| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
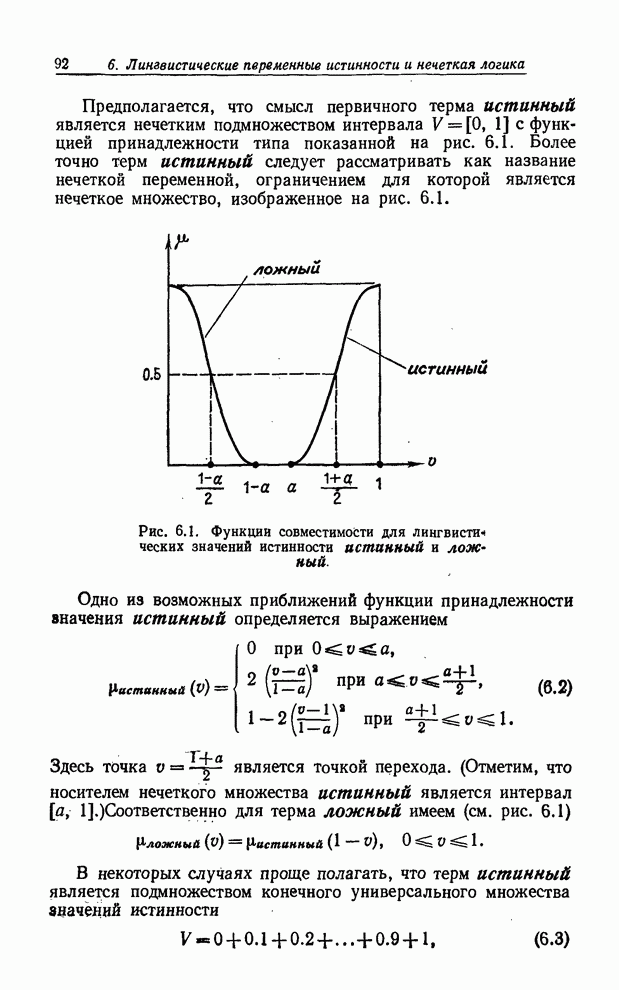
ЗНАЧЕНИЯ ИСТИННОСТИ
неизвестно и не определено
Среди
возможных значений истинности лингвистической переменной Истинность два
значения привлекают особое внимание, а именно пустое множество ![]() и единичный интервал
и единичный интервал
![]() , которые
соответствуют наименьшему и наибольшему элементам (по отношению включения)
решетки нечетких подмножеств интервала
, которые
соответствуют наименьшему и наибольшему элементам (по отношению включения)
решетки нечетких подмножеств интервала ![]() . Важность именно этих значений
истинности обусловлена тем, что их можно интерпретировать как значения истинности
не определено и неизвестно соответственно. Для
удобства будем обозначать эти значения истинности символами
. Важность именно этих значений
истинности обусловлена тем, что их можно интерпретировать как значения истинности
не определено и неизвестно соответственно. Для
удобства будем обозначать эти значения истинности символами ![]() и
и ![]() , понимая при этом, что
, понимая при этом, что ![]() и
и ![]() определяются
выражениями
определяются
выражениями
 (6.51)
(6.51)
и
 (6.52)
(6.52)
Значения
неизвестно и не определено, интерпретируемые как
степени принадлежности, используются также в представлении нечетких множеств типа
1. В этом случае имеются три возможности выражения степени принадлежности точки
![]() в
в ![]() : 1) число из
интервала
: 1) число из
интервала ![]() ;
2)
;
2) ![]() (не
определено); 3)
(не
определено); 3) ![]() (неизвестно).
(неизвестно).
Рассмотрим простой пример. Пусть
![]() . (6.53)
. (6.53)
Возьмем
нечеткое подмножество множества ![]() вида
вида
![]() . (6.54)
. (6.54)
В
этом случае степень принадлежности элемента ![]() множеству
множеству ![]() есть неизвестно, а
степень принадлежности
есть неизвестно, а
степень принадлежности ![]() есть не определено. В
более общем случае
есть не определено. В
более общем случае ![]() может
быть
может
быть
![]() , (6.55)
, (6.55)
где
имеется в виду, что степень принадлежности элемента ![]() множеству
множеству ![]() частично неизвестна, причем
член
частично неизвестна, причем
член ![]() интерпретируется
следующим образом:
интерпретируется
следующим образом:
 . (6.56)
. (6.56)
Важно
четко понимать разницу между ![]() и
и ![]() . Когда мы говорим, что степень
принадлежности точки
. Когда мы говорим, что степень
принадлежности точки ![]() множеству
множеству ![]() есть
есть ![]() , мы имеем в виду, что функция
принадлежности
, мы имеем в виду, что функция
принадлежности ![]() не
определена в точке
не
определена в точке ![]() .
Предположим, например, что
.
Предположим, например, что ![]() — множество действительных чисел, а
— множество действительных чисел, а ![]() — функция,
определенная на множестве целых чисел, причем
— функция,
определенная на множестве целых чисел, причем ![]() , если
, если ![]() — четное, и
— четное, и ![]() , если
, если ![]() — нечетное. Тогда степень
принадлежности числа
— нечетное. Тогда степень
принадлежности числа ![]() множеству
множеству ![]() есть
есть ![]() , а не 0. С другой стороны, если бы
, а не 0. С другой стороны, если бы ![]() была определена на
множестве действительных чисел и
была определена на
множестве действительных чисел и ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() — четное число, то
степень принадлежности числа
— четное число, то
степень принадлежности числа ![]() множеству
множеству ![]() была бы равна 0.
была бы равна 0.
Поскольку
мы умеем вычислять значения истинности высказываний ![]() и
и![]() ,
, ![]() или
или![]() и не
и не![]() по заданным
лингвистическим значениям истинности высказываний
по заданным
лингвистическим значениям истинности высказываний ![]() и
и ![]() , нетрудно вычислить и значения
, нетрудно вычислить и значения ![]() ,
, ![]() ,
, ![]() , когда
, когда ![]() . Предположим, например, что
. Предположим, например, что
 , (6.57)
, (6.57)
 . (6.58)
. (6.58)
Применяя принцип обобщения, как в (6.25), получим
 , (6.59)
, (6.59)
где
 (6.60)
(6.60)
После упрощения (6.59) сводится к выражению
 . (6.61)
. (6.61)
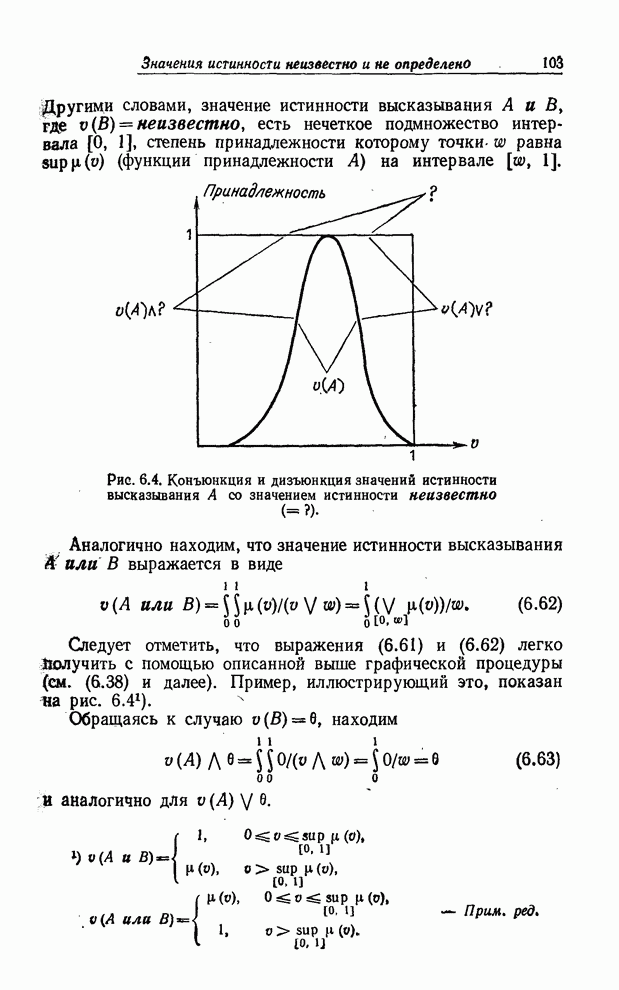
Другими
словами, значение истинности высказывания ![]() и
и ![]() , где
, где ![]() , есть нечеткое подмножество
интервала
, есть нечеткое подмножество
интервала ![]() ,
степень принадлежности которому точки
,
степень принадлежности которому точки ![]() равна
равна ![]() (функции принадлежности
(функции принадлежности ![]() ) на интервале
) на интервале ![]() .
.

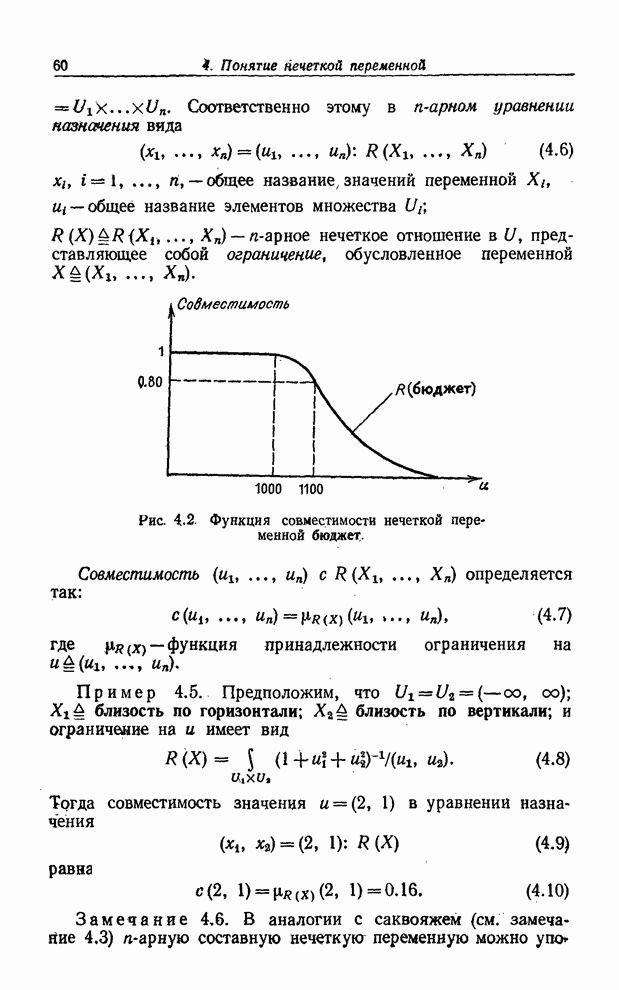
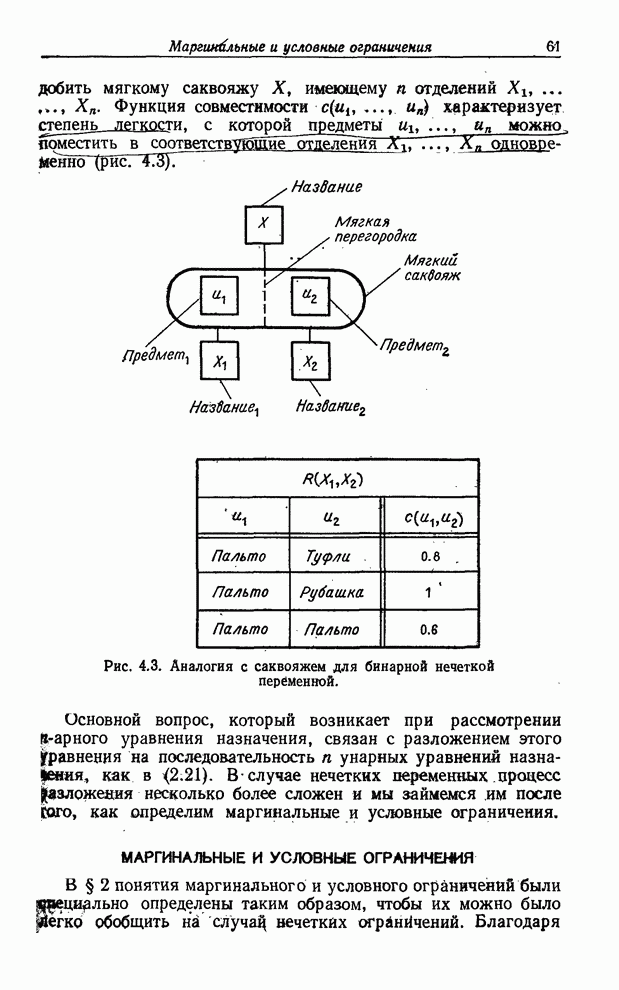
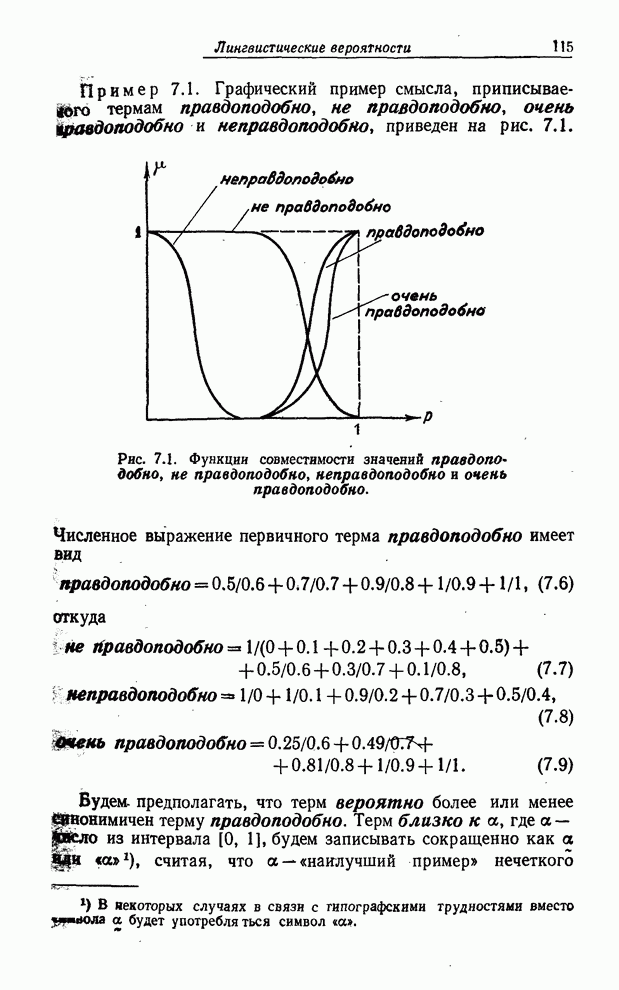
Рис. 6.4. Конъюнкция и дизъюнкция значений
истинности высказывания ![]() со значением истинности неизвестно (
со значением истинности неизвестно (![]() ).
).
Аналогично
находим, что значение истинности высказывания ![]() или
или ![]() выражается в виде
выражается в виде
 . (6.62)
. (6.62)
Следует отметить, что выражения (6.61) и (6.62) легко получить с помощью описанной выше графической процедуры (см. (6.38) и далее). Пример, иллюстрирующий это, показан на рис. 6.4.
Обращаясь
к случаю ![]() ,
находим
,
находим
 (6.63)
(6.63)
и
аналогично для ![]() .
.

Поучительно проследить, что происходит с приведенными выше соотношениями, когда мы применяем их к частному случаю двузначной логики, т. е. к случаю, когда универсальное множество имеет вид
![]() , (6.64)
, (6.64)
или в более привычном виде
![]() , (6.65)
, (6.65)
где
![]() означает истинный,
а
означает истинный,
а ![]() — ложный.
Поскольку
— ложный.
Поскольку ![]() есть
есть
![]() , мы можем
отождествить значение истинности неизвестно со значением истинный
или ложный, т. е.
, мы можем
отождествить значение истинности неизвестно со значением истинный
или ложный, т. е.
![]() . (6.66)
. (6.66)
Результирующая
логика имеет четыре значения истинности ![]() ,
, ![]() ,
, ![]() и
и ![]() и является обобщением двузначной логики
в смысле замечания 6.5.
и является обобщением двузначной логики
в смысле замечания 6.5.
Поскольку
универсальное множество значений истинности состоит лишь из двух элементов,
целесообразно построить таблицы истинности для операций ![]() ,
, ![]() и
и ![]() в этой четырехзначной логике
непосредственно, т. е. без использования общих формул (6.25), (6.29) и (6.31).
Так, применяя принцип обобщения к операции
в этой четырехзначной логике
непосредственно, т. е. без использования общих формул (6.25), (6.29) и (6.31).
Так, применяя принцип обобщения к операции ![]() , сразу получаем
, сразу получаем
![]() (6.67)
(6.67)
![]() (6.68)
(6.68)
![]() (6.69)
(6.69)
 (6.70)
(6.70)
и
поэтому расширенная таблица истинности для операции ![]() имеет следующий вид (см.
табл. 6.5).
имеет следующий вид (см.
табл. 6.5).
Таблица 6.5

Выбросив
из нее элементы ![]() ,
получим табл. 6.6.
,
получим табл. 6.6.
Таблица 6.6.

Аналогично,
для операции ![]() получим
табл. 6.7
получим
табл. 6.7
Таблица 6.7

Как
и следовало ожидать, эти таблицы согласуются с таблицами истинности для
операций ![]() и
и
![]() в обычной
трехзначной логике [46].
в обычной
трехзначной логике [46].
Описанный
выше подход проливает некоторый свет на определение операции ![]() в двузначной логике
— в некотором смысле спорный вопрос, который мотивировал развитие модальной
логики [45], [47]. В частности, вместо общепринятого определения связки
в двузначной логике
— в некотором смысле спорный вопрос, который мотивировал развитие модальной
логики [45], [47]. В частности, вместо общепринятого определения связки ![]() мы можем определить
ее как связку в трехзначной логике с помощью неполной таблицы истинности (табл.
6.8), которая отражает интуитивно понятную
мы можем определить
ее как связку в трехзначной логике с помощью неполной таблицы истинности (табл.
6.8), которая отражает интуитивно понятную
Таблица 6.8

идею
о том, что если ![]() истинно
и
истинно
и ![]() ложно,
то значение истинности высказывания
ложно,
то значение истинности высказывания ![]() неизвестно. Теперь можно
поставить вопрос: как следует заполнить пустые клетки в табл. 6.8, чтобы в
результате применения принципа обобщения получить значение (2,3)-го элемента,
равное
неизвестно. Теперь можно
поставить вопрос: как следует заполнить пустые клетки в табл. 6.8, чтобы в
результате применения принципа обобщения получить значение (2,3)-го элемента,
равное ![]() ?
Итак, обозначая неизвестные (2,1)-й и (2,2)-й элементы через
?
Итак, обозначая неизвестные (2,1)-й и (2,2)-й элементы через ![]() и
и ![]() соответственно, мы
должны получить
соответственно, мы
должны получить
![]() (6.71)
(6.71)
откуда с необходимостью следует, что
![]() . (6.72)
. (6.72)
На этом пути мы приходим к обычному определению связки ⟹ в двузначной логике в виде следующей таблицы истинности:

Как показывает рассмотренный выше пример, понятие значения истинности неизвестно в сочетании с принципом обобщения помогает уяснить некоторые из понятий и соотношений обычных двузначной и трехзначной логик. Эти логики, конечно, можно рассматривать как вырожденные случаи нечеткой логики, в которой значением истинности неизвестно является весь единичный интервал, а не множество 0 + 1.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
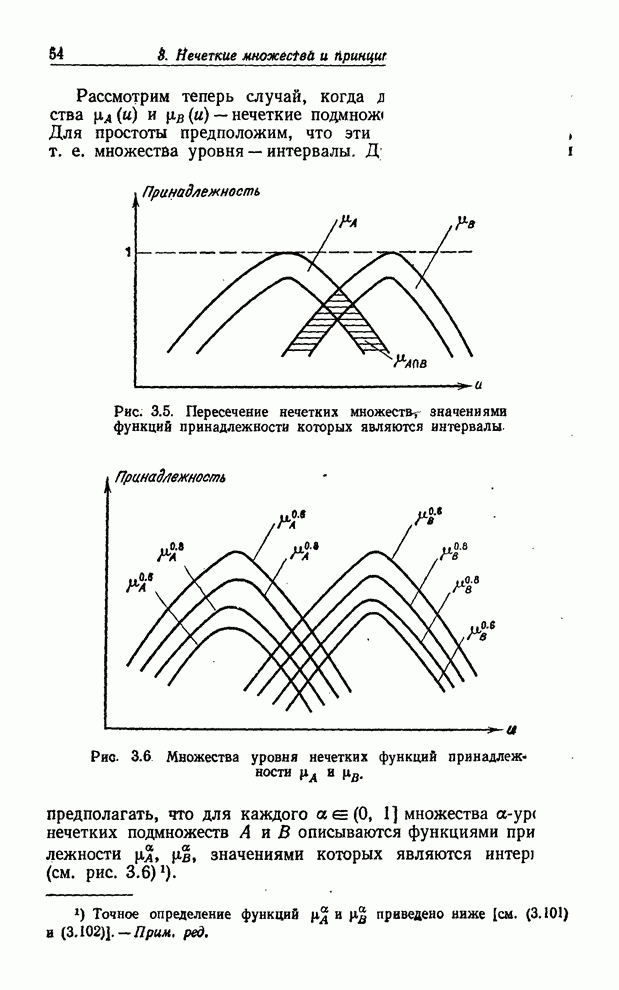
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
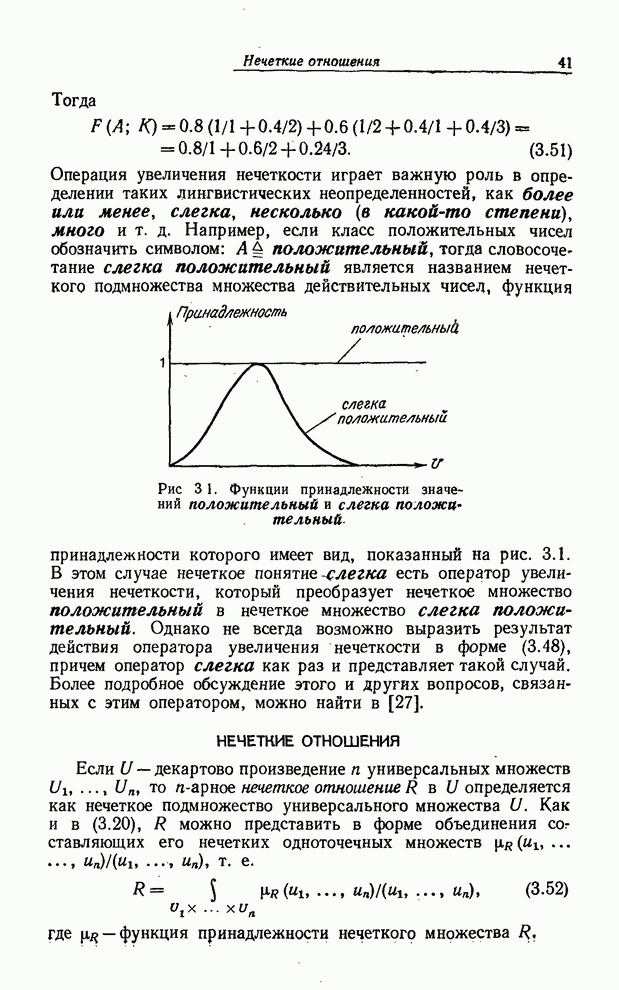
- НЕЧЕТКИЕ ОТНОШЕНИЯ
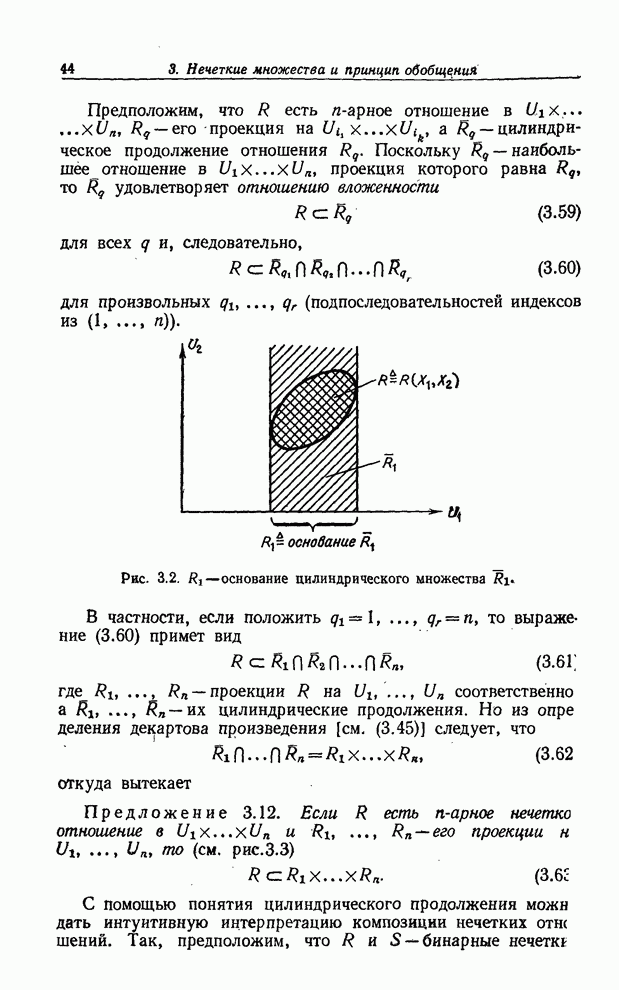
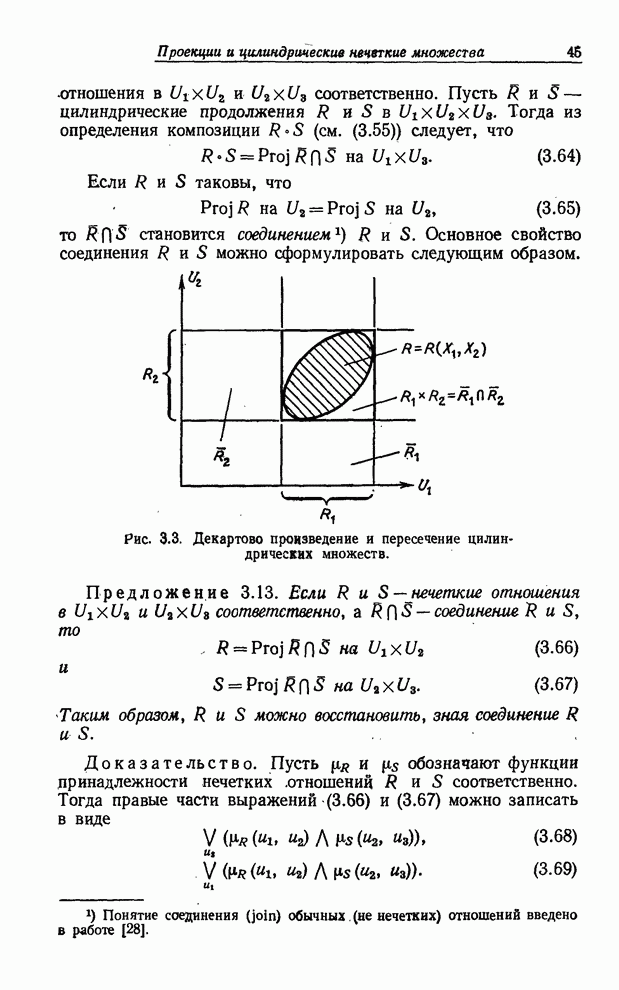
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
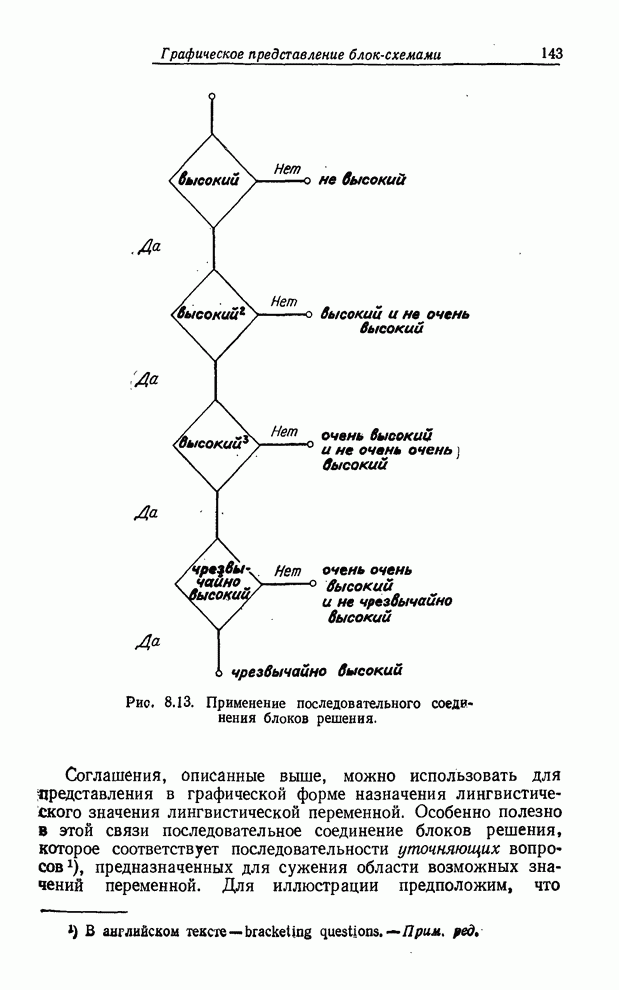
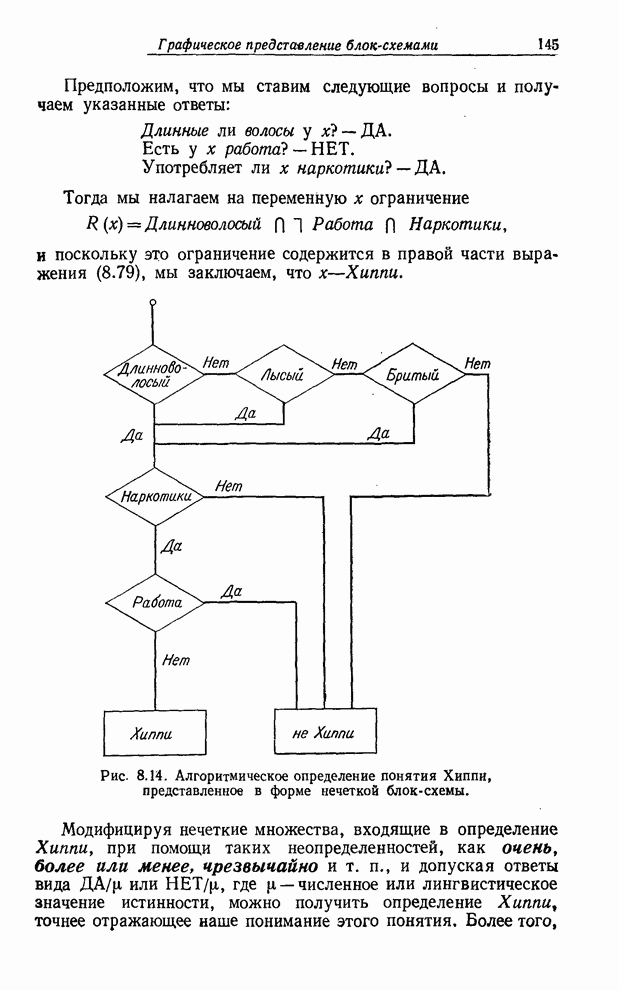
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ