| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Условия (уравнения) равновесия пространственной произвольной системы сил
Если система сил находится в равновесии, то ее главный вектор и главный момент равны нулю:

Эти векторные равенства приводят к следующим шести скалярным равенствам:

которые называются условиями равновесия пространственной произвольной системы сил.
Первые три условия выражают равенство нулю главного вектора, следующие три - равенство нулю главного момента системы сил.
В этих условиях равновесия должны учитываться все действующие силы - как активные (задаваемые), так и реакции связей. Последние заранее неизвестны, и условия равновесия становятся уравнениями для определения этих неизвестных - уравнениями равновесия.
Поскольку максимальное число уравнений равно шести, то в задаче на равновесие тела под действием произвольной пространственной систе-мы сил можно определить шесть неизвестных реакций. При большем количестве неизвестных задача становится статически неопределенной.
И еще одно замечание. Если главный вектор и главный момент относительно некоторого центра О равны нулю, то они будут равны нулю относительно любого другого центра. Это прямо следует из материала о перемене центра приведения (доказать самостоятельно). Следовательно, если условия равновесия тела выполняются в одной системе координат, то они будут выполняться и в любой другой неподвижной системе координат. Иными словами, выбор координатных осей при составлении уравнений равновесия совершенно произволен.
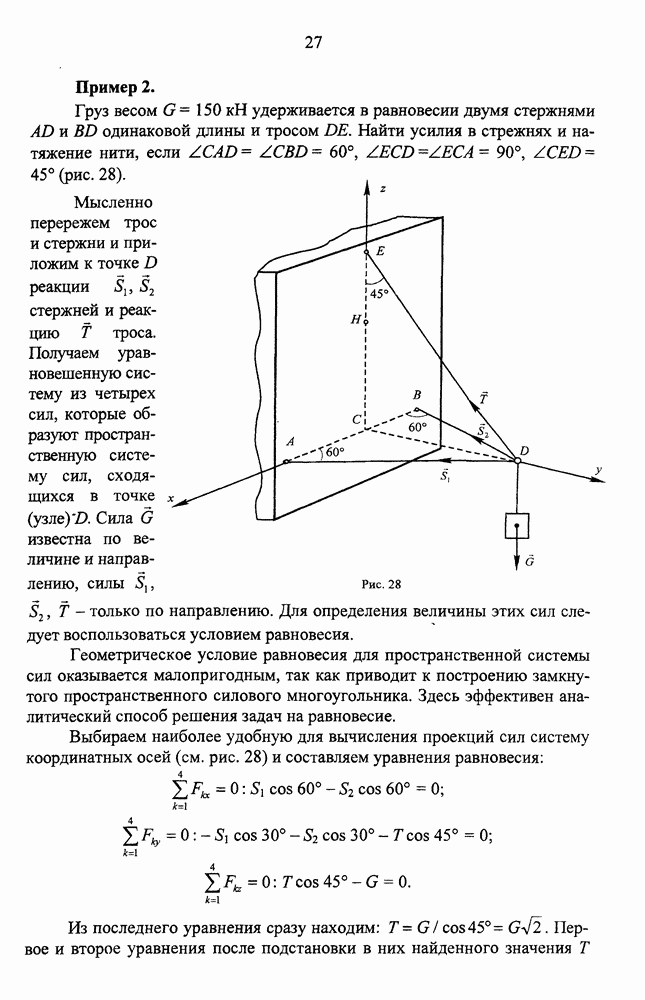
Пример.
Прямоугольная плита (рис. 51, а) весом  удерживается в горизонтальном положении сферическим шарниром О, подшипником А и тросом BE, причем точки
удерживается в горизонтальном положении сферическим шарниром О, подшипником А и тросом BE, причем точки  находятся на одной вертикали. В точке D к плите приложена сила
находятся на одной вертикали. В точке D к плите приложена сила  , перпендикулярная стороне OD и наклоненная к плоскости плиты под углом 45°. Определить натяжение троса и реакции опор в точках Он А, если
, перпендикулярная стороне OD и наклоненная к плоскости плиты под углом 45°. Определить натяжение троса и реакции опор в точках Он А, если  и
и  .
.

Рис. 51.
Для решения задачи рассматриваем равновесие плиты. К активным силам Р, G добавляем реакции связей - составляющие  реакции сферического шарнира, реакции
реакции сферического шарнира, реакции  ,
,  подшипника, реакцию
подшипника, реакцию  троса. Одновременно вводим координатные оси Oxyz (рис. 51, б). Видно, что полученная совокупность сил образует произвольную пространственную систему, в которой силы
троса. Одновременно вводим координатные оси Oxyz (рис. 51, б). Видно, что полученная совокупность сил образует произвольную пространственную систему, в которой силы  неизвестны.
неизвестны.
Для определения неизвестных составляем уравнения равновесия.
Начинаем с уравнения проекций сил на ось  :
:

Поясним определение проекции  вычисление осуществляется в два приема- вначале определяется проекция силы Т на плоскость
вычисление осуществляется в два приема- вначале определяется проекция силы Т на плоскость  , далее, проектируя
, далее, проектируя  на осъ х (удобнее на ось
на осъ х (удобнее на ось  , параллельную
, параллельную  ), находим
), находим  (см. рис. 51,б):
(см. рис. 51,б):

Этим способом двойного проектирования удобно пользоваться, когда линия действия силы и ось не пересекаются. Далее составляем:

Уравнение моментов сил относительно оси  имеет вид:
имеет вид:

Моменты сил  в уравнении отсутствуют, так как эти силы либо пересекают ось х(
в уравнении отсутствуют, так как эти силы либо пересекают ось х( ), либо ей параллельны
), либо ей параллельны  . В обоих этих случаях момент силы относительно оси равен нулю (см. с. 41).
. В обоих этих случаях момент силы относительно оси равен нулю (см. с. 41).
Вычисление момента силы часто облегчается, если силу разложить подходящим образом на составляющие и воспользоваться теоремой Вариньона. В данном случае это удобно сделать для силы  . Разлагая ее на горизонтальную
. Разлагая ее на горизонтальную  и вертикальную
и вертикальную  составляющие, можем написать:
составляющие, можем написать:

Но  (сила
(сила  пересекает ось х), второе же слагаемое легко вычисляется:
пересекает ось х), второе же слагаемое легко вычисляется:

Далее составляем остальные уравнения моментов:

Момент силы Т в последнем уравнении отсутствует, так как линия действия силы пересекается с осью z (в точке Е).
Мы получили шесть уравнений, содержащих шесть неизвестных. Решая их, определяем все искомые реакции.
Из последних двух уравнений, содержащих лишь по одной неизвестной, сразу находим  и Т:
и Т:

Подставляя найденные значения реакций в остальные уравнения, определяем значения других неизвестных:

Отрицательный знак реакции  означает, что ее действительное
означает, что ее действительное  противоположно принятому в расчетах (указанному на рис. 51, б).
противоположно принятому в расчетах (указанному на рис. 51, б).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
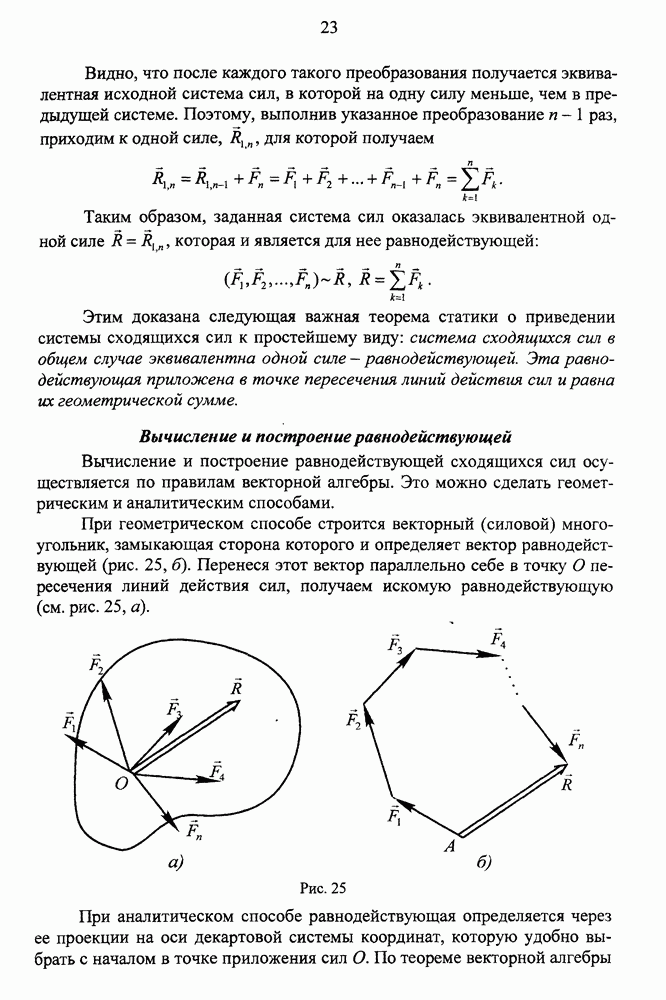
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
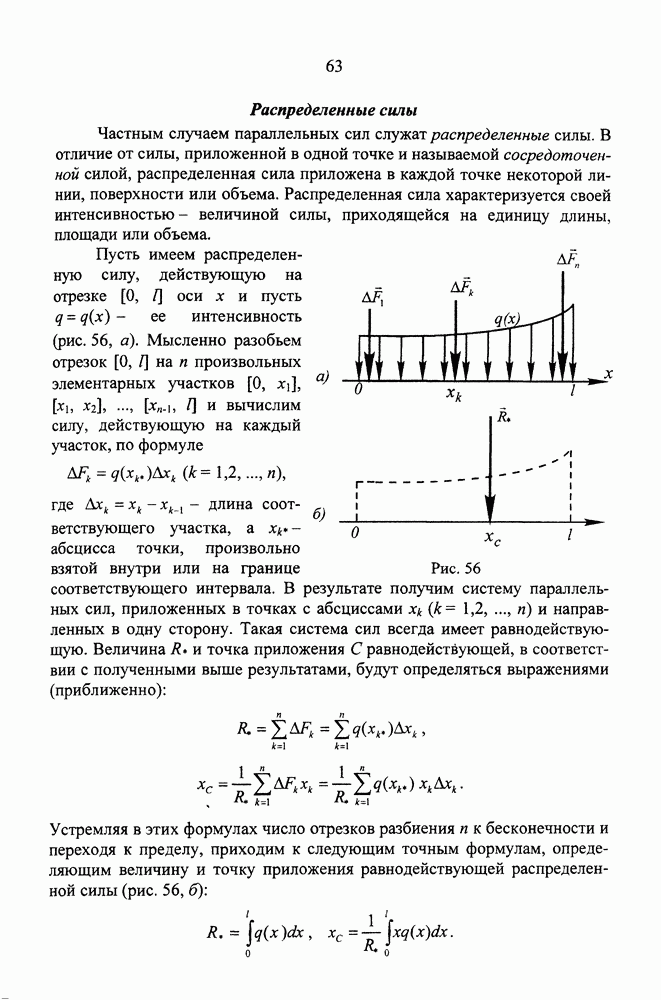
- Распределенные силы
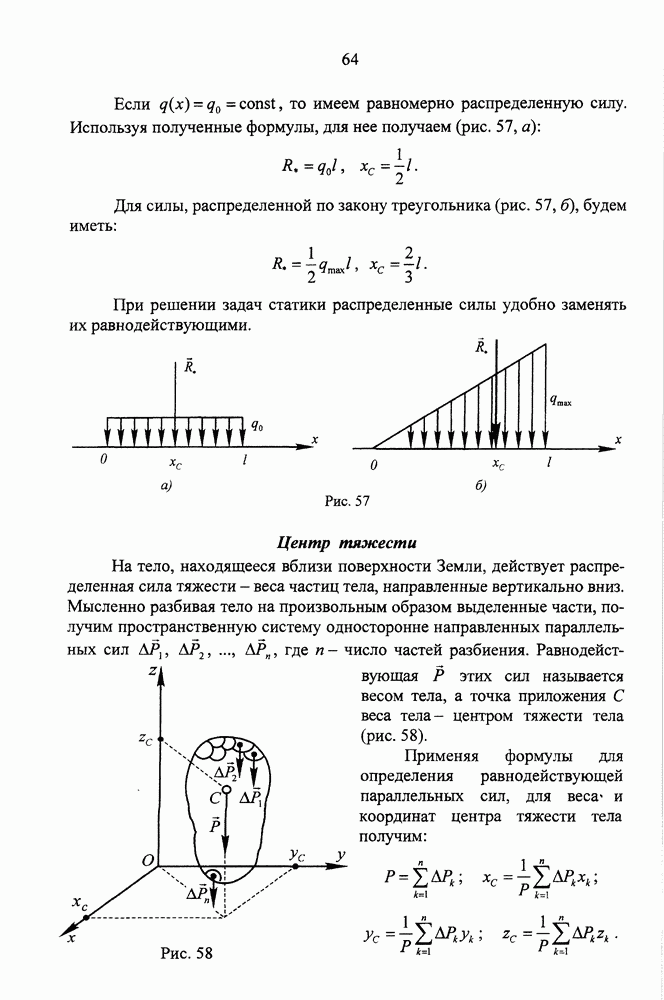
- Центр тяжести
- Интегральные формулы для координат центра тяжести
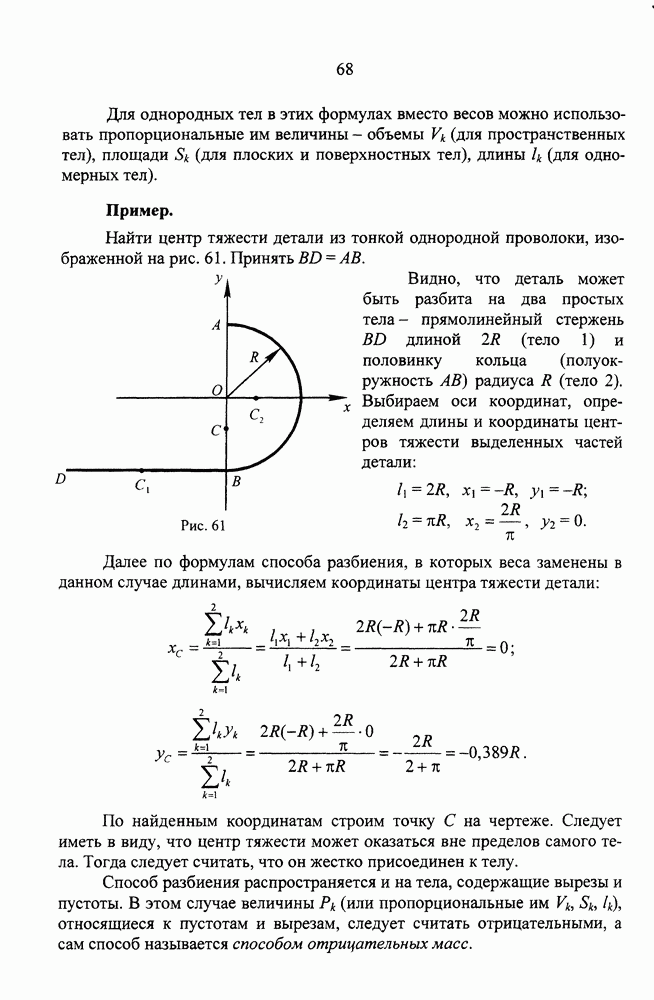
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
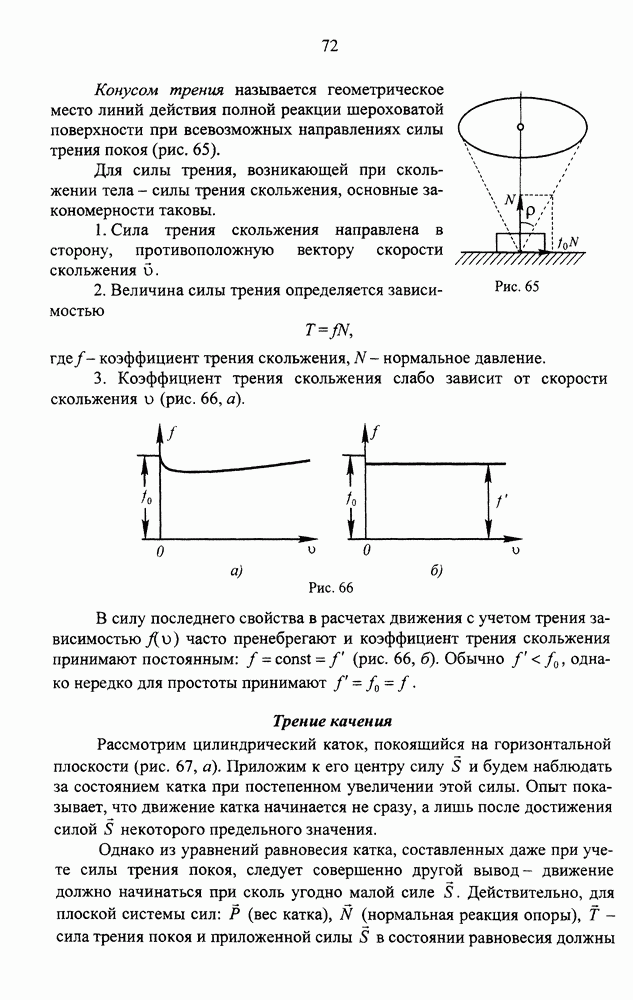
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
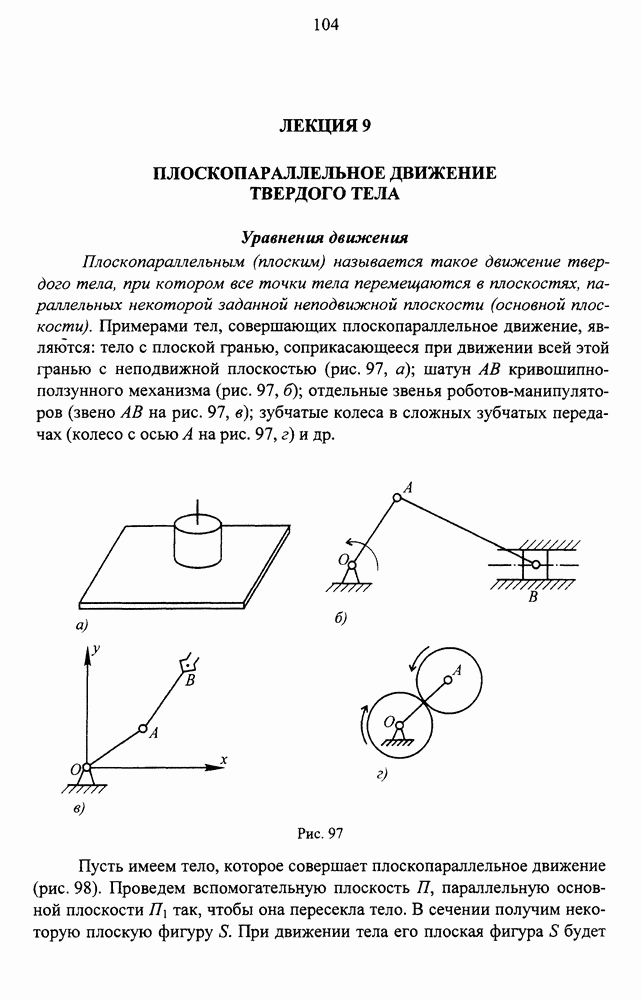
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
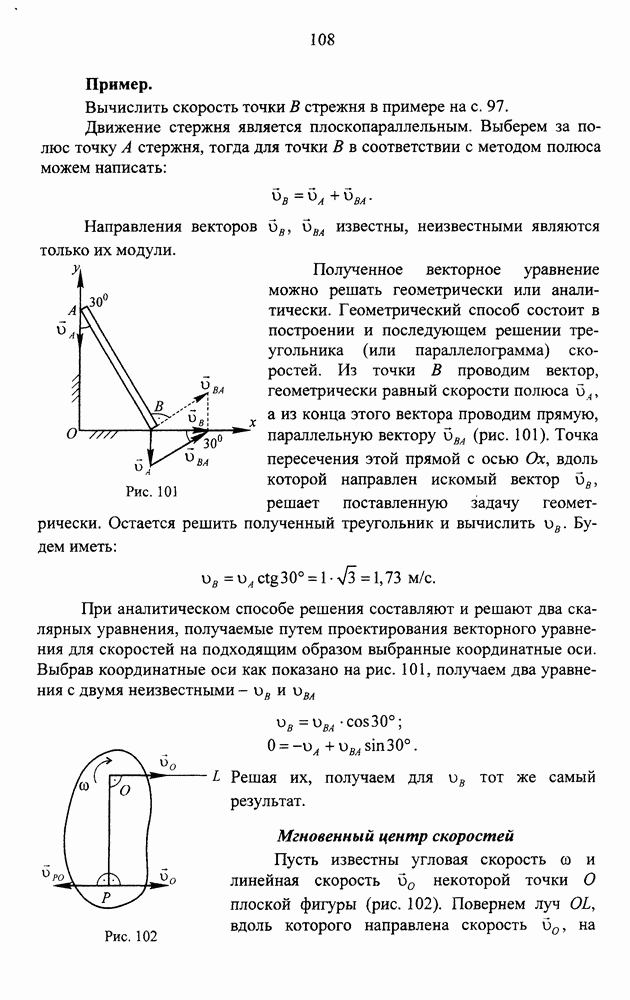
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
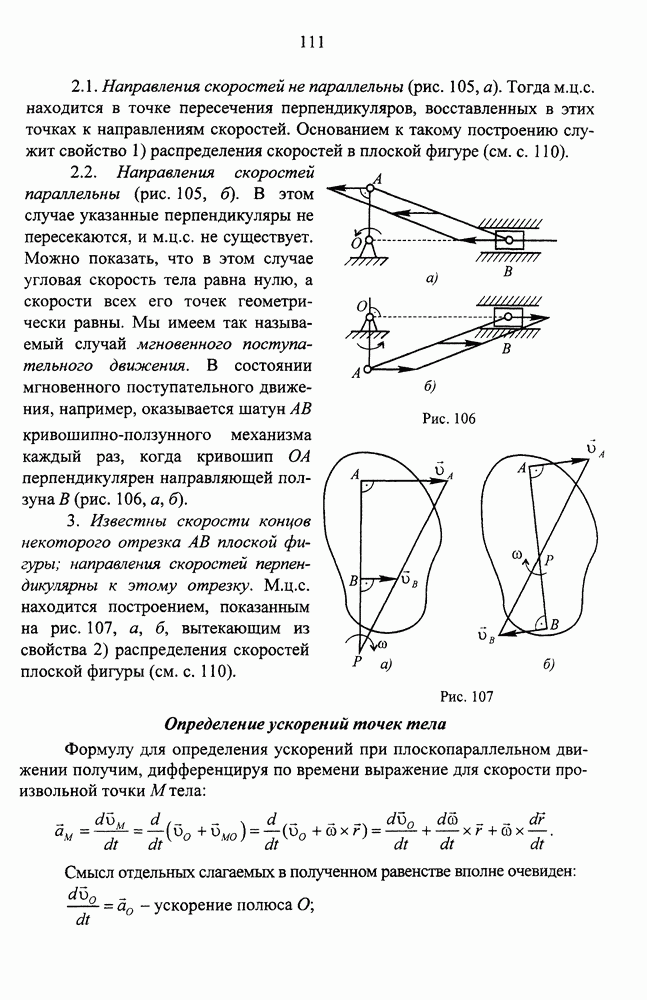
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
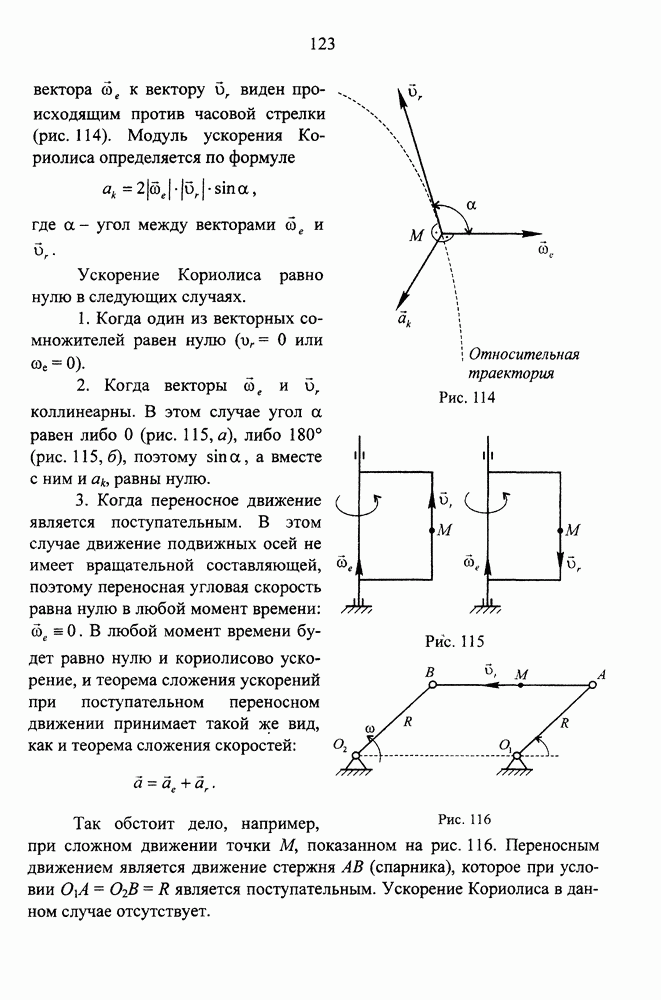
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
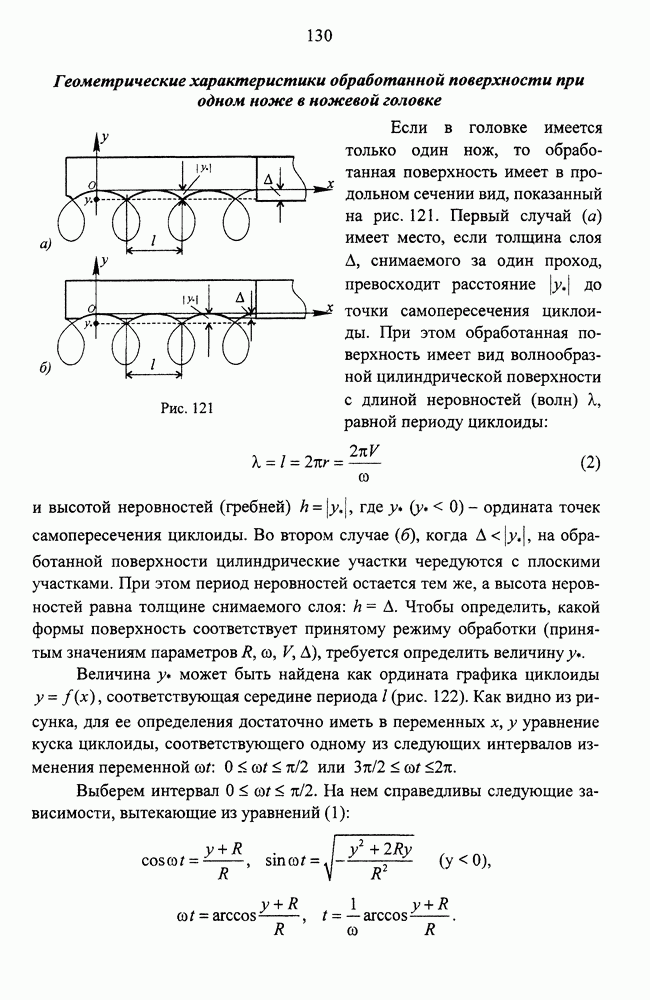
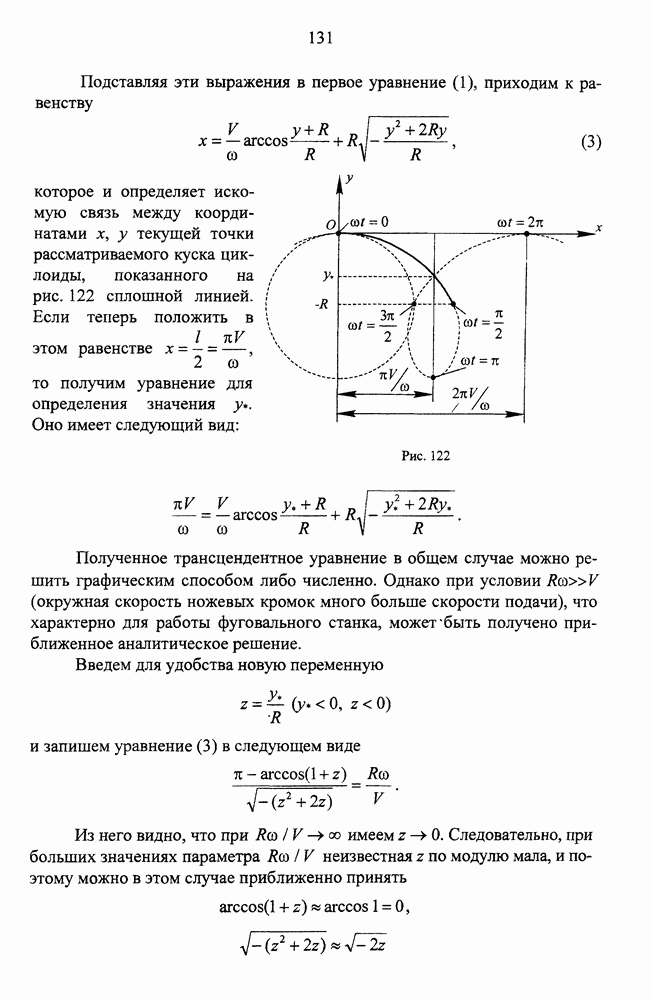
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА