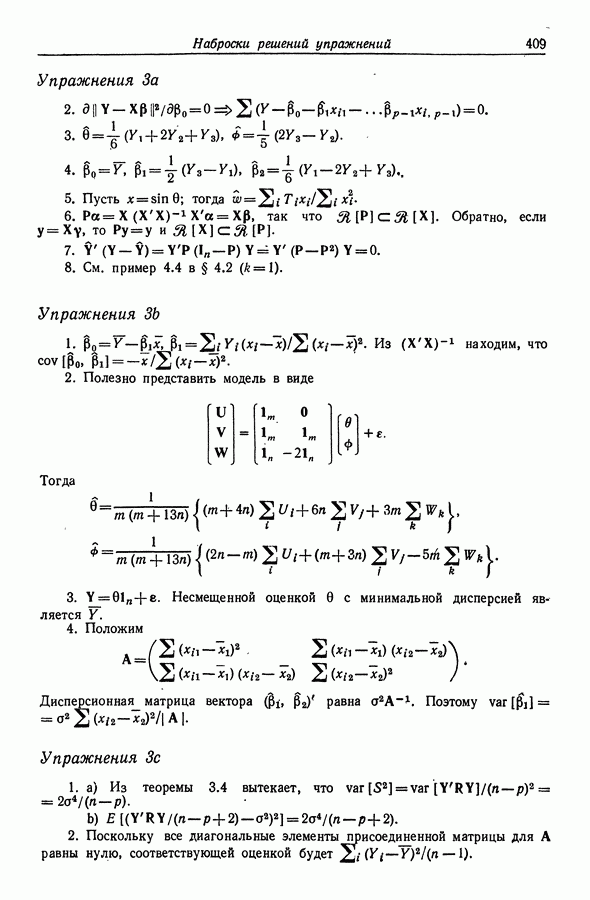| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2.3. Метод ковариационного анализа
В случаях, когда пропущено более одного наблюдения, Yates (1933) предложил применять повторное использование формулы для одного пропущенного наблюдения, начиная этот процесс с предположительных значений для всех пропущенных наблюдений, кроме одного. Итерации производятся до тех пор, пока все остатки, соответствующие пропущенным наблюдениям, не станут пренебрежимо малыми. Однако такой метод не пригоден, например, для программ для универсальных ЭВМ, поскольку каждому плану соответствуют свои собственные формулы для  и
и 
Более общая итерационная процедура описана Hartley (1956). Если пропущено только одно наблюдение, то для него можно найти приемлемую оценку, трижды анализируя имеющиеся данные и придавая при этом пропущенному наблюдению три различных равноотстоящих значения (например, —1, 0, 1). Соответствующая оценка задается простой формулой, включающей лишь эти три выбранных значения и полученные при этом остаточные суммы квадратов. Если пропущено более одного наблюдения, то этот метод применяется итеративным образом.
Другая общая итерационная процедура, описанная Healey, Westmacott (1956), требует только использования подпрограммы для отыскания остатков в индивидуальных ячейках. Начиная с предположенных значений для пропущенных наблюдений (например, со средних по имеющимся данным значений ячейки, строки или столбца), мы производим анализ полной модели и затем вычитаем полученный остаток из каждого из предположенных значений пропущенных наблюдений. Полученные разности образуют новые оценки для пропущенных наблюдений, и мы продолжаем этот процесс до тех пор, пока все остатки для пропущенных наблюдений не станут пренебрежимо малыми. Хотя эта процедура является итерационной даже при одном пропущенном наблюдении, она весьма быстро сходится к решению, получаемому методом наименьших квадратов. Модификация этой процедуры [Реагсе (1965, § 7.3); Реагсе, Jeffers (1971); Ргеесе (1971)] увеличивает скорость сходимости, так что при пропуске только одного наблюдения требуется не более двух итераций. Эту модификацию можно применять и в случае перепутанных значений [Ргеесе, Gower (1974)]. Другую итерационную процедуру для факторных планов, которая при единственном пропущенном наблюдении становится неитеративной, предложил Shearer (1973).
Не являющуюся итерационной процедуру обработки пропущенных наблюдений предложил Bartlett (1937b, с. 151). Имеющиеся данные дополняются произвольными значениями (например, нулями) для  пропущенных наблюдений, и влияние выбора этих значений на анализ пополненной совокупности данных ликвидируется путем проведения ковариационного анализа над
пропущенных наблюдений, и влияние выбора этих значений на анализ пополненной совокупности данных ликвидируется путем проведения ковариационного анализа над  фиктивными сопутствующими переменными. При этом
фиктивными сопутствующими переменными. При этом  фиктивная переменная равна 1 в позиции, соответствующей
фиктивная переменная равна 1 в позиции, соответствующей  пропущенному наблюдению, а во всех остальных случаях равна 0. Мы увидим ниже, что, когда все пропущенные наблюдения полагаются равными нулю, оценка наименьших квадратов для
пропущенному наблюдению, а во всех остальных случаях равна 0. Мы увидим ниже, что, когда все пропущенные наблюдения полагаются равными нулю, оценка наименьших квадратов для  пропущенного наблюдения отличается лишь знаком от коэффициента регрессии
пропущенного наблюдения отличается лишь знаком от коэффициента регрессии  фиктивной переменной. Этот метод описан в ряде работ (например, Tocher (1952), Wilkinson (1960) и Seber (1966)) и иллюстрируется примером 10.8. Неитерационная процедура обработки пропущенных наблюдений в перекрестных классификациях описана Haseman, Gaylor (1973).
фиктивной переменной. Этот метод описан в ряде работ (например, Tocher (1952), Wilkinson (1960) и Seber (1966)) и иллюстрируется примером 10.8. Неитерационная процедура обработки пропущенных наблюдений в перекрестных классификациях описана Haseman, Gaylor (1973).
Пример 10.8. Предположим, что в плане с рандомизированными блоками, описанном в примере 10.5, пропущено наблюдение  Тогда мы предполагаем модель
Тогда мы предполагаем модель

где  (произвольная постоянная) и
(произвольная постоянная) и  Оценку наименьших квадратов у для у легко найти методом наименьших
Оценку наименьших квадратов у для у легко найти методом наименьших
квадратов, описанным в примере 10.1 (разд. 10.1.1). Таким образом,

где

и

Если  то из (10.18) видно; что
то из (10.18) видно; что

Полученный результат следовало ожидать, поскольку двухшаговый метод наименьших квадратов в применении к (10.21) сводится просто к замене  на
на  т. е. к замене
т. е. к замене  на —у и минимизации остаточной суммы квадратов относительно у. Это равносильно методу Иэйтса минимизации
на —у и минимизации остаточной суммы квадратов относительно у. Это равносильно методу Иэйтса минимизации  относительно
относительно  Попутно отметим, что
Попутно отметим, что  с (10.4)]
с (10.4)]

Продемонстрировав суть метода ковариационного анализа на простом примере, приведем теперь общую теорию и процедуру вычислений для случая  пропущенных наблюдений. Рассмотрим модель ковариационного анализа
пропущенных наблюдений. Рассмотрим модель ковариационного анализа

где 

Если матрица X имеет полный ранг и  то оценка наименьших квадратов для у является решением (ср. с (3.22) в § 3,7) уравнения
то оценка наименьших квадратов для у является решением (ср. с (3.22) в § 3,7) уравнения

 т. е. уравнения
т. е. уравнения

Из уравнения (10.16) замечаем, что  этого опять-таки следовало ожидать ввиду эквивалентности двухшагового метода наименьших квадратов и метода Иэйтса. Метод ковариационного анализа используется при пропущенных наблюдениях, по-видимому, не очень широко, поскольку на первый взгляд он требует компьютерной программы для общего ковариационного анализа с
этого опять-таки следовало ожидать ввиду эквивалентности двухшагового метода наименьших квадратов и метода Иэйтса. Метод ковариационного анализа используется при пропущенных наблюдениях, по-видимому, не очень широко, поскольку на первый взгляд он требует компьютерной программы для общего ковариационного анализа с  сопутствующими переменными. Однако Rubin (1972) указал, что в действительности это не так. Все, что здесь требуется, — это программа для отыскания остатков и подпрограмма для обращения матрицы размера
сопутствующими переменными. Однако Rubin (1972) указал, что в действительности это не так. Все, что здесь требуется, — это программа для отыскания остатков и подпрограмма для обращения матрицы размера  Чтобы убедиться в этом, заметим прежде всего, что
Чтобы убедиться в этом, заметим прежде всего, что  является вектором остатков, который получился бы, если бы мы использовали
является вектором остатков, который получился бы, если бы мы использовали  в качестве вектора наблюдений
в качестве вектора наблюдений  Поскольку
Поскольку  элементов вектора
элементов вектора  равны единице, а остальные его элементы равны нулю, то
равны единице, а остальные его элементы равны нулю, то

является  элементом вектора
элементом вектора  т. е. остатком, соответствующим
т. е. остатком, соответствующим  пропущенному наблюдению, когда все наблюдения, включая и пропущенные, полагаются равными нулю, за исключением
пропущенному наблюдению, когда все наблюдения, включая и пропущенные, полагаются равными нулю, за исключением  пропущенного наблюдения, которому приписывается значение 1. Аналогично
пропущенного наблюдения, которому приписывается значение 1. Аналогично

можно рассматривать как остаток, соответствующий  пропущенному наблюдению, когда все пропущенные наблюдения (но не элементы вектора
пропущенному наблюдению, когда все пропущенные наблюдения (но не элементы вектора  полагаются равными нулю. Таким образом, из уравнения (10.22) находим
полагаются равными нулю. Таким образом, из уравнения (10.22) находим

или в обозначениях Рубина (с векторами-столбцами вместо векторов-строк)  Если матрица
Если матрица  вырождена, то нужно использовать обобщенную обратную [Wilkinson (1958а)]. Из общей теории разд. 10.2.1 вытекает, что таковой будет всякое решение уравнения (10.16), т.е.
вырождена, то нужно использовать обобщенную обратную [Wilkinson (1958а)]. Из общей теории разд. 10.2.1 вытекает, что таковой будет всякое решение уравнения (10.16), т.е.  На практике вырожденность возникает, когда пропущены такие части плана, как блоки.
На практике вырожденность возникает, когда пропущены такие части плана, как блоки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
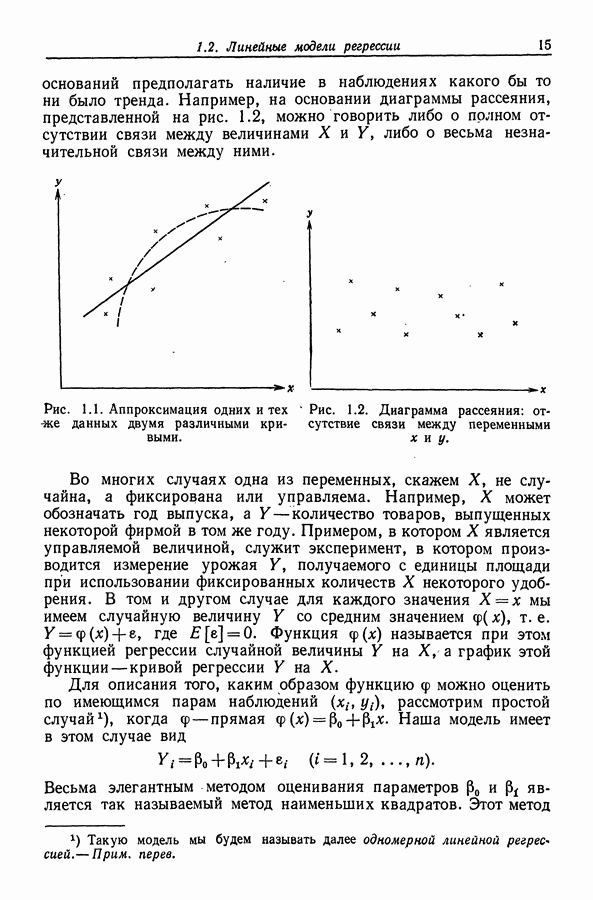
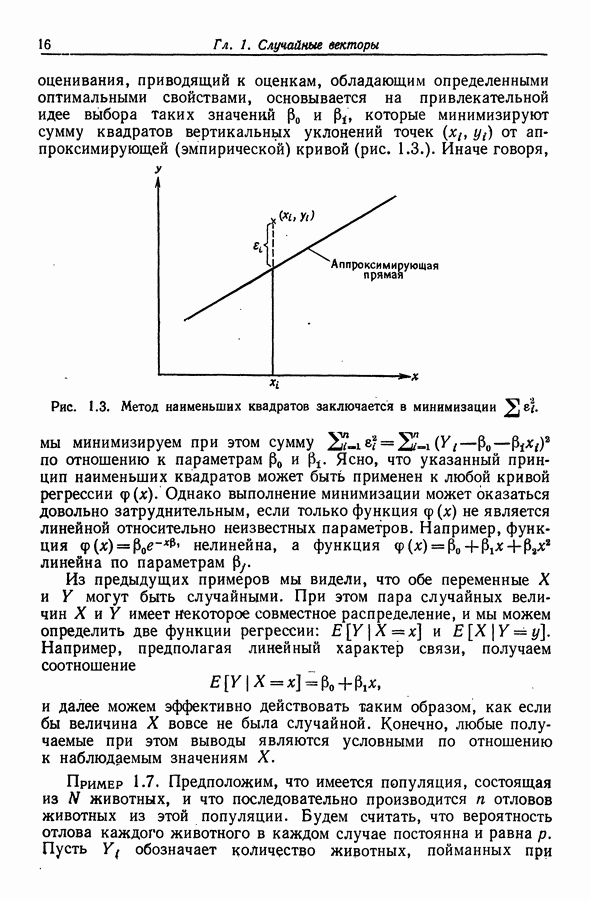
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
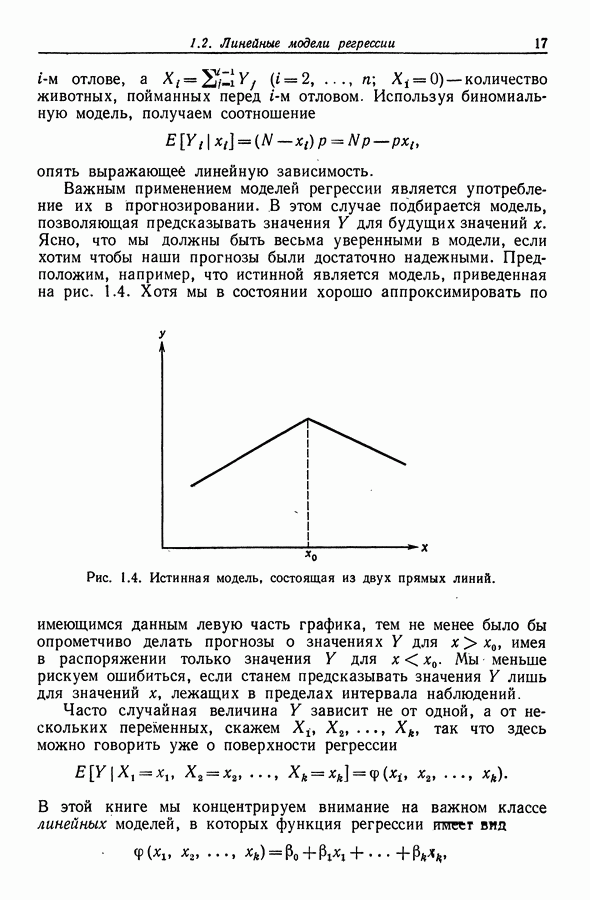
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
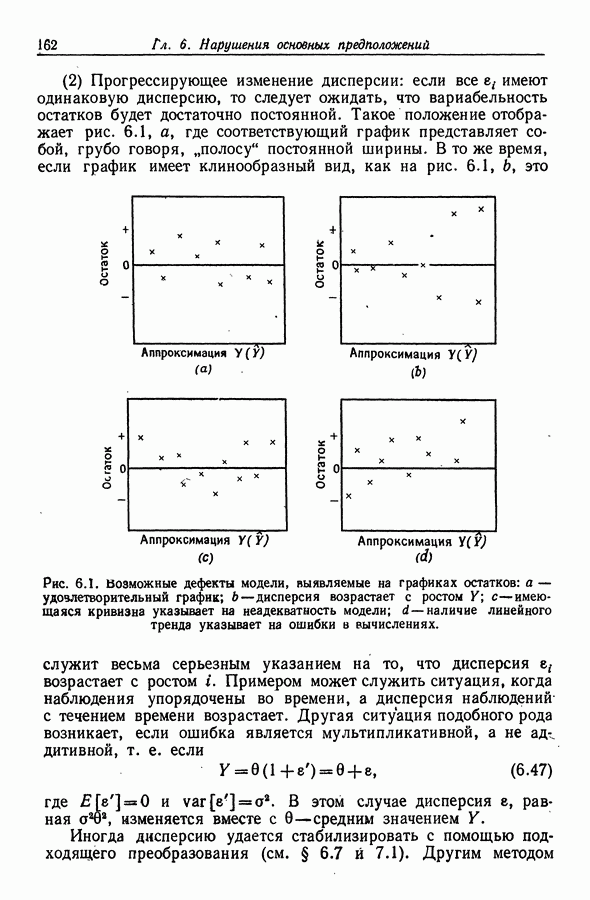
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
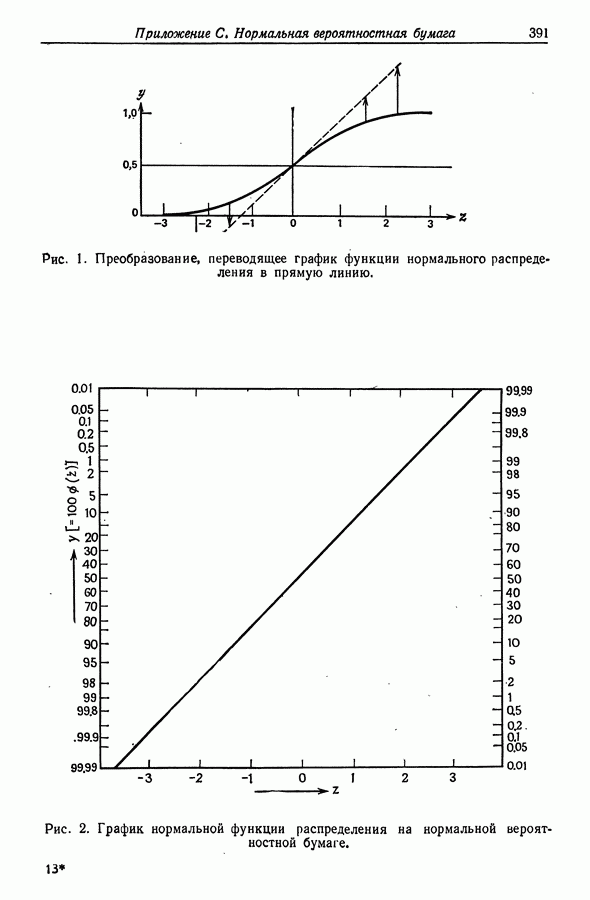
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
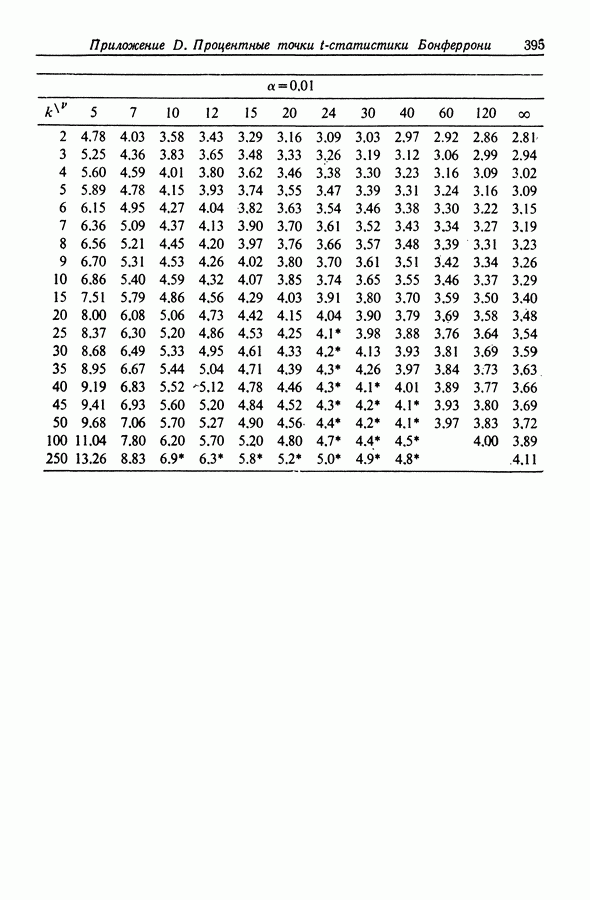
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
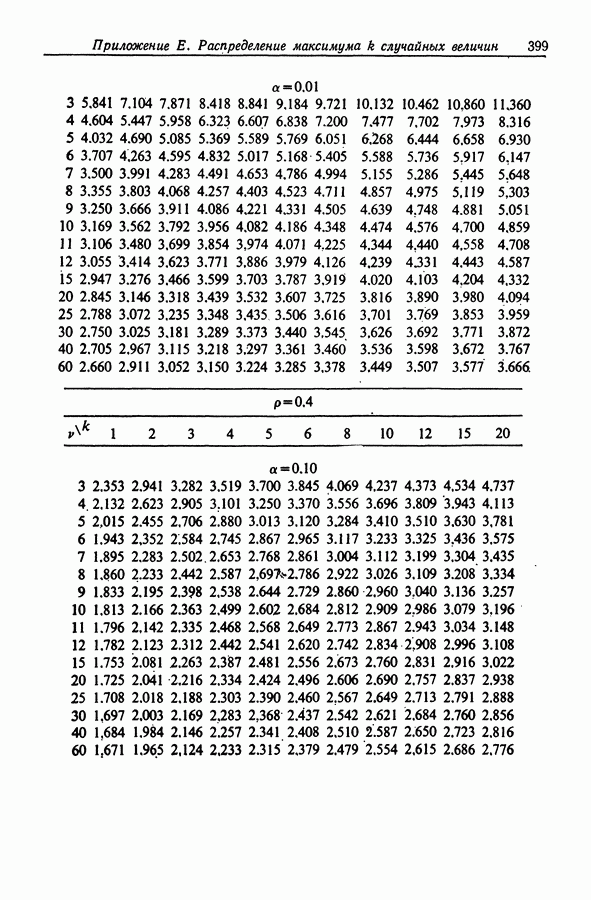
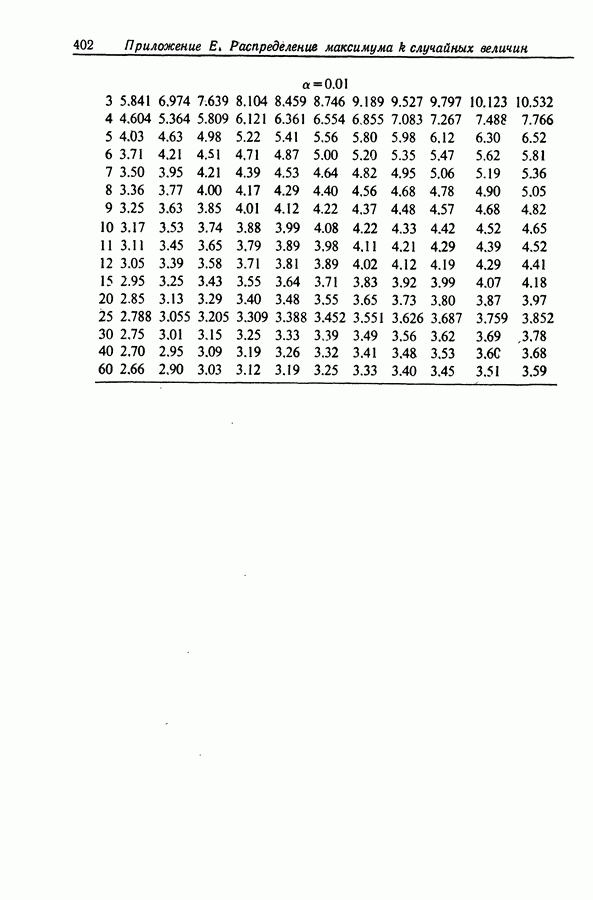
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
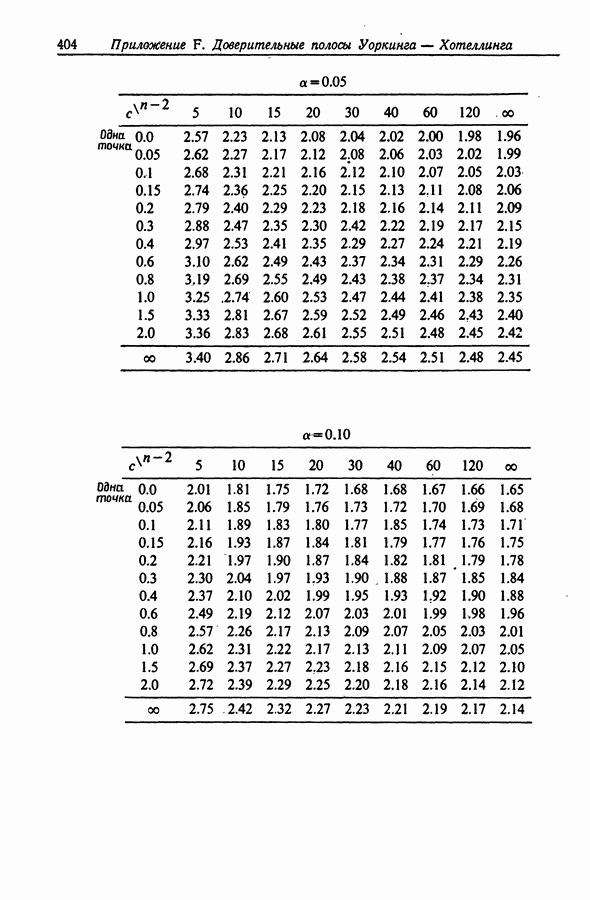
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ