| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
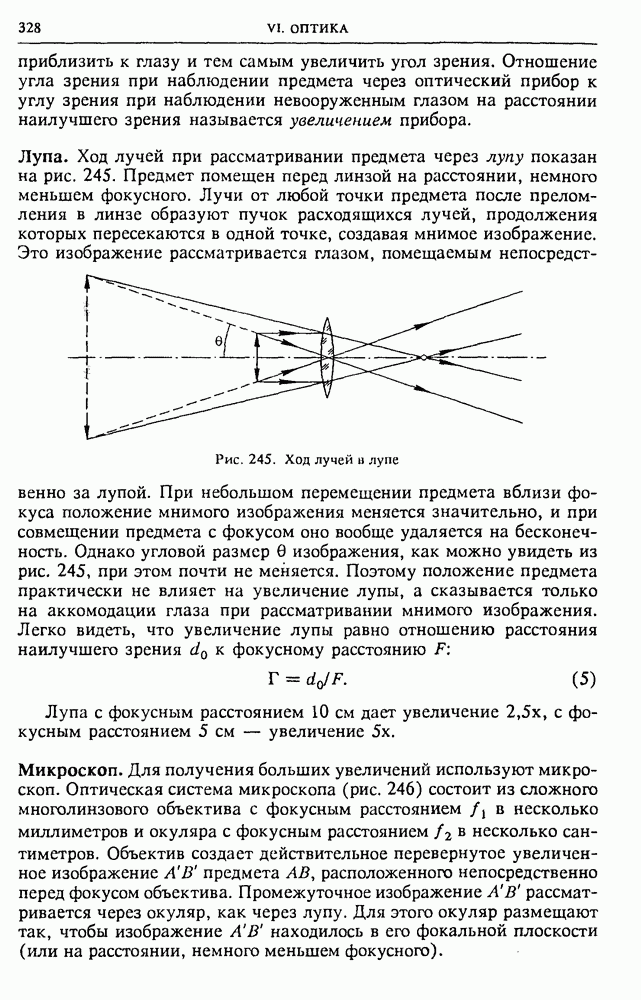
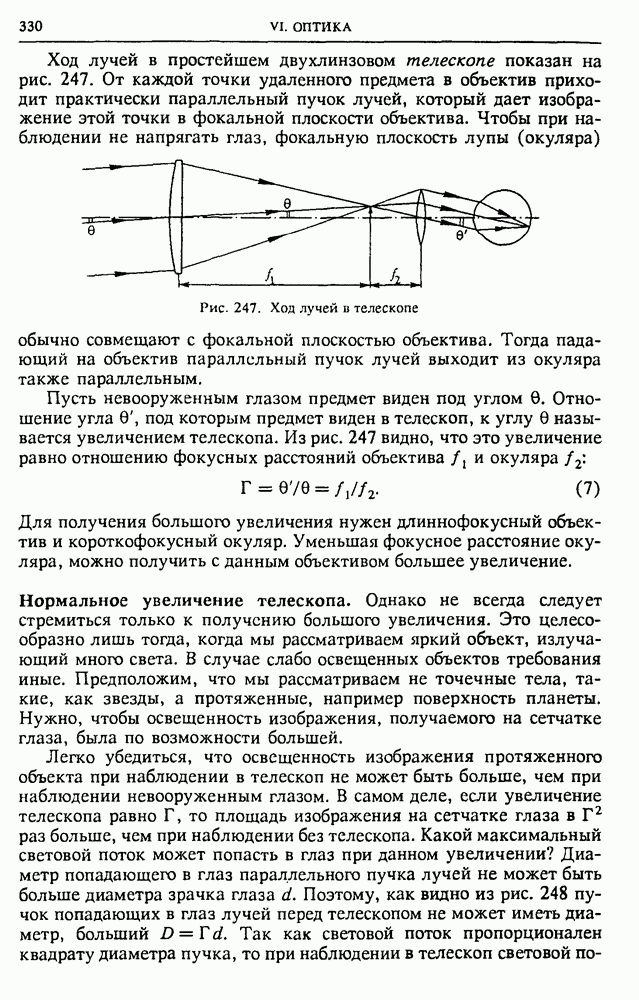
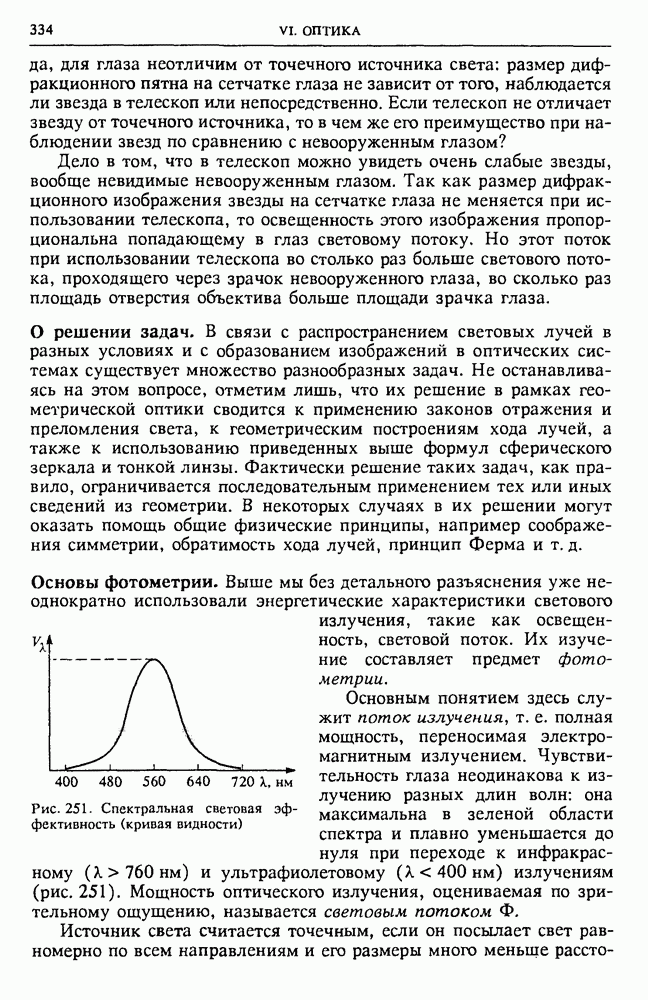
§ 36. Геометрическая оптика
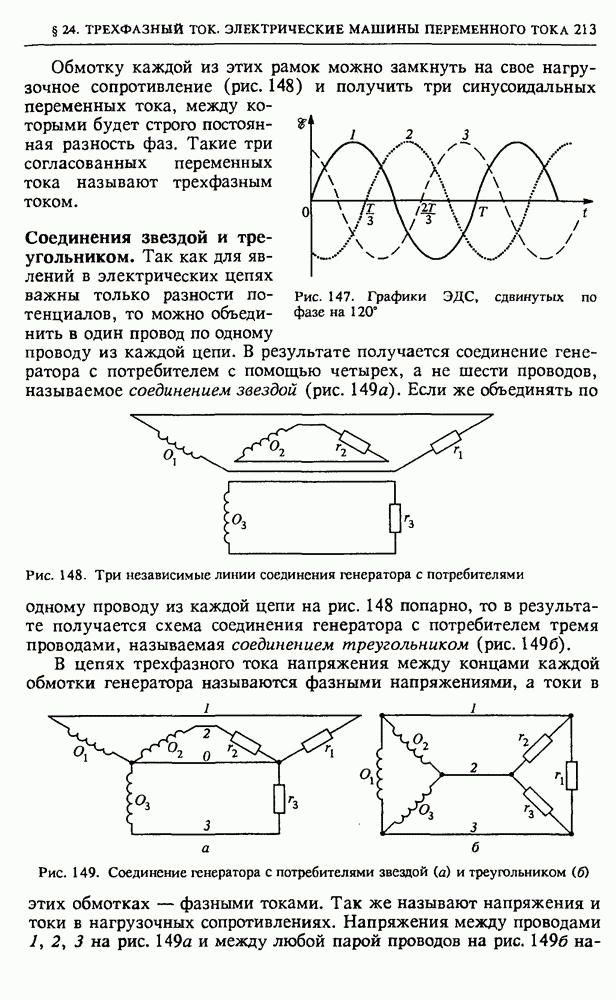
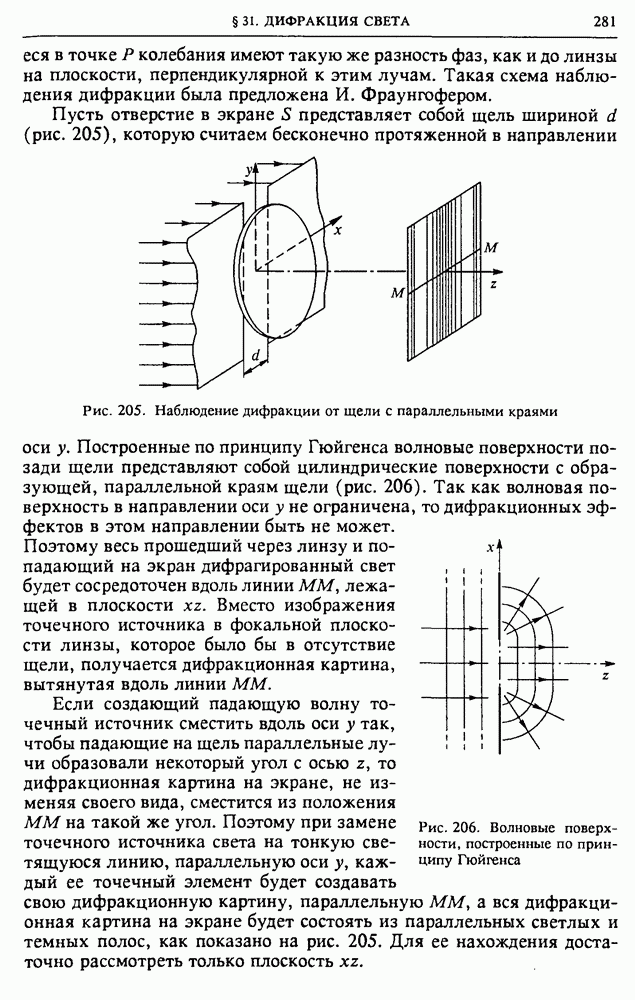
Геометрическая оптика использует представление о световых лучах, распространяющихся независимо друг от друга, прямолинейных в однородной среде, отражающихся и преломляющихся на границах сред с разными оптическими свойствами. Вдоль лучей происходит перенос энергии световых колебаний.
Показатель преломления среды. Оптические свойства прозрачной среды характеризуются показателем преломления  который определяет скорость
который определяет скорость  (точнее, фазовую скорость) световых волн:
(точнее, фазовую скорость) световых волн:

где с — скорость света в вакууме. Показатель преломления воздуха близок к единице (пвозд  воды его значение равно 1,33, а у стекла в зависимости от сорта может составлять от 1,5 до 1,95. Особенно велик показатель преломления алмаза — приблизительно 2,5.
воды его значение равно 1,33, а у стекла в зависимости от сорта может составлять от 1,5 до 1,95. Особенно велик показатель преломления алмаза — приблизительно 2,5.
Значение показателя преломления, вообще говоря, зависит от длины волны Я (или от частоты  :
:  Эту зависимость называют дисперсией света. Например, у хрусталя (свинцового стекла) показатель преломления плавно меняется от 1,87 для красного света с длиной волны
Эту зависимость называют дисперсией света. Например, у хрусталя (свинцового стекла) показатель преломления плавно меняется от 1,87 для красного света с длиной волны  до 1,95 для синего света с
до 1,95 для синего света с 
Показатель преломления связан с диэлектрической проницаемостью среды  (для данной длины волны или частоты) соотношением
(для данной длины волны или частоты) соотношением  Среда с большим значением показателя преломления называется оптически более плотной.
Среда с большим значением показателя преломления называется оптически более плотной.
Законы геометрической оптики. Поведение световых лучей подчиняется основным законам геометрической оптики.
1. В однородной среде световые лучи прямолинейны (закон прямолинейного распространения света).
2. На границе двух сред (или на границе среды с вакуумом) возникает отраженный луч, лежащий в плоскости, образуемой падающим лучом и нормалью к границе, т. е. в плоскости падения, причем угол отражения  равен углу падения
равен углу падения  (рис. 224):
(рис. 224):

(закон отражения, света).
3. Преломленный луч лежит в плоскости падения (при падении света на границу изотропной среды) и образует с нормалью к границе угол  (угол преломления), определяемый соотношением
(угол преломления), определяемый соотношением

или

(закон преломления света или закон Снеллиуса).
При переходе света в оптически более плотную среду  луч приближается к нормали
луч приближается к нормали  Отношение
Отношение  называют относительным показателем преломления двух сред (или показателем преломления второй среды относительно первой).
называют относительным показателем преломления двух сред (или показателем преломления второй среды относительно первой).

Рис. 224. Отражение и преломление спета на плоской границе двух сред
При падении света из вакуума на границу среды с показателем преломления  закон преломления принимает вид
закон преломления принимает вид

Для воздуха показатель преломления близок к единице  поэтому и при падении света из воздуха на некоторую среду можно пользоваться формулой (4).
поэтому и при падении света из воздуха на некоторую среду можно пользоваться формулой (4).
При переходе света в оптически менее плотную среду  угол падения не может превышать предельного значения
угол падения не может превышать предельного значения  так как угол преломления
так как угол преломления  не может превышать
не может превышать  (рис. 225):
(рис. 225):

Если угол падения  происходит полное отражение, т. е. вся энергия падающего света возвращается в первую, оптически более плотную, среду. Для границы стекло — воздух
происходит полное отражение, т. е. вся энергия падающего света возвращается в первую, оптически более плотную, среду. Для границы стекло — воздух 

Рис. 225. Предельный угол полного отражения
Принцип Гюйгенса и законы геометрической оптики. Законы геометрической оптики были установлены задолго до выяснения природы света. Эти законы могут быть выведены из волновой теории на основе принципа Гюйгенса. Их применимость ограничена явлениями дифракции.
Остановимся подробнее на переходе от волновых представлений о распространении света к представлениям геометрической оптики. С помощью принципа Гюйгенса по заданной волновой поверхности падающей волны можно построить волновые поверхности преломленной и отраженной волн. При этом следует учесть, что световые лучи перпендикулярны волновым поверхностям.
Рассмотрим плоскую световую волну, падающую из среды 1 (с показателем преломления  на плоскую границу раздела со средой 2 (с показателем преломления
на плоскую границу раздела со средой 2 (с показателем преломления  под углом (рис. 226). Угол падения — это угол между падающим лучом и нормалью к границе раздела.
под углом (рис. 226). Угол падения — это угол между падающим лучом и нормалью к границе раздела.

Рис. 226. Построение Гюйгенса для отражения и преломления света
В то же время  — это угол между границей раздела и волновой поверхностью падающей волны. Пусть в некоторый момент эта волновая поверхность занимает положение
— это угол между границей раздела и волновой поверхностью падающей волны. Пусть в некоторый момент эта волновая поверхность занимает положение  Спустя время
Спустя время  она достигнет точки В границы раздела. За это же время вторичная волна из точки А, распространяющаяся в среде X, расширится до радиуса
она достигнет точки В границы раздела. За это же время вторичная волна из точки А, распространяющаяся в среде X, расширится до радиуса  Подставляя сюда
Подставляя сюда  получаем
получаем  Отсюда ясно, что волновая поверхность
Отсюда ясно, что волновая поверхность  отраженной волны, представляющая собой огибающую всех вторичных сферических волн с центрами на отрезке
отраженной волны, представляющая собой огибающую всех вторичных сферических волн с центрами на отрезке  наклонена к границе раздела на угол
наклонена к границе раздела на угол  который равен
который равен  (равенство углов и
(равенство углов и  следует из равенства прямоугольных треугольников
следует из равенства прямоугольных треугольников  и
и  имеющих общую гипотенузу
имеющих общую гипотенузу  и равные катеты
и равные катеты  и
и  Таким образом, отраженный луч
Таким образом, отраженный луч  перпендикулярный фронту отраженной волны, образует с нормалью угол
перпендикулярный фронту отраженной волны, образует с нормалью угол  равный углу падения
равный углу падения 
Аналогично из этого построения Гюйгенса можно получить и закон преломления. В среде 2 вторичные волны распространяются со скоростью  и поэтому выходящая из точки А сферическая волна спустя время
и поэтому выходящая из точки А сферическая волна спустя время  имеет радиус
имеет радиус  Подставляя сюда
Подставляя сюда  находим
находим  Разделив обе части этого равенства на
Разделив обе части этого равенства на  приходим к соотношению
приходим к соотношению

которое, очевидно, совпадает с законом преломления (3), так как угол  наклона волновой поверхности волны в среде 2 есть в то же время и угол между преломленным лучом и нормалью к границе раздела (угол преломления, рис. 226).
наклона волновой поверхности волны в среде 2 есть в то же время и угол между преломленным лучом и нормалью к границе раздела (угол преломления, рис. 226).
Отражение и преломление на искривленной поверхности. Плоская волна характеризуется тем свойством, что ее волновые поверхности представляют собой неограниченные плоскости, а направление ее распространения и амплитуда везде одинаковы. Часто электромагнитные волны, не являющиеся плоскими, можно приближенно рассматривать как плоские на небольшом участке пространства. Для этого необходимо, чтобы амплитуда и направление распространения волны почти не менялись на протяжении расстояний порядка длины волны. Тогда также можно ввести понятие лучей, т. е. линий, касательная к которым в каждой точке совпадает с направлением распространения волны. Если при этом граница раздела двух сред, например поверхность линзы, может считаться приблизительно плоской на расстояниях порядка длины волны, то поведение лучей света на такой границе будет описываться теми же законами отражения и преломления.
Изучение законов распространения световых волн в этом случае составляет предмет геометрической оптики, поскольку в этом приближении оптические законы можно сформулировать на языке геометрии. Многие оптические явления, такие, как, например, прохождение света через оптические системы, формирующие изображение, можно рассматривать исходя из представления о световых лучах, совершенно отвлекаясь от волновой природы света. Поэтому представления геометрической оптики справедливы лишь в той степени, в какой можно пренебречь явлениями дифракции световых волн. Дифракция сказывается тем слабее, чем меньше длина волны. Это значит, что геометрическая оптика соответствует предельному случаю малых длин волн: 
Физическую модель пучка световых лучей можно получить, если пропустить свет от источника пренебрежимо малого размера через небольшое отверстие в непрозрачном экране. Выходящий из отверстия свет заполняет некоторую область, и если длина волны пренебрежимо мала по сравнению с размерами отверстия, то на небольшом расстоянии от него можно говорить о пучке световых лучей с резкой границей.
Интенсивность отраженного и преломленного света. Законы отражения и преломления позволяют определить только направление соответствующих световых лучей, но ничего не говорят об их интенсивности. Между тем опыт показывает, что соотношение интенсивностей отраженного и преломленного лучей, на которые расщепляется исходный луч на границе раздела, сильно зависит от угла падения. Например, при нормальном падении света на поверхность стекла отражается около 4% энергии падающего светового пучка, а при падении на поверхность воды — только 2 %. Но при скользящем падении поверхности стекла и воды отражают почти все падающее излучение. Благодаря этому мы можем любоваться зеркальными отражениями берегов в спокойной прозрачной воде горных озер.

Рис. 227. У естественного спета колебания сектора Е происходят по всевозможных направлениях в плоскости, перпендикулярной лучу
Естественный свет. Световая волна, как и любая электромагнитная волна, поперечна: вектор Е лежит в плоскости, перпендикулярной направлению распространения. Испускаемый обычными источниками (например, раскаленными телами) свет неполяризован. Это значит, что в световом луче колебания вектора Е происходят во всевозможных направлениях в плоскости, перпендикулярной направлению луча (рис. 227). Такой неполяризованный свет называется естественным. Его можно представить как некогерентную смесь двух световых волн одинаковой интенсивности, линейно поляризованных в двух взаимно перпендикулярных направлениях. Эти направления можно выбрать произвольно.
Поляризация света при отражении. При изучении отражения неполяризованного света от границы раздела сред удобно выбрать одно из двух независимых направлений вектора Е в плоскости падения, а второе — перпендикулярно ей. Условия отражения этих двух волн оказываются различными: волна, у которой вектор Е перпендикулярен плоскости падения (т. е. параллелен границе раздела) при всех углах падения (кроме 0 и 90°), отражается сильнее. Поэтому отраженный свет оказывается частично поляризованным, а при отражении под некоторым определенным углом (для стекла около 56°) — полностью поляризованным.
Этим обстоятельством пользуются для устранения бликов, например при фотографировании пейзажа с водной поверхностью. Подбирая должным образом ориентацию поляризационного светофильтра, пропускающего световые колебания только определенной поляризации, можно практически полностью устранить блики на фотографии.
Принцип Ферма. Основные законы геометрической оптики — закон прямолинейного распространения света в однородной среде, законы отражения и преломления света на границе раздела двух сред — могут быть получены с помощью принципа Ферма. Согласно этому принципу действительный путь распространения монохроматического луча света есть путь, для прохождения которого свету требуется экстремальное (как правило, минимальное) время по сравнению с любым другим близким к нему мыслимым путем между теми же точками.

Рис. 228. К выводу закона отражения света из принципа Ферма
Возьмем для примера закон отражения света. Сразу видно, что он непосредственно следует из принципа Ферма. Пусть луч света, вышедшего из точки А, отражается от зеркала в некоторой точке С и приходит в заданную точку В (рис. 228). Согласно принципу Ферма, проходимый светом путь  должен быть короче любого другого пути по близкой траектории, например
должен быть короче любого другого пути по близкой траектории, например  Чтобы найти положение точки отражения С, отложим на опущенном из точки А перпендикуляре к зеркалу отрезок
Чтобы найти положение точки отражения С, отложим на опущенном из точки А перпендикуляре к зеркалу отрезок  равный
равный  и соединим точки А и В отрезком прямой.
и соединим точки А и В отрезком прямой.
Пересечение этого отрезка с поверхностью зеркала и дает положение точки С. Действительно, легко видеть, что  и потому путь света
и потому путь света  из точки А в точку В равен отрезку
из точки А в точку В равен отрезку  Путь света из А в В через любую другую точку
Путь света из А в В через любую другую точку  равный
равный  будет длиннее, так как прямая
будет длиннее, так как прямая  — это кратчайшее расстояние между двумя точками А и В. Из рис. 228 сразу видно, что именно такое положение точки С соответствует равенству углов падения и отражения:
— это кратчайшее расстояние между двумя точками А и В. Из рис. 228 сразу видно, что именно такое положение точки С соответствует равенству углов падения и отражения: 

Рис. 229. Мнимое изображение точки А в плоском зеркале
Изображение в плоском зеркале. Точка А, расположенная симметрично точке А относительно поверхности плоского зеркала, представляет собой изображение точки А в этом зеркале. В самом деле, узкий пучок лучей, выходящих из
А, отражающихся в зеркале и попадающих в глаз наблюдателя (рис. 229), будет казаться выходящим из точки А. Создаваемое плоским зеркалом изображение называется мнимым, так как в точке А пересекаются не сами отраженные лучи, а их продолжения назад. Очевидно, что изображение протяженного предмета в плоском зеркале будет равным по размерам самому предмету.
• Что такое световые лучи? Как это понятие соотносится с понятием волновой поверхности? Какое отношение имеют лучи к направлению распространения световых колебаний?
• В каких условиях можно использовать представление о световых лучах?
• Что такое показатель преломления среды? Как он связан со скоростью распространения света?
• Сформулируйте основные законы геометрической оптики. Что такое плоскость падения? Объясните на основе соображений симметрии, почему луч как при отражении, так и при преломлении не выходит из этой плоскости.
• При каких условиях отражение света на границе раздела будет полным? Что такое предельный угол полного отражения?
• Поясните, как можно получить законы прямолинейного распространения, отражения и преломления на основе принципа Гюйгенса.
• Почему законы отражения и преломления света, сформулированные для плоской границы раздела, можно применять и в случае искривленных поверхностей (линзы, капли воды и др.)?
• Приведите примеры наблюдавшихся вами явлений, свидетельствующих о зависимости интенсивности отраженного света от угла падения.
• Почему при отражении естественного света получается частично поляризованный свет?
• Сформулируйте принцип Ферма и покажите, что из него следует закон отражения света.
• Докажите, что изображение предмета в плоском зеркале равно по размерам самому предмету.
Принцип Ферма и формула линзы. Скорость света в среде с показателем преломления  равна
равна  Поэтому принцип Ферма можно сформулировать как требование минимальности оптической длины луча при распространении света между двумя заданными точками. Под оптической длиной луча понимается произведение показателя преломления на длину пути луча. В неоднородной среде оптическая длина складывается из оптических длин на отдельных участках. Использование этого принципа позволяет рассмотреть некоторые задачи с несколько иной точки зрения, чем при непосредственном применении законов отражения и преломления. Например, при рассмотрении фокусирующей оптической системы вместо применения закона преломления можно просто потребовать равенства оптических длин всех лучей.
Поэтому принцип Ферма можно сформулировать как требование минимальности оптической длины луча при распространении света между двумя заданными точками. Под оптической длиной луча понимается произведение показателя преломления на длину пути луча. В неоднородной среде оптическая длина складывается из оптических длин на отдельных участках. Использование этого принципа позволяет рассмотреть некоторые задачи с несколько иной точки зрения, чем при непосредственном применении законов отражения и преломления. Например, при рассмотрении фокусирующей оптической системы вместо применения закона преломления можно просто потребовать равенства оптических длин всех лучей.
Получим с помощью принципа Ферма формулу тонкой линзы, не прибегая к закону преломления. Для определенности будем рассматривать двояковыпуклую линзу со сферическими преломляющими поверхностями, радиусы кривизны которых равны  (рис. 230).
(рис. 230).
Хорошо известно, что с помощью собирающей линзы можно получить действительное изображение точки. Пусть  предмет,
предмет,  его изображение. Все лучи, исходящие из
его изображение. Все лучи, исходящие из  и прошедшие через линзу, собираются в одной точке
и прошедшие через линзу, собираются в одной точке  Пусть
Пусть  лежит на главной оптической оси линзы, тогда изображение
лежит на главной оптической оси линзы, тогда изображение  также лежит на оси. Что значит получить формулу линзы? Это значит установить связь между расстояниями
также лежит на оси. Что значит получить формулу линзы? Это значит установить связь между расстояниями  от предмета до линзы и
от предмета до линзы и  от линзы до изображения и величинами, характеризующими данную линзу: радиусами кривизны ее поверхностей
от линзы до изображения и величинами, характеризующими данную линзу: радиусами кривизны ее поверхностей  и показателем преломления
и показателем преломления 
Из принципа Ферма следует, что оптические длины всех лучей, выходящих из источника и собирающихся в точке, являющейся его изображением, одинаковы. Рассмотрим два из этих лучей: один, идущий вдоль оптической оси, второй — через край линзы (рис. 230а).

Рис. 230. К вьшоду формулы тонкой линзы
Несмотря на то, что второй луч проходит большее расстояние, его путь в стекле короче, чем у первого, так что время распространения света  для них одинаково. Выразим это математически. Обозначения величин всех отрезков указаны на рисунке. Приравняем оптические длины первого и второго лучей:
для них одинаково. Выразим это математически. Обозначения величин всех отрезков указаны на рисунке. Приравняем оптические длины первого и второго лучей:

Выразим  по теореме Пифагора:
по теореме Пифагора:

Теперь воспользуемся приближенной формулой  которая справедлива при
которая справедлива при  с точностью до членов порядка
с точностью до членов порядка  Считая
Считая  малым по сравнению с
малым по сравнению с  с точностью до членов порядка
с точностью до членов порядка  имеем
имеем

Аналогично для  получаем
получаем

Подставляем выражения (8) и (9) в основное соотношение (7) и приводим подобные члены:

В этой формуле в случае тонкой линзы можно пренебречь величинами  в знаменателях правой части по сравнению с
в знаменателях правой части по сравнению с  и
и  очевидно, что в левой части выражения
очевидно, что в левой части выражения  следует сохранить, ибо этот член стоит множителем.
следует сохранить, ибо этот член стоит множителем.
С той же точностью, что и в формулах (8) и (9),  с помощью теоремы Пифагора можно представить в виде (рис. 230б)
с помощью теоремы Пифагора можно представить в виде (рис. 230б)

Теперь остается только подставить эти выражения в левую часть формулы (10) и сократить обе части равенства на  :
:

Это и есть искомая формула тонкой линзы. Вводя обозначение

ее можно переписать в виде

Фокусное расстояние линзы. Из формулы (12) нетрудно понять, что  есть фокусное расстояние линзы: если источник находится на бесконечности (т.е. на линзу падает параллельный пучок лучей), его изображение находится в фокусе. Полагая
есть фокусное расстояние линзы: если источник находится на бесконечности (т.е. на линзу падает параллельный пучок лучей), его изображение находится в фокусе. Полагая  получаем
получаем 
Аберрации. Полученное свойство фокусировки параллельного пучка монохроматических лучей является, как видно из проделанного вывода, приближенным и справедливо лишь для узкого пучка, т. е. для лучей, не слишком сильно отстоящих от оптической оси. Для широких пучков лучей имеет место сферическая аберрация, проявляющаяся в том, что далекие от оптической оси лучи пересекают ее не в фокусе (рис. 231). В результате изображение бесконечно удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается несколько размытым.
Кроме сферической аберрации, линза как оптический прибор, формирующий изображение, обладает рядом других недостатков.
Например, даже узкий параллельный пучок монохроматических лучей, образующий некоторый угол с оптической осью линзы, после преломления не собирается в одну точку. При использовании немонохроматического света у линзы проявляется еще и хроматическая аберрация, связанная с тем, что показатель преломления  зависит от длины волны. В результате, как видно из формулы (11), узкий параллельный пучок лучей белого света пересекается после преломления в линзе не в одной точке: лучи каждого цвета имеют свой фокус.
зависит от длины волны. В результате, как видно из формулы (11), узкий параллельный пучок лучей белого света пересекается после преломления в линзе не в одной точке: лучи каждого цвета имеют свой фокус.
При конструировании оптических приборов удается в большей или меньшей степени устранить эти недостатки путем применения специально рассчитанных сложных многолинзовых систем. Однако одновременно устранить все недостатки невозможно. Поэтому приходится идти на компромисс и, рассчитывая оптические приборы, предназначенные для определенной цели, добиваться устранения одних недостатков и мириться с присутствием других. Например, объективы, предназначенные для наблюдения объектов малой яркости, должны пропускать возможно больше света, что вынуждает мириться с некоторыми аберрациями, неизбежными при использовании широких пучков света.

Рис. 231. Сферическая аберрация линзы
Для объективов телескопов, где изучаемыми объектами являются звезды — точечные источники, расположенные вблизи оптической оси прибора, особенно важно устранить сферическую и хроматическую аберрацию для широких пучков, параллельных оптической оси. Устранить хроматическую аберрацию проще всего путем использования в оптической системе отражения вместо преломления. Так как лучи всех длин волн отражаются одинаково, то телескоп-рефлектор, в отличие от рефрактора, полностью лишен хроматической аберрации. Если при этом еще надлежащим образом выбрать форму поверхности отражающего зеркала, то можно полностью избавиться и от сферической аберрации для пучков, параллельных оптической оси. Для получения точечного осевого изображения зеркало должно быть параболическим.
Покажем это. Пусть плоская волна, т. е. пучок лучей, параллельных оси у, падает на зеркальную поверхность, обладающую тем свойством, что после отражения все лучи собираются в одной точке  (рис. 232). Из симметрии ясно, что искомая поверхность зеркала представляет собой поверхность вращения вокруг оси у, поэтому достаточно рассмотреть сечение этой поверхности плоскостью ху, т. е. кривую
(рис. 232). Из симметрии ясно, что искомая поверхность зеркала представляет собой поверхность вращения вокруг оси у, поэтому достаточно рассмотреть сечение этой поверхности плоскостью ху, т. е. кривую  Рассмотрим центральный луч и луч, падающий на зеркало в произвольной точке С с координатами х и у. На основании принципа Ферма оптическая длина
Рассмотрим центральный луч и луч, падающий на зеркало в произвольной точке С с координатами х и у. На основании принципа Ферма оптическая длина
этих лучей от произвольной волновой поверхности  до фокуса
до фокуса  должна быть одной и той же:
должна быть одной и той же:

Из рис. 232 видно, что  Подставляя эти значения в (13), получим
Подставляя эти значения в (13), получим

Возводя обе части в квадрат и приводя подобные члены, найдем

Это уравнение параболы.

Рис. 232. Все параллельные лучи после отражения от параболического зеркала собираются в точке 
Параболические зеркала используются во всех крупнейших телескопах. В этих телескопах устранены сферическая и хроматическая аберрации; однако параллельные пучки, идущие даже под небольшими углами к оптической оси, после отражения не пересекаются в одной точке и дают сильно искаженные внеосевые изображения. Поэтому пригодное для работы поле зрения оказывается очень небольшим, порядка нескольких десятков угловых минут,
• Поясните, почему применительно к фокусирующей оптической системе принцип Ферма формулируется как условие равенства оптических длин всех лучей от точки предмета до ее изображения.
• Выведите с помощью принципа Ферма закон преломления света на границе раздела двух сред.
• Сформулируйте приближения, при выполнении которых справедлива формула тонкой линзы.
• В чем проявляются сферическая и хроматическая аберрации линзы?
• Какие преимущества и какие недостатки имеет параболическое зеркало по сравнению со сферическим?
• Покажите, что эллиптическое зеркало отражает все лучи, вышедшие из одного фокуса эллипсоида, в другой фокус.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
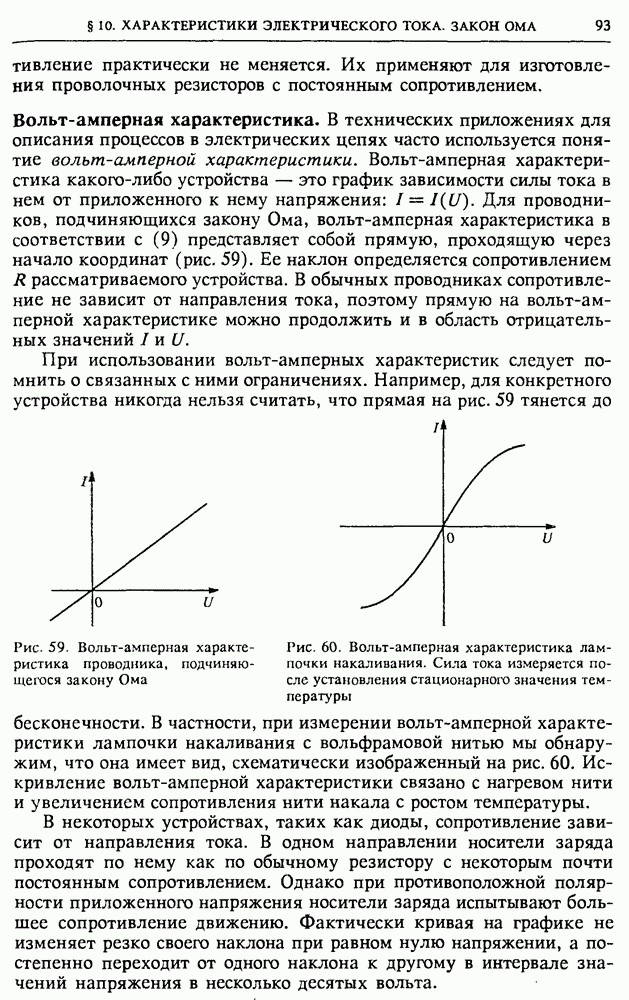
- § 10. Характеристики электрического тока. Закон Ома
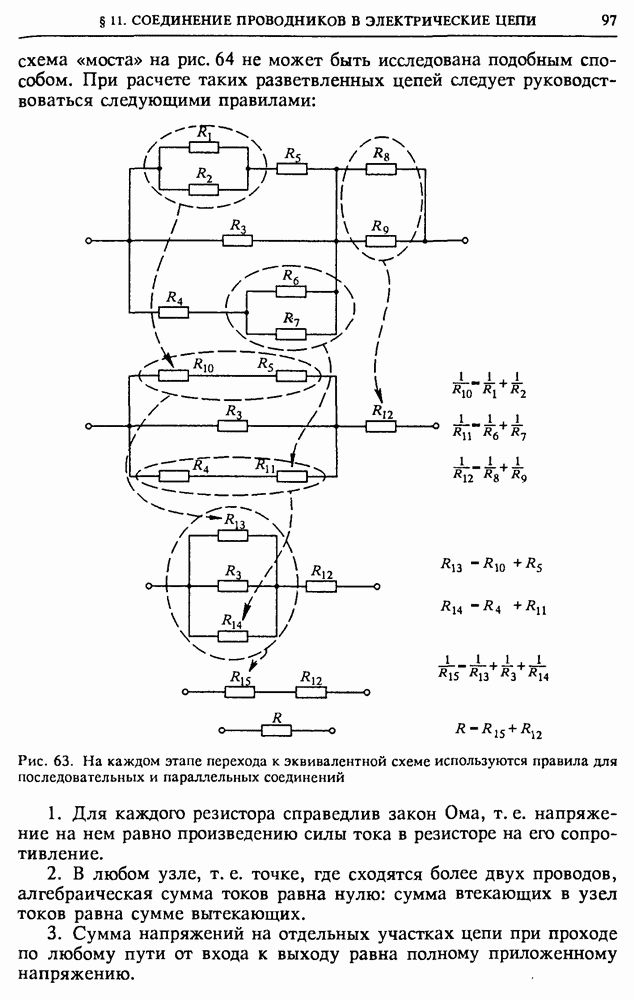
- § 11. Соединение проводников в электрические цепи
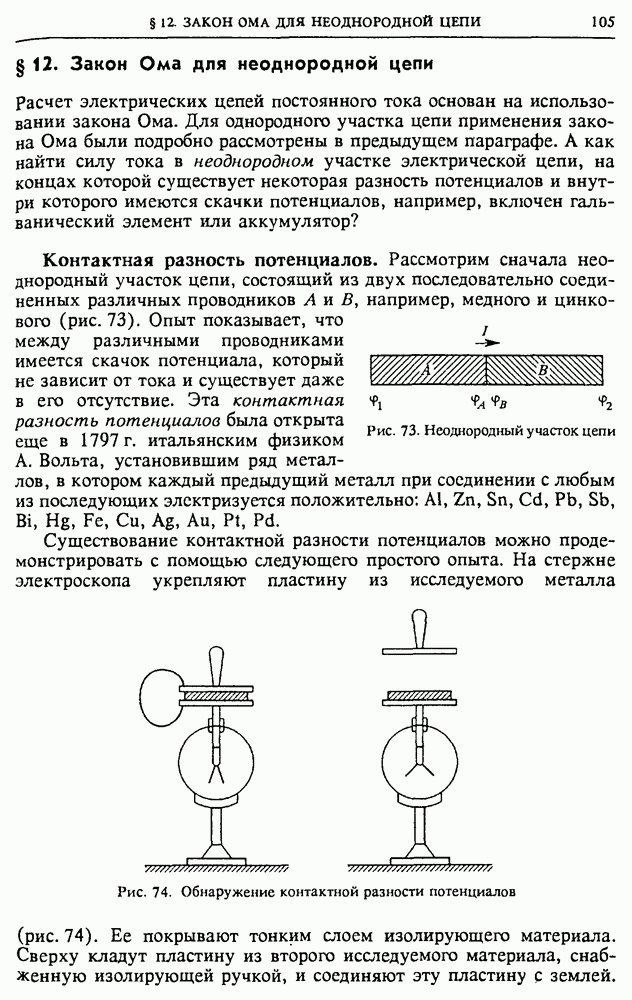
- § 12. Закон Ома для неоднородной цепи
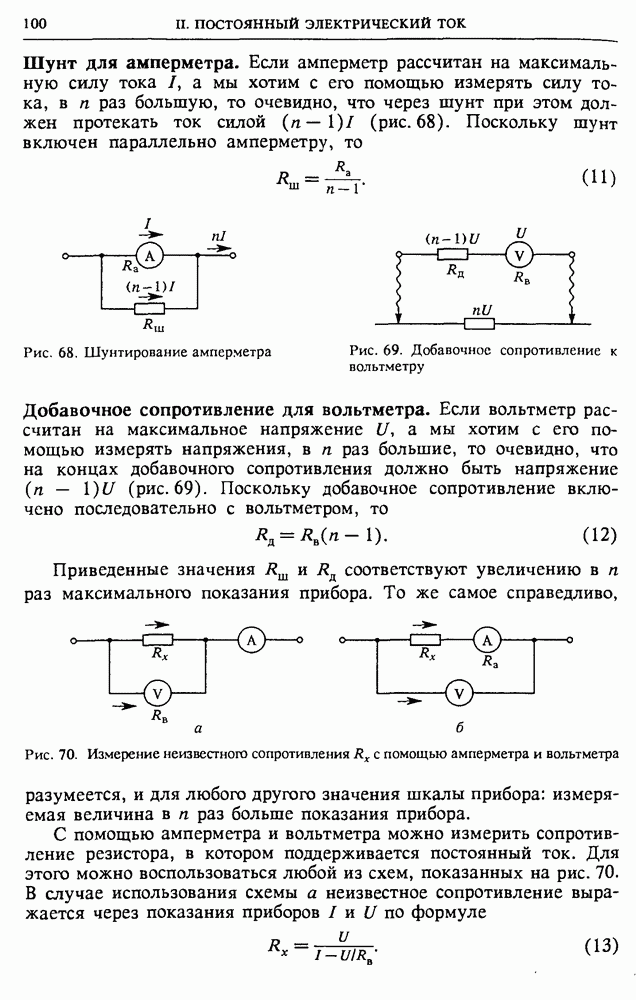
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
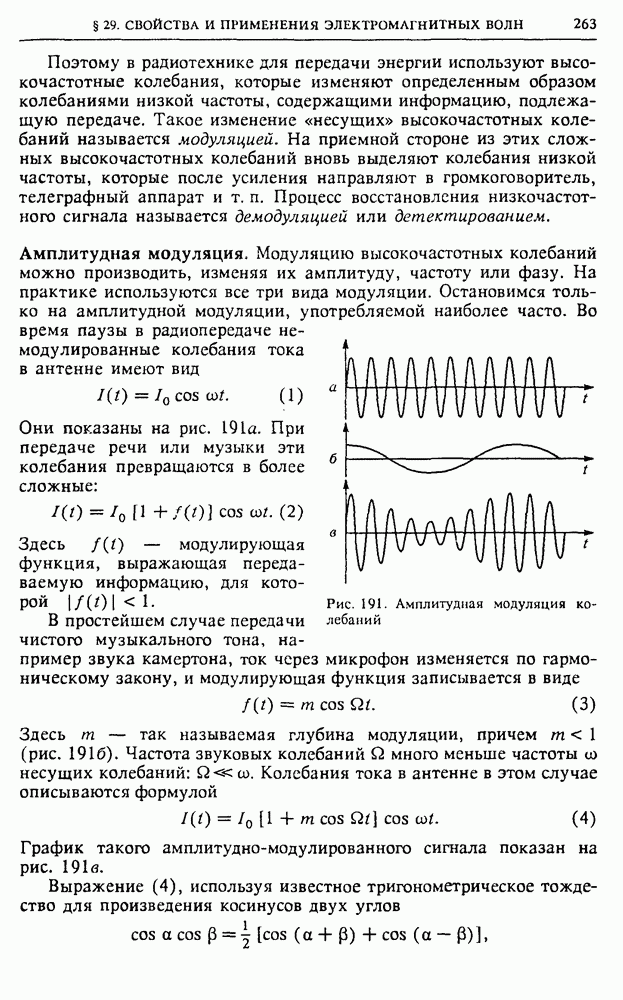
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
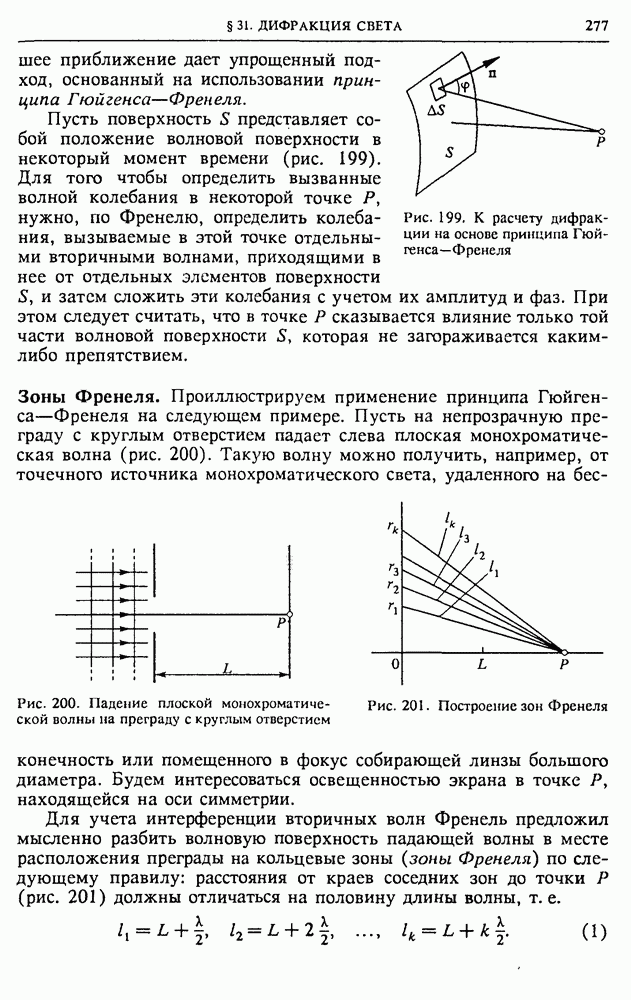
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение