| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2.1. Матричная форма
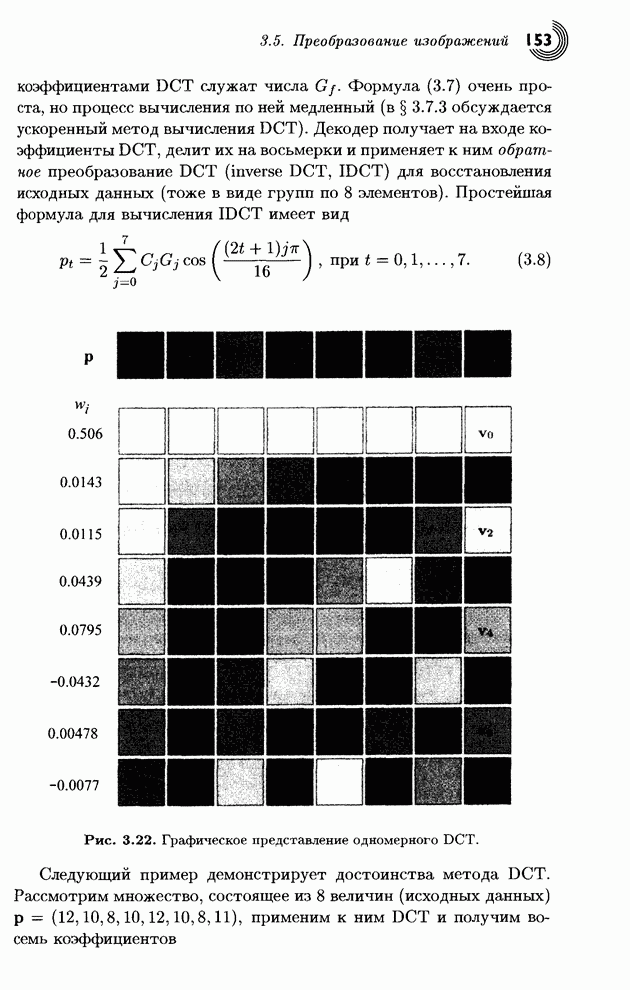
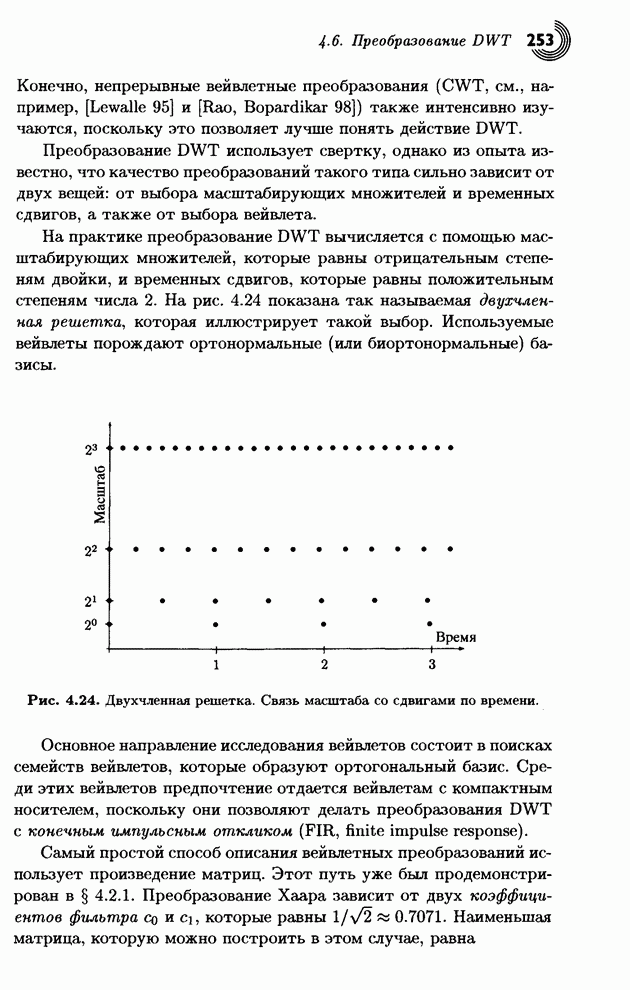
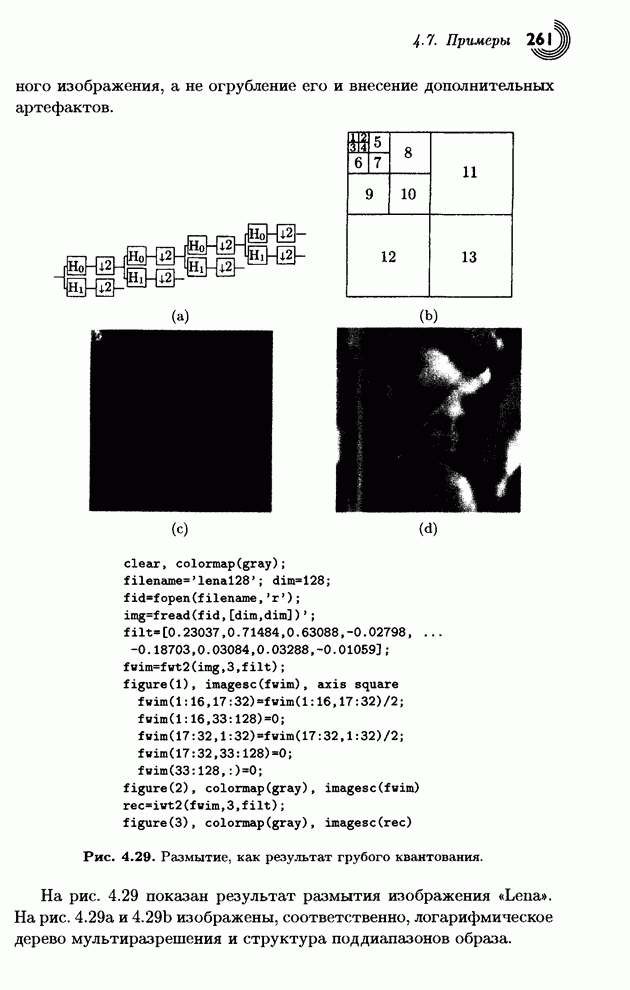
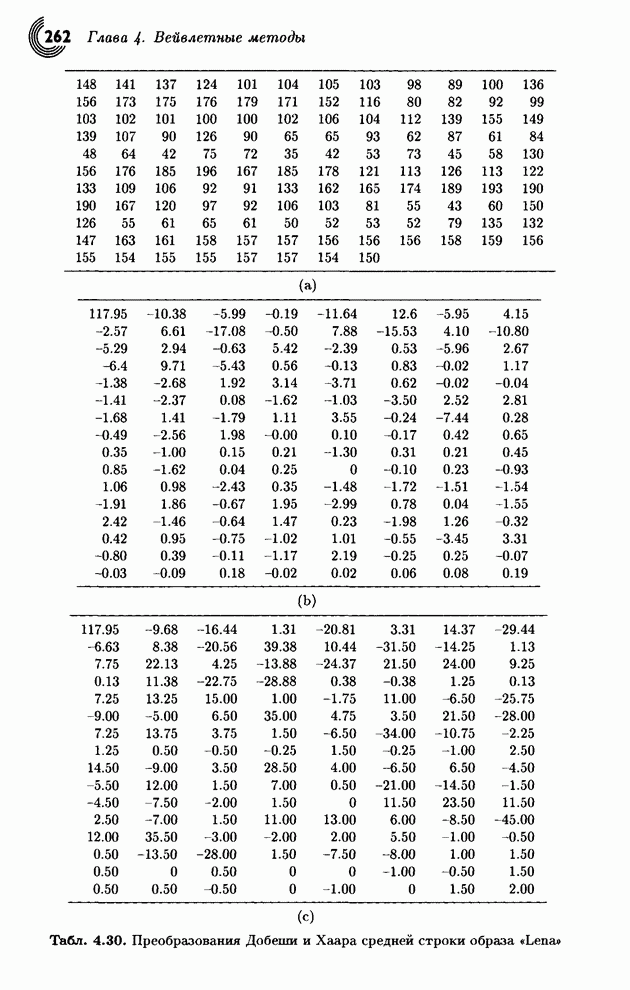
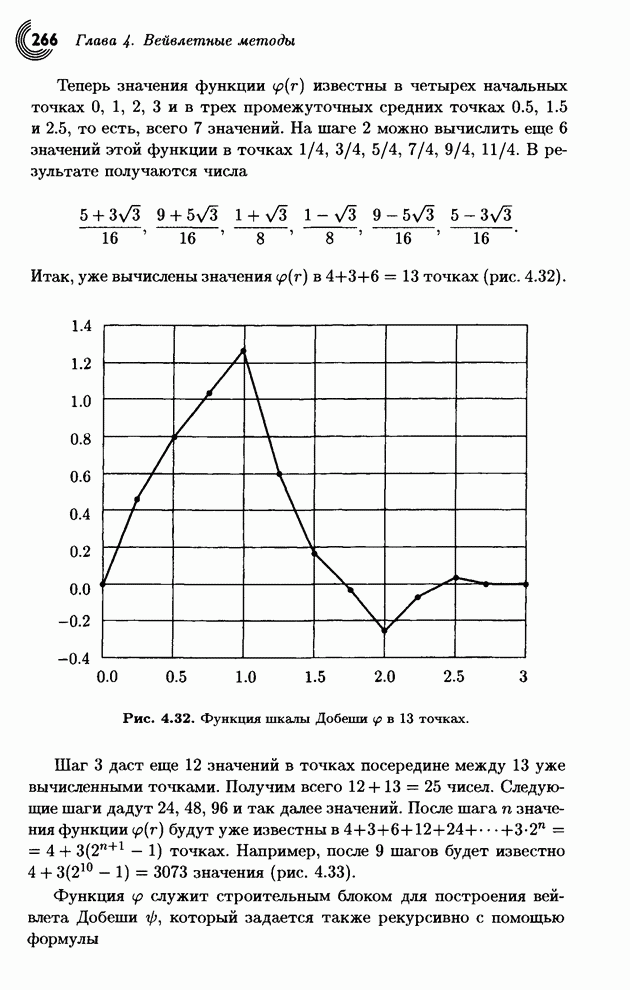
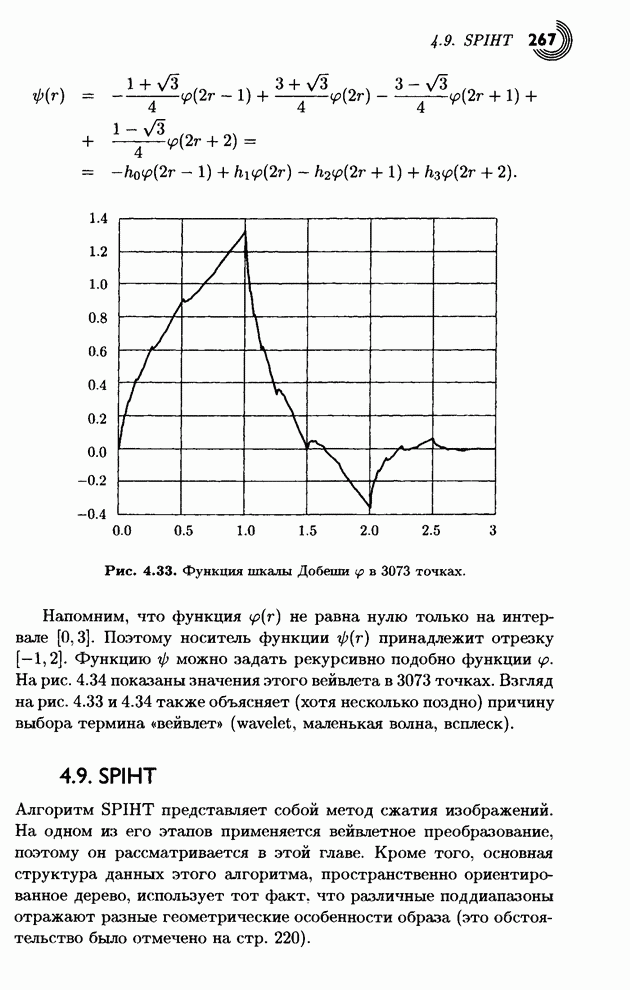
В основе преобразования Хаара
лежит вычисление средних и разностей. Оказывается, .что эти операции можно
легко выразить с помощью умножений соответствующих матриц (см. [Mulcahy 96] и [Mulcahy 97]). Для примера рассмотрим
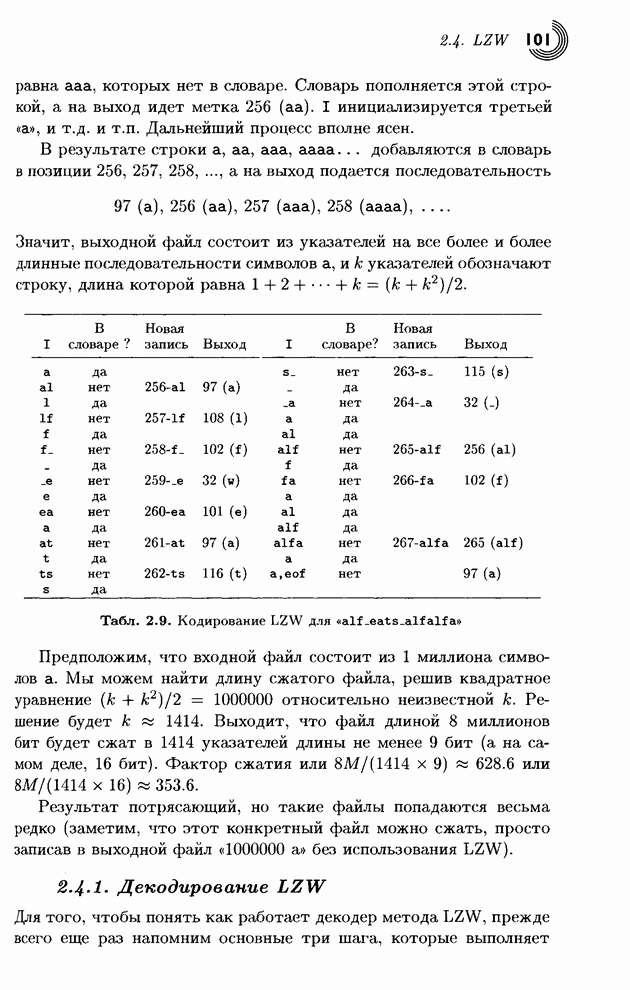
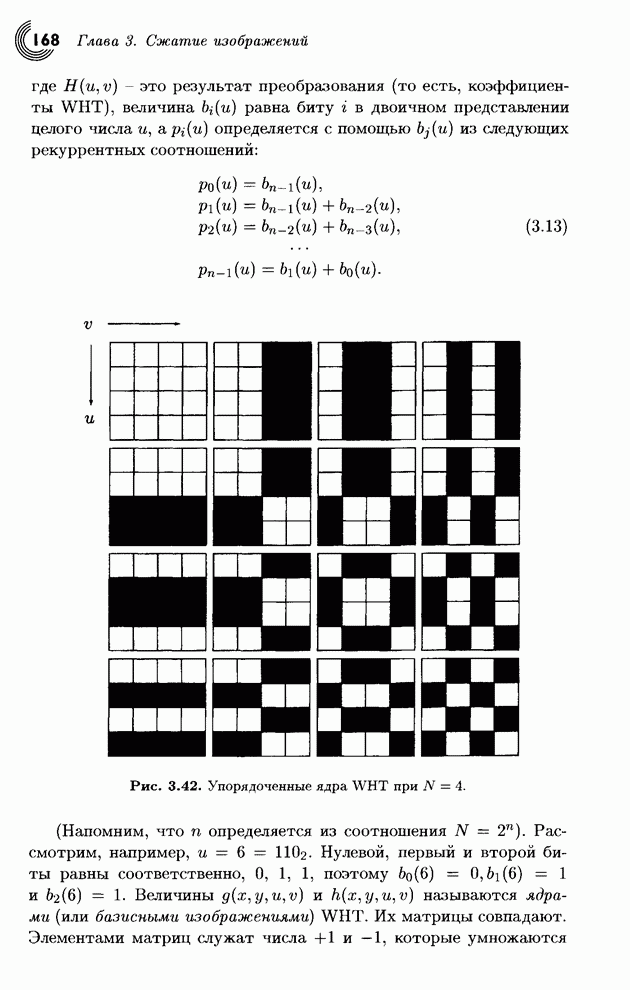
верхнюю строку простого изображения размера 8х8 из рис. 4.8. Каждый, кто
немного знаком с операциями над матрицами, легко построит матрицу, которая при
умножении на некоторый вектор дает другой вектор, состоящий из четырех полусумм
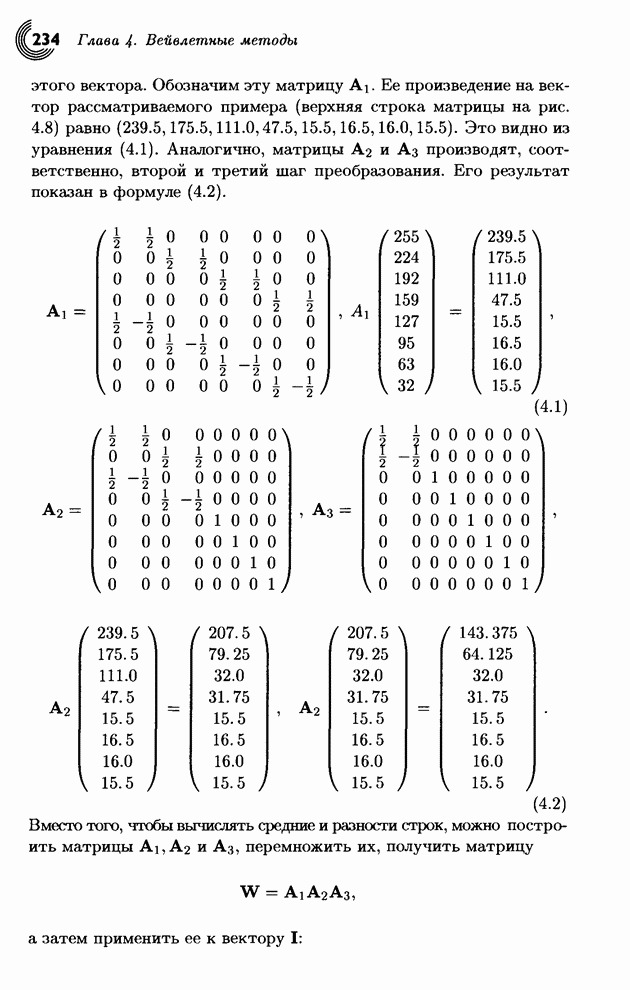
и четырех полуразностей элементов этого вектора. Обозначим эту матрицу ![]() . Ее произведение на
вектор рассматриваемого примера (верхняя строка матрицы на рис. 4.8) равно
(239.5, 175.5, 111.0, 47.5, 15.5, 16.5, 16.0, 15.5). Это видно из уравнения
(4.1). Аналогично, матрицы
. Ее произведение на
вектор рассматриваемого примера (верхняя строка матрицы на рис. 4.8) равно
(239.5, 175.5, 111.0, 47.5, 15.5, 16.5, 16.0, 15.5). Это видно из уравнения
(4.1). Аналогично, матрицы ![]() и
и ![]() производят, соответственно, второй и
третий шаг преобразования. Его результат показан в формуле (4.2).
производят, соответственно, второй и
третий шаг преобразования. Его результат показан в формуле (4.2).
 ,
,  , (4.1)
, (4.1)
 ,
,  ,
,
 ,
,  . (4.2)
. (4.2)
Вместо того, чтобы вычислять
средние и разности строк, можно построить матрицы ![]() ,
, ![]() и
и ![]() , перемножить их, получить матрицу
, перемножить их, получить матрицу
![]() ,
,
а
затем применить ее к вектору ![]() :
:
 .
.
В этом заключается только
половина работы. Для того, чтобы сделать полное преобразование, необходимо
применить ![]() к
строкам произведения
к
строкам произведения ![]() , или, что то же самое, умножим
, или, что то же самое, умножим ![]() на
на ![]() . Результат для
удобства тоже транспонируем. Полное преобразование (см. строку timg=w*img*w’ рис. 4.12)
равно
. Результат для
удобства тоже транспонируем. Полное преобразование (см. строку timg=w*img*w’ рис. 4.12)
равно
![]() .
.
Для обратного преобразования справедлива формула
![]() .
.
В
этом месте становится важным нормализованное преобразование Хаара (упомянутое
на стр. 216). Вместо вычисления средних (выражений ![]() и разностей (выражений
и разностей (выражений ![]() лучше вычислять
величины
лучше вычислять
величины ![]() и
и
![]() . Это
приводит к ортогональной матрицы
. Это
приводит к ортогональной матрицы ![]() , а хорошо известно, что обращение такой
матрицы сводится к ее транспонированию. Следовательно, обратное преобразование
запишется в простом виде
, а хорошо известно, что обращение такой
матрицы сводится к ее транспонированию. Следовательно, обратное преобразование
запишется в простом виде ![]() (см. строку cimg=full(w‘*sparse(dimg)*w на рис. 4.12).
(см. строку cimg=full(w‘*sparse(dimg)*w на рис. 4.12).
Между процедурами прямого и
обратного преобразования некоторые коэффициенты могут быть квантованы или
отброшены. Кроме того, для лучшего сжатия, матрицу ![]() можно кодировать по методу RLE и/или по методу Хаффмана.
можно кодировать по методу RLE и/или по методу Хаффмана.
Функция individ(n) на рис. 4.12 начинается с матрицы преобразования
Хаара размера 2x2 (заметим, что вместо знаменателя 2 взято число ![]() ), затем использует
эту матрицу для построения необходимого числа матриц
), затем использует
эту матрицу для построения необходимого числа матриц ![]() . Функция harmatt(dim) формирует окончательную матрицу Хаара для
изображения, состоящего из dim строк и dim столбцов.
. Функция harmatt(dim) формирует окончательную матрицу Хаара для
изображения, состоящего из dim строк и dim столбцов.
Пример: Программа Matlab на рис. 4.15 вычисляет ![]() в виде произведения
трех матриц
в виде произведения
трех матриц ![]() ,
,
![]() и
и ![]() , после чего делает
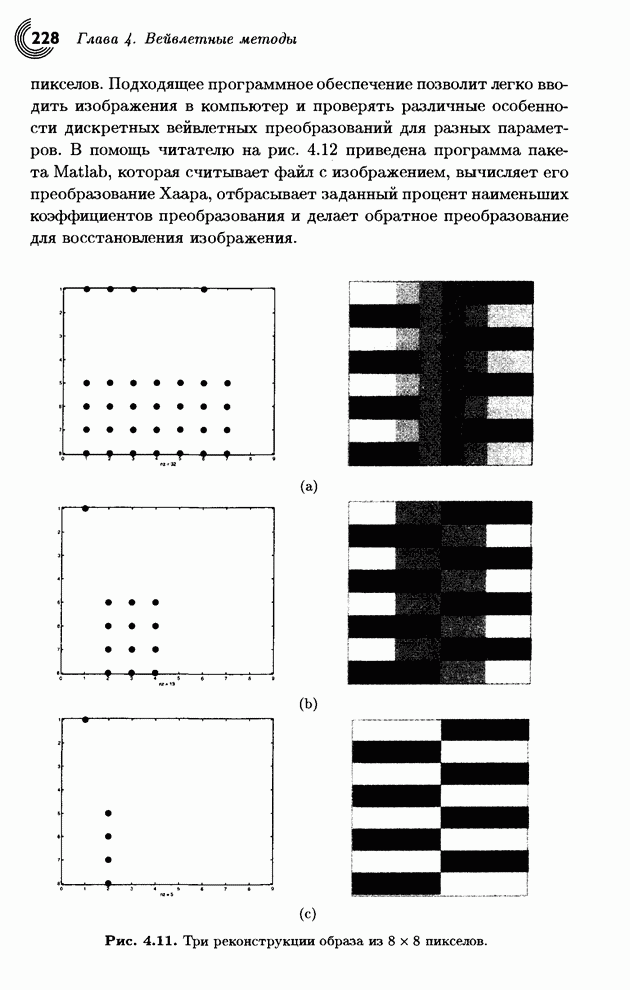
преобразования изображения размера 8х8 из рис. 4.8. Результатом становится
матрица 8x8, состоящая из коэффициентов преобразования, в которой верхний левый
коэффициент 131.375 равен среднему всех 64 пикселов исходного изображения.
, после чего делает
преобразования изображения размера 8х8 из рис. 4.8. Результатом становится
матрица 8x8, состоящая из коэффициентов преобразования, в которой верхний левый
коэффициент 131.375 равен среднему всех 64 пикселов исходного изображения.

Рис. 4.16. Программа и результат
матричного вейвлетного преобразования ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
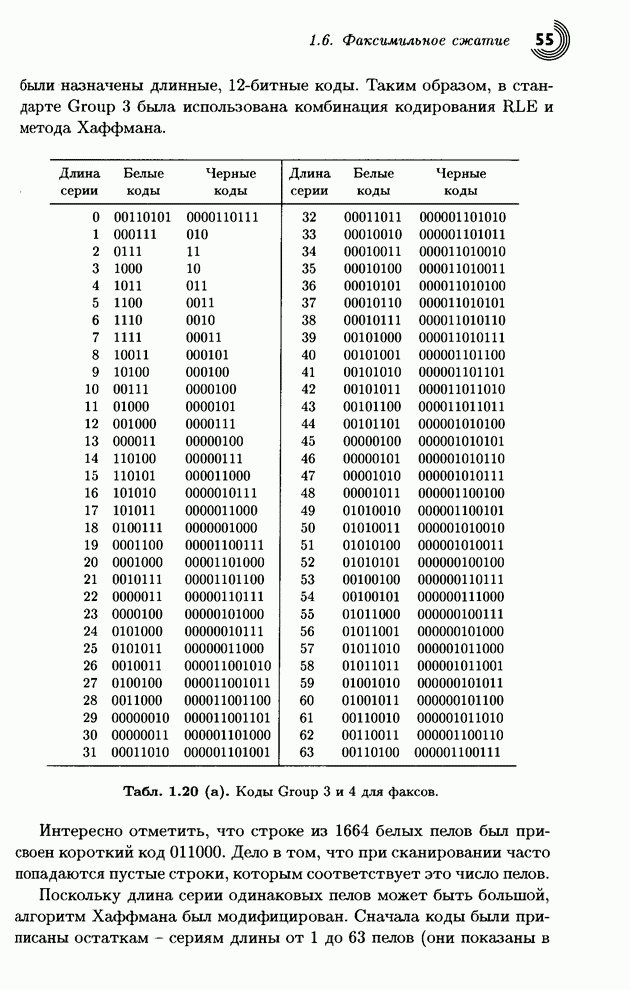
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий