| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 29. Интерференция
§ 1. Электромагнитные волны
В этой главе мы будем обсуждать те же вопросы, что и в предыдущей, но с большими математическими подробностями. Качественно мы уже показали, что поле излучения двух источников имеет максимумы и минимумы, и теперь наша задача — дать математическое, a не просто качественное описание поля.
Мы вполне
удовлетворительно разобрали физический смысл формулы (28.6), рассмотрим теперь
некоторые ее математические черты. Прежде всего поле заряда, движущегося вверх
и вниз с малой амплитудой в направлении ![]() от оси движения, перпендикулярно
лучу зрения и лежит в плоскости ускорения и луча зрения (фиг. 29.1). Обозначим
расстояние через
от оси движения, перпендикулярно
лучу зрения и лежит в плоскости ускорения и луча зрения (фиг. 29.1). Обозначим
расстояние через ![]() , тогда в момент времени
, тогда в момент времени ![]() величина
электрического поля равна
величина
электрического поля равна
![]() , (29.1)
, (29.1)
где ![]() — ускорение в момент
времени
— ускорение в момент
времени ![]() ,
или запаздывающее ускорение.
,
или запаздывающее ускорение.

Фигура 29.1. Напряженность поля ![]() , создаваемая положительным зарядом с
запаздывающим ускорением
, создаваемая положительным зарядом с
запаздывающим ускорением ![]()
Интересно нарисовать
картину распределения поля в разных случаях. Наиболее характерный множитель в
формуле (29.1) — это ![]() ; чтобы его понять, возьмем
простейший случай
; чтобы его понять, возьмем
простейший случай ![]() и изобразим поле на графике. Раньше
мы были заняты вопросом, как ведет себя поле в данной фиксированной точке
пространства с течением времени. Теперь посмотрим, как выглядит поле в разных
точках пространства в один и тот же момент времени. Иначе говоря, нам нужен
«моментальный снимок» поля, из которого будет ясно, каково оно в разных местах.
Разумеется, картина распределения поля зависит от ускорения заряда. Зададим
характер движения заряда: пусть сначала он покоится, затем внезапно начнет
определенным образом ускоряться (как показано на фиг. 29.2) и, наконец,
остановится. Затем, чуть позже, измерим поле в разных точках пространства. Мы
можем утверждать, что поле будет иметь вид, приведенный на фиг. 29.3. В самом
деле, поле в каждой точке определяется ускорением заряда в предыдущий момент
времени, причем под словом «предыдущий» понимается
и изобразим поле на графике. Раньше
мы были заняты вопросом, как ведет себя поле в данной фиксированной точке
пространства с течением времени. Теперь посмотрим, как выглядит поле в разных
точках пространства в один и тот же момент времени. Иначе говоря, нам нужен
«моментальный снимок» поля, из которого будет ясно, каково оно в разных местах.
Разумеется, картина распределения поля зависит от ускорения заряда. Зададим
характер движения заряда: пусть сначала он покоится, затем внезапно начнет
определенным образом ускоряться (как показано на фиг. 29.2) и, наконец,
остановится. Затем, чуть позже, измерим поле в разных точках пространства. Мы
можем утверждать, что поле будет иметь вид, приведенный на фиг. 29.3. В самом
деле, поле в каждой точке определяется ускорением заряда в предыдущий момент
времени, причем под словом «предыдущий» понимается ![]() секунд назад. Чем дальше
точка, тем более ранним моментом времени определяется для нее ускорение.
Поэтому кривая на фиг. 29.3 в некотором смысле есть «обращенный» во времени
график ускорения; время и расстояние отличаются постоянным множителем
секунд назад. Чем дальше
точка, тем более ранним моментом времени определяется для нее ускорение.
Поэтому кривая на фиг. 29.3 в некотором смысле есть «обращенный» во времени
график ускорения; время и расстояние отличаются постоянным множителем ![]() , который часто
выбирается равным единице. Этот факт легко заметить и в математической записи
, который часто
выбирается равным единице. Этот факт легко заметить и в математической записи ![]() . Ясно, что
добавка интервала времени
. Ясно, что
добавка интервала времени ![]() и вычитание отрезка пути
и вычитание отрезка пути ![]() дают одну и ту же
величину
дают одну и ту же
величину ![]() .
.

Фигура 29.2. Ускорение некоторого заряда как функция времени

Фигура 29.3. Электрическое поле как функция положения точки
наблюдения спустя некоторый промежуток времени. Множителем ![]() пренебрегаем.
пренебрегаем. ![]() добавлением отрезка
добавлением отрезка
![]() , т. е.
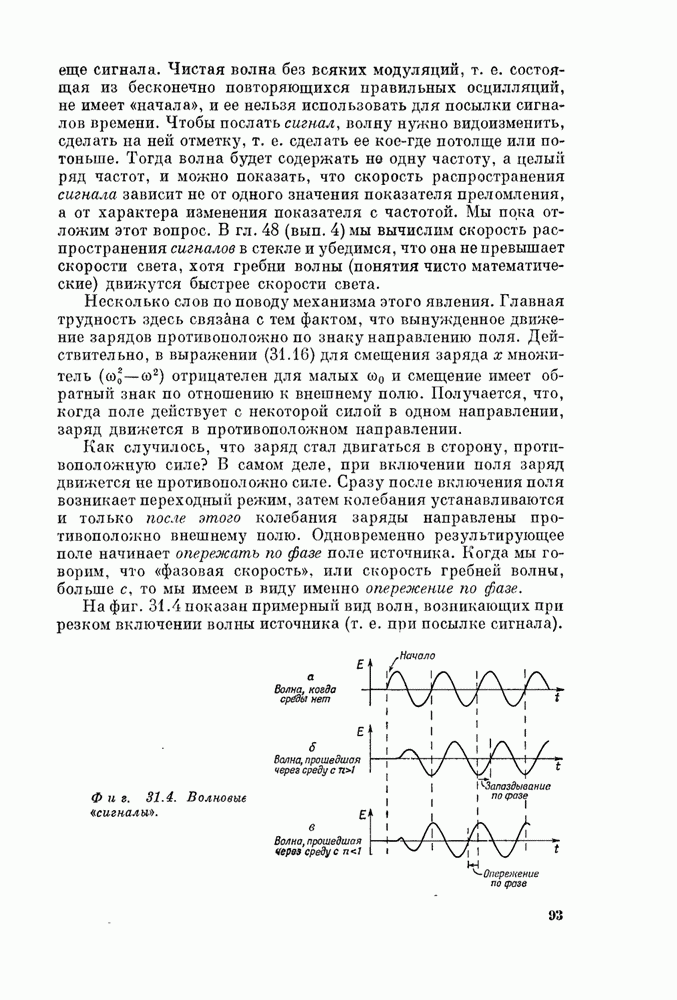
поле распространяется со временем как волна, уходящая от источника. Вот почему
иногда говорят, что свет движется как волна. Можно также сказать, что поле
запаздывает во времени, или иначе, что поле распространяется вширь с течением
времени.
, т. е.
поле распространяется со временем как волна, уходящая от источника. Вот почему
иногда говорят, что свет движется как волна. Можно также сказать, что поле
запаздывает во времени, или иначе, что поле распространяется вширь с течением
времени.
Особый интерес представляет
случай периодических колебаний заряда ![]() . В опыте, рассмотренном в гл. 28,
смещение зарядов
. В опыте, рассмотренном в гл. 28,
смещение зарядов ![]() в момент
в момент ![]() равнялось некоторой константе
равнялось некоторой константе
![]() ,
амплитуде колебаний, умноженной на
,
амплитуде колебаний, умноженной на ![]() . Ускорение в этом случае равно
. Ускорение в этом случае равно
![]() , (29.2)
, (29.2)
где ![]() , равное
, равное ![]() , и есть амплитуда
ускорения. Подставляя эту формулу в (29.1), находим
, и есть амплитуда
ускорения. Подставляя эту формулу в (29.1), находим
![]() . (29.3)
. (29.3)
Отвлечемся пока от угла ![]() и постоянных и
посмотрим, как ведет себя Е (29.3) в зависимости от времени или координат.
и постоянных и
посмотрим, как ведет себя Е (29.3) в зависимости от времени или координат.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
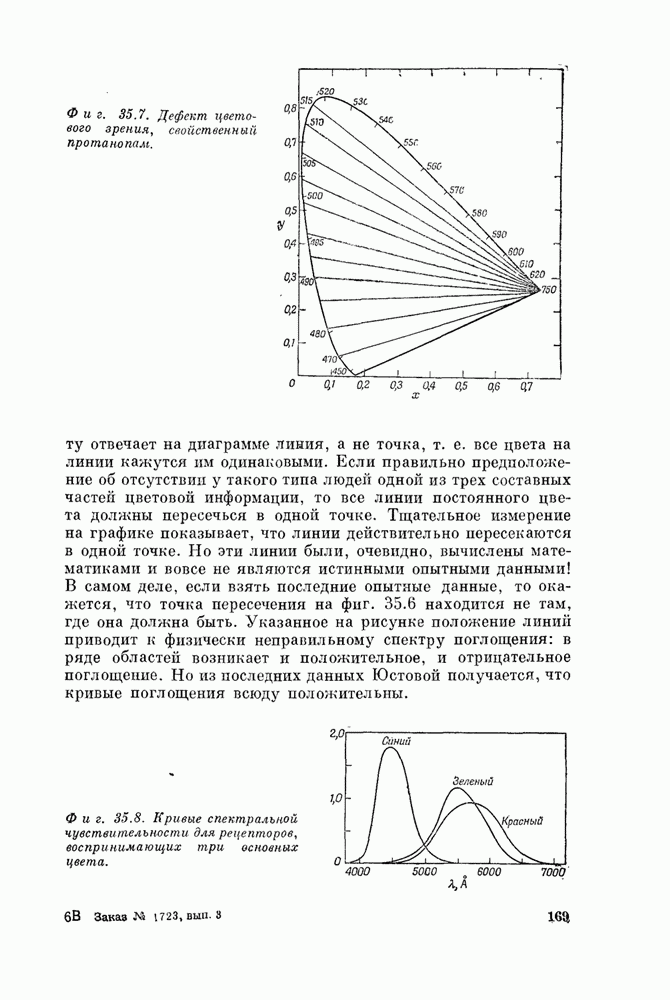
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
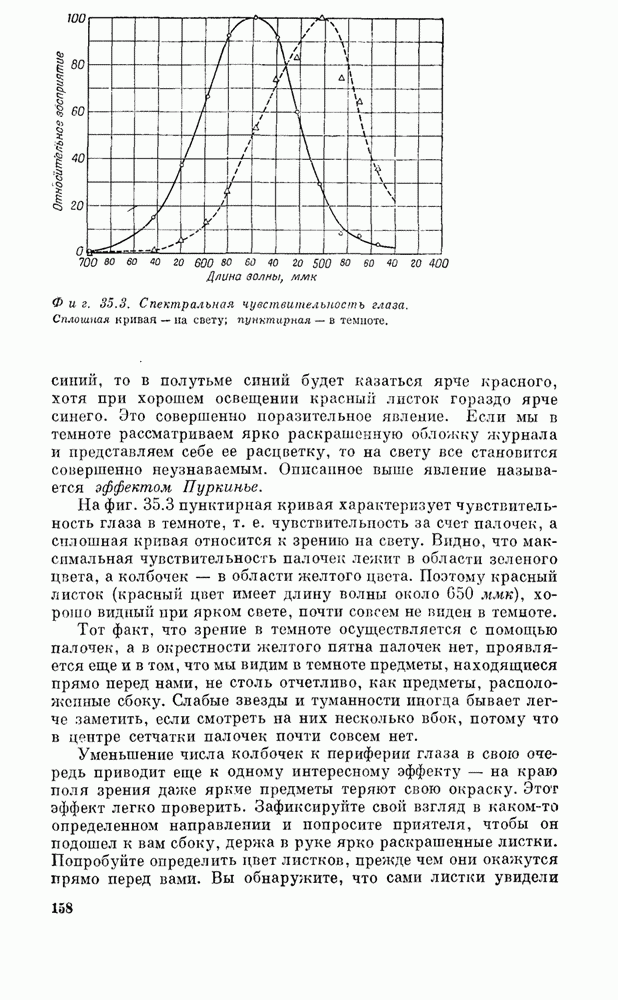
- § 3. Измерение восприятия цвета
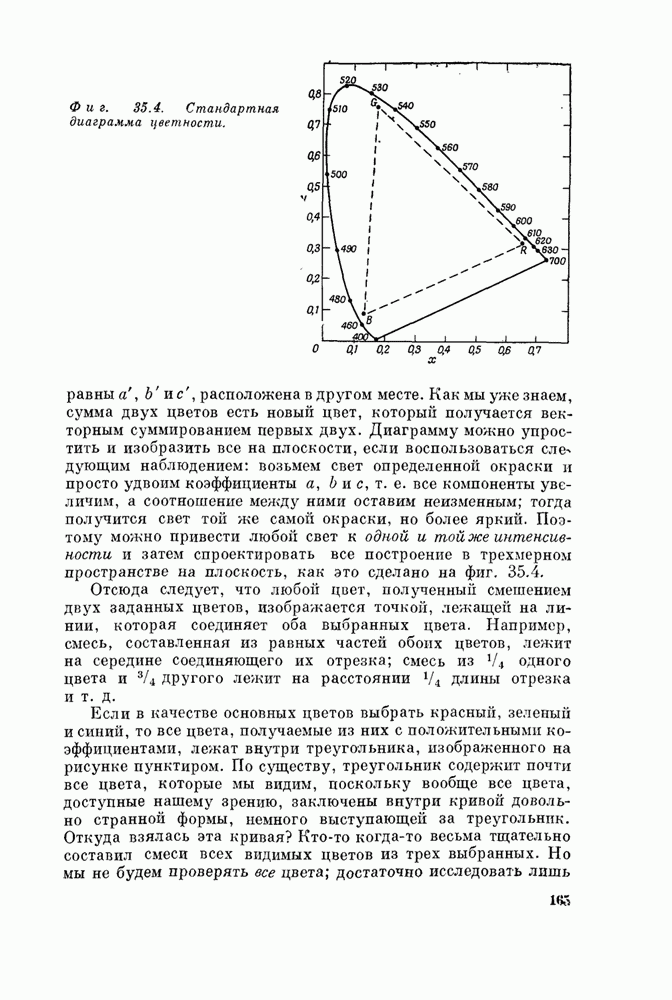
- § 4. Диаграмма цветности
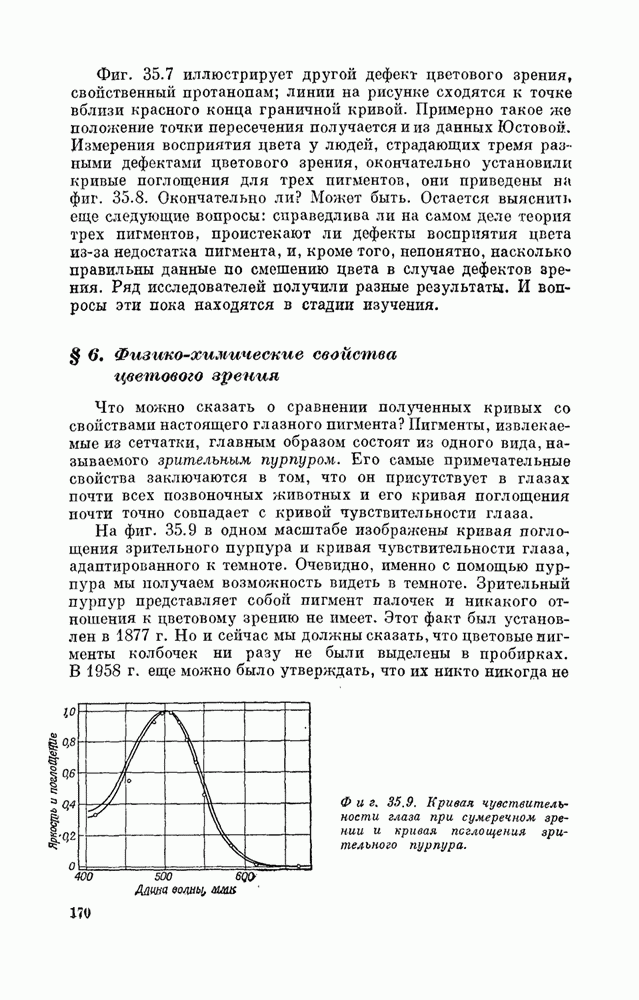
- § 5. Механизм цветового зрения
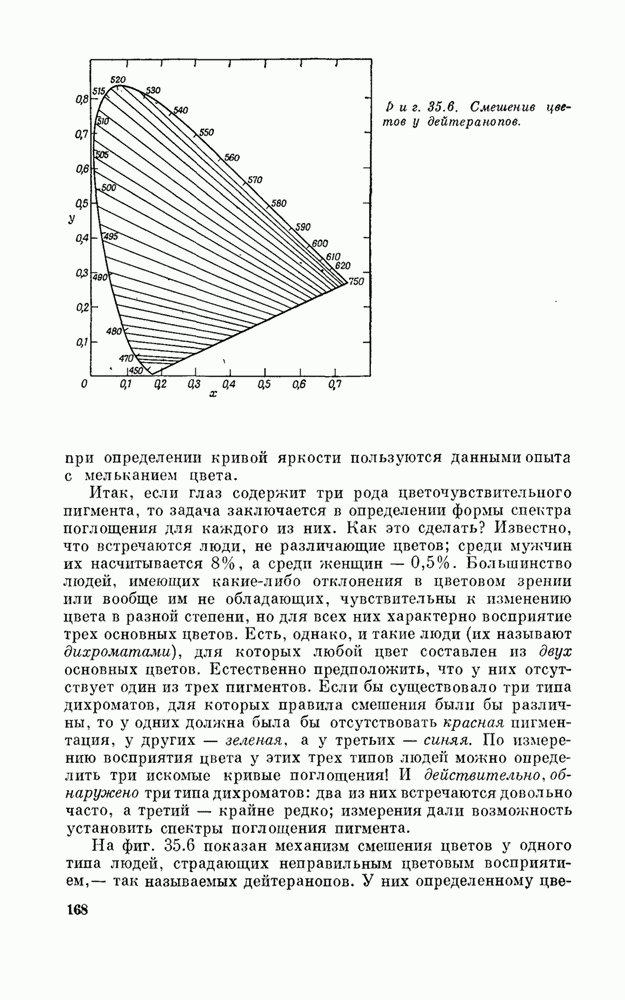
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии