| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Аберрация
При выводе формул (34.17)
и (34.18) мы взяли простой пример, когда ![]() лежит в направлении движения системы
координат; но мы можем обобщить теперь эти формулы на другие возможные случаи.
Пусть источник посылает луч света в определенном направлении; это направление
фиксируется неподвижным наблюдателем, а мы движемся, скажем, по поверхности
Земли в горизонтальном направлении (фиг. 34.12, а). В каком направлении падает
луч света с нашей точки зрения? Можно получить ответ, записав четыре компоненты
лежит в направлении движения системы
координат; но мы можем обобщить теперь эти формулы на другие возможные случаи.
Пусть источник посылает луч света в определенном направлении; это направление
фиксируется неподвижным наблюдателем, а мы движемся, скажем, по поверхности
Земли в горизонтальном направлении (фиг. 34.12, а). В каком направлении падает
луч света с нашей точки зрения? Можно получить ответ, записав четыре компоненты
![]() и
совершив преобразования Лоренца. Но можно воспользоваться и следующим
рассуждением: чтобы увидеть луч следует наш телескоп повернуть на некоторый
угол (фиг. 34.12, б). Почему? Потому что свет падает сверху со скоростью
и
совершив преобразования Лоренца. Но можно воспользоваться и следующим
рассуждением: чтобы увидеть луч следует наш телескоп повернуть на некоторый
угол (фиг. 34.12, б). Почему? Потому что свет падает сверху со скоростью ![]() , а мы движемся
горизонтально со скоростью
, а мы движемся
горизонтально со скоростью ![]() , и свет пройдет «прямо через
телескоп, если последний наклонить на некоторый угол. Легко понять, что
расстояние по горизонтали равно
, и свет пройдет «прямо через
телескоп, если последний наклонить на некоторый угол. Легко понять, что
расстояние по горизонтали равно ![]() , а по вертикали
, а по вертикали ![]() , и, обозначив угол наклона
через
, и, обозначив угол наклона
через ![]() ,
мы получим
,
мы получим ![]() .
Замечательно! В самом деле, замечательно, если бы не одна маленькая деталь:
.
Замечательно! В самом деле, замечательно, если бы не одна маленькая деталь: ![]() не есть тот угол,
под которым надо установить телескоп по отношению к поверхности Земли, потому
что наш анализ проводился с точки зрения неподвижного наблюдателя.
Горизонтальное расстояние, которое мы считали равным
не есть тот угол,
под которым надо установить телескоп по отношению к поверхности Земли, потому
что наш анализ проводился с точки зрения неподвижного наблюдателя.
Горизонтальное расстояние, которое мы считали равным ![]() , неподвижный по отношению
к Земле наблюдатель найдет равным совсем другой величине, так как он
пользуется, с нашей точки зрения, «сжатой» линейкой. Из-за эффекта сокращения
возникает совсем другое соотношение:
, неподвижный по отношению
к Земле наблюдатель найдет равным совсем другой величине, так как он
пользуется, с нашей точки зрения, «сжатой» линейкой. Из-за эффекта сокращения
возникает совсем другое соотношение:
![]() (34.22)
(34.22)
что эквивалентно
![]() (34.23)
(34.23)

Фигура 34.12. Удаленный источник света ![]() .
.
а — наблюдаемый через неподвижный телескоп; б — наблюдаемый через телескоп, движущийся в боковом направлении.
Полезно вам самим получить это соотношение с помощью преобразования Лоренца.
Описанный выше эффект кажущегося изменения направления луча называется аберрацией и обнаружен на опыте. Казалось бы, как он может проявиться? Ведь никто не знает, где на самом деле расположена звезда. Пусть мы действительно смотрим на звезду в неправильном, кажущемся направлении, откуда нам известно, что оно неправильное? Известно; потому, что Земля обращается вокруг Солнца. Сегодня мы устанавливаем телескоп под одним углом, а через шесть месяцев мы должны его уже повернуть. Вот откуда мы знаем о существовании этого эффекта.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
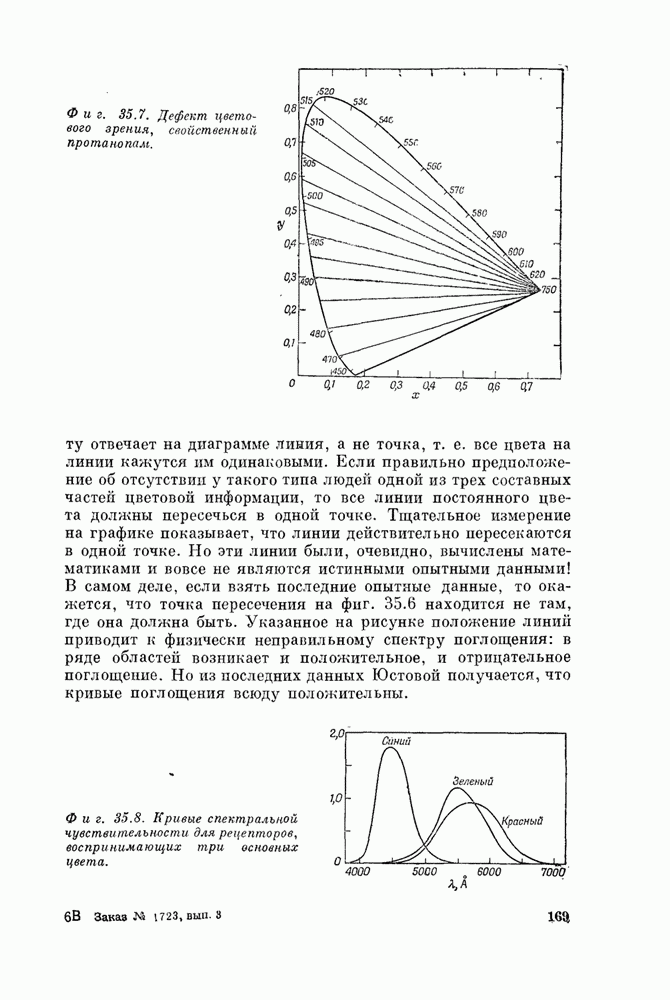
- § 4. Диаграмма цветности
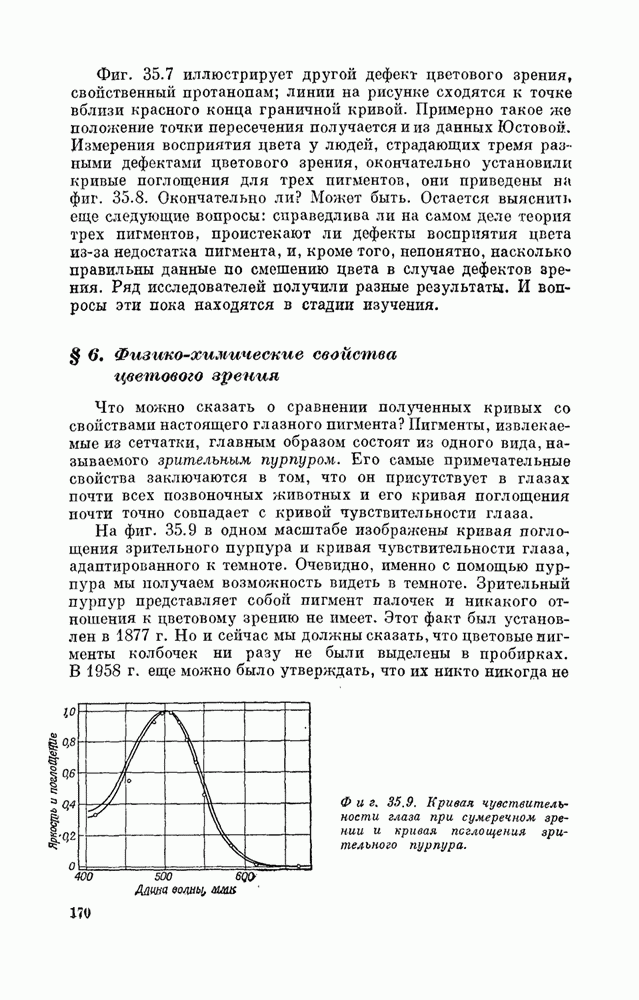
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии