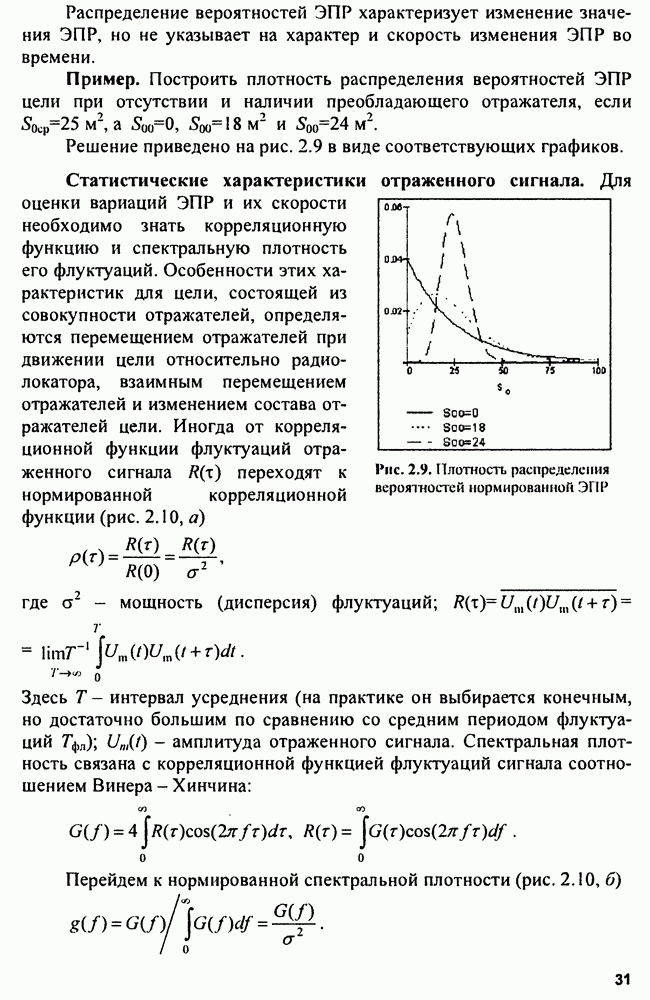
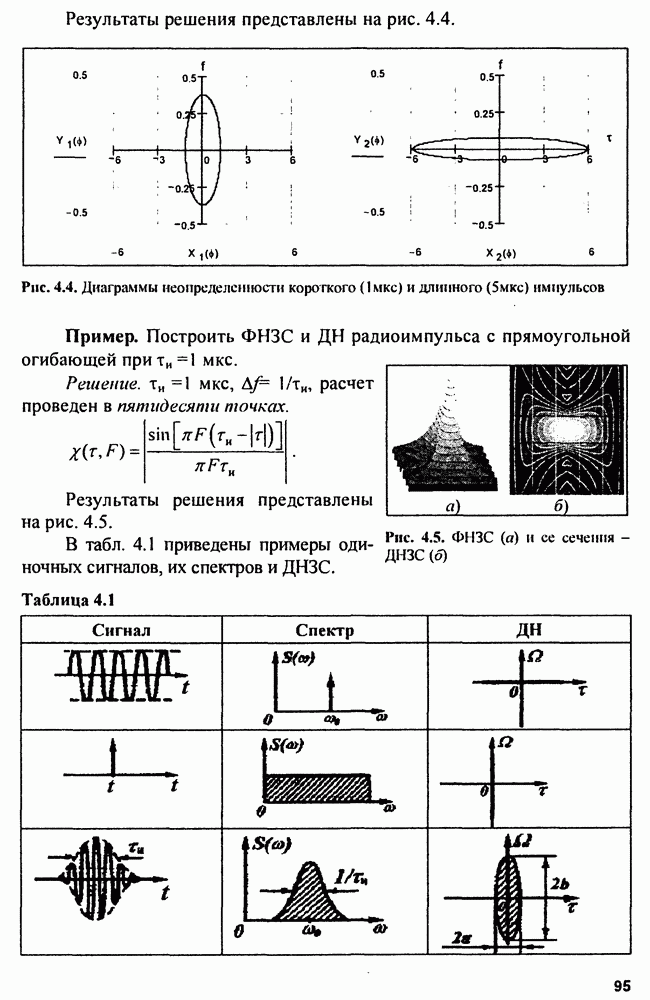
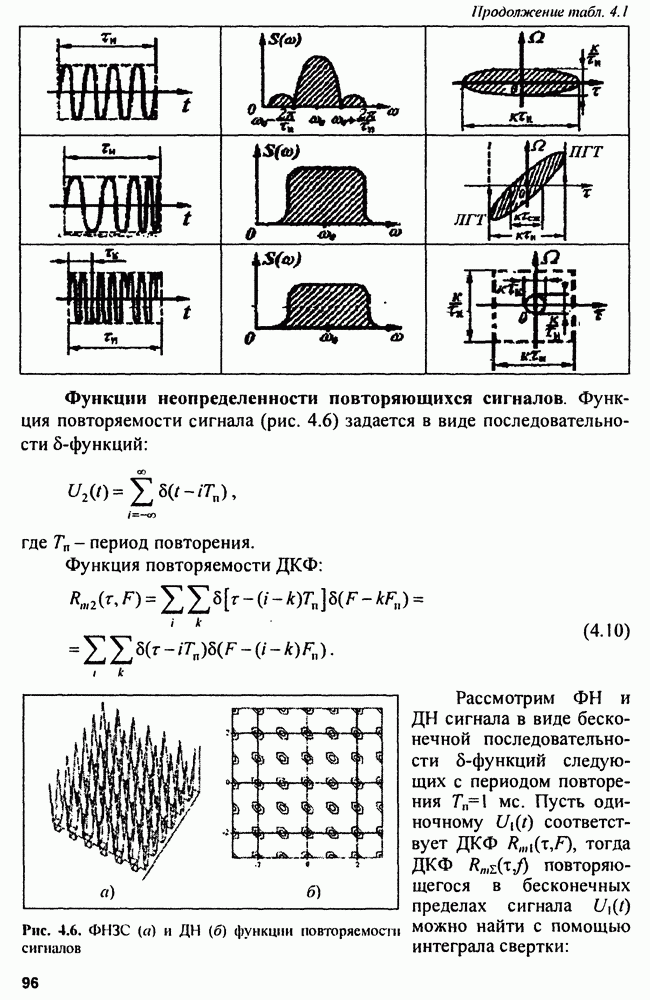
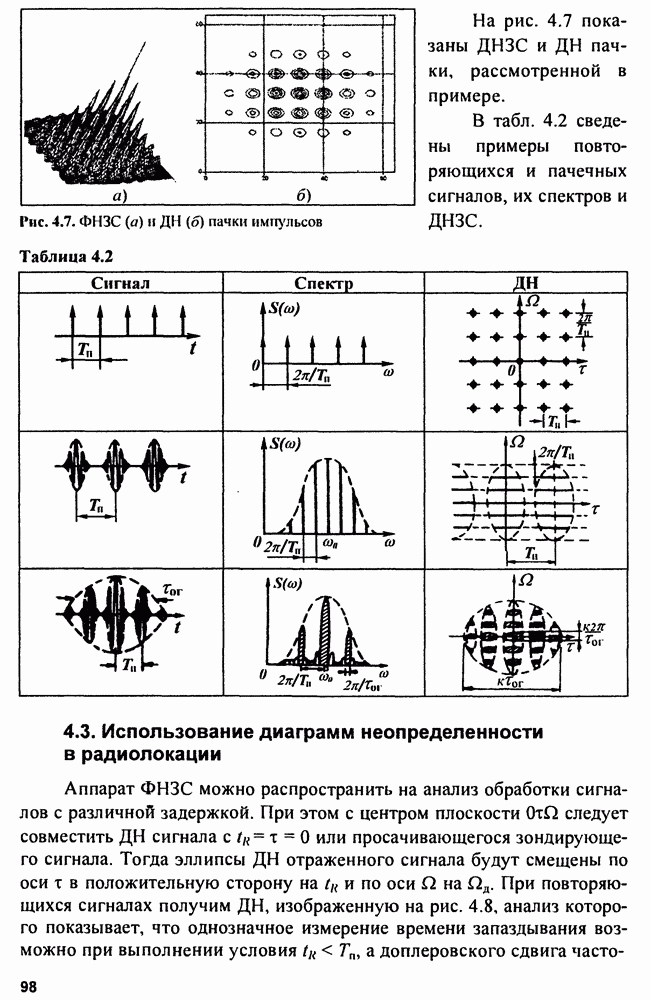
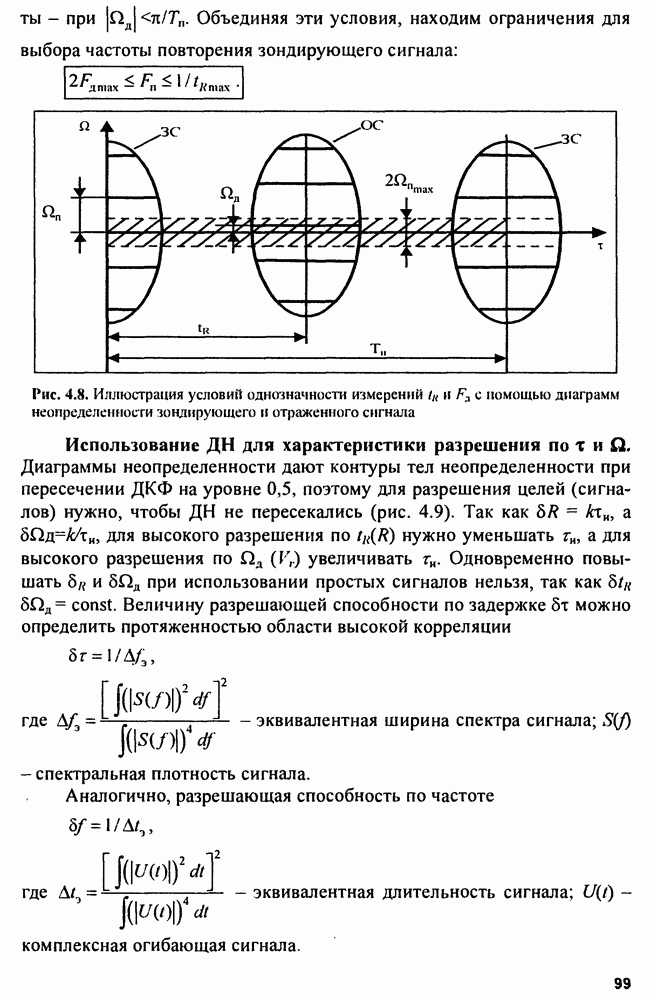
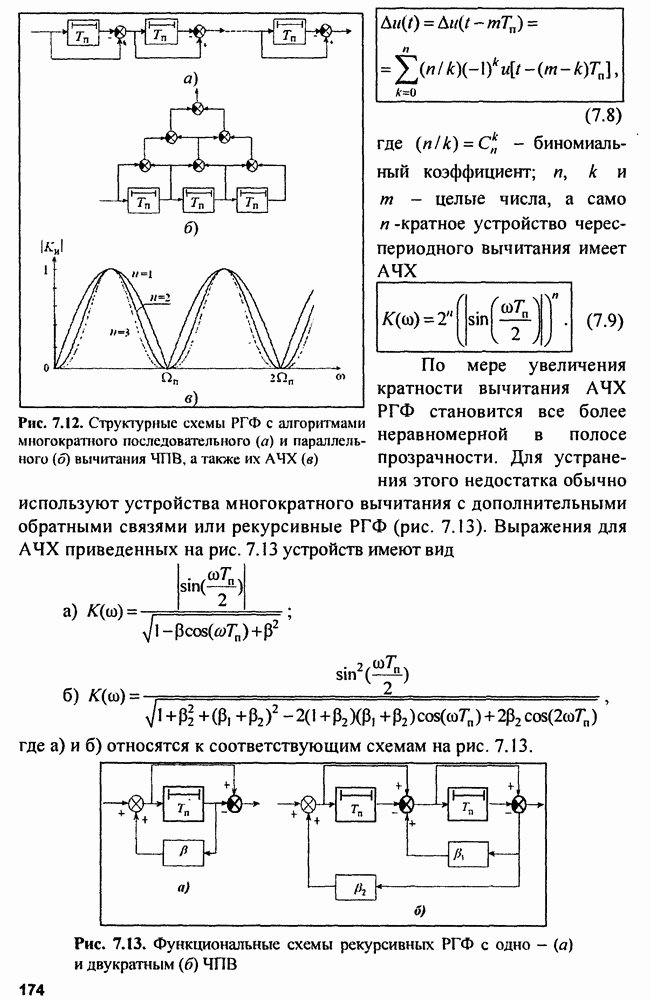
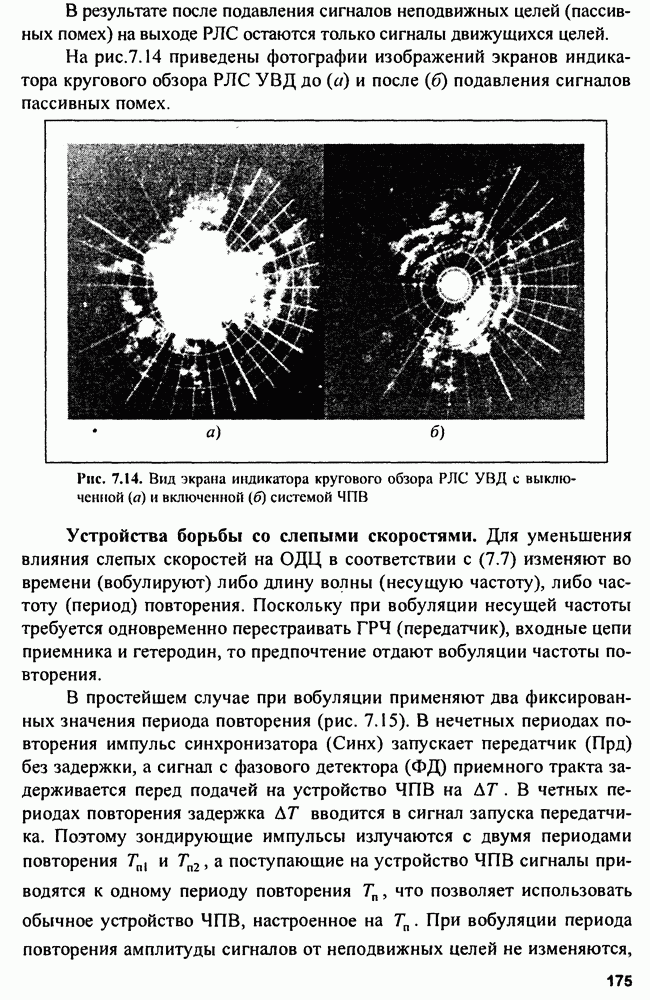
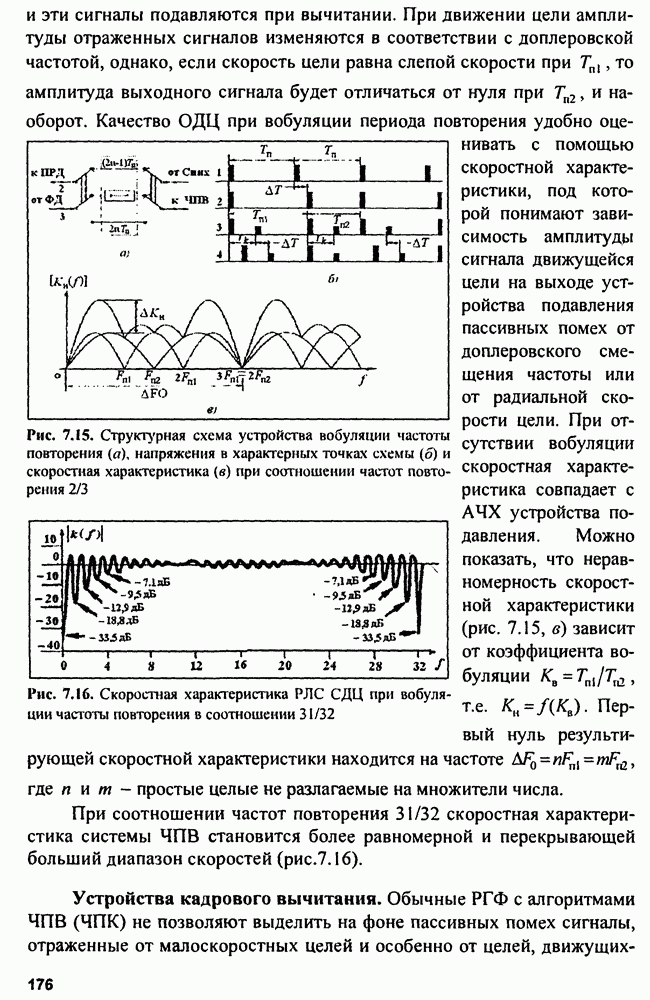
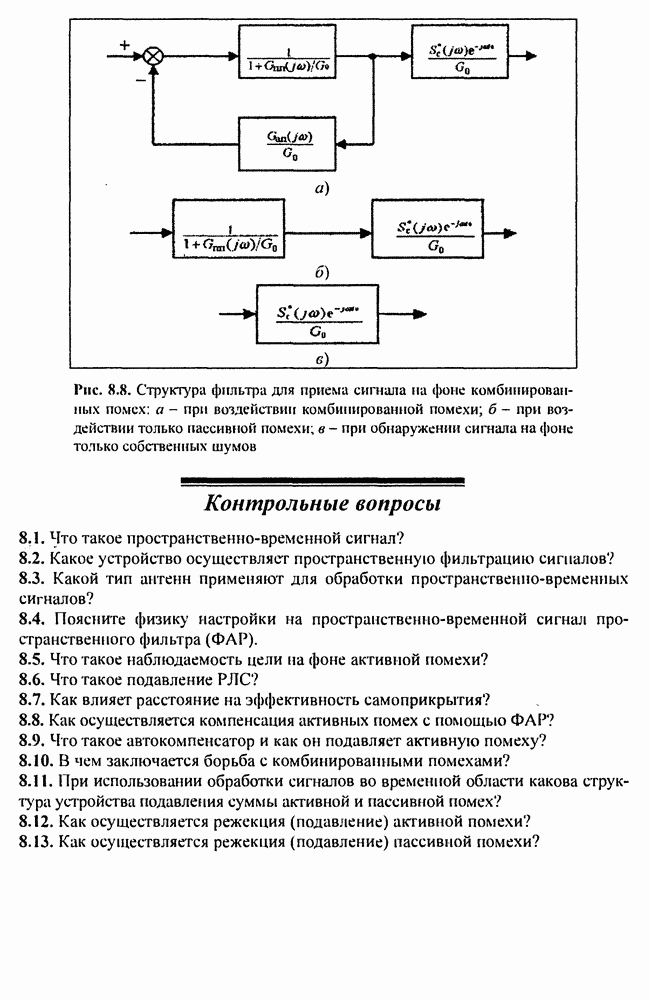
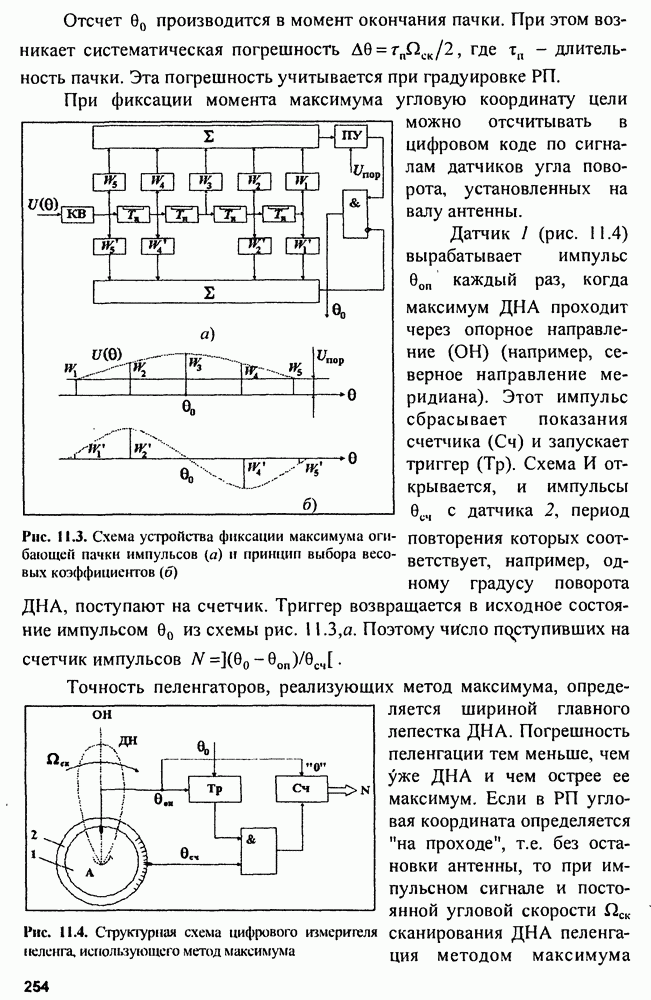
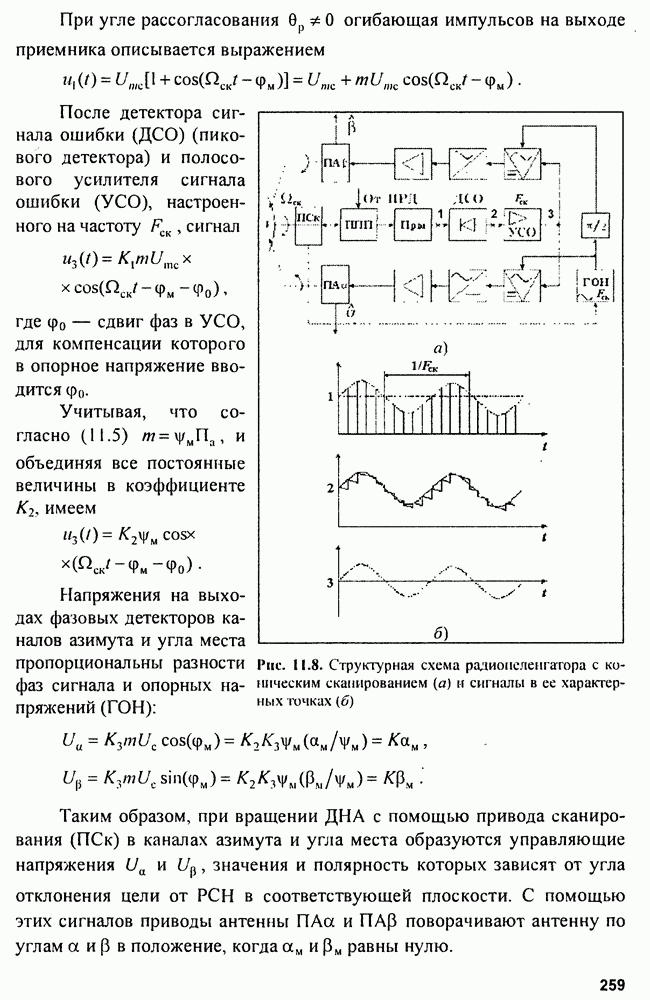
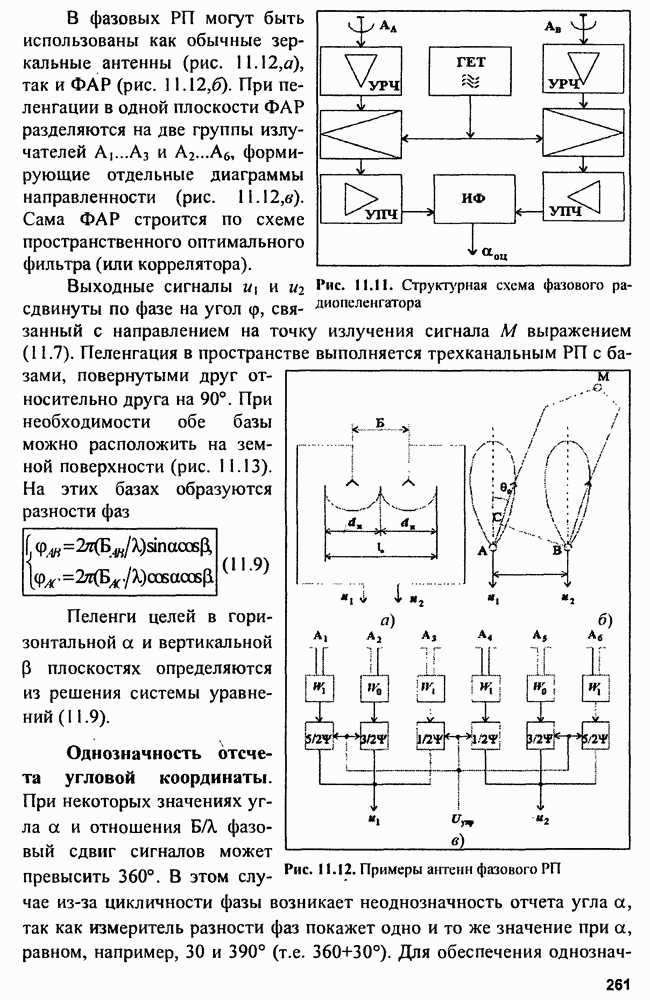
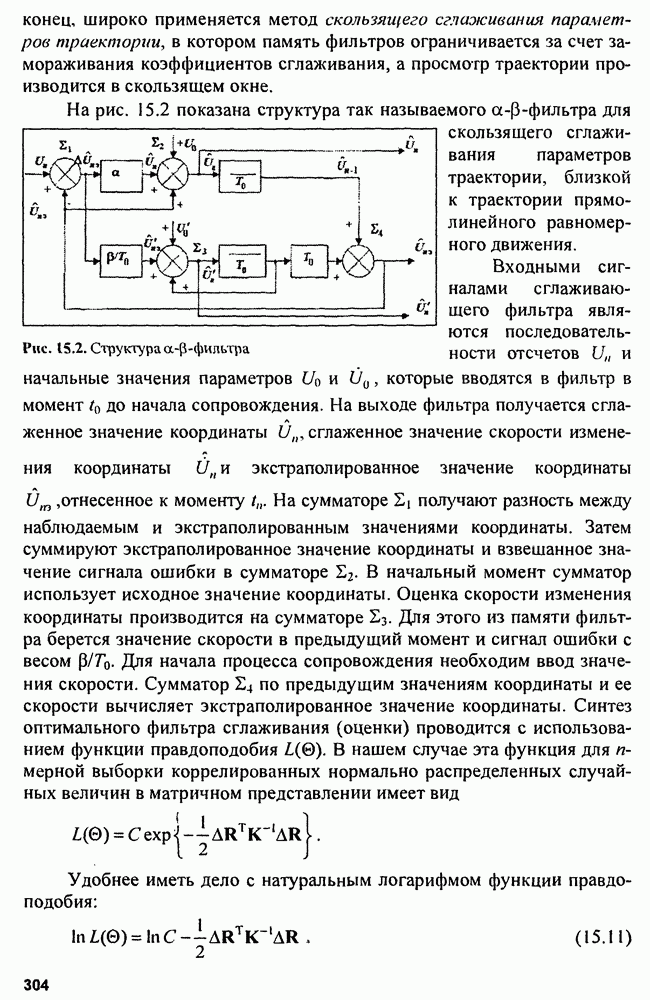
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
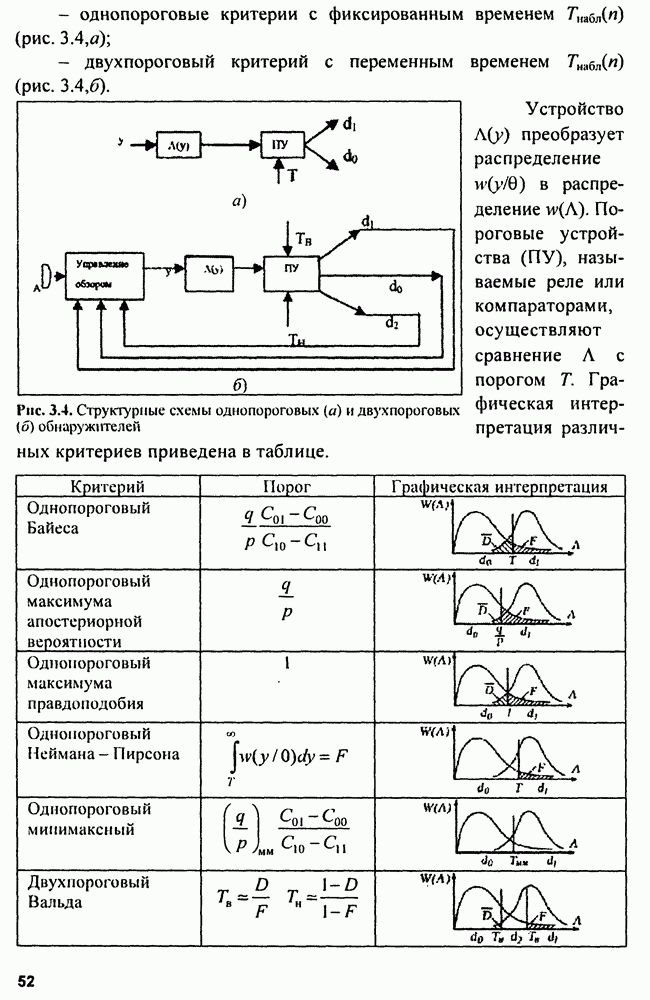
3.4. Синтез оптимальных обнаружителей
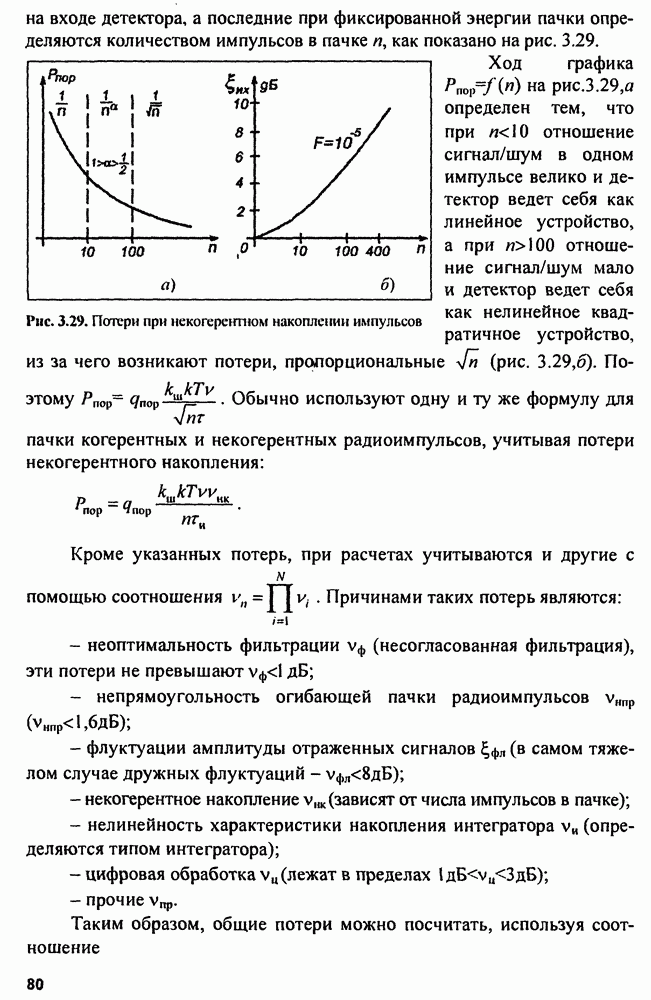
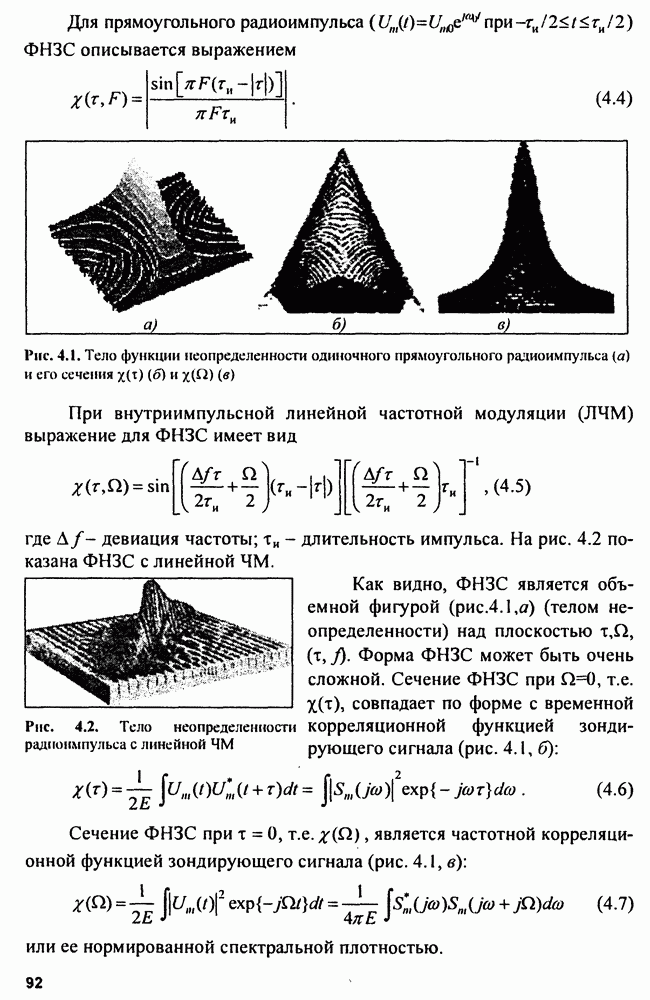
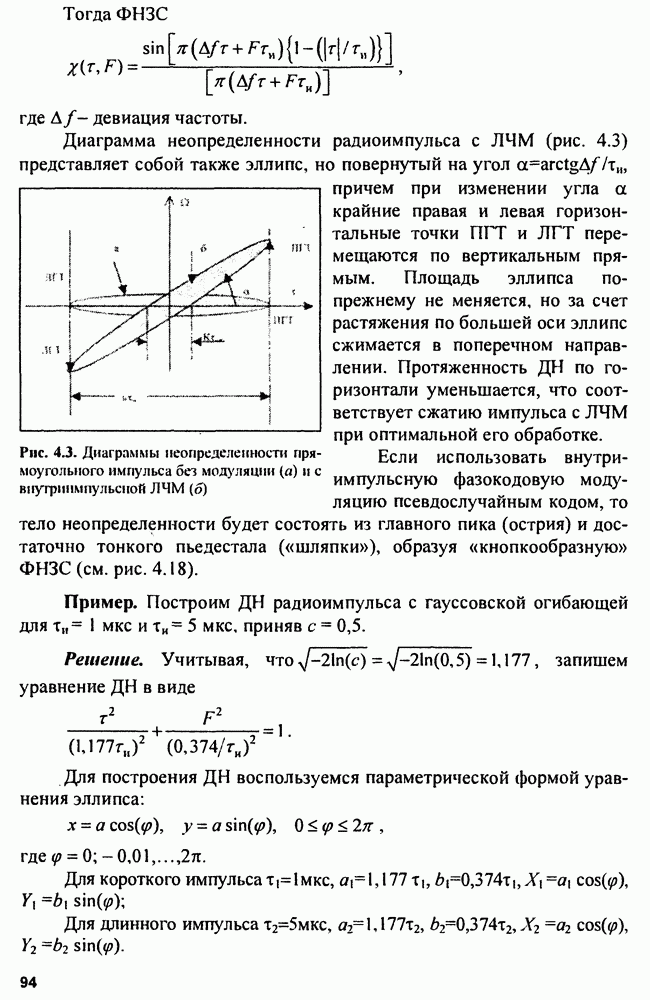
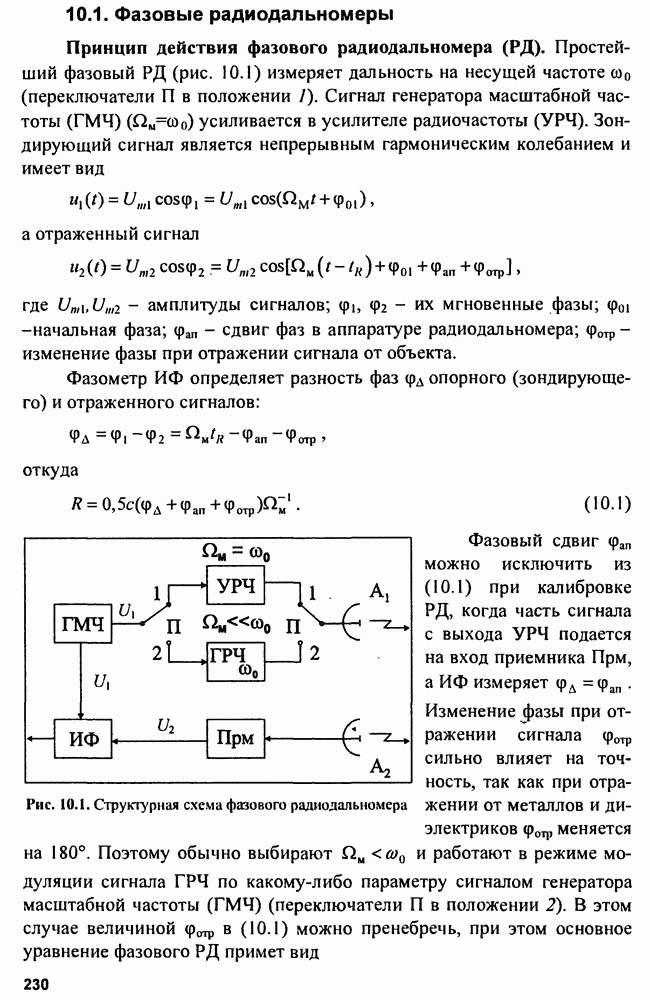
Обнаружение одиночного радиоимпульса с полностью известными параметрами на фоне «белого» шума. «Белый» шум складывается с сигналом аддитивно:  при этом
при этом 

- мощность шума на входе приемника.
В пределах полосы пропускания приемника  где
где  коэффициент шума приемника
коэффициент шума приемника  Для прикидочных расчетов можно ориентироваться на следующие значения коэффициентов шума.
Для прикидочных расчетов можно ориентироваться на следующие значения коэффициентов шума.

Пусть наблюдение входной реализации ведется дискретно через интервалы времени  в моменты времени
в моменты времени  Поскольку
Поскольку  отсчеты в моменты
отсчеты в моменты  независимы:
независимы:  . В этом случае «белый» шум имеет нормальный закон распределения вероятностей
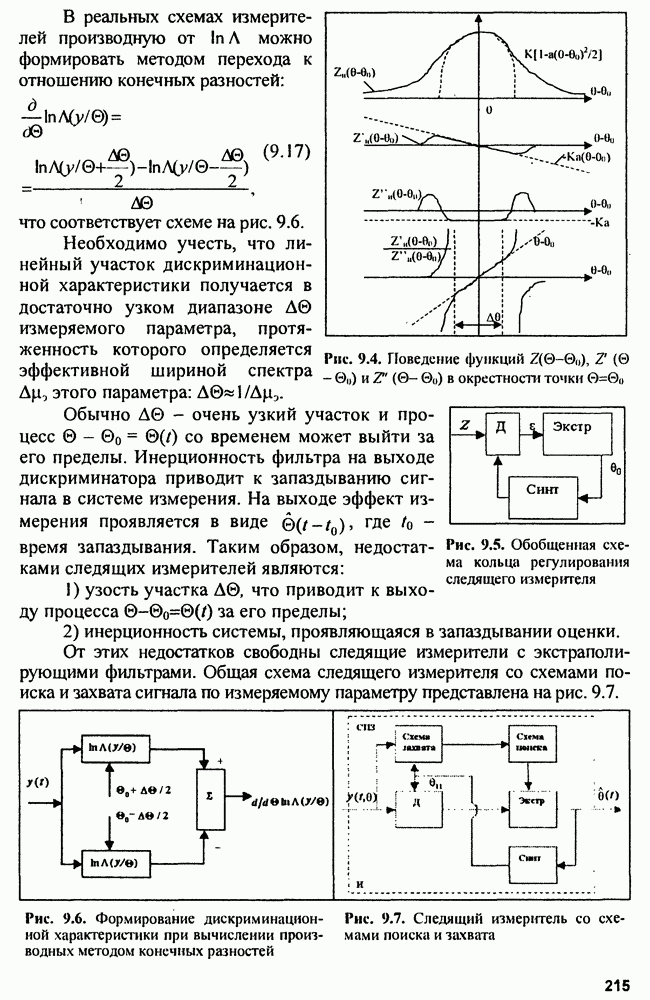
. В этом случае «белый» шум имеет нормальный закон распределения вероятностей  и плотность распределения вероятностей
и плотность распределения вероятностей  имеет вид
имеет вид

В силу независимости отсчетов совместная ПРВ

При  отсчеты входной выборки
отсчеты входной выборки  поэтому
поэтому  и тогда
и тогда

С учетом независимости отсчетов

Подставляя  в выражение для
в выражение для  получаем
получаем

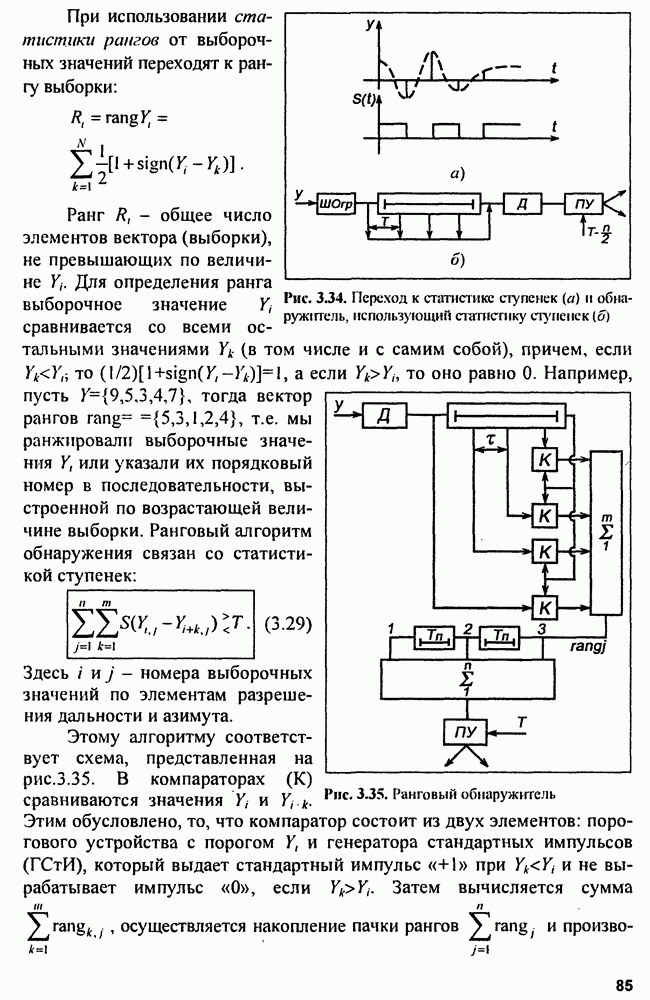
Можно сравнивать А с порогом решения  можно также сравнивать монотонную функцию от А с такой же функцией порога. Например, часто используют сравнение
можно также сравнивать монотонную функцию от А с такой же функцией порога. Например, часто используют сравнение  Учитывая, что
Учитывая, что

и обозначая  получаем алгоритм оптимального обнаружения икук
получаем алгоритм оптимального обнаружения икук 
Если перейти к непрерывному времени, то нужно устремить интервал дискретизации к нулю  при этом
при этом 
Обозначим  и заметим, что это корреляционный интеграл,
и заметим, что это корреляционный интеграл,  энергия сигнала. Объединяя
энергия сигнала. Объединяя  получаем алгоритм обнаружения:
получаем алгоритм обнаружения:

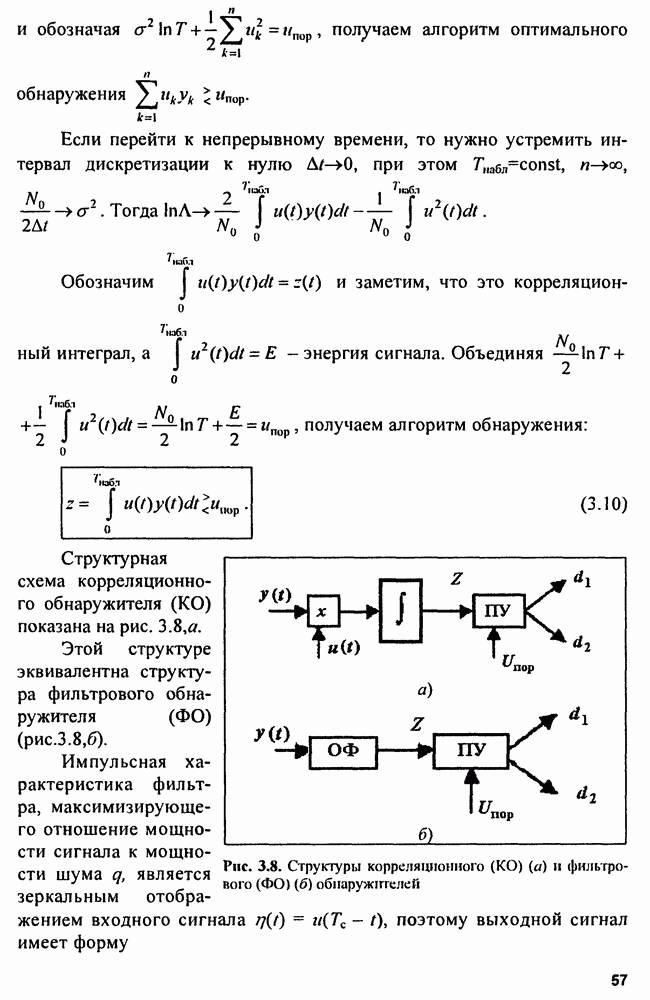
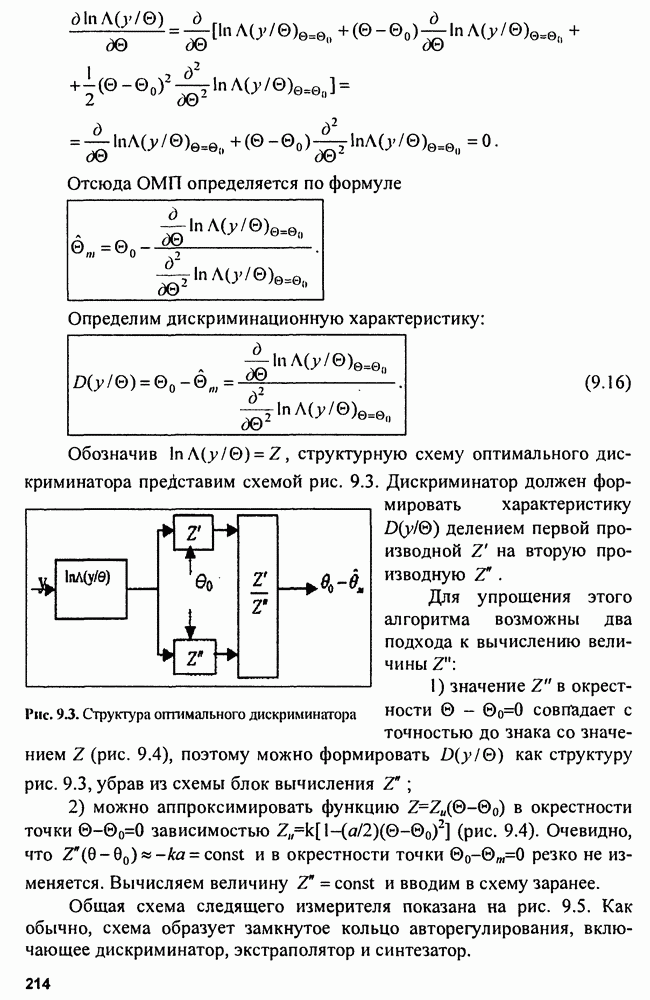
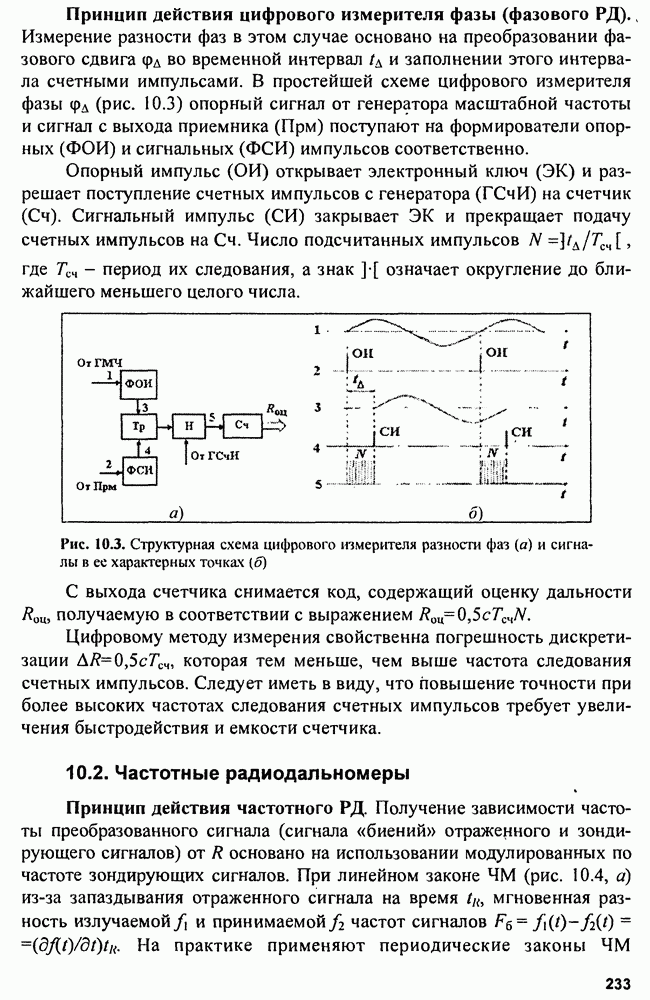
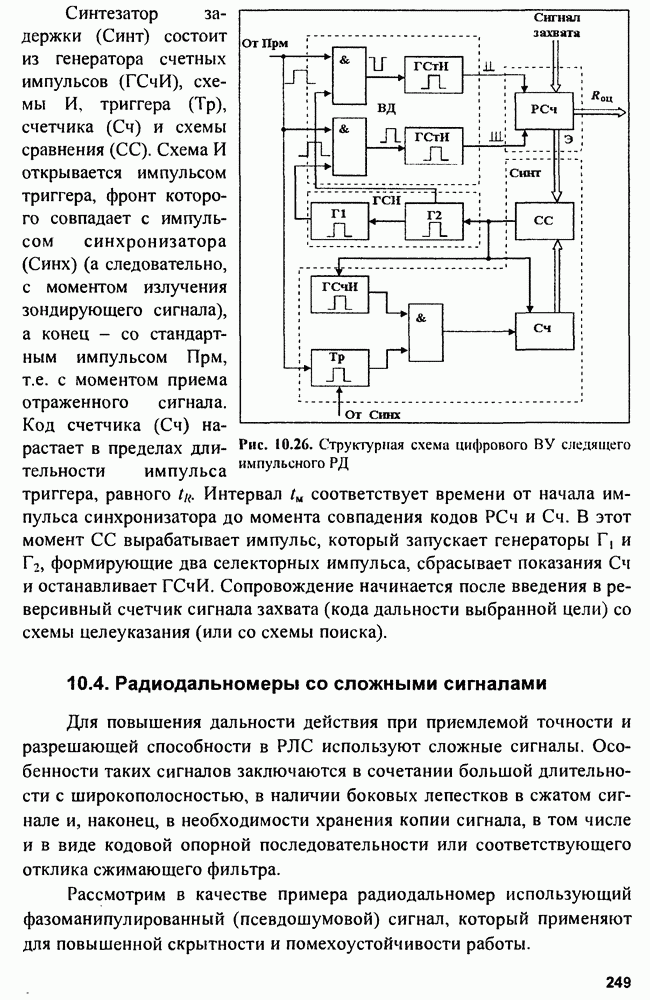
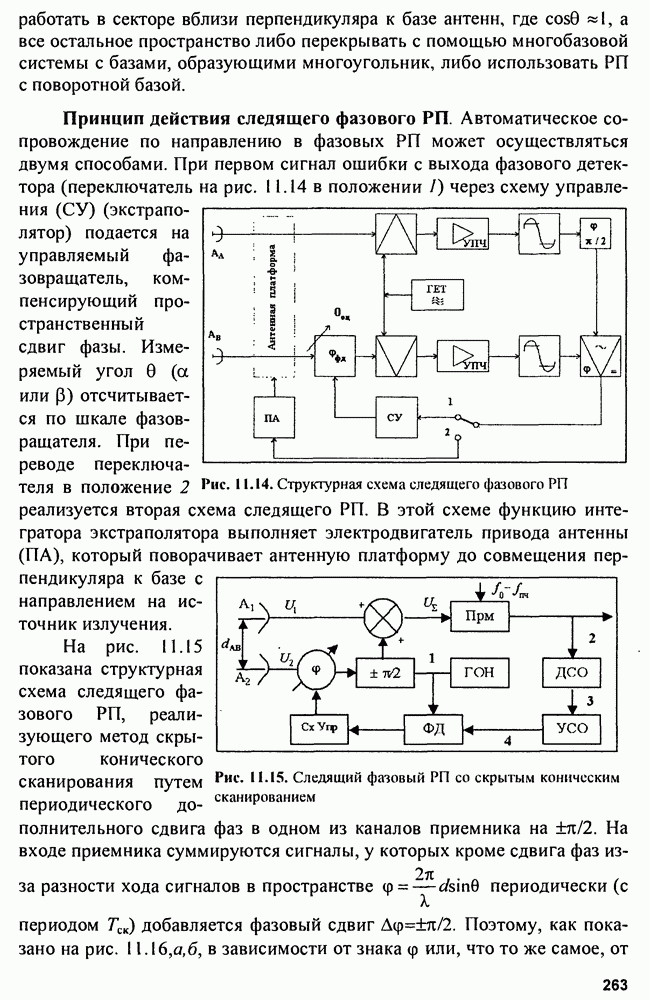
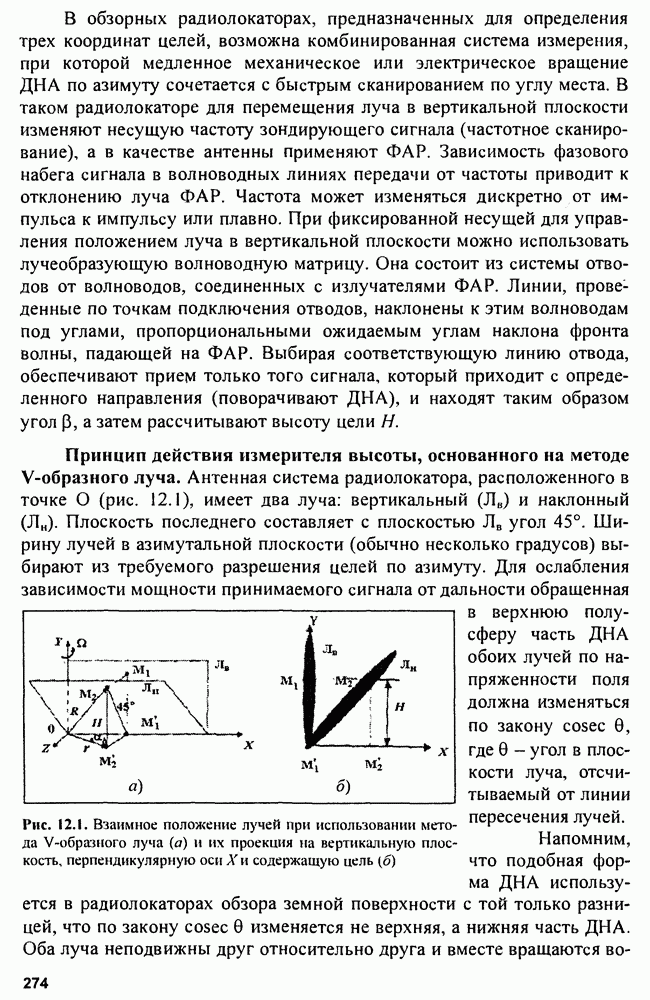
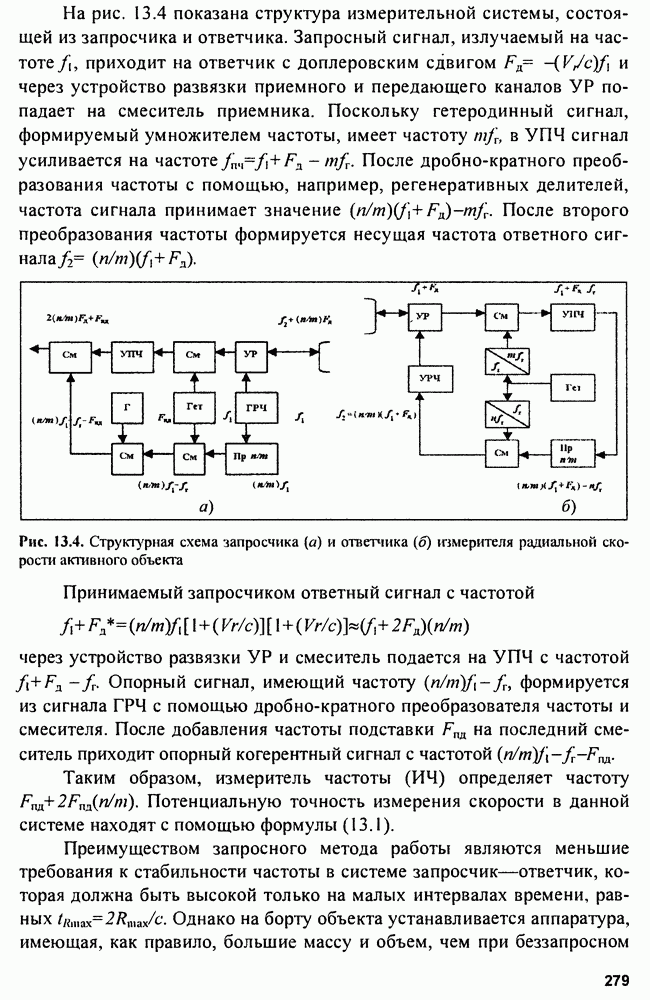
Структурная схема корреляционного обнаружителя (КО) показана на рис. 3.8, а.

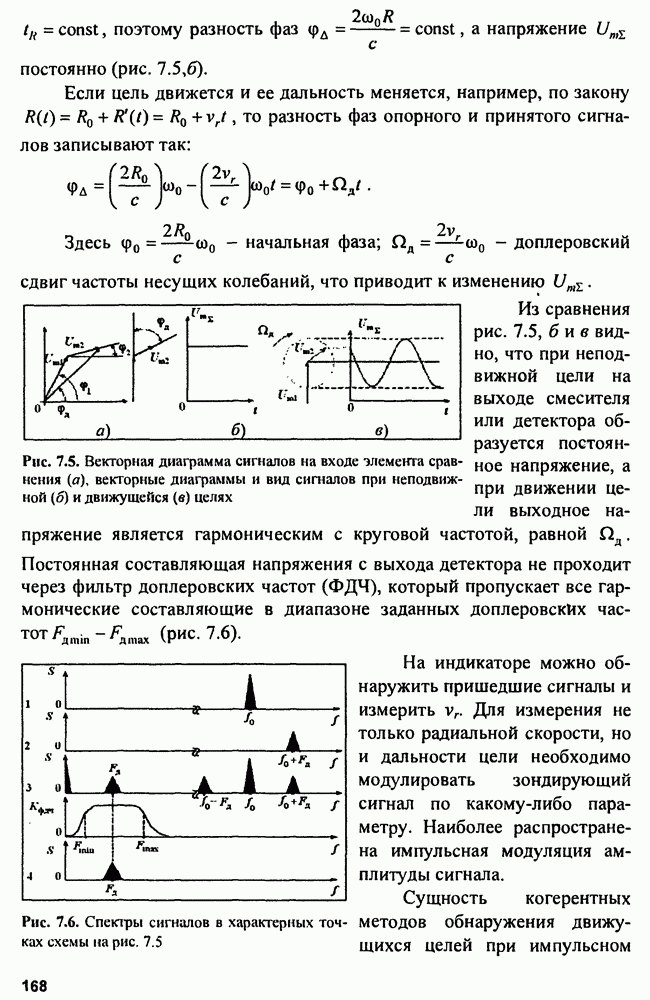
Рис. 3.8. Структуры корреляционного (КО) (а) и фильтрового (ФО) (б) обнаружителей
Этой структуре эквивалентна структура фильтрового обнаружителя 
Импульсная характеристика фильтра, максимизирующего отношение мощности сигнала к мощности шума  является зеркальным отображением входного сигнала
является зеркальным отображением входного сигнала  поэтому выходной сигнал имеет форму
поэтому выходной сигнал имеет форму

Соотношение для коэффициента передачи согласованного фильтра получаем по формуле

при этом формируется максимальное отношение сигнала к шуму:  (при реальных шумах в диапазоне частот
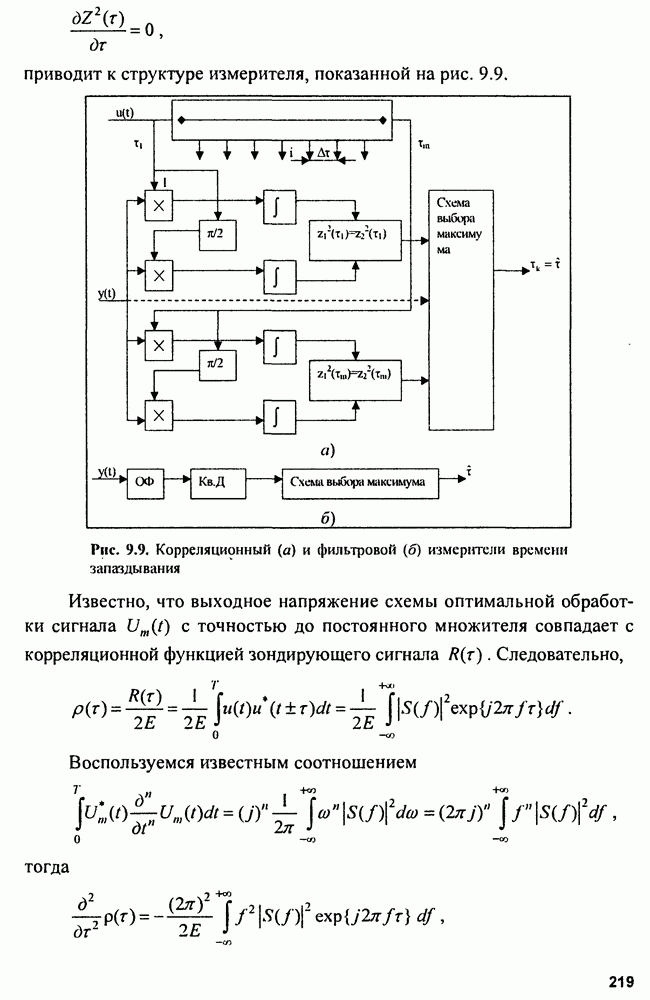
(при реальных шумах в диапазоне частот  Поскольку выходной сигнал обнаружителей, описываемый корреляционным интегралом, зависит от времени запаздывания
Поскольку выходной сигнал обнаружителей, описываемый корреляционным интегралом, зависит от времени запаздывания  и расстройки по частоте
и расстройки по частоте  корреляционный обнаружитель оказывается многоканальным по дальности и скорости. Фильтровой обнаружитель многоканален только по скорости.
корреляционный обнаружитель оказывается многоканальным по дальности и скорости. Фильтровой обнаружитель многоканален только по скорости.
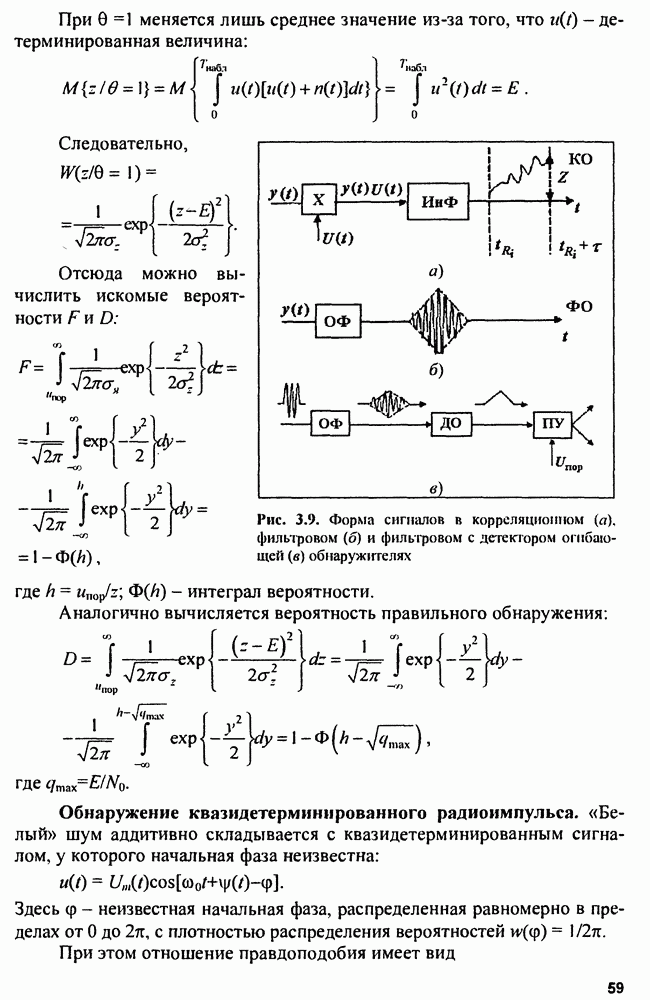
В КО на выходе инерционного фильтра  будет нарастающее напряжение в момент равное
будет нарастающее напряжение в момент равное  в то время как в ФО на выходе возникает радиоимпульс, по форме совпадающий с корреляционной функцией входного сигнала. Для устранения колебаний внутри огибающей радиоимпульса на выходе
в то время как в ФО на выходе возникает радиоимпульс, по форме совпадающий с корреляционной функцией входного сигнала. Для устранения колебаний внутри огибающей радиоимпульса на выходе  ставят детектор огибающей
ставят детектор огибающей  (рис. 3.9, а-г).
(рис. 3.9, а-г).
Для определения величины вероятностей правильного обнаружения  и ложной тревоги
и ложной тревоги  надо знать плотности распределения вероятностей величины
надо знать плотности распределения вероятностей величины  на входе порогового устройства при
на входе порогового устройства при  Если
Если  то на входе - только шум
то на входе - только шум  поэтому
поэтому  Операция интегрирования является линейной,
Операция интегрирования является линейной,  детерминированная величина. Следовательно
детерминированная величина. Следовательно  будет иметь то же распределение вероятностей, что и
будет иметь то же распределение вероятностей, что и  т.е. нормальное распределение с параметрами
т.е. нормальное распределение с параметрами

Таким образом,

При  меняется лишь среднее значение из-за того, что
меняется лишь среднее значение из-за того, что  детерминированная величина:
детерминированная величина:

Следовательно, 


Рис. 3.9. Форма сигналов в корреляционном (а), фильтровом (б) и фильтровом с детектором огибающей (в) обнаружителях
Отсюда можно вычислить искомые вероятности 

где  интеграл вероятности.
интеграл вероятности.
Аналогично вычисляется вероятность правильного обнаружения:

где 
Обнаружение квазидетерминированного радиоимпульса. «Белый» шум аддитивно складывается с квазидетерминированным сигналом, у которого начальная фаза неизвестна:

Здесь  неизвестная начальная фаза, распределенная равномерно в пределах от
неизвестная начальная фаза, распределенная равномерно в пределах от  до
до  с плотностью распределения вероятностей
с плотностью распределения вероятностей  При этом отношение правдоподобия имеет вид
При этом отношение правдоподобия имеет вид

Представим сигнал в виде двух ортогональных составляющих 

где  квадратурные корреляционные интегралы.
квадратурные корреляционные интегралы.
Можно показать, что  где
где  следовательно,
следовательно,

Усредняя по неизвестной начальной фазе  получаем
получаем

Поскольку  а модифицированная функция Бесселя
а модифицированная функция Бесселя  монотонная функция х, можно перейти к следующему алгоритму обнаружения:
монотонная функция х, можно перейти к следующему алгоритму обнаружения:

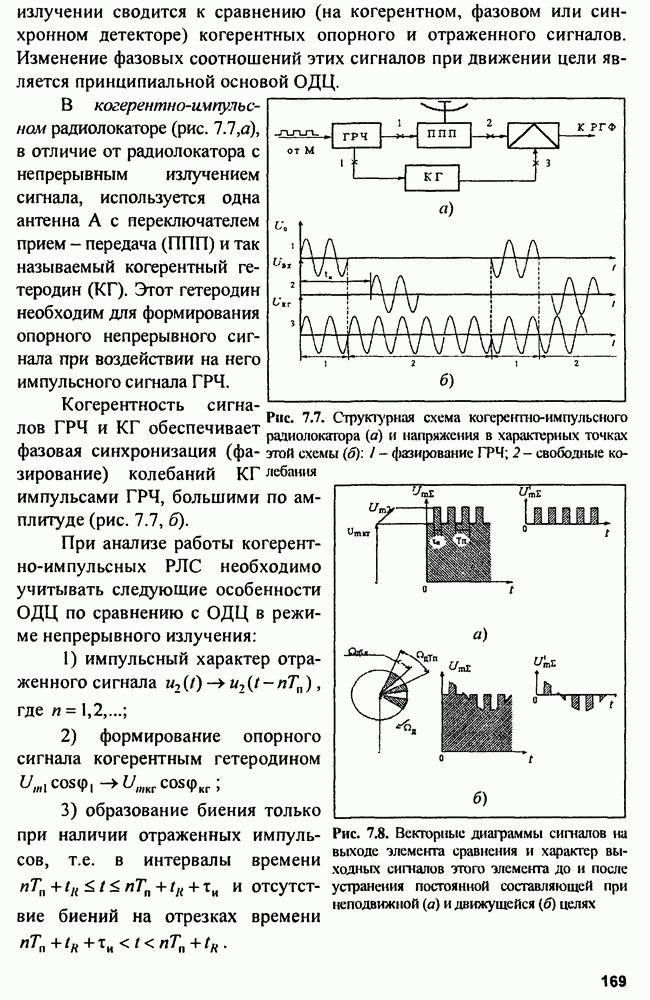
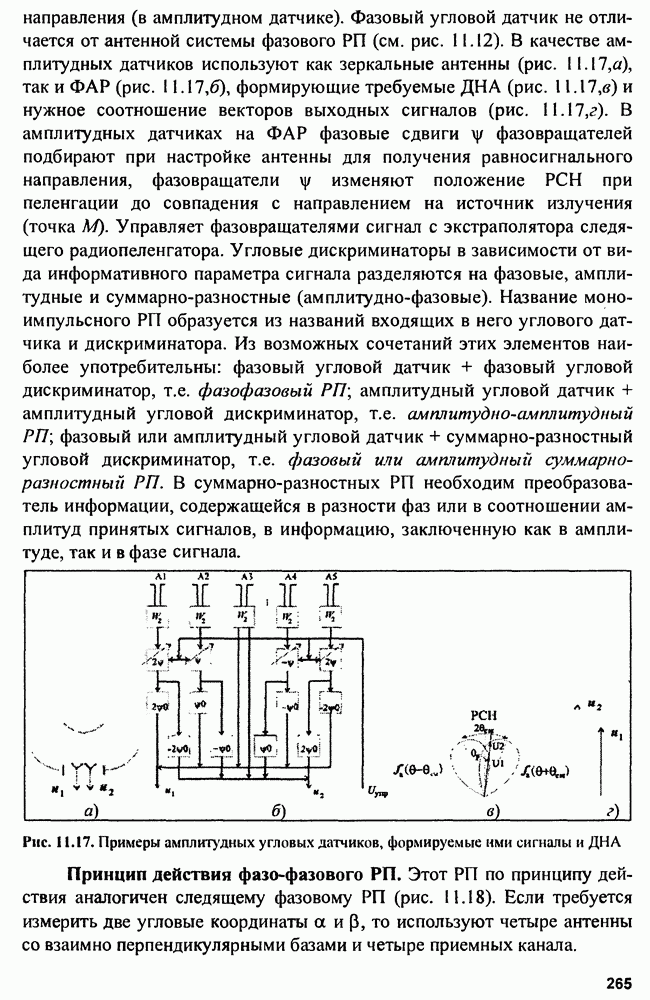
что соответствует структуре  показанной на рис. 3.10,а.
показанной на рис. 3.10,а.
Те же операции можно осуществить с помощью  если продетектировать колебания на выходе
если продетектировать колебания на выходе  с импульсной переходной характеристикой
с импульсной переходной характеристикой  и выделить огибающую
и выделить огибающую  (см. рис. 3.10, б).
(см. рис. 3.10, б).
Так как шум и смесь сигнала с шумом распределены на выходе детектора огибающей (ДО) по законам Рэлея и обобщенного Рэлея (Райса), вероятности

где  нормированный порог.
нормированный порог.

Рис. 3.10. Корреляционный (а) и фильтровой (б) обнаружители радиоимпульса с неизвестной начальной фазой
Обнаружение флуктуирующего радиоимпульса. «Белый» шум складывается с радиоимпульсом, имеющим неизвестную начальную фазу и флуктуирующую амплитуду:  Плотности распределения вероятностей амплитуды и фазы задаются соотношениями
Плотности распределения вероятностей амплитуды и фазы задаются соотношениями  закон распределения Рэлея.
закон распределения Рэлея.

Усредняя А по  получаем
получаем

где  энергия сигнала при
энергия сигнала при 
Средняя энергия сигнала  . С учетом этого вычисляем отношение правдоподобия:
. С учетом этого вычисляем отношение правдоподобия:
Воспользуемся интегралом

и получим окончательное соотношение

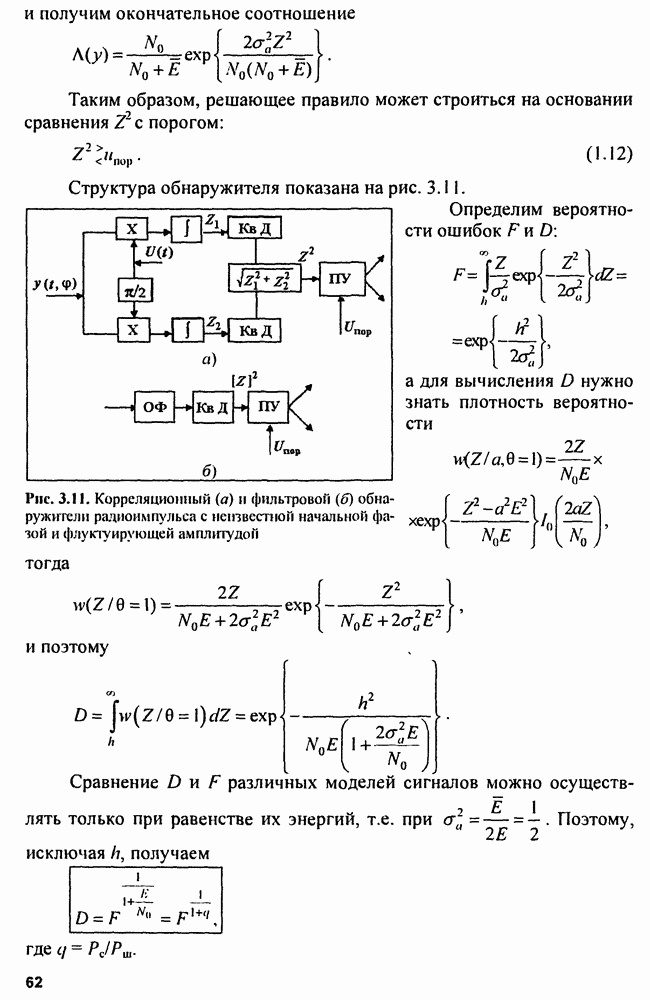
Таким образом, решающее правило может строиться на основании сравнения  с порогом:
с порогом:

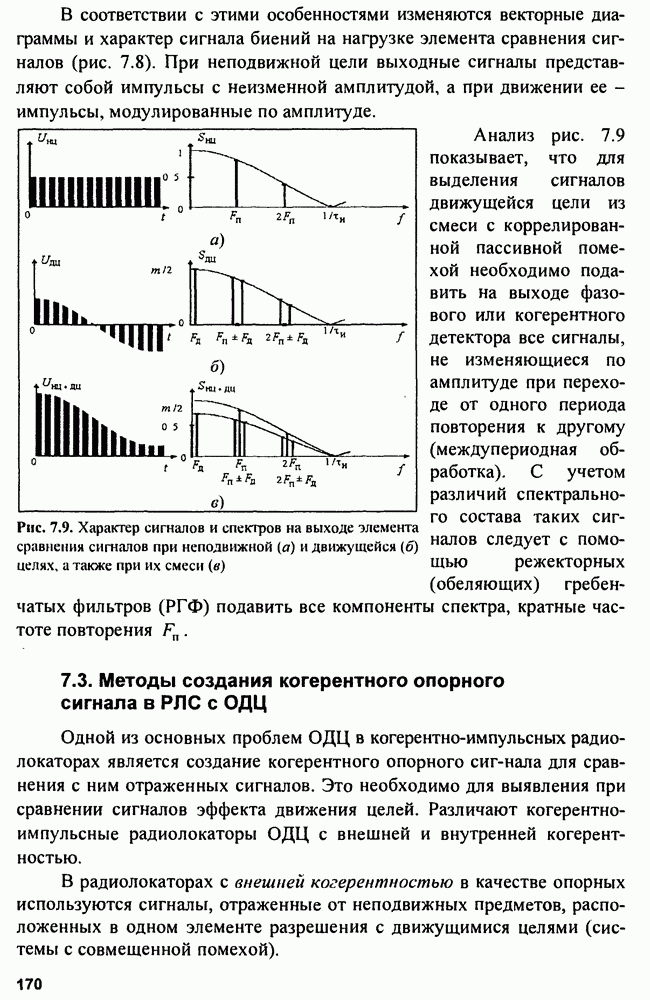
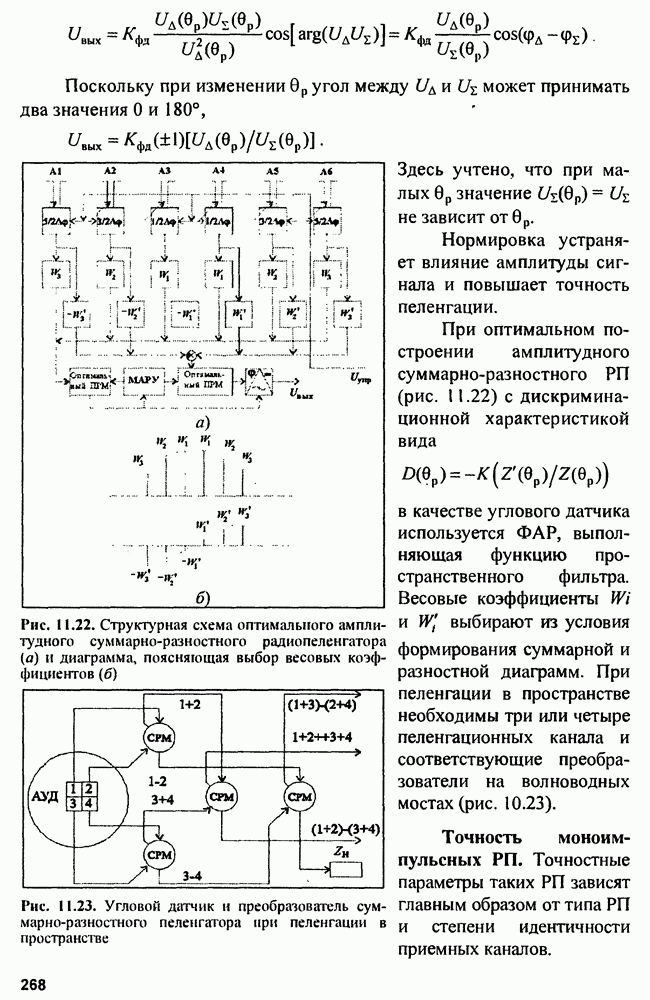
Структура обнаружителя показана на рис. 3.11.

Рис. 3.11. Корреляционный (а) и фильтровой (б) обнаружители радиоимпульса с неизвестной начальной фазой и флуктуирующей амплитудой
Определим вероятности ошибок 

а для вычисления  нужно знать плотность вероятности
нужно знать плотность вероятности

тогда

и поэтому

Сравнение  различных моделей сигналов можно осуществлять только при равенстве их энергий, т.е. при
различных моделей сигналов можно осуществлять только при равенстве их энергий, т.е. при  Поэтому, исключая
Поэтому, исключая  получаем
получаем 

Обнаружение флуктуирующего радиоимпульса с неизвестным (случайным) временем прихода ... и с расстройкой по частоте В этом случае сигнал имеет вид

где  случайные величины с известными априорными распределениями вероятностей.
случайные величины с известными априорными распределениями вероятностей.
Тогда нужно найти  Поскольку известно
Поскольку известно  введем в
введем в  новые случайные параметры
новые случайные параметры  и усредним
и усредним  по этим параметрам. При этом будем считать, что они изменяют свои значения дискретно, т.е.
по этим параметрам. При этом будем считать, что они изменяют свои значения дискретно, т.е.  с вероятностями
с вероятностями 
Определить  можно как и ранее:
можно как и ранее:

поэтому

Таким образом, синтезированный обнаружитель состоит из  каналов по времени запаздывания (дальности) и
каналов по времени запаздывания (дальности) и  каналов по частоте (скорости). В действительности и время запаздывания, и смещение частоты - непрерывные величины, поэтому многоканальный обнаружитель является квазиоптимальным. Только по мере увеличения числа каналов (в пределе до бесконечности) он будет приближаться к оптимальному. Многоканальность по дальности необходима при использовании
каналов по частоте (скорости). В действительности и время запаздывания, и смещение частоты - непрерывные величины, поэтому многоканальный обнаружитель является квазиоптимальным. Только по мере увеличения числа каналов (в пределе до бесконечности) он будет приближаться к оптимальному. Многоканальность по дальности необходима при использовании  в этом случае для каждого канала формируется свой опорный сигнал, сдвинутый по сравнению с соседними каналами на величину элемента разрешения по времени
в этом случае для каждого канала формируется свой опорный сигнал, сдвинутый по сравнению с соседними каналами на величину элемента разрешения по времени  . В ФО из-за инвариантности согласованного фильтра ко времени прихода сигнала многоканальность по дальности не нужна, а многоканальность по скорости обеспечивается набором (гребенкой) фильтров, расстроенных друг относительно друга на величину элемента разрешения по частоте (скорости)
. В ФО из-за инвариантности согласованного фильтра ко времени прихода сигнала многоканальность по дальности не нужна, а многоканальность по скорости обеспечивается набором (гребенкой) фильтров, расстроенных друг относительно друга на величину элемента разрешения по частоте (скорости) 
Обнаружение пачки когерентных радиоимпульсов. Реализации аддитивной смеси «белого» шума с когерентными радиоимпульсами пачки в каждом периоде повторения имеют ту особенность, что шум в них не коррелирован, так как время корреляции шума  меньше периода повторения
меньше периода повторения 

Плотности распределения вероятностей

поэтому

Соответственно 
В согласии со случаем обнаружения для модели сигнала с полностью известными параметрами получаем

следовательно,

откуда

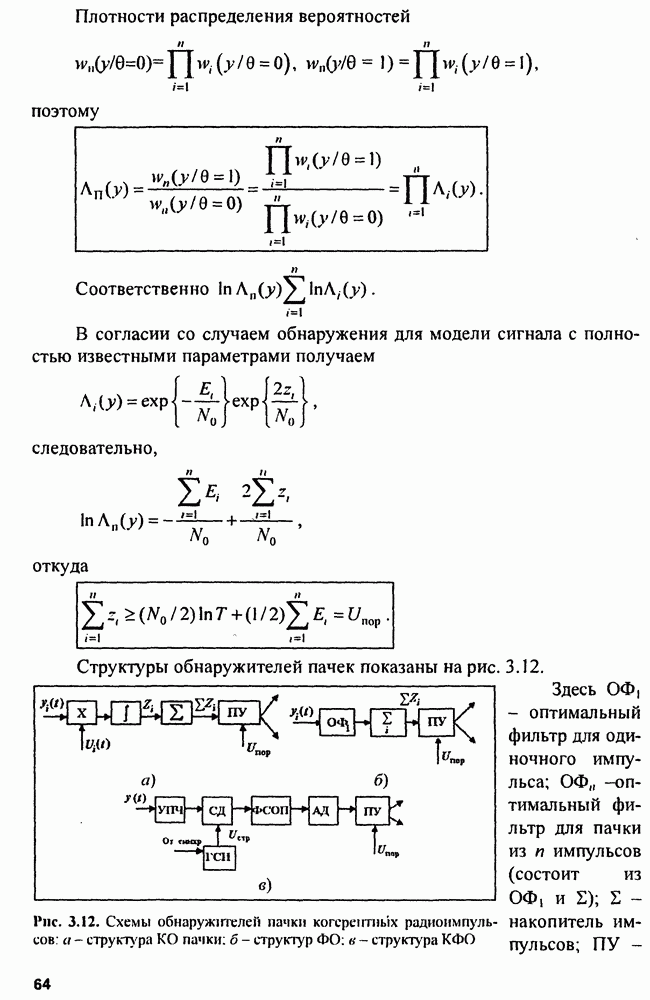
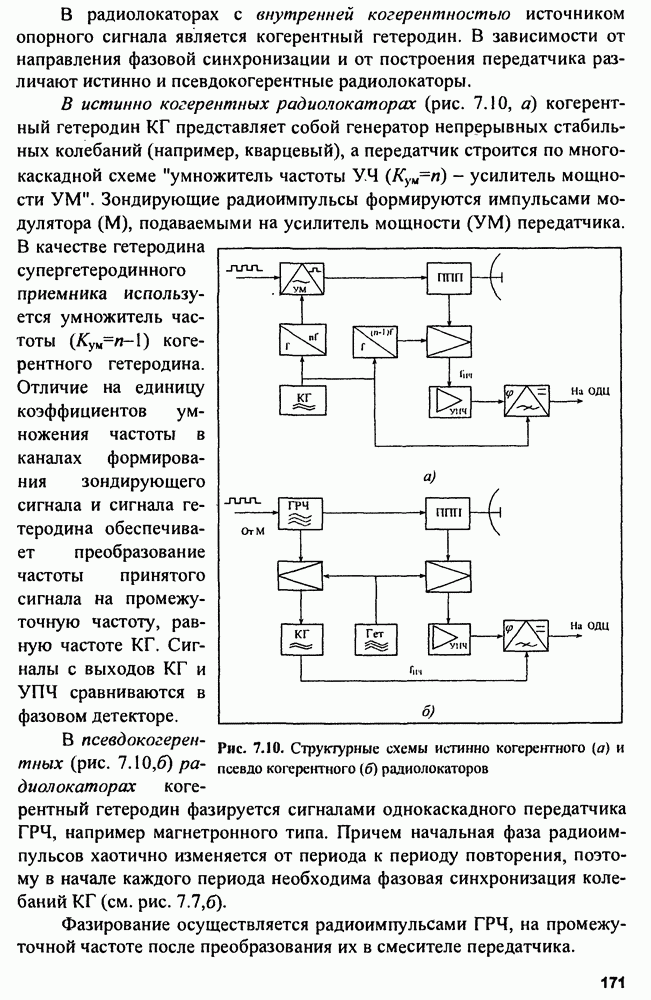
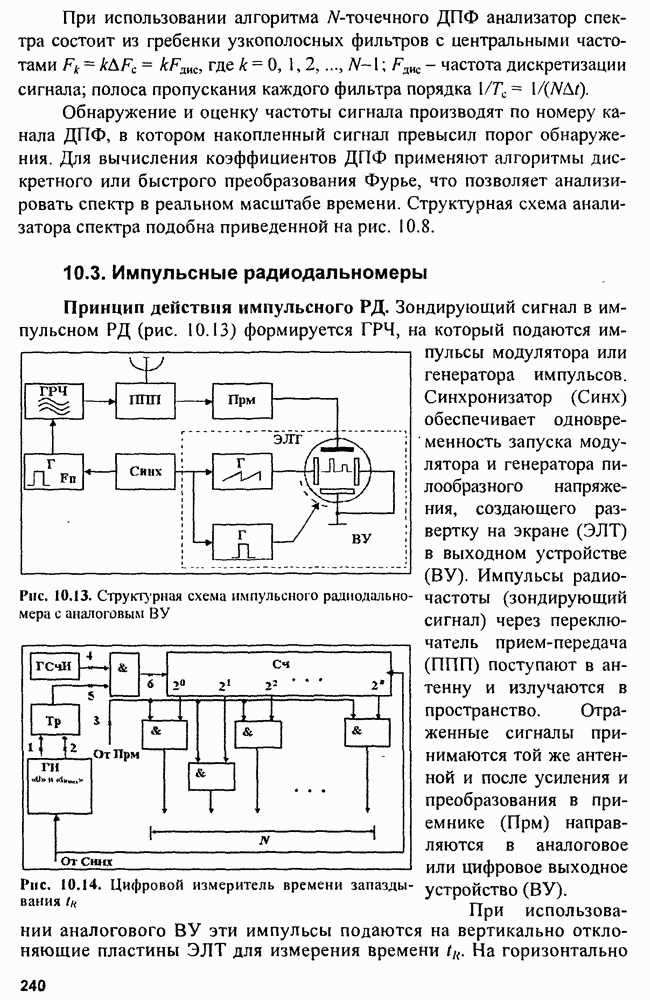
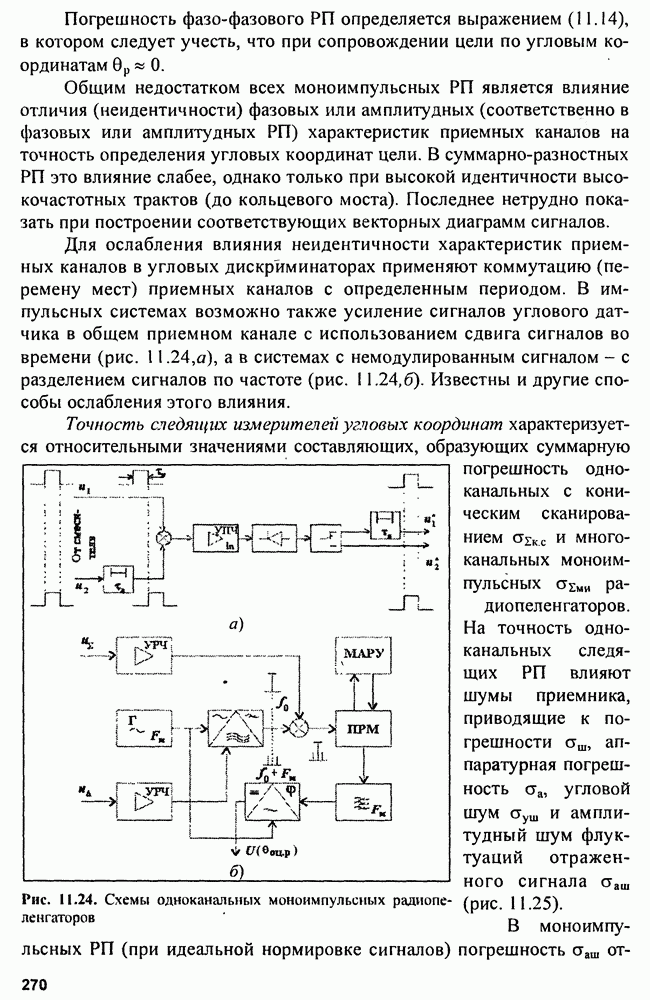
Структуры обнаружителей пачек показаны на рис. 3.12.
Здесь  оптимальный фильтр для одиночного импульса;
оптимальный фильтр для одиночного импульса;  оптимальный фильтр для пачки из
оптимальный фильтр для пачки из  импульсов (состоит из
импульсов (состоит из  и
и  накопитель импульсов; ПУ
накопитель импульсов; ПУ

Рис. 3.12. Схемы обнаружителей памкн когерентных радиоимпульсов: а - структура КО пачки; б - структур ФО: в - структура КФО
пороговое устройство; СД - селектор дальности; ГСИ - генератор стробирующих импульсов; ФСОП - фильтр, согласованный с огибающей пачки.
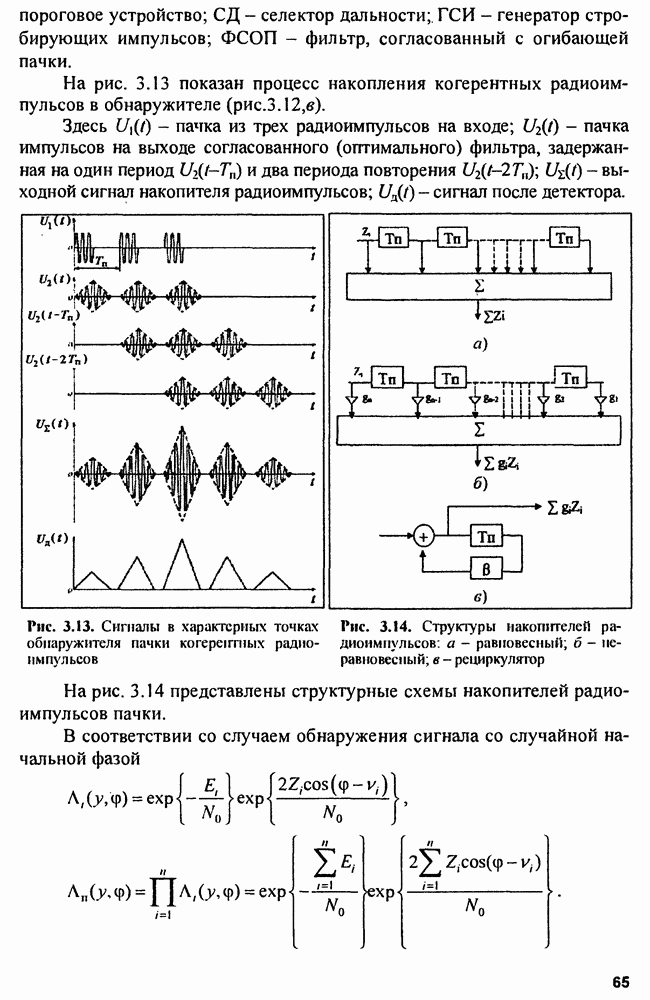
На рис. 3.13 показан процесс накопления когерентных радиоимпульсов в обнаружителе (рис.3.12,в).
Здесь  пачка из трех радиоимпульсов на входе;
пачка из трех радиоимпульсов на входе;  пачка импульсов на выходе согласованного (оптимального) фильтра, задержанная на один период
пачка импульсов на выходе согласованного (оптимального) фильтра, задержанная на один период  и два периода повторения
и два периода повторения  выходной сигнал накопителя радиоимпульсов;
выходной сигнал накопителя радиоимпульсов;  сигнал после детектора.
сигнал после детектора.

Рис. 3.13. Сигналы в характерных точках обнаружителя пачки когерентных радиоимпульсов

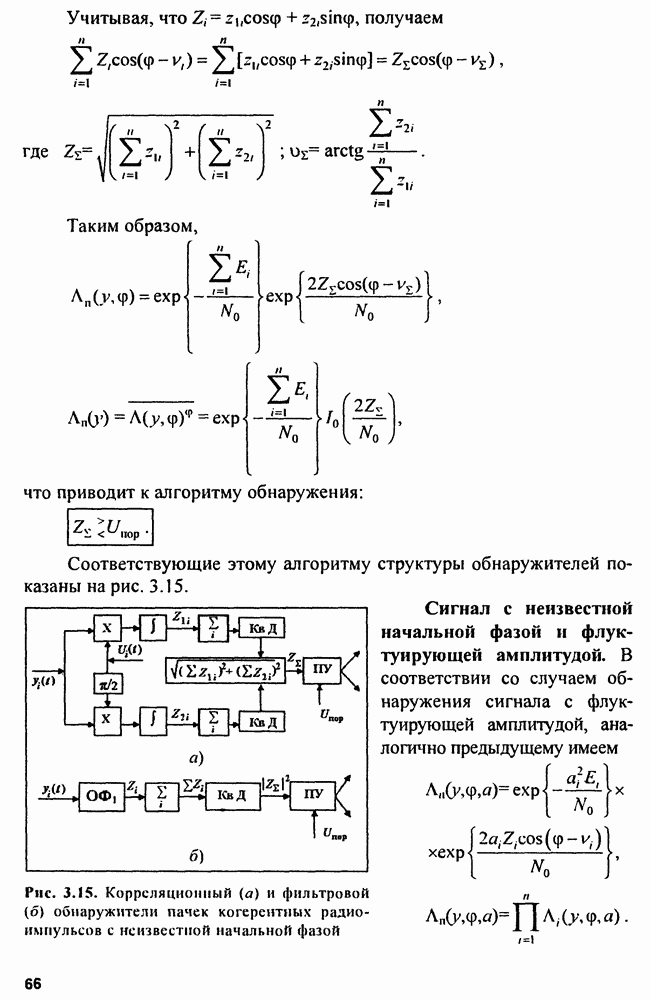
Рис. 3.14. Структуры накопителей радиоимпульсов: а - равновесный;  неравновесный; в - рециркулятор
неравновесный; в - рециркулятор
На рис. 3.14 представлены структурные схемы накопителей радиоимпульсов пачки.
В соответствии со случаем обнаружения сигнала со случайной начальной фазой

Учитывая, что  получаем
получаем

где 
Таким образом,

что приводит к алгоритму обнаружения:

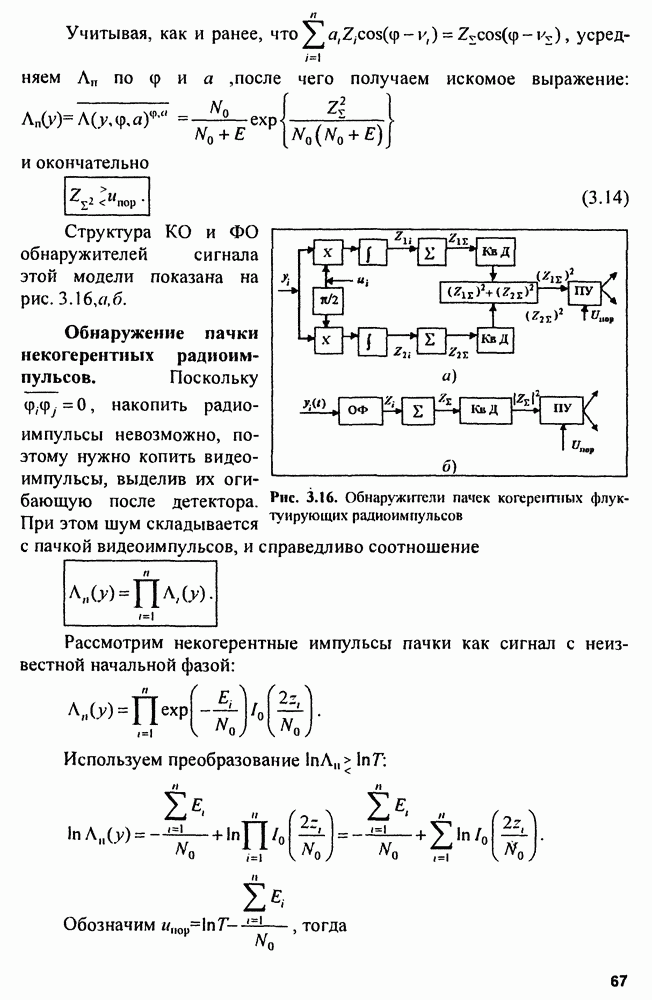
Соответствующие этому алгоритму структуры обнаружителей показаны на рис. 3.15.
Сигнал с неизвестной начальной фазой и флуктуирующей амплитудой. В соответствии со случаем обнаружения сигнала с флуктуирующей амплитудой, аналогично предыдущему имеем


Рис. 3.15. Корреляционный (а) и фильтровой (б) обнаружители пачек когерентных радиоимпульсов с неизвестной начальной фазой
Учитывая, как и ранее, что  усредняем
усредняем  по
по  после чего получаем искомое выражение:
после чего получаем искомое выражение:  и окончательно
и окончательно

Структура КО и ФО обнаружителей сигнала этой модели показана на рис. 3.16, а, б.

Рис. 3.16. Обнаружители пачек когерентных флуктуирующих радиоимпульсов
Обнаружение пачки некогерентных радиоимпульсов. Поскольку  накопить радиоимпульсы невозможно, поэтому нужно копить видеоимпульсы, выделив их огибающую после детектора. При этом шум складывается с пачкой видеоимпульсов, и справедливо соотношение
накопить радиоимпульсы невозможно, поэтому нужно копить видеоимпульсы, выделив их огибающую после детектора. При этом шум складывается с пачкой видеоимпульсов, и справедливо соотношение

Рассмотрим некогерентные импульсы пачки как сигнал с неизвестной начальной фазой:

Используем преобразование 

Обозначим  тогда
тогда

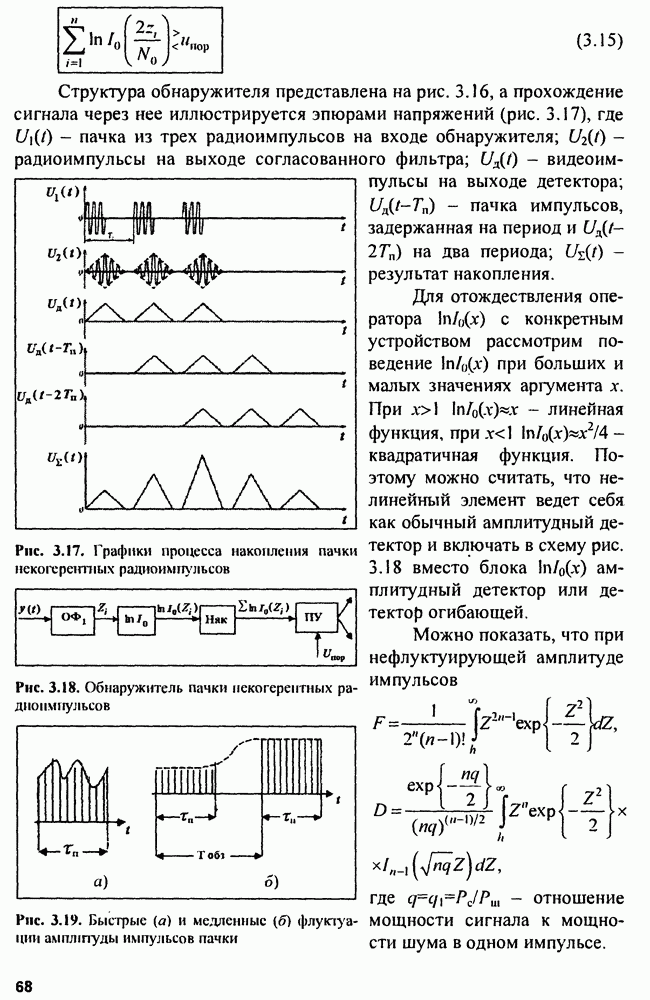
Структура обнаружителя представлена на рис. 3.16, а прохождение сигнала через нее иллюстрируется эпюрами напряжений (рис. 3.17), где  пачка из трех радиоимпульсов на входе обнаружителя;
пачка из трех радиоимпульсов на входе обнаружителя;  радиоимпульсы на выходе согласованного фильтра;
радиоимпульсы на выходе согласованного фильтра;  видеоимпульсы на выходе детектора;
видеоимпульсы на выходе детектора;  пачка импульсов, задержанная на период и
пачка импульсов, задержанная на период и  на два периода;
на два периода;  результат накопления.
результат накопления.

Рис. 3.17. Графики процесса накопления пачки некогерентных радиоимпульсов

Рис. 3.18. Обнаружитель пачки некогереитных радиоимпульсов

Рис. 3.19. Быстрые (а) и медленные (б) флуктуации амплитуды импульсов пачки
Для отождествления оператора  с конкретным устройством рассмотрим поведение
с конкретным устройством рассмотрим поведение  при больших и малых значениях аргумента
при больших и малых значениях аргумента  При
При  линейная функция, при
линейная функция, при  квадратичная функция. Поэтому можно считать, что нелинейный элемент ведет себя как обычный амплитудный детектор и включать в схему рис. 3.18 вместо блока
квадратичная функция. Поэтому можно считать, что нелинейный элемент ведет себя как обычный амплитудный детектор и включать в схему рис. 3.18 вместо блока  амплитудный детектор или детектор огибающей.
амплитудный детектор или детектор огибающей.
Можно показать, что при нефлуктуирующей амплитуде импульсов

где  отношение мощности сигнала к мощности шума в одном импульсе.
отношение мощности сигнала к мощности шума в одном импульсе.
При флуктуации амплитуды импульсов пачки различают два. случая: быстрые (независимые) флуктуации, когда амплитуды успевают изменяться от импульса к импульсу, и медленные (дружные) флуктуации, когда амплитуды импульсов меняются от пачки к пачке (рис. 3.19, а,б). Если флуктуации быстрые и описываются законом Релея, то получаем алгоритм обнаружения:

что соответствует схеме обнаружителя, показанной на рис. 3.20.
Для медленных флуктуаций алгоритм усложняется:

Подставив в это соотношение  и взяв интеграл, находим схему обнаружителя, показанную на рис. 3.18.
и взяв интеграл, находим схему обнаружителя, показанную на рис. 3.18.

Рис. 3.20. Обнаружитель пачки быстро флуктуирующих импульсов

Рис. 3.21. Характеристики обнаружения флуктуирующих импульсов
На рис. 3.21 приведены характеристики обнаружения для этих случаев с  Для одинаковых
Для одинаковых  большая вероятность
большая вероятность  при обнаружении обеспечивается в случае быстрых флуктуаций. Следовательно, целесообразно убыстрить (декоррелировать) флуктуации отраженных сигналов, делая их независимыми от импульса к импульсу. Декорреляцию осуществляют путем изменения частоты зондирующих импульсов на величину
при обнаружении обеспечивается в случае быстрых флуктуаций. Следовательно, целесообразно убыстрить (декоррелировать) флуктуации отраженных сигналов, делая их независимыми от импульса к импульсу. Декорреляцию осуществляют путем изменения частоты зондирующих импульсов на величину  за период повторения, причем
за период повторения, причем  Здесь
Здесь  наибольший размер цели
наибольший размер цели 
Обнаружение детерминированного сигнала на фоне коррелированной аддитивной гауссовой помехи. Будем считать, что случайный гауссов процесс  с нулевым средним значением и корреляционной функцией
с нулевым средним значением и корреляционной функцией  рассматривается в интервале
рассматривается в интервале  При дискретном времени
При дискретном времени  где
где  известна корреляционная матрица помехи
известна корреляционная матрица помехи  симметричная с ненулевым
симметричная с ненулевым
определителем, и обратная ей корреляционная матрица  Причем алгоритм обращения корреляционной матрицы
Причем алгоритм обращения корреляционной матрицы

где  так называемый символ Кронекера, который равен 1 при
так называемый символ Кронекера, который равен 1 при  или
или  при
при 
Пусть последовательность выборочных значений  образует вектор
образует вектор  Совместные плотности распределения вероятностей выборочных значений можно представить в виде
Совместные плотности распределения вероятностей выборочных значений можно представить в виде

Найдем отношение правдоподобия

и перейдем к его логарифму для сравнения с порогом решения 

Объединяя слагаемые этого выражения, не зависящие от  в пороговое напряжение мпор, получаем алгоритм
в пороговое напряжение мпор, получаем алгоритм

Если обозначить  отождествляя
отождествляя  с весовыми коэффициентами фильтра, то алгоритм обнаружения становится более понятным:
с весовыми коэффициентами фильтра, то алгоритм обнаружения становится более понятным:

Перейдем к непрерывному времени:  тогда плотности распределения вероятностей переходят в гауссовы функционалы:
тогда плотности распределения вероятностей переходят в гауссовы функционалы:

Для  эти функционалы выглядят следующим образом:
эти функционалы выглядят следующим образом:

Уравнение обращения корреляционной матрицы становится интегральным:

при этом отношение правдоподобия имеет вид 

Введем весовой коэффициент фильтра обработки  и получим алгоритм обнаружения
и получим алгоритм обнаружения

Перейдем в частотную область, для чего применим преобразование Фурье к левой и правой частям уравнения фильтра обработки:

С использованием интеграла свертки получаем

Полагая  по теореме о спектре свертки имеем
по теореме о спектре свертки имеем

где 
Таким образом,  Вычисляя интеграл Фурье от уравнения обращения корреляционной матрицы, находим
Вычисляя интеграл Фурье от уравнения обращения корреляционной матрицы, находим

где 

Решая уравнения (3.18) и (3.19) совместно и исключая  приходим к уравнению коэффициента передачи оптимального фильтра (устройства):
приходим к уравнению коэффициента передачи оптимального фильтра (устройства):

На рис. 3.22, а показана структурная схема такого обнаружителя. Он состоит из последовательно включенных «обеляющего» фильтра с коэффициентом передачи  и фильтра, оптимального для обнаружения сигнала на фоне «обеленной» помехи с коэффициентом передачи
и фильтра, оптимального для обнаружения сигнала на фоне «обеленной» помехи с коэффициентом передачи  На рис.
На рис.  показано прохождение спектральных составляющих через "обеляющий" фильтр.
показано прохождение спектральных составляющих через "обеляющий" фильтр.
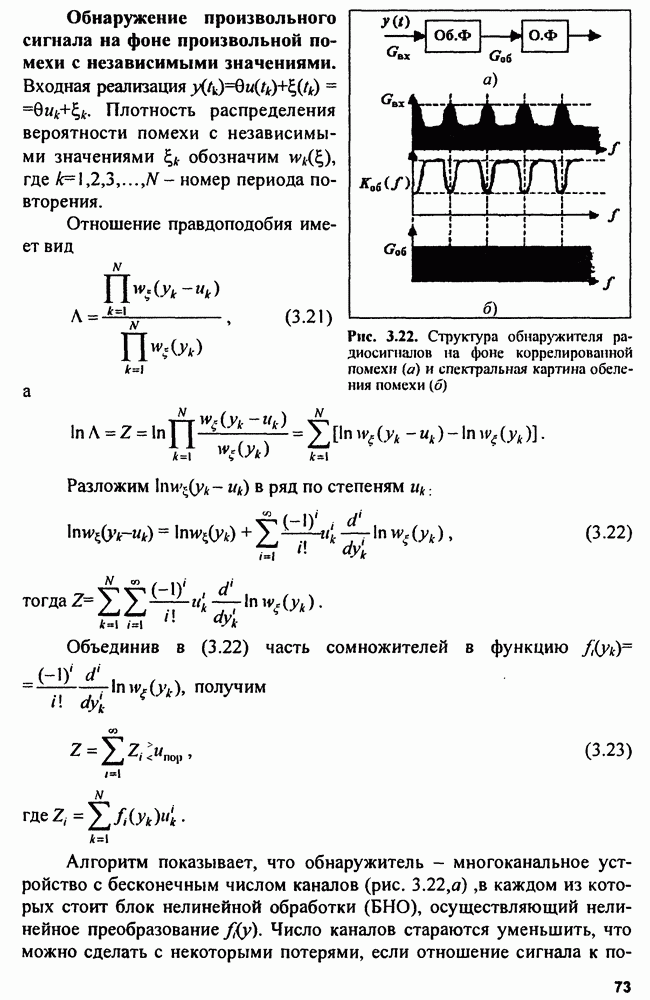
Обнаружение произвольного сигнала на фоне произвольной помехи с независимыми значениями. Входная реализация  Плотность распределения вероятности помехи с независимыми значениями обозначим
Плотность распределения вероятности помехи с независимыми значениями обозначим  где
где  номер периода повторения.
номер периода повторения.

Рис. 3.22. Структура обнаружителя радиосигналов на фоне коррелированной помехи (а) и спектральная картина обеления помехи (б)
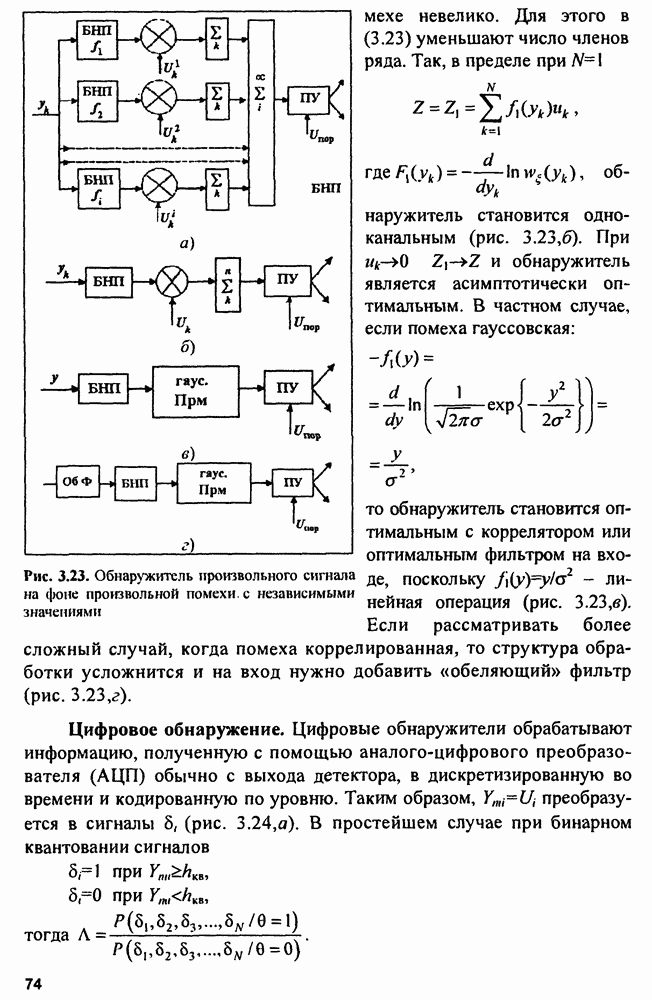
Отношение правдоподобия имеет вид

а

Разложим  в ряд по степеням
в ряд по степеням 

тогда 
Объединив в (3.22) часть сомножителей в функцию  получим
получим

Алгоритм показывает, что обнаружитель - многоканальное устройство с бесконечным числом каналов (рис. 3.22,а) в каждом из которых стоит блок нелинейной обработки БНО), осуществляющий нелинейное преобразование  Число каналов стараются уменьшить, что можно сделать с некоторыми потерями, если отношение сигнала к
Число каналов стараются уменьшить, что можно сделать с некоторыми потерями, если отношение сигнала к

Рис. 3.23. Обнаружитель произвольного сигнала на фоне произвольной помехи, с независимыми значениями
помехе невелико. Для этого в (3.23) уменьшают число членов ряда. Так, в пределе при 

где  обнаружитель становится одноканальным (рис. 3.23,6). При
обнаружитель становится одноканальным (рис. 3.23,6). При  и обнаружитель является асимптотически оптимальным. В частном случае, если помеха гауссовская:
и обнаружитель является асимптотически оптимальным. В частном случае, если помеха гауссовская:

то обнаружитель становится оптимальным с коррелятором или оптимальным фильтром на входе, поскольку  линейная операция (рис. 3.23,в). Если рассматривать более сложный случай, когда помеха коррелированная, то структура обработки усложнится и на вход нужно добавить «обеляющий» фильтр (рис. 3.23,г).
линейная операция (рис. 3.23,в). Если рассматривать более сложный случай, когда помеха коррелированная, то структура обработки усложнится и на вход нужно добавить «обеляющий» фильтр (рис. 3.23,г).
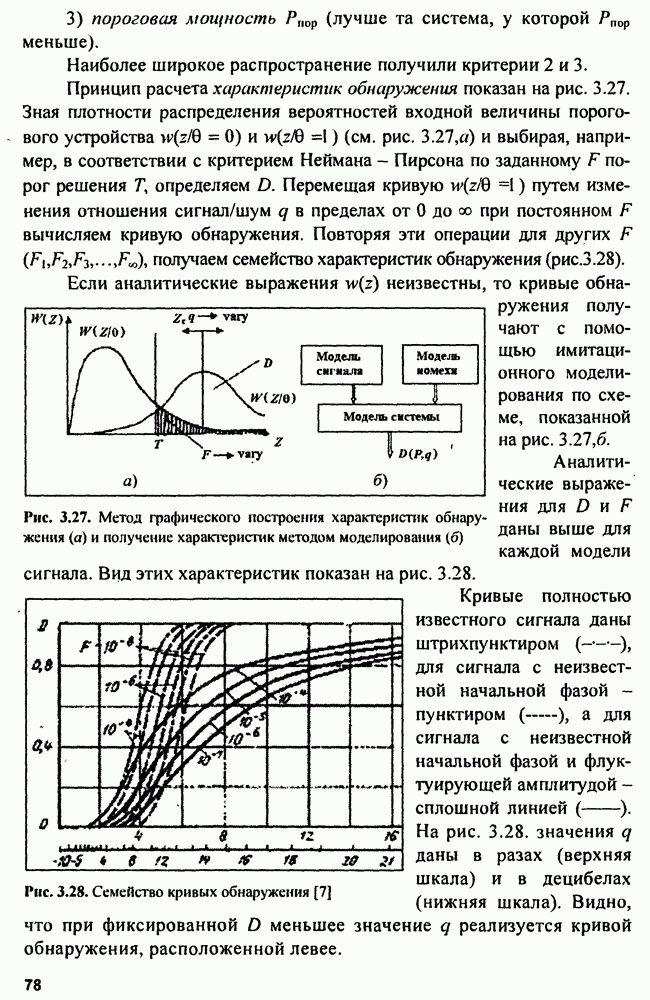
Цифровое обнаружение. Цифровые обнаружители обрабатывают информацию, полученную с помощью аналого-цифрового преобразователя  обычно с выхода детектора, в дискретизированную во времени и кодированную по уровню. Таким образом,
обычно с выхода детектора, в дискретизированную во времени и кодированную по уровню. Таким образом,  преобразуется в сигналы 8, (рис. 3.24,а). В простейшем случае при бинарном квантовании сигналов
преобразуется в сигналы 8, (рис. 3.24,а). В простейшем случае при бинарном квантовании сигналов

тогда 
На выходе АЦП заданы условные плотности распределения вероятностей  Вычислим вероятность появления единицы на
Вычислим вероятность появления единицы на  -й позиции при наличии только шума:
-й позиции при наличии только шума:


Рис. 3.24. Иллюстрация работы цифрового обнаружителя: а - схема; б - квантование; в - вероятности превышения порога шумом  и сигналом с шумом
и сигналом с шумом 
Такая же вероятность при наличии сигнала:

где  вероятности появления нуля на
вероятности появления нуля на  позиции.
позиции.
Условные вероятности принятия случайной величиной 5 любого из двух возможных значений (0,1), показанных на рис. 3.24, б,

При статистически независимых наблюдениях

поэтому  или
или

где  весовой коэффициент:
весовой коэффициент: 
Этот алгоритм соответствует структуре весового накопителя (интегратора). Если шум стационарный:  а пачка импульсов имеет
а пачка импульсов имеет
прямоугольную огибающую  Реш, то
Реш, то  В этом случае алгоритм упрощается:
В этом случае алгоритм упрощается:

например, пусть распределение реализаций после детектора

тогда вероятности для одной реализации  и
и 

Если задана вероятность  то порог квантования можно найти из соотношения
то порог квантования можно найти из соотношения

При  и
и  статистика пачки имеет биноминальное распределение:
статистика пачки имеет биноминальное распределение:

где  биномиальный коэффициент;
биномиальный коэффициент;  наибольшее целое число, удовлетворяющее неравенству
наибольшее целое число, удовлетворяющее неравенству 
Понятно, что одинаковые вероятности  можно получить при различных сочетаниях
можно получить при различных сочетаниях  т.е. при разных сочетаниях порогов
т.е. при разных сочетаниях порогов  Рассмотренный метод обнаружения с накоплением бинарно-квантованных импульсов по любым к реализациям из
Рассмотренный метод обнаружения с накоплением бинарно-квантованных импульсов по любым к реализациям из  соответствует так называемому обнаружителю Типа «к из
соответствует так называемому обнаружителю Типа «к из 
Обычно выбирают порог  из соотношения
из соотношения  Проигрыш аналоговому обнаружителю не превышает
Проигрыш аналоговому обнаружителю не превышает  Пример схемы бинарного обнаружителя (обнаружитель в «скользящем» окне) показан на рис. 3.25.
Пример схемы бинарного обнаружителя (обнаружитель в «скользящем» окне) показан на рис. 3.25.
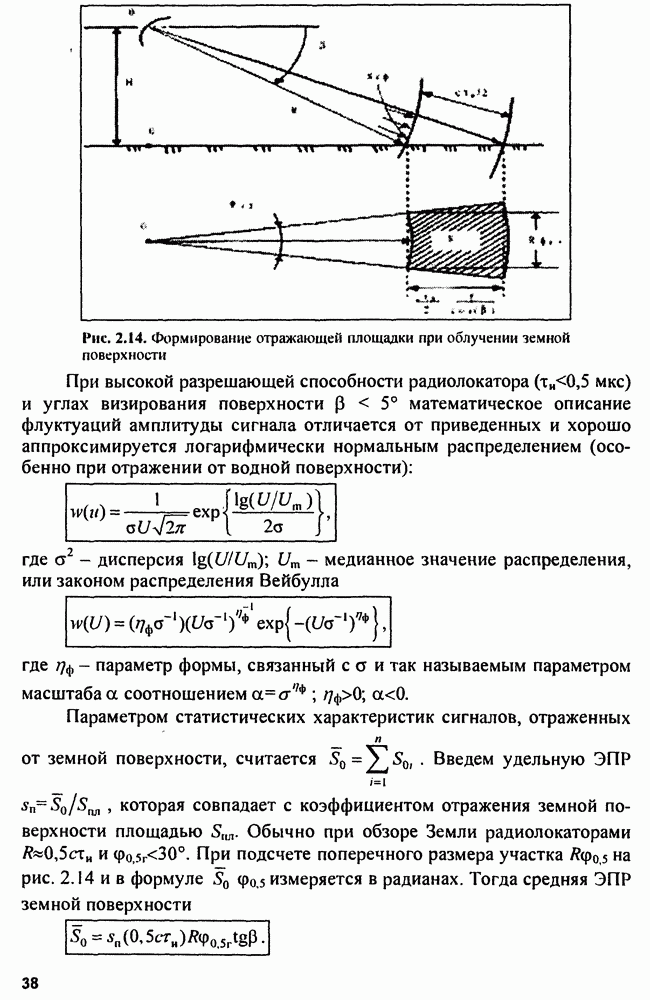
Графики сигналов в различных точках схемы приведены на рис. 3.26,б. В режиме обзора пространства на вход поступают видеоимпульсы пачки, промодулированные по амплитуде вследствие движения диаграммы направленности антенны  на рис.3.26,а). Селектор дальности (Сел
на рис.3.26,а). Селектор дальности (Сел  пропускает на квантователь
пропускает на квантователь  импульсы цели только с определенного элемента разрешения по дальности. Квантователь работает по алгоритму: если
импульсы цели только с определенного элемента разрешения по дальности. Квантователь работает по алгоритму: если  то на выходе появляется стандартный импульс
то на выходе появляется стандартный импульс  а если
а если  то
то  на рис. 3.26,а).
на рис. 3.26,а).
Таким образом, на регистр сдвига  и реверсивный счетчик
и реверсивный счетчик  подается последовательность единиц и нулей в
подается последовательность единиц и нулей в  периодах повторения, где
периодах повторения, где  число импульсов в пачке
число импульсов в пачке  на рис. 3.26,а). Регистр сдвига имеет число ячеек, равное
на рис. 3.26,а). Регистр сдвига имеет число ячеек, равное  и управляется тактовыми импульсами
и управляется тактовыми импульсами  . С выхода
. С выхода  стандартные импульсы попадают на вход
стандартные импульсы попадают на вход  и на суммирующий вход
и на суммирующий вход  На вычитающий вход
На вычитающий вход  импульсы подаются с выхода
импульсы подаются с выхода  Код числа накопленной пачки стандартных импульсов сравнивается в пороговом устройстве
Код числа накопленной пачки стандартных импульсов сравнивается в пороговом устройстве  с порогом
с порогом  после чего выносится решение об обнаружении цели.
после чего выносится решение об обнаружении цели.

Рис. 3.25. Бинарный обнаружитель, работающий в «скользящем окне»

Рис. 3.26. Схема квантователя (а) и графики сигналов (б) в точках  и 3 устройства рис. 3.26
и 3 устройства рис. 3.26
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
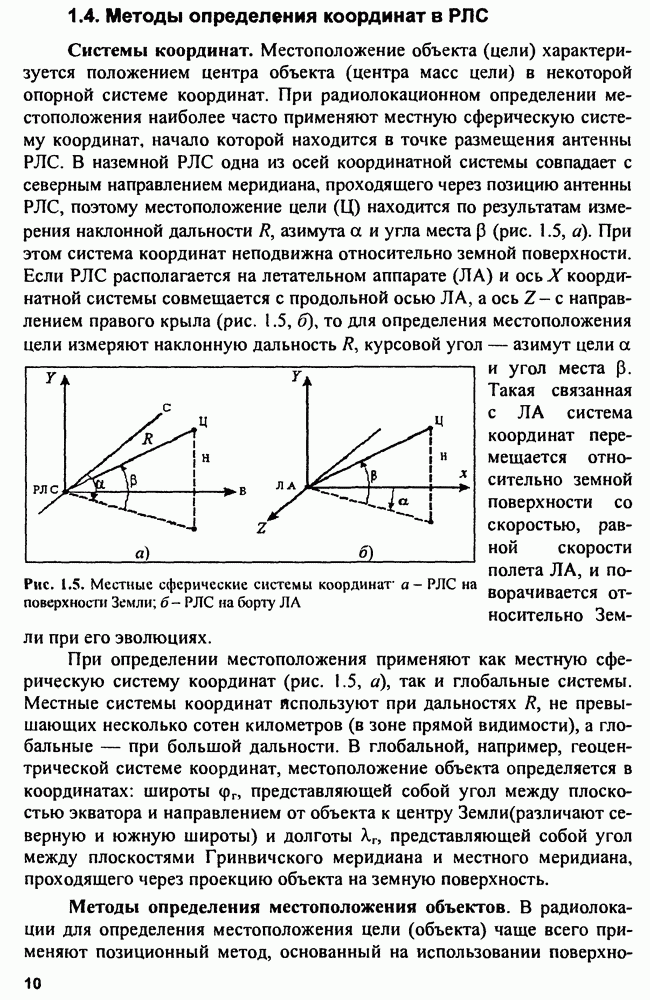
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
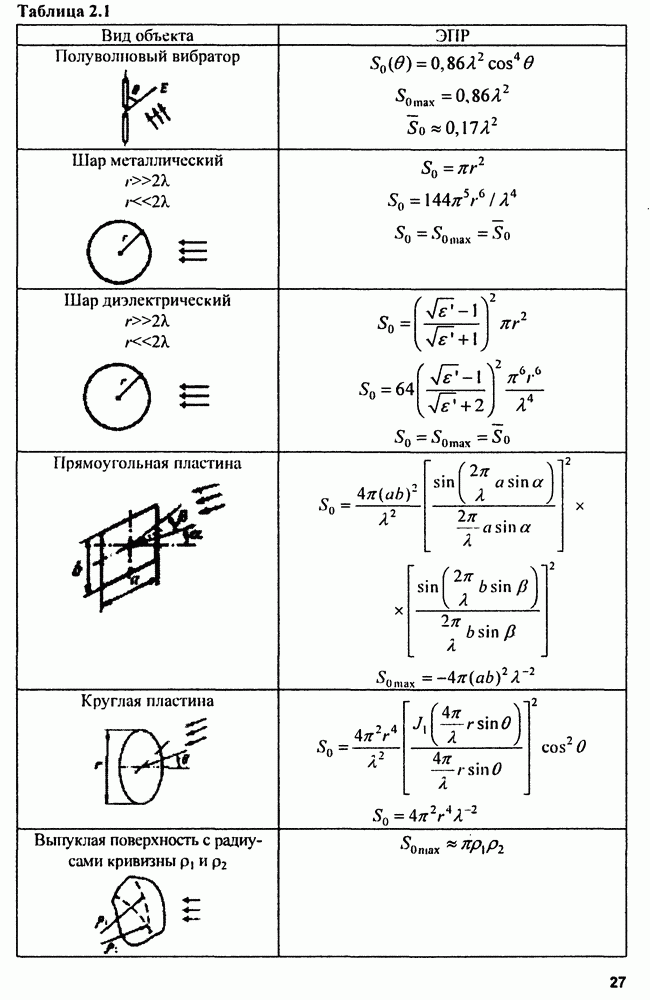
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
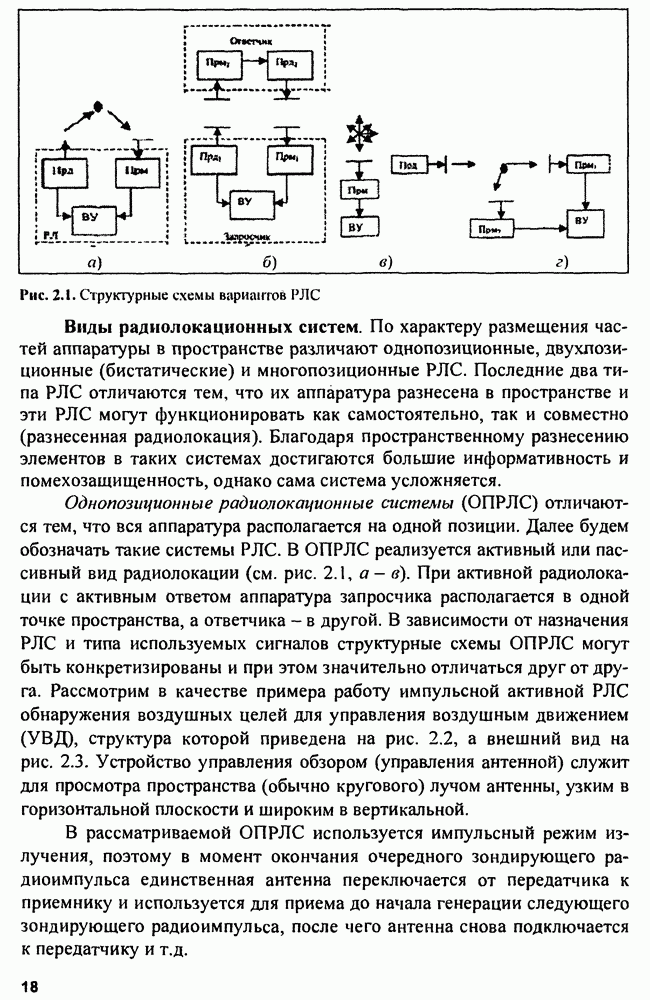
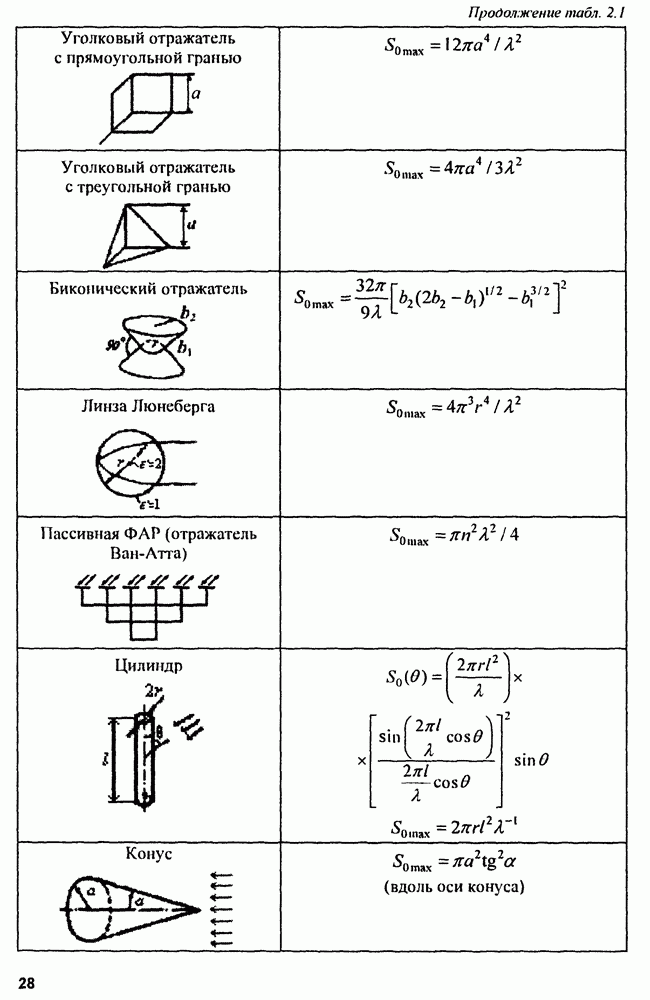
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
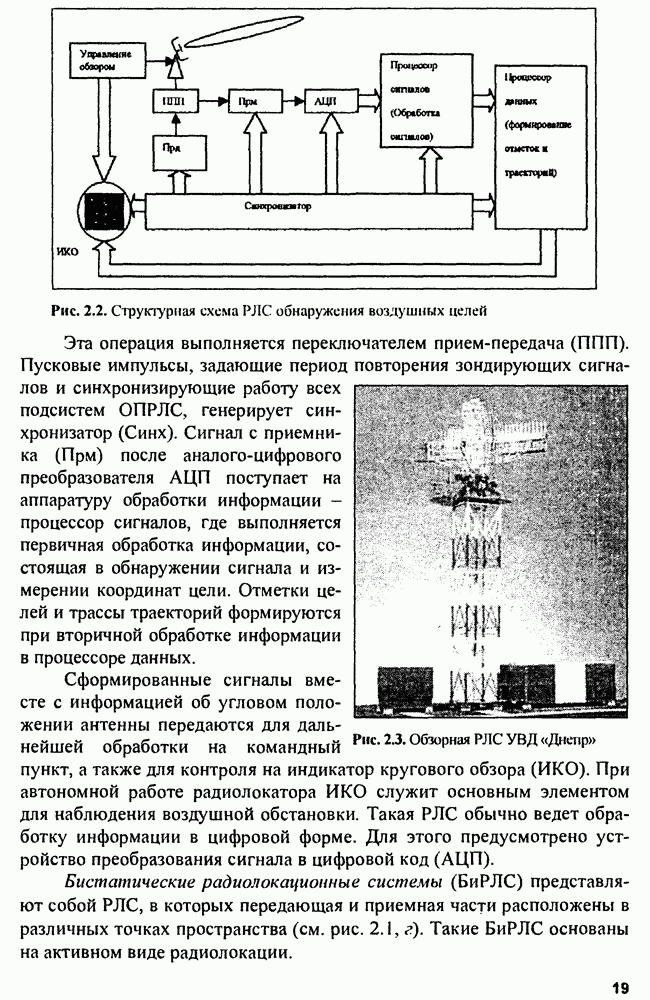
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
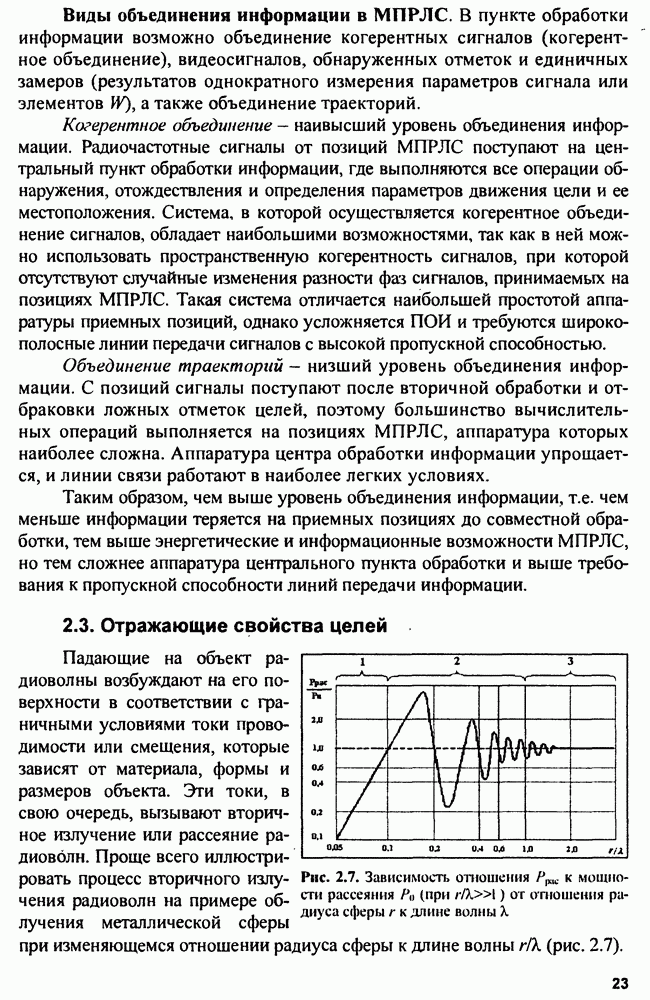
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение