| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3 Марковские случайные процессы
Марковские случайные процессы играют важную роль при исследовании СМО. Поэтому приведем некоторые сведения из теории таких процессов, которые будут использоваться в дальнейшем изложении.
Определение 10. Случайный процесс  заданный на некотором вероятностном пространстве и принимающий значения в некотором числовом множестве Y, называется марковским, если для любого натурального числа
заданный на некотором вероятностном пространстве и принимающий значения в некотором числовом множестве Y, называется марковским, если для любого натурального числа  , любых
, любых  и любых
и любых  упорядоченных следующим образом:
упорядоченных следующим образом:  выполняется соотношение:
выполняется соотношение:

Параметр t процесса будем рассматривать как время. Если  - будущий момент времени, t - настоящий момент времени,
- будущий момент времени, t - настоящий момент времени,  - прошлые моменты времени, то условие (1) можно трактовать следующим образом: будущее поведение марковского процесса полностью определяется его состоянием в настоящий момент времени. У немарковского процесса будущее поведение зависит также от состояний процесса в прошлом.
- прошлые моменты времени, то условие (1) можно трактовать следующим образом: будущее поведение марковского процесса полностью определяется его состоянием в настоящий момент времени. У немарковского процесса будущее поведение зависит также от состояний процесса в прошлом.
В случае, если пространство состояний Y марковского процесса  является конечным или счетным, марковский процесс называется цепью Маркова. Если параметр t принимает значения только в дискретном множестве, то цепь Маркова называется цепью с дискретным временем. Если же параметр t принимает значения в некотором непрерывном множестве, то цепь Маркова называется цепью с непрерывным временем.
является конечным или счетным, марковский процесс называется цепью Маркова. Если параметр t принимает значения только в дискретном множестве, то цепь Маркова называется цепью с дискретным временем. Если же параметр t принимает значения в некотором непрерывном множестве, то цепь Маркова называется цепью с непрерывным временем.
Важным частным случаем цепи Маркова с непрерывным временем является так называемый процесс гибели и размножения.
1.3.1 Процессы гибели и размножения
Определение 11. Случайный процесс  называется процессом гибели и размножения, если он удовлетворяет условиям:
называется процессом гибели и размножения, если он удовлетворяет условиям:
• пространство состояний процесса есть множество неотрицательных целых чисел (или его некоторое подмножество);
• время пребывания процесса в состоянии  имеет показательное распределение с параметром
имеет показательное распределение с параметром  и не зависит от предыдущего поведения процесса;
и не зависит от предыдущего поведения процесса;
• после завершения пребывания процесса в состоянии  он переходит в состояние
он переходит в состояние  вероятностью
вероятностью  и в состояние
и в состояние  с вероятностью
с вероятностью  Вероятность
Вероятность  полагается равной 1.
полагается равной 1.
Состояние процесса  в момент времени t можно трактовать как размер некоторой популяции в этот момент времени. Переход из состояния i в состояние
в момент времени t можно трактовать как размер некоторой популяции в этот момент времени. Переход из состояния i в состояние  трактуется как рождение нового члена популяции, а переход в состояние
трактуется как рождение нового члена популяции, а переход в состояние  - как гибель члена популяции. Такая трактовка процесса и объясняет его название.
- как гибель члена популяции. Такая трактовка процесса и объясняет его название.
Обозначим  вероятность того, что в момент t процесс
вероятность того, что в момент t процесс  находится в состоянии
находится в состоянии  .
.
Утверждение 8. Вероятности  удовлетворяют следующей системе линейных дифференциальных уравнений:
удовлетворяют следующей системе линейных дифференциальных уравнений:

где 
Для доказательства применим так называемый  - метод». Этот метод широко используется при анализе цепей Маркова и марковских процессов с непрерывным временем.
- метод». Этот метод широко используется при анализе цепей Маркова и марковских процессов с непрерывным временем.
Сущность этого метода состоит в следующем. Фиксируется некоторый момент времени t и некоторое малое приращение времени  Распределение вероятностей состояний марковского процесса в момент времени
Распределение вероятностей состояний марковского процесса в момент времени  выражается через его распределение вероятностей в момент t и вероятности возможных переходов процесса за время
выражается через его распределение вероятностей в момент t и вероятности возможных переходов процесса за время  . В результате получается система разностных уравнений для вероятностей
. В результате получается система разностных уравнений для вероятностей  Деля обе части этих уравнений на
Деля обе части этих уравнений на  и устремляя величину
и устремляя величину  к нулю, получаем систему дифференциальных уравнений для искомых вероятностей.
к нулю, получаем систему дифференциальных уравнений для искомых вероятностей.
Применяем этот метод для вывода уравнений (1.3). Обозначим через  вероятность перехода процесса
вероятность перехода процесса  из состояния
из состояния  в состояние j за интервал времени
в состояние j за интервал времени  Поскольку распределение времени пребывания процесса
Поскольку распределение времени пребывания процесса  в состоянии i имеет показательное распределение, обладающее свойством отсутствия последействия, то время до окончания пребывания в состоянии
в состоянии i имеет показательное распределение, обладающее свойством отсутствия последействия, то время до окончания пребывания в состоянии  , начиная с момента времени t, также распределено по показательному закону с параметром
, начиная с момента времени t, также распределено по показательному закону с параметром 
Вероятность того, что процесс  осуществит переход из состояния i за время
осуществит переход из состояния i за время  есть вероятность того, что за время
есть вероятность того, что за время  показательно распределенное с параметром
показательно распределенное с параметром  время закончилось. По определению функции распределения эта вероятность равна
время закончилось. По определению функции распределения эта вероятность равна

то есть, вероятность изменения состояния процесса за время  есть величина порядка
есть величина порядка  Отсюда следует, что вероятность того, что за время
Отсюда следует, что вероятность того, что за время  произойдет два или более перехода процесса
произойдет два или более перехода процесса  есть величина порядка
есть величина порядка  Учитывая то, что процесс гибели и размножения осуществляет переходы за один шаг только в соседние состояния, заключаем, что
Учитывая то, что процесс гибели и размножения осуществляет переходы за один шаг только в соседние состояния, заключаем, что  для
для 
Используя приведенные рассуждения и формулу полной вероятности, мы получаем соотношения:

Из описания процесса и формулы (1.4) следует, что:

Подставляя соотношения (1.6) в (1.5) и используя введенные обозначения переписываем (1.5) в виде:

Деля обе части этого уравнения на  и устремляя
и устремляя  к нулю, получаем уравнение (1.3). Уравнение (1.2) выводится аналогично.
к нулю, получаем уравнение (1.3). Уравнение (1.2) выводится аналогично.
Утверждение 8 доказано.
Для решения бесконечной системы дифференциальных уравнений (1.2), (1.3) путем перехода к преобразованиям Лапласа (см. ниже)  вероятностей
вероятностей  ее сводят к бесконечной системе линейных алгебраических уравнений.
ее сводят к бесконечной системе линейных алгебраических уравнений.
Однако, и эта система может быть решена в явном виде только в некоторых случаях, когда трехдиагональная матрица этой системы имеет дополнительную специфику (например,  ). Ситуация, когда полученная система уравнений для вероятностей
). Ситуация, когда полученная система уравнений для вероятностей  не может быть решена, достаточно типична в теории массового обслуживания. Поэтому, несмотря на то, что значительный практический интерес иногда представляют именно эти вероятности, зависящие
не может быть решена, достаточно типична в теории массового обслуживания. Поэтому, несмотря на то, что значительный практический интерес иногда представляют именно эти вероятности, зависящие  характеризующие (при известном начальном состоянии процесса
характеризующие (при известном начальном состоянии процесса  или известном распределении вероятностей начального состояния) динамику рассматриваемого процесса, обычно приходится довольствоваться так называемым стационарным распределением вероятностей процесса:
или известном распределении вероятностей начального состояния) динамику рассматриваемого процесса, обычно приходится довольствоваться так называемым стационарным распределением вероятностей процесса:

Положительные предельные (стационарные) вероятности  могут существовать не всегда и условия их существования обычно устанавливаются с помощью так называемых эргодических теорем.
могут существовать не всегда и условия их существования обычно устанавливаются с помощью так называемых эргодических теорем.
Для рассматриваемого нами процесса гибели и размножения можно доказать следующий результат.
Утверждение 9. Стационарное распределение вероятностей (1.8) рассматриваемого процесса гибели и размножения существует, если сходится ряд

где

и расходится ряд

При этом стационарные вероятности  вычисляются следующим образом:
вычисляются следующим образом:

Последняя часть утверждения доказывается элементарно. Предполагаем, что условия (1.9) и (1.10) выполняются и пределы (1.8) существуют. Устремляем в (1.2), (1.3) t к бесконечности. При этом производные  стремятся к нулю.
стремятся к нулю.
Существование пределов этих производных следует из существования пределов в правой части системы (1-2), (1.3). Равенство пределов производных нулю следует из того, что предположение о том, что пределы ненулевые, противоречит ограниченности вероятностей: 
В результате, из (1.2), (1.3) получаем систему линейных алгебраических уравнений для распределения 

Введя обозначение  , систему (1.12),(1.13) можно переписать в виде:
, систему (1.12),(1.13) можно переписать в виде:

откуда следует, что  что влечет выполнение соотношений
что влечет выполнение соотношений

Отсюда следует, что  . Формула для вероятности
. Формула для вероятности  следует из условия нормировки.
следует из условия нормировки.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
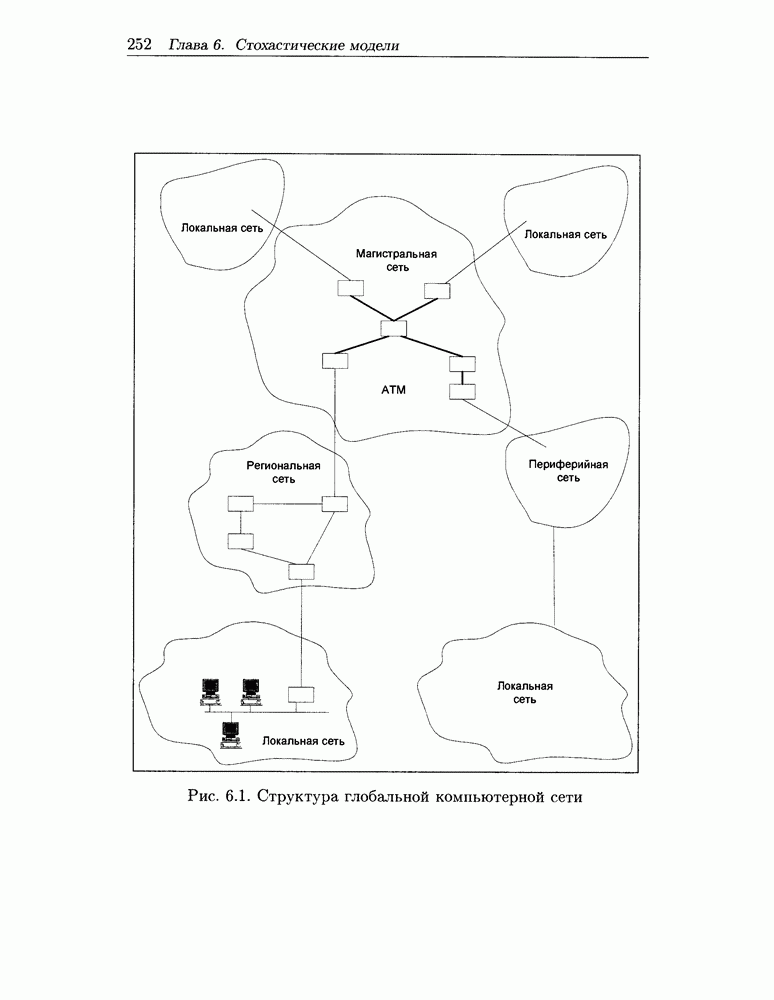
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
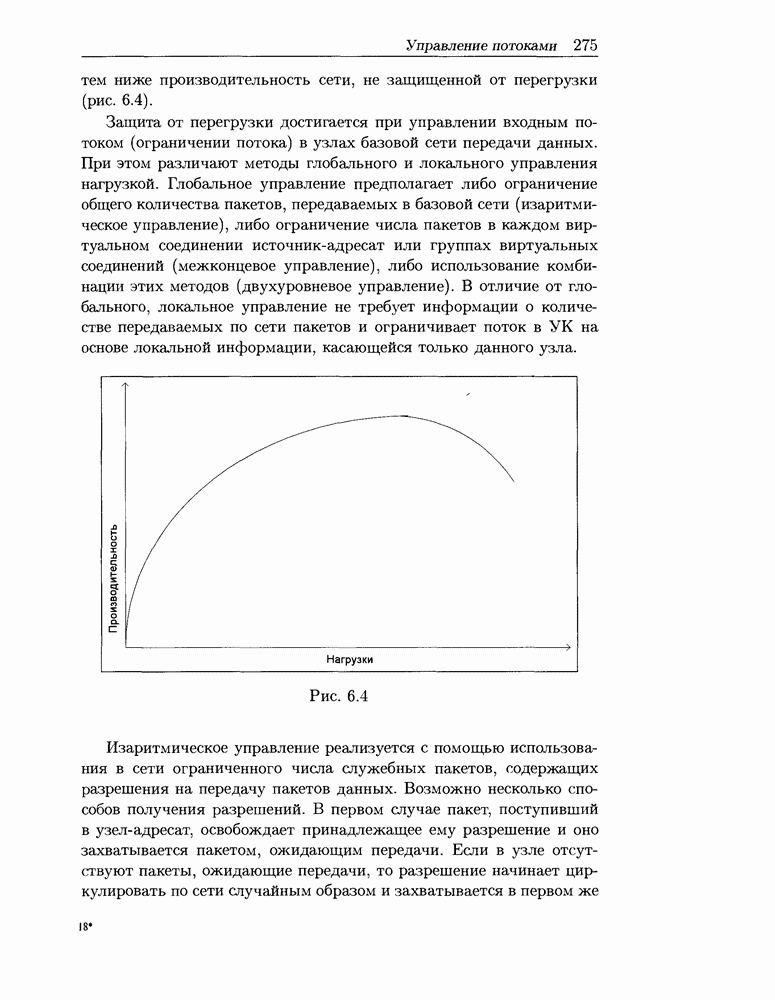
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
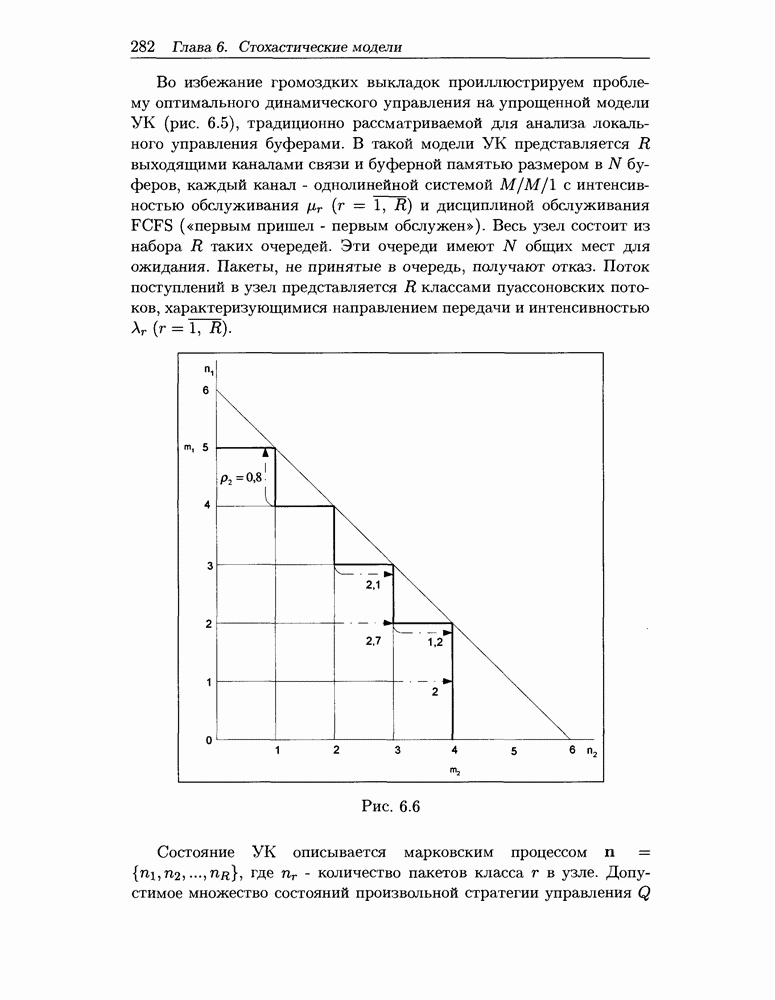
- 6.3.3 Локальное управление буферами
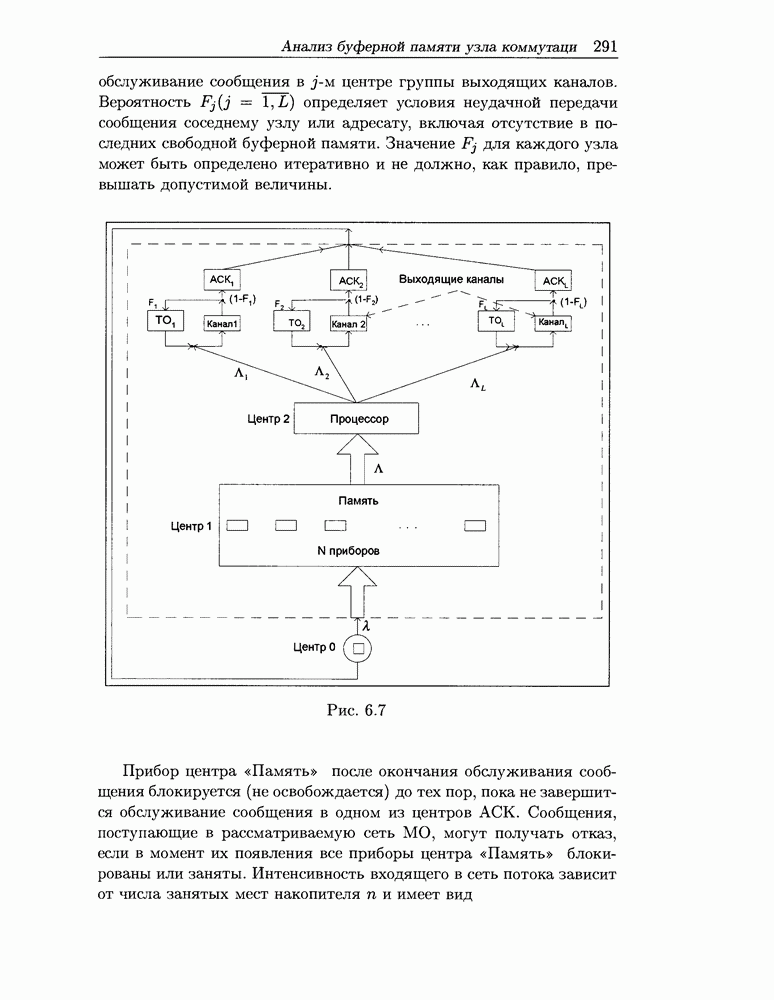
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
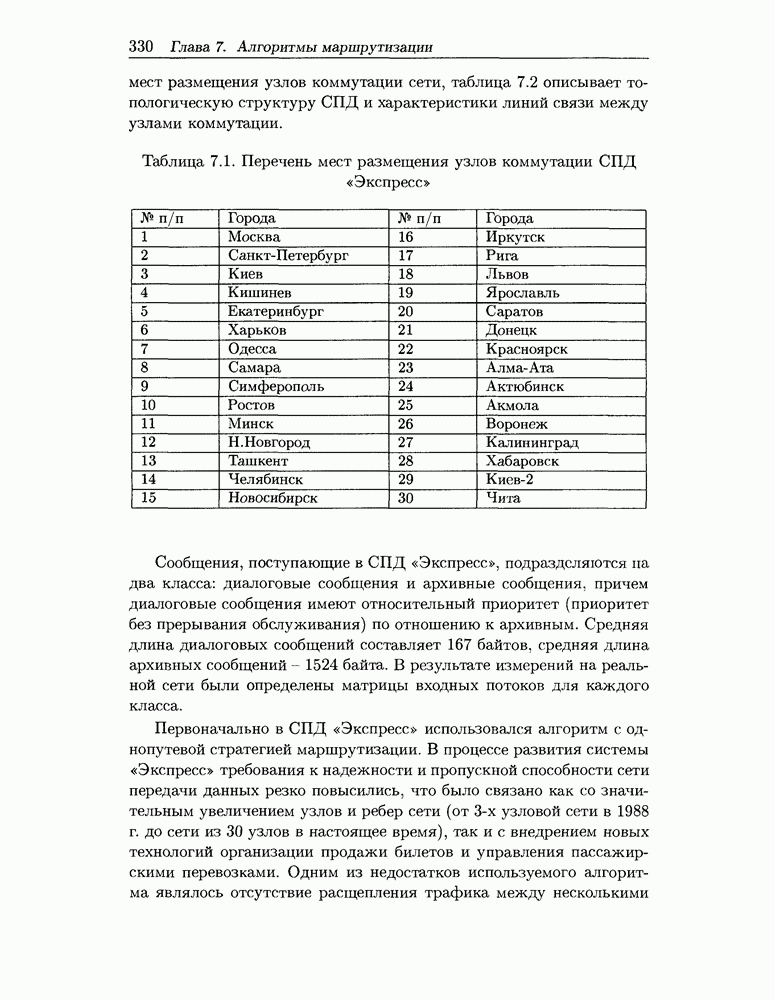
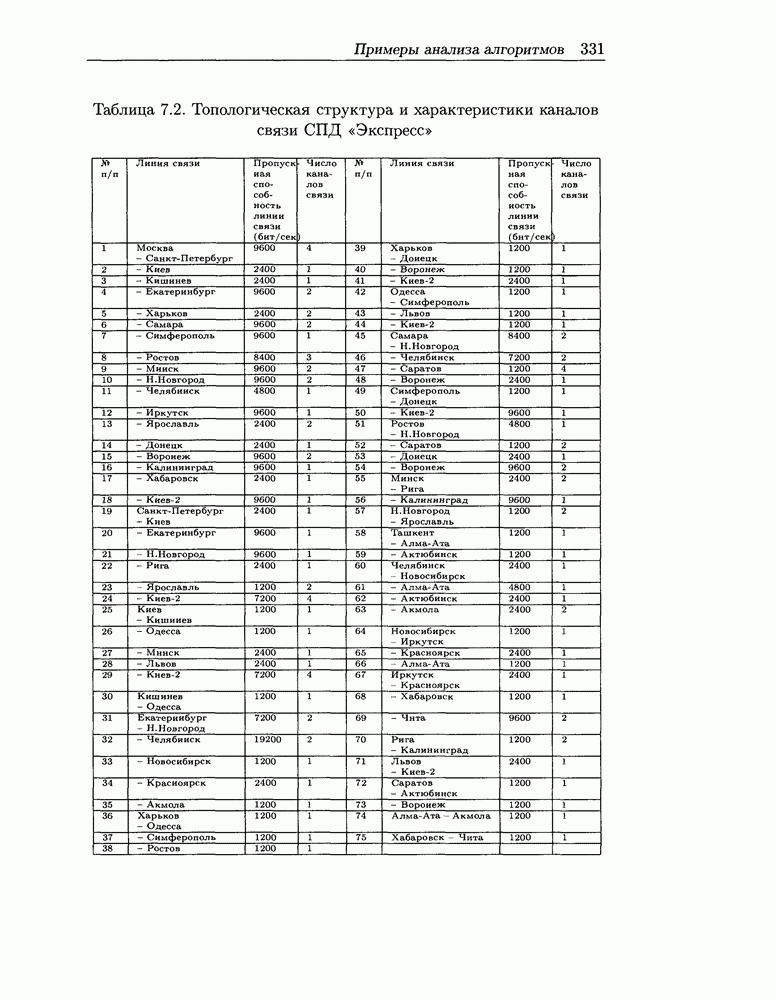
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
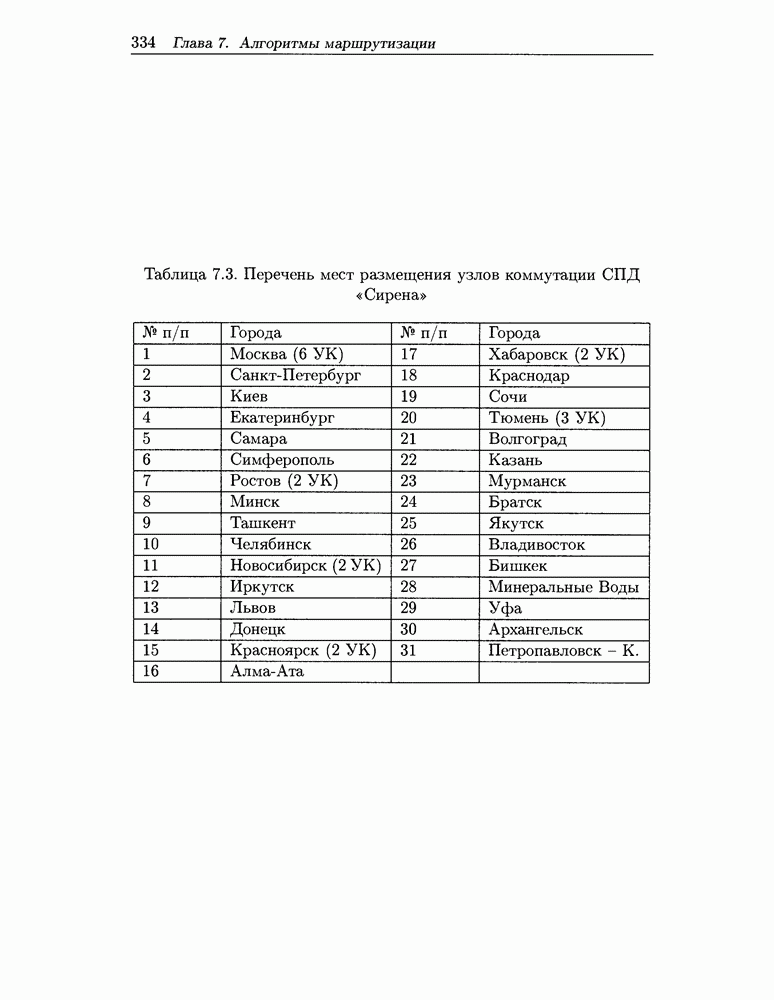
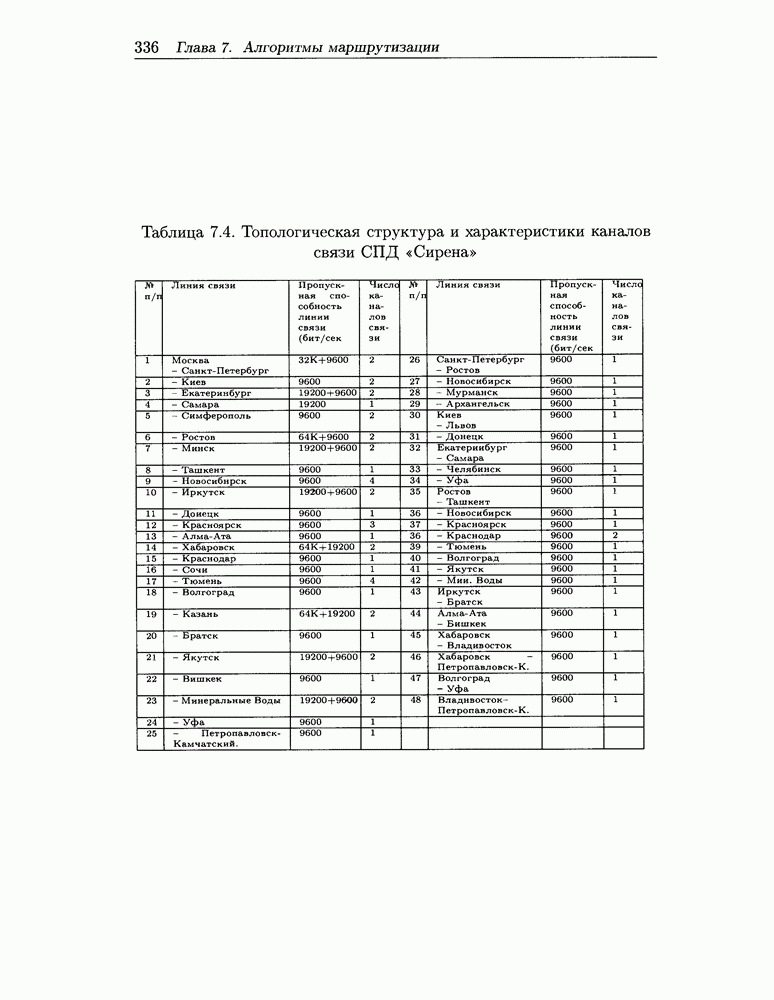
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
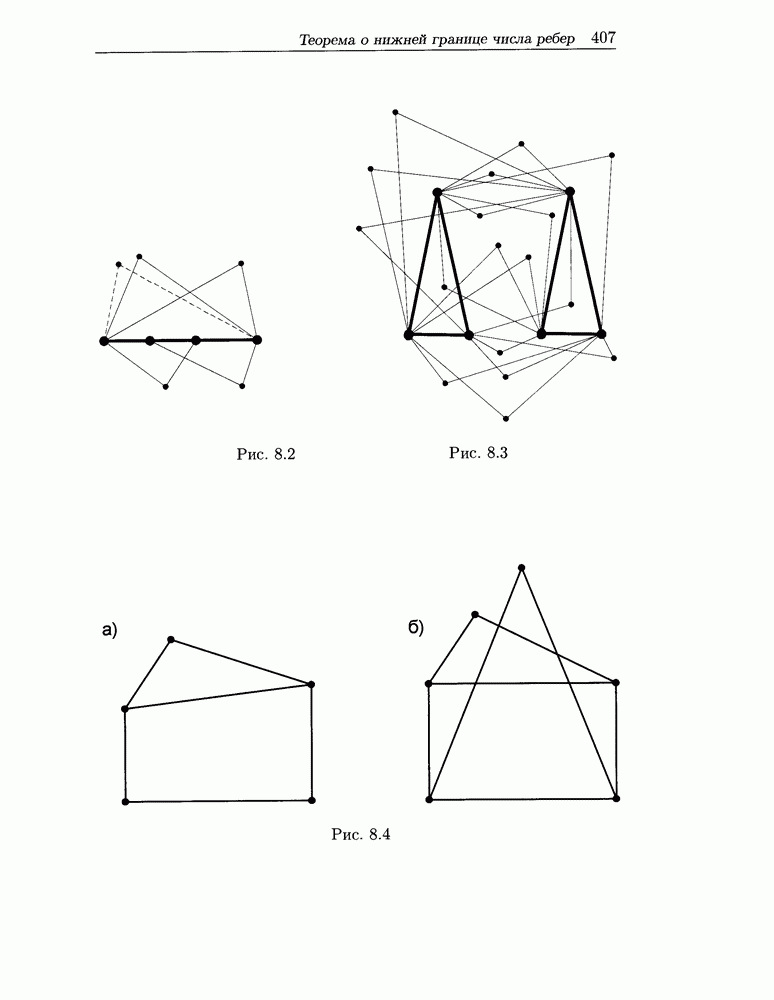
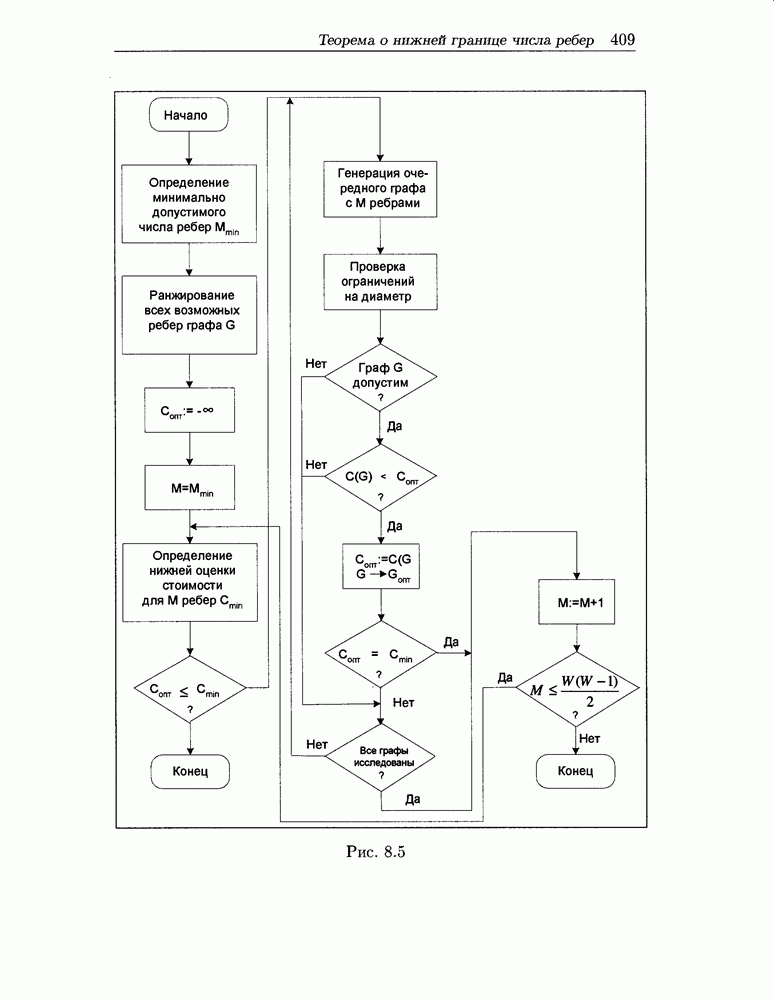
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
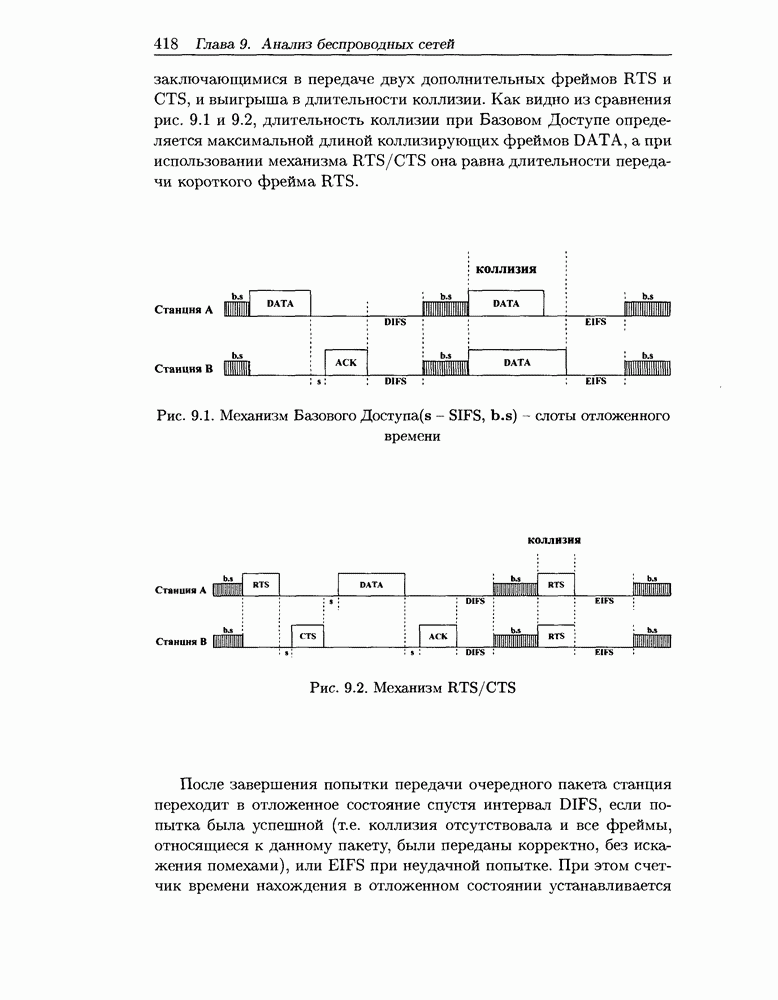
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
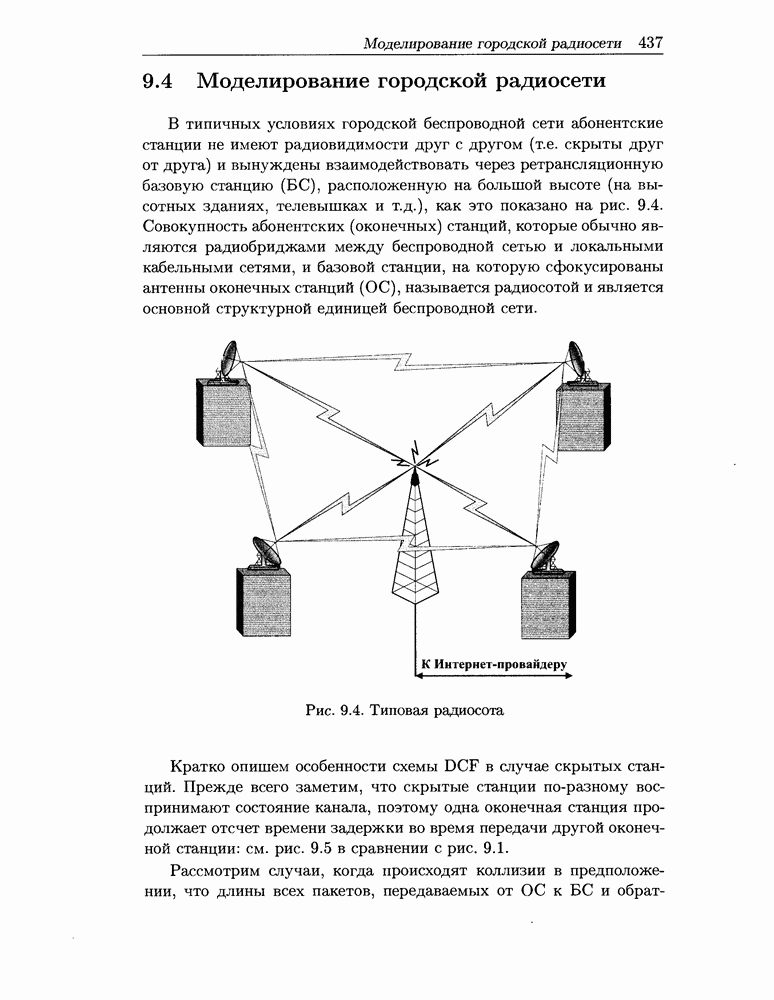
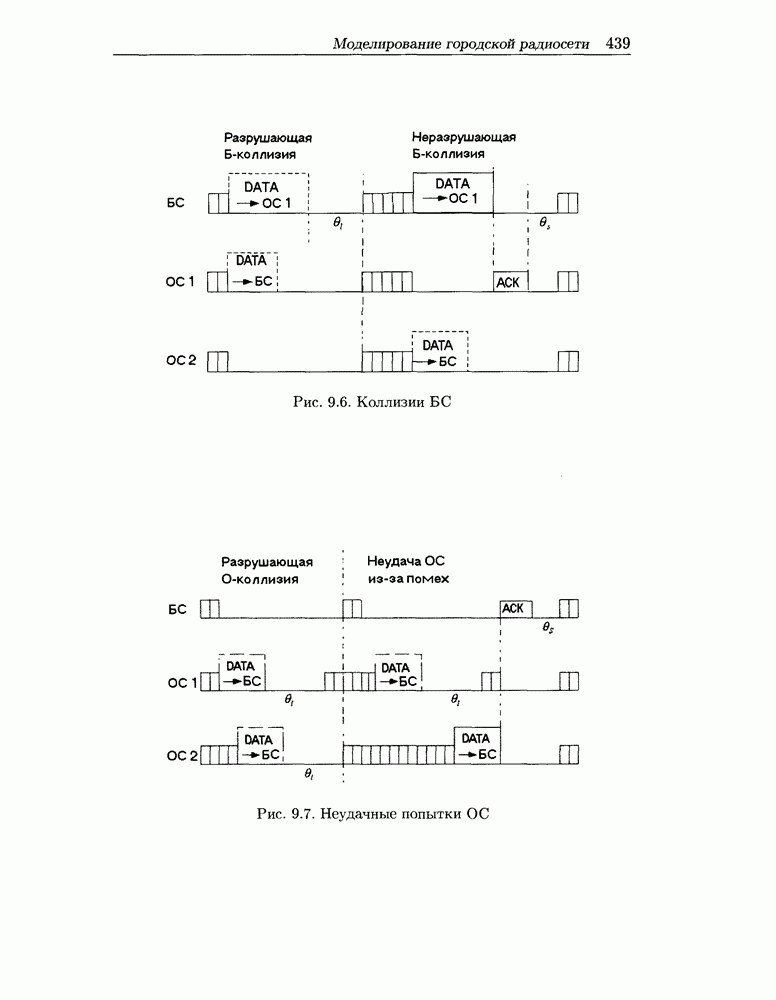
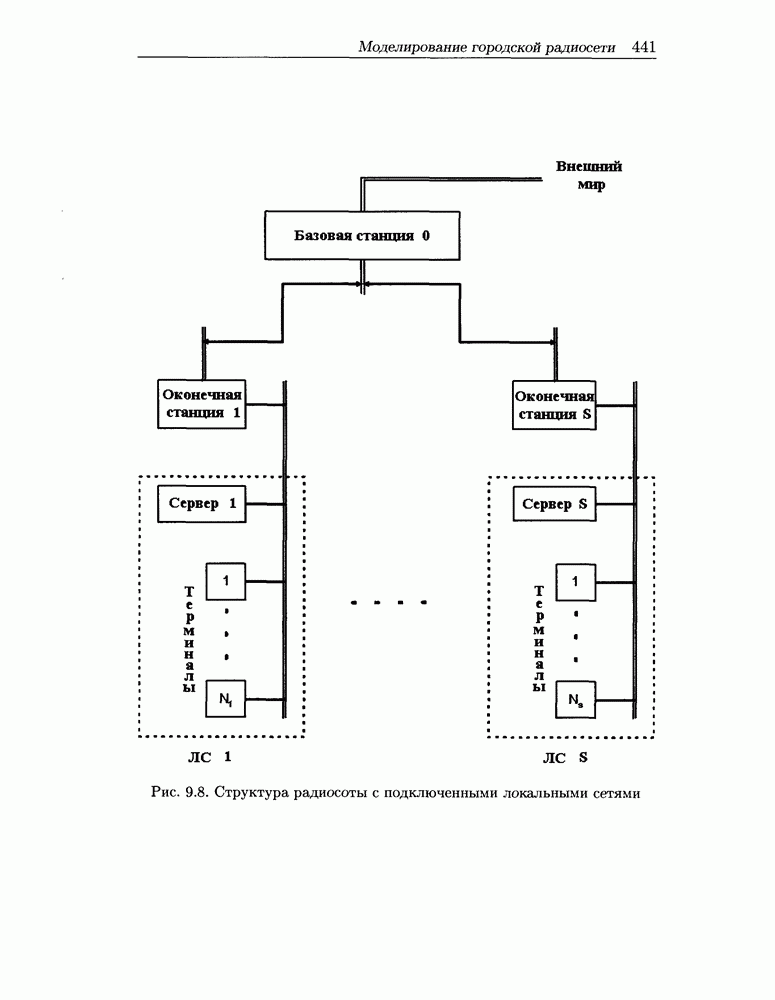
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
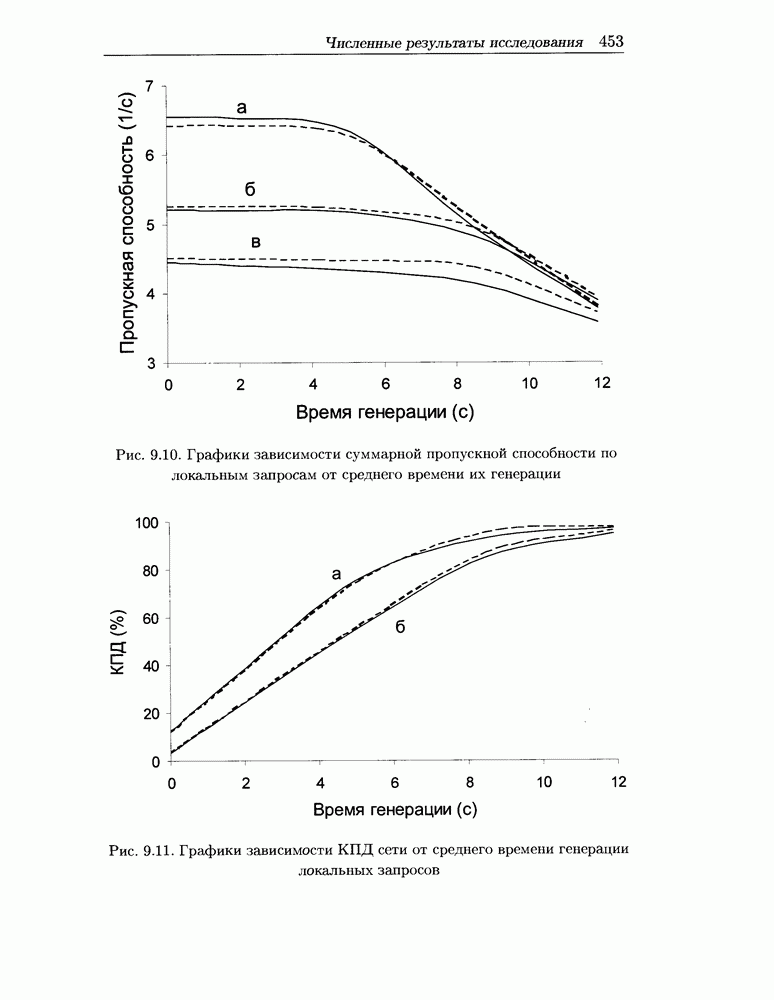
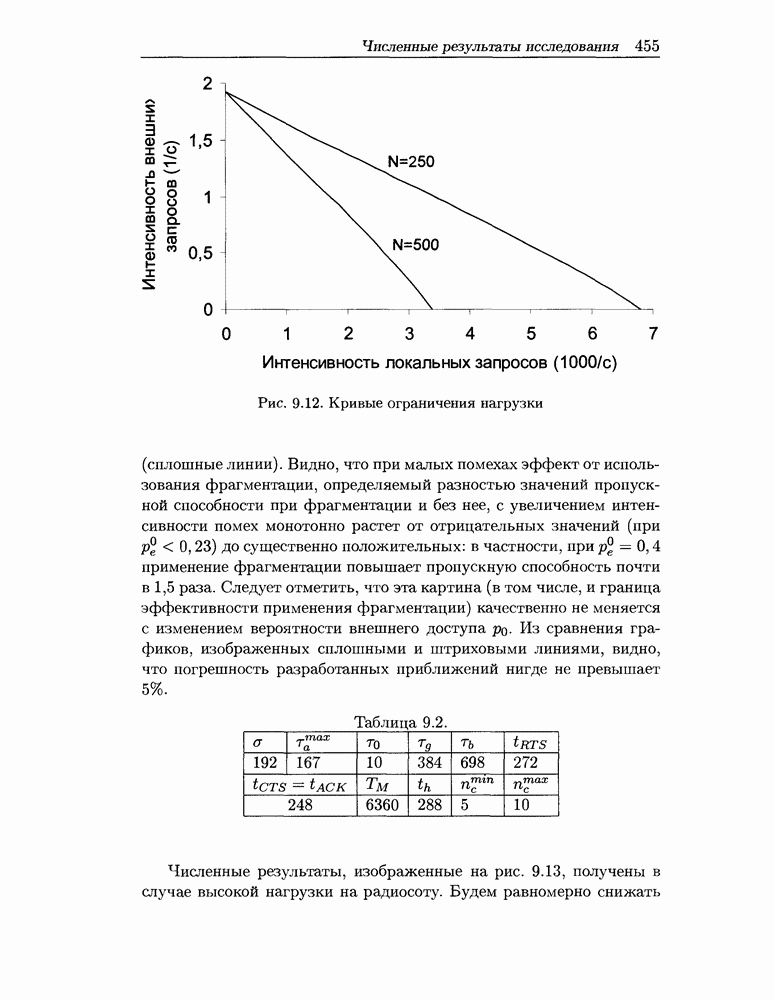
- 9.5 Численные результаты исследования городской радиосоты
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература