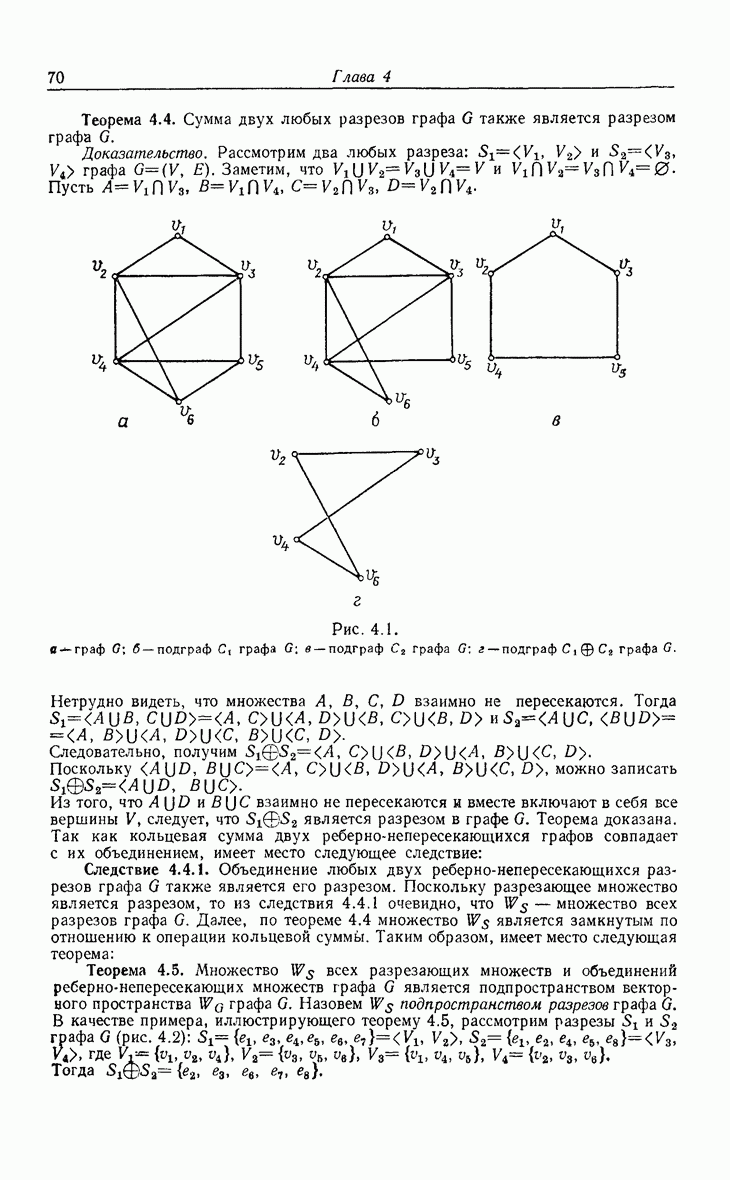
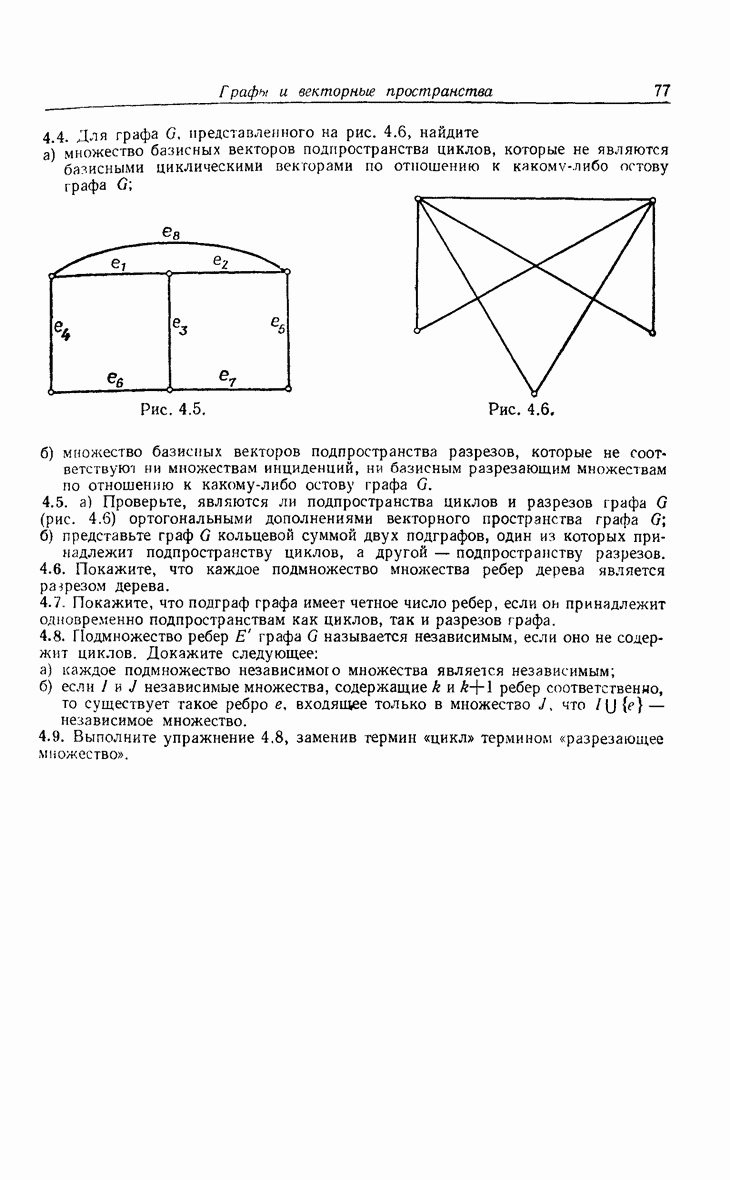
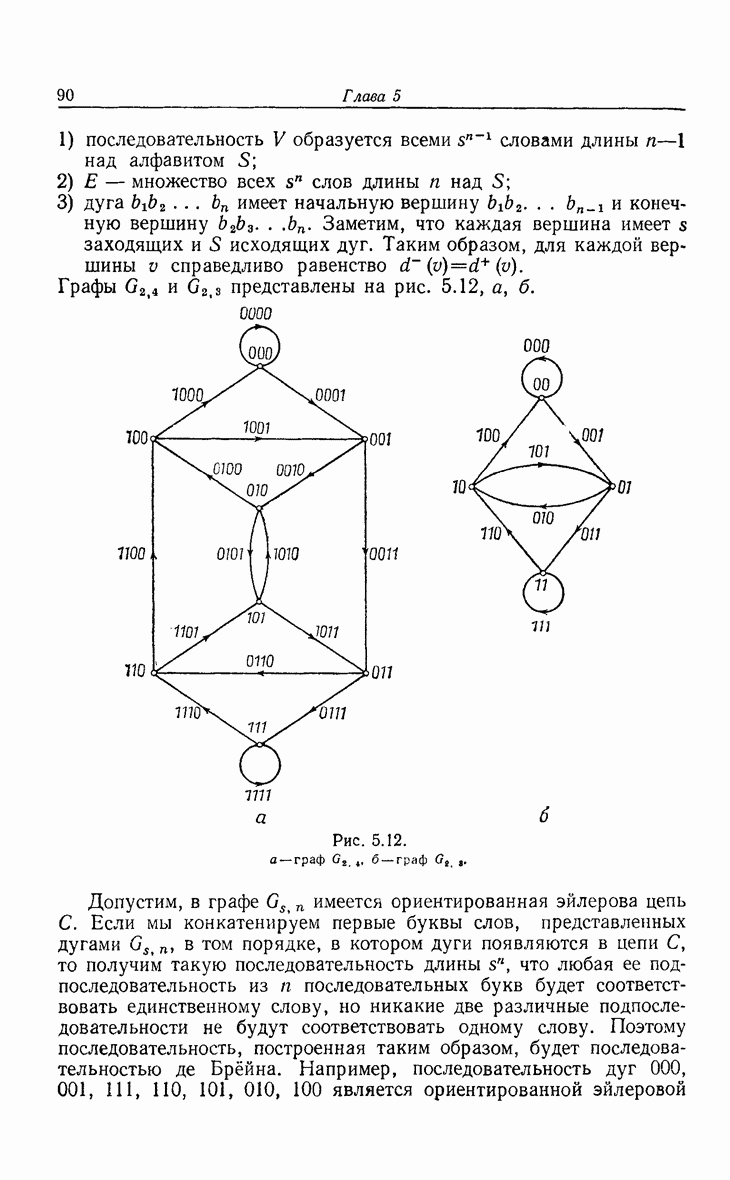
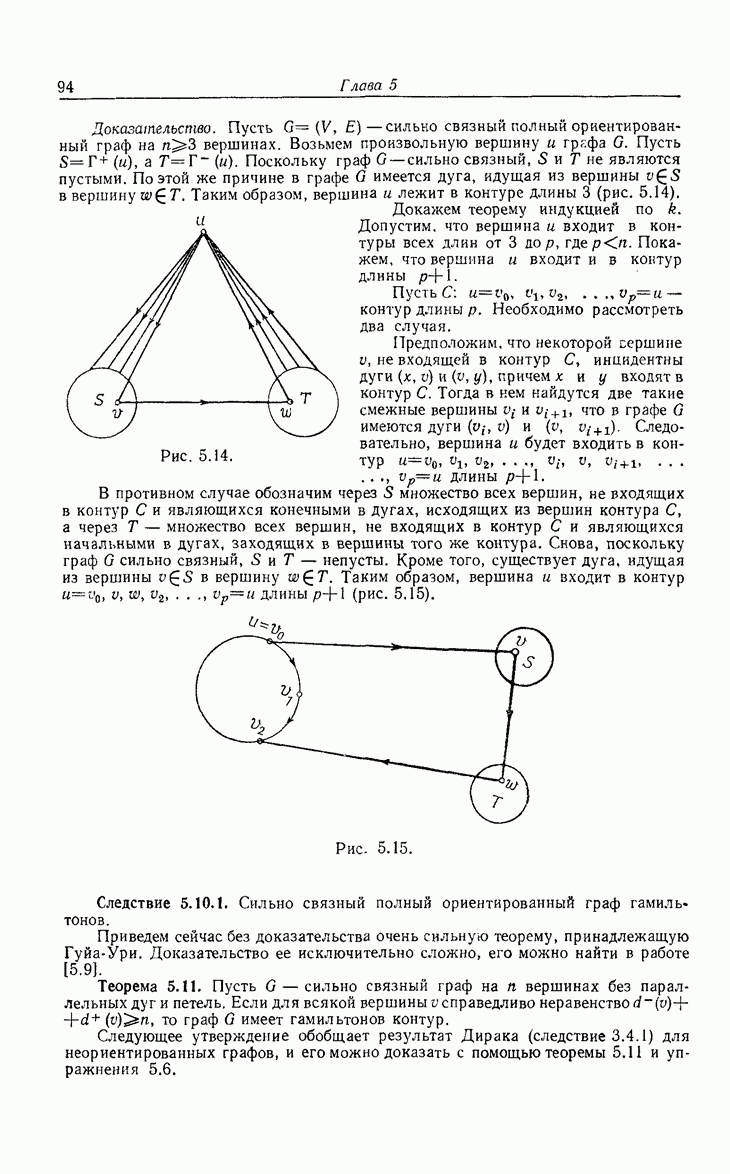
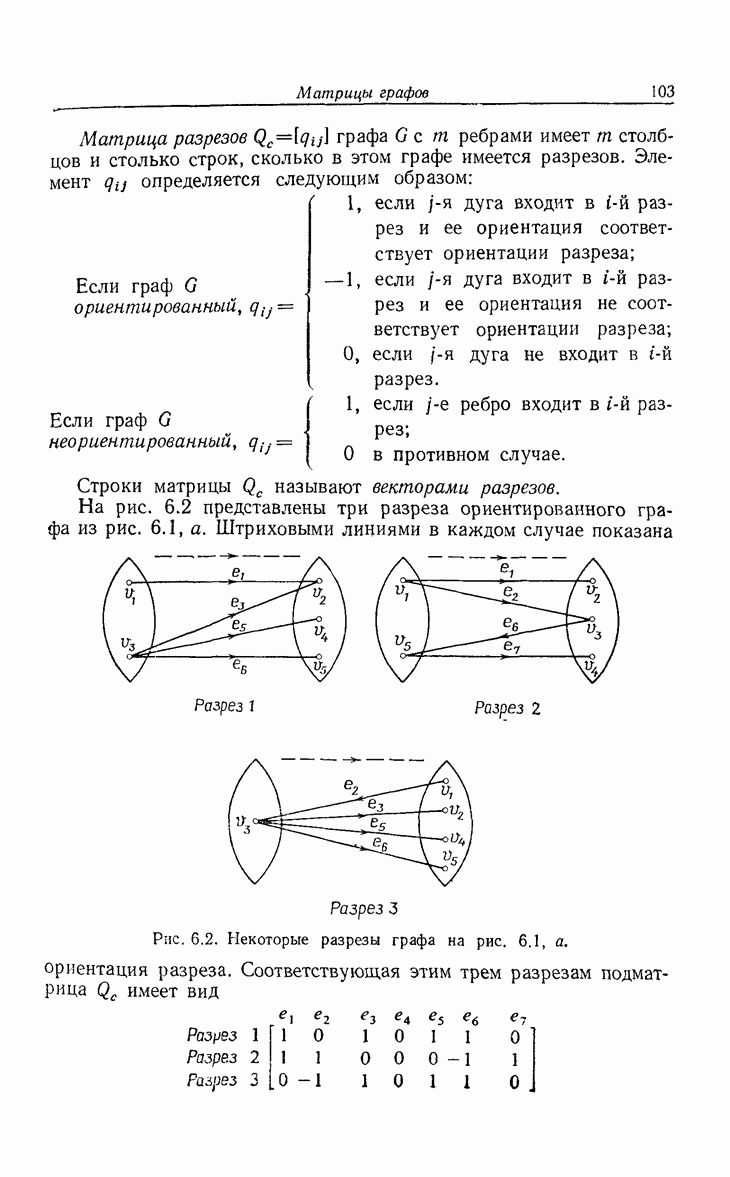
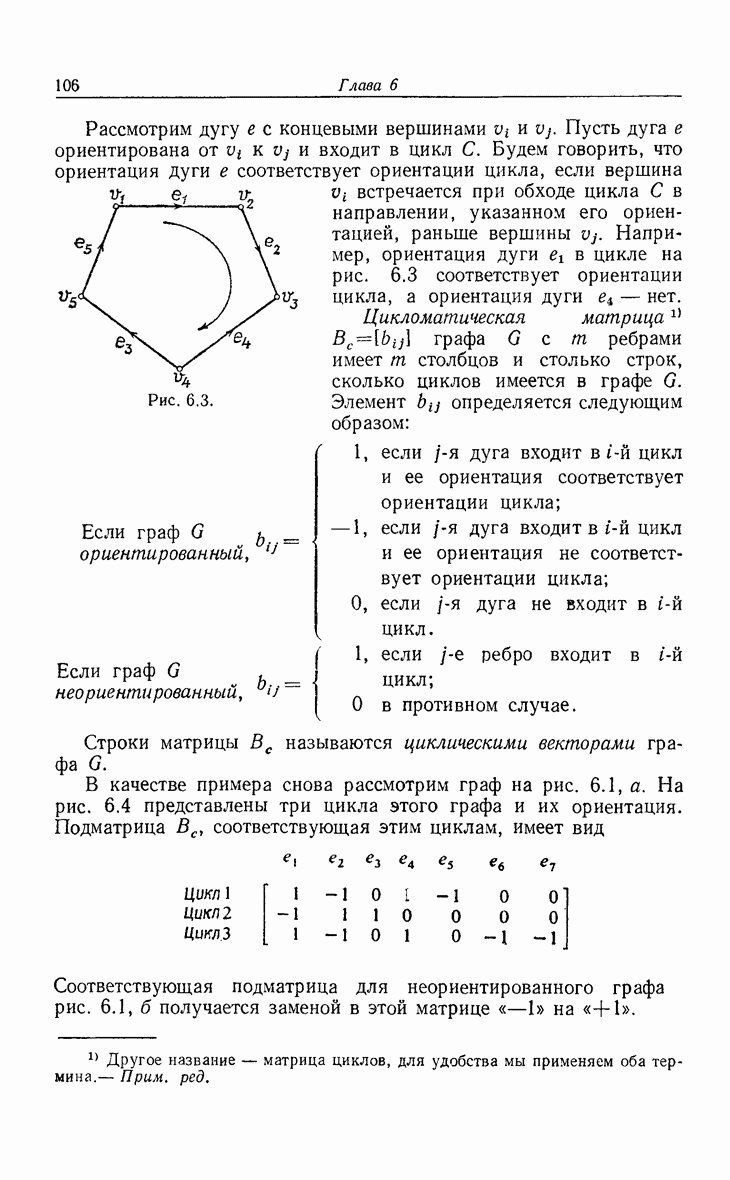
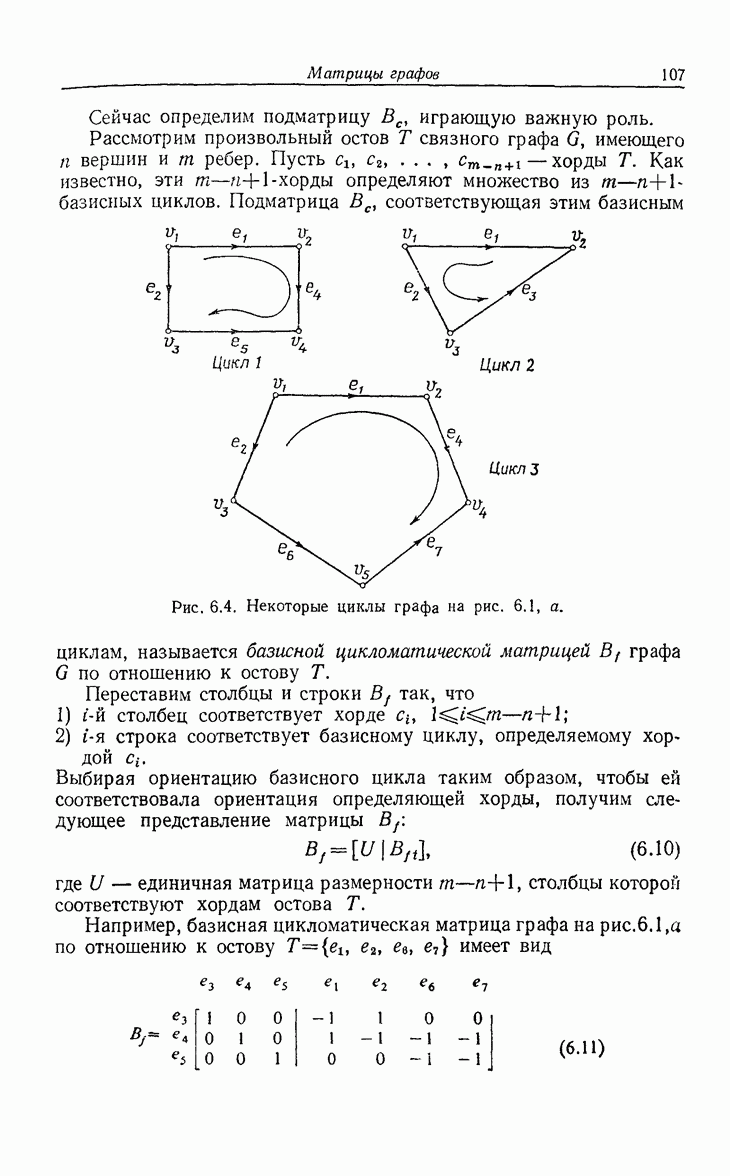
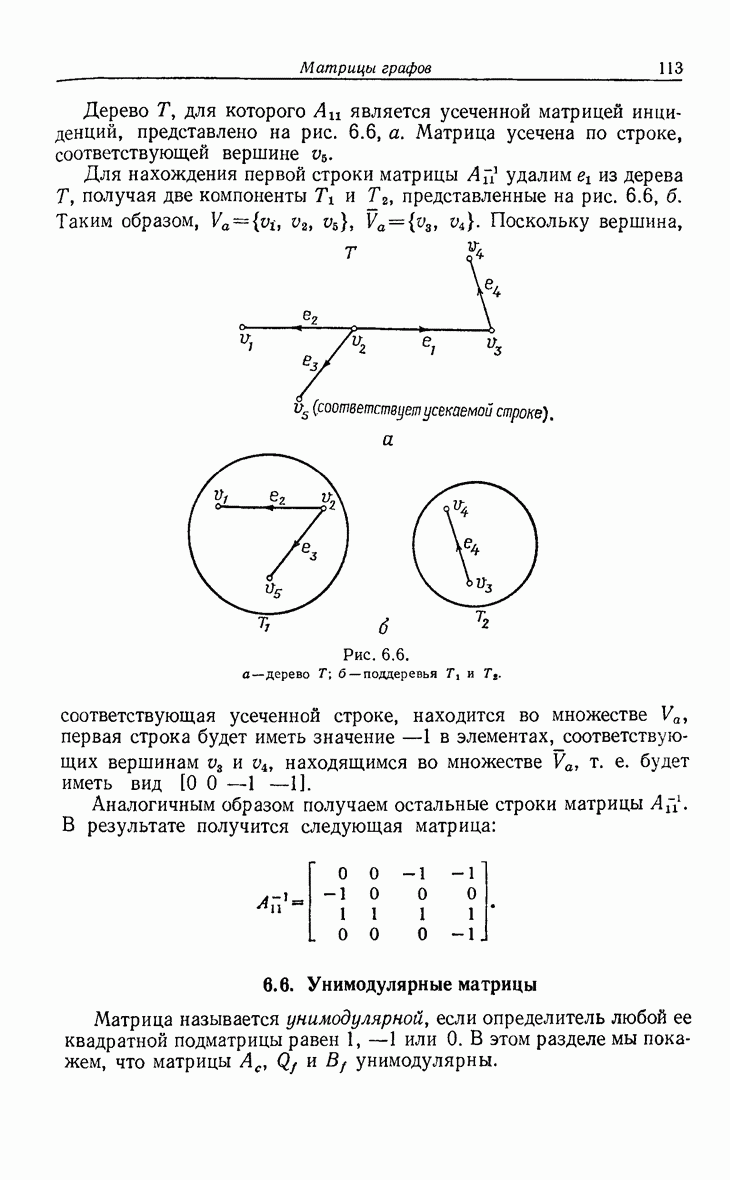
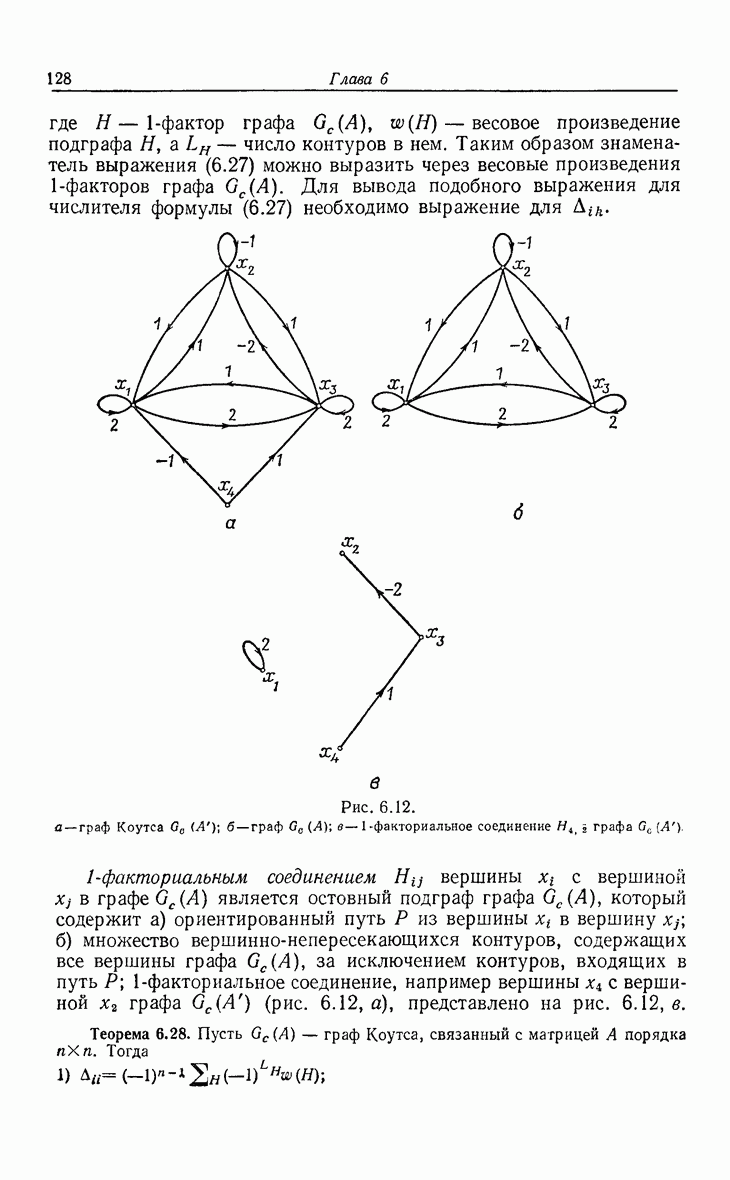
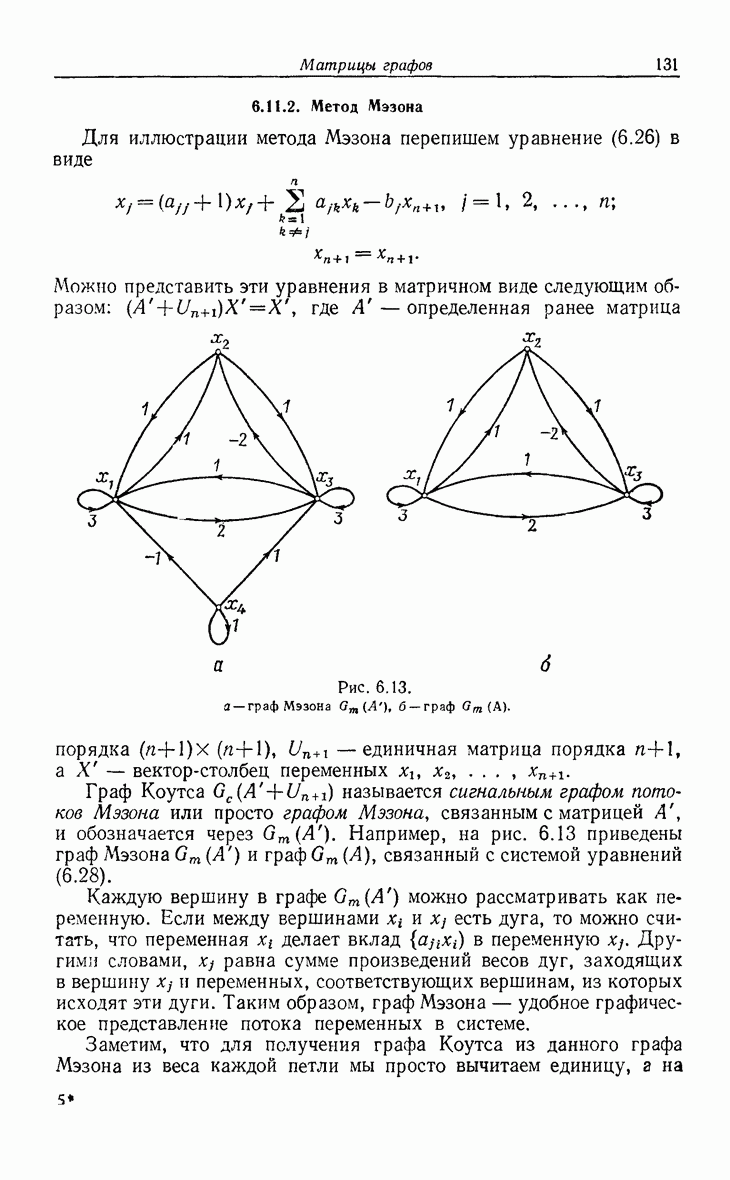
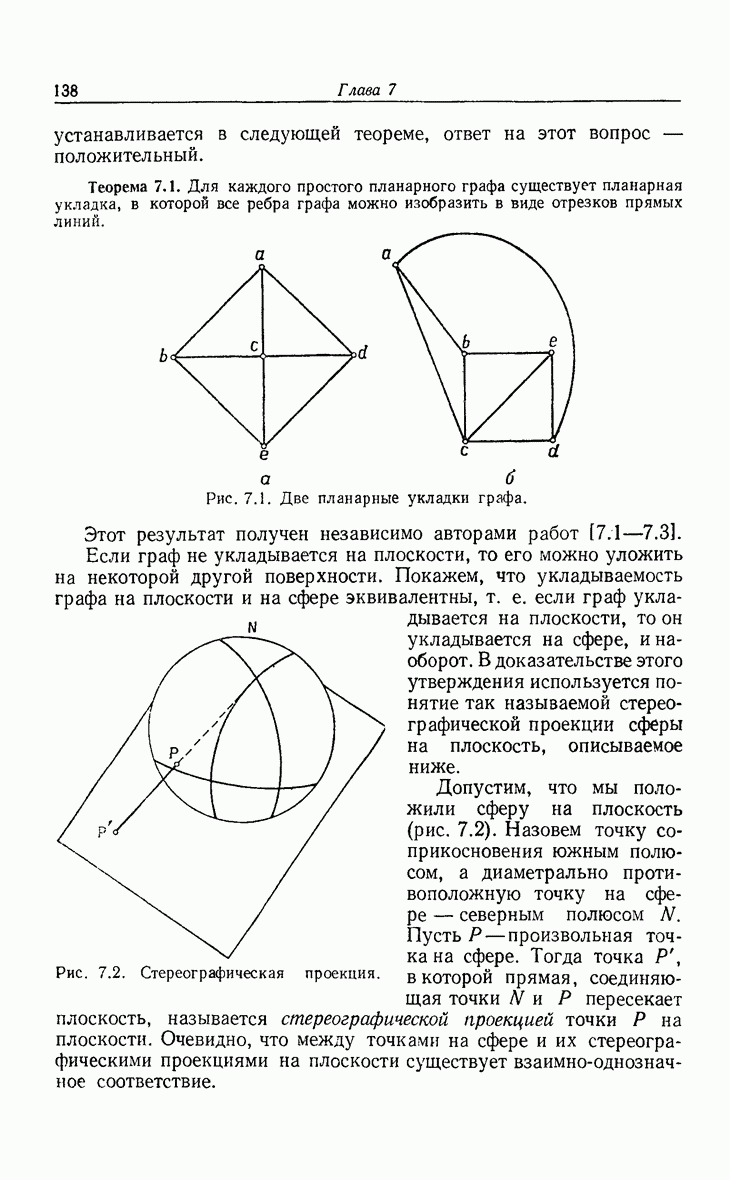
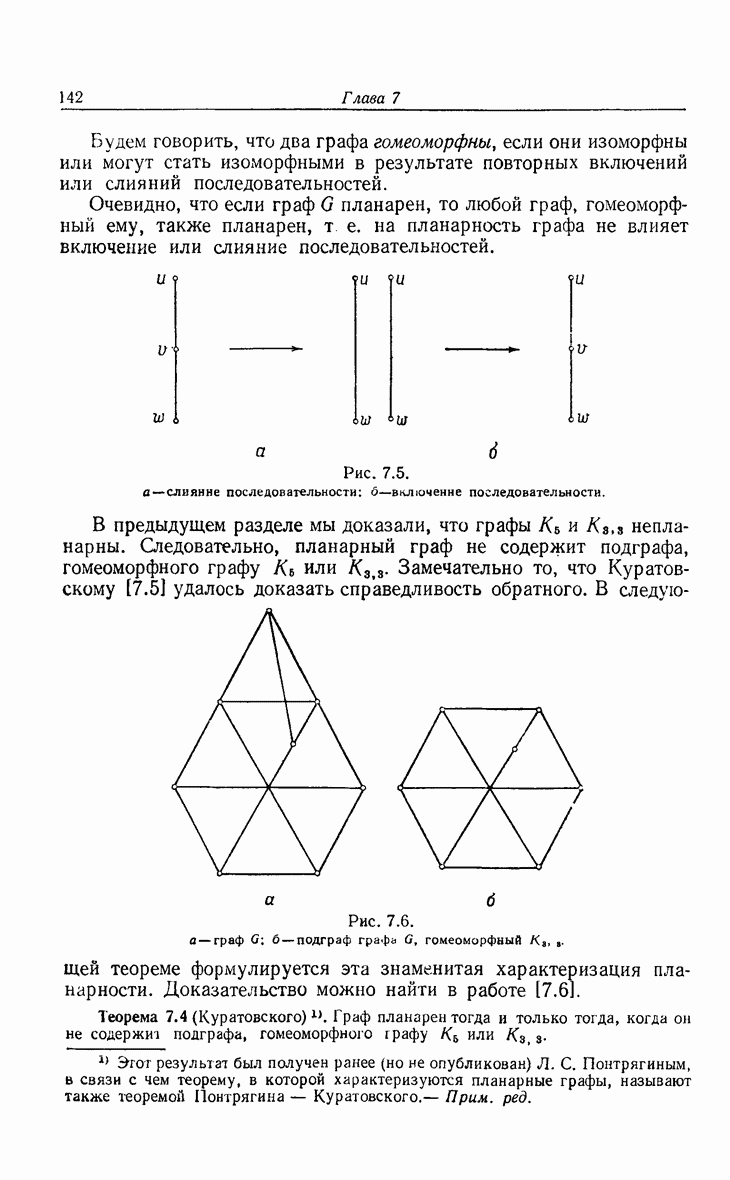
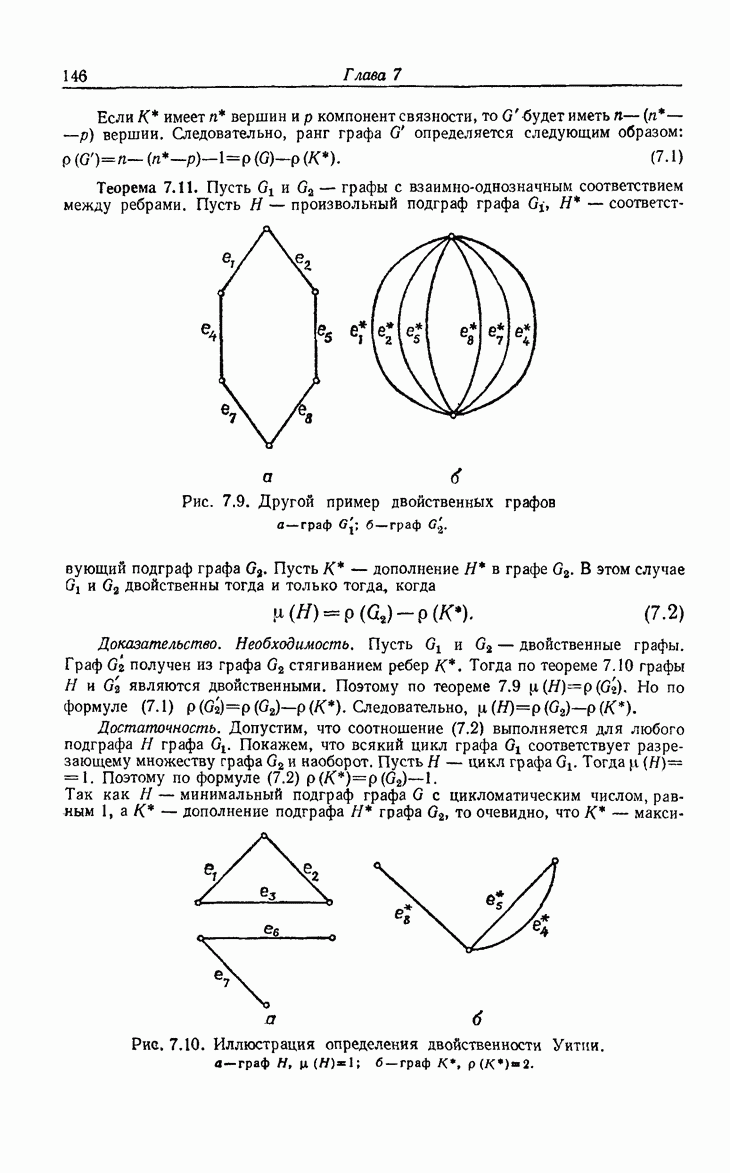
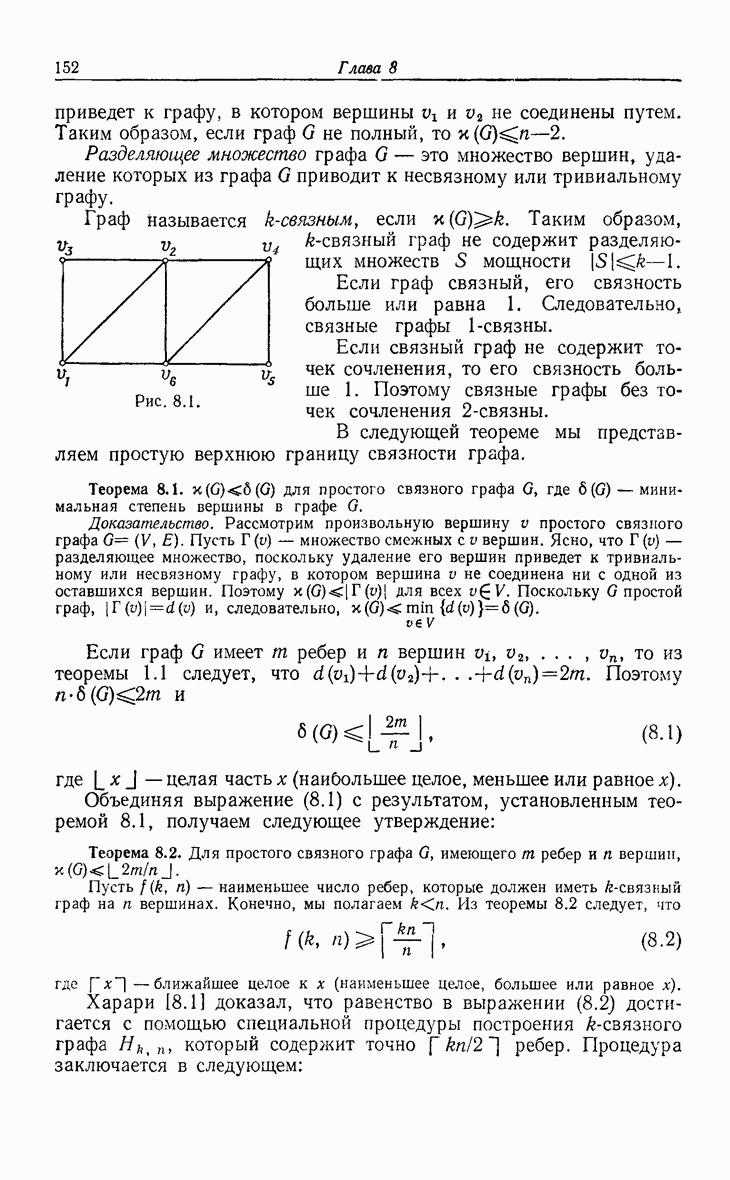
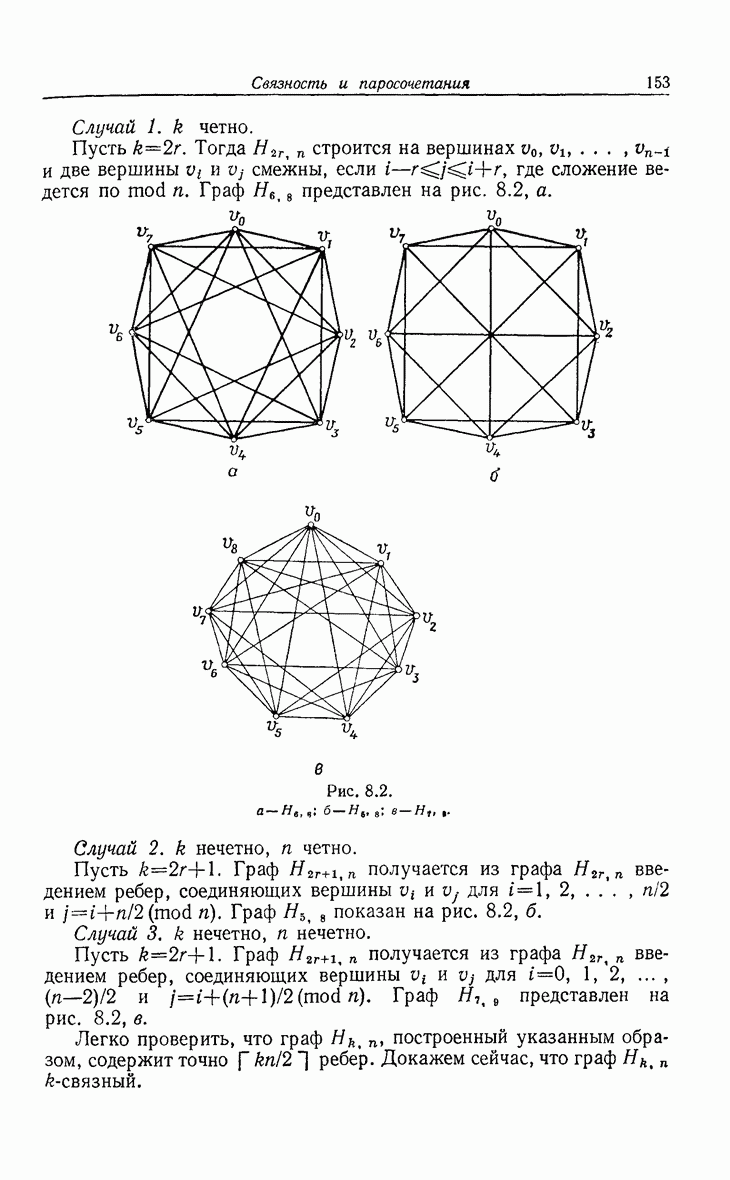
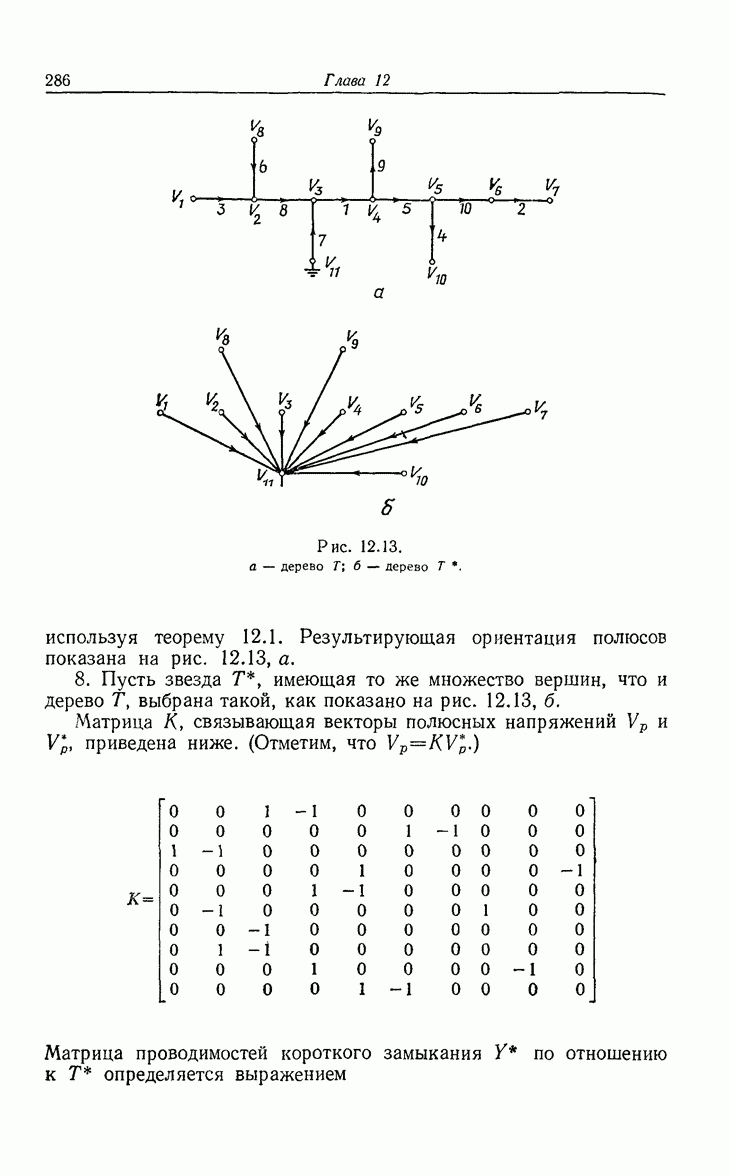
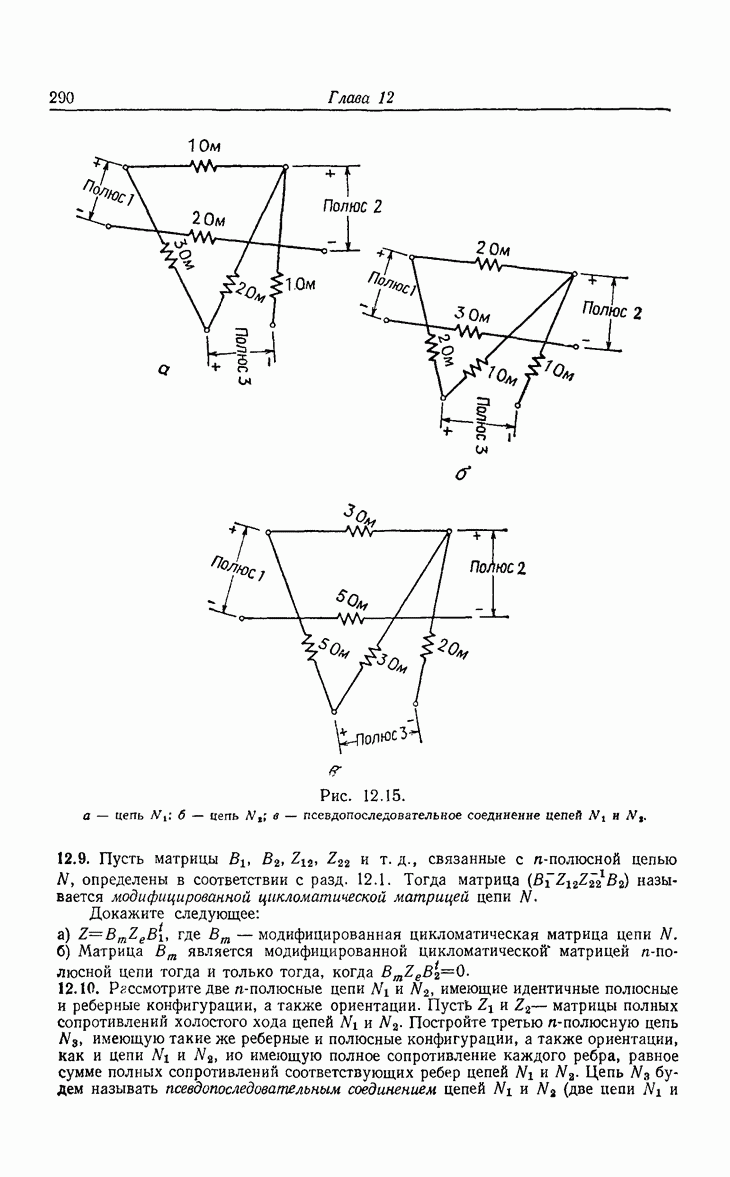
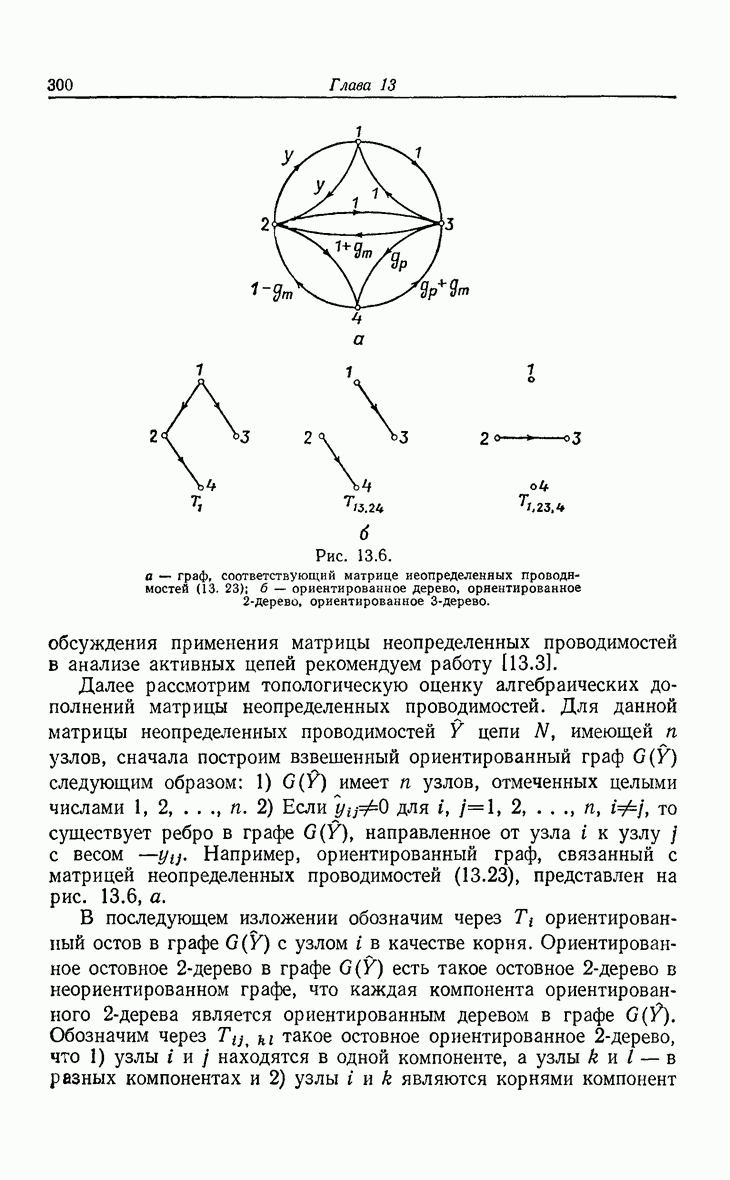
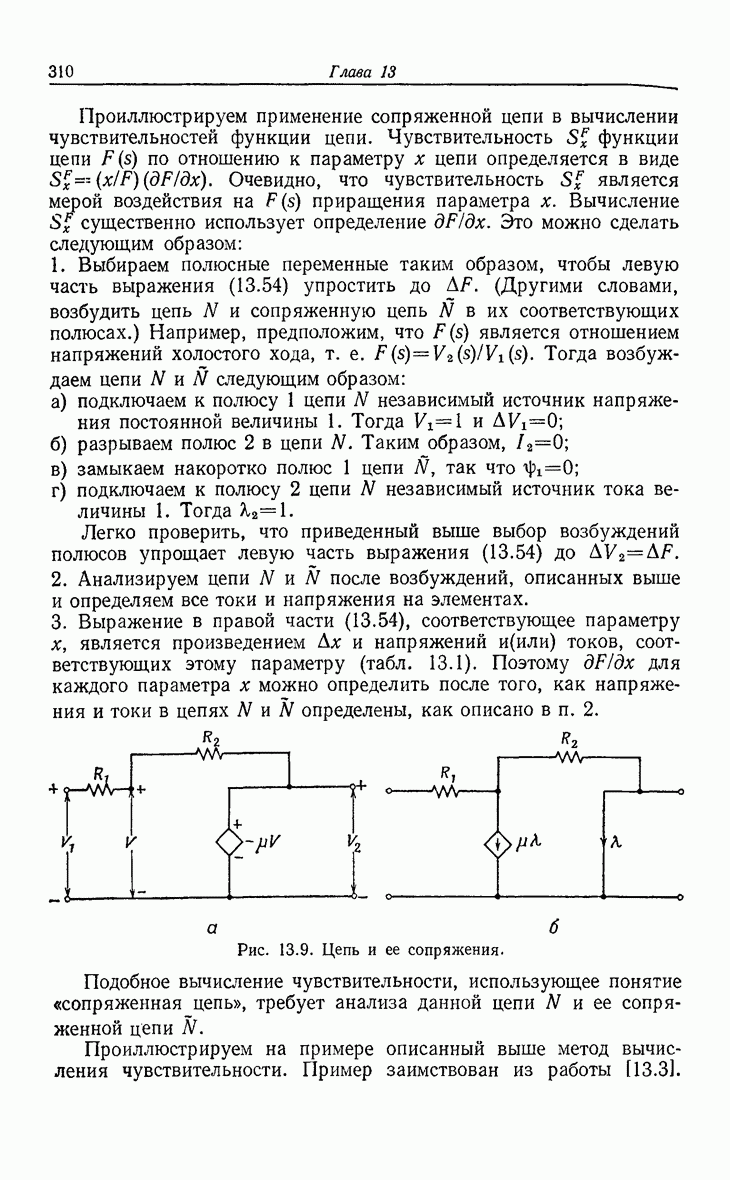
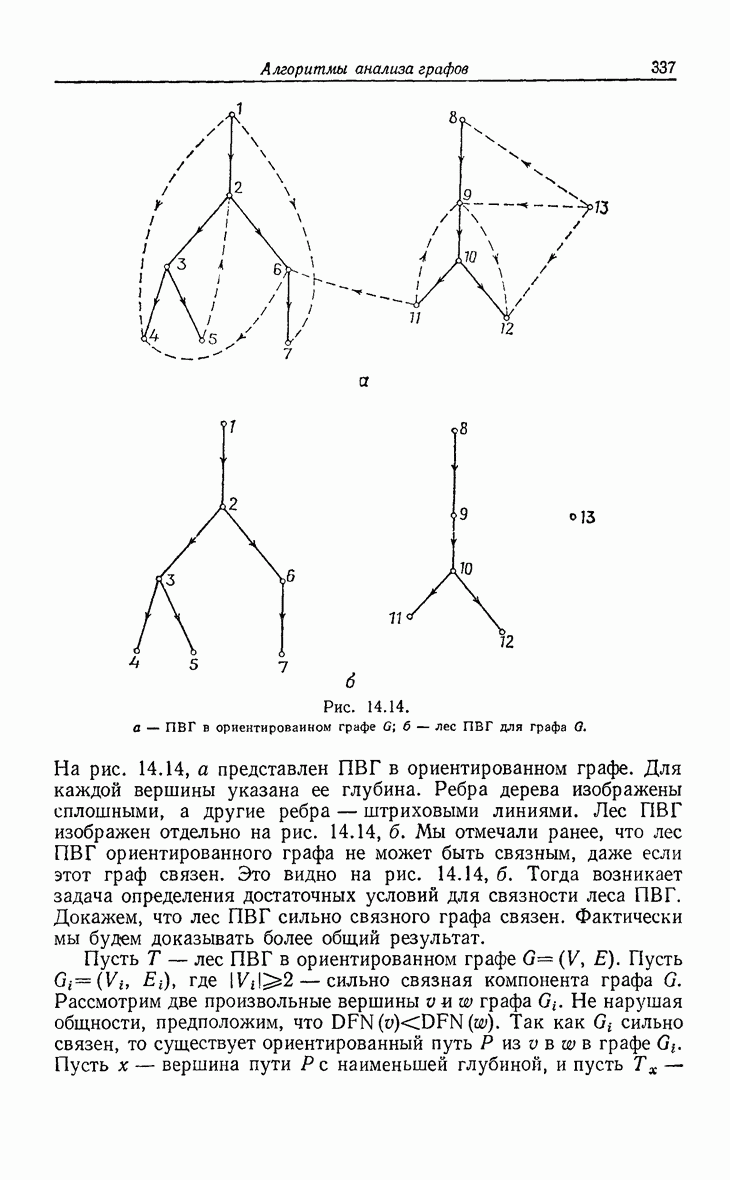
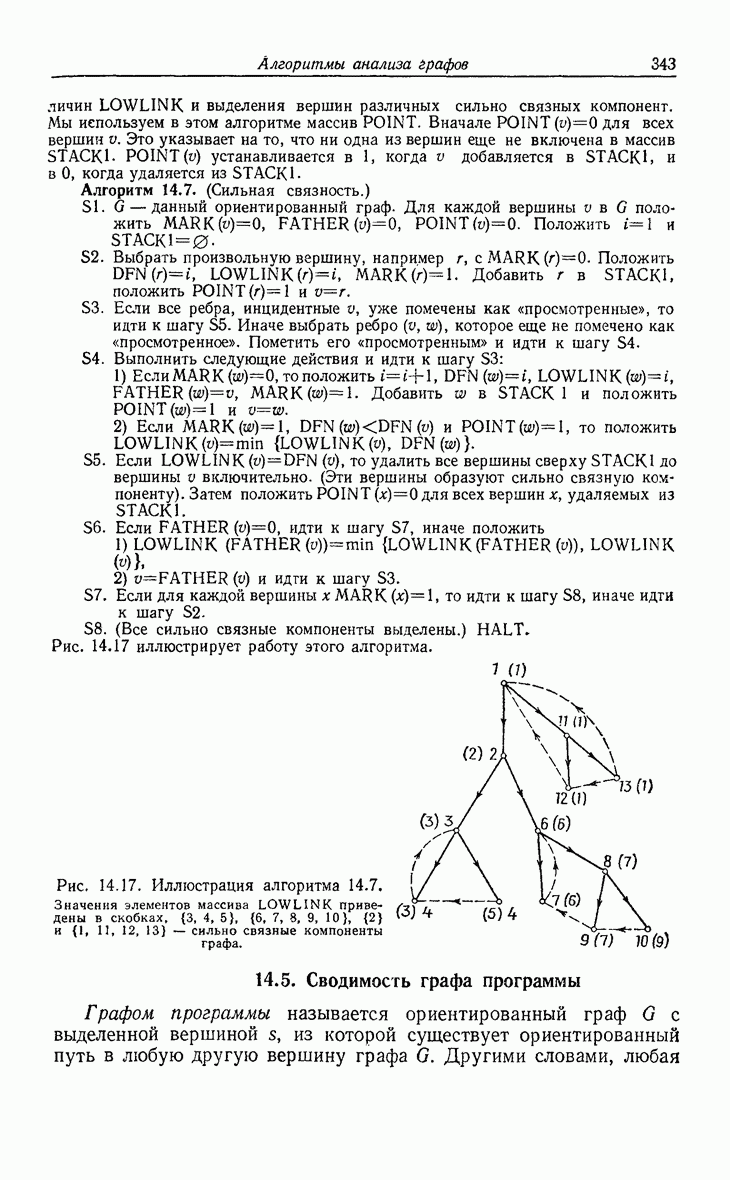
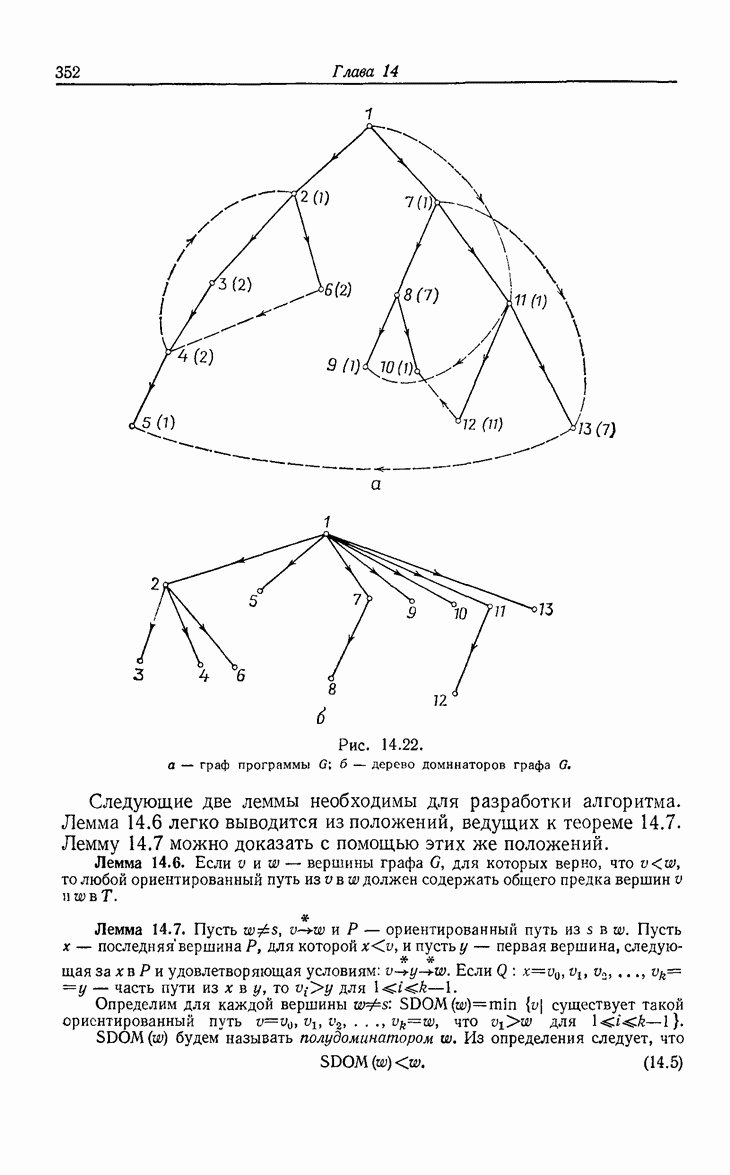
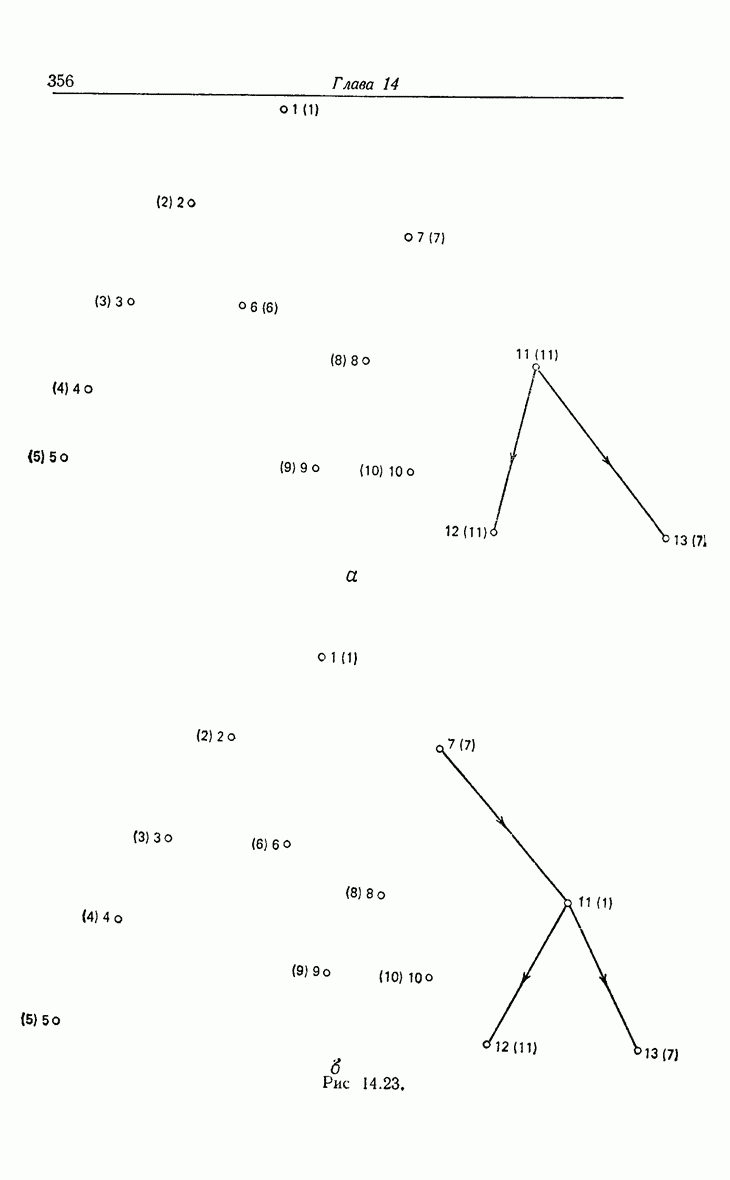
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Векторные пространства
Рассмотрим множество S с бинарной операцией  Пусть F — поле, где символы
Пусть F — поле, где символы  обозначают операции сложения и умножения соответственно. Пусть также определена операция умножения, обозначаемая символом
обозначают операции сложения и умножения соответственно. Пусть также определена операция умножения, обозначаемая символом  между элементами F и
между элементами F и  . Эта операция сопоставляет каждой упорядоченной паре
. Эта операция сопоставляет каждой упорядоченной паре  , где а принадлежит F, a s принадлежит
, где а принадлежит F, a s принадлежит  , единственный элемент множества S, обозначаемый
, единственный элемент множества S, обозначаемый  Множество S называется векторным пространством над полем F, если выполнены следующие аксиомы:
Множество S называется векторным пространством над полем F, если выполнены следующие аксиомы:
1)  — абелева группа относительно операции
— абелева группа относительно операции 
2) Для любых элементов  поля F и любых s и
поля F и любых s и  принадлежащих S, имеем
принадлежащих S, имеем 
3) Для любых элементов  , принадлежащих F, и любого элемента s из множества
, принадлежащих F, и любого элемента s из множества  имеет место равенство
имеет место равенство  Для любого элемента s множества
Для любого элемента s множества  выполняется равенство
выполняется равенство  , где
, где  — мультипликативный нулевой элемент поля F. Приведем важный пример векторного пространства.
— мультипликативный нулевой элемент поля F. Приведем важный пример векторного пространства.
Рассмотрим множество W всех  - векторов 11 над полем F. (Заметим, что элементы
- векторов 11 над полем F. (Заметим, что элементы  -векторов принадлежат F.) Символы
-векторов принадлежат F.) Символы  будут обозначать операции сложения и умножения в F соответственно, а
будут обозначать операции сложения и умножения в F соответственно, а  и
и  — аддитивный и мультипликативный нулевые элементы в F Пусть
— аддитивный и мультипликативный нулевые элементы в F Пусть  — операция сложения на множестве W, а — операция
— операция сложения на множестве W, а — операция
умножения между элементами F и W, определенные следующим образом:
1. Если  элементы
элементы  , то
, то 
2. Если а принадлежит F, то  . Нетрудно установить, что W — абелева группа относительно операции
. Нетрудно установить, что W — абелева группа относительно операции  в которой нулевым элементом считается
в которой нулевым элементом считается  -вектор
-вектор  Таким образом, множество W удовлетворяет первой аксиоме в определении векторного пространства. Легко убедиться в том, что элементы множеств W и F удовлетворяют и трем другим аксиомам этого определения.
Таким образом, множество W удовлетворяет первой аксиоме в определении векторного пространства. Легко убедиться в том, что элементы множеств W и F удовлетворяют и трем другим аксиомам этого определения.
Например, множество W, состоящее из восьми  -векторов, приведенных ниже, является векторным пространством над
-векторов, приведенных ниже, является векторным пространством над  Это векторное пространство будем использовать во всех, примерах данного раздела.
Это векторное пространство будем использовать во всех, примерах данного раздела.
Теперь приведем несколько важных определений и результатов (без доказательств), связанных с векторным пространством.
Рассмотрим векторное пространство S над полем 
Векторы и скаляры. Элементы множества  называются векторами, а элементы множества F — скалярами.
называются векторами, а элементы множества F — скалярами.
Линейная комбинация. Если элемент  множества S можно представить в виде
множества S можно представить в виде  где
где  — векторы, а
— векторы, а  — скаляры, то говорят, что s является линейной комбинацией
— скаляры, то говорят, что s является линейной комбинацией 
Линейная независимость. Векторы  — линейнонезависимы, если никакой из векторов этого множества нельзя представить в виде линейной комбинации остальных.
— линейнонезависимы, если никакой из векторов этого множества нельзя представить в виде линейной комбинации остальных.
Базисные векторы. Векторы  образуют базис в векторном пространстве S, если они линейно-независимы и любой вектор в этом пространстве можно представить в виде линейной комбинации этих векторов. Векторы
образуют базис в векторном пространстве S, если они линейно-независимы и любой вектор в этом пространстве можно представить в виде линейной комбинации этих векторов. Векторы  называются базисными. Представление вектора в виде линейной комбинации базисных векторов единственно для данного базиса. Векторное пространство может иметь и несколько базисов. Однако можно доказать, что все базисы, имеют одинаковое число векторов.
называются базисными. Представление вектора в виде линейной комбинации базисных векторов единственно для данного базиса. Векторное пространство может иметь и несколько базисов. Однако можно доказать, что все базисы, имеют одинаковое число векторов.
Размерность. Размерность векторного пространства S, обозначаемая  определяется числом базисных векторов в базисе S. Подпространство. Если S — подмножество векторного пространства S над полем F, то S — подпространство пространства S, если S также векторное пространство над
определяется числом базисных векторов в базисе S. Подпространство. Если S — подмножество векторного пространства S над полем F, то S — подпространство пространства S, если S также векторное пространство над 
Прямая сумма. Прямой суммой  двух подпространств и
двух подпространств и  пространства S называется множество всех векторов вида
пространства S называется множество всех векторов вида  , где
, где  — принадлежит подпространству
— принадлежит подпространству  — подпространству
— подпространству  также является подпространством, и размерность его определяется следующим образом:
также является подпространством, и размерность его определяется следующим образом: 
 . Заметим, что если
. Заметим, что если  подпространства, то
подпространства, то  также подпространство. Проиллюстрируем эти определения с помощью векторного подпространства W
также подпространство. Проиллюстрируем эти определения с помощью векторного подпространства W  -векторов над полем GF (2). Векторы
-векторов над полем GF (2). Векторы  принадлежащие подпространству W, определены ранее.
принадлежащие подпространству W, определены ранее.
1.  — линейная комбинация
— линейная комбинация  поскольку
поскольку 
2. Векторы  — линейно-независимы, так как ни один из них нельзя выразить через другой. Следует отметить, что
— линейно-независимы, так как ни один из них нельзя выразить через другой. Следует отметить, что  линейно-независимы для любого
линейно-независимы для любого 
3. Векторы  образуют в пространстве W базис, поскольку они линейно-независимы, а оставшиеся векторы, как показано ниже, можно представить в виде линейной комбинации этих векторов:
образуют в пространстве W базис, поскольку они линейно-независимы, а оставшиеся векторы, как показано ниже, можно представить в виде линейной комбинации этих векторов:  Можно проверить, что векторы
Можно проверить, что векторы  , также образуют базис.
, также образуют базис.
4. Размерность векторного пространства W равна 3, так как три вектора образуют его базис.
5. Множества  — подпространства пространства W. Базисами
— подпространства пространства W. Базисами  являются
являются  соответственно. Таким образом,
соответственно. Таким образом, 
6. Если  и W" определены как в п. 5, то
и W" определены как в п. 5, то 
7. Размерность  определяется следующим равенством:
определяется следующим равенством:  (ГПГ).
(ГПГ).
Поскольку  имеем
имеем  Таким образом, получаем
Таким образом, получаем  Того же самого результата можно достичь с учетом
Того же самого результата можно достичь с учетом 
Теперь определим изоморфизм между двумя векторными пространствами над одним и тем же полем.
Пусть S и S — два n-мерных векторных подпространства над полем F. Говорят, что S и S изоморфны, если между ними существует такое взаимно-однозначное соответствие, что справедливы утверждения:
1. Если векторам s, и  принадлежащим подпространству S, соответствуют векторы и
принадлежащим подпространству S, соответствуют векторы и  пространства S, то вектору
пространства S, то вектору  соответствует вектор
соответствует вектор  где
где  и А — операции в S и S соответственно.
и А — операции в S и S соответственно.
2. Для любого а в поле F вектору  соответствует вектор a A s, если вектор s пространства S соответствует вектору s пространства
соответствует вектор a A s, если вектор s пространства S соответствует вектору s пространства  , где и А — операции в
, где и А — операции в  соответственно.
соответственно.
Рассмотрим  -мерное векторное пространство S над полем F и
-мерное векторное пространство S над полем F и  -мерное векторное пространство W векторов над полем F. Пусть
-мерное векторное пространство W векторов над полем F. Пусть
векторы  образуют базис в пространстве S. Сопоставим вектору s из пространства S вектор
образуют базис в пространстве S. Сопоставим вектору s из пространства S вектор  из пространства W тогда и только тогда, когда
из пространства W тогда и только тогда, когда 
Нетрудно видеть, что это взаимно-однозначное соответствие определяет изоморфизм между пространствами  и
и 
Таким образом, сформулируем следующий важный вывод:
Теорема 4.1. Любое  -мерное векторное пространство над полем F является изоморфным векторному пространству W
-мерное векторное пространство над полем F является изоморфным векторному пространству W  -векторов над полем
-векторов над полем 
Эта теорема является главным звеном, связывающим векторные пространства и матрицы. Она предполагает, что  -мерное векторное пространство над полем F можно исследовать с использованием
-мерное векторное пространство над полем F можно исследовать с использованием  -мерного векторного пространства W всех
-мерного векторного пространства W всех  -векторов над полем
-векторов над полем 
Завершим этот раздел определением двух наиболее важных понятий — скалярное произведение и ортогональность. Пусть  — два элемента векторного пространства W
— два элемента векторного пространства W  -векторов над полем F. Скалярным произведением
-векторов над полем F. Скалярным произведением  обозначаемым через
обозначаемым через  называется скаляр, определяемый выражением
называется скаляр, определяемый выражением  . Например, если
. Например, если  то
то  Векторы
Векторы  ортогональны относительно друг друга, если
ортогональны относительно друг друга, если  , где 0 — аддитивный нулевой элемент поля F. Например, векторы
, где 0 — аддитивный нулевой элемент поля F. Например, векторы  ортогональны над полем GF (2), поскольку
ортогональны над полем GF (2), поскольку  Два подпространства W и W" векторного пространства W являются ортогональными подпространствами этого же пространства, если каждый вектор одного подпространства ортогонален любому вектору другого подпространства. Два подпространства W и W" пространства W называются ортогональными дополнениями пространства W, если они ортогональны друг другу и их прямая сумма
Два подпространства W и W" векторного пространства W являются ортогональными подпространствами этого же пространства, если каждый вектор одного подпространства ортогонален любому вектору другого подпространства. Два подпространства W и W" пространства W называются ортогональными дополнениями пространства W, если они ортогональны друг другу и их прямая сумма  равна векторному пространству W. В качестве примера вновь рассмотрим
равна векторному пространству W. В качестве примера вновь рассмотрим  -мерное векторное пространство W
-мерное векторное пространство W  -векторов над полем GF (2). В этом векторном пространстве подпространства
-векторов над полем GF (2). В этом векторном пространстве подпространства  ортогональны Друг другу. Нетрудно убедиться, что прямая сумма W и W" равна W. Следовательно, они являются ортогональными дополнениями.
ортогональны Друг другу. Нетрудно убедиться, что прямая сумма W и W" равна W. Следовательно, они являются ортогональными дополнениями.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Часть I. Теория графов
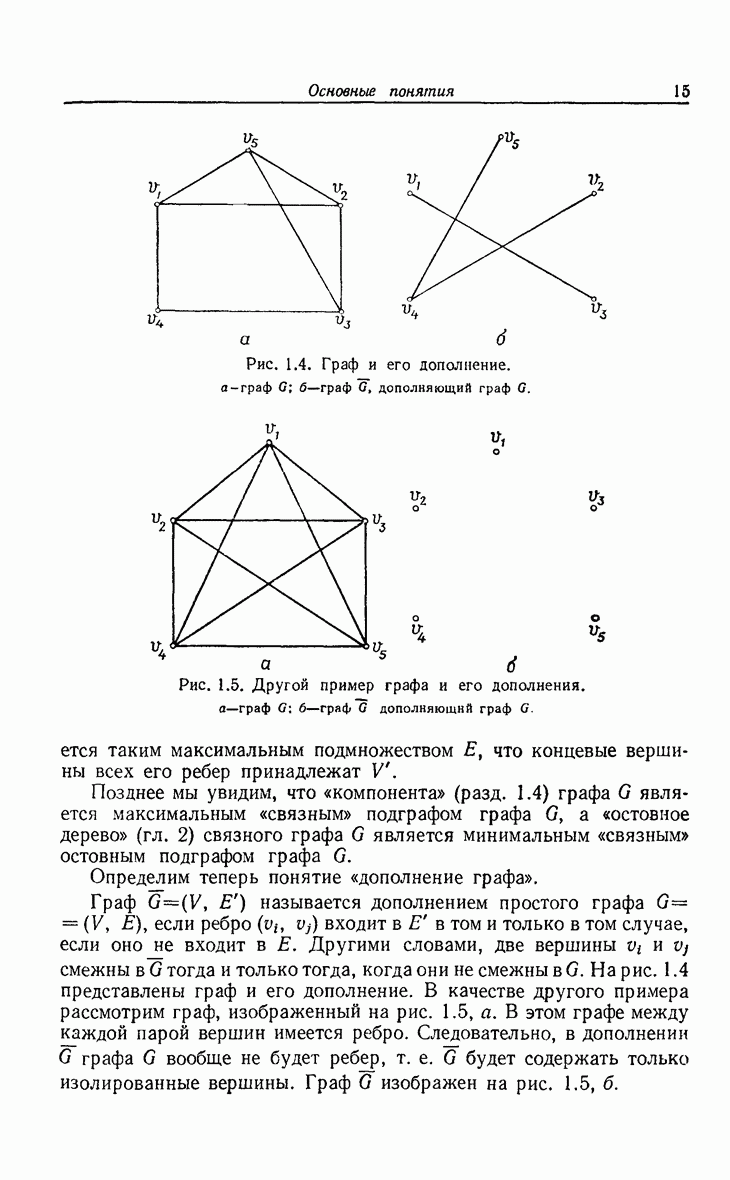
- 1.2. Подграфы и дополнения
- 1.3. Маршруты, цепи, пути и циклы
- 1.4. Связность и компоненты графа
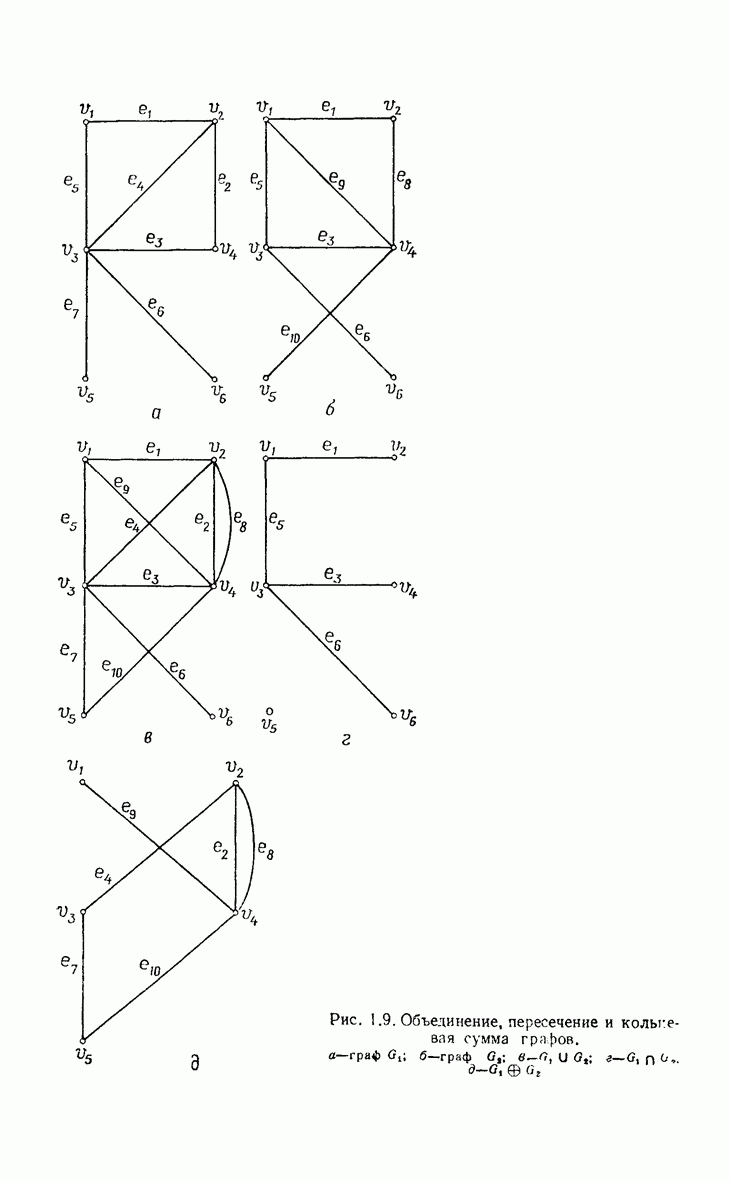
- 1.5. Операции над графами
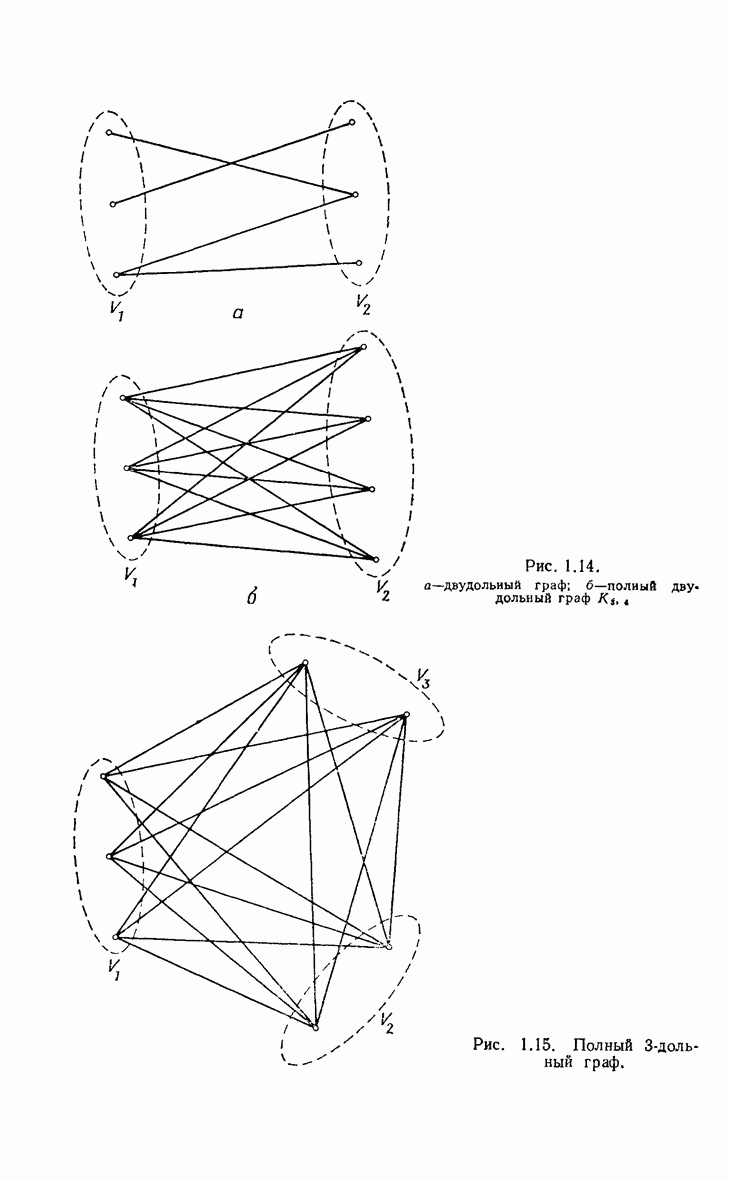
- 1.6. Специальные графы
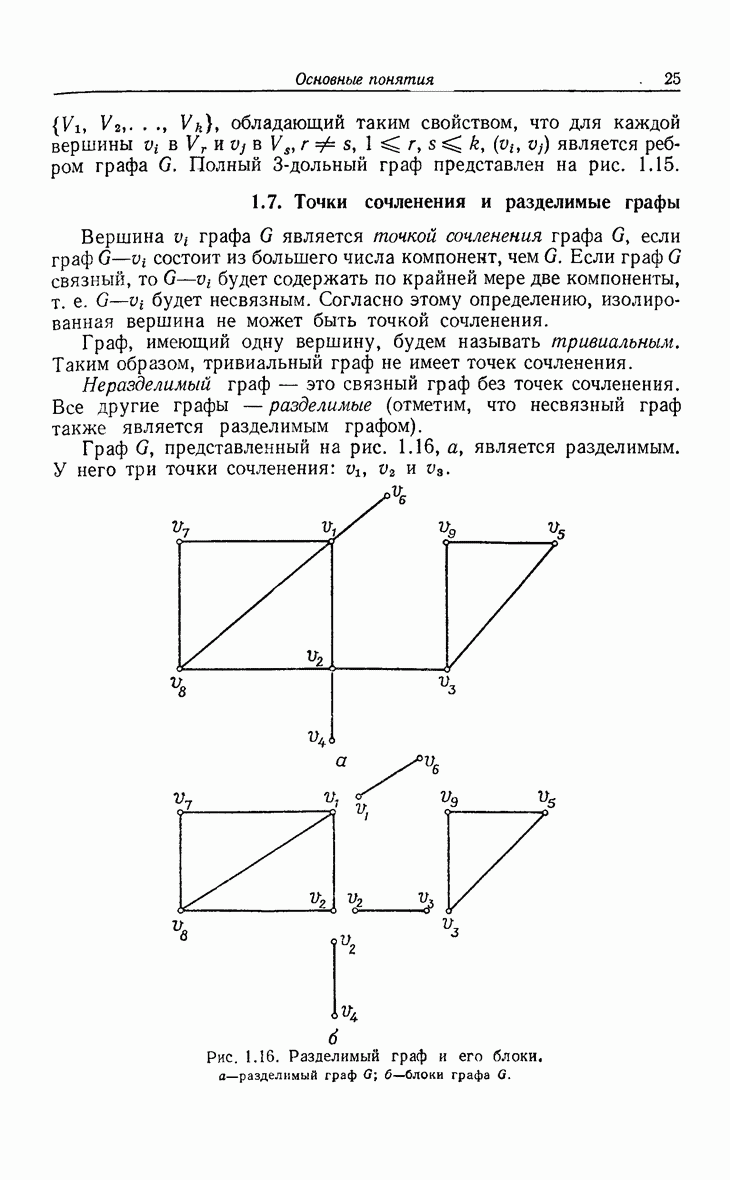
- 1.7. Точки сочленения и разделимые графы
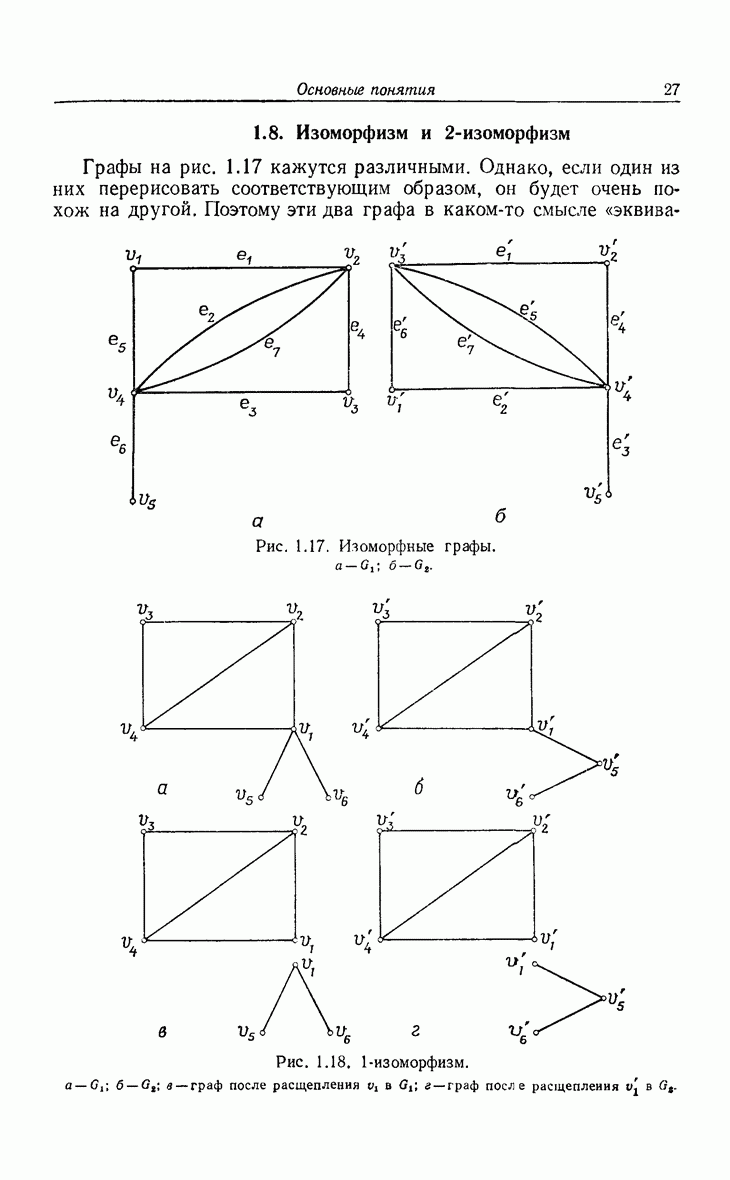
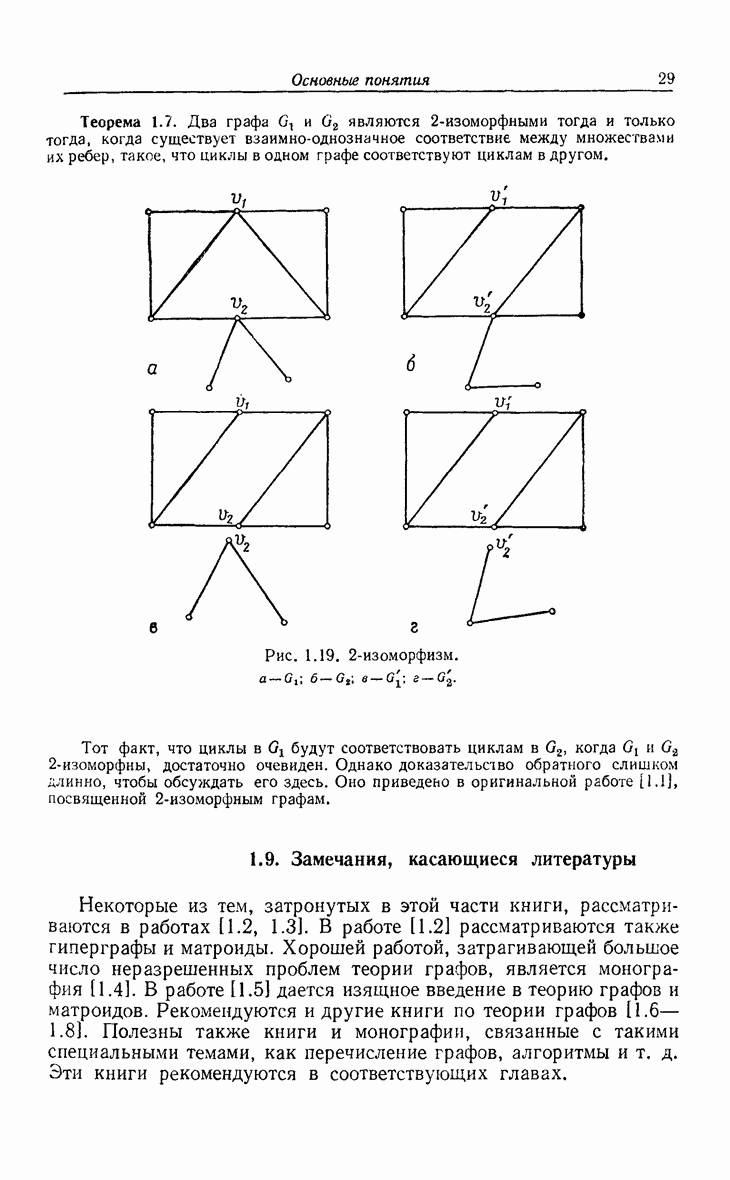
- 1.8. Изоморфизм и 2-изоморфизм
- 1.9. Замечания, касающиеся литературы
- Упражнения
- 2. Деревья, разрезающие множества и циклы
- 2.1. Деревья, остовы и кодеревья
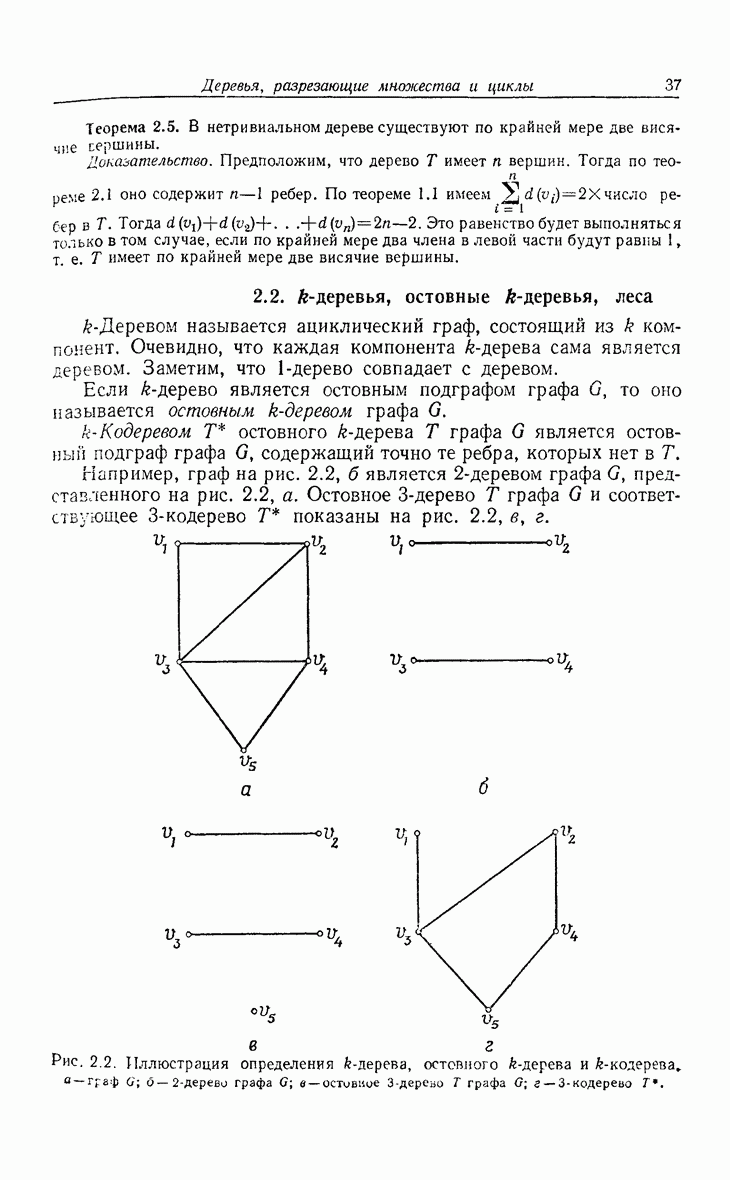
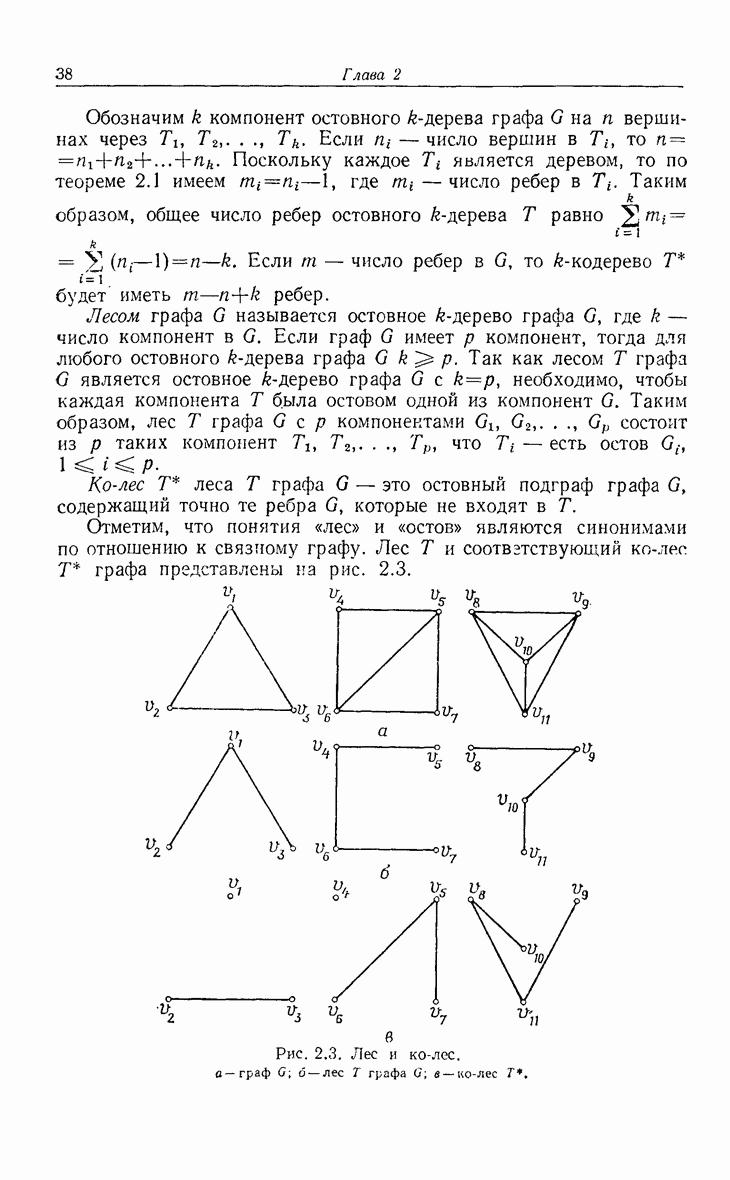
- 2.2. k-деревья, остовные k-деревья, леса
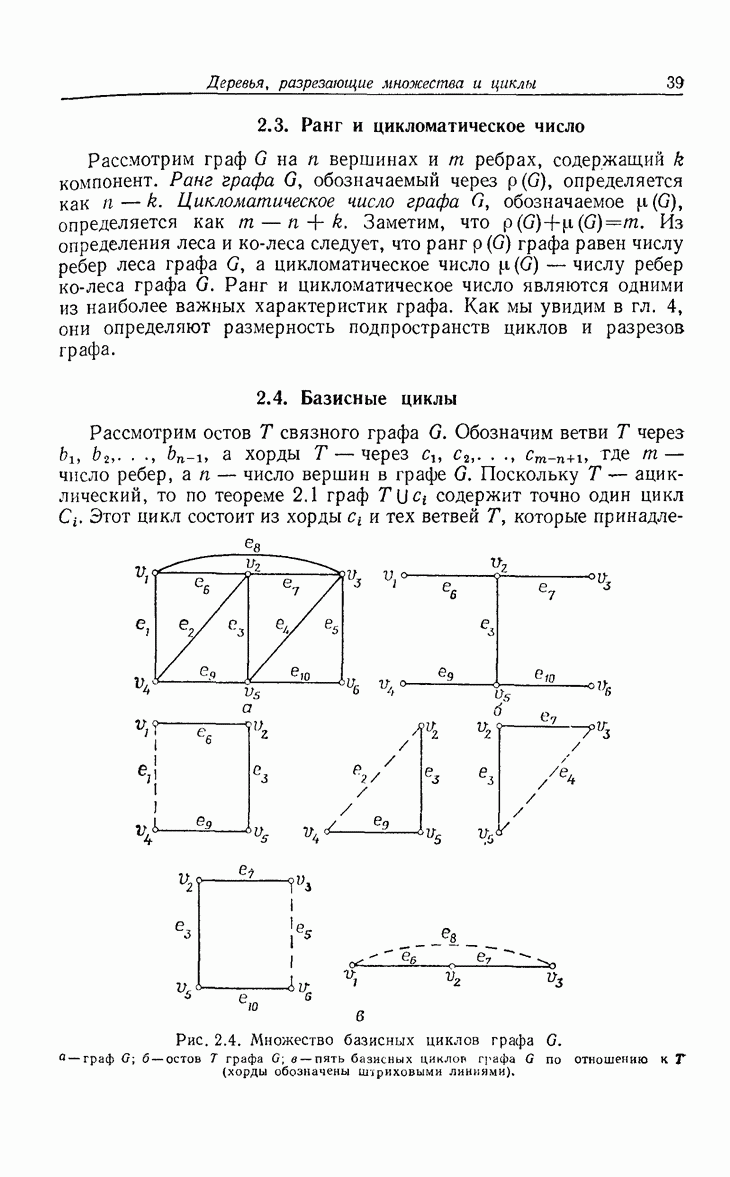
- 2.4. Базисные циклы
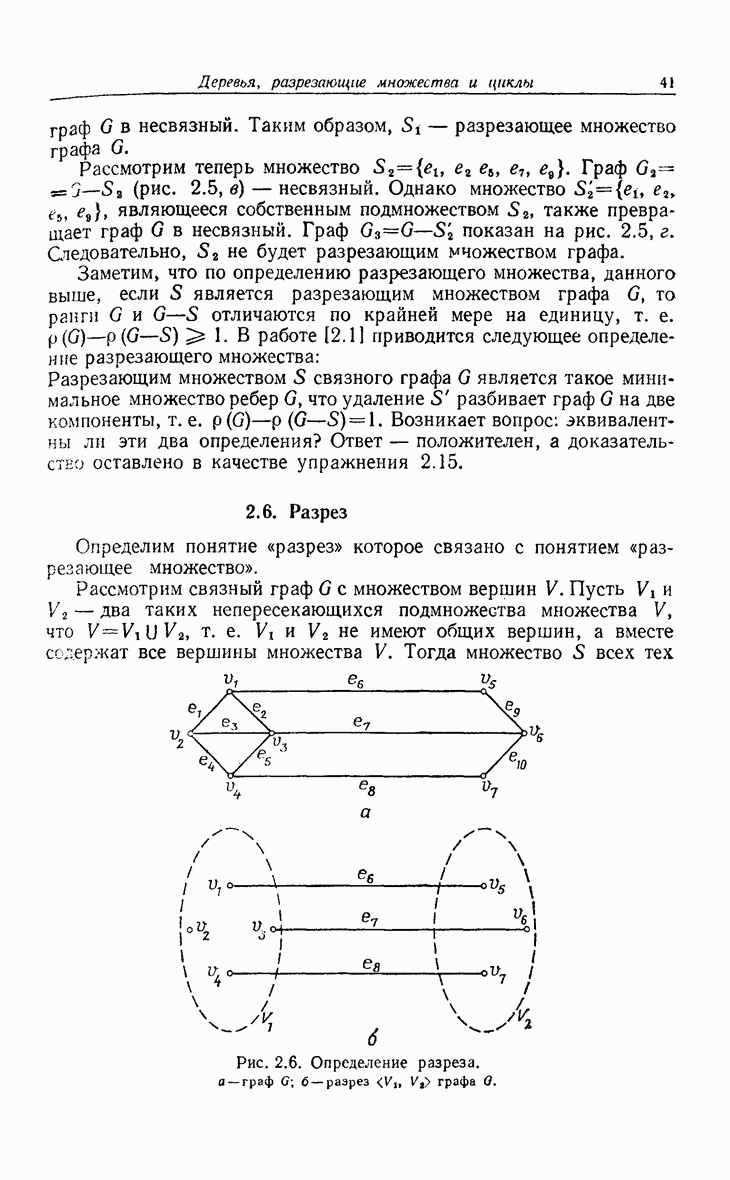
- 2.5. Разрезающие множества
- 2.6. Разрез
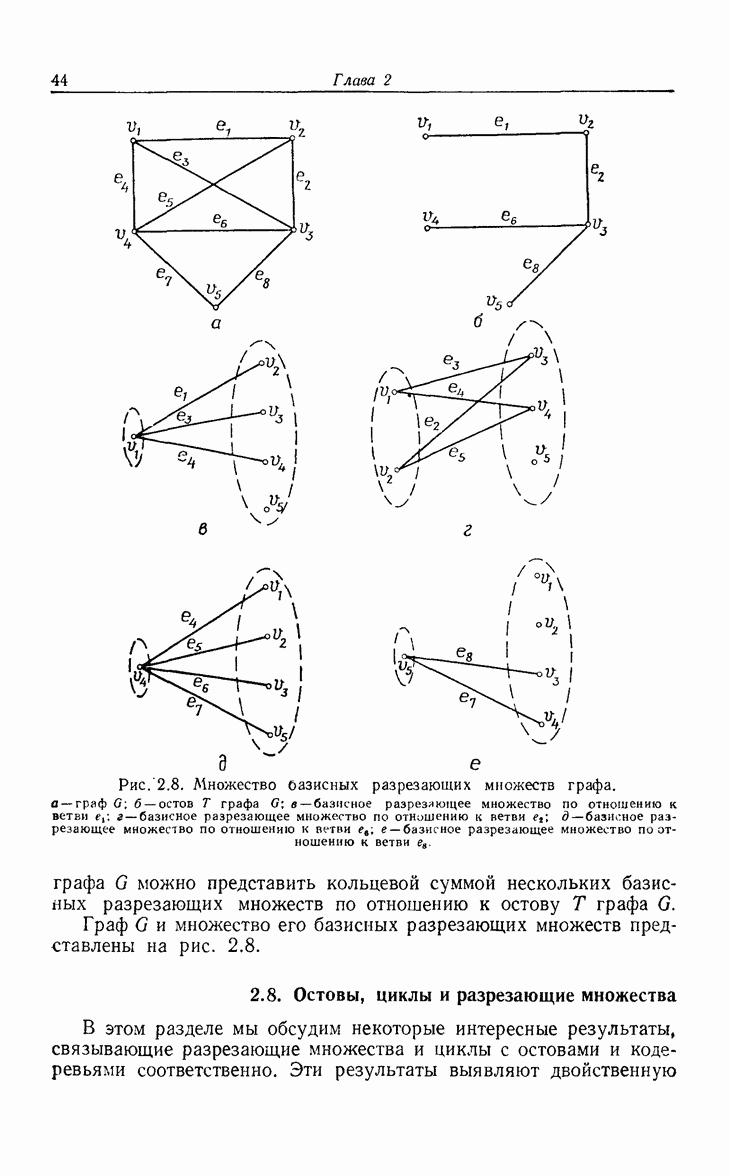
- 2.7. Базисные разрезающие множества
- 2.8. Остовы, циклы и разрезающие множества
- 2.9. Замечения, касающиеся литературы
- Упражнения
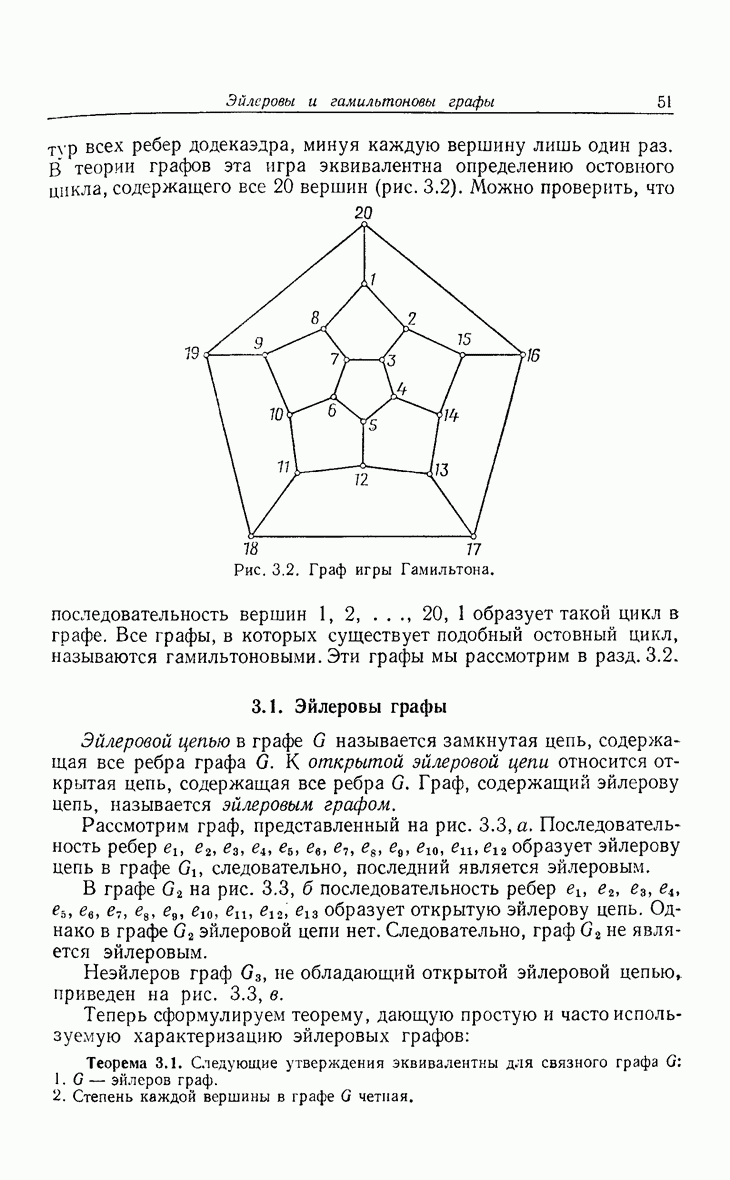
- 3. Эйлеровы и гамильтоновы графы
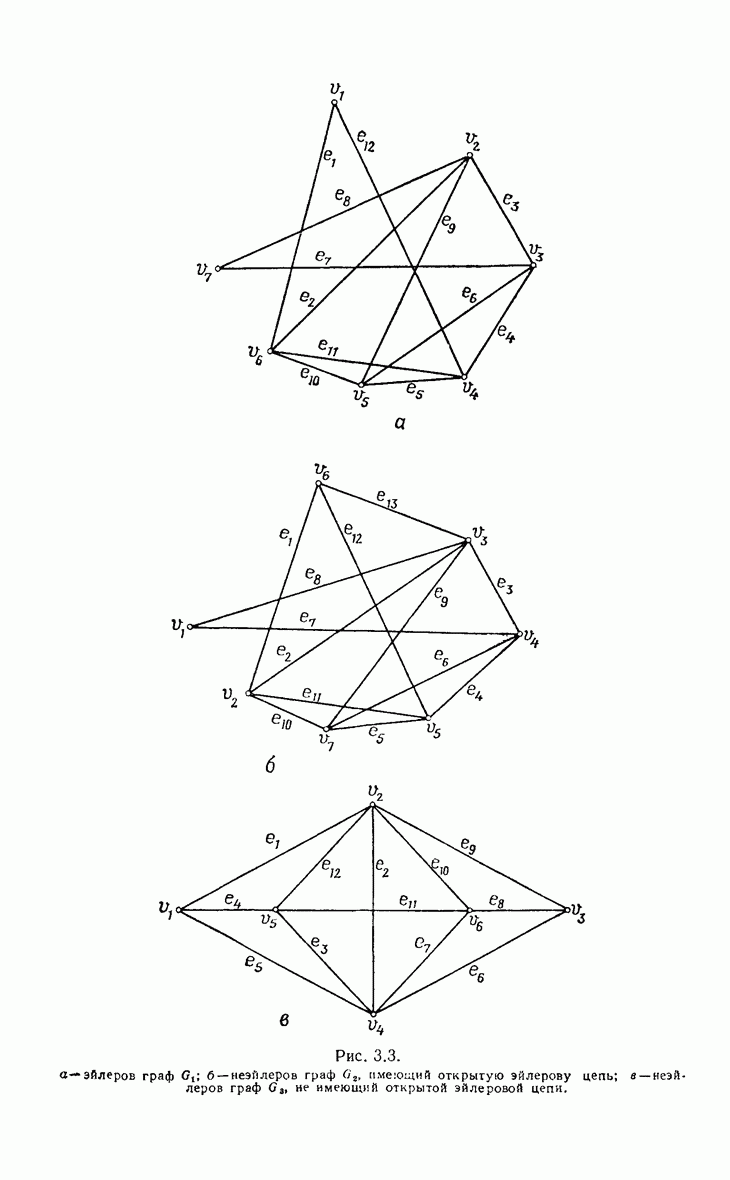
- 3.1. Эйлеровы графы
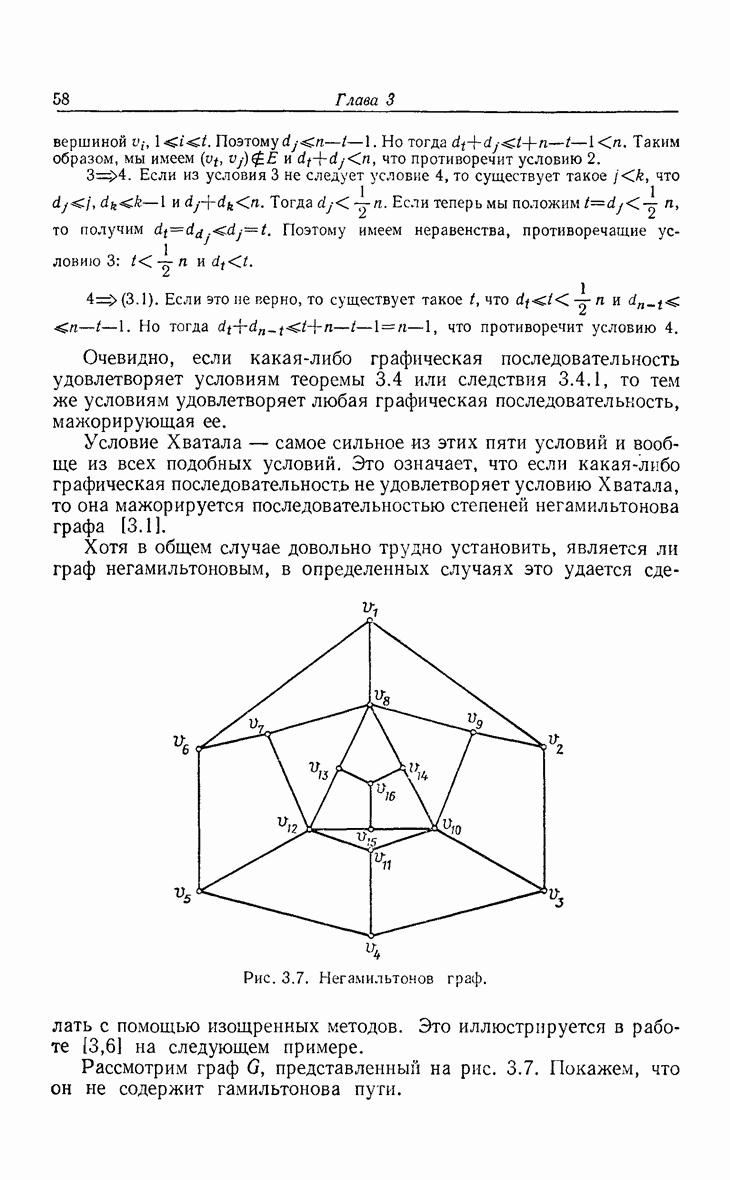
- 3.2. Гамильтоновы графы
- 3.3. Замечания, касающиеся литературы
- Упражнения
- 4. Графы и векторные пространства
- 4.2. Векторные пространства
- 4.3. Векторное пространство графа
- 4.4. Размерность подпространств циклов и разрезов
- 4.5. Связь между подпространствами циклов и разрезов
- 4.6. Ортогональность подпространств циклов и разрезов
- 4.7. Замечания, касающиеся литературы
- Упражнения
- 5. Ориентированные графы
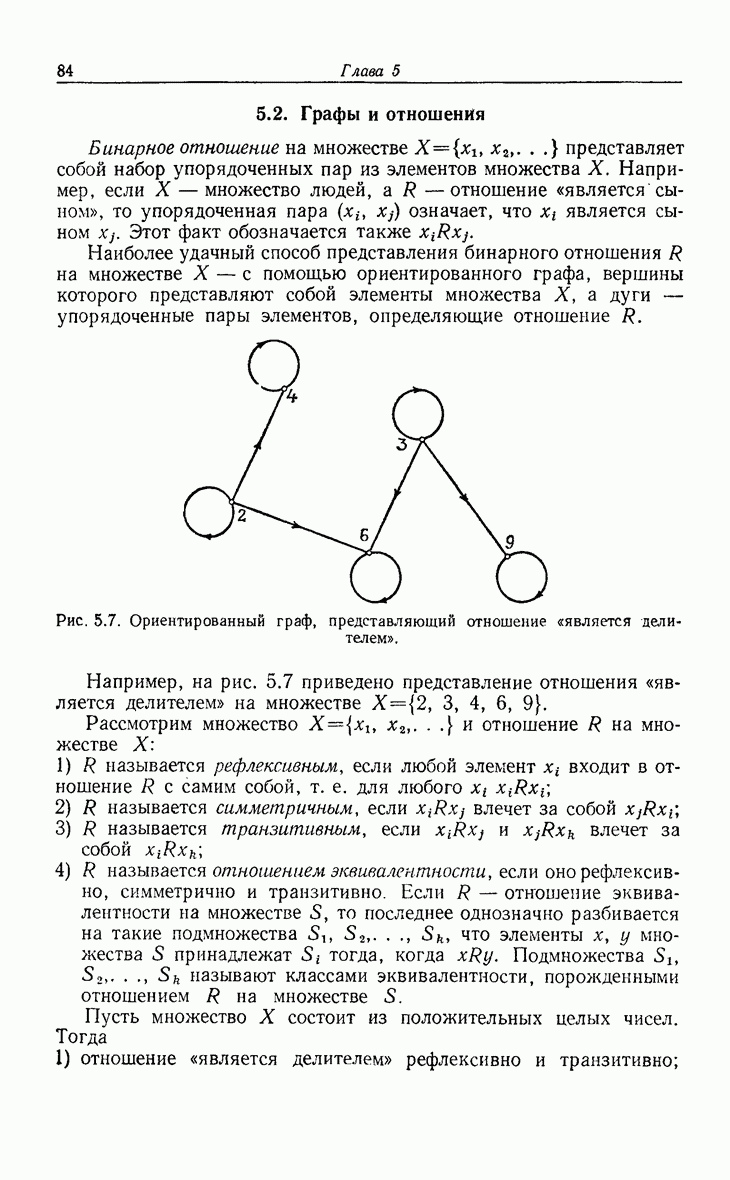
- 5.2. Графы и отношения
- 5.3. Ориентированные или корневые деревья
- 5.4. Ориентированные эйлеровы графы
- 5.5. Ориентированные остовы и ориентированные эйлеровы цепи
- 5.6. Ориентированные гамильтоновы графы
- 5.7. Ациклические ориентированные графы
- 5.8. Турниры
- 5.9. Замечания, касающиеся литературы
- Упражнения
- 6. Матрицы графов
- 6.2. Матрица разрезов
- 6.3. Цикломатическая матрица
- 6.4. Соотношение ортогональности
- 6.5. Подматрицы матриц разрезов, инциденций и циклов
- 6.6. Унимодулярные матрицы
- 6.7. Число остовов
- 6.8 Число остовных 2-деревьев
- 6.9 Число ориентированных остовов в ориентированном графе
- 6.10. Матрица смежности
- 6.11. Графы Коутса и Мэзона
- 6.12. Замечания, касающиеся литературы
- Упражнения
- 7. Планарность и двойственность
- 7.2. Формула Эйлера
- 7.3. Теорема Куратовского и другие характеризации планарности
- 7.4. Двойственные графы
- 7.5. Планарность и двойственность
- 7.6. Замечания, касающиеся литературы
- Упражнения
- 8. Связность и паросочетания
- 8.2. Реберная связность
- 8.3. Графы с заданными степенями
- 8.4. Теорема Менгера
- 8.5. Паросочетания
- 8.6. Паросочетания в двудольных графах
- 8.7. Паросочетания графов общего вида
- 8.8. Замечания, касающиеся литературы
- Упражнения
- 9. Покрытия и раскраски
- 9.1. Независимые множества и вершинные покрытия
- 9.2. Реберные покрытия
- 9.3. Реберная раскраска и хроматический индекс
- 9.4. Вершинная раскраска и хроматическое число
- 9.5. Хроматические полиномы
- 9.6. Проблема четырех красок
- 9.7. Замечания, касающиеся литературы
- Упражнения
- 10. Матроиды
- 10.2. Фундаментальные свойства
- 10.3. Эквивалентные системы аксиом
- 10.4. Двойственность матроидов и графоиды
- 10.5. Ограничение, сужение и миноры матроида
- 10.6. Представимость матроидов
- 10.7. Бинарные матроиды
- 10.8. Ориентируемые матроиды
- 10.9. Матроиды и «жадный» алгоритм
- 10.10. Замечания, касающиеся литературы
- Упражнения
- Часть II. Теория электрических цепей
- 11. Графы и электрические цепи
- 11.1. Преобразование контуров и сечений
- 11.2. Системы контурных уравнений и уравнений сечений
- 11.3. Метод смешанных переменных
- 11.4. Главное разбиение графа
- 11.5. Уравнения состояния
- 11.6. Свойство неусиления в резистивных цепях
- 11.7. Замечания, касающиеся литературы
- Упражнения
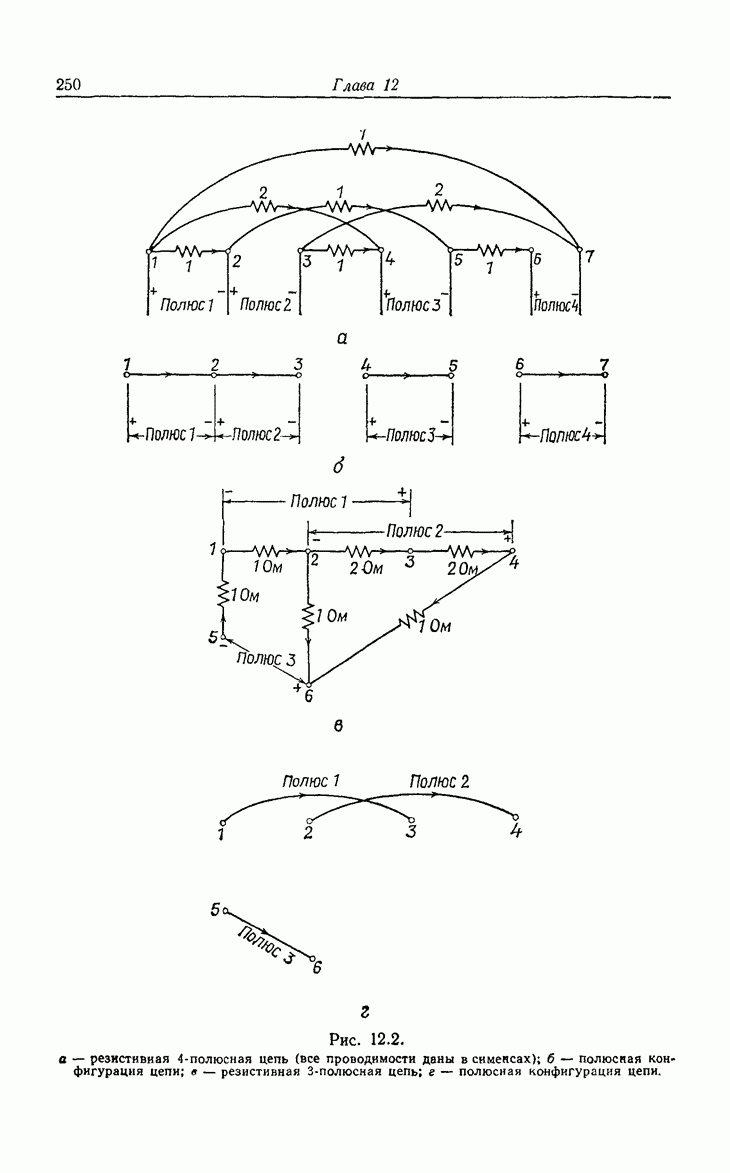
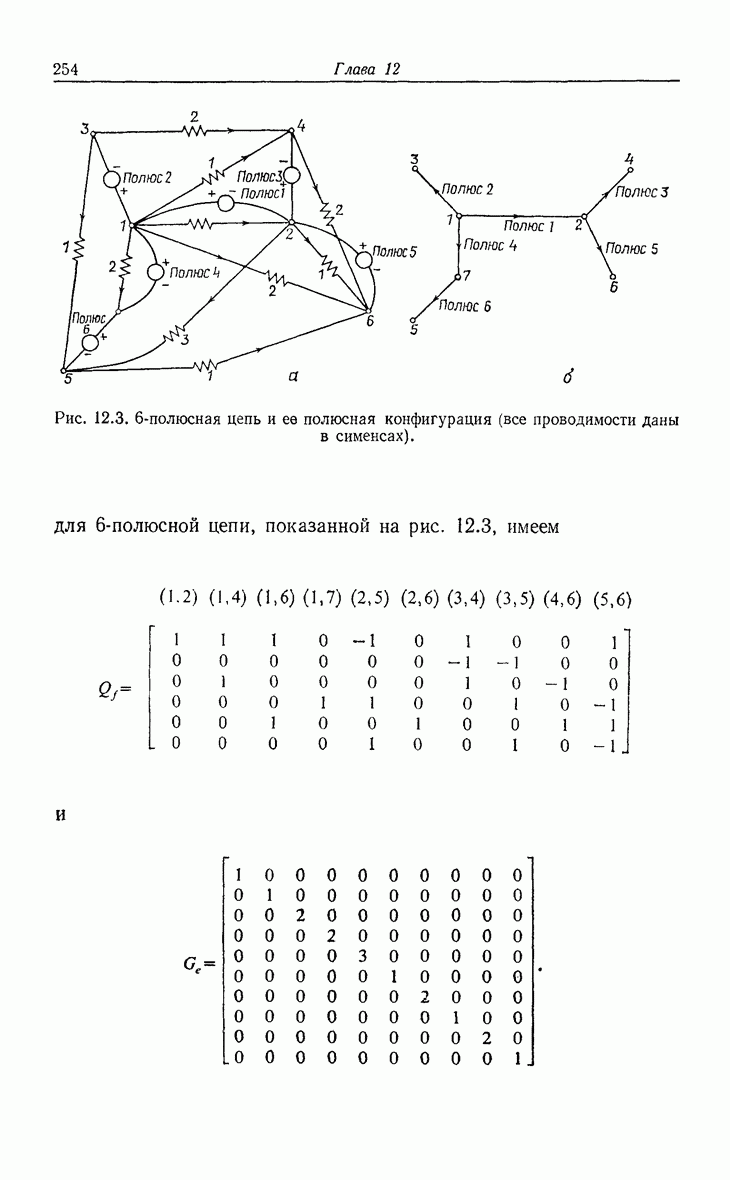
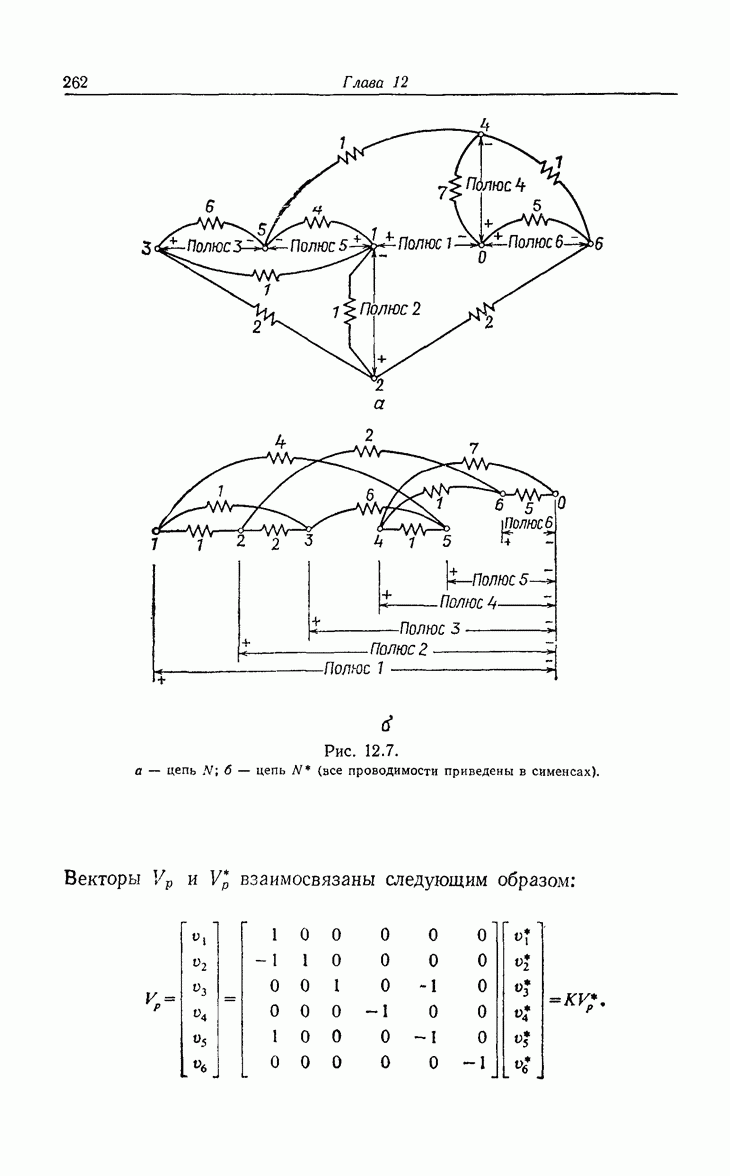
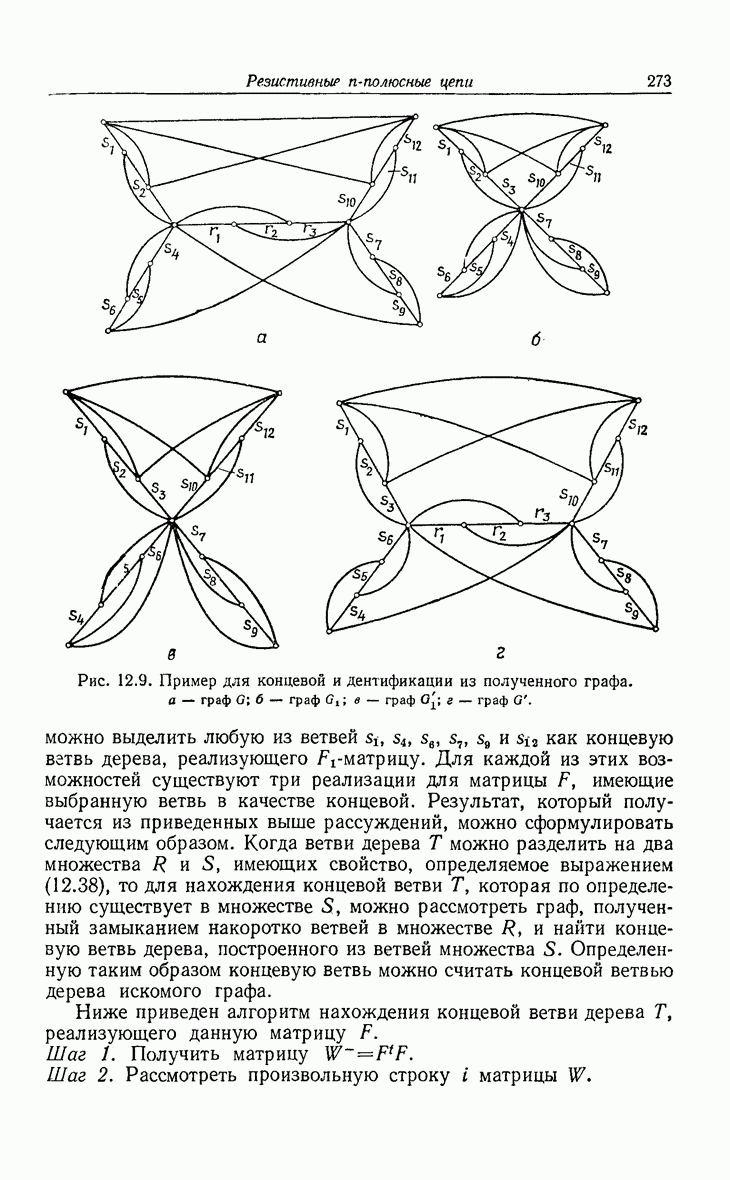
- 12. Резистивные n-полюсные цепи
- 12.2. K-матрицы резистивной (n-полюсной цепи ранга n)
- 12.3. Реализация (n+1)-узловых резистивных n-полюсных цепей (подход Седербаума)
- 12.4. Реализация цикломатической матрицы и матрицы сечений
- 12.5. Реализация (n+1)-узловых резистивных n-полюсных цепей (подход Гуиллемина)
- 12.6. Замечания, касающиеся литературы
- Упражнения
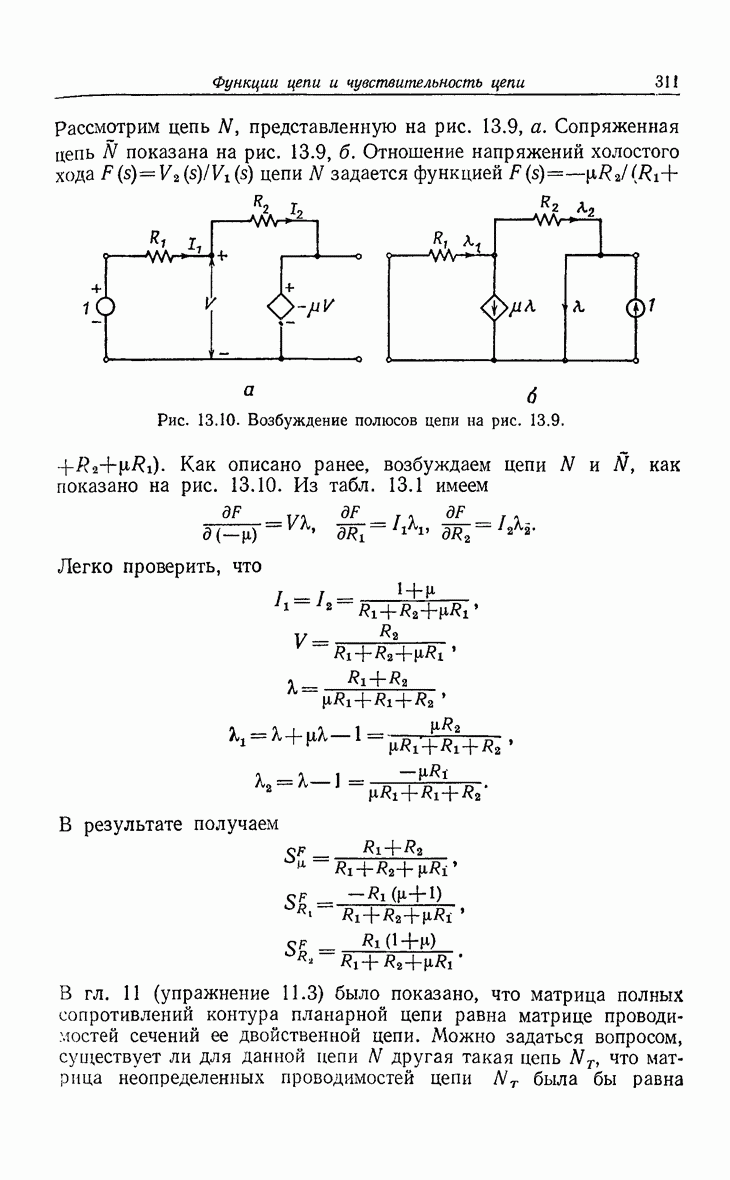
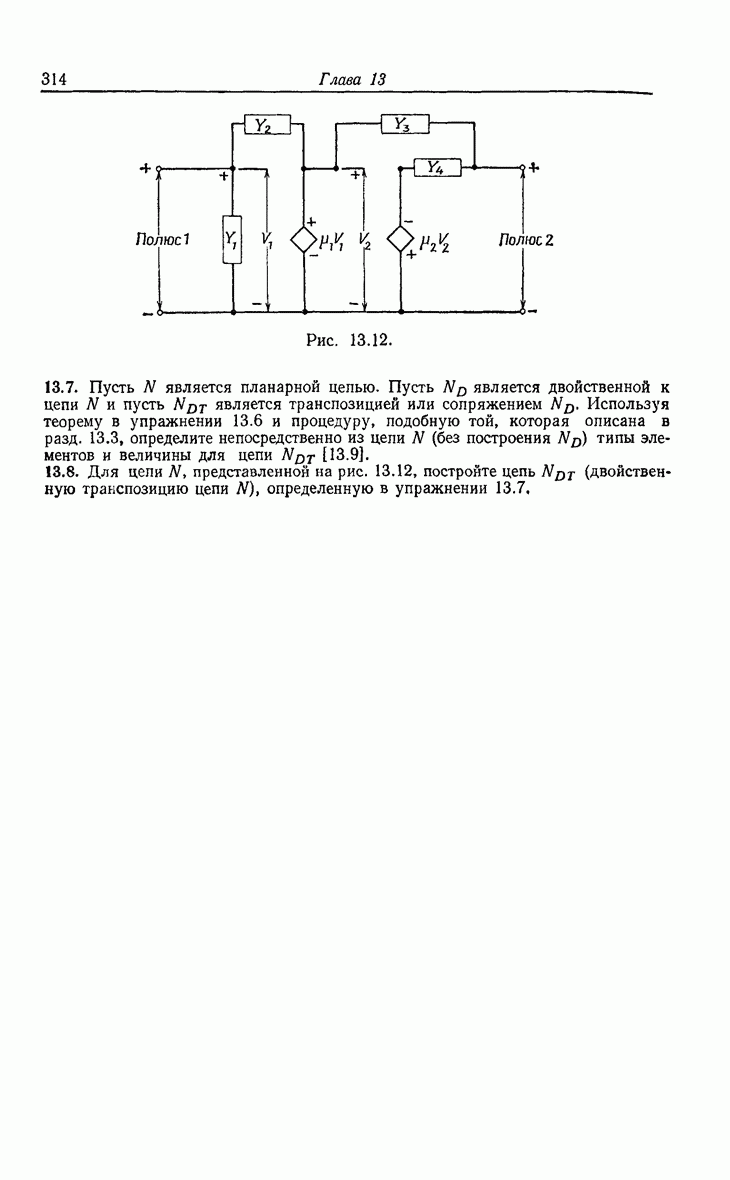
- 13. Функции цепи и чувствительность цепи
- 13.1. Топологические формулы для RLC-цепей без взаимных индуктивностей
- 13.2. Топологические формулы для общих линейных цепей
- 13.3. Сопряженная цепь и вычисление чувствительности цепи
- 13.4. Замечания, касающиеся литературы
- Упражнения
- Часть III. Теория электрических цепей
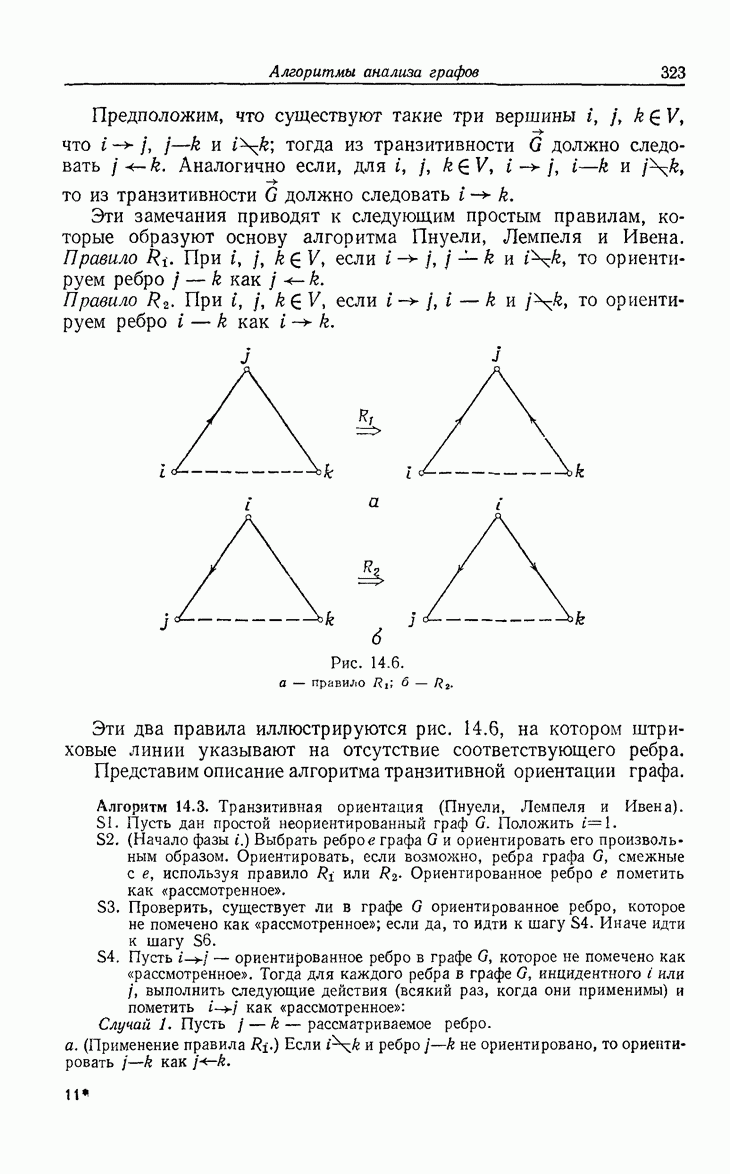
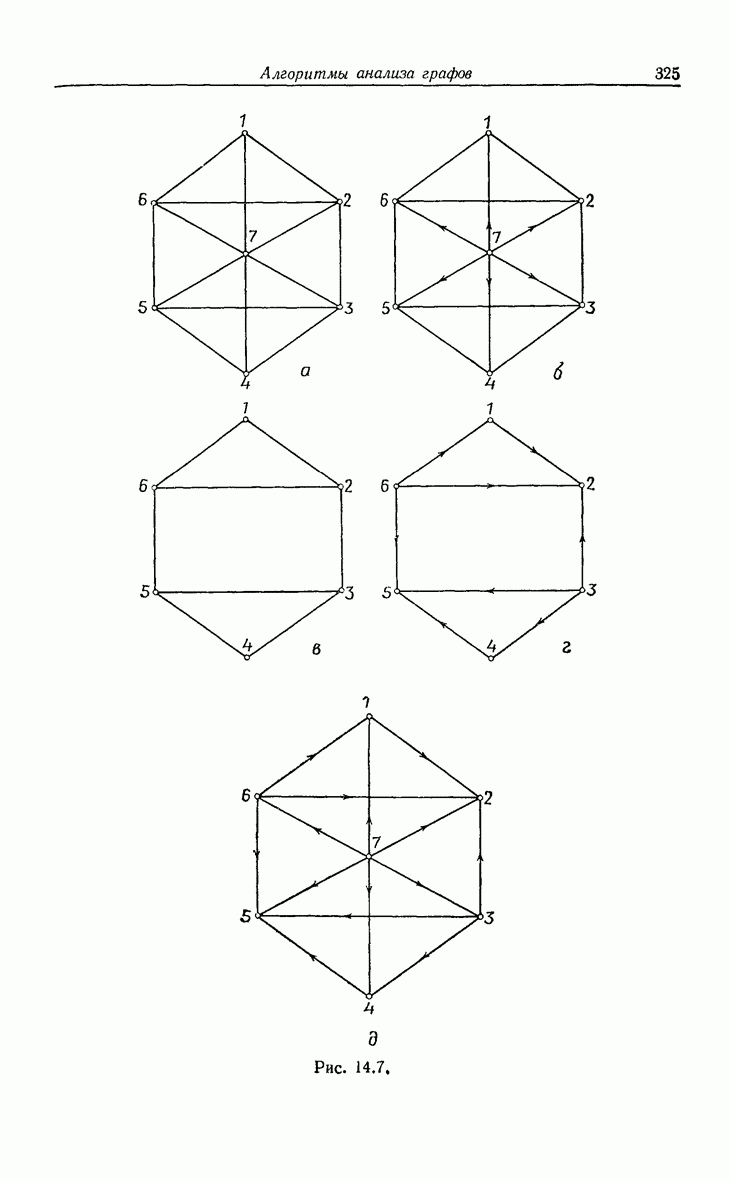
- 14. Алгоритмы анализа графов
- 14.1. Транзитивное замыкание
- 14.2. Транзитивная ориентация
- 14.3. Поиск в глубину
- 14.4. Двусвязность и сильная связность
- 14.6. Доминаторы в графе программы
- 14.7. Замечания, касающиеся литературы
- Упражнения
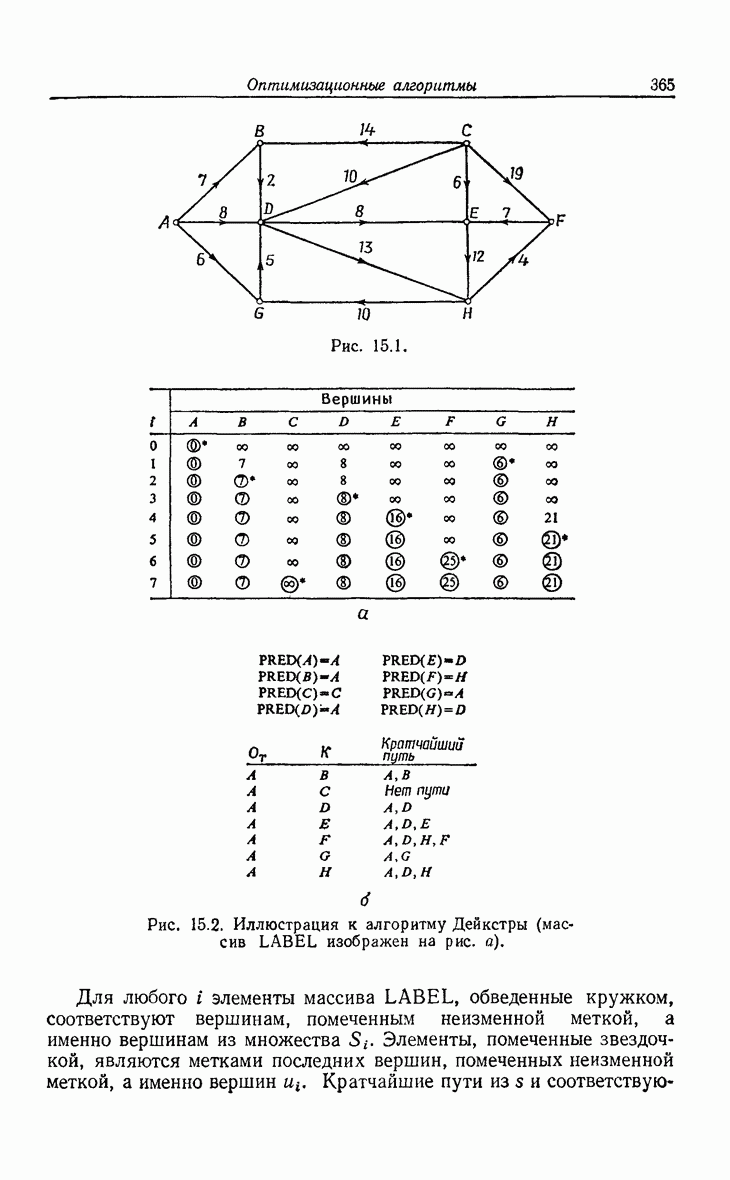
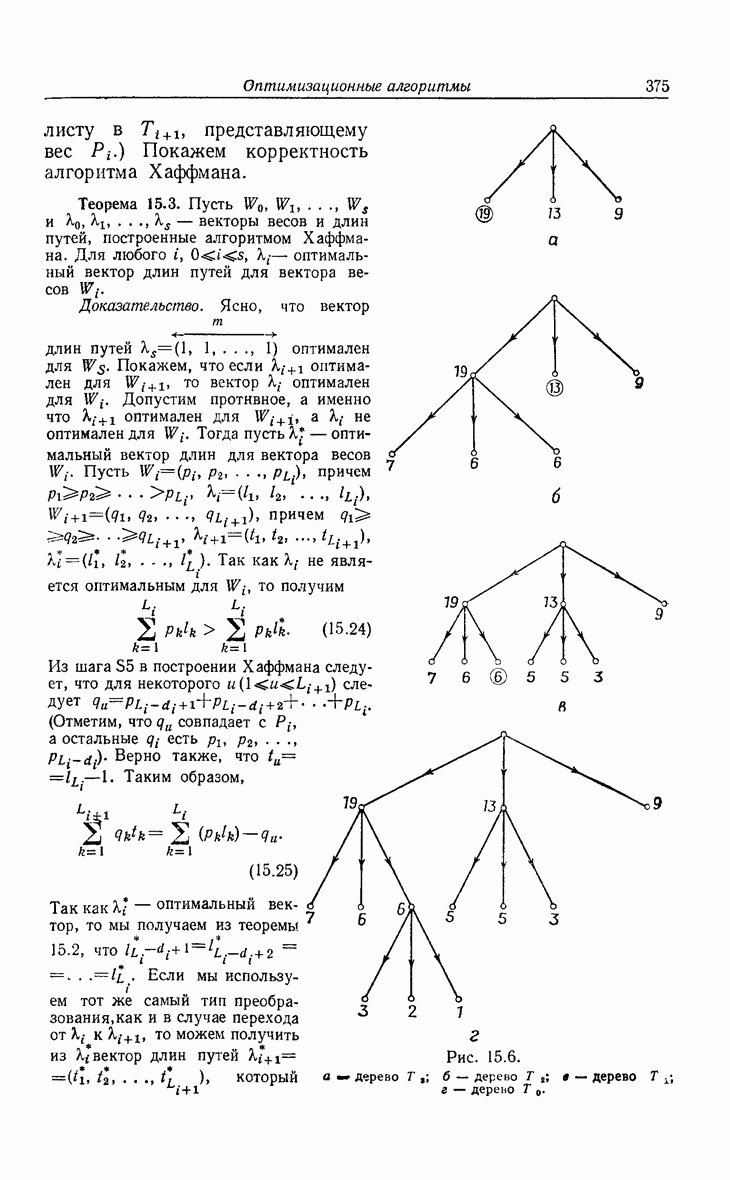
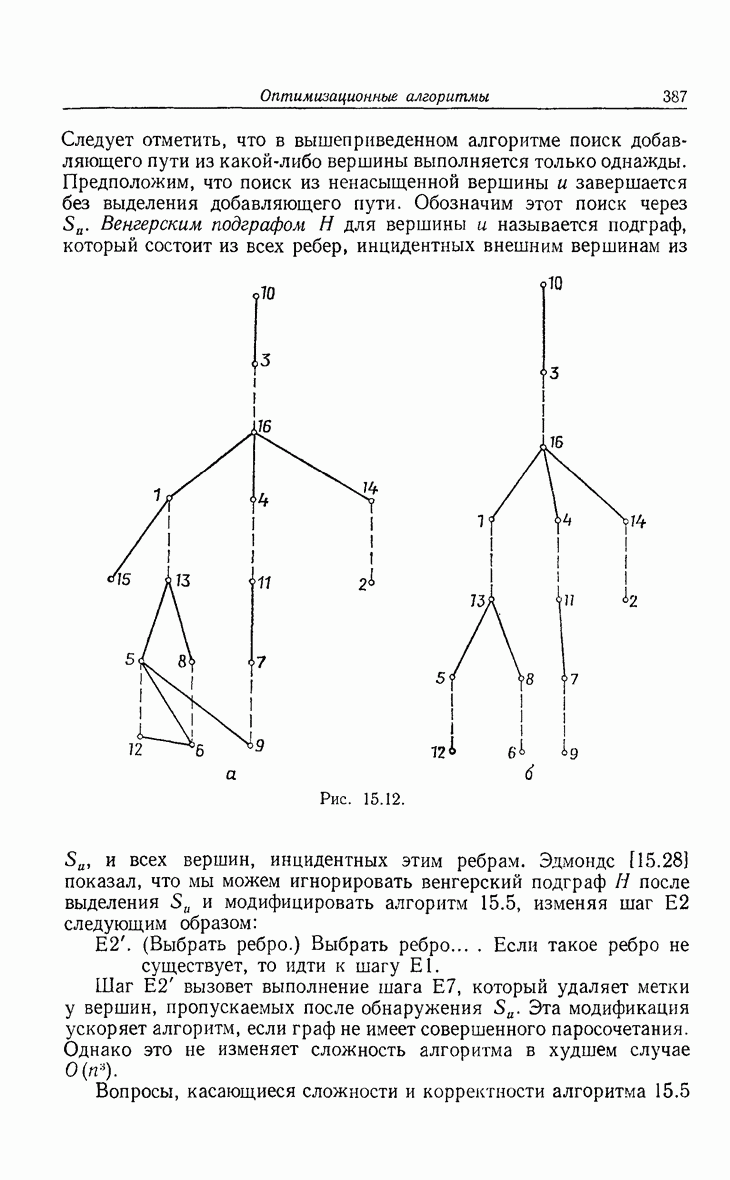
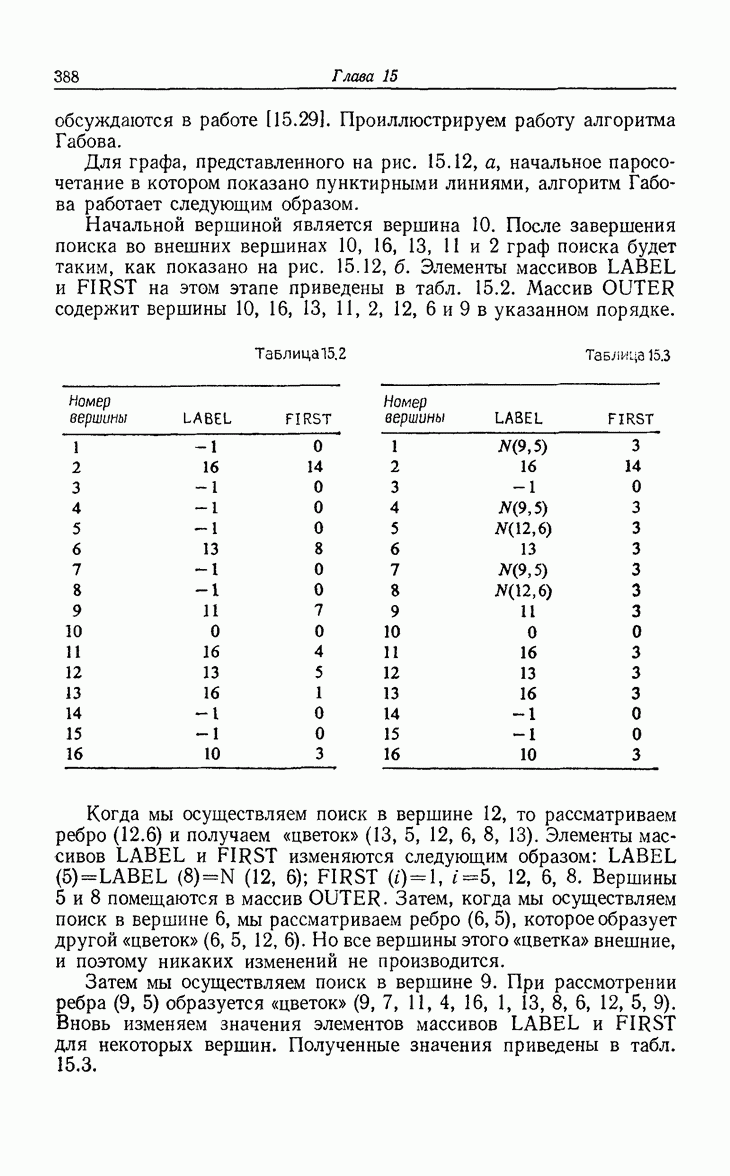
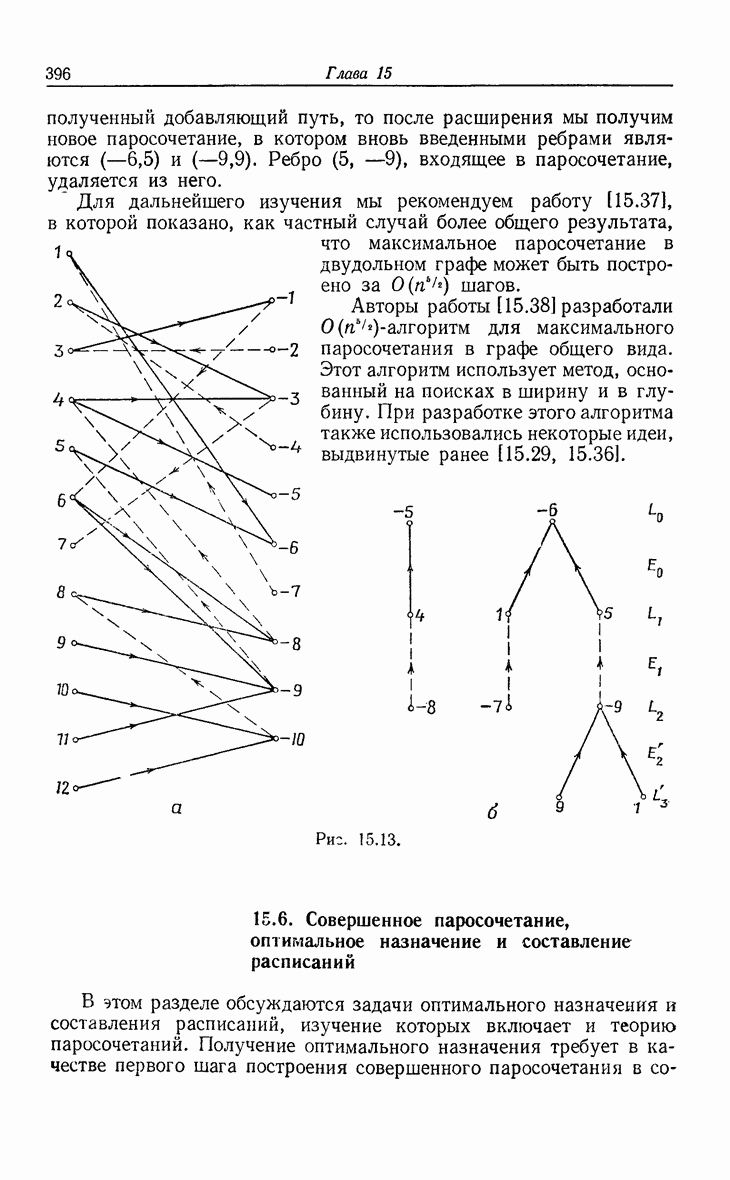
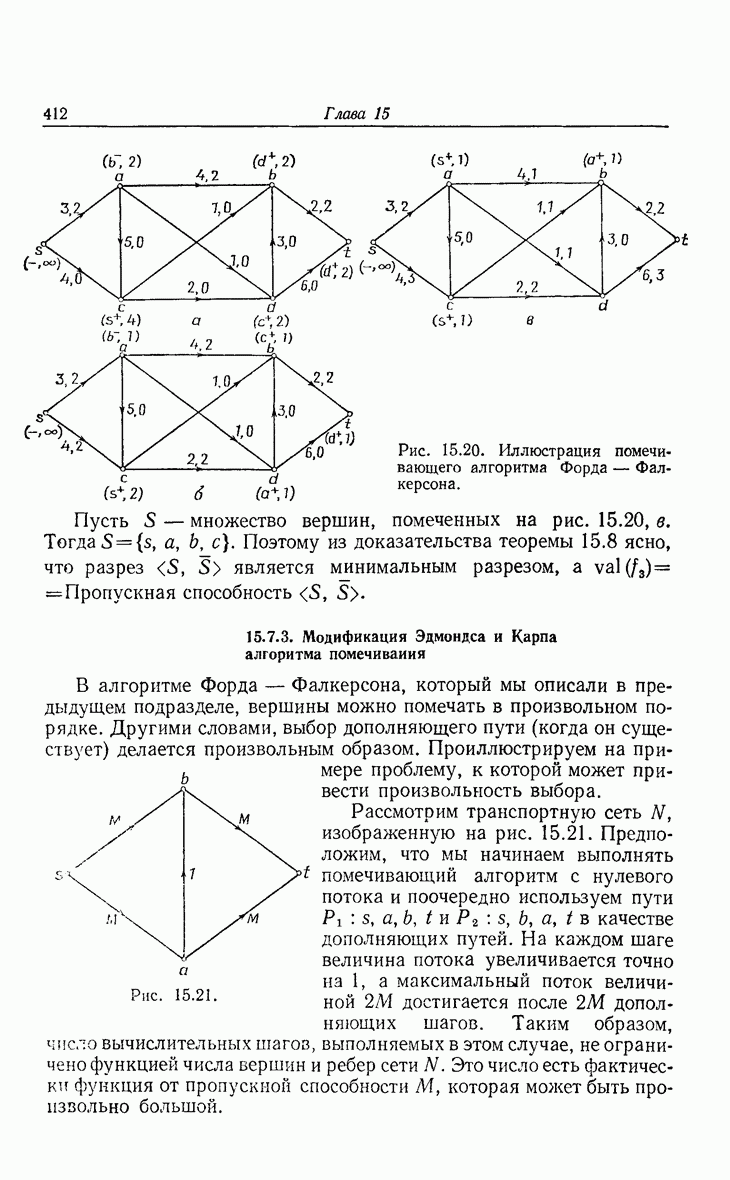
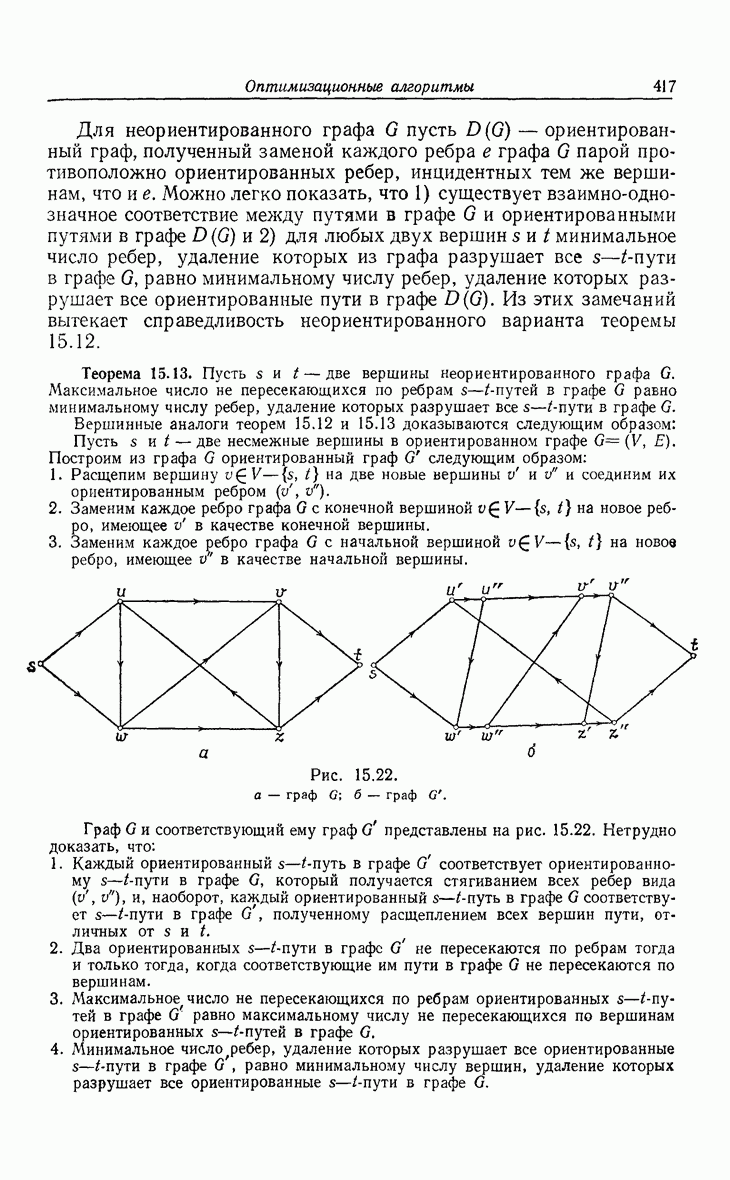
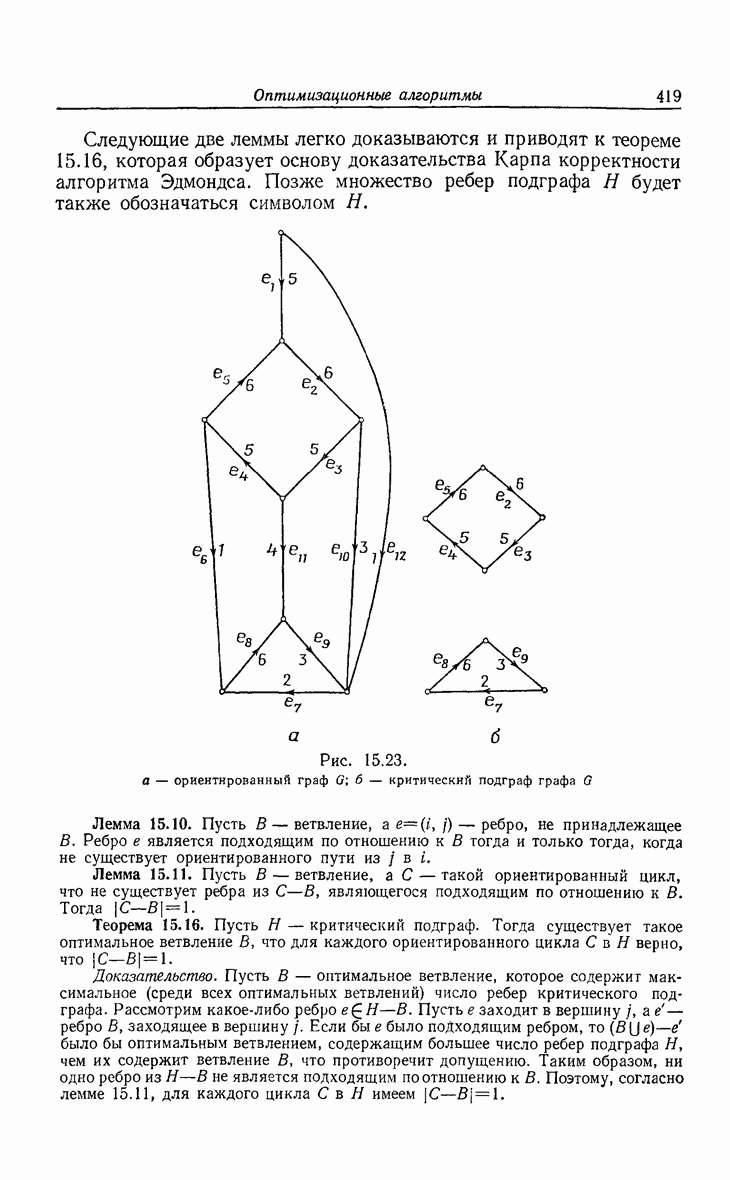
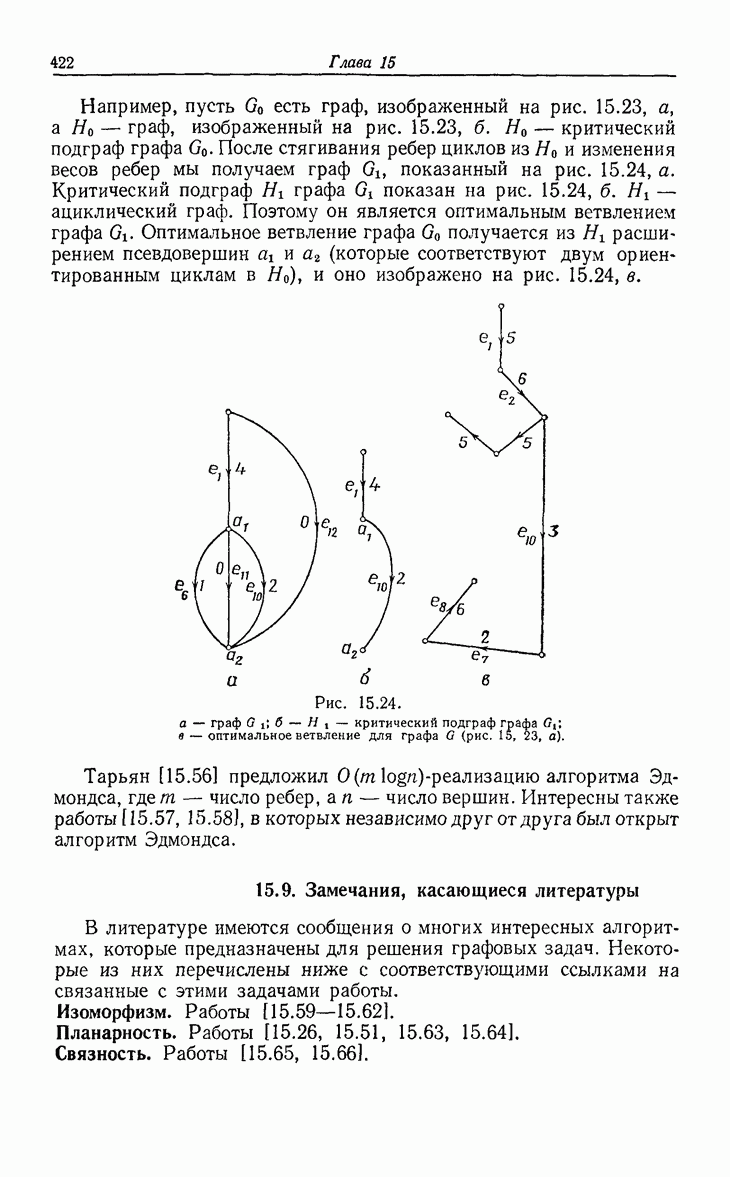
- 15. Оптимизационные алгоритмы
- 15.2. Деревья с минимальной длиной взвешенных путей.
- 15.3. Оптимальные деревья бинарного поиска
- 15.4. Максимальные паросочетания в графе
- 15.5. Максимальные паросочетания в двудольном графе
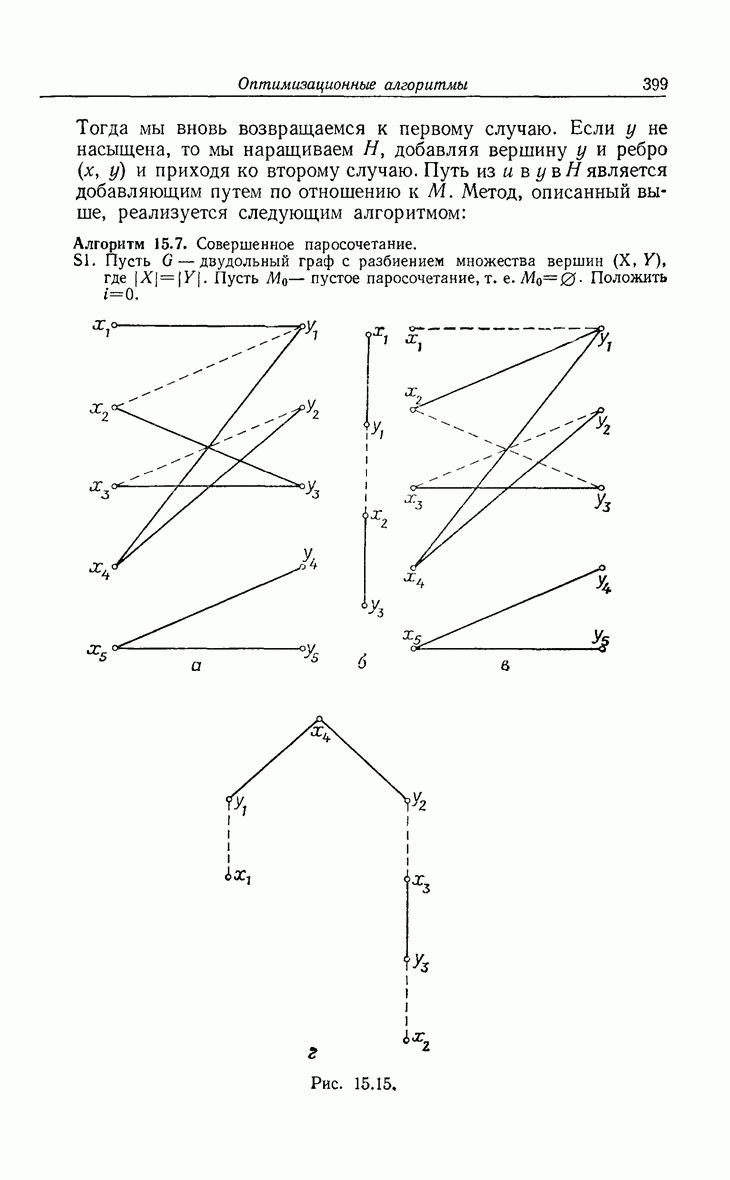
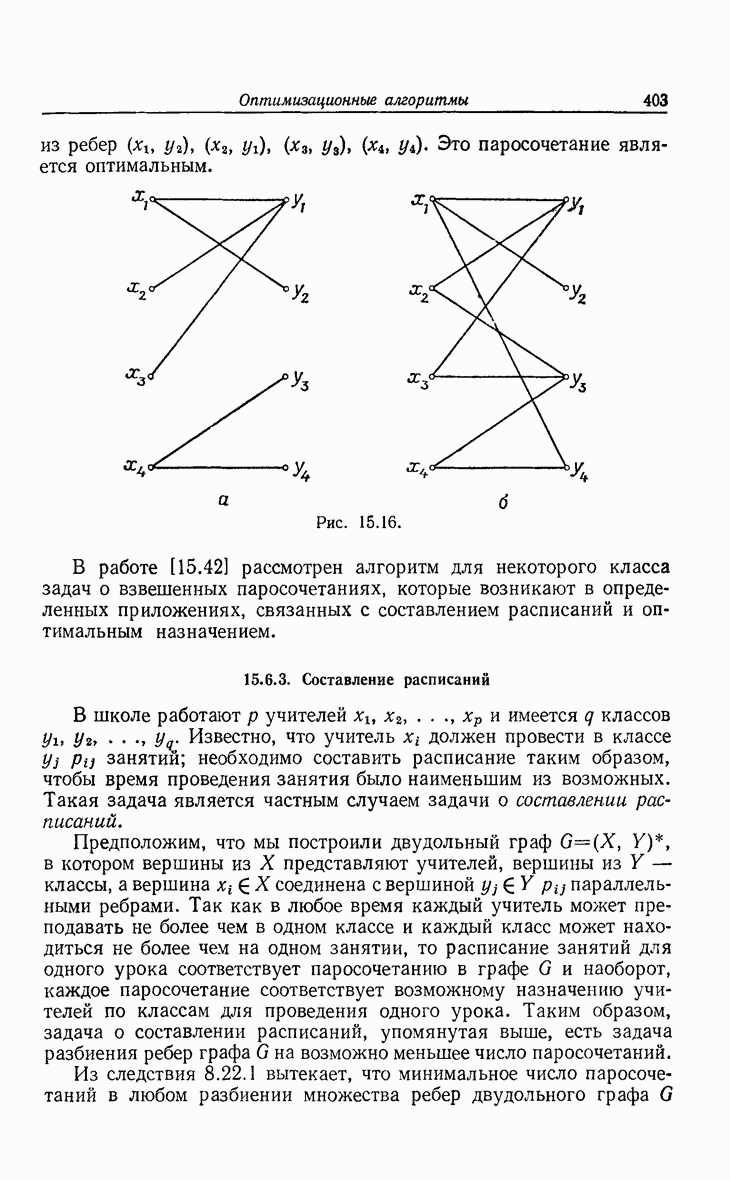
- 15.6. Совершенное паросочетание, оптимальное назначение и составление расписаний
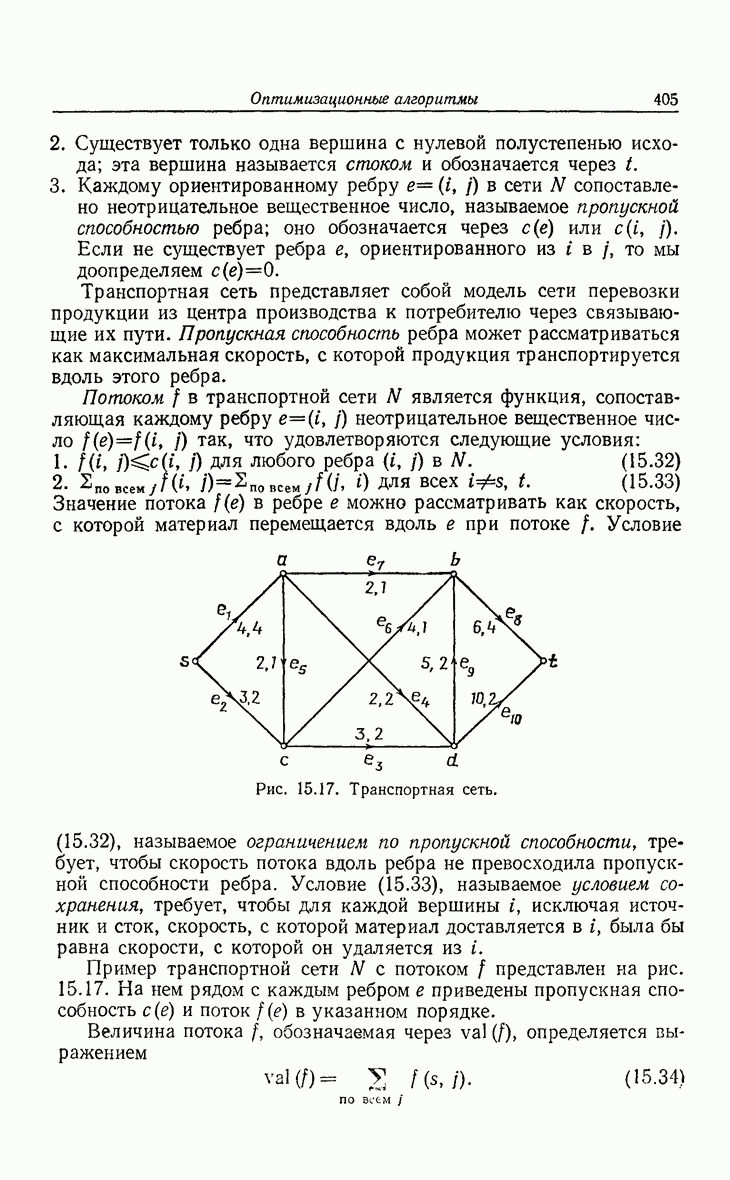
- 15.7. Потоки в транспортной сети
- 15.8. Оптимальное ветвление
- 15.9. Замечания, касающиеся литературы
- Упражнения
- ЛИТЕРАТУРА