3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений

В предыдущем параграфе рассматривались оптимальный и близкий к оптимальному алгоритмы оценивания двумерных СП на основе модели кратности . Для того, чтобы применить методику, изложенную в предыдущем параграфе, для построения алгоритмов фильтрации СП с кратными корнями характеристических уравнений, прежде всего необходимо сформулировать задачу фильтрации кадра в терминах пространства состояний. Для этого нужно решить задачу нахождения обобщенной векторной формы представления данного класса моделей.

            Для начала рассмотрим случай кратности 2 по обеим осям. Модель в этом случае должна иметь следующий вид:

,                          (3.28)

где  – вектор, содержащий элементы -й строки;  – порождающий вектор стандартных СВ;  – матричные коэффициенты модели;  – размер изображения. Таким образом, необходимо определить матричные коэффициенты  на основании соответствующей модели (2.14) с кратными корнями, таким образом, чтобы они стали эквивалентны.

            Для определения элементов неизвестных матриц  домножим (3.28) на  справа и найдем математическое ожидание:

,      (3.29)

.                                (3.30)

            Пусть  – ковариационная матрица поля  на расстоянии . Очевидно, что, . Тогда формулы (3.29) и (3.30) принимают следующий вид:

,

.                                  (3.31)

Точно также, после домножения (3.18) на  получим

,

.                                  (3.32)

Умножим теперь (3.28) на :

и найдем математическое ожидание

.                                        (3.33)

Здесь  – матрица дисперсии порождающего поля. Для стандартно распределенных СВ  она тождественно равна единичной матрице.

            Рассмотрим структуру элементов матрицы :

.

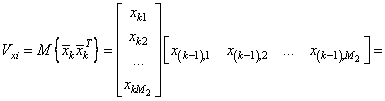
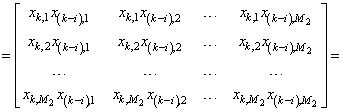
            Принимая во внимание разделимость модели по координатным осям, можем записать

.

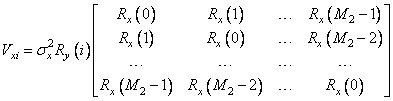            Матрица в последнем выражении является ковариационной матрицей одномерной модели по строке, т.е. . С учетом этого, полученное выражение может быть переписано в следующем виде:

.                                    (3.34)

            Теперь, с учетом последнего выражения, найдем коэффициенты модели . Решим систему матричных уравнений (3.22), (3.23) относительно неизвестных :

;   .

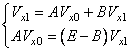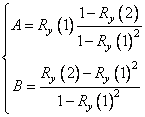Подставив в полученные выражения значения КФ, получим окончательное решение 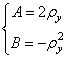. Таким образом, коэффициенты  и  векторной модели с кратными корнями порядка 2 по обеим осям являются скалярами.

            Для того, чтобы полностью определить параметры модели (3.28), необходимо найти еще коэффициент . Для этого подставим полученные варажения  и  в формулу (3.33) и с учетом того, что , получим:

,

.            (3.35)

            Явное выражение для  можно получить с использованием известного разложения Холесского [31].

            Таким образом, все коэффициенты модели (3.28) полностью определены. Теперь необходимо привести (3.28) к виду

.                                     (3.36)

Это может быть сделано следующим образом. Включим в вектор состояния  две строки изображения – -ю и -ю: . С учетом этого перепишем (3.28) в форме (3.36):

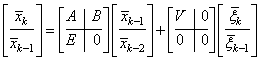.      (3.37)

Таким образом, модель (3.28) полностью построена.

            Полученное представление модели СП (3.36) дает возможность применить для фильтрации СП на основе моделей кратности  стандартную калмановскую процедуру фильтрации векторной случайной последовательности. Здесь 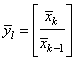 – вектор состояния,  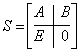– переходная матрица системы; 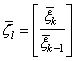 – вектор некоррелированных стандартных СВ, Е – единичная матрица.

            Модель наблюдения запишется следующим образом:

,                       (3.38)

где  – строка зашумленного изображения;  – белый гауссовский шум с дисперсией , а  – матрица наблюдения. Соотношения (3.26), (3.28) приводят к следующему алгоритму векторной калмановской фильтрации:

, ,                     (3.39)

,   .          (3.40)

            Вычислительная сложность алгоритма (3.39), (3.40) существенно выше, чем у алгоритма (3.15) – (3.17). Тем не менее, далее будут высказаны предложения по сокращению вычислительной сложности подобных алгоритмов.

            Дальнейший анализ приведенных выражений показывает, что возможно обобщение векторной модели (3.36) на случай любой кратности. Пусть заданы  – кратность корней, и  – вектор параметров двумерной модели (2.14). Включим в вектор состояния   строк изображения – с -й по -ю:  и перепишем с учетом этого (3.28) в форме (3.36):

,     (3.41)

где  – соответствующий коэффициент скалярной модели вдоль оси .

            Найдем теперь коэффициент . Для этого перепишем (3.31) в векторном виде

,

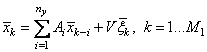и домножим его справа на :

.

Найдем теперь математическое ожидание от обеих частей:

,

.

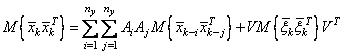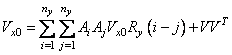Из последнего равенства получаем:

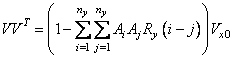,            (3.42)

причем выражение в скобках представляет собой скаляр. Общий вид коэффициента  может быть получен из (3.42) при помощи разложения Холесского.

            Таким образом, обобщенный вид модели с кратными корнями для случая двух измерений полностью определен и мы можем применить для оценивания подобных СП процедуры векторной калмановской фильтрации в форме (3.39) – (3.40).

            Увеличение размера вектора состояния влечет за собой увеличение объема вычислений. Тем не менее, можно заметить, что алгоритм (3.39)-(3.40) может быть в значительной степени упрощен. Действительно, во-первых переходная матрица системы  содержит в себе большое количество нулей, а во-вторых, на каждом шаге наблюдается, и, соответственно, оценивается фактически лишь одна строка изображения. Кроме того, пересчет коэффициента усиления (3.39), в силу стационарности модели, может быть осуществлен заранее. Исходя из этих соображений, можно оценить вычислительную сложность алгоритма. Предварительный пересчет матричных коэффициентов фильтра в (3.39) требует  элементарных операций умножения, где  – длина строки изображения. При условии предварительного пересчета (3.39), вычислительная сложность оценки одной строки (3.40) будет .

            Рассмотрим теперь возможность сокращения числа арифметических операций в (3.40) и синтеза квазиоптимального скалярного алгоритма оценивания.

            Рассмотрим структуру матрицы усиления . Она состоит из  матричных блоков размера :

,

где  – матрица ковариации ошибок оценивания -й и -й строк изображения.

            Пусть пересчет установившегося значения коэффициента усиления (3.29) уже осуществлен. В этом случае

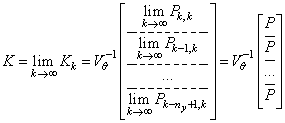,  (3.43)

где  – установившееся значение матрицы ковариации ошибки оценивания одной строки изображения;  – дисперсия шума наблюдения. Поскольку на каждом шаге наблюдаются, и, соответственно, оцениваются лишь первые  элементов вектора , то для вычисления оценки используется лишь первые  строк матрицы .

            Анализ данного выражения и формулы (3.40) показывает, все соображения, использованные для синтеза квазиоптимального алгоритма фильтрации СП на основе моделей кратности 1, могут быть применены и в данном случае. Действительно, выделим -ю строку соотношения (3.40) и применим к ней все выше изложенные рассуждения. Очевидно, что и все коэффициенты, определяющие скалярную АР‑модель состояния и наблюдения для  будут верны и в данном случае.

            Рассмотрим возможность использования для представления процесса изменения  авторегрессий более высоких порядков. Допустим, что модель состояния  записывается следующим образом:

.     (3.44)

            Для каждого элемента  необходимо определить неизвестные параметры  и дисперсию порождающего шума . Для этого домножим (3.44) на  и найдем математическое ожидание:

.                 (3.45)

Полученное выражение представляет собой систему  линейных уравнений относительно неизвестных . Возведя (3.44) в квадрат, при условии известных , получим уравнение для нахождения :

.                  (3.46)

            Из приведенных рассуждений ясно, вычислительная сложность квазиоптимального алгоритма в случае модели с корнями произвольной кратности имеет тот же порядок, что и в случае кратности 1. При использовании в модели (3.34) авторегрессий более высокого порядка, вычислительная сложность вырастает пропорционально порядку авторегрессии.