| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. Авторегрессионные модели
Остановимся вначале на основных вероятностных характеристиках многомерных авторегрессионных моделей СП. Этот класс СП порождается линейными стохастическими разностными уравнениями следующего вида:
![]() , (1.21)
, (1.21)
где ![]() – моделируемое СП, определенное на
– моделируемое СП, определенное на ![]() -мерной сетке
-мерной сетке ![]() ;
; ![]() – коэффициенты модели;
– коэффициенты модели; ![]() – порождающее белое
СП;
– порождающее белое
СП; ![]() –
каузальная область локальных состояний.
–
каузальная область локальных состояний.
Наиболее часто в качестве
порождающего поля ![]() выбирают
нормально распределенное СП с независимыми компонентами. В этом случае СП
выбирают
нормально распределенное СП с независимыми компонентами. В этом случае СП ![]() также имеет гауссовское
распределение.
также имеет гауссовское
распределение.
Задача анализа моделей (1.21) в общем виде рассматривалась в [23, 64]. Модели (1.21) соответствует пространственный линейный фильтр с передаточной функцией
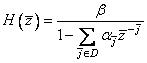 , (1.22)
, (1.22)
где ![]() . При этом спектральная плотность СП
. При этом спектральная плотность СП ![]() записывается следующим
образом:
записывается следующим
образом:
![]() , (1.23)
, (1.23)
где ![]() – дисперсия СП
– дисперсия СП ![]() .
.
Корреляционная функция
поля ![]() может
быть найдена с помощью обратного
может
быть найдена с помощью обратного ![]() -преобразования спектральной плотности:
-преобразования спектральной плотности:
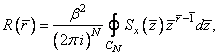 (1.24)
(1.24)
где ![]() – единичная полиокружность в многомерном
комплексном пространстве.
– единичная полиокружность в многомерном
комплексном пространстве.
Как показано в работах
[46, 51, 52], анализ вероятностных свойств СП сильно упрощается, если их
спектральная плотность может быть факторизована. Такие «разделимые» СП, со
спектральной плотностью 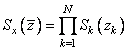 , представляют собой удобный объект для
исследований. Поскольку у таких полей передаточная функция многомерного фильтра
, представляют собой удобный объект для
исследований. Поскольку у таких полей передаточная функция многомерного фильтра
 и КФ
и КФ  также факторизуются,
то для решения задачи статистического анализа многомерного СП достаточно
исследовать свойства случайных последовательностей, порожденных одномерными
авторегрессиями с характеристиками
также факторизуются,
то для решения задачи статистического анализа многомерного СП достаточно
исследовать свойства случайных последовательностей, порожденных одномерными
авторегрессиями с характеристиками ![]() ,
, ![]() и
и ![]() .
.
К недостаткам таких
моделей следует отнести невозможность описания с их помощью изотропных СП,
например, с КФ ![]() .
Однако, как показывает анализ, подбором соответствующих одномерных моделей
удается достичь вполне приемлемых аппроксимаций.
.
Однако, как показывает анализ, подбором соответствующих одномерных моделей
удается достичь вполне приемлемых аппроксимаций.
В работе [46] для
получения близких к изотропным СП предложено выбирать одномерные фильтры с
кратными корнями характеристических уравнений: 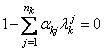 , где
, где ![]() – порядки одномерных авторегрессий.
– порядки одномерных авторегрессий.
В настоящей главе решаются задачи синтеза модели N-мерного СП с кратными корнями характеристических уравнений одномерных фильтров и анализа ее вероятностных свойств. Решим сначала эти задачи для одномерной модели.
Рассмотрим одномерную
авторегрессию длины ![]() :
:
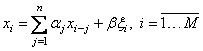 . (1.25)
. (1.25)
Здесь ![]() – гауссовская последовательность независимых
компонент с математическим ожиданием 0 и дисперсией
– гауссовская последовательность независимых
компонент с математическим ожиданием 0 и дисперсией ![]() . Решение задачи синтеза будет
заключаться в том, чтобы по заданным
. Решение задачи синтеза будет
заключаться в том, чтобы по заданным ![]() – корню характеристического уравнения,
– корню характеристического уравнения, ![]() – его кратности и
– его кратности и ![]() – требуемой дисперсии
поля определить неизвестные коэффициенты авторегрессии
– требуемой дисперсии
поля определить неизвестные коэффициенты авторегрессии ![]() .
.
В случае с кратными корнями это уравнение можно записать в операторной форме следующим образом:
![]() , (1.26)
, (1.26)
где ![]() – оператор сдвига. Учитывая, что действие
оператора сдвига на
– оператор сдвига. Учитывая, что действие
оператора сдвига на ![]() -й
элемент последовательности определяется как
-й
элемент последовательности определяется как ![]() , перепишем (1.26) в явном виде:
, перепишем (1.26) в явном виде:
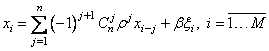 . (1.27)
. (1.27)
Сравнение (1.26) и (1.27)
дает возможность записать выражение для коэффициентов ![]() :
:
![]() . (1.28)
. (1.28)
Значение неизвестного
параметра ![]() ,
являющегося коэффициентом усиления в передаточной функции (1.22), должно выбираться
так, чтобы фильтр был устойчив. Далее будет показано, как можно определить
,
являющегося коэффициентом усиления в передаточной функции (1.22), должно выбираться
так, чтобы фильтр был устойчив. Далее будет показано, как можно определить ![]() на основе КФ модели.
на основе КФ модели.
Одной из задач
статистического анализа модели, является получение ее КФ. Найдем вначале
нормированную КФ, т.е. будем полагать ![]() . Для решения этой задачи воспользуемся
формулой (1.24), записанной для одномерного случая
. Для решения этой задачи воспользуемся
формулой (1.24), записанной для одномерного случая
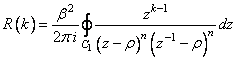 .
.
Так как подынтегральная
функция имеет в точке ![]() полюс
порядка n, то интеграл представляет собой коэффициент
полюс
порядка n, то интеграл представляет собой коэффициент ![]() ее разложения в ряд Лорана, и
поэтому может быть найден с использованием методов теории вычетов
ее разложения в ряд Лорана, и
поэтому может быть найден с использованием методов теории вычетов
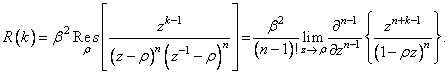
Используя правила дифференцирования произведения функций, после предельного перехода получаем
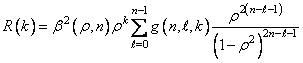 , (1.29)
, (1.29)
где
![]() , (1.30)
, (1.30)
а коэффициент ![]() находится из условия
находится из условия ![]() :
:
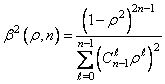 . (1.31)
. (1.31)
Формулы (1.29) – (1.31)
дают, при заданных ![]() и
и
![]() , общий вид
нормированной КФ одномерной модели (1.25). Для того, чтобы получить КФ при не
равных единице дисперсиях
, общий вид
нормированной КФ одномерной модели (1.25). Для того, чтобы получить КФ при не
равных единице дисперсиях ![]() и
и ![]() , необходимо домножить правую часть (1.31)
на
, необходимо домножить правую часть (1.31)
на ![]() . Тем
самым, получаем выражение и для коэффициента
. Тем
самым, получаем выражение и для коэффициента ![]() :
:
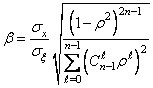 . (1.32)
. (1.32)
Формулы (1.28) и (1.32) полностью определяют неизвестные коэффициенты одномерной АР-модели (1.25) с кратными корнями характеристических уравнений.
Рассмотрим теперь случай ![]() измерений. Модель СП,
при заданной дисперсии
измерений. Модель СП,
при заданной дисперсии ![]() , полностью определяется вектором
параметров
, полностью определяется вектором
параметров ![]() и
вектором кратностей
и
вектором кратностей ![]() характеристических
корней.
характеристических
корней.
Пусть многомерное разделимое СП порождается следующими АР-уравнениями, записанными в операторной форме:
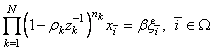 , (1.33)
, (1.33)
где ![]() – размерность поля;
– размерность поля; ![]() и
и ![]() – параметр и кратность корней модели вдоль
– параметр и кратность корней модели вдоль
![]() -й оси;
-й оси; ![]() – сетка, на которой
определено поле
– сетка, на которой
определено поле ![]() .
.
Определим коэффициенты авторегрессии для многомерной модели с кратными корнями. Для этого раскроем в (1.33) скобки:
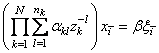 ,
,
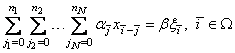 . (1.34)
. (1.34)
Шаблон коэффициентов модели ![]() определен на
определен на ![]() -мерном параллелепипеде
размера
-мерном параллелепипеде
размера ![]() . Из
(1.33) и (1.34) следует, что коэффициенты
. Из
(1.33) и (1.34) следует, что коэффициенты ![]() являются произведениями соответствующих
коэффициентов
являются произведениями соответствующих
коэффициентов ![]() одномерных
авторегрессий вдоль
одномерных
авторегрессий вдоль ![]() -й
оси:
-й
оси:
 , (1.35)
, (1.35)
где ![]() . Коэффициент
. Коэффициент ![]() многомерной модели (1.34) находится
аналогично:
многомерной модели (1.34) находится
аналогично:
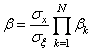 , (1.36)
, (1.36)
где ![]() – соответствующий нормированный одномерный
коэффициент.
– соответствующий нормированный одномерный
коэффициент.
Таким образом, выражение (1.34) дает общий вид АР‑модели многомерного разделимого гауссовского СП, а формулы (1.35) и (1.36) полностью определяют ее коэффициенты, т.е. задача синтеза модели решена. КФ модели (1.34), как уже отмечалось, является произведением КФ соответствующих одномерных авторегрессий:
 . (1.37)
. (1.37)
Для того, чтобы корни
характеристического уравнения были действительными, необходимо, чтобы параметр ![]() выбирался из диапазона
от нуля до единицы.. Чем больше значение
выбирался из диапазона
от нуля до единицы.. Чем больше значение ![]() , тем более крупные детали появляются на
моделируемом изображении, т.е. этот параметр характеризует величину связи между
соседними элементами.
, тем более крупные детали появляются на
моделируемом изображении, т.е. этот параметр характеризует величину связи между
соседними элементами.
Рассмотрим некоторые
примеры. Хорошо изученная трехточечная модель Хабиби (1.5) является частным
случаем 2‑мерной модели (1.34) кратности (1,1), причем значение параметра
![]() задает
коэффициент корреляции соседних элементов. Легко видеть, что ее КФ, вычисленная
по формулам (1.29), (1.37), совпадает с (1.26):
задает
коэффициент корреляции соседних элементов. Легко видеть, что ее КФ, вычисленная
по формулам (1.29), (1.37), совпадает с (1.26):
![]() .
.
Для 2‑мерной модели кратности (2,2) КФ записывается более сложно:
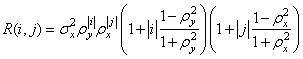 ,
,
и также совпадает с (1.11), приведенной в первой главе. Вид коэффициентов, согласно (1.10), и рассчитанный по формулам (1.35), (1.36), также одинаков.
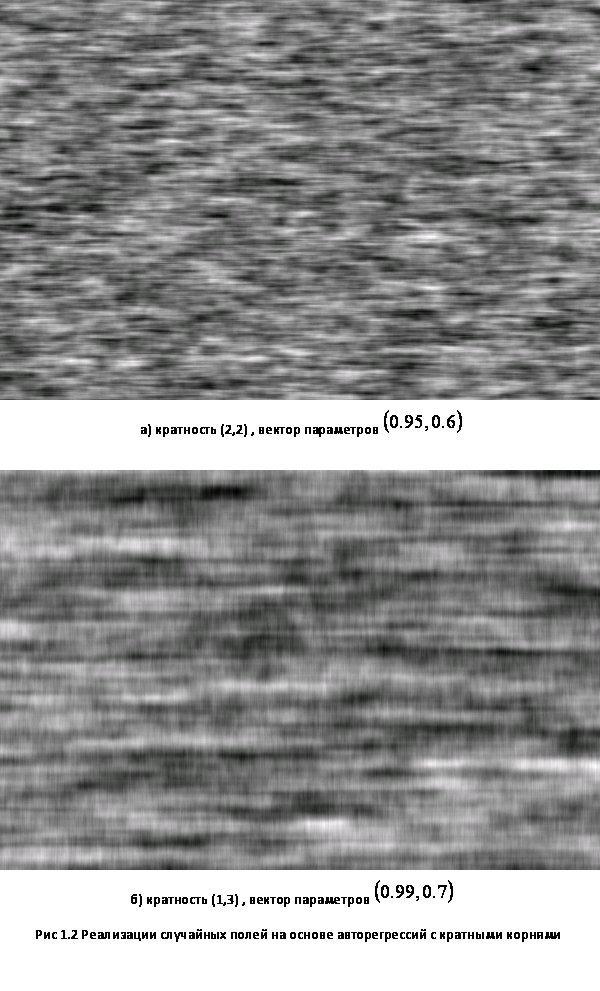
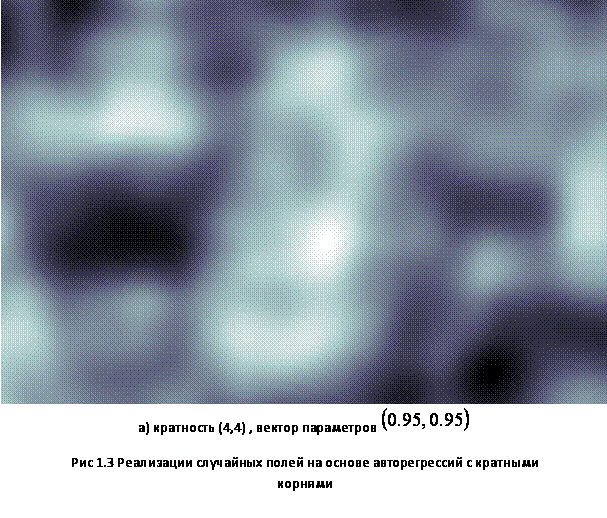
На на рис. 2.1, 2.2 и .2.3
приведены кадры изображений размера 600х400 элементов на основе моделей с
кратными корнями при различных наборах параметров (первый параметр относится к
оси ![]() , второй –
к оси
, второй –
к оси ![]() ). Анализ приведенных и других
результатов показывает, что, варьируя параметры связи и соотношения кратностей,
можно получить широкий спектр разнотипных текстур, на основе которых возможно
построение комплексных моделей многозональных изображений, причем, с ростом
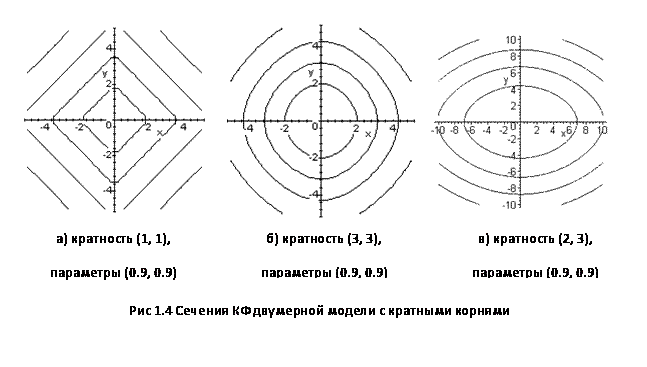
кратности корней, СП приближается по свойствам к изотропному. Это
подтверждается также видом сечений равного уровня КФ, приведенных на рис. 2.4.
). Анализ приведенных и других
результатов показывает, что, варьируя параметры связи и соотношения кратностей,
можно получить широкий спектр разнотипных текстур, на основе которых возможно
построение комплексных моделей многозональных изображений, причем, с ростом
кратности корней, СП приближается по свойствам к изотропному. Это
подтверждается также видом сечений равного уровня КФ, приведенных на рис. 2.4.

Проведем оценку вычислительной сложности предложенной модели.
Для получения реализации ![]() -мерного СП, определенного на сетке
размером
-мерного СП, определенного на сетке
размером ![]() элементов,
требуется
элементов,
требуется 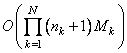 операций
умножения.
операций
умножения.
Полезный во многих приложениях вариант модели
многомерного СП можно получить, взяв за основу одномерную авторегрессию с
кратными корнями. Пусть необходимо сформировать реализации ![]() -мерного СП
-мерного СП ![]() заданного на сетке
заданного на сетке ![]() . Это можно сделать
следующим образом: вначале моделируется
. Это можно сделать
следующим образом: вначале моделируется ![]() одномерных АР последовательностей
одномерных АР последовательностей ![]() на основе модели с
кратными корнями (1.27) (
на основе модели с
кратными корнями (1.27) (![]() – вектор кратностей вдоль соответствующих
осей). Далее, элемент
– вектор кратностей вдоль соответствующих
осей). Далее, элемент ![]() поля
поля
![]() получается
перемножением соответствующих элементов одномерных последовательностей:
получается
перемножением соответствующих элементов одномерных последовательностей:
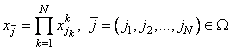 (1.38)
(1.38)
Найдем КФ данной модели.
Домножим (1.38) на ![]() и
найдем
и
найдем
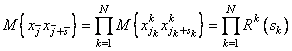 . (1.39)
. (1.39)
Здесь ![]() – КФ (1.29) одномерной АР-модели
вдоль
– КФ (1.29) одномерной АР-модели
вдоль ![]() -й оси.
Таким образом, данная модель является разделимой моделью СП, причем ее КФ
совпадает с КФ
-й оси.
Таким образом, данная модель является разделимой моделью СП, причем ее КФ
совпадает с КФ ![]() -мерной
АР-модели с кратными корнями. Закон распределения вероятностей такого СП
оказывается негауссовским и, в общем случае
-мерной
АР-модели с кратными корнями. Закон распределения вероятностей такого СП
оказывается негауссовским и, в общем случае ![]() , достаточно сложным. По видимому, именно
из-за негауссовости СП и малых значений параметра
, достаточно сложным. По видимому, именно
из-за негауссовости СП и малых значений параметра ![]() кадры обладают ярко выраженной осевой
структурой, что редко встречается на реальных изображениях (за исключением,
может быть, аэрофотоснимков городов). Вместе с тем, предложенная модель
отличается простотой и очень малыми вычислительными затратами (
кадры обладают ярко выраженной осевой
структурой, что редко встречается на реальных изображениях (за исключением,
может быть, аэрофотоснимков городов). Вместе с тем, предложенная модель
отличается простотой и очень малыми вычислительными затратами (![]() операций умножения).
Пример реализации кадра размером 600´400 элементов на основе множительной модели (1.38) приведен
на рис. 2.5. Действительно, даже для простейшего случая
операций умножения).
Пример реализации кадра размером 600´400 элементов на основе множительной модели (1.38) приведен
на рис. 2.5. Действительно, даже для простейшего случая ![]() одномерная плотность
распределения вероятностей (ПРВ) СП находится как ПРВ произведения двух
гауссовских СВ в виде [81]:
одномерная плотность
распределения вероятностей (ПРВ) СП находится как ПРВ произведения двух
гауссовских СВ в виде [81]:
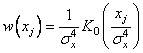 , (1.30)
, (1.30)
где ![]() – модифицированная функция Бесселя 3 рода
0-го порядка.
– модифицированная функция Бесселя 3 рода
0-го порядка.

Анализ КФ моделей с кратными корнями показывает, что сечения КФ СП, полученных с помощью разделимых многомерных моделей, с ростом кратности корней характеристических уравнений приближаются к гиперэллипсоидам. Для оценки приближенности таких СП к изотропным желательно иметь количественную оценку анизотропии поля. Для этого можно воспользоваться известным коэффициентом анизотропии двумерного СП [81]:
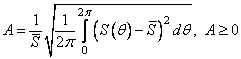 , (1.41)
, (1.41)
где ![]() – спектральная плотность поля в
направлении
– спектральная плотность поля в
направлении ![]() ,
, 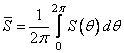 – "среднее
значение" углового спектра.
– "среднее
значение" углового спектра.
Коэффициент A имеет смысл
среднеквадратического расстояния между ![]() и
и ![]() и характеризует величину суммарного
отклонения углового спектра от ее «среднего» значения. Недостатком данного
метода оценки изотропности является предположение о том, что спектральная
плотность поля
и характеризует величину суммарного
отклонения углового спектра от ее «среднего» значения. Недостатком данного
метода оценки изотропности является предположение о том, что спектральная
плотность поля ![]() в
полярных координатах
в
полярных координатах ![]() является
функцией лишь одной переменной – направления
является
функцией лишь одной переменной – направления ![]() , что верно лишь для изотропных полей.
Другим недостатком является необходимость вычисления спектральной плотности в
полярных координатах, что в рассматриваемом случае вызывает трудности для
многих СП.
, что верно лишь для изотропных полей.
Другим недостатком является необходимость вычисления спектральной плотности в
полярных координатах, что в рассматриваемом случае вызывает трудности для
многих СП.
Поэтому представляется
целесообразным характеризовать анизотропность многомерного СП на основе
корреляционного расстояния ![]() в направлении
в направлении ![]() :
:
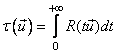 ,
,
где ![]() – точка на гиперсфере. При этом
предлагается следующий коэффициент анизотропии:
– точка на гиперсфере. При этом
предлагается следующий коэффициент анизотропии:
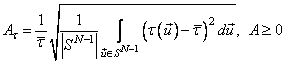 , (1.42)
, (1.42)
где 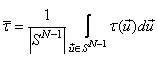 – «среднее» угловое корреляционное расстояние;
– «среднее» угловое корреляционное расстояние;
![]() – площадь
поверхности гиперсферы.
– площадь
поверхности гиперсферы.
Достоинствами
предложенного коэффициента анизотропии является необходимость знания только КФ
поля, и а также возможность его вычисления с применением стандартных численных
методов. Значения ![]() ,
найденные с помощью полученной формулы, для модели (1.34) при
,
найденные с помощью полученной формулы, для модели (1.34) при ![]() ,
, ![]() и различных соотношения
кратностей приведены в табл. 1. Параметры
и различных соотношения
кратностей приведены в табл. 1. Параметры ![]() в случае различающихся кратностей
выбирались, исходя из равенства корреляционных расстояний по обеим осям.
в случае различающихся кратностей
выбирались, исходя из равенства корреляционных расстояний по обеим осям.
Анализ показывает, что
значения коэффициента, близкие к нулю, говорят о высокой степени изотропности
поля. Из приведенной таблицы видно, что с увеличением кратности корней модели,
при условии соответствующего подбора параметров ![]() , изотропность поля увеличивается. Наиболее
близкие к изотропным реализации получаются при равных по обеим координатным
осям кратностях. Как видно из рис. 2.4 и табл. 1, если зафиксировать кратность
поля по одной из осей, и увеличивать кратность по другой оси, не изменяя
параметров
, изотропность поля увеличивается. Наиболее
близкие к изотропным реализации получаются при равных по обеим координатным
осям кратностях. Как видно из рис. 2.4 и табл. 1, если зафиксировать кратность
поля по одной из осей, и увеличивать кратность по другой оси, не изменяя
параметров ![]() ,
значения коэффициента
,
значения коэффициента ![]() растут.
растут.
Таблица 2.1
|
|
1 |
2 |
3 |
4 |
|
1 |
0.1232 |
0.0861 |
0.0826 |
0.0772 |
|
2 |
0.0861 |
0.0443 |
0.0394 |
0.0331 |
|
3 |
0.0826 |
0.0394 |
0.0270 |
0.0249 |
|
4 |
0.0772 |
0.0331 |
0.0249 |
0.0194 |
Преимуществами данной методики оценки изотропности СП являются относительная простота вычисления, а также возможность ее применения на разнообразных выборках реальных данных.
На этапе применения описанных моделей к обработке реальных данных возникает задача идентификации параметров. Идентификация одномерных АР-моделей в общем случае описана в литературе, например в [6].
Будем исходить из предположения, что задано многомерное СП, являющееся реализацией некоторой разделимой АР-модели. Ставится задача определения параметров этой модели.
Рассмотрим предлагаемую
методику оценивания параметров в двумерном случае. При этом обобщение на СП
большей размерности принципиальных трудностей не вызывает. Пусть двумерное СП ![]() описывается следующим
АР уравнением:
описывается следующим
АР уравнением:
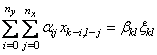 , (1.43)
, (1.43)
где ![]() – стандартное порождающее СП. Для
нахождения неизвестных коэффициентов
– стандартное порождающее СП. Для
нахождения неизвестных коэффициентов ![]() будем следовать основным правилам вывода
системы Юла-Уокера для одномерных последовательностей.
будем следовать основным правилам вывода
системы Юла-Уокера для одномерных последовательностей.
Домножим (1.43) на ![]()
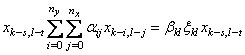 ,
,
и найдем математическое ожидание:
 (1.44)
(1.44)
Полученное выражение
представляет собой систему ![]() уравнений относительно неизвестных
уравнений относительно неизвестных ![]() , причем
, причем ![]() . Значения КФ
. Значения КФ ![]() находятся из
экспериментальных данных.
находятся из
экспериментальных данных.
Найдем коэффициенты ![]() . Для этого возведем
(1.43) в квадрат и найдем математическое ожидание:
. Для этого возведем
(1.43) в квадрат и найдем математическое ожидание:
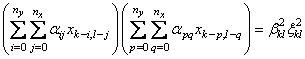 ,
,
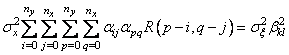 . (1.45)
. (1.45)
Система линейных
уравнений (1.44), (1.45) позволяет найти неизвестные коэффициенты ![]() и тем самым полностью
определить коэффициенты модели.
и тем самым полностью
определить коэффициенты модели.
Заметим, что для случая ![]() измерений система
(1.44), (1.45) уравнений для идентификации параметров модели запишется в виде:
измерений система
(1.44), (1.45) уравнений для идентификации параметров модели запишется в виде:
 (1.46)
(1.46)
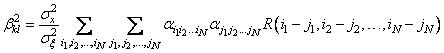 . (1.47)
. (1.47)
Отметим, что для того, чтобы система (1.46), (1.47) имела решение, матрица системы должна быть неособенной.
Рассмотрим теперь модель с кратными корнями для двумерного СП. В этом случае
![]() ,
,
и нам необходимо определить только
четыре параметра – ![]() и
и
![]() . Однако
система (1.44), (1.45) для кратных корней становится нелинейной относительно
неизвестных параметров и решение задачи идентификации требует другого подхода.
. Однако
система (1.44), (1.45) для кратных корней становится нелинейной относительно
неизвестных параметров и решение задачи идентификации требует другого подхода.
Для идентификации моделей
с кратными корнями предлагается использовать двухэтапную процедуру, проводимую
независимо по каждой из осей. На первом этапе необходимо определить кратности
модели по всем осям. Решение задачи нахождения кратности, по существу, является
задачей определения порядка авторегрессии. Эта задача может быть решена на
основе методики определения порядка авторегрессии одномерной последовательности
[11]. Пусть имеется случайная последовательность ![]() и известно, что она порождается одномерной
АР-моделью
и известно, что она порождается одномерной
АР-моделью
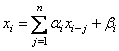 ,
,
где ![]() – последовательность независимых
стандартных СВ.
– последовательность независимых
стандартных СВ.
В [11] показано, что,
если отсчеты ![]() -й
разностной последовательности
-й
разностной последовательности ![]() некоррелированны, то порядок авторегрессии
последовательности
некоррелированны, то порядок авторегрессии
последовательности ![]() равен
равен
![]() . Методика
заключается в последовательном вычислении разностей
. Методика
заключается в последовательном вычислении разностей ![]() и вычислении их КФ. Как только
последовательность перестает быть коррелированной, можно считать, что порядок
авторегрессии определен. В случае модели с кратными корнями, знание порядка
авторегрессии означает знание кратности модели. В [11] приведены примеры
применения данной методики, основанные на принятии статистической гипотезы о
некоррелированности отсчетов случайной последовательности.
и вычислении их КФ. Как только
последовательность перестает быть коррелированной, можно считать, что порядок
авторегрессии определен. В случае модели с кратными корнями, знание порядка
авторегрессии означает знание кратности модели. В [11] приведены примеры
применения данной методики, основанные на принятии статистической гипотезы о
некоррелированности отсчетов случайной последовательности.
На втором этапе процедуры
производится определение значения параметра ![]() . Для этого можно воспользоваться формулой
(1.28), из которой следует, что
. Для этого можно воспользоваться формулой
(1.28), из которой следует, что ![]() , или
, или  . Значения коэффициентов
. Значения коэффициентов ![]() могут быть получены на
основе выборочных значений КФ, как решение системы Юла-Уокера. Для повышения
достоверности можно повторить процедуру для всех значений
могут быть получены на
основе выборочных значений КФ, как решение системы Юла-Уокера. Для повышения
достоверности можно повторить процедуру для всех значений ![]() , и на основе полученных оценок
выбрать наилучшее значение параметра
, и на основе полученных оценок
выбрать наилучшее значение параметра ![]() .
.
Эксперименты показывают,
что описанная процедура идентификации обеспечивает приемлемую точность оценки
параметров. Так, для различных реализаций модели с кратными корнями ошибка
оценки параметра ![]() составляла
в среднем 5-10%.
составляла
в среднем 5-10%.
Таким образом, применив изложенную методику по каждой из осей, получим полностью идентифицированную многомерную модель СП с кратными корнями.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Введение
- 1.1. Тензорные стохастические разностные уравнения
- 1.1. Тензорные стохастические разностные уравнения
- 1.2. Каузальные модели изображений
- 1.2. Каузальные модели изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.2. Эффективность обнаружения аномалий
- 2.2. Эффективность обнаружения аномалий
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.2. Тензорный фильтр Калмана
- 3.2. Тензорный фильтр Калмана
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- Заключение
- Заключение
- Литература
- Литература