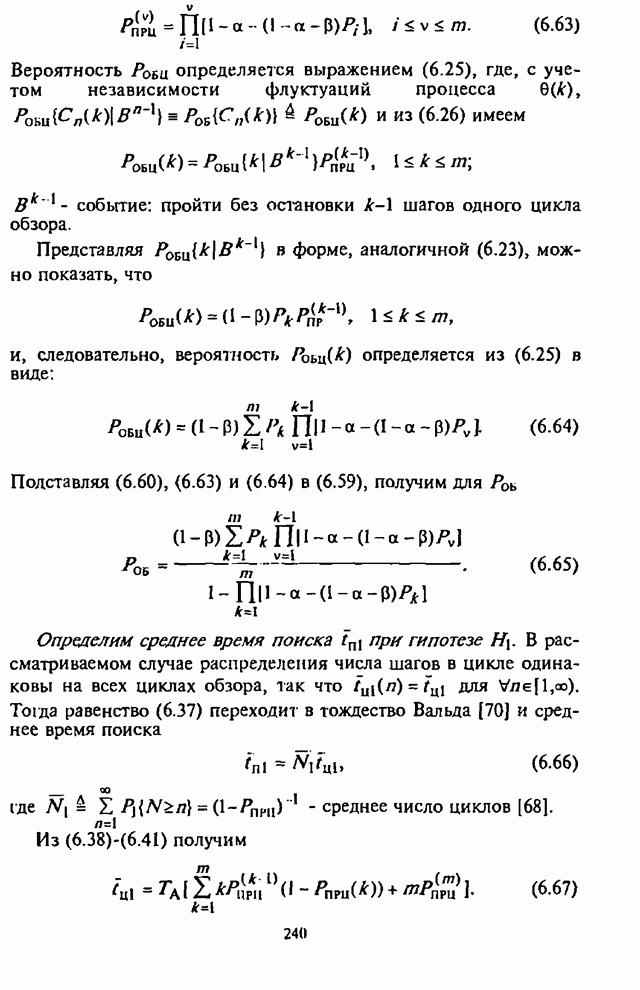| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
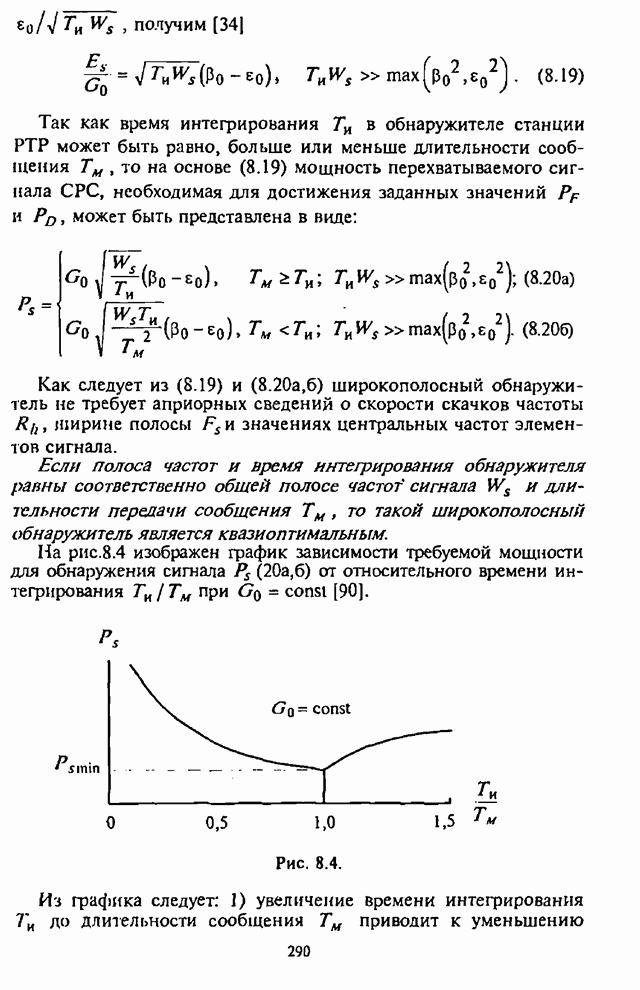
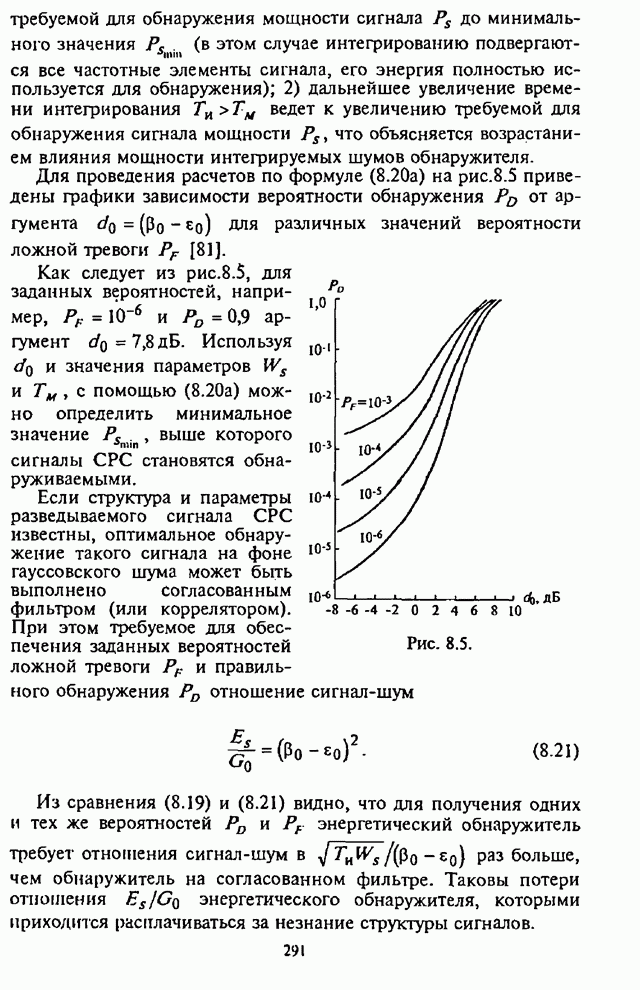
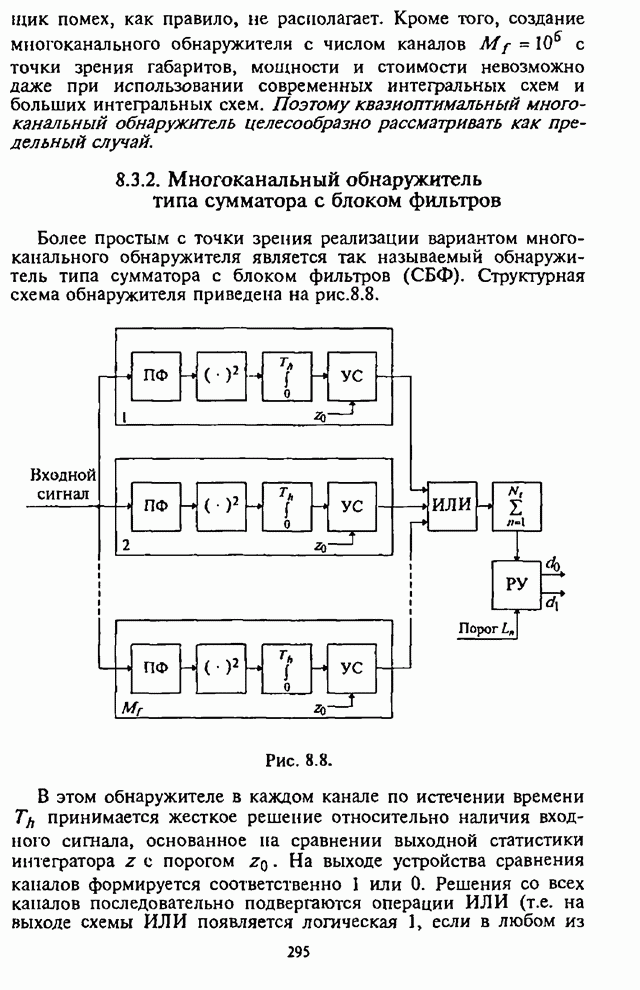
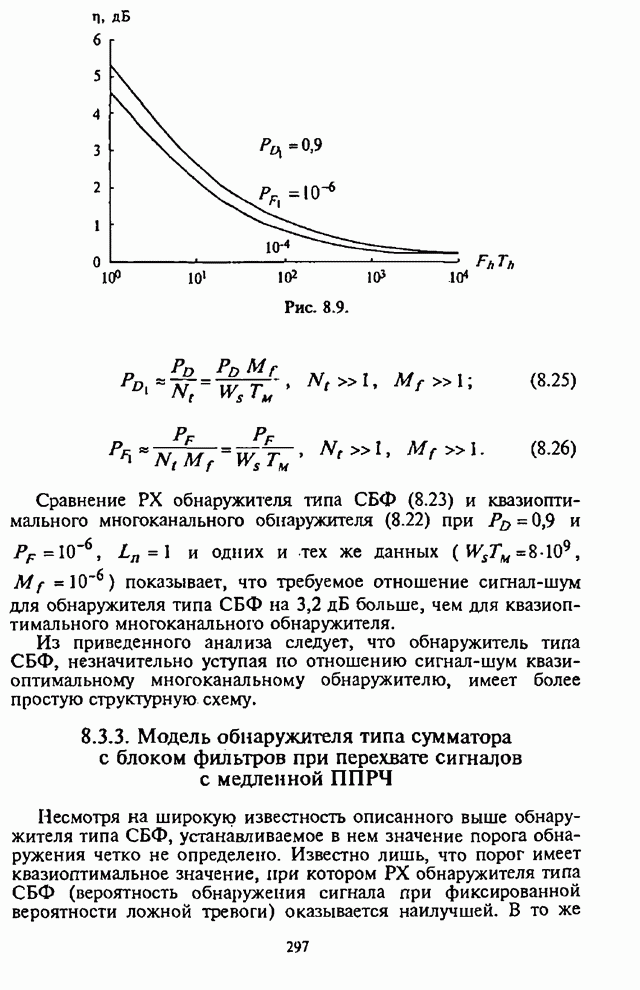
6.3. Показатели и оценка эффективности циклических процедур поиска
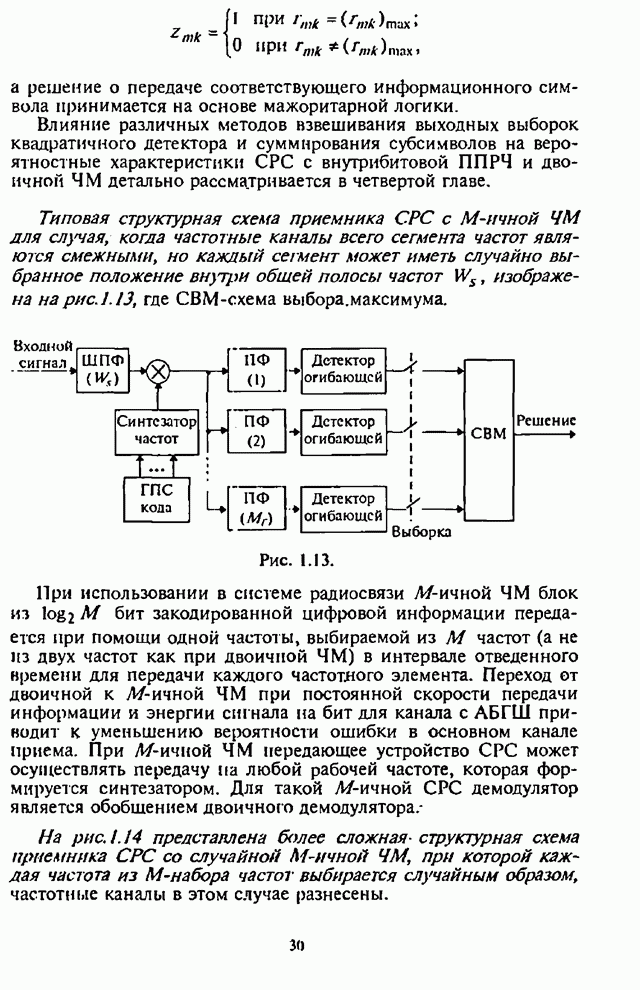
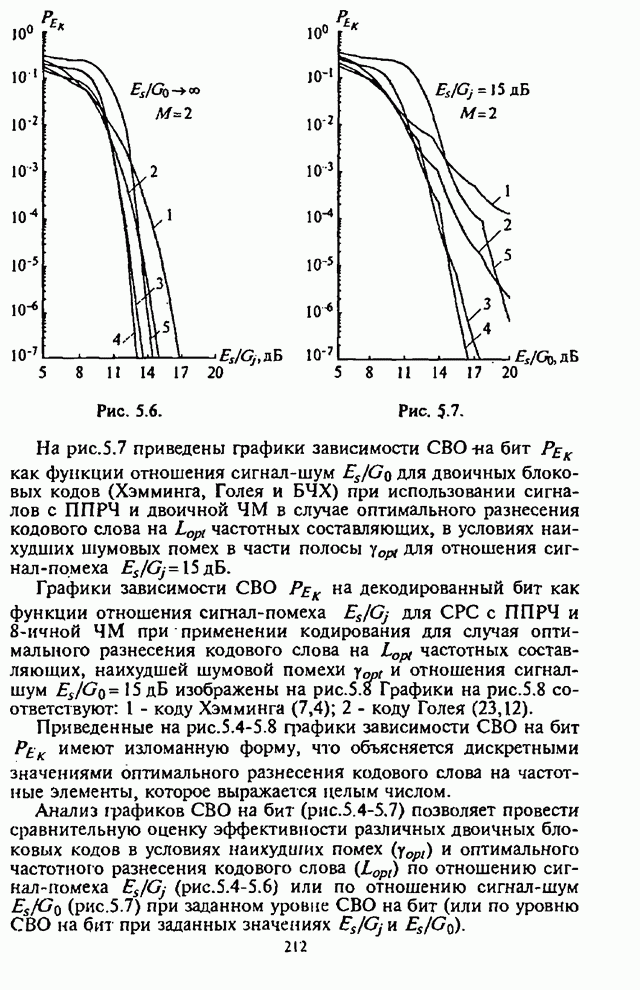
Как отмечалось выше, назначением подсистемы синхронизации является введение СРС в работоспособное состояние и поддержание этого состояния в течение передачи сообщения. Исходя из назначения подсистемы синхронизации, определяются показатели эффективности и их характеристики.
Рассмотрим
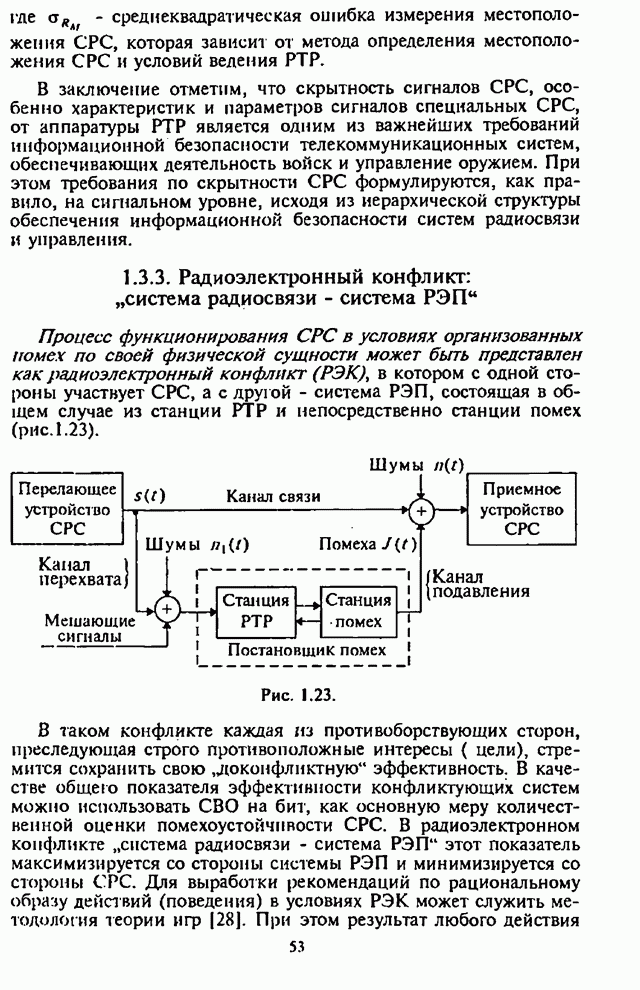
эффективность циклических процедур поиска с поочередным алгоритмом обзора
поискового пространства ![]() . Правила функционирования таких процедур поиска подробно
описаны в [56,57,59,65,66] и имеющейся в них библиографии. Далее используются
модель, терминология и обозначения, принятые в [66].
. Правила функционирования таких процедур поиска подробно
описаны в [56,57,59,65,66] и имеющейся в них библиографии. Далее используются
модель, терминология и обозначения, принятые в [66].
Будем
рассматривать упрощенную математическую модель, когда случайный процесс ![]() , аппроксимируется дискретным
марковским процессом
, аппроксимируется дискретным
марковским процессом ![]() с конечным числом состояний из дискретного множества
с конечным числом состояний из дискретного множества ![]() , полагая
, полагая ![]() при
при ![]() - длительность
одного шага поиска (рис.6.13).
- длительность
одного шага поиска (рис.6.13).

Рис. 6.13.
При
этом на каждом шаге поиска анализируется только одна точка из ![]() . Диаграмма
циклического поиска для этого случая изображена на рис.6.14, где пунктиром
показан процесс
. Диаграмма
циклического поиска для этого случая изображена на рис.6.14, где пунктиром
показан процесс ![]() ,
а сплошной линией - траектория сканирования поисковой системы;
,
а сплошной линией - траектория сканирования поисковой системы; ![]() - правило
обзора точек
- правило
обзора точек ![]() :
если
:
если ![]() то
на
то
на ![]() шаге анализируется точка
шаге анализируется точка ![]() .
.

Рис. 6.14.
В
общем случае [67] статистические характеристики дискретного марковского
процесса ![]() ,
задаются вектором вероятностей начальных состояний
,
задаются вектором вероятностей начальных состояний
![]() (6.15)
(6.15)
и
совокупностью матриц переходных вероятностей состояний процесса ![]() от
от ![]() шага к
шага к ![]() шагу
шагу
![]()
![]() (6.16)
(6.16)
где ![]() обозначает
транспонирование;
обозначает
транспонирование;
 (6.17)
(6.17)
Здесь
и далее символом ![]() обозначается вероятность
события
обозначается вероятность
события ![]() , а символом
, а символом ![]() - условная
вероятность.
- условная
вероятность.
Для упрощения дальнейших выкладок и возможности получения обозримых результатов примем ряд ограничений на класс рассматриваемых марковских процессов. Будем полагать, что матрицы (6.16) могут быть различны на разных шагах поиска внутри одного цикла обзора, но повторяются от цикла к циклу
![]() .
.
Кроме
того, исключим возможность перехода процесса ![]() через траекторию обзора
через траекторию обзора ![]() на каждом цикле
на каждом цикле ![]() без совпадения
горизонтальных участков (см. рис.6.14), а также - возможность многократных
пересечений на одном цикле процесса
без совпадения
горизонтальных участков (см. рис.6.14), а также - возможность многократных
пересечений на одном цикле процесса ![]() с траекторией обзора
с траекторией обзора ![]() ,
, ![]() и - возможность «скольжения» по ней. Для дискретных
марковских процессов такого типа элементы матриц
и - возможность «скольжения» по ней. Для дискретных
марковских процессов такого типа элементы матриц ![]() должны
удовлетворять внутри цикла
должны
удовлетворять внутри цикла ![]() , например, следующей системе ограничений:
, например, следующей системе ограничений:
![]() ,
, ![]() ,
, ![]() (6.18)
(6.18)
при ![]()
Элементы
матриц ![]() могут быть любыми, удовлетворяющими обычным ограничениям
(6.17). Решение о наличии (отсутствии) сигнала на каждом шаге поиска (т.е. в
каждой точке
могут быть любыми, удовлетворяющими обычным ограничениям
(6.17). Решение о наличии (отсутствии) сигнала на каждом шаге поиска (т.е. в
каждой точке ![]() )
выносится по правилу бинарного обнаружения, оптимальному в смысле критерия
Неймана-Пирсона [54]. При этом вероятности
)
выносится по правилу бинарного обнаружения, оптимальному в смысле критерия
Неймана-Пирсона [54]. При этом вероятности ![]() - пропуска сигнала в точках
- пропуска сигнала в точках ![]() , содержащих сигнал, и
вероятности
, содержащих сигнал, и
вероятности ![]() -
ложного обнаружения в точках
-
ложного обнаружения в точках ![]() , не содержащих сигнал, полагаем
постоянными на всех шагах и циклах поиска. Наблюдаемые реализации помех
полагаем статистически независимыми на разных шагах поиска [68].
, не содержащих сигнал, полагаем
постоянными на всех шагах и циклах поиска. Наблюдаемые реализации помех
полагаем статистически независимыми на разных шагах поиска [68].
Эффективность поиска при
гипотезе ![]() - о наличии
сигнала, будем характеризовать вероятностями
- о наличии
сигнала, будем характеризовать вероятностями ![]() - правильных
и
- правильных
и ![]() - ошибочных решений
о значении
параметра сигнала и средним временем поиска
- ошибочных решений
о значении
параметра сигнала и средним временем поиска ![]() при гипотезе
при гипотезе
![]() -
об отсутствии
сигнала - вероятностью
-
об отсутствии
сигнала - вероятностью ![]() - ложного обнаружения
(ложных тревог) за
- ложного обнаружения
(ложных тревог) за ![]() циклов обзора и средним
временем
циклов обзора и средним
временем ![]() до окончания
поиска ложным обнаружением [68].
до окончания
поиска ложным обнаружением [68].
Определим вероятности ![]() и
и ![]() . Вероятность окончания поиска
на первых
. Вероятность окончания поиска
на первых ![]() циклах
правильным обнаружением равна
циклах
правильным обнаружением равна
![]() (6.19)
(6.19)
где ![]() - событие правильного обнаружения на
- событие правильного обнаружения на ![]() -м цикле;
-м цикле;  ,
, ![]() - событие - пройти без остановки
- событие - пройти без остановки ![]() -й цикл;
-й цикл;![]()
Вероятность окончания поиска на первых циклах ошибочным решением -
![]() (6.20)
(6.20)
где ![]() .
.
Поскольку
наблюдаемые реализации предполагаются статистически независимыми, а ![]() и
и ![]() -
постоянными на всех шагах и циклах поиска,
-
постоянными на всех шагах и циклах поиска, ![]() для
для ![]()
 (6.21)
(6.21)
Вероятности
![]() в (6.19) можно представить
как
в (6.19) можно представить
как
![]() (6.22)
(6.22)
где ![]() - событие
правильною обнаружения на
- событие
правильною обнаружения на ![]() шаге
шаге ![]() цикла обзора,
цикла обзора,  .
.
Пусть
![]() - событие остановки на
- событие остановки на ![]() шаге
шаге ![]() цикла. Тогда
цикла. Тогда
![]() (6.23)
(6.23)
где
для ![]() вероятность
вероятность
![]() (6.24)
(6.24)
Используя известные соотношения [67,69], получим для вероятностей
 (6.25)
(6.25)
где ![]() - элементы матрицы
- элементы матрицы
 (6.26)
(6.26)
переходных
вероятностей процесса ![]() на
на ![]() шаге
шаге ![]() -гo цикла;
-гo цикла; ![]() - единичная матрица
|69];
- единичная матрица
|69];
![]() (6.27)
(6.27)
координаты вектора
![]() (6.28)
(6.28)
вероятностей
начального состояния процесса ![]() на
на ![]() цикле,
цикле,
![]() (6.29)
(6.29)
Подставляя (6.26), (6.27) в (6.25) и (6.23)-(6.25) в (6.22), получим для (6.19)
![]() (6.30)
(6.30)
где ![]() - матрица,
обратная к
- матрица,
обратная к ![]() ;
;
![]() (6.31)
(6.31)
Финальные
вероятности ![]() и
и ![]() равны
пределам
равны
пределам
![]() (6.32)
(6.32)
Поскольку,
как это следует из (6.21), ![]() , то из (6.20) имеем
, то из (6.20) имеем
![]() (6.33)
(6.33)
и, следовательно, поиск всегда заканчивается с вероятностью единица. Из (6.30), (6.32) и (6.33) окончательно получим
 (6.34)
(6.34)
В
отсутствие сигнала (гипотеза ![]() ) вероятность ложных тревог
) вероятность ложных тревог ![]() первых циклов равна [68]
первых циклов равна [68]
![]() (6.35)
(6.35)
Определим среднее время
поиска. Если условия регулярности ![]() при обнаружении
выполнены, то среднее время поиска
при обнаружении
выполнены, то среднее время поиска ![]() можно представить как условное (при
можно представить как условное (при ![]() и
и ![]() ) математическое ожидание
) математическое ожидание
 (6.36)
(6.36)
суммы
случайного числа ![]() случайных величин -
длительностей циклов
случайных величин -
длительностей циклов ![]() ,
где
,
где ![]() - математическое ожидание по
- математическое ожидание по ![]() .
.
В
рассматриваемой поисковой модели (см. рис.6.14) целочисленная случайная
величина ![]() -
число циклов - не зависит от будущего и
-
число циклов - не зависит от будущего и ![]() . Тогда, согласно теореме
Колмогорова-Смирнова [70], имеет место тождество
. Тогда, согласно теореме
Колмогорова-Смирнова [70], имеет место тождество
 (6.37)
(6.37)
которым воспользуемся для вычисления (6.36).
Определим среднее время поиска
![]() при гипотезе
при гипотезе
![]() . Среднюю длительность
. Среднюю длительность ![]() произвольного
произвольного ![]() цикла можно представить как
цикла можно представить как
![]() (6.38)
(6.38)
где
![]() (6.39)
(6.39)
![]() - вероятность остановки
поиска на
- вероятность остановки
поиска на ![]() шаге
шаге
![]() цикла при условии, что
цикла при условии, что ![]() и пройдено без остановки
и пройдено без остановки ![]() циклов.
циклов.
Можно
показать, что вероятность ![]() не зависит от события
не зависит от события ![]() и определяется следующим выражением:
и определяется следующим выражением:
 (6.40)
(6.40)
Подставляя (6.40) в (6.39), получим для (6.38)
 (6.41)
(6.41)
Выражение
в квадратных скобках в (6.41) равно среднему числу поисковых шагов на ![]() цикле, которое
обозначим
цикле, которое
обозначим ![]() .
Тогда
.
Тогда
![]() (6.42)
(6.42)
Используя (6.25)-(6.28), получим
 (6.43)
(6.43)
Для
вероятности ![]() в (6.37) имеем с учетом (6.31)
в (6.37) имеем с учетом (6.31)
![]() (6.44)
(6.44)
Подстакляя (6.42)-(6.44) в (6.37), получим для среднего времени поиска
![]() (6.45)
(6.45)
где
![]() (6.46)
(6.46)
- среднее
число поисковых шагов длительностью ![]() (среднее нормированное время
поиска) при наличии сигнала [68]. Подставляя (6.43) в (6.46), окончательно
получим
(среднее нормированное время
поиска) при наличии сигнала [68]. Подставляя (6.43) в (6.46), окончательно
получим
![]() (6.47)
(6.47)
Сопоставляя
выражения (6.34) и (6.43), можно видеть, что при ![]() среднее время поиска
среднее время поиска ![]() и вероятность правильного обнаружения
и вероятность правильного обнаружения ![]() связаны
простыми соотношениями
связаны
простыми соотношениями
![]()
 ,
,
которые
удобны при оптимизации параметров ![]() циклических процедур поиска.
циклических процедур поиска.
Вычислим среднее время
![]() до
окончания поиска ложным обнаружением. Средняя длительность одного цикла обзора при
гипотезе
до
окончания поиска ложным обнаружением. Средняя длительность одного цикла обзора при
гипотезе ![]()
![]() ,
,
где среднее число шагов на одном цикле -
 .
.
Среднее нормированное время
![]() (6.48)
(6.48)
и, следовательно,
![]() (6.49)
(6.49)
Если на каждом шаге поиска используется несмещенное правило обнаружения [54], т.е. когда
![]() (6.50)
(6.50)
то
при ![]() выполняется
неравенство
выполняется
неравенство
![]() или
или ![]() . (6.51)
. (6.51)
Следовательно,
![]() является
верхней границей для
является
верхней границей для ![]() при всех возможных
значениях параметров несмещенных алгоритмов обнаружения (6.50); в частности, при любых
значениях отношения сигнал-помеха. Доказательство этого факта дано в приложении
П.6.1.
при всех возможных
значениях параметров несмещенных алгоритмов обнаружения (6.50); в частности, при любых
значениях отношения сигнал-помеха. Доказательство этого факта дано в приложении
П.6.1.
Рассмотрим
конкретные примеры использования соотношений (6.34), (6.47). Выражения (6.36) и (6.48) для ![]() и
и ![]() остаются неизменными для
всех рассматриваемых ниже примеров.
остаются неизменными для
всех рассматриваемых ниже примеров.
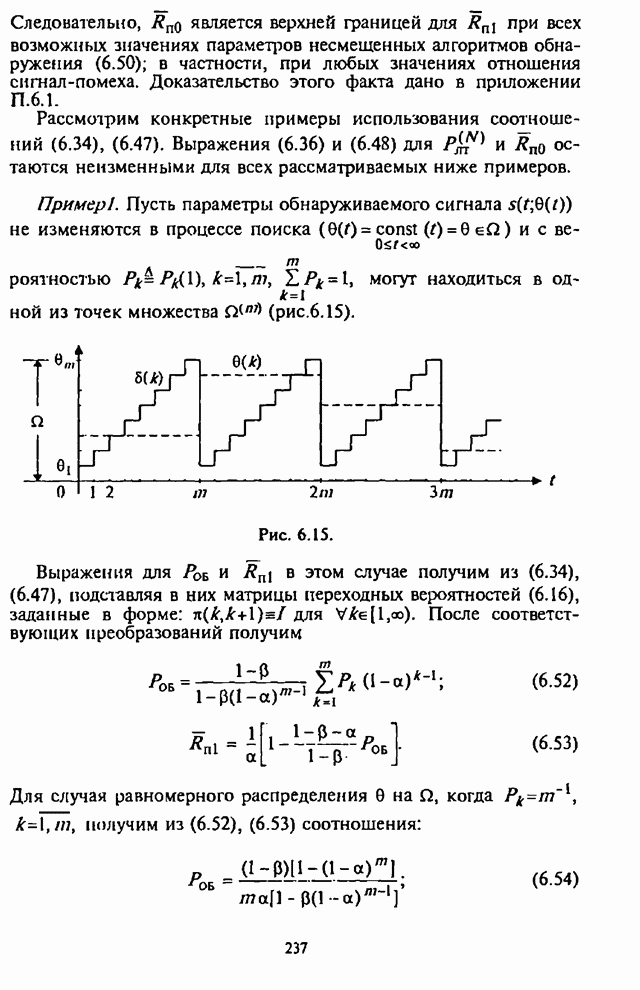
Пример 1. Пусть параметры
обнаруживаемого сигнала ![]() не изменяются в процессе поиска
не изменяются в процессе поиска ![]() и с вероятностью
и с вероятностью ![]() , могут находиться в
одной из точек множества
, могут находиться в
одной из точек множества ![]() (рис.6.15).
(рис.6.15).

Рис. 6.15.
Выражения
для ![]() и
и ![]() в этом случае получим из (6.34), (6.47), подставляя в них матрицы
переходных вероятностей (6.16), заданные в форме:
в этом случае получим из (6.34), (6.47), подставляя в них матрицы
переходных вероятностей (6.16), заданные в форме: ![]() для
для ![]() . После соответствующих
преобразований получим
. После соответствующих
преобразований получим
 (6.52)
(6.52)
![]() (6.53)
(6.53)
Для случая
равномерного распределения ![]() на
на ![]() , когда
, когда ![]() , получим из (6.52), (6.53)
соотношения:
, получим из (6.52), (6.53)
соотношения:
 ; (6.54)
; (6.54)
 (6.55)
(6.55)
Пример 2. Пусть процесс ![]() , не изменяется в течение одного цикла обзора, но изменяется
как марковская последовательность от цикла к циклу, т.е.
, не изменяется в течение одного цикла обзора, но изменяется
как марковская последовательность от цикла к циклу, т.е. ![]() при
при ![]() (рис.6.16).
(рис.6.16).

Рис. 6.16.
Требование
постоянства процесса ![]() внутри цикла формально
означает, что
внутри цикла формально
означает, что ![]() для
для ![]() . Тогда из (6.26), (6.29) имеем:
. Тогда из (6.26), (6.29) имеем: ![]() . Будем полагать,
что процесс
. Будем полагать,
что процесс ![]() ,
однородный [67,69], т.е.
,
однородный [67,69], т.е.
![]()
Подставляя
![]() и
и ![]() (6.34), (6.47), получим для
(6.34), (6.47), получим для ![]() и
и ![]() следующие
выражения:
следующие
выражения:
![]() (6.56)
(6.56)
![]() . (6.57)
. (6.57)
Соотношения
(6.56), (6.57) являются более общими по сравнению с (6.34), (6.47), поскольку
в данном случае на элементы матриц переходных вероятностей ![]() никаких ограничений, кроме обычных (6.16), не накладывается.
Для иллюстрации этого факта рассмотрим следующие примеры.
никаких ограничений, кроме обычных (6.16), не накладывается.
Для иллюстрации этого факта рассмотрим следующие примеры.
Пример 3. Пусть случайный процесс ![]() ,
, ![]() , флуктуирует независимо от цикла к циклу.
Это означает [67], что элементы матрицы
, флуктуирует независимо от цикла к циклу.
Это означает [67], что элементы матрицы ![]() удовлетворяют условию
удовлетворяют условию![]() . Тогда
. Тогда![]() и из (6.56), (6.57) получим, что
выражения для
и из (6.56), (6.57) получим, что
выражения для ![]() и
и
![]() в этом случае совпадают с
(6.52), (6.53). Таким образом, эффективность циклического поиска оказывается
одинаковой как в случае неизменяющегося параметра сигнала, так и при независимых
флуктуациях от цикла к циклу.
в этом случае совпадают с
(6.52), (6.53). Таким образом, эффективность циклического поиска оказывается
одинаковой как в случае неизменяющегося параметра сигнала, так и при независимых
флуктуациях от цикла к циклу.
Пример 4. Процесс ![]() , независимо флуктуирует от шага к шагу
поиска. Это означает [67], что элементы матрицы
, независимо флуктуирует от шага к шагу
поиска. Это означает [67], что элементы матрицы ![]() (6.16) внутри цикла
(6.16) внутри цикла ![]() должны удовлетворять условию
должны удовлетворять условию ![]() . Получить в этом случае выражения
для
. Получить в этом случае выражения
для ![]() и
и ![]() непосредственно из
(6.34),(6.47) нельзя, поскольку ограничения (6.18), при которых справедливы
(6.34), (6.47), теперь не выполняются.
непосредственно из
(6.34),(6.47) нельзя, поскольку ограничения (6.18), при которых справедливы
(6.34), (6.47), теперь не выполняются.
Определим вероятности ![]() и
и![]() . Из
(6.19)-(6.30), с учетом статистической независимости
флуктуации процесса
. Из
(6.19)-(6.30), с учетом статистической независимости
флуктуации процесса ![]() ,
после преобразований, аналогичных тем, которые описаны в примере 3, получим
для
,
после преобразований, аналогичных тем, которые описаны в примере 3, получим
для ![]() (6.19)
(6.19)
 (6.58)
(6.58)
где ![]() и
и ![]() для
для ![]() .
.
Тогда из (6.32), (6.33) для рассматриваемого случая (6.58) имеем
 (6.59)
(6.59)
Вероятность пройти без остановки один цикл обзора -
![]() (6.60)
(6.60)
где
 (6.61)
(6.61)
![]() (6.62)
(6.62)
Подставляя
в (6.62) для рассматриваемого случая ![]()
![]() получим
получим
 . (6.63)
. (6.63)
Вероятность
![]() определяется
выражением (6.25), где, с учетом независимости флуктуации процесса
определяется
выражением (6.25), где, с учетом независимости флуктуации процесса ![]() и
из (6.26) имеем
и
из (6.26) имеем
![]() ;
;
![]() -
событие: пройти без остановки
-
событие: пройти без остановки ![]() шагов одного цикла обзора.
шагов одного цикла обзора.
Представляя
![]() в форме,
аналогичной (6.23), можно показать, что
в форме,
аналогичной (6.23), можно показать, что
![]() ,
,
и,
следовательно, вероятность ![]() определяется из (6.25) в виде:
определяется из (6.25) в виде:
 . (6.64)
. (6.64)
Подставляя
(6.60), (6.63) и (6.64) в (6.59), получим для ![]()
 . (6.65)
. (6.65)
Определим
среднее время поиска ![]() при
гипотезе
при
гипотезе ![]() . В
рассматриваемом случае распределения числа шагов в цикле одинаковы на всех
циклах обзора, так что
. В
рассматриваемом случае распределения числа шагов в цикле одинаковы на всех
циклах обзора, так что ![]() для
для ![]() . Тогда равенство (6.37) переходит в
тождество Вальда [70] и среднее время поиска
. Тогда равенство (6.37) переходит в
тождество Вальда [70] и среднее время поиска
![]() , (6.66)
, (6.66)
где
![]() - среднее
число циклов [68].
- среднее
число циклов [68].
Из (6.38)-(6.41) получим
 . (6.67)
. (6.67)
Подставляя (6.60), (6.63) в (6.67), имеем для
 . (6.68)
. (6.68)
В
частном случае равномерного распределения значений случайного процесса ![]() на
на ![]() , т.е.
, т.е. ![]() получим из (6.65), (6.68)
получим из (6.65), (6.68)
![]() ; (6.69)
; (6.69)
![]() . (6.70)
. (6.70)
И
в этом случае при выполнении условия несмещенности (6.50) для ![]() справедливо
неравенство
справедливо
неравенство ![]() (6.51).
(6.51).
Для
случая равномерного распределения значений случайного процесса сравним
показатели эффективности (6.54), (6.55) при постоянном (нефлуктуирующем)
параметре сигнала (пример 3) с показателями эффективности (6.69), (6.70) при
независимых флуктуациях процесса ![]() (пример 4).
(пример 4).
Сначала
рассмотрим асимптотический случай ![]() (очень большое отношение сигнал-помеха).
Обозначим через
(очень большое отношение сигнал-помеха).
Обозначим через ![]() показатели
эффективности (6.54), (6.55) при постоянном параметре сигнала, а через
показатели
эффективности (6.54), (6.55) при постоянном параметре сигнала, а через ![]() - для случая
независимых флуктуации (6.69), (6.70). Устремляя
- для случая
независимых флуктуации (6.69), (6.70). Устремляя ![]() и
и ![]() к нулю, получим из (6.54), (6.55) и
(6.69), (6.70)
к нулю, получим из (6.54), (6.55) и
(6.69), (6.70)

Таким
образом, в этом предельном случае при одинаковых вероятностях правильного
обнаружения среднее время поиска при нефлуктуирующем параметре сигнала в два
раза меньше, чем при флуктуирующем (для ![]() ).
).
Сравнение
в этом частном случае для произвольных ![]() показывает (см. приложение П.6.2), что
всегда
показывает (см. приложение П.6.2), что
всегда
![]() и
и
![]() .
.
Другими
словами, флуктуации параметра ![]() , по которому осуществляется поиск сигнала
, по которому осуществляется поиск сигнала
![]() , приводит к
уменьшению вероятности правильного обнаружения и возрастанию среднего времени
поиска, т.е. - к снижению эффективности циклических процедур поиска
рассмотренного вида.
, приводит к
уменьшению вероятности правильного обнаружения и возрастанию среднего времени
поиска, т.е. - к снижению эффективности циклических процедур поиска
рассмотренного вида.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
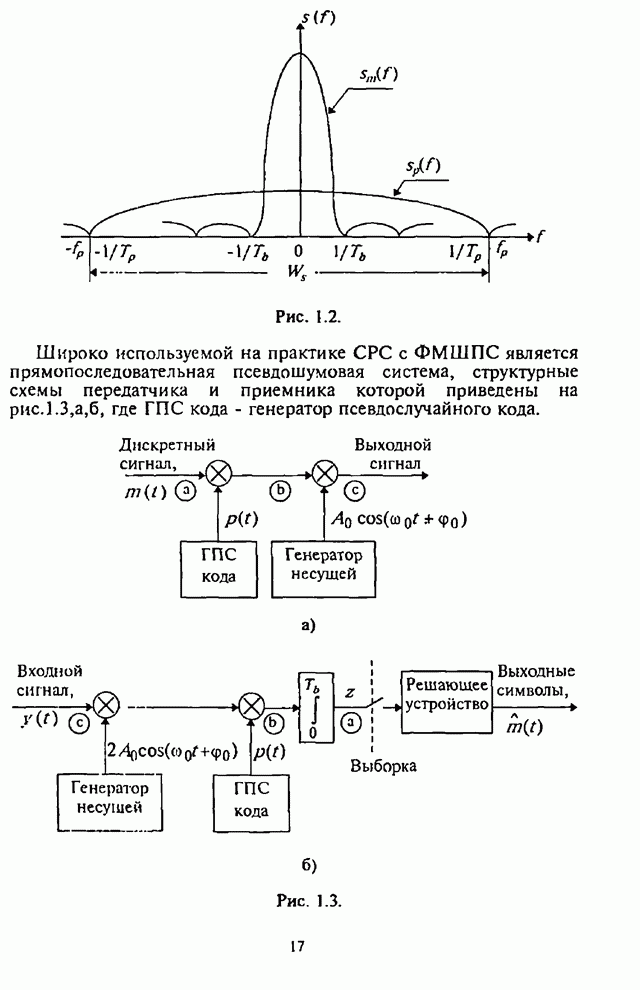
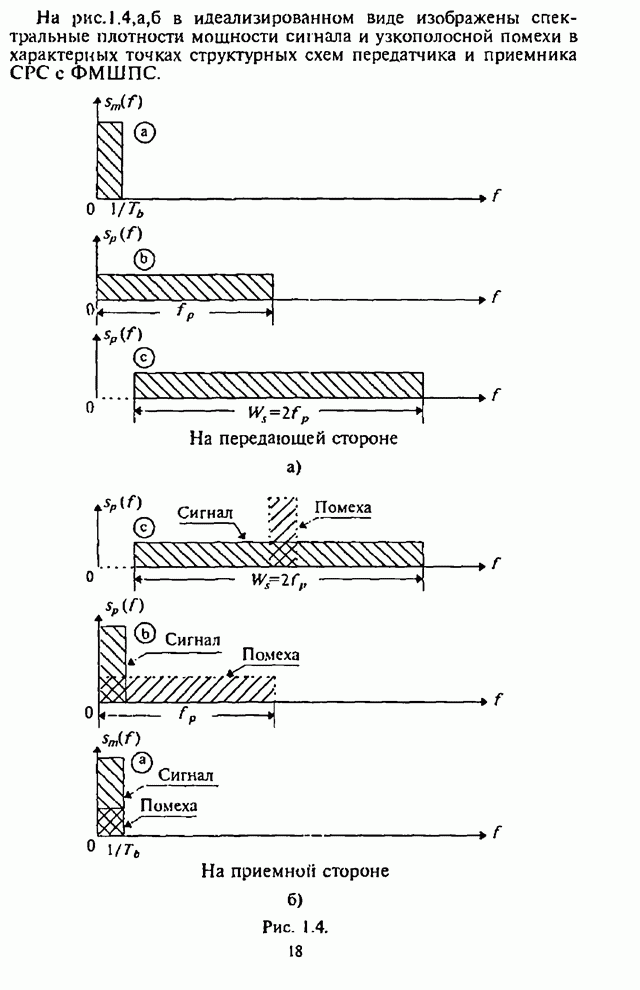
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
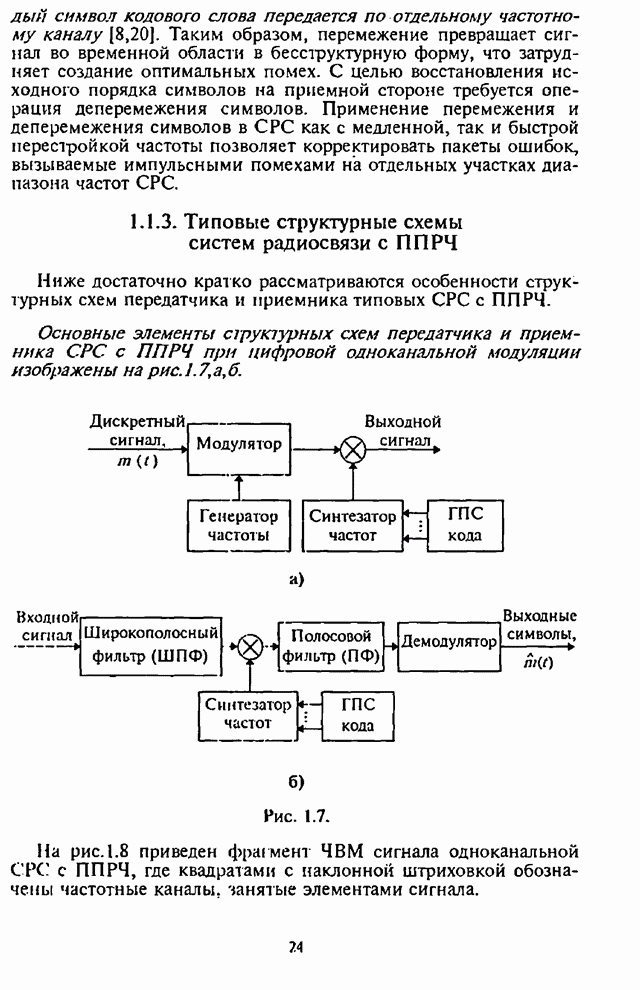
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
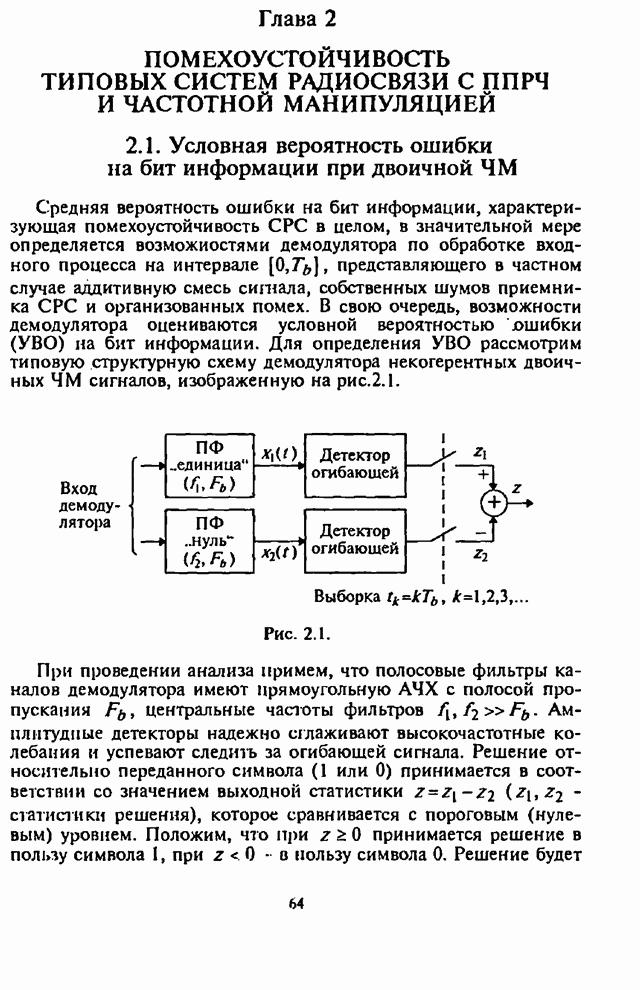
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
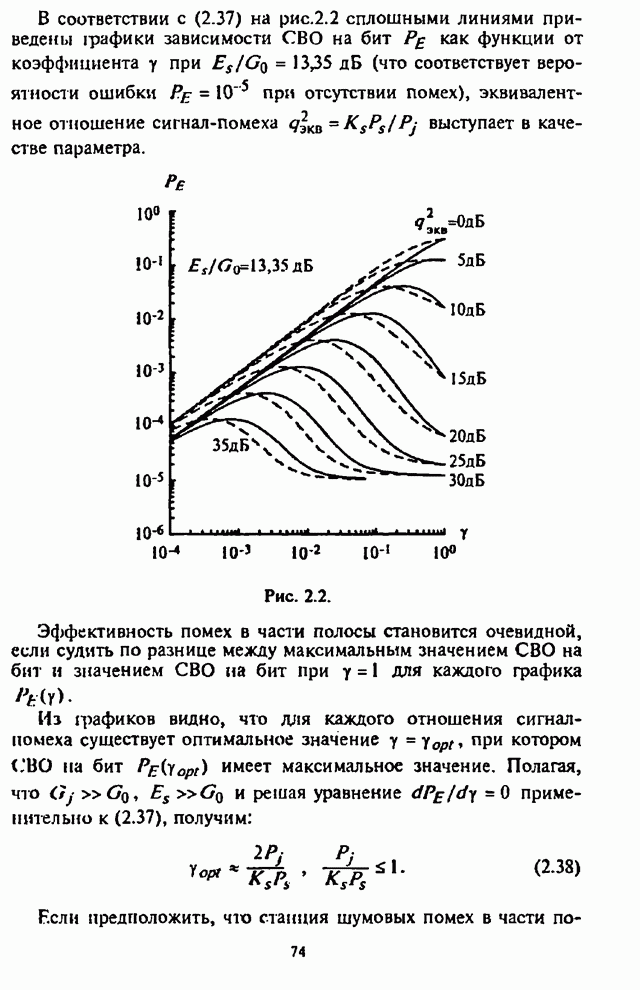
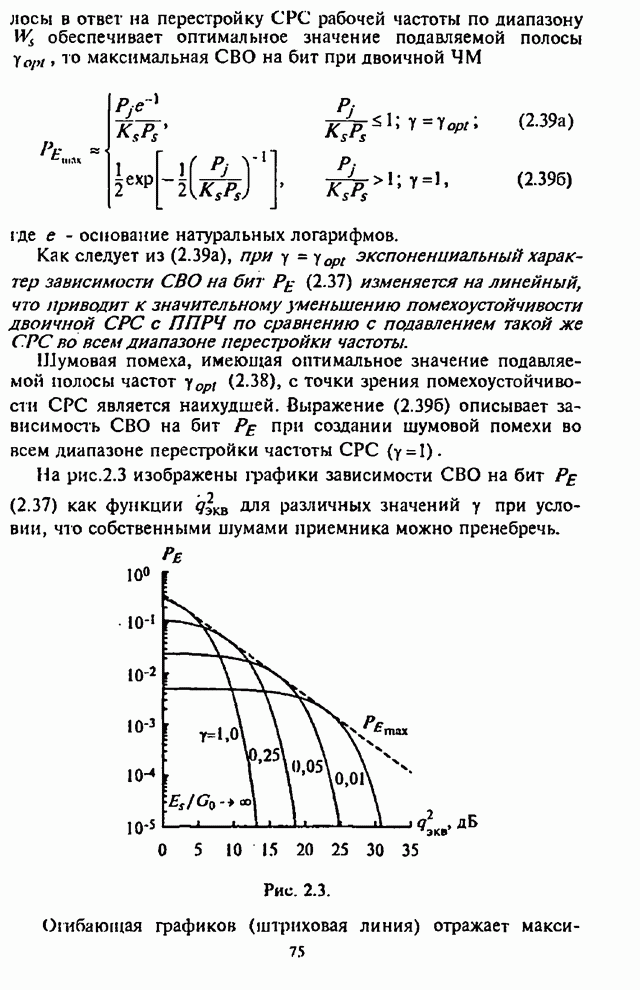
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
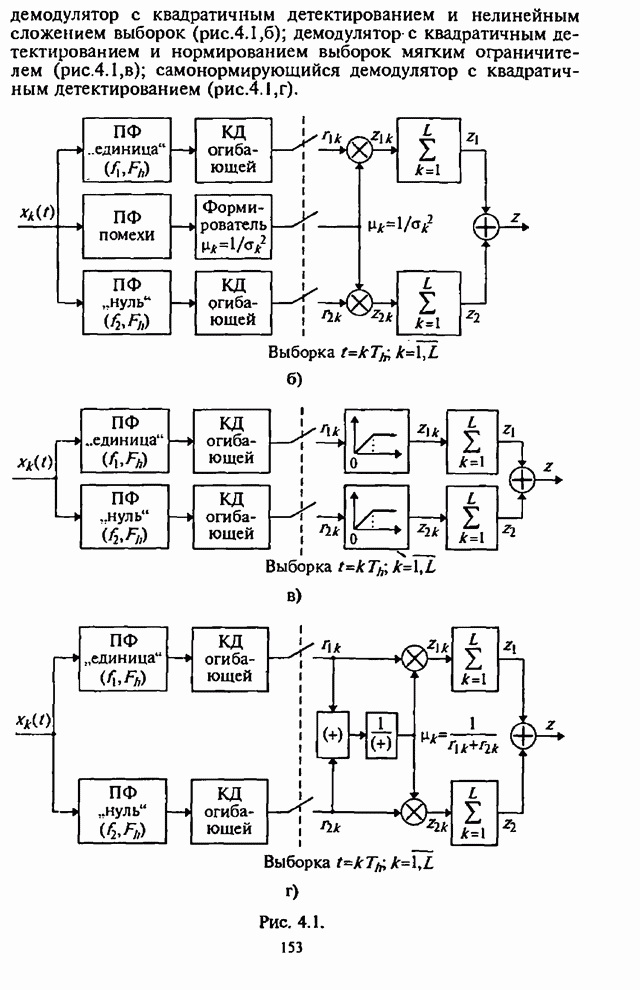
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
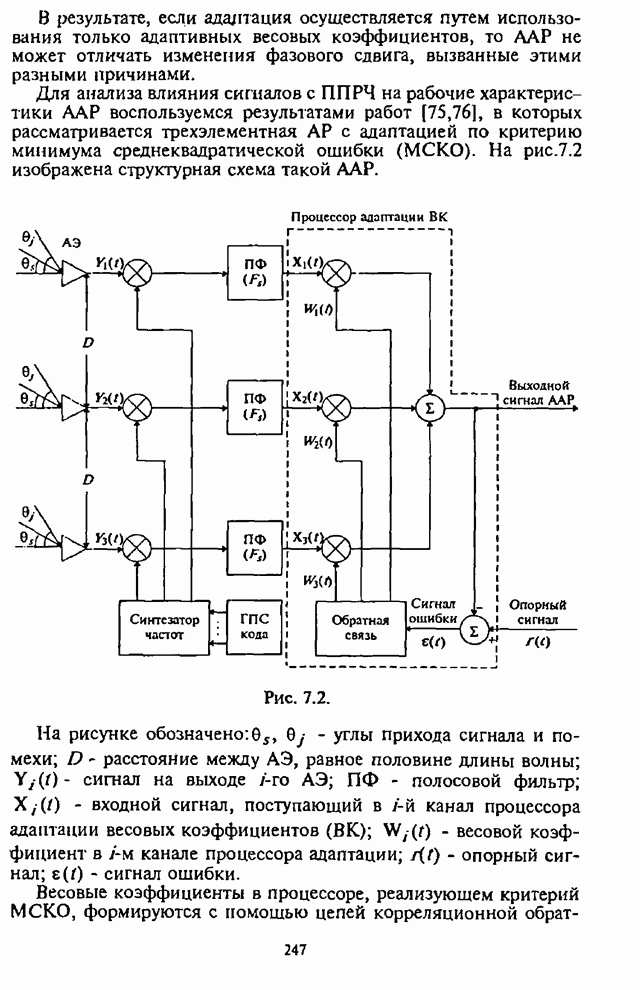
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
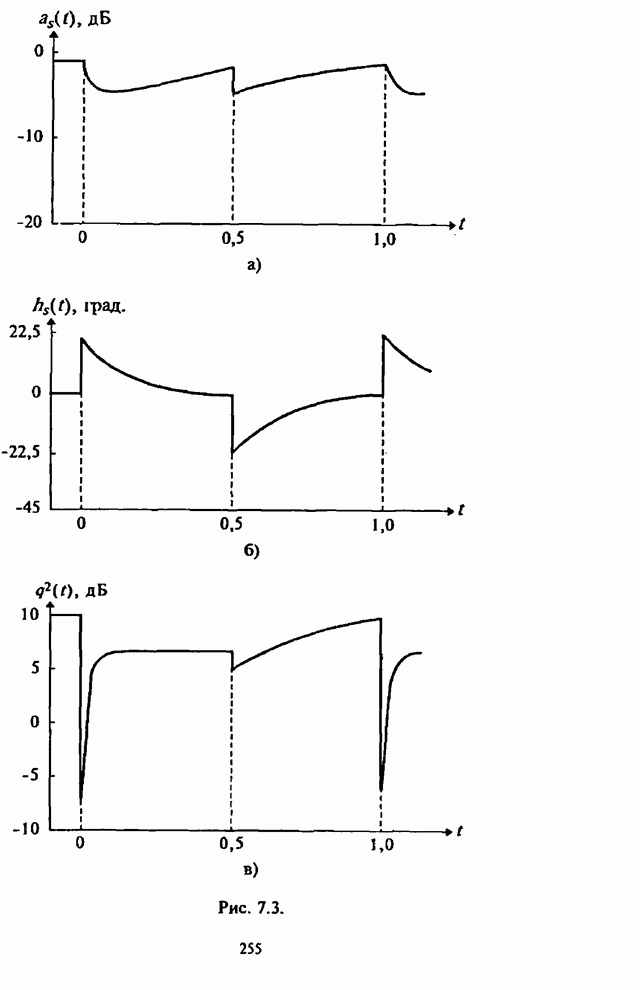
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ