1. Коды Хаффмана

Работа алгоритма начинается с составления списка символов (чисел) алфавита в порядке убывания их частоты (вероятности). Лучше всего продемонстрировать этот алгоритм на простом примере. Пусть имеется пять символов:  с известными вероятностями: , , ,  и . Для построения кодов, выбираем сначала пару символов с наименьшими вероятностями – это символы  и . Наименее вероятному символу ставим в соответствие битовый ноль, а более вероятному – битовую единицу:

Символы  и  условно объединяются в единый символ  с вероятностью появления 0,2. Затем берется третий символ из упорядоченного списка – это символ  с вероятностью 0,2. Поэтому код символа  будет начинаться с битовой 1, а к кодам символов  и  дописывается битовый ноль:

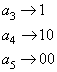
Далее, условно объединяем все три символа, в символ  с вероятностью появления 0,4 и рассматриваем его со следующим символом списка - , вероятность которого 0,2. Так как вероятность появления символа  меньше вероятности появления условного символа , то код символа  будет начинаться с нуля, а кодам символов ,  и  приписывается битовая единица:

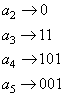
Аналогично, получаем для последнего символа :

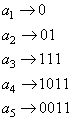
В итоге получаем коды Хаффмана, но записанные в обратном порядке, т.е. для кодирования символа  имеем код 0, для  - код 10, для  - 111,  - 1101 и  - 1100. Заметим, что данные коды могут быть корректно декодированы, например, последовательность символов  будет представлена последовательностью бит

01011111011100

В этой последовательности первым встречается битовый ноль, но с нуля начинается только один код – код символа , поэтому он так и декодируется. Затем видим код, начинающийся с битовой единицы. Таких кодов несколько, поэтому необходимо прочитать следующий бит, который равен 0. Код 10 – единственный, соответствующий символу . После этого видим код с тремя единицами подряд (111). Это говорит о том, что это символ . Наконец последние два кода точно декодируют символы  и .

Построенные таким образом однозначные коды будут в среднем тратить 2,2 бита на символ:

 бит/символ

Для сравнения, обычный двоичный код потребовал бы 3 бита для представления одного символа, т.е. в этом случае последовательность можно было бы сжать в 3/2,2=1,36 раза.

Однако чтобы произвести декодирование данных необходимо знать построенные коды. Самый лучший способ передать декодеру частоты появления символов в потоке, т.е. в данном случае дополнительно пять чисел. На основе этих частот декодер строит коды, а затем применяет их для декодирования последовательности. Поэтому, чем длиннее кодированная последовательность, тем меньше удельный вес служебной информации переданной декодеру.

И здесь возникает вопрос: а как можно численно определить степень статистической избыточности в заданной цифровой последовательности? Ведь тогда, зная эту характеристику мы могли бы определять максимально возможную степень сжатия этой последовательности и сравнивать конкретный алгоритм с этой нижней границей, т.е. мы могли бы объективно оценивать качество работы алгоритма сжатия. Оказывается, что такой величиной является энтропия, которая определяет минимальное число бит, необходимое для представления заданной последовательности чисел с последующей возможностью полного восстановления информации.

В 1948 г. сотрудник лаборатории Bell Labs Клод Шеннон показал, что минимальное число бит, которое необходимо затратить для представления одного символа той или иной информации можно найти с помощью формулы

,

где  - частота (вероятность) появления -го числа в последовательности;  - число уникальных чисел в последовательности. Например, применяя данную формулу к нашей последовательности чисел, определяем, что число уникальных символов равно 5 – это  и . Частота появления цифр равна , , ,  и . В результате, минимальное число бит для представления одного символа в такой последовательности равно

 бит/символ.

Сравнивая полученный результат с ранее полученным для кодов Хаффмана (2,2 бит/символ), видим, что коды Хаффмана оказываются более близкими к нижней границе, чем равномерный код, которому необходимо 3 бита/символ.

Также можно посчитать и степень сжатия последовательности. Если равномерный код будет расходовать 3 бита на символ, то потенциальное сжатие будет равно

 раз,

а с помощью неравномерных кодов Хаффмана получим

 раз.

Следовательно, представленный алгоритм сжатия не является лучшим. Кроме того, с помощью энтропии можно показать, что если последовательность содержит случайный набор чисел (не имеет закономерностей), то вероятности , а возможность сжатия , т.е. случайный набор данных сжать невозможно. Это положение в частности говорит о том, что если один раз к данным был применен хороший алгоритм сжатия, например, zip, то повторное сжатие этим или другим алгоритмом не приведет к лучшим результатам, скорее наоборот. Таким образом, на выходе любого хорошего алгоритма сжатия будет получаться почти случайный набор данных.