| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Тензоры высших рангов
Тензор
напряжений ![]() описывает
внутренние силы в веществе. Если при этом материал упругий, то внутренние
деформации удобно описывать с помощью другого тензора
описывает
внутренние силы в веществе. Если при этом материал упругий, то внутренние
деформации удобно описывать с помощью другого тензора ![]() - так называемого тензора
деформаций. Для простого объекта, подобного бруску из металла, изменение длины
- так называемого тензора
деформаций. Для простого объекта, подобного бруску из металла, изменение длины ![]() , как вы знаете,
приблизительно пропорционально силе, т. е. он подчиняется закону Гука
, как вы знаете,
приблизительно пропорционально силе, т. е. он подчиняется закону Гука
![]() .
.
Для
произвольных деформаций упругого твердого тела тензор деформаций ![]() связан с тензором
напряжений
связан с тензором
напряжений ![]() системой
линейных уравнений
системой
линейных уравнений
 . (31.26)
. (31.26)
Вы знаете также, что потенциальная энергия пружины (или бруска) равна
![]() ,
,
а обобщением плотности упругой энергии для твердого тела будет выражение
 . (31.27)
. (31.27)
Полное
описание упругих свойств кристалла должно задаваться коэффициентами ![]() . Это знакомит нас
с новым зверем - тензором четвертого ранга. Поскольку каждый из индексов может
принимать одно из трех значений -
. Это знакомит нас
с новым зверем - тензором четвертого ранга. Поскольку каждый из индексов может
принимать одно из трех значений - ![]() ,
, ![]() или
или ![]() , то всего оказывается
, то всего оказывается ![]() коэффициент. Но
различны из них на самом деле только 21. Во-первых, поскольку тензор
коэффициент. Но
различны из них на самом деле только 21. Во-первых, поскольку тензор ![]() симметричен, у
него остается только шесть различных величин, и поэтому в уравнении (31.27)
нужны только 36 различных коэффициентов. Затем, не изменяя энергии, мы можем
переставить
симметричен, у
него остается только шесть различных величин, и поэтому в уравнении (31.27)
нужны только 36 различных коэффициентов. Затем, не изменяя энергии, мы можем
переставить ![]() и
и
![]() , так
что
, так
что ![]() должно
быть симметрично при перестановке пары индексов
должно
быть симметрично при перестановке пары индексов ![]() и
и ![]() . Это уменьшает число коэффициентов
до 21. Итак, чтобы описать упругие свойства кристалла низшей возможной
симметрии, требуется 21 упругая постоянная! Разумеется, для кристаллов с более
высокой симметрией число необходимых постоянных уменьшается. Так, кубический
кристалл описывается всего тремя упругими постоянными, а для изотропного
вещества хватит и двух.
. Это уменьшает число коэффициентов
до 21. Итак, чтобы описать упругие свойства кристалла низшей возможной
симметрии, требуется 21 упругая постоянная! Разумеется, для кристаллов с более
высокой симметрией число необходимых постоянных уменьшается. Так, кубический
кристалл описывается всего тремя упругими постоянными, а для изотропного
вещества хватит и двух.
В
справедливости последнего утверждения можно убедиться следующим образом. В
случае изотропного материала компоненты ![]() не должны зависеть от поворота осей.
Как это может быть? Ответ: они могут быть независимы, только когда выражаются
через тензоры
не должны зависеть от поворота осей.
Как это может быть? Ответ: они могут быть независимы, только когда выражаются
через тензоры ![]() .
Но существует лишь два возможных выражения, имеющих требуемую симметрию, - это
.
Но существует лишь два возможных выражения, имеющих требуемую симметрию, - это ![]() и
и ![]() , так что
, так что ![]() должно быть их
линейной комбинацией. Таким образом, для изотропного материала
должно быть их
линейной комбинацией. Таким образом, для изотропного материала
![]() ;
;
следовательно,
чтобы описать упругие свойства материала, требуются две постоянные: ![]() и
и ![]() . Я предоставляю
вам самим доказать, что для кубического кристалла требуются три такие
постоянные.
. Я предоставляю
вам самим доказать, что для кубического кристалла требуются три такие
постоянные.
И еще один последний пример (на этот раз пример тензора третьего ранга) дает нам пьезоэлектрический эффект. При напряженном состоянии в кристалле возникает электрическое поле, пропорциональное тензору напряжений. Общий закон пропорциональности имеет вид
 ,
,
где
![]() -
электрическое поле, a
-
электрическое поле, a ![]() - пьезоэлектрические коэффициенты
(пьезомодули), составляющие тензор. Можете ли вы сами доказать, что если у
кристалла есть центр инверсии (т. е. если он инвариантен относительно замены
- пьезоэлектрические коэффициенты
(пьезомодули), составляющие тензор. Можете ли вы сами доказать, что если у
кристалла есть центр инверсии (т. е. если он инвариантен относительно замены ![]() ), то все его
пьезоэлектрические коэффициенты равны нулю.
), то все его
пьезоэлектрические коэффициенты равны нулю.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
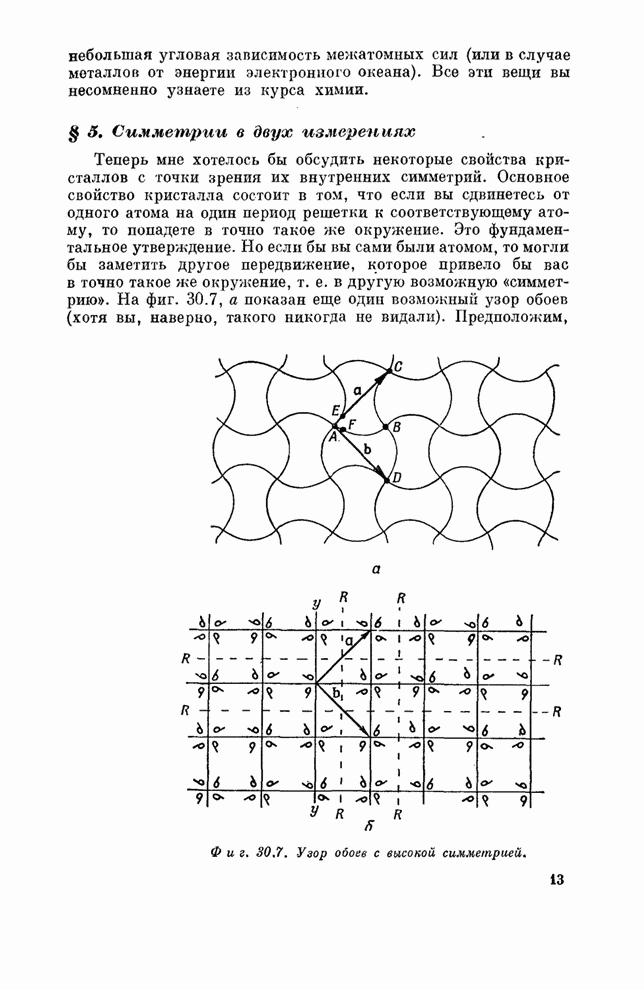
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)