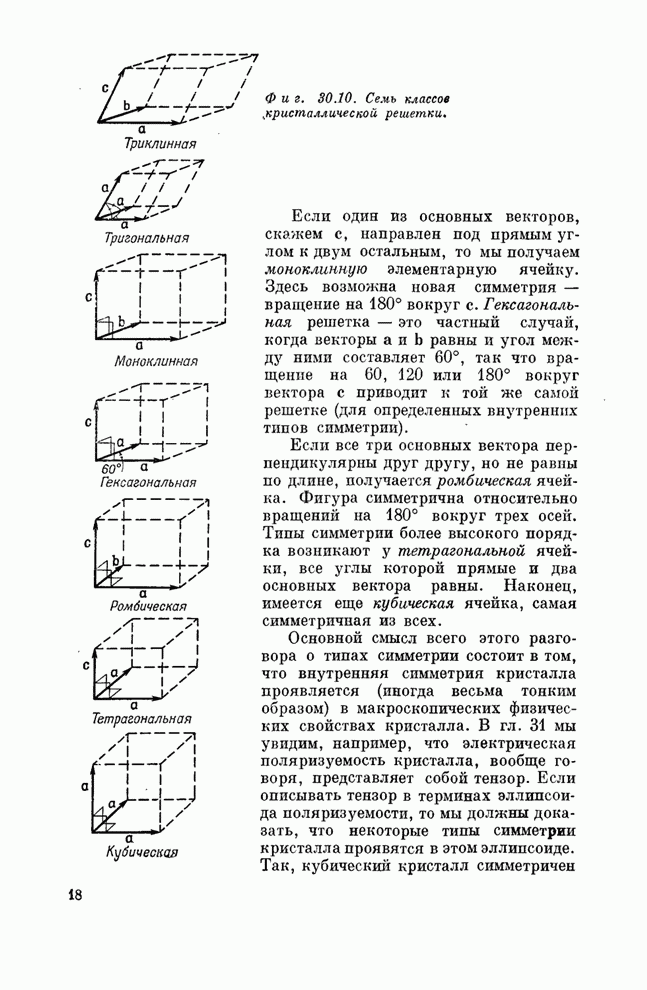
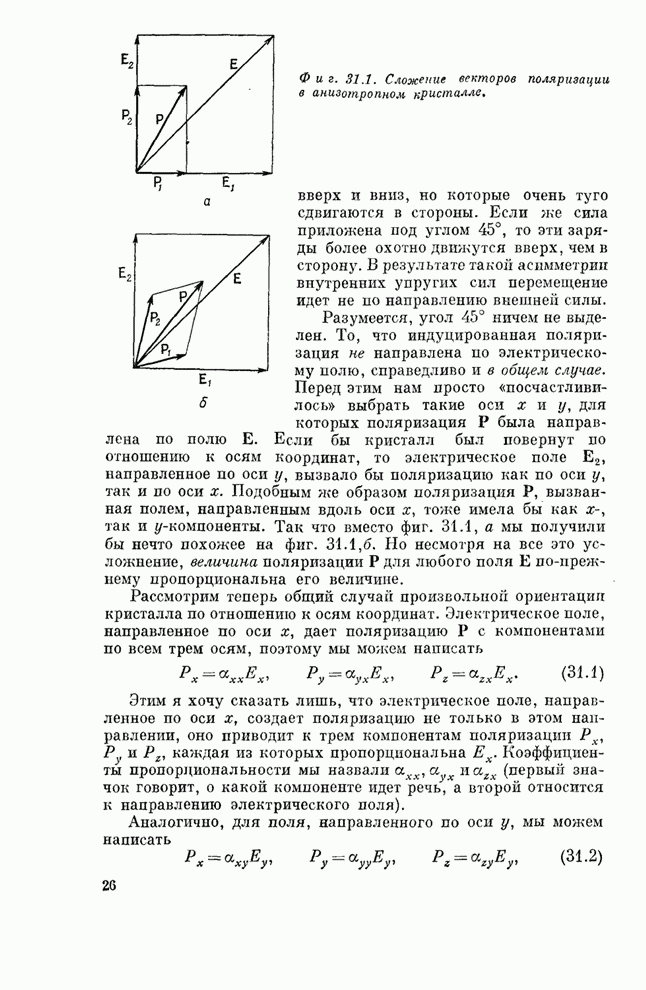
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Симметрии в двух измерениях
Теперь
мне хотелось бы обсудить некоторые свойства кристаллов с точки зрения их
внутренних симметрий. Основное свойство кристалла состоит в том, что если вы
сдвинетесь от одного атома на один период решетки к соответствующему атому, то
попадете в точно такое же окружение. Это фундаментальное утверждение. Но если
бы вы сами были атомом, то могли бы заметить другое передвижение, которое
привело бы вас в точно такое же окружение, т. е. в другую возможную
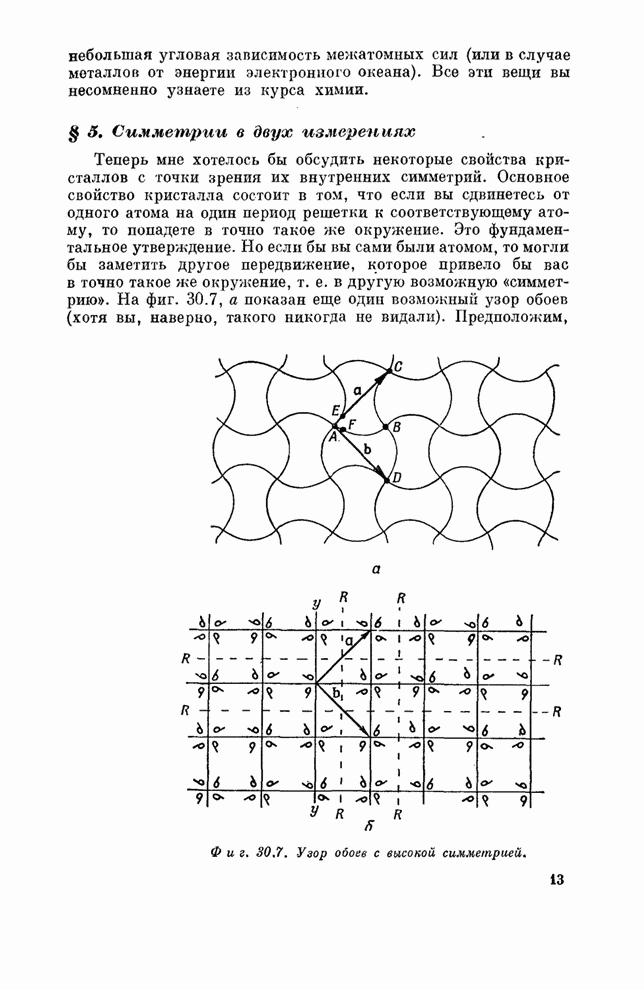
«симметрию». На фиг. 30.7,а показан еще один возможный узор обоев (хотя вы,
наверно, такого никогда не видали). Предположим, что мы сравниваем окружения в
точках ![]() и
и
![]() . Вы
могли бы сперва подумать, что они одинаковы Не совсем. Точки
. Вы
могли бы сперва подумать, что они одинаковы Не совсем. Точки ![]() и
и ![]() эквивалентны
эквивалентны ![]() , но окружение
, но окружение ![]() подобно
подобно ![]() , только если все
рядом обращать как будто в зеркале.
, только если все
рядом обращать как будто в зеркале.

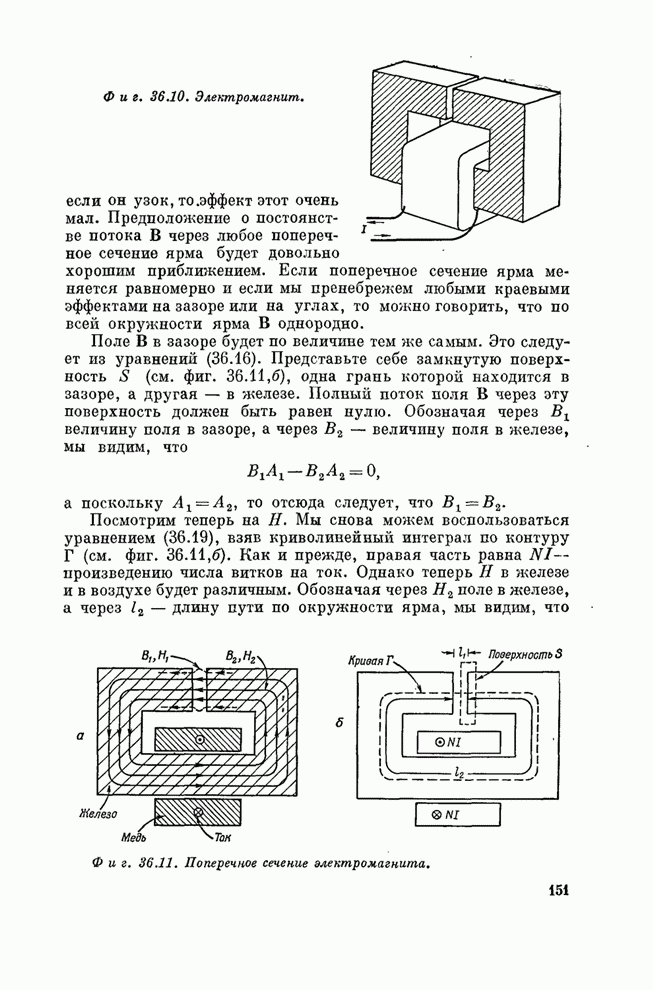
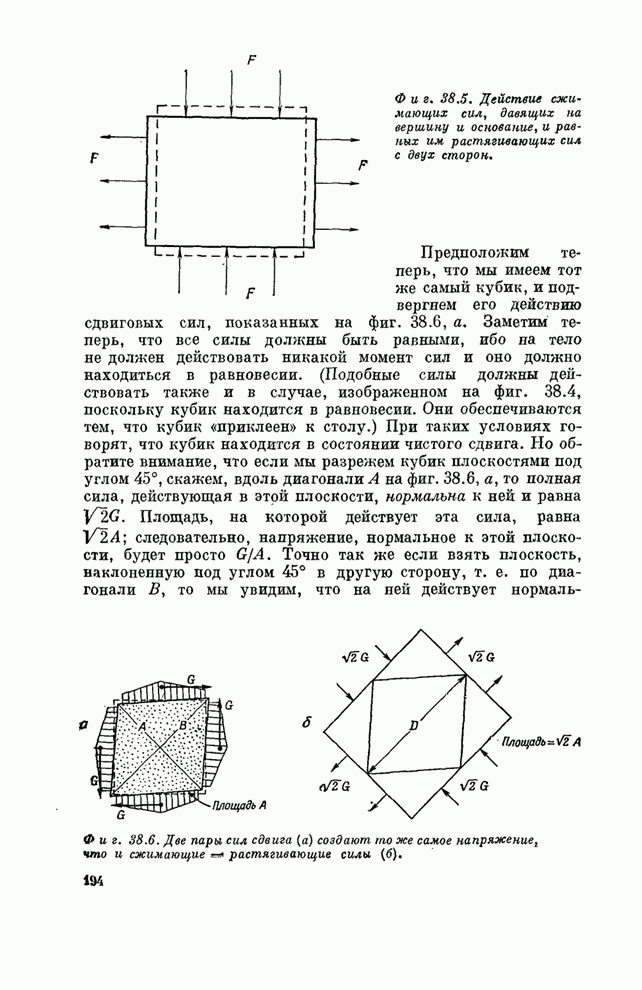
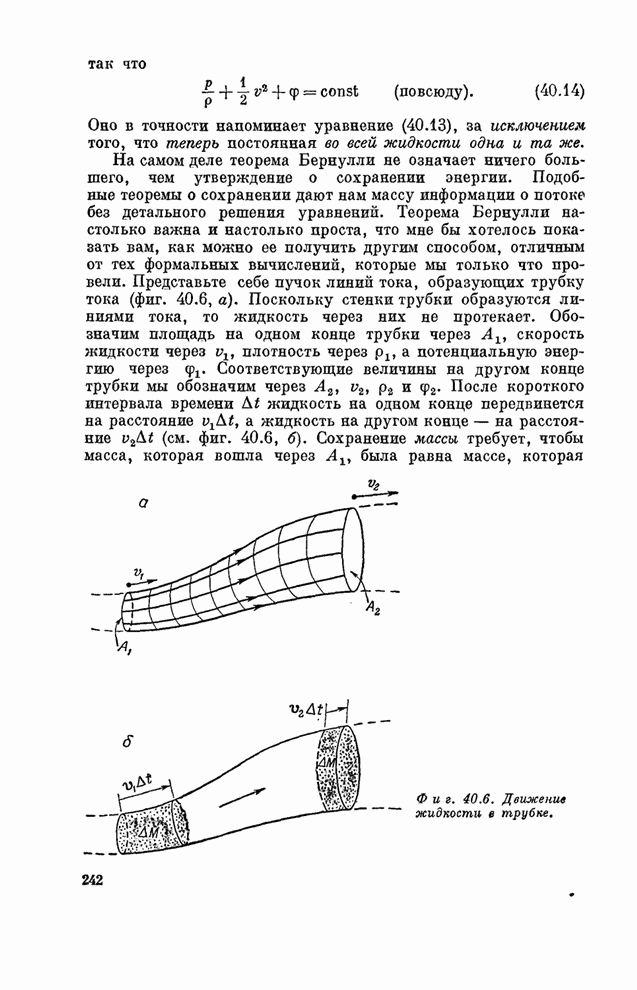
Фиг. 30.7. Узор обоев с высокой симметрией.
В
этом узоре имеются еще и другие виды «эквивалентных» точек. Так, точки ![]() и
и ![]() обладают
«одинаковыми» окружениями, за тем исключением, что одно повернуто на 90° по
отношению к другому. Узор особенный. Вращение на 90°, проделанное сколько
угодно раз вокруг такой вершины, как
обладают
«одинаковыми» окружениями, за тем исключением, что одно повернуто на 90° по
отношению к другому. Узор особенный. Вращение на 90°, проделанное сколько
угодно раз вокруг такой вершины, как ![]() , снова дает тот же узор. Кристалл с
такой структурой имел бы на поверхности прямые углы, но внутри он устроен
сложнее, чем простой куб.
, снова дает тот же узор. Кристалл с
такой структурой имел бы на поверхности прямые углы, но внутри он устроен
сложнее, чем простой куб.
Теперь,
когда мы описали ряд частных случаев, попытаемся вывести все возможные типы
симметрии, какие может иметь кристалл. Прежде всего посмотрим, что получается в
плоскости. Плоская решетка может быть определена с помощью двух так называемых
основных векторов, которые идут от одной точки решетки к двум ближайшим
эквивалентным точкам. Два вектора 1 и 2 суть основные векторы решетки на фиг.
30.1. Два вектора ![]() и
и ![]() на фиг. 30.7,а - основные векторы для
изображенного там узора. Мы могли бы, конечно, с тем же успехом заменить
на фиг. 30.7,а - основные векторы для
изображенного там узора. Мы могли бы, конечно, с тем же успехом заменить ![]() на
на ![]() или
или ![]() на
на ![]() . Раз
. Раз ![]() и
и ![]() одинаковы по
величине и перпендикулярны друг другу, то вращение на 90° переводит
одинаковы по
величине и перпендикулярны друг другу, то вращение на 90° переводит ![]() в
в ![]() и
и ![]() в
в ![]() и снова дает ту же
решетку.
и снова дает ту же
решетку.
Итак, мы видим, что существуют решетки, обладающие «четырехсторонней» симметрией. А раньше мы описали плотную упаковку, основанную на шестиугольнике и обладающую шестисторонней симметрией. Вращение набора кружков на фиг. 30.5,а на угол 60° вокруг центра любого шарика переводит рисунок сам в себя.
Какие
виды вращательной симметрии существуют еще? Может ли быть, например,
вращательная симметрия пятого или восьмого порядка? Легко понять, что они
невозможны. Единственная симметрия, связанная с фигурой, имеющей более четырех
сторон, есть симметрия шестого порядка. Прежде всего покажем, что симметрия
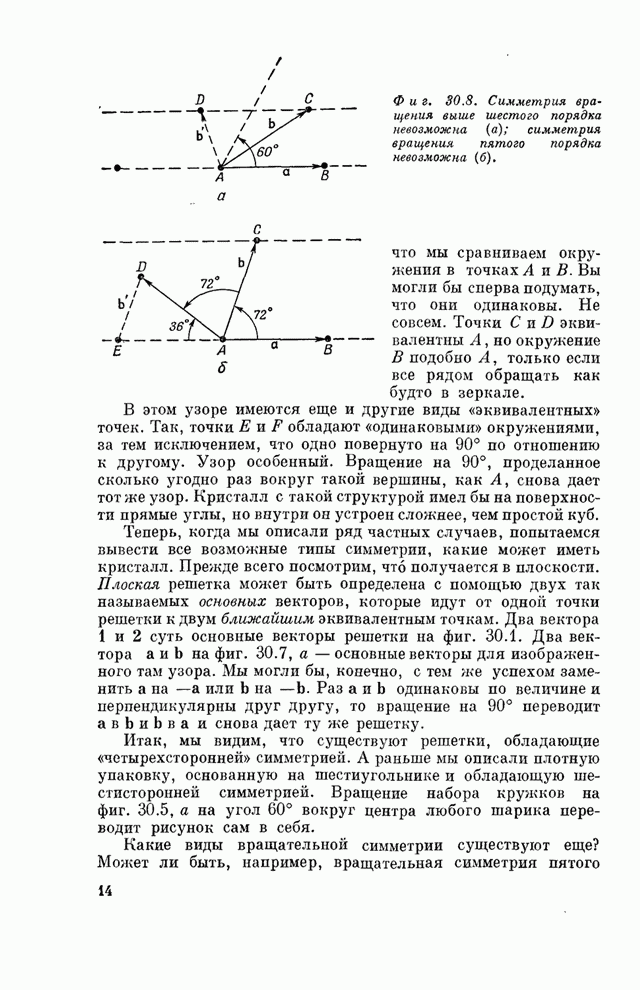
более чем шестого порядка невозможна. Попытаемся вообразить решетку с двумя
равными основными векторами, образующими угол менее 60° (фиг. 30.8,а). Мы
должны предположить, что точки ![]() и
и ![]() эквивалентны
эквивалентны ![]() и что
и что ![]() и
и ![]() - наиболее короткие
векторы, проведенные из
- наиболее короткие
векторы, проведенные из ![]() до эквивалентных соседей. Но это,
безусловно, неверно, потому что расстояние между
до эквивалентных соседей. Но это,
безусловно, неверно, потому что расстояние между ![]() и
и ![]() короче, чем от любого из них до
короче, чем от любого из них до ![]() . Должна
существовать соседняя точка
. Должна
существовать соседняя точка ![]() , эквивалентная
, эквивалентная ![]() , которая ближе к
, которая ближе к ![]() , чем к
, чем к ![]() или
или ![]() . Мы должны были бы
выбрать
. Мы должны были бы
выбрать ![]() в
качестве одного из основных векторов. Поэтому угол между основными векторами
должен быть равен 60° или еще больше. Октагональная симметрия невозможна.
в
качестве одного из основных векторов. Поэтому угол между основными векторами
должен быть равен 60° или еще больше. Октагональная симметрия невозможна.

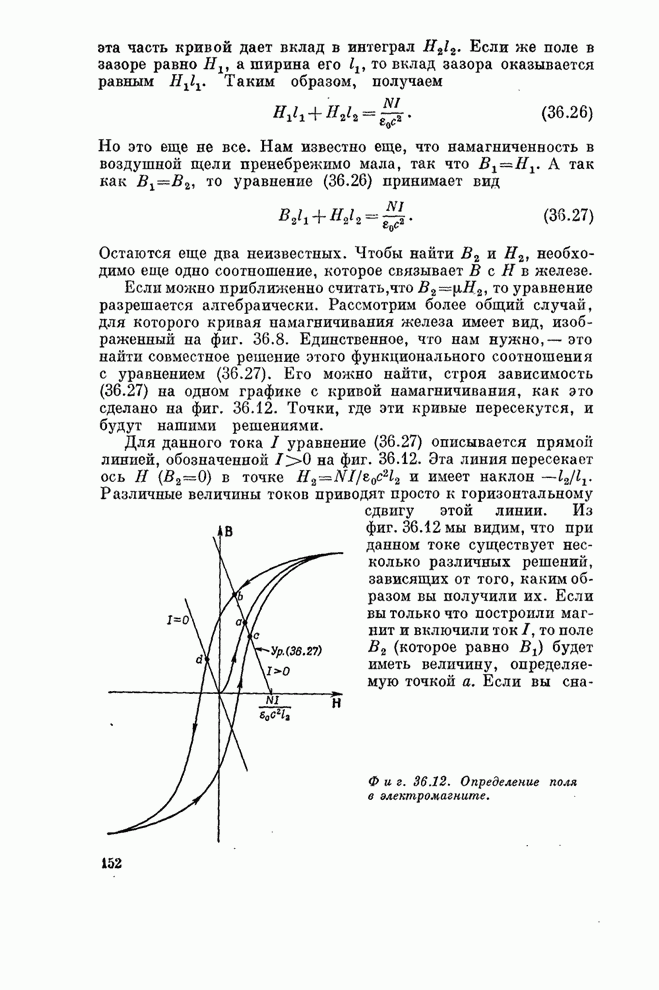
Фиг. 30.8. Симметрия вращения выше шестого порядка невозможна (а); симметрия вращения пятого порядка невозможна (б).
А
как быть с пятикратной симметрией? Если мы предположим, что основные векторы ![]() и
и ![]() имеют одинаковую
длину и образуют угол
имеют одинаковую
длину и образуют угол ![]() (фиг. 30.8,б), то должна существовать
эквивалентная точка решетки в
(фиг. 30.8,б), то должна существовать
эквивалентная точка решетки в ![]() под 72° к линии
под 72° к линии ![]() . Но вектор
. Но вектор ![]() от
от ![]() к
к ![]() тогда короче
тогда короче ![]() , и
, и ![]() уже не основной
вектор. Пятикратной симметрии быть не может. Единственные возможности, не
приводящие к подобным трудностям, это
уже не основной
вектор. Пятикратной симметрии быть не может. Единственные возможности, не
приводящие к подобным трудностям, это ![]() , 90 или 120°. Очевидно, допустимы
также нуль и 180°. Можно еще так выразить полученный нами результат: рисунок
может не меняться при повороте на полный оборот (ничего не изменяется),
полоборота, одну треть, одну четверть или одну шестую оборота. И этим
исчерпываются все возможные вращательные симметрии на плоскости - всего их
пять. Если
, 90 или 120°. Очевидно, допустимы
также нуль и 180°. Можно еще так выразить полученный нами результат: рисунок
может не меняться при повороте на полный оборот (ничего не изменяется),
полоборота, одну треть, одну четверть или одну шестую оборота. И этим
исчерпываются все возможные вращательные симметрии на плоскости - всего их
пять. Если ![]() ,
то мы говорим об «
,
то мы говорим об «![]() -кратной» симметрии, или симметрии
-кратной» симметрии, или симметрии ![]() -го порядка. Мы
говорим, что узор, для которого
-го порядка. Мы
говорим, что узор, для которого ![]() равно 4 или 6, обладает более
«высокой симметрией», чем узор с
равно 4 или 6, обладает более
«высокой симметрией», чем узор с ![]() , равным 1 или 2.
, равным 1 или 2.
Вернемся
к фиг. 30.7,а. Мы видим, что узор там обладает четырехкратной вращательной
симметрией. На фиг. 30.7,б мы нарисовали другое расположение, которое обладает
теми же свойствами симметрии, что и фиг. 30.7,а. Маленькие фигурки, похожие на
запятые, - это асимметричные объекты, которые служат для определения симметрии
изображения внутри каждого квадратика. Заметьте, что запятые в соседних
квадратиках перевернуты попеременно, так что элементарная ячейка больше одного
квадратика. Если бы запятых не было, рисунок по-прежнему обладал бы
четырехкратной симметрией, но элементарная ячейка была бы меньше. Посмотрим
внимательно на фиг. 30.7; мы обнаружим, что они обладают еще и другими типами
симметрии. Так, отражение относительно каждой пунктирной линии ![]() воспроизводит
рисунок без изменений. Но это еще не все. У них есть еще один тип симметрии.
Если отразить рисунок относительно линии
воспроизводит
рисунок без изменений. Но это еще не все. У них есть еще один тип симметрии.
Если отразить рисунок относительно линии ![]() , а затем сдвинуть на один квадратик
вправо (или влево), то снова получится первоначальный рисунок. Линия
, а затем сдвинуть на один квадратик
вправо (или влево), то снова получится первоначальный рисунок. Линия ![]() называется линией
скольжения.
называется линией
скольжения.
Этим
исчерпываются все типы симметрии в пространстве двух измерений. Есть еще одна
пространственная операция симметрии, которая на плоскости эквивалентна вращению
на 180°, однако в трехмерном пространстве она не сводится к этому вращению, а
есть совсем другая операция. Я говорю об инверсии. Под инверсией мы
подразумеваем такую операцию, когда любая точка, отвечающая вектору смещения из
начала координат ![]() (например,
точка
(например,
точка ![]() на
фиг. 30.9,б), переносится в точку
на
фиг. 30.9,б), переносится в точку ![]() .
.

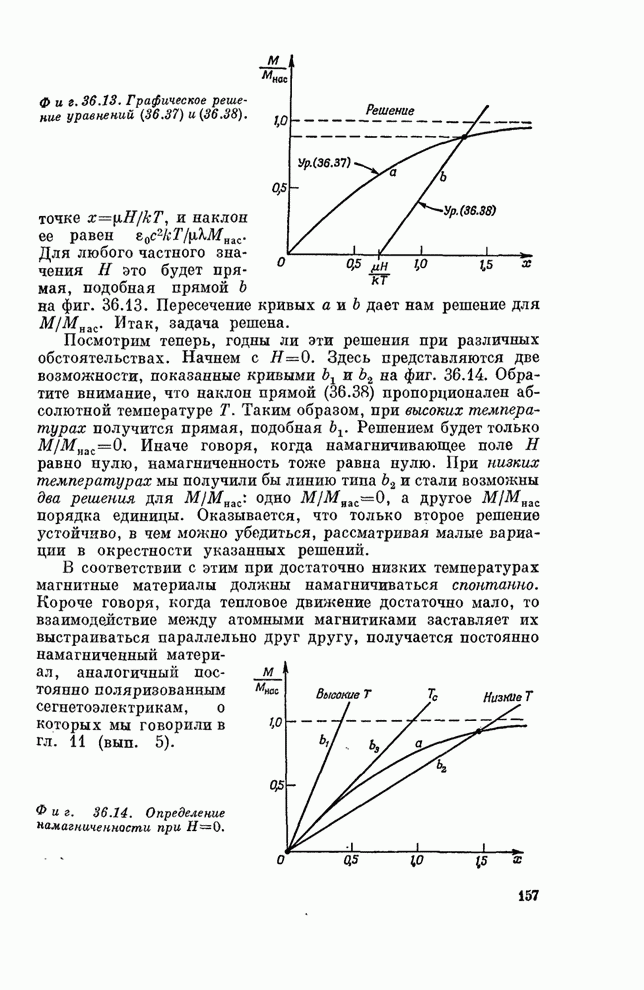
Фиг. 30.9. Операция симметрии, называемая инверсией.
а - рисунок меняется; б - рисунок
не меняется при преобразовании ![]() ; в - в трех измерениях рисунок не
симметричен после операции инверсии; г - рисунок симметричен в трех измерениях.
; в - в трех измерениях рисунок не
симметричен после операции инверсии; г - рисунок симметричен в трех измерениях.
Инверсия
рисунка а на фиг. 30.9 дает новый рисунок, а инверсия рисунка б приводит к
такому же рисунку. На двумерном узоре (вы можете это видеть) инверсия рисунка б
в точке ![]() эквивалентна
повороту на 180° вокруг той же самой точки. Предположим, однако, что мы сделали
узор на фиг. 30.9,б трехмерным, вообразив на маленьких шестерках и девятках
«стрелочки», смотрящие из страницы кверху. В результате инверсии в трехмерном
пространстве все стрелочки перевернутся и направятся вниз, так что узор не
воспроизведется. Если мы обозначим острия и хвосты стрелок точками и
крестиками, то сможем образовать трехмерный рисунок (фиг. 30.9,в), который
несимметричен относительно инверсии, или же мы можем получить рисунок, который
такой симметрией обладает (фиг. 30.9,г). Заметьте, что трехмерную инверсию
нельзя получить никакой комбинацией вращений.
эквивалентна
повороту на 180° вокруг той же самой точки. Предположим, однако, что мы сделали
узор на фиг. 30.9,б трехмерным, вообразив на маленьких шестерках и девятках
«стрелочки», смотрящие из страницы кверху. В результате инверсии в трехмерном
пространстве все стрелочки перевернутся и направятся вниз, так что узор не
воспроизведется. Если мы обозначим острия и хвосты стрелок точками и
крестиками, то сможем образовать трехмерный рисунок (фиг. 30.9,в), который
несимметричен относительно инверсии, или же мы можем получить рисунок, который
такой симметрией обладает (фиг. 30.9,г). Заметьте, что трехмерную инверсию
нельзя получить никакой комбинацией вращений.
Если мы будем характеризовать «симметрию» рисунка (или решетки) разного рода операциями симметрии, которые мы только что описали, то окажется, что в двумерном случае существуют 17 различных форм узоров. Узор с наинизшей возможной симметрией мы изобразили на фиг. 30.1, а узор с одной из наивысших симметрий - на фиг. 30.7. Отыщите сами все 17 возможных форм рисунков.
Удивительно, как мало типов из этих 17 используется при изготовлении обоев и тканей! Всегда видишь одни и те же три или четыре основных типа. В чем здесь дело? Неужели так убога фантазия художников или, может быть, многие из возможных типов рисунков не будут радовать глаз?
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
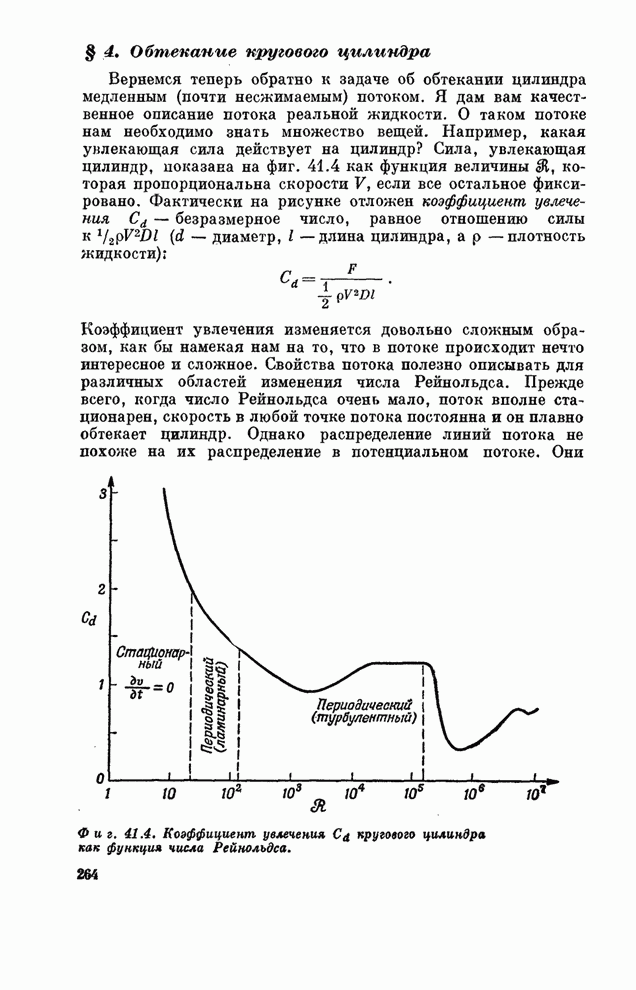
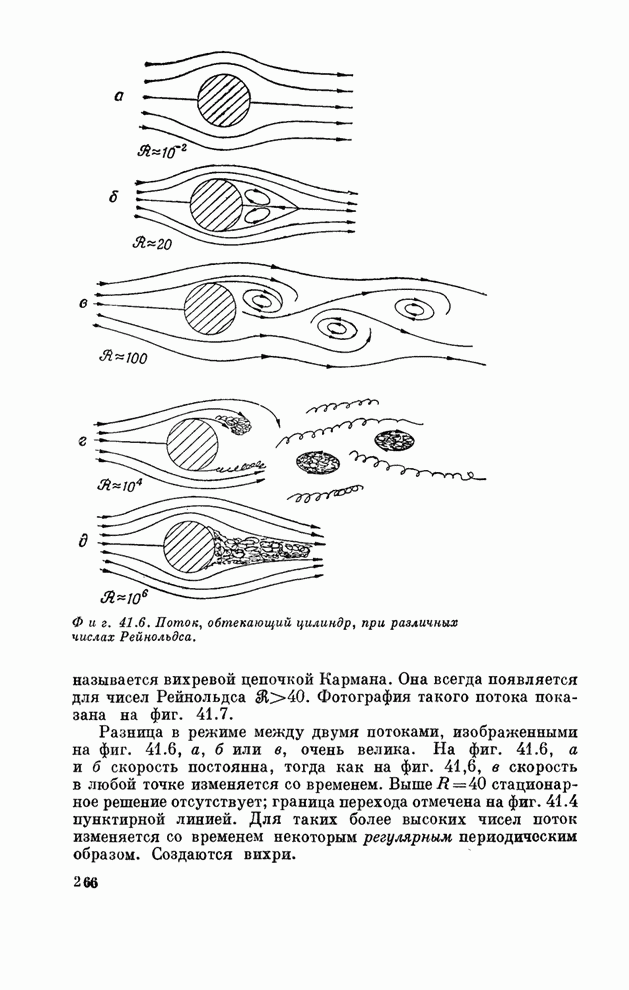
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)