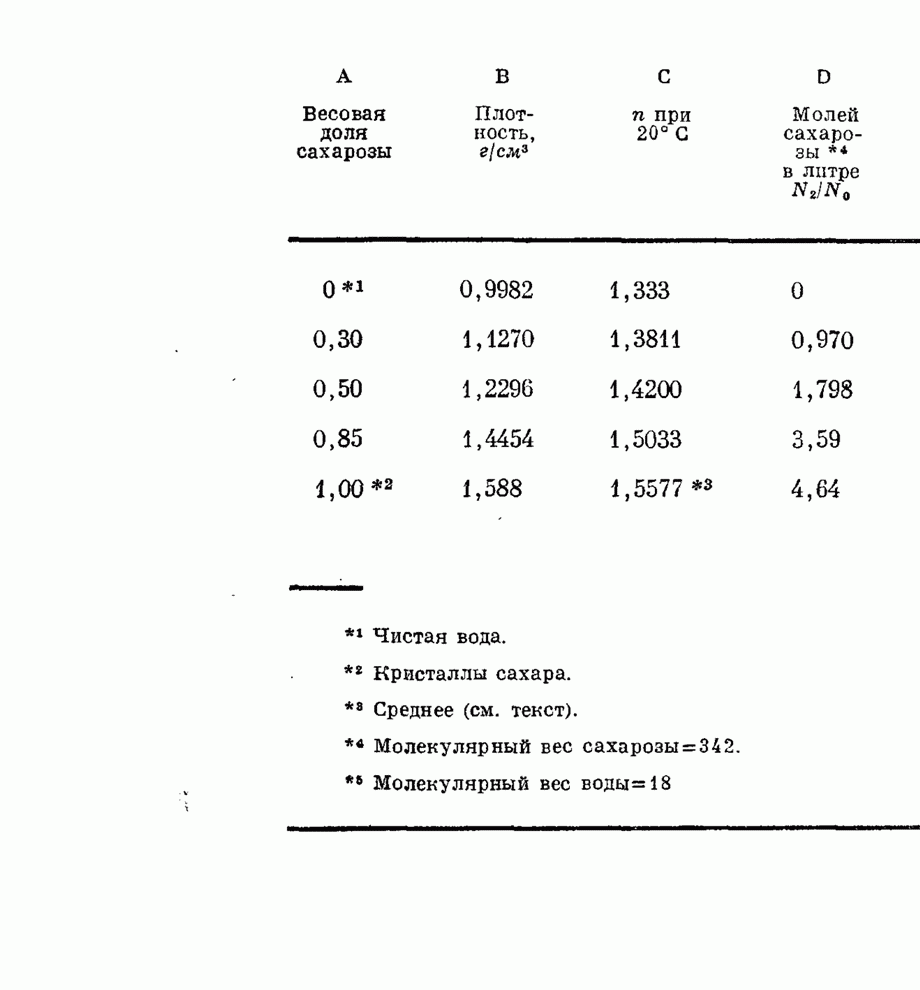
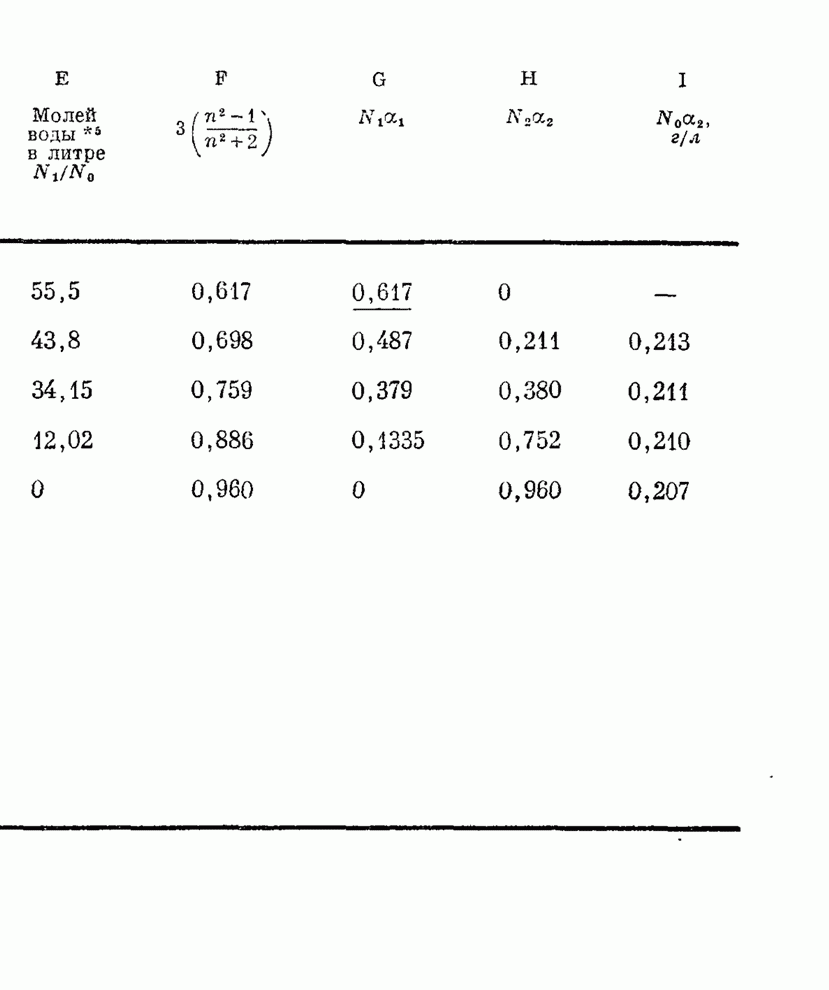
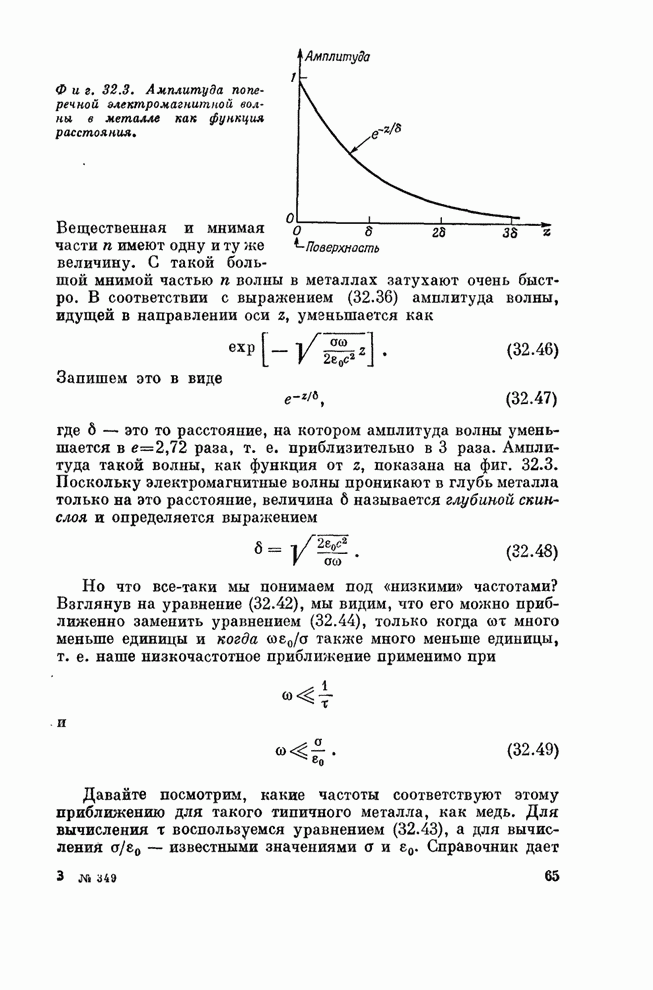
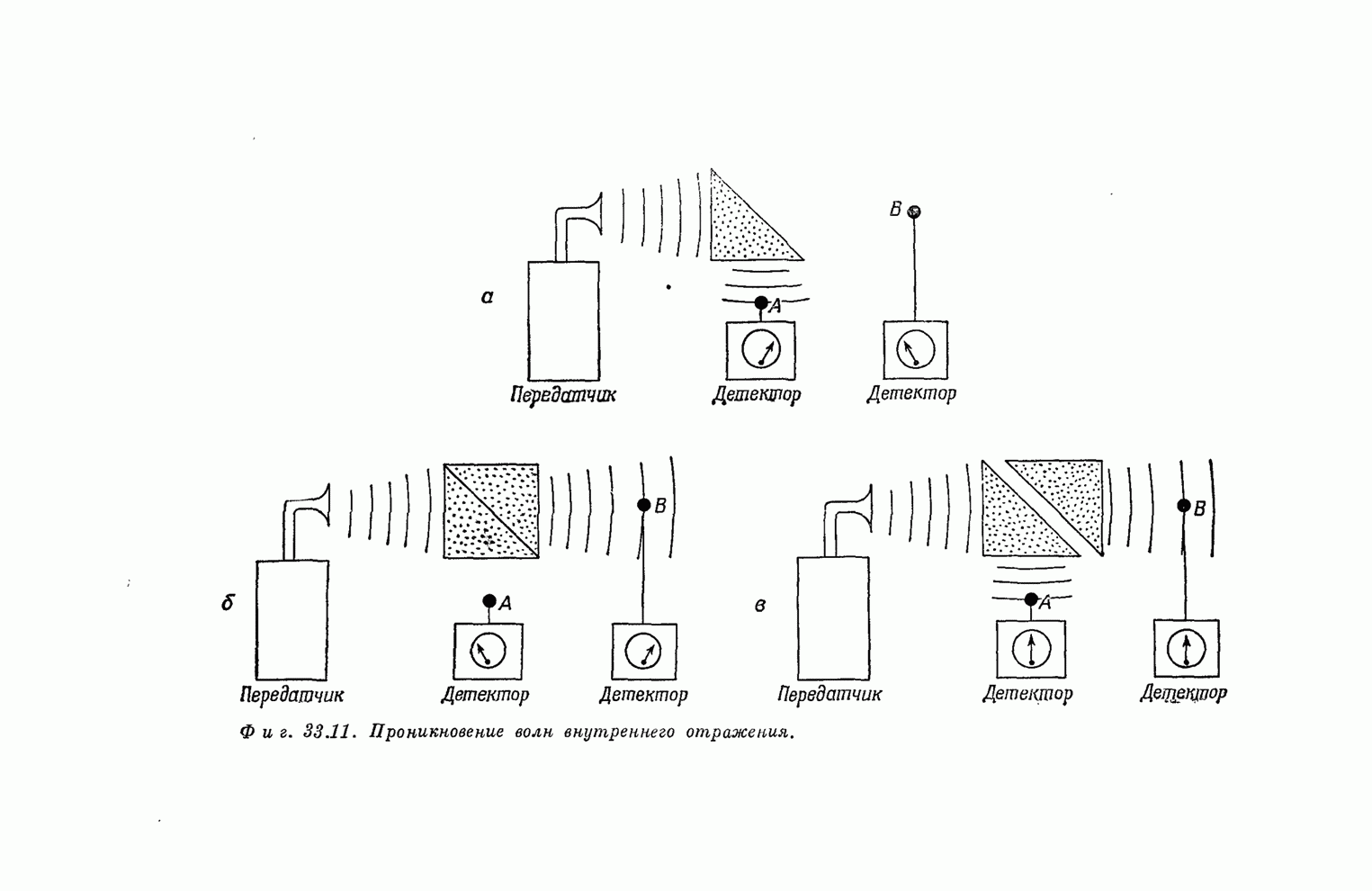
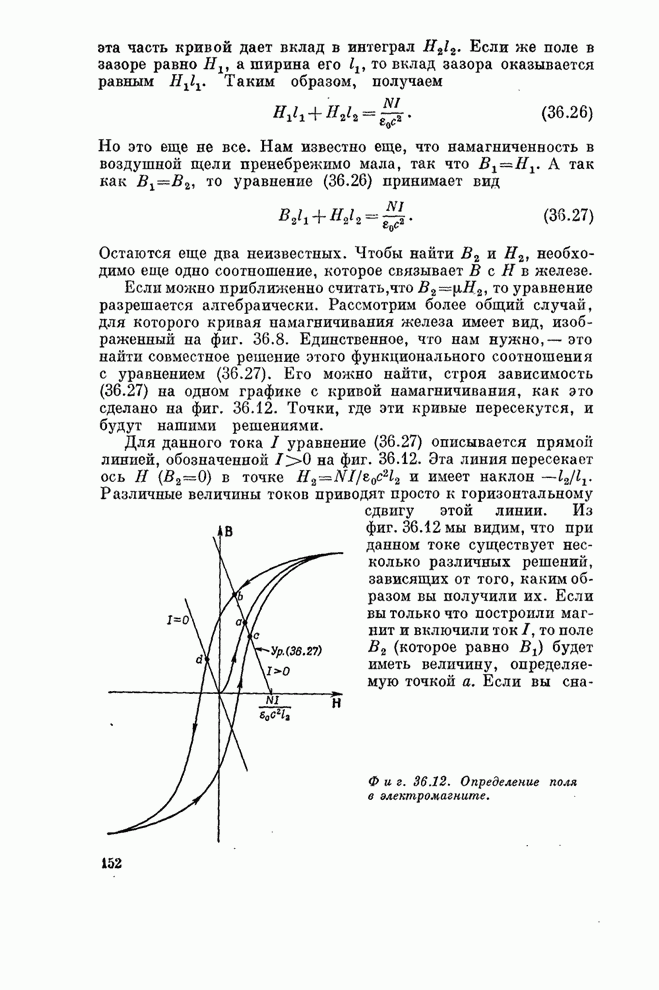
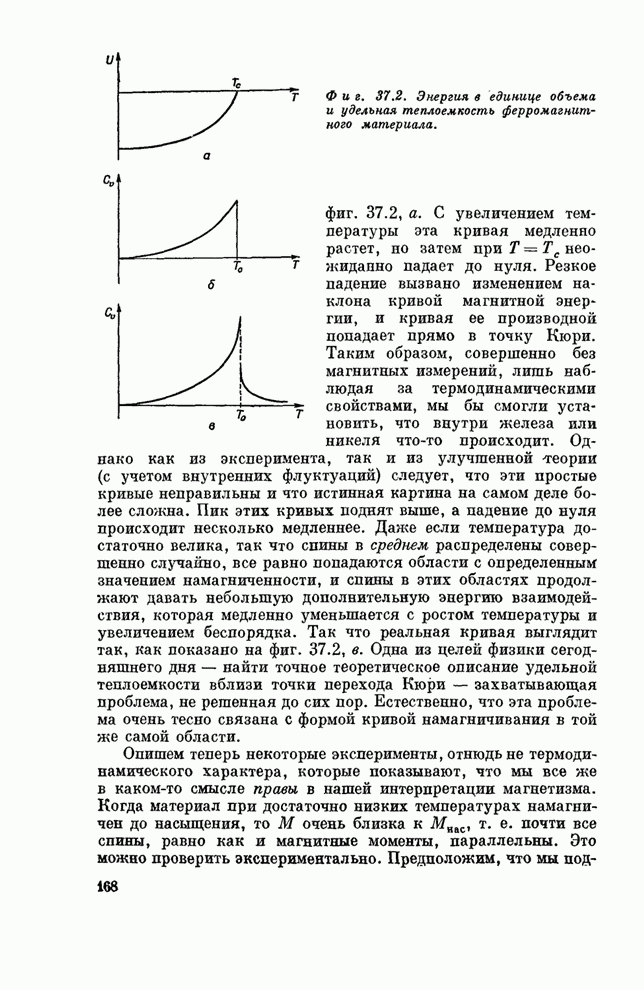
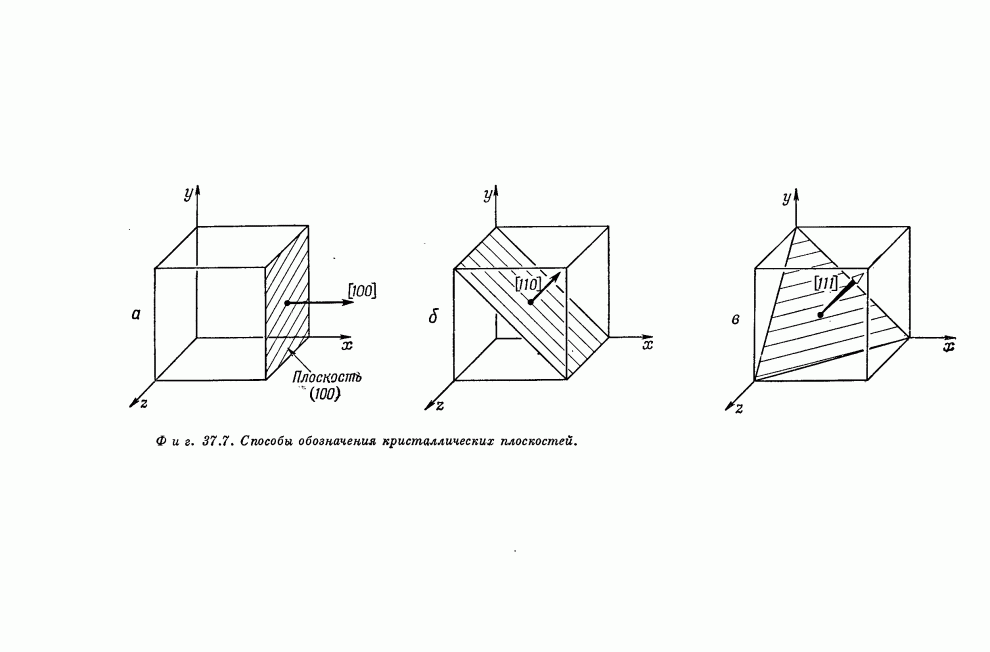
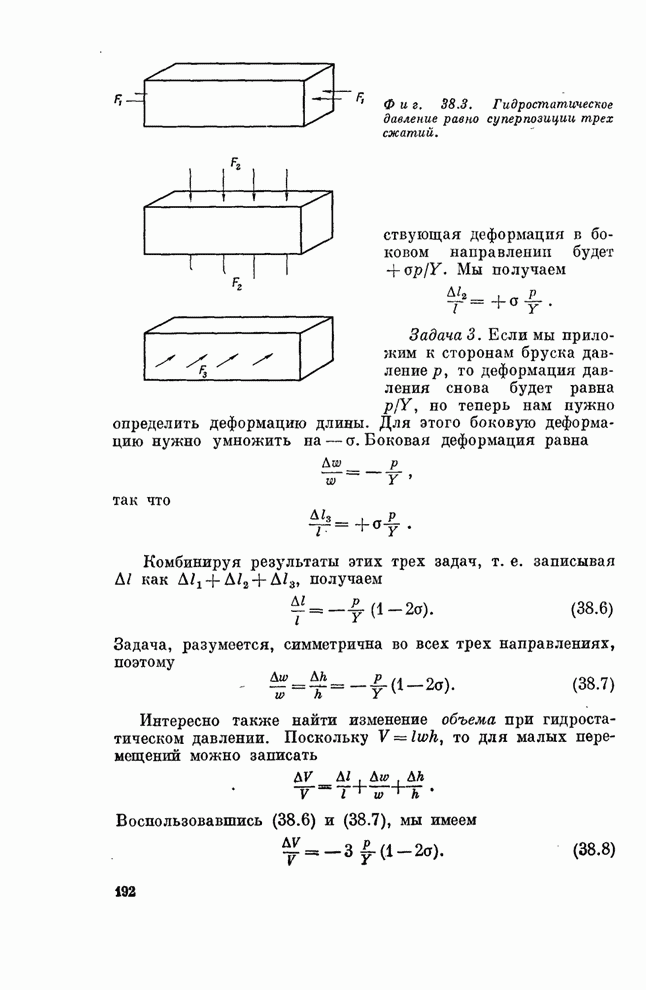
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИЛОЖЕНИЕ (к главе 30)
A dynamical model of a crystal structure
By Sir Lawrence Bragg, F.R.S. and J. F. Nye
Cavendish Laboratory University of Cambridge
(Received 9 January 1947 - Read 19 June 1947)
[Plates 8 to 21]
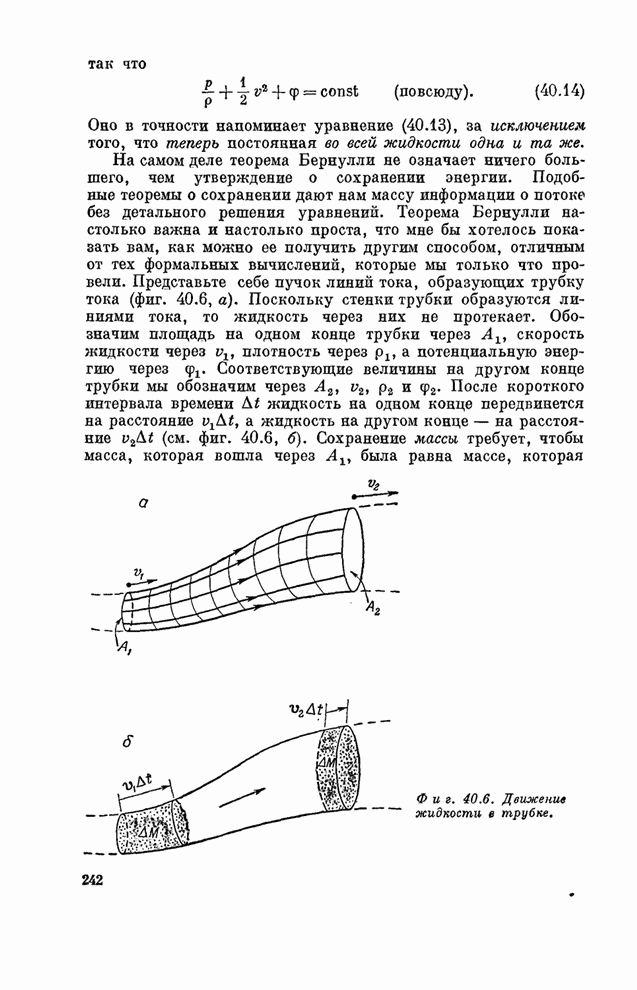
The crystal structure of a metal is represented by an assemblage of bubbles, a millimetre or less in diameter, floating on the surface of a soap solution. The bubbles are blown from a fine pipette beneath the surface with a constant air pressure, and are remarkably uniform in size. They are held together by surface tension, either in a single layer on the surface or in a three, dimensional mass. An assemblage may contain hundreds of thousands of bubbles and persists for an hour or more. The assemblages show structures which have been supposed to exist in metals, and simulate effects which have been observed, such as grain boundaries, dislocations and other types of fault, slip, recrystallization, annealing, and strains due to 'foreign' atoms.
1. The bubble model
Models of crystal structure have been described from time to time in which the atoms are represented by small floating or suspended magnets, or by circular disks floating on a water surface and held together by the forces of capillary attraction. These models have certain disadvantages; for instance, in the case of floating objects in contact, frictional forces impede their free relative movement. A more serious disadvantage is that the number of components is limited, for a large number of components is required in order to approach the state of affairs in a real crystal.
ДИНАМИЧЕСКАЯ МОДЕЛЬ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ
Л. Брэгг и Джо Най
Кристаллическая структура металла моделируется скоплением пузырьков диаметром 1 мм и меньше, плавающих на поверхности мыльного раствора. Пузырьки выдуваются из маленькой пипетки, расположенной ниже поверхности раствора; давление воздуха в пипетке постоянно, и размеры пузырьков чрезвычайно мало отличаются друг от друга. Пузырьки удерживаются вместе за счет поверхностного натяжения, выстраиваясь в один слой на поверхности или образуя трехмерную массу. Скопление может содержать сотни тысяч пузырьков и сохраняется в течение часа или более. Скопление образует структуры, которые, как предполагают, имеются в металлах, и имитируют эффекты, которые уже наблюдались, такие, как формирование границ между зернами, дислокаций и других типов дефектов, процессы скольжения, явления рекристаллизации и отжига, возникновение напряжений, связанных с «посторонними» атомами.
1. Пузырьковая модель
Время от времени предлагались модели кристалла, в которых атомы представлялись маленькими плавающими или подвешенными магнитами, или же кружками, плавающими на поверхности воды и притягивающимися за счет капиллярных сил.
Эти модели имеют серьезные недостатки; например, в случае плавающих и соприкасающихся объектов силы трения мешают их свободному относительному движению. Более серьезным недостатком является ограниченное число компонент, потому что приблизиться к положению дел в реальном кристалле можно только с большим числом компонент.
A dynamical model of a crystal structure
The present paper describes the behavior
of a model in which the atoms are represented by small bubbles from ![]() to
to ![]() mm. in diameter
floating on the surface of a soap solution. These small bubbles are
sufficiently persistent for experiments lasting an hour or more, they slide
past each other without friction, and they can be produced in large numbers.
Some of the illustrations in this paper were taken from assemblages of bubbles
numbering 100,000 or more. The model most nearly represents the behavior of a
metal structure, because the bubbles are of one type only and are held together
by a general capillary attraction, which represents the binding force of the
free electrons in the metal. A brief description of the model has been given in
the Journal of Scientific Instruments (Bragg 1942b).
mm. in diameter
floating on the surface of a soap solution. These small bubbles are
sufficiently persistent for experiments lasting an hour or more, they slide
past each other without friction, and they can be produced in large numbers.
Some of the illustrations in this paper were taken from assemblages of bubbles
numbering 100,000 or more. The model most nearly represents the behavior of a
metal structure, because the bubbles are of one type only and are held together
by a general capillary attraction, which represents the binding force of the
free electrons in the metal. A brief description of the model has been given in
the Journal of Scientific Instruments (Bragg 1942b).

Figure 1. Apparatus for producing rafts of bubbles.
2. Method of formation
The bubbles are blown from a fine
orifice, beneath the surface of a soap solution. We have had the best results
with a solution the formula of which was given to us by Mr Green of the Royal
Institution. ![]() c.c.
of oleic acid (pure redistilled) is well shaken in 50 c.c. of distilled water.
This is mixed thoroughly with 73 c.c. of 10% solution of tri-ethsnolamine and
the mixture made up to 200 c.c. To this is added 164 c.c. of pure glycerine. It
is left to stand and the clear liquid is drawn off from below. In some
experiments this was diluted in three times its volume of water to reduce
viscosity. The orifice of the jet is about 5 mm. below the surface. A constant
air pressure of 50 to 200 cm. of water is supplied by means of two Winchester
flasks. Normally the bubbles are remarkably uniform in size. Occasionally they
issue in an irregular manner, but this can be corrected by a change of jet or
of pressure. Unwanted bubbles can easily be destroyed by playing a small flame
over the surface. Figure 1 shows the apparatus. We have found it of advantage
to blacken the bottom of the vessel, because details of structure, such as
grain boundaries and dislocations, then show up more clearly.
c.c.
of oleic acid (pure redistilled) is well shaken in 50 c.c. of distilled water.
This is mixed thoroughly with 73 c.c. of 10% solution of tri-ethsnolamine and
the mixture made up to 200 c.c. To this is added 164 c.c. of pure glycerine. It
is left to stand and the clear liquid is drawn off from below. In some
experiments this was diluted in three times its volume of water to reduce
viscosity. The orifice of the jet is about 5 mm. below the surface. A constant
air pressure of 50 to 200 cm. of water is supplied by means of two Winchester
flasks. Normally the bubbles are remarkably uniform in size. Occasionally they
issue in an irregular manner, but this can be corrected by a change of jet or
of pressure. Unwanted bubbles can easily be destroyed by playing a small flame
over the surface. Figure 1 shows the apparatus. We have found it of advantage
to blacken the bottom of the vessel, because details of structure, such as
grain boundaries and dislocations, then show up more clearly.
Figure 2, plate 8, shows a portion of a 'raft' or two-dimensional crystal of bubbles. Its regularity can be judged by looking at the figure in a glancing direction. The size of the bubbles varies with the aperture, but does not appear to vary to any marked degree with the pressure or the depth of the orifice beneath the surface.
В настоящей работе описано поведение модели, в которой атомы представлены маленькими пузырьками диаметром от 0,1 до 2 мм, плавающими на поверхности мыльного раствора. Эти маленькие пузырьки достаточно устойчивы для экспериментов длительностью 1 час и более, они скользят друг по другу без трения и могут быть приготовлены в больших количествах. Ряд снимков для этой статьи был сделан на скоплениях, насчитывающих 100 000 пузырьков и более. Модель ближе всего соответствует поведению металлической структуры, потому что все пузырьки только одного типа и держатся вместе за счет общего капиллярного притяжения, которое изображает силу связи свободных электронов в металле. Краткое описание этой модели было дано в работе Брэгга).
Способ образования пузырьков
Пузырьки
выдуваются из тонкой пипетки, расположенной под поверхностью мыльного раствора.
Наилучшие результаты мы получили с помощью раствора, состав которого нам
сообщил мистер Грин из Королевского института: 15,2 ![]() олеиновой кислоты (двойной
дистилляции) тщательно взбалтывается с 50
олеиновой кислоты (двойной
дистилляции) тщательно взбалтывается с 50 ![]() дистиллированной воды. Все это
тщательно смешивается с 73
дистиллированной воды. Все это
тщательно смешивается с 73 ![]() 10 %-ного раствора триэтаноламина, и
всю смесь доливают водой до 200
10 %-ного раствора триэтаноламина, и
всю смесь доливают водой до 200 ![]() . К этому добавляют 164
. К этому добавляют 164 ![]() чистого
глицерина. Смеси дают отстояться и берут чистую жидкость внизу. В некоторых
экспериментах ее разбавляли в тройном количестве (по объему) воды для
уменьшения вязкости. Отверстие пипетки расположено примерно на 5 мм ниже уровня
раствора. Постоянное давление воздуха (составлявшее 50-200 см водяного столба)
поддерживается с помощью двух колб Винчестера. Обычно пузырьки удивительно
однородны по размерам. Иногда вдруг они выходят беспорядочным образом, но этого
можно избежать, меняя пипетку или давление. Ненужные пузырьки легко уничтожить,
проведя над поверхностью слабым пламенем. На фиг. 1 показан наш прибор. Мы
сочли удобным зачернить дно сосуда, потому что в этом случае детали структуры,
такие, как границы зерен и дислокации, проявляются более ярко.
чистого
глицерина. Смеси дают отстояться и берут чистую жидкость внизу. В некоторых
экспериментах ее разбавляли в тройном количестве (по объему) воды для
уменьшения вязкости. Отверстие пипетки расположено примерно на 5 мм ниже уровня
раствора. Постоянное давление воздуха (составлявшее 50-200 см водяного столба)
поддерживается с помощью двух колб Винчестера. Обычно пузырьки удивительно
однородны по размерам. Иногда вдруг они выходят беспорядочным образом, но этого
можно избежать, меняя пипетку или давление. Ненужные пузырьки легко уничтожить,
проведя над поверхностью слабым пламенем. На фиг. 1 показан наш прибор. Мы
сочли удобным зачернить дно сосуда, потому что в этом случае детали структуры,
такие, как границы зерен и дислокации, проявляются более ярко.
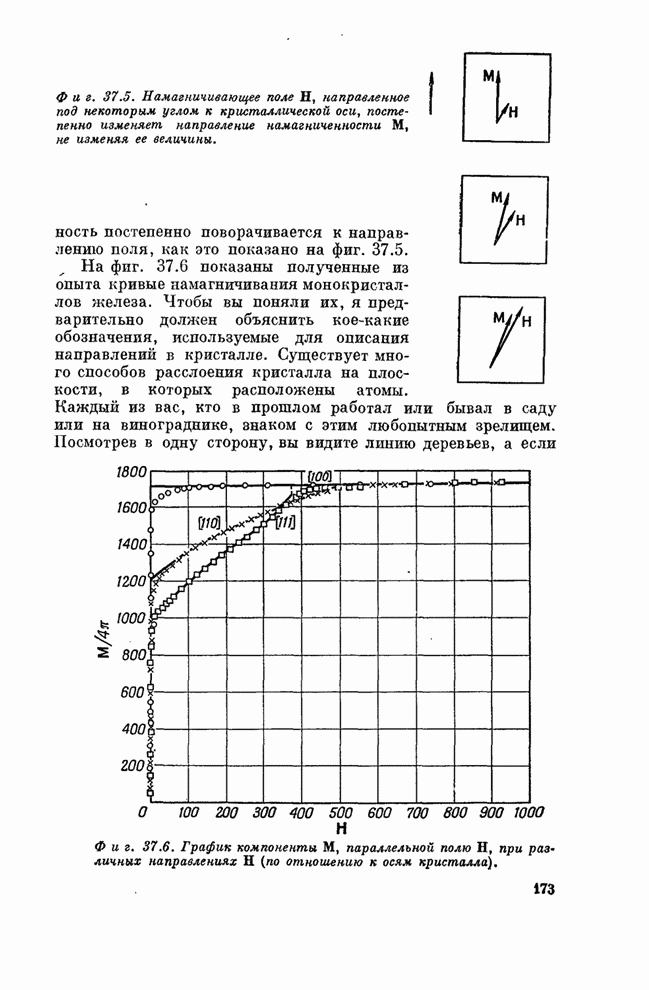
На фиг. 2 (лист 1) показана часть «плота» или двумерного кристалла из пузырьков. О правильности расположения можно судить, если взглянуть на снимок под небольшим углом к плоскости страницы. Размер пузырьков меняется с апертурой
The main effect of increasing the
pressure is to increase the rate of issue of the bubbles. As an example, a
thick-walled jet of ![]() bore with a pressure of 100 cm.
produced bubbles of 1-2 mm. in diameter. A thin-wailed jet of
bore with a pressure of 100 cm.
produced bubbles of 1-2 mm. in diameter. A thin-wailed jet of ![]() diameter and a
pressure of 180cm. produced bubbles of
diameter and a
pressure of 180cm. produced bubbles of ![]() mm diameter. It is convenient to
refer to bubbles of
mm diameter. It is convenient to
refer to bubbles of ![]() to
to ![]() mm. diameter as 'large' bubbles,
those from
mm. diameter as 'large' bubbles,
those from ![]() to
to
![]() mm.
diameter as 'medium' bubbles, and those from
mm.
diameter as 'medium' bubbles, and those from ![]() to
to ![]() mm. diameter as 'small' bubbles,
since their behavior varies with their size.
mm. diameter as 'small' bubbles,
since their behavior varies with their size.

Figure 3. Apparatus for producing bubbles of small size.
With this apparatus we have not
found it possible to reduce the size of the jet and sо produce bubbles of smaller
diameter than ![]() mm.
As it was desired to experiment with very small bubbles, we had recourse to
placing the soap solution in a rotating vessel and introducing a fine jet as
nearly as possible parallel to a stream line. The bubbles are swept away as
they form, and under steady conditions are reasonably uniform. They issue at a
rate of one thousand or more per second, giving a high-pitched note. The soap
solution mounts up in a steep wall around the perimeter of the vessel while it
is rotating, but carries back most of the bubbles with it when rotation ceases.
With this device, illustrated in figure 3, bubbles down to
mm.
As it was desired to experiment with very small bubbles, we had recourse to
placing the soap solution in a rotating vessel and introducing a fine jet as
nearly as possible parallel to a stream line. The bubbles are swept away as
they form, and under steady conditions are reasonably uniform. They issue at a
rate of one thousand or more per second, giving a high-pitched note. The soap
solution mounts up in a steep wall around the perimeter of the vessel while it
is rotating, but carries back most of the bubbles with it when rotation ceases.
With this device, illustrated in figure 3, bubbles down to ![]() mm. in diameter can be
obtained. As an example, an orifice
mm. in diameter can be
obtained. As an example, an orifice ![]() across in a thin-walled jet, with a
pressure of 190 cm. of water, and a speed of the fluid of 180cm./sec. past the
orifice, produced bubbles of
across in a thin-walled jet, with a
pressure of 190 cm. of water, and a speed of the fluid of 180cm./sec. past the
orifice, produced bubbles of ![]() mm. diameter. In this case a dish of
diameter
mm. diameter. In this case a dish of
diameter ![]() cm.
and speed of 6 rev./sec. was used. Figure 4, plate 8, is an enlarged picture of
these 'small' bubbles and shows their degree of regularity; the pattern is not
as perfect with a rotating as with a stationary vessel, the rows being seen to
be slightly irregular when viewed in a glancing direction.
cm.
and speed of 6 rev./sec. was used. Figure 4, plate 8, is an enlarged picture of
these 'small' bubbles and shows their degree of regularity; the pattern is not
as perfect with a rotating as with a stationary vessel, the rows being seen to
be slightly irregular when viewed in a glancing direction.
These two-dimensional crystals show structures which have been supposed to exist in metals, and simulate effects which have been observed, such as grain boundaries, dislocations and other types of fault, slip, recrystallization, annealing, and strains due to 'foreign' atoms.
(размером отверстия), но не зависит сколько-нибудь заметным образом от давления или глубины расположения отверстия ниже уровня раствора. Основной эффект, к которому приводит увеличение давления, - это увеличение скорости рождения пузырьков.
Например, толстостенная трубка с внутренним диаметром 49 мк и давлением 100 см образовывала пузырьки диаметром 1,2 мм. Тонкостенная трубка с внутренним диаметром 27 мк и давлением 180 см образовывала пузырьки диаметром 0,6 мм. Пузырьки диаметром от 2 до 1 мм удобно называть «большими», диаметром от 0,8 до 0,6 мм - «средними», а пузырьки диаметром от 0,3 до 1,1 мм - «маленькими», так как поведение пузырьков зависит от их размеров.
С помощью такого прибора нам не удалось уменьшить размеры отверстия и получить пузырьки диаметром менее 0,6 мм.
Поскольку было желательно поставить опыты с очень маленькими пузырьками, мы влили мыльный раствор во вращающийся сосуд и ввели тонкую трубочку, расположив как можно более точно параллельно линии потока. По мере образования пузырьки уносятся и при постоянных условиях довольно близки по размерам. Образуются они со скоростью тысяча или более в секунду, причем издается пронзительный звук. При вращении сосуда мыльный раствор круто поднимается по его стенкам по всей окружности, а когда вращение прекращается, раствор уносит с собой большинство пузырьков. С помощью этого устройства, показанного на фиг. 3, могут быть получены пузырьки диаметром до 0,12 мм. Так, тонкостенная трубка с поперечным отверстием 38 мк, при давлении воздуха 190 см водяного столба и скорости потока у отверстия в 180см/сек образует пузырьки диаметром 0,14 мм. В этом случае использовался сосуд диаметром 9,5 см, а скорость вращения достигала 6 оборотов в 1 сек.
На фиг. 4 (лист 1) приведен увеличенный снимок этих «маленьких» пузырьков, иллюстрирующий степень их регулярности; при вращении порядок получается не таким полным, как в неподвижном сосуде; когда смотришь в плоскости страницы, видно, что ряды слегка нерегулярны.
Эти двумерные кристаллы образуют структуры, которые, как полагают, существуют в металлах, и имитируют такие наблюденные эффекты, как границы зерен, дислокации и другие дефекты, процессы скольжения, явление рекристаллизации и отжига и возникновение напряжений, вызванных «посторонними» атомами.
A dynamical model of a crystal structure
3. Grain boundaries
Figures 5a, 5b and 5c, plates 9
and 10, show typical grain boundaries for bubbles of ![]() ,
, ![]() and
and ![]() mm. diameter respectively.
The width of the disturbed area at the boundary, where the bubbles have an
irregular distribution, is in general greater the smaller the bubbles. In
figure 5a, which shows portions of several adjacent grains, bubbles at a
boundary between two grains adhere definitely to one crystalline arrangement or
the other. In figure 5c there is a marked 'Beilby layer' between the two
grains. The small bubbles, as will be seen, have a greater rigidity than the
large ones, and this appears to give rise to more irregularity at the
interface.
mm. diameter respectively.
The width of the disturbed area at the boundary, where the bubbles have an
irregular distribution, is in general greater the smaller the bubbles. In
figure 5a, which shows portions of several adjacent grains, bubbles at a
boundary between two grains adhere definitely to one crystalline arrangement or
the other. In figure 5c there is a marked 'Beilby layer' between the two
grains. The small bubbles, as will be seen, have a greater rigidity than the
large ones, and this appears to give rise to more irregularity at the
interface.
Separate grains show up distinctly when photographs of polycrystalline rafts such as figures 5a to 5c, plates 9 and 10, and figures 12a to 12e, plates 14 to 16, are viewed obliquely. With suitable lighting, the floating raft of bubbles itself when viewed obliquely resembles a polished and etched metal in a remarkable way.
It often happens that some 'impurity atoms', or bubbles which are markedly larger or smaller than the average, are found in a polycrystalline raft, and when this is so a large proportion of them are situated at the grain boundaries. It would be incorrect to say that the irregular bubbles make their way to the boundaries; it is a defect of the model that no diffusion of bubbles through the structure can take place, mutual adjustments of neighbors alone being possible. It appears that the boundaries tend to readjust themselves by the growth of one crystal at the expense of another till they pass through the irregular atoms.
4. Dislocations
When a single crystal or polycrystalline raft is compressed, extended, or otherwise deformed it exhibits a behavior very similar to that which has been pictured for metals subjected to strain. Up to a certain limit the model is within its elastic range. Beyond that point it yields by slip along one of the three equally inclined directions of closely packed rows. Slip takes place by the bubbles in one row moving forward over those in the next row by an amount equal to the distance between neighbors. It is very interesting to watch this process taking place. The movement is not simultaneous along the whole row but begins at one end with the appearance of a 'dislocation', where there is locally one more bubble in the rows on one side of the slip line as compared with those on the other. This dislocation then runs along the slip line from one side of the crystal to the other, the final result being a slip by one 'inter-atomic' distance. Such a process has been invoked by Orowan, by Polanyi and by Taylor to explain the small forces required to produce plastic gliding in metal structures. The theory put forward by Taylor (1934) to explain the mechanism of plastic deformation of crystals considers the mutual action and equilibrium of such dislocations. The bubbles afford a very striking picture of what has been supposed to take place in the metal. Sometimes the dislocations run along quite slowly, taking a matter of seconds to cross a crystal; stationary dislocations also are to be seen in crystals which are not homogeneously
3. Границы зерен
На фиг. 5 (лист 2) показаны типичные границы зерен для пузырьков диаметром соответственно 1,87, 0,76 и 0,30 мм. Ширина возмущенной поверхности на границе, где пузырьки имеют нерегулярное распределение, в основном бывает тем больше, чем меньше пузырьки. На фиг. 5,а, где показано несколько соседних зерен, пузырьки на границе между двумя зернами явно придерживаются либо одного, либо другого кристаллического порядка. На фиг. 5,в ясно обозначился «слой Бейлби» между двумя зернами. Маленькие пузырьки, как будет видно далее, обладают большей жесткостью, чем большие, а это приводит к значительной беспорядочности на границах. Отдельные зерна ясно видны, если рассматривать фотографии поликристаллических слоев. При подходящем освещении сами плавающие слои пузырьков, рассматриваемые вдоль страницы, удивительно напоминают полированный и травленый металл. Часто случается, что в поликристаллический плот попадают «атомы примеси», т. е. пузырьки, заметно отличающиеся по размерам от средних, и в этом случае большая доля их размещается на границах зерен. Было бы неправильно утверждать, что несоразмерные пузырьки проталкиваются к границам; невозможность диффузии пузырьков сквозь структуру составляет дефект модели. Может возникать только взаимное приспособление соседей. Оказывается, что границы стремятся перестроиться благодаря росту одного кристалла за счет другого, пока граница не пройдет через атомы примесей.
4. Дислокации
Если монокристалл или поликристаллический плот подвергается сжатию, растяжению или другой деформации, его поведение очень похоже на поведение металлов, на которые действует напряжение. До известного предела модель находится в области упругой деформации. За этой границей модель начинает скользить вдоль одного из трех равноправных направлений, вдоль плотно упакованных рядов. Скольжение происходит за счет перехода пузырьков в одном ряду над пузырьками соседнего ряда на расстояние, равное промежутку между соседними пузырьками. Очень интересно наблюдать за этим процессом. Движение вдоль всего ряда не одновременное, начинается оно на одном конце с появления «дислокации», где в рядах по одну сторону линии скольжения в одном месте оказывается на один пузырек больше, нежели в рядах по другую сторону. Эта дислокация затем пробегает вдоль линии скольжения от одного конца кристалла до другого; в результате происходит проскальзывание на одно «межатомное» расстояние. Процесс такого рода
strained. They appear as short black lines, and can be seen in the series of photographs, figures 12a to 12e, plates 14 to 16. When a polycrystalline raft is compressed, these dark lines are seen to be dashing about in all directions across the crystals.
Figures 6a, 6b and 6c, plates 10
and 11, show examples of dislocations. In figure 6a, where the diameter of the
bubbles is ![]() mm.,
the dislocation is very local, extending over about six bubbles. In figure 6b
(diameter
mm.,
the dislocation is very local, extending over about six bubbles. In figure 6b
(diameter ![]() mm.)
it extends over twelve bubbles, and in figure 6c (diameter
mm.)
it extends over twelve bubbles, and in figure 6c (diameter ![]() mm.) its influence can be
traced for a length of about fifty bubbles. The greater rigidity of the small
bubbles leads to longer dislocations. The study of any mass of bubbles shows,
however, that there is not a standard length of dislocation for each size. The
length depends upon the nature of the strain in the crystal. A boundary between
two crystals with corresponding axes at approximately 30° (the maximum angle
which can occur) may be regarded as a series of dislocations in alternate rows,
and in this case the dislocations are very short. As the angle between the neighboring
crystals decreases, the dislocations occur at wider intervals and at the same
time become longer, till one finally has single dislocations in a large body of
perfect structure as shown in figures 6a, 6b and 6c.
mm.) its influence can be
traced for a length of about fifty bubbles. The greater rigidity of the small
bubbles leads to longer dislocations. The study of any mass of bubbles shows,
however, that there is not a standard length of dislocation for each size. The
length depends upon the nature of the strain in the crystal. A boundary between
two crystals with corresponding axes at approximately 30° (the maximum angle
which can occur) may be regarded as a series of dislocations in alternate rows,
and in this case the dislocations are very short. As the angle between the neighboring
crystals decreases, the dislocations occur at wider intervals and at the same
time become longer, till one finally has single dislocations in a large body of
perfect structure as shown in figures 6a, 6b and 6c.
Figure 7, plate 11, shows three parallel dislocations. If we call them positive and negative (following Taylor) they are positive, negative, positive, reading from left to right. The strip between the last two has three bubbles in excess, as can be seen by looking along the rows in a horizontal direction. Figure 8, plate 12, shows a dislocation projecting from a grain boundary, an effect often observed.
Figure 9, plate 12, shows a place where two bubbles take the place of one. This may be regarded as a limiting case of positive and negative dislocations on neighboring rows, with the compressive sides of the dislocations facing each other. The contrary case would lead to a hole in the structure, one bubble being missing at the point where the dislocations met.
предположили Орован, Поляни и Тэйлор для объяснения малости силы, вызывающей пластическое скольжение в металлических структурах. В теории, выдвинутой Тэйлором для объяснения механизма пластической деформации кристаллов, рассматривается взаимодействие и равновесие таких дислокаций. Пузырьки дают поразительную иллюстрацию того, что, как думают, происходит в металлах. Иногда дислокации движутся совсем медленно и на прохождение кристалла им требуется время порядка секунд; можно увидеть и неподвижные дислокации в кристаллах, напряжение в которых неоднородно. Они выглядят как короткие черные черточки. При сжатии поликристаллического плота эти черточки разбегаются во всех направлениях по кристаллу.
На фиг. 6 (лист 3) показаны примеры дислокаций. На фиг. 6,а дислокации имеют ограниченный характер, протягиваясь на длину около шести пузырьков. На фиг. 6,б дислокации простираются на двенадцать пузырьков, а на фиг. 6,в влияние дислокаций можно проследить на протяжении примерно пятидесяти пузырьков. Большая жесткость маленьких пузырьков приводит к более длинным дислокациям. Изучение любой массы пузырьков показывает, однако, что для каждого размера пузырьков не существует стандартной длины дислокаций. Она зависит от природы напряжений в кристалле. Границу между двумя кристаллами с осями под углом 30° друг к другу (максимальный возможный угол) можно рассматривать как серию дислокаций в чередующихся рядах, и в этом случае дислокации очень короткие. При уменьшении угла между соседними кристаллами дислокации возникают в более широких интервалах и в то же время становятся длиннее, пока, наконец, не образуется единственная дислокация в большом объеме с совершенной структурой (фиг. 6).
На фиг. 7 (лист 4) показаны три параллельные дислокации. Если (следуя Тэйлору) различать положительные и отрицательные дислокации, то это положительная, отрицательная и снова положительная, считая слева направо. Полоса между двумя последними имеет три лишних пузырька, что можно увидеть, если смотреть вдоль рядов в горизонтальном направлении. На фиг. 8 (лист 4) показана дислокация, распространяющаяся от границ зерна, что представляет собой часто встречающийся эффект. На фиг. 9 (лист 4) показано то место, где стоят два пузырька, а не один. Это можно рассматривать как предельный случай положительной и отрицательной дислокаций в соседних рядах, когда сжатые стороны дислокаций находятся друг против друга. Противоположный случай привел бы к возникновению дырки, т. е. одного пузырька не хватало бы там, где встречаются дислокации.
| << Предыдущий параграф |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
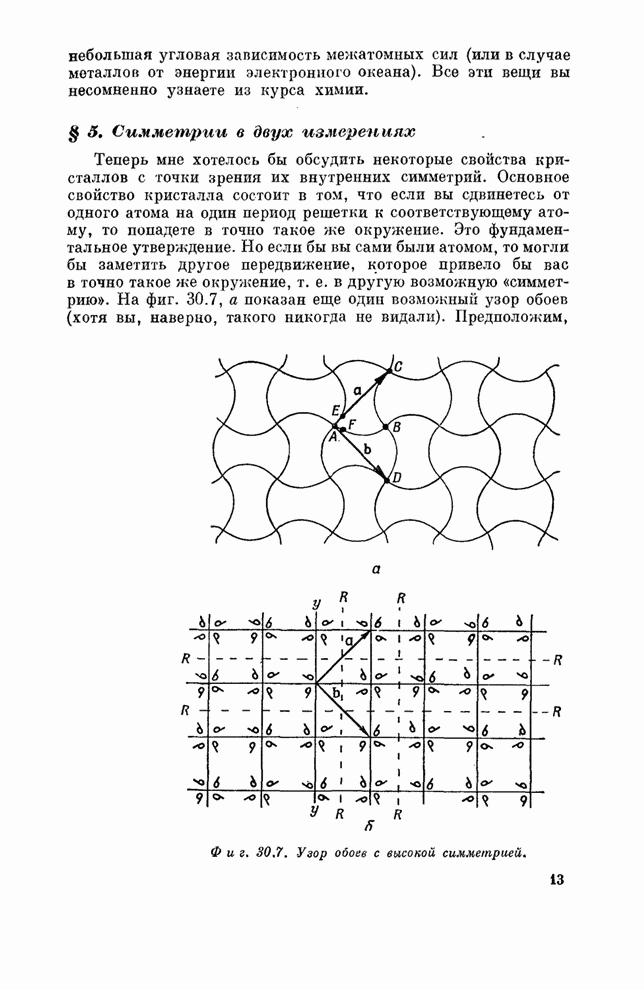
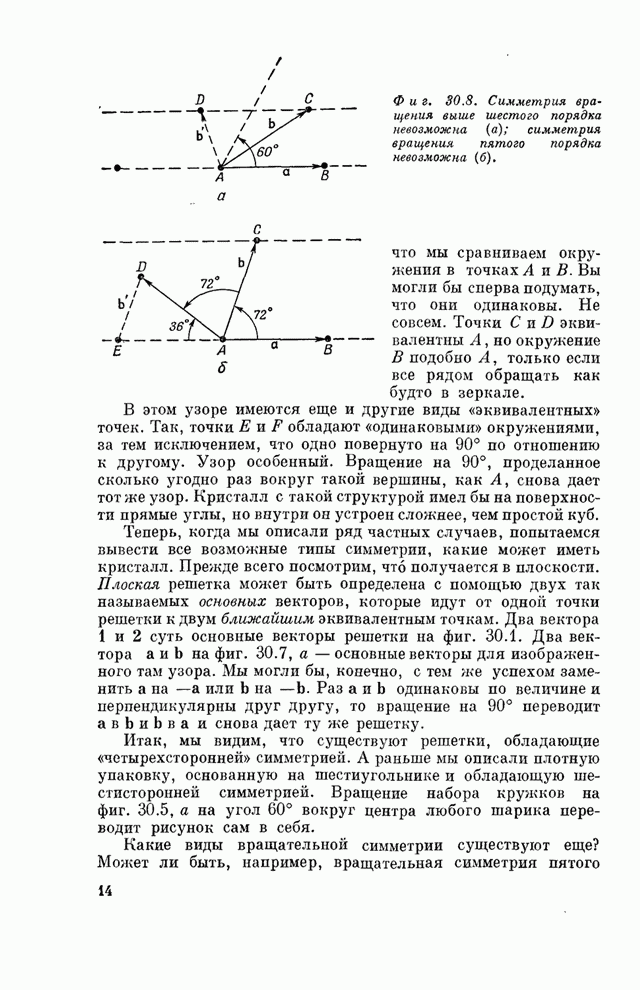
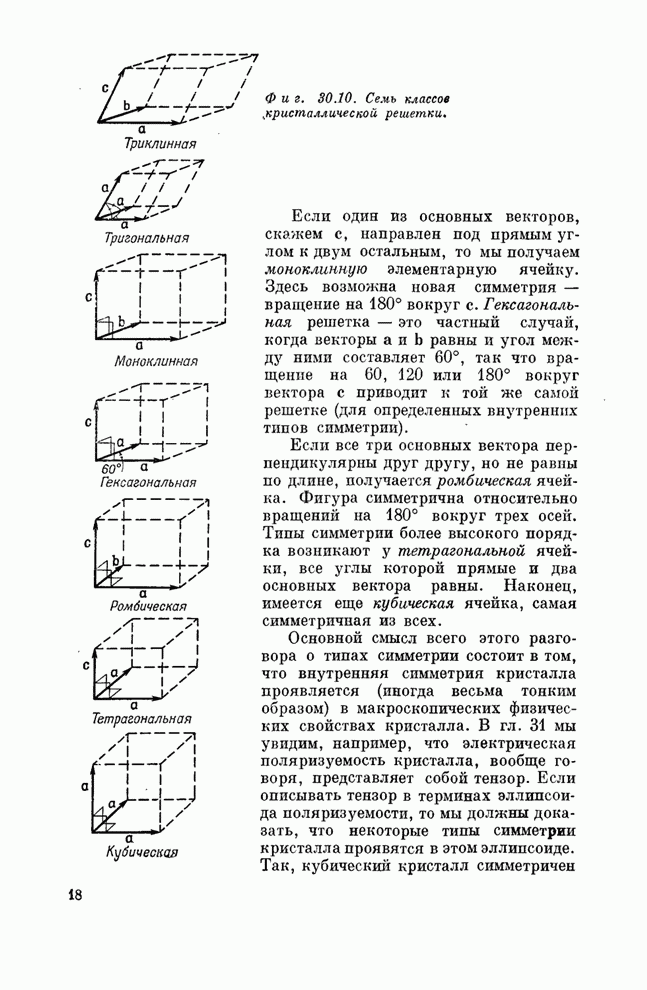
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
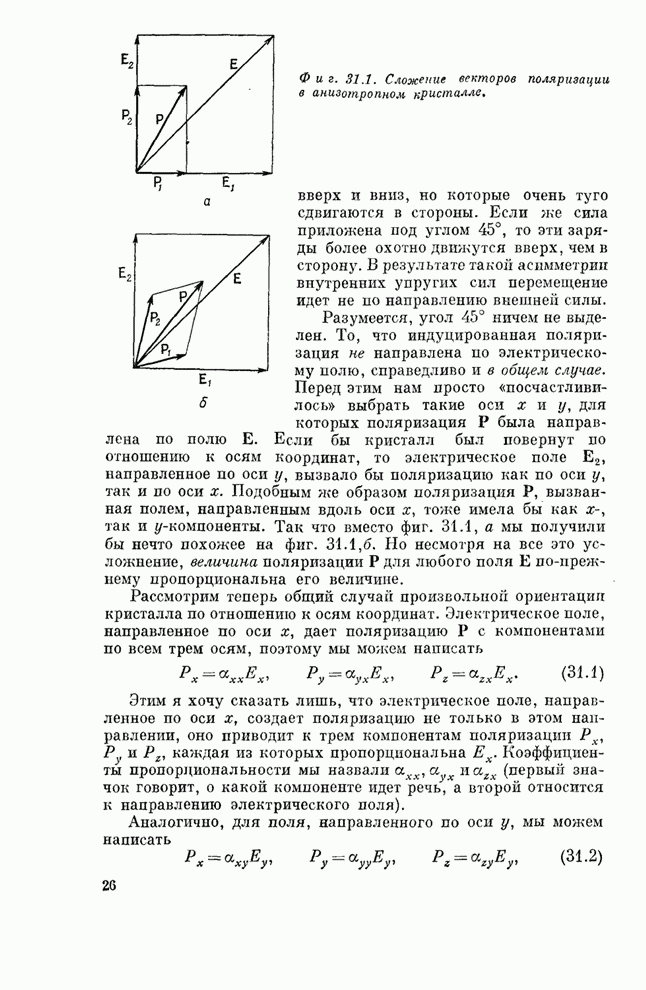
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
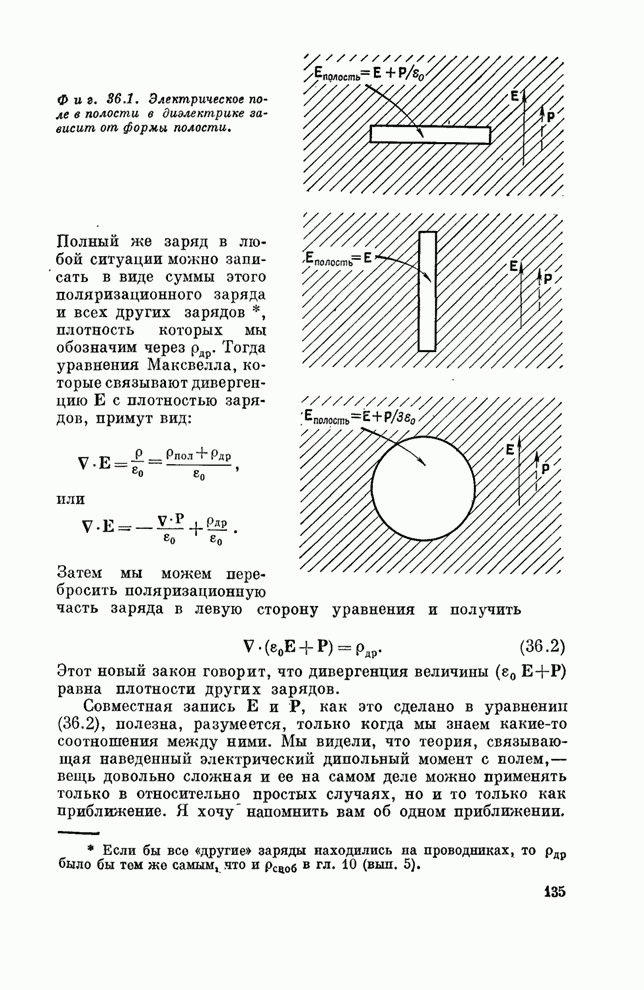
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
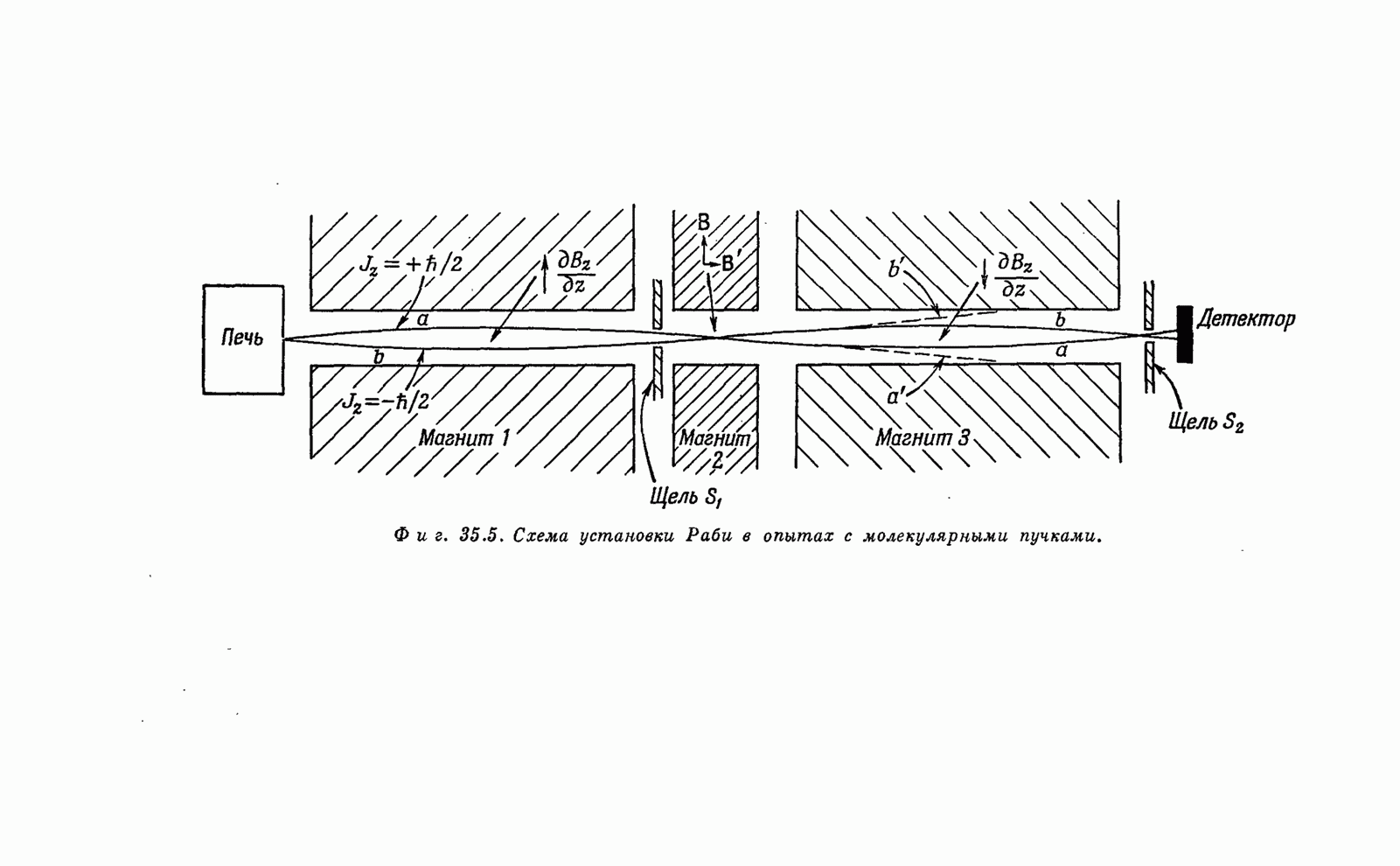
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
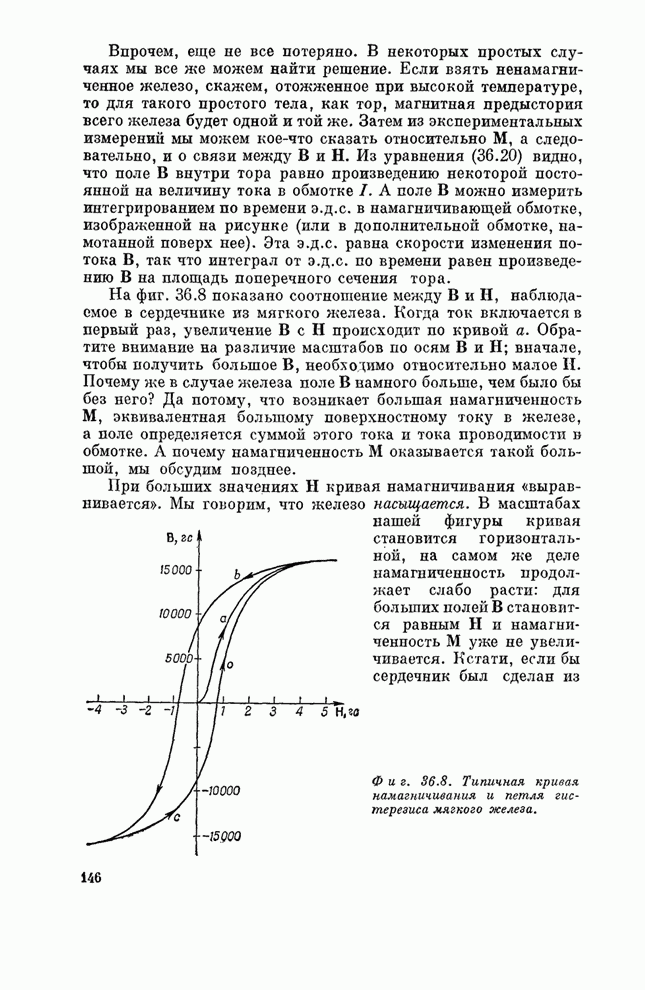
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
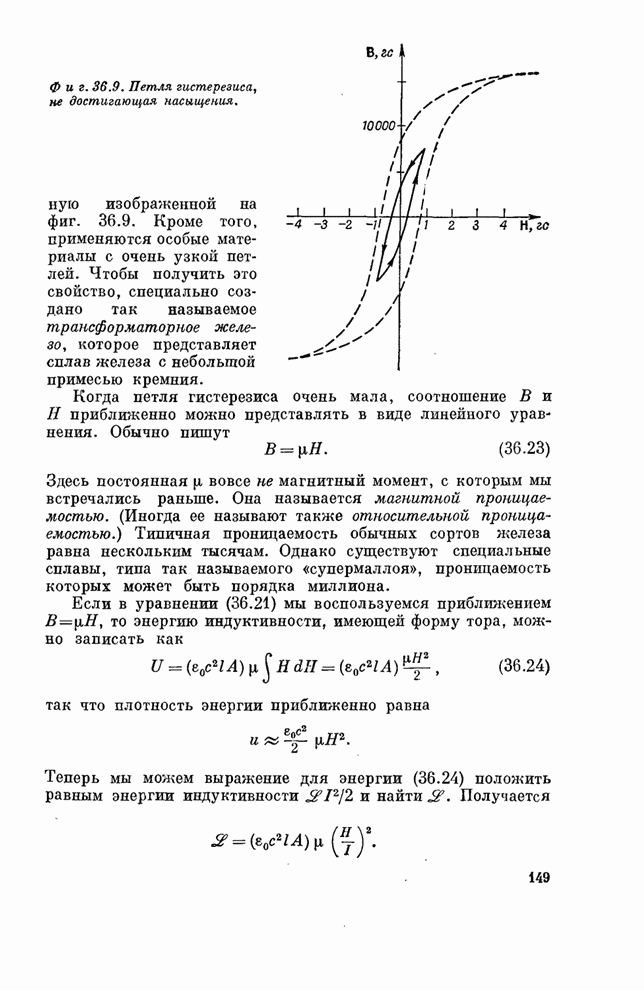
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
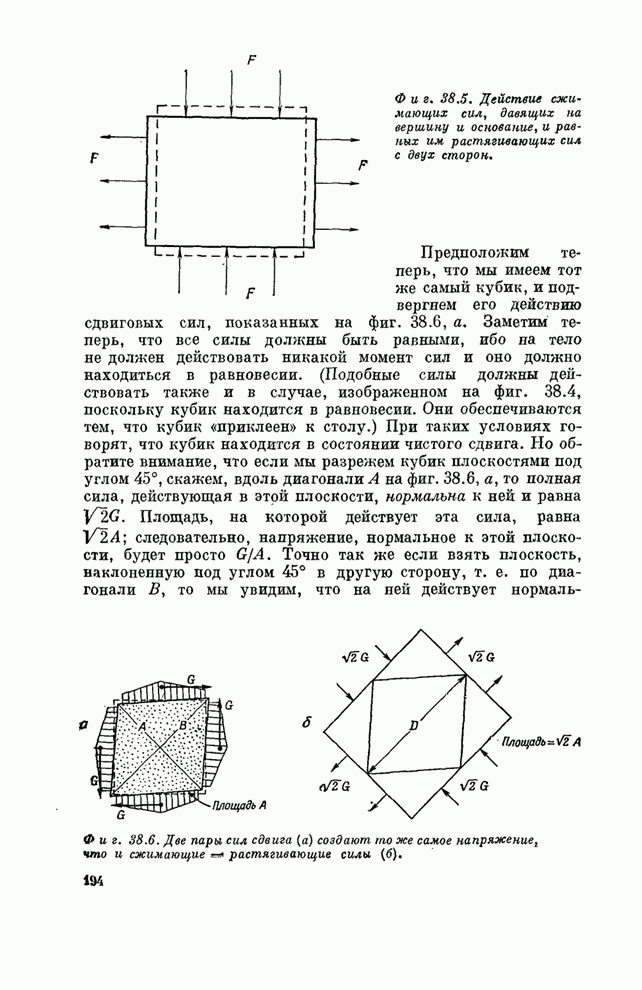
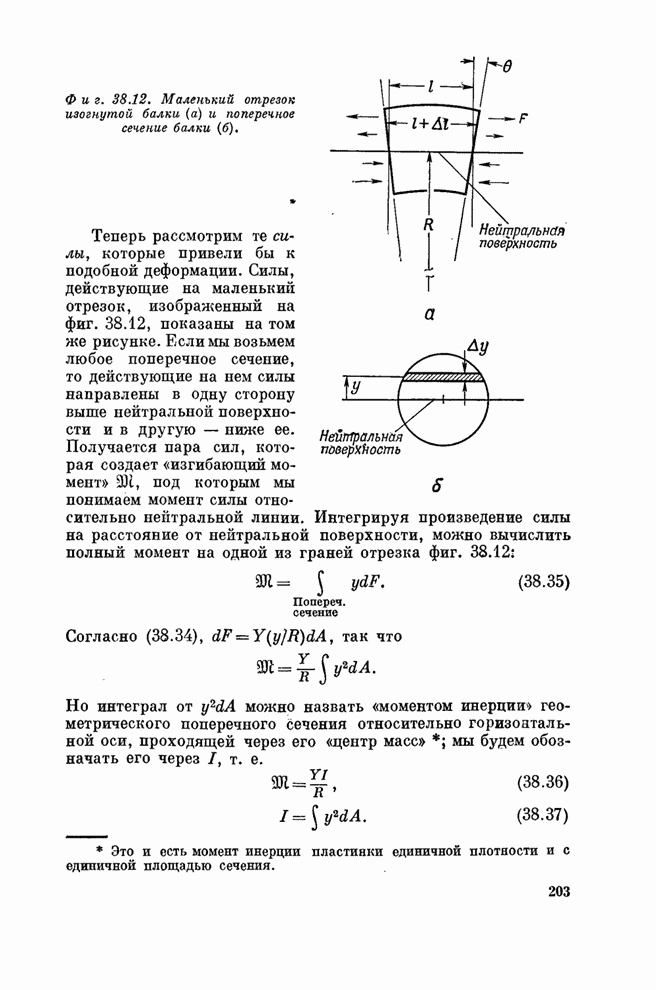
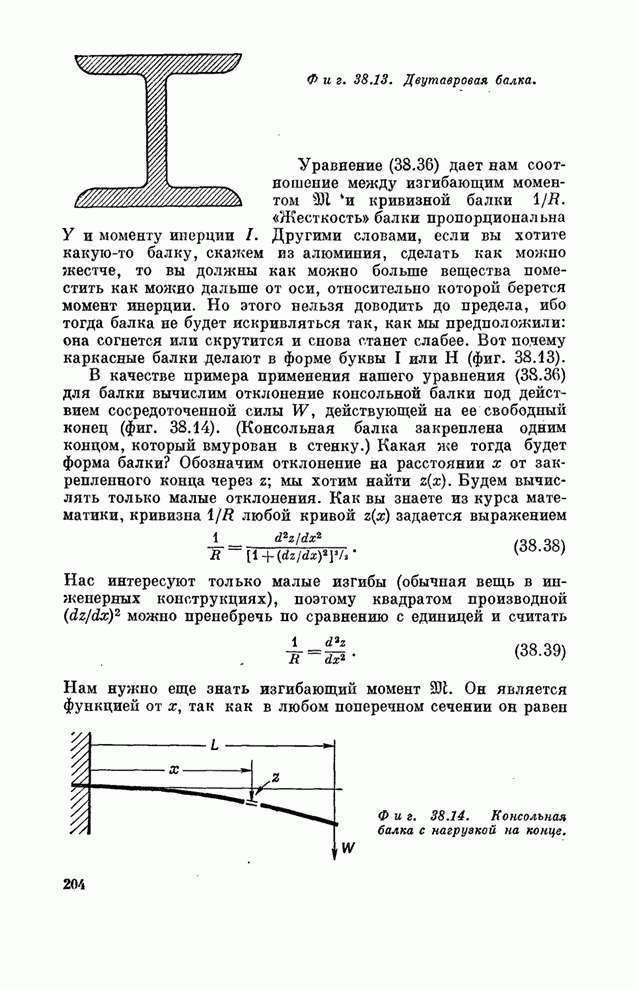
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
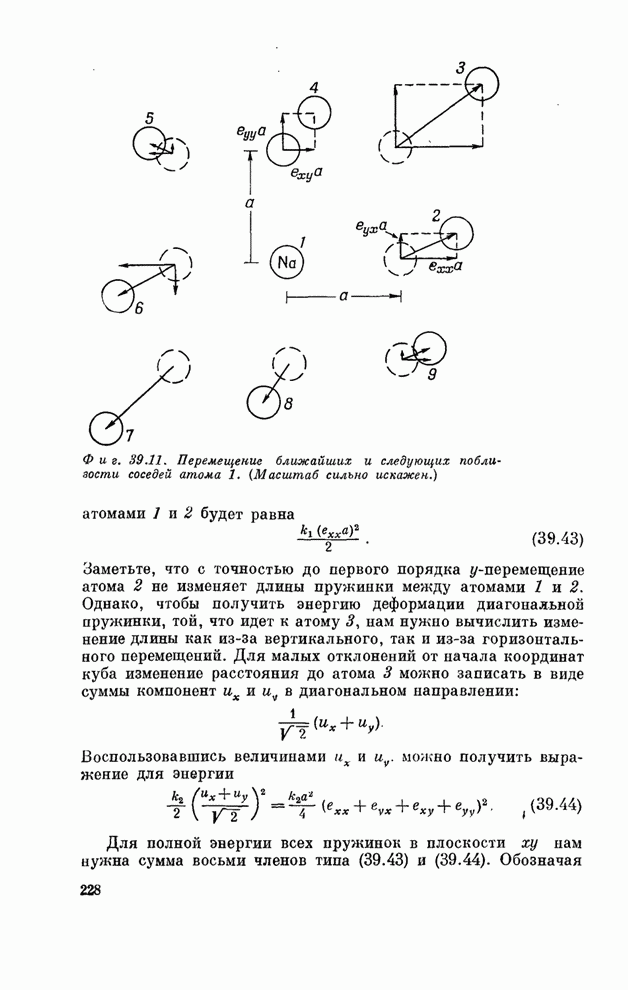
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
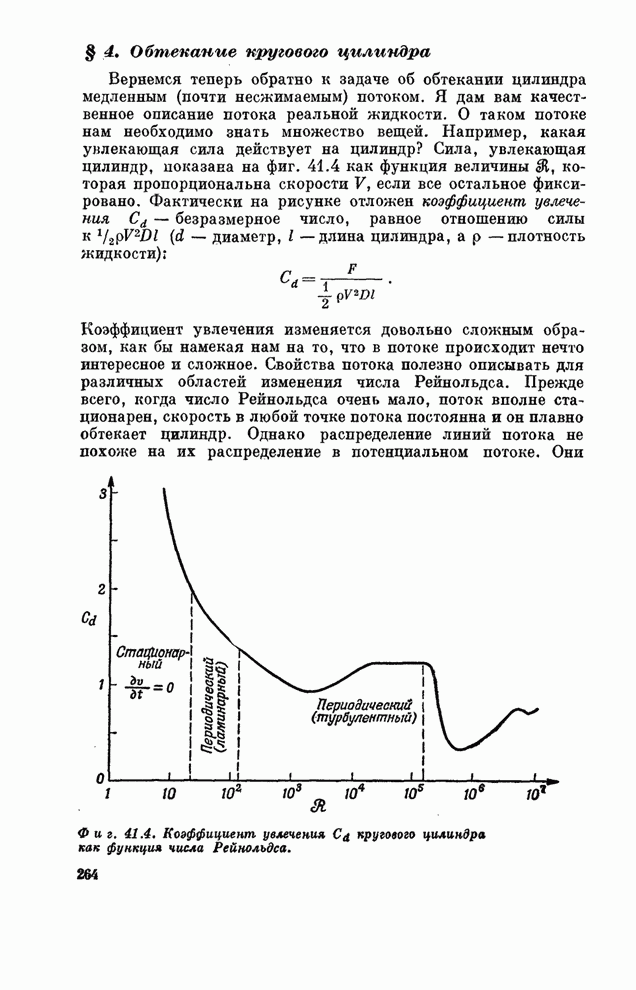
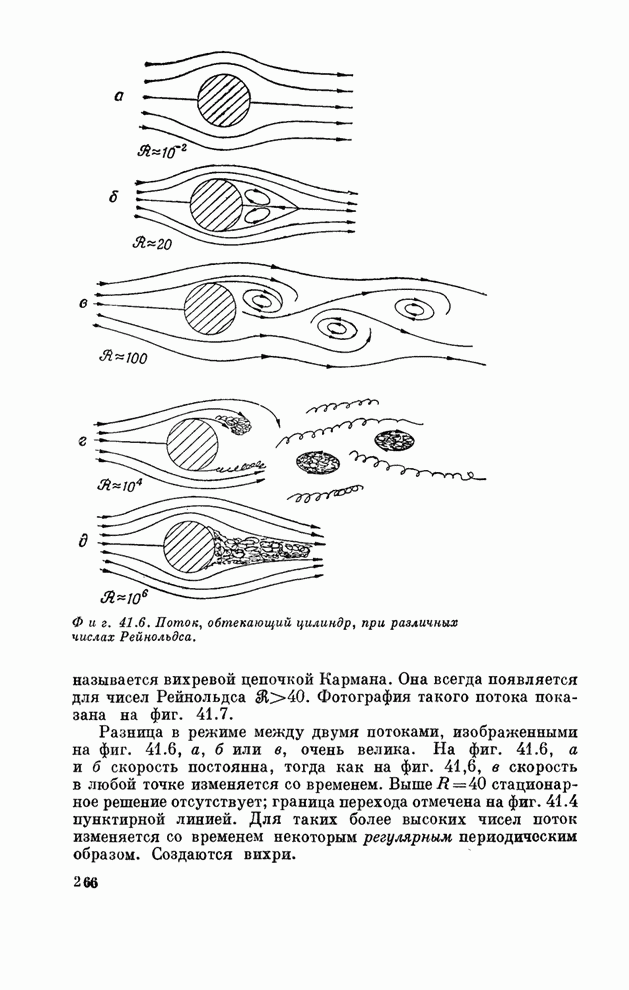
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)