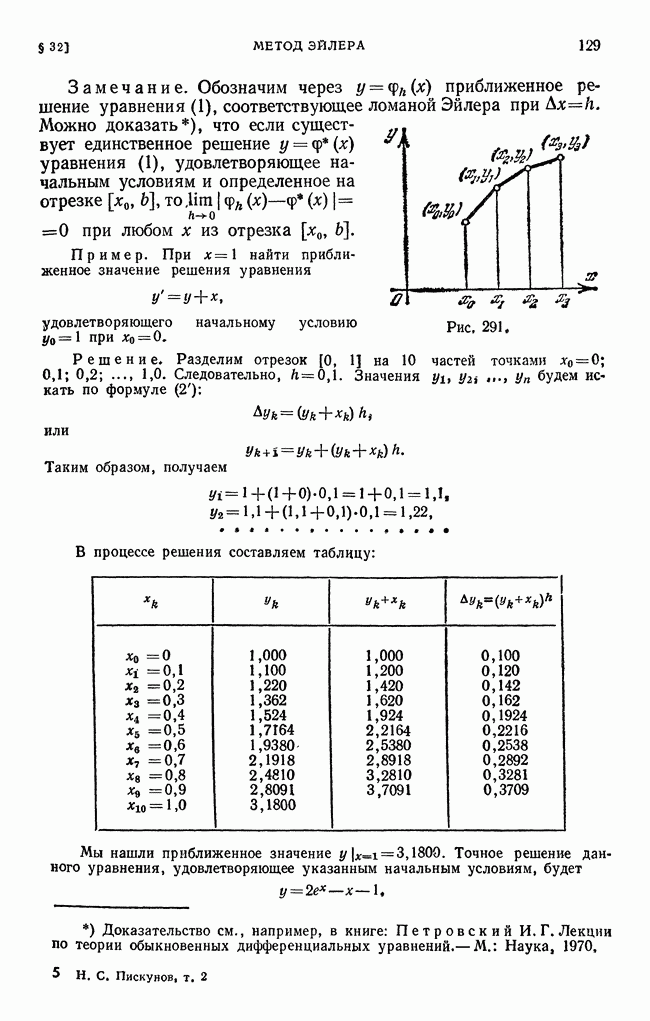
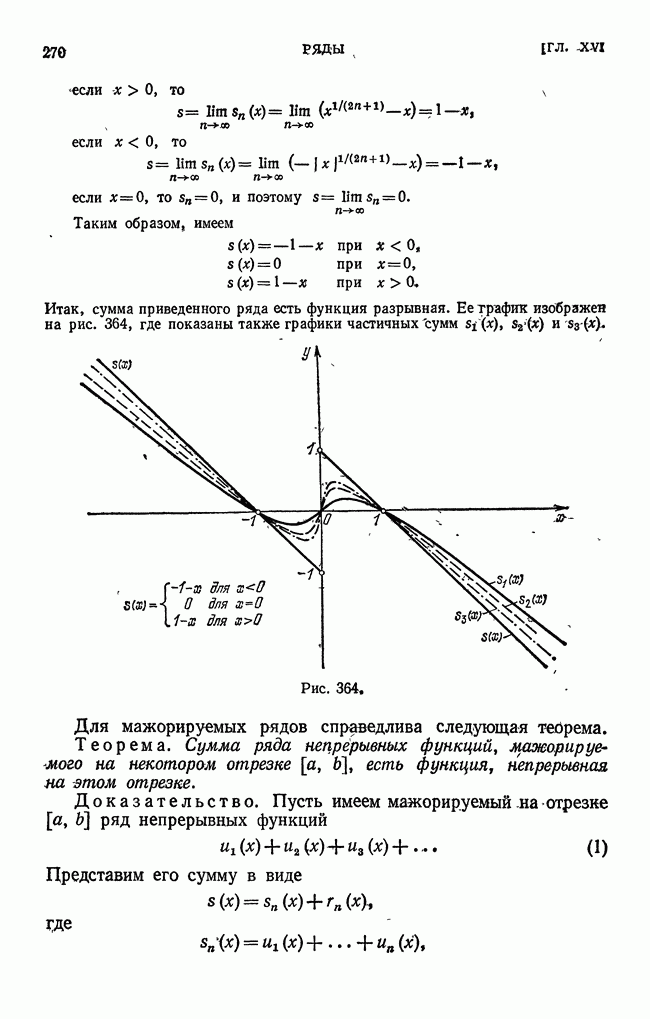
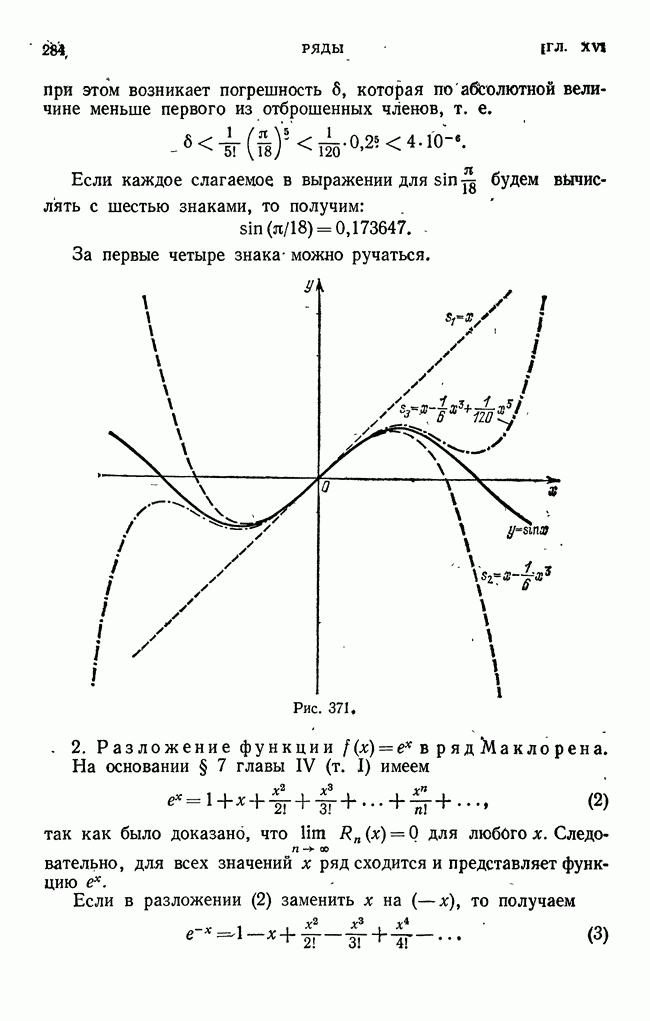
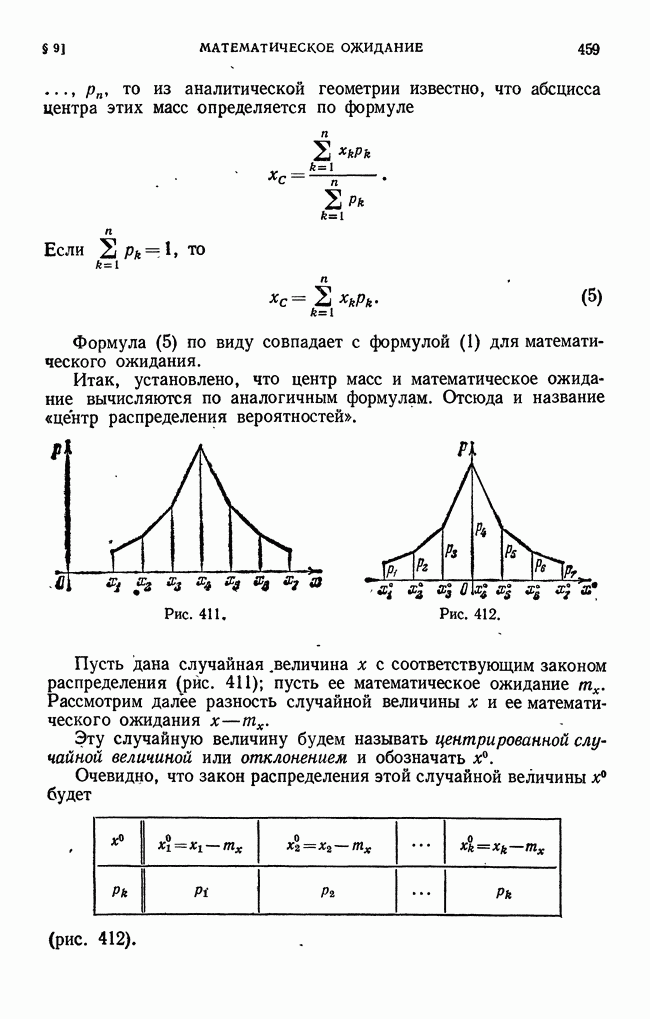
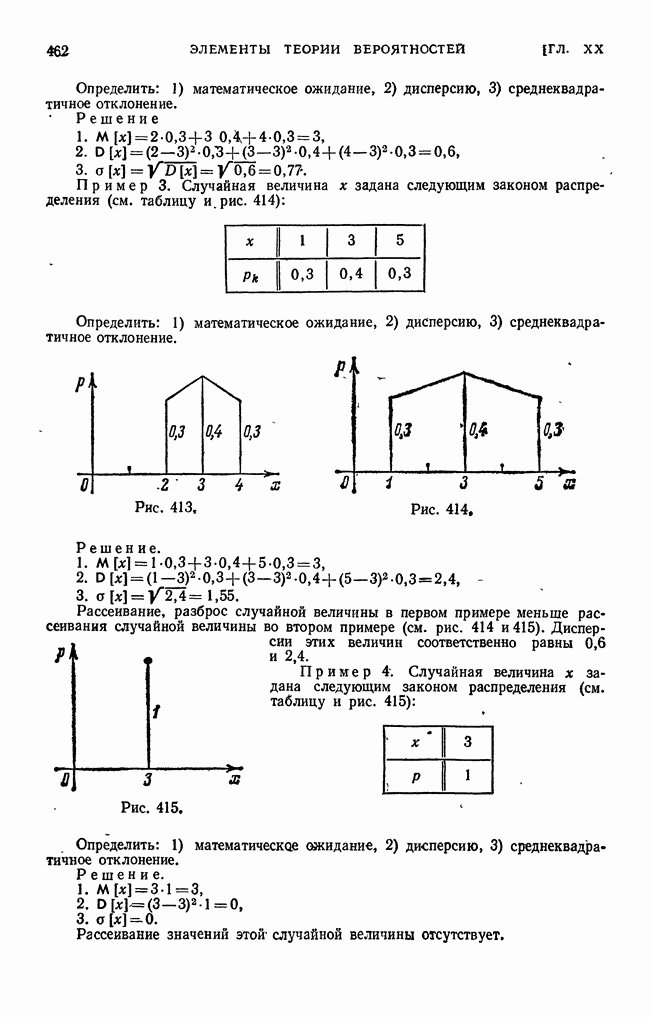
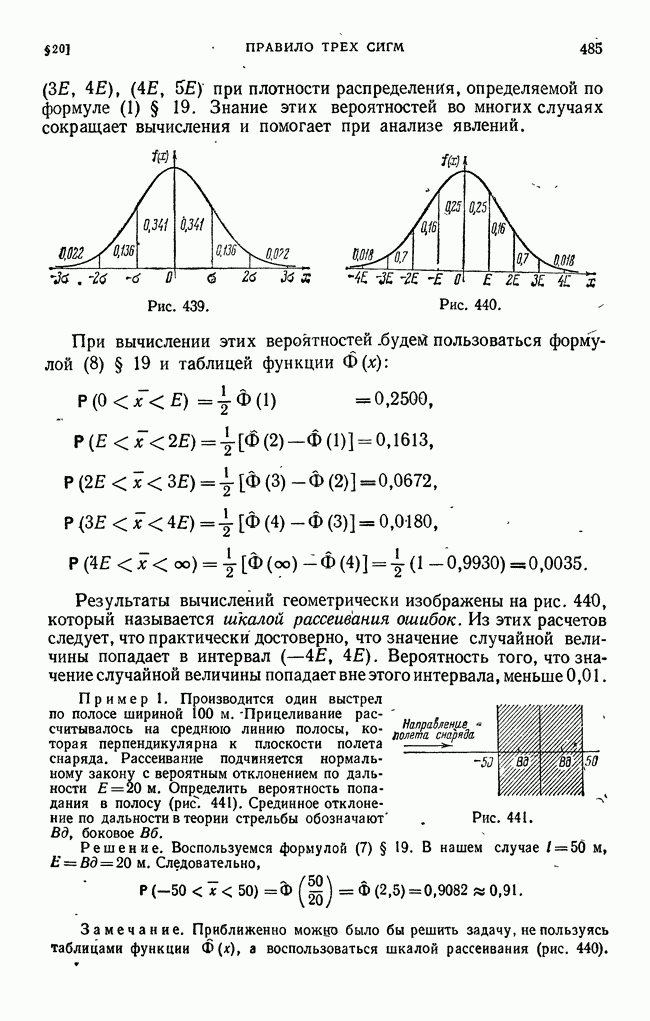
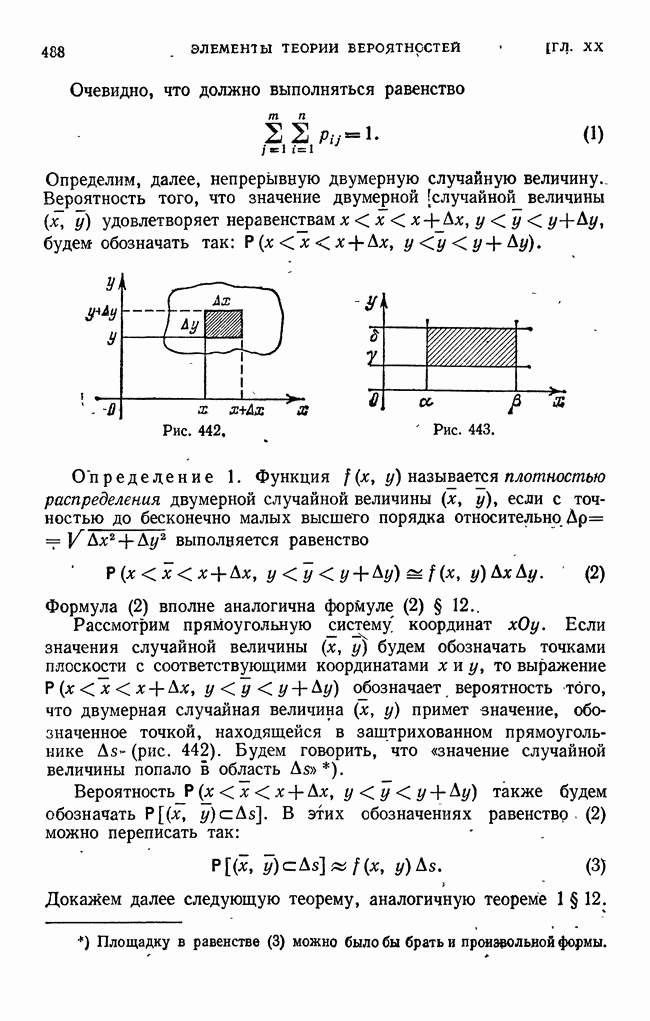
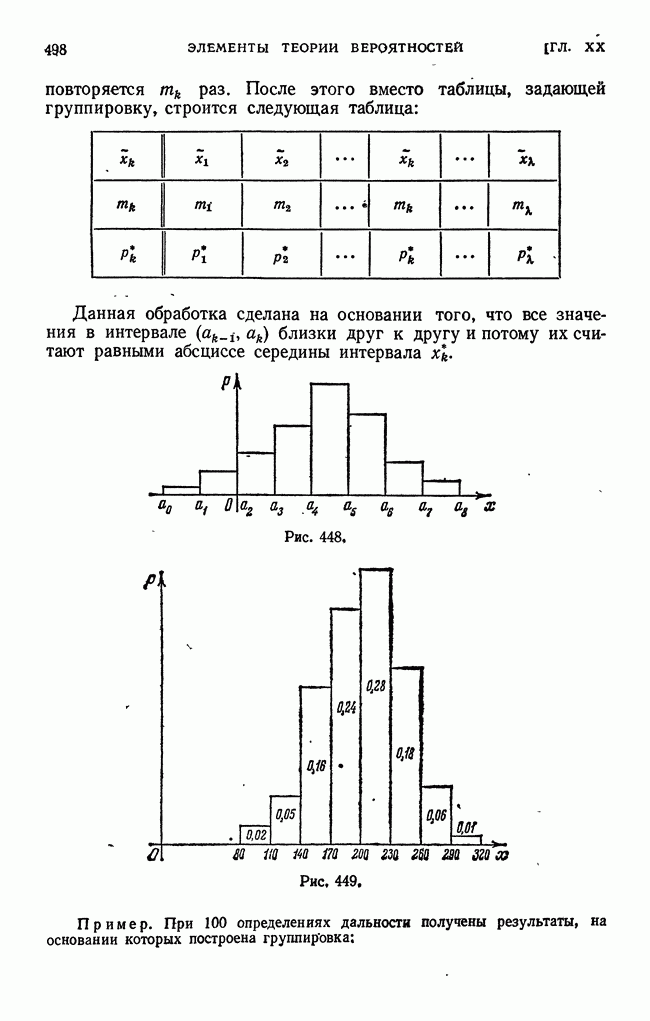
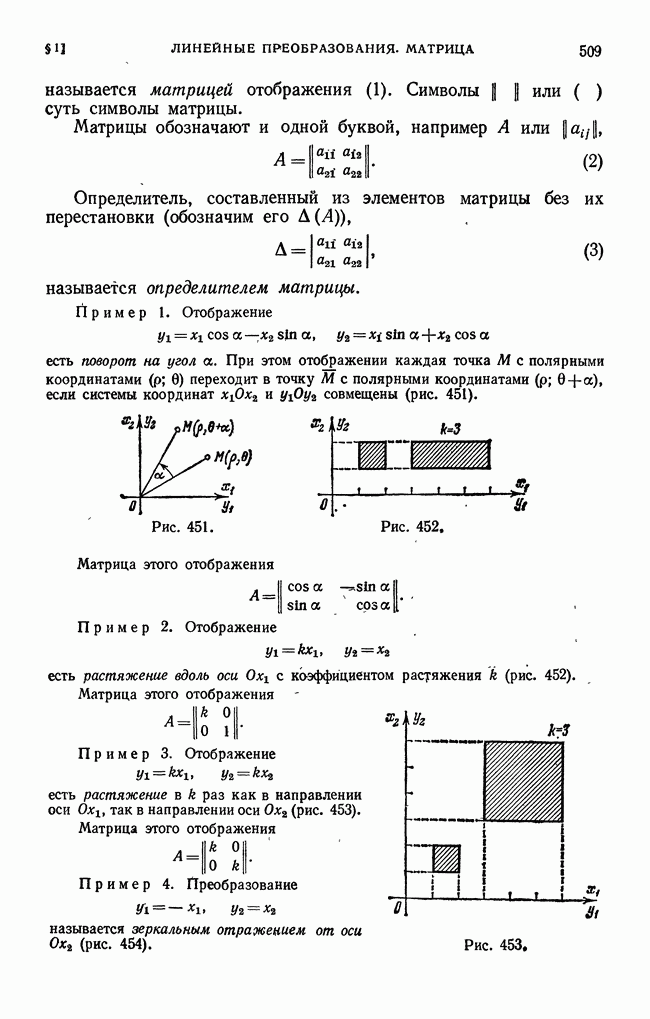
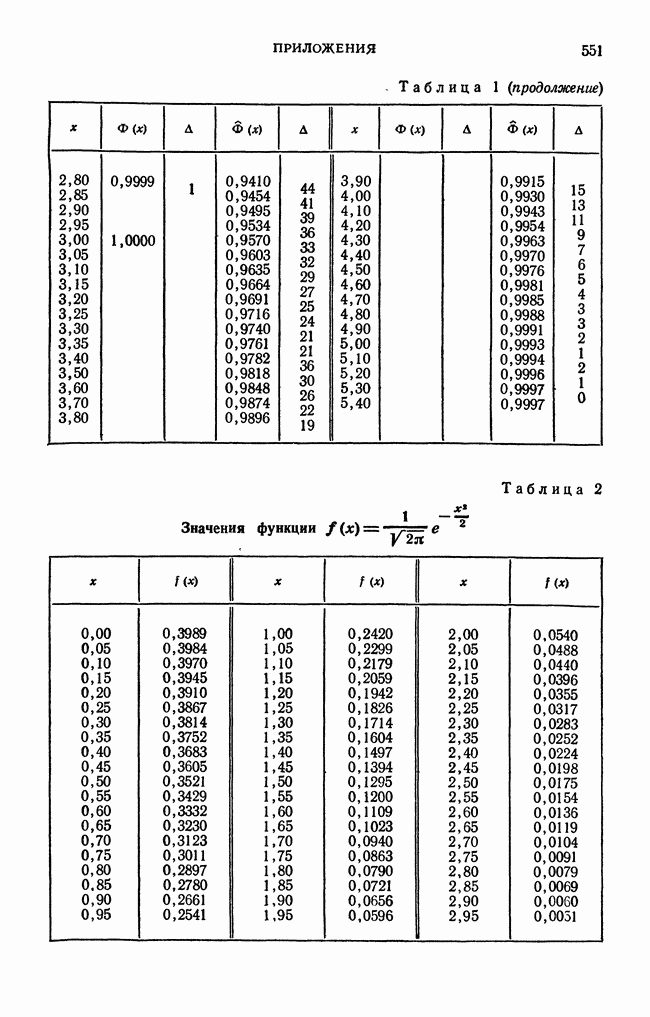
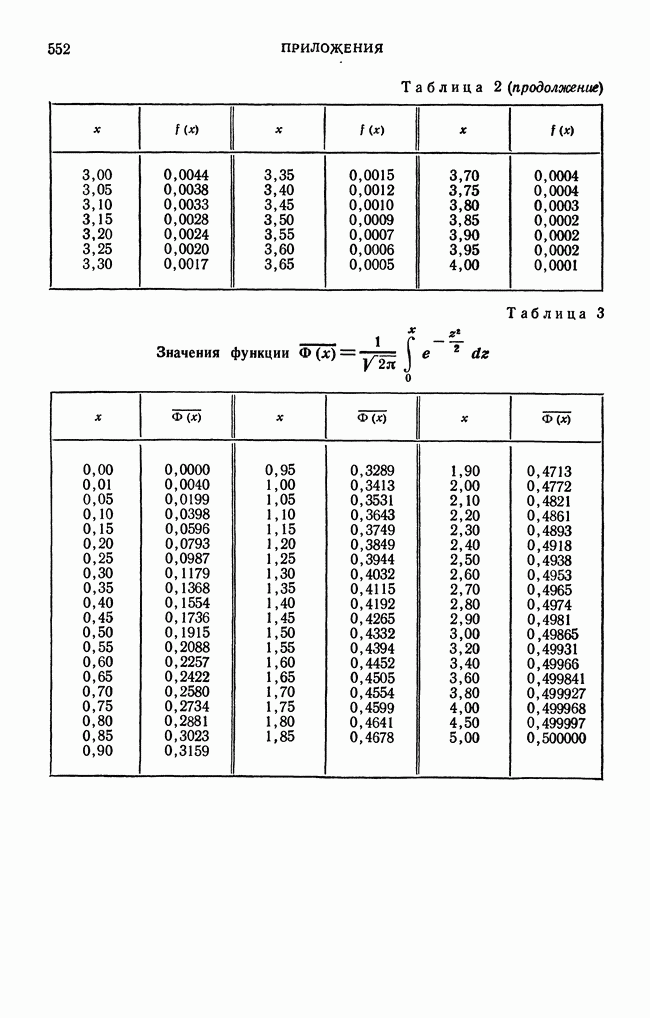
| << Предыдущий параграф | Следующий параграф >> |
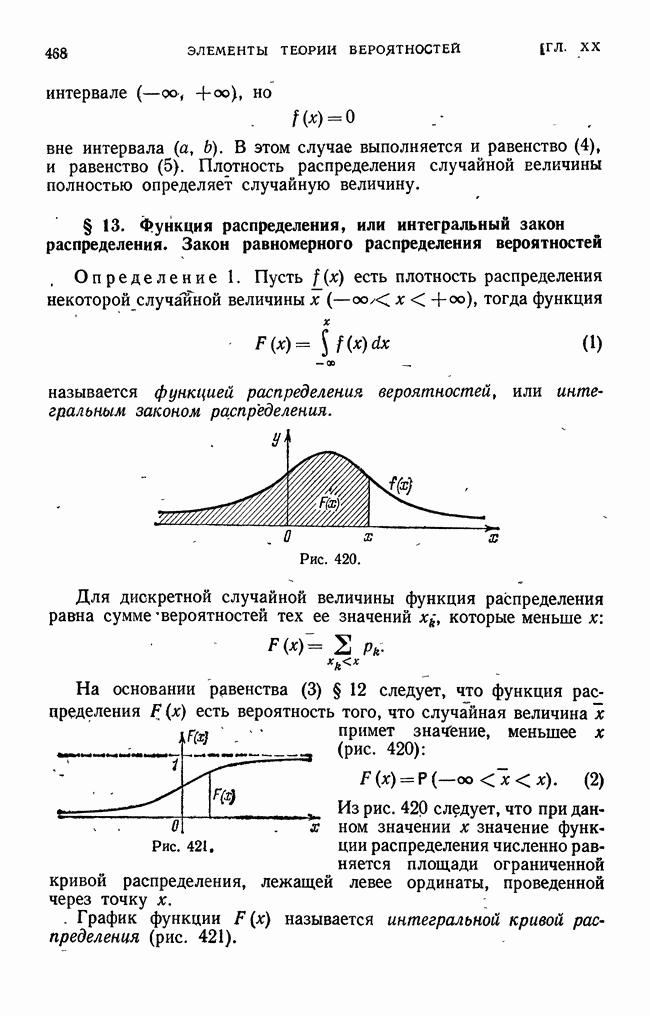
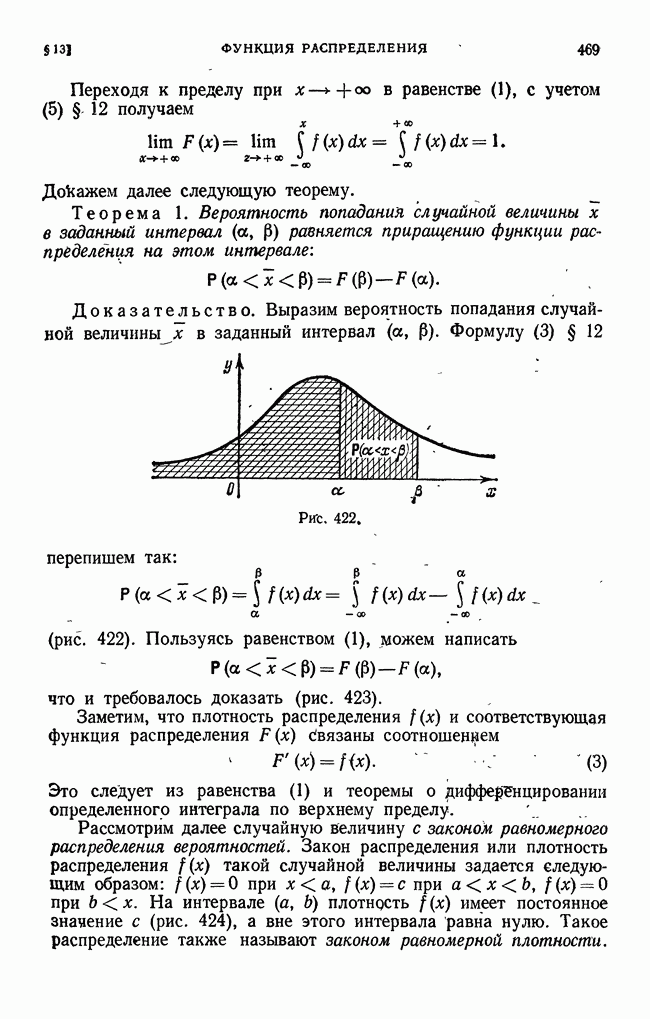
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена
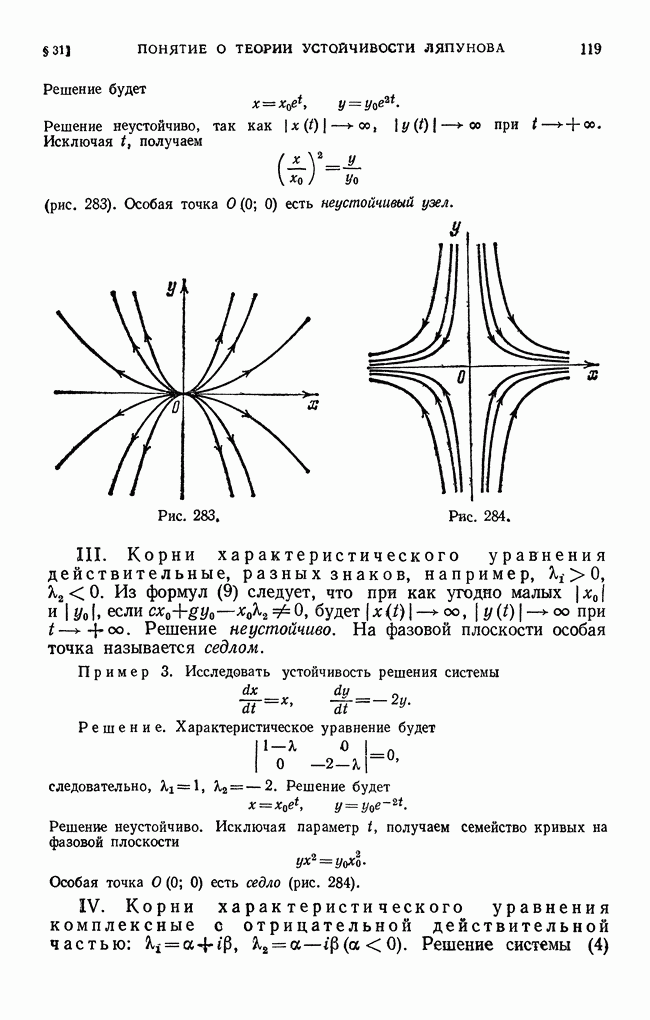
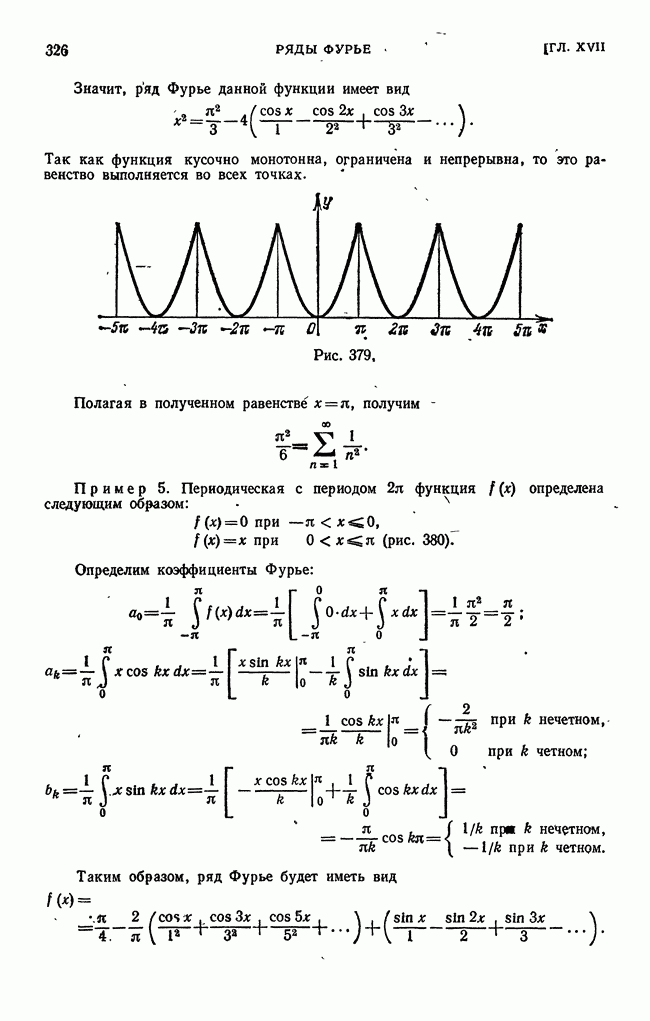
Представление функции бесконечным рядом (Фурье, Тейлора и т. д.) имеет на практике тот смысл, что конечная сумма, получающаяся при обрывании ряда на  члене, является приближенным выражением разлагаемой функции; это приближенное выражение можно довести до какой угодно степени точности путем выбора достаточно большого значения
члене, является приближенным выражением разлагаемой функции; это приближенное выражение можно довести до какой угодно степени точности путем выбора достаточно большого значения  Однако характер приближенного представления может быть различным.
Однако характер приближенного представления может быть различным.

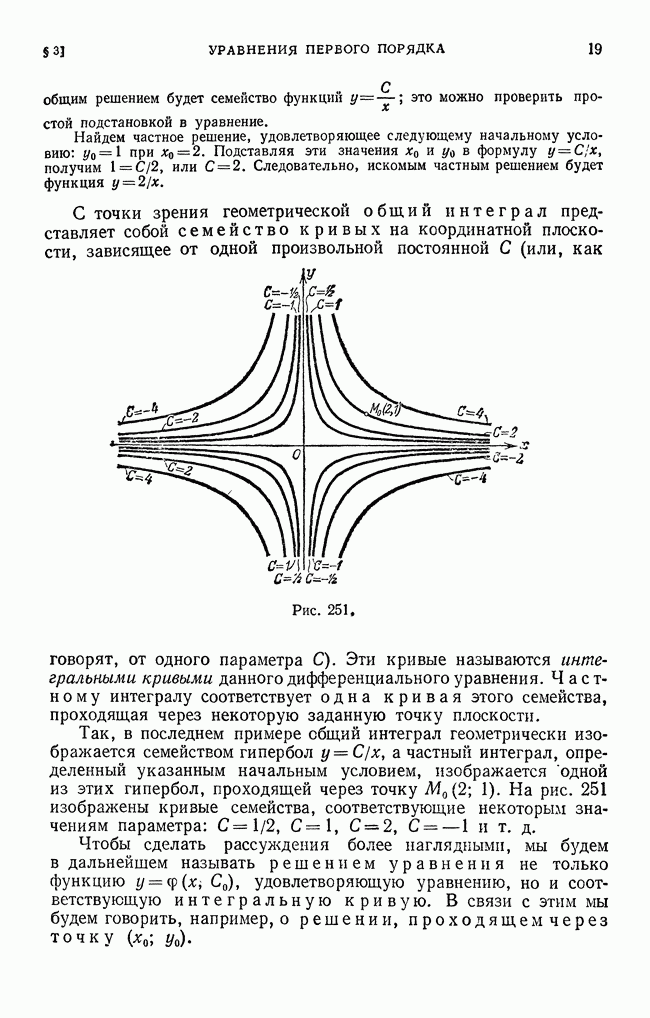
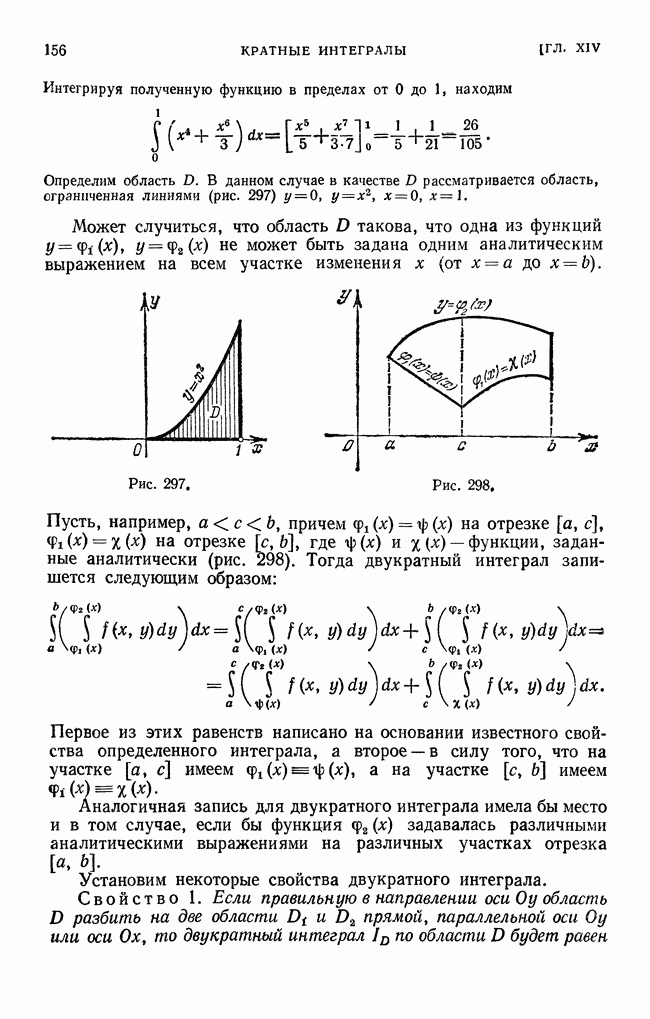
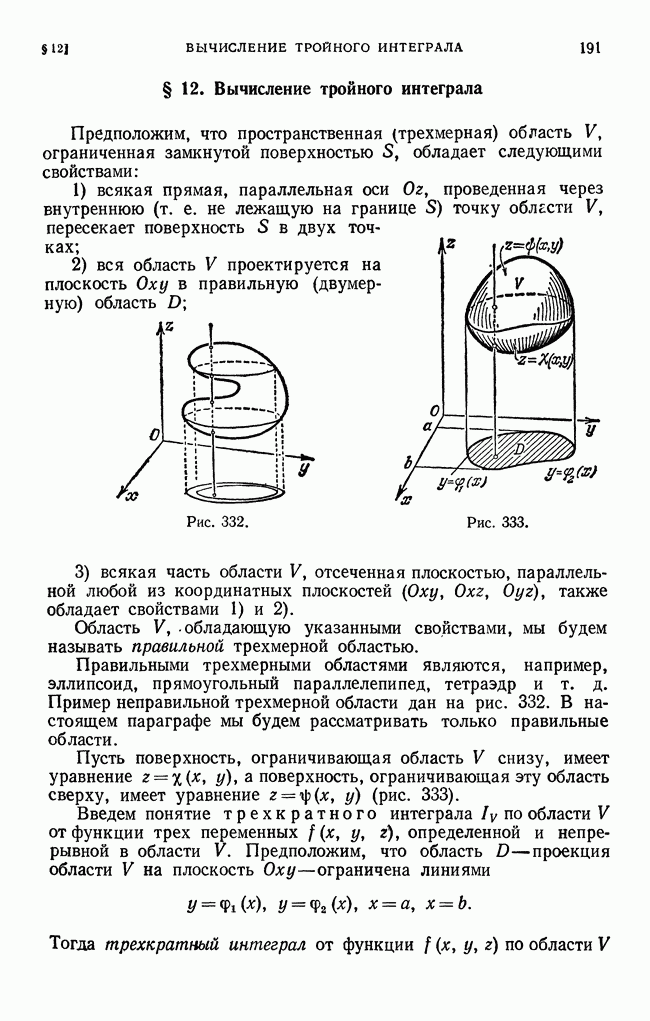
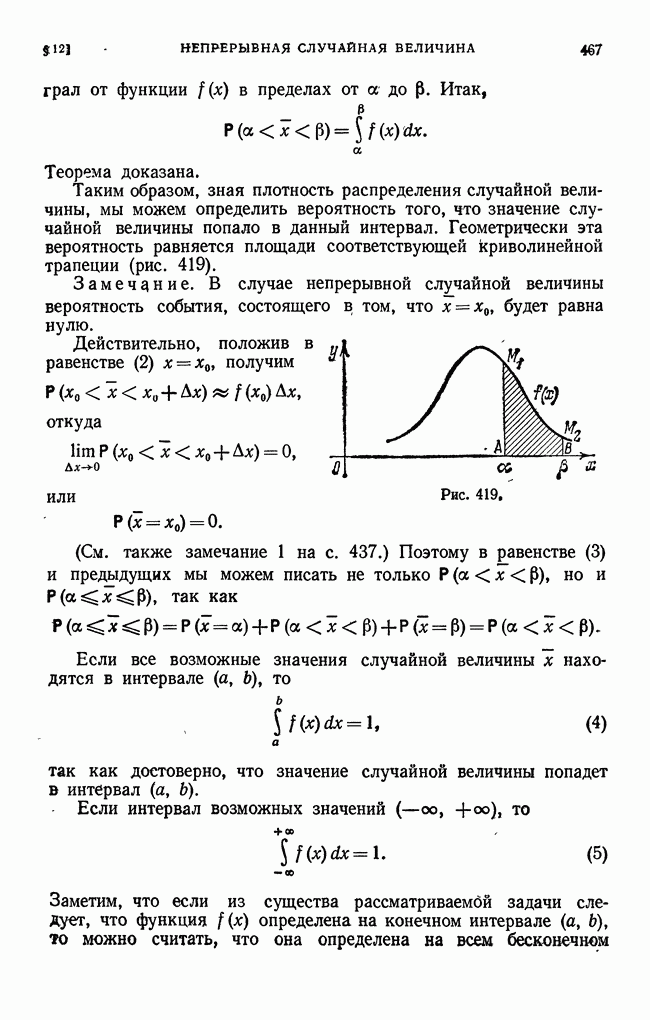
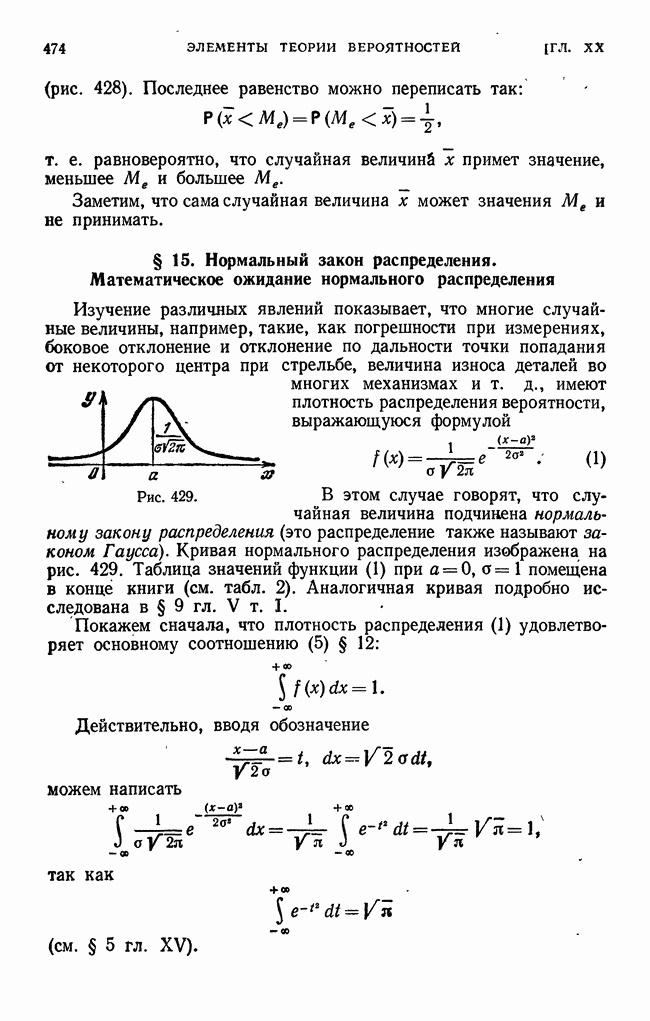
Рис. 387,
Так, например, сумма  первых членов ряда Тейлора
первых членов ряда Тейлора  совпадает с рассматриваемой функцией в одной точке и в этой точке имеет производные до
совпадает с рассматриваемой функцией в одной точке и в этой точке имеет производные до  порядка, совпадающие с производными рассматриваемой функции. Многочлен Лагранжа
порядка, совпадающие с производными рассматриваемой функции. Многочлен Лагранжа  степени (см. § 9 гл. VII, т. I) совпадает с рассматриваемой функцией в
степени (см. § 9 гл. VII, т. I) совпадает с рассматриваемой функцией в  точках.
точках.
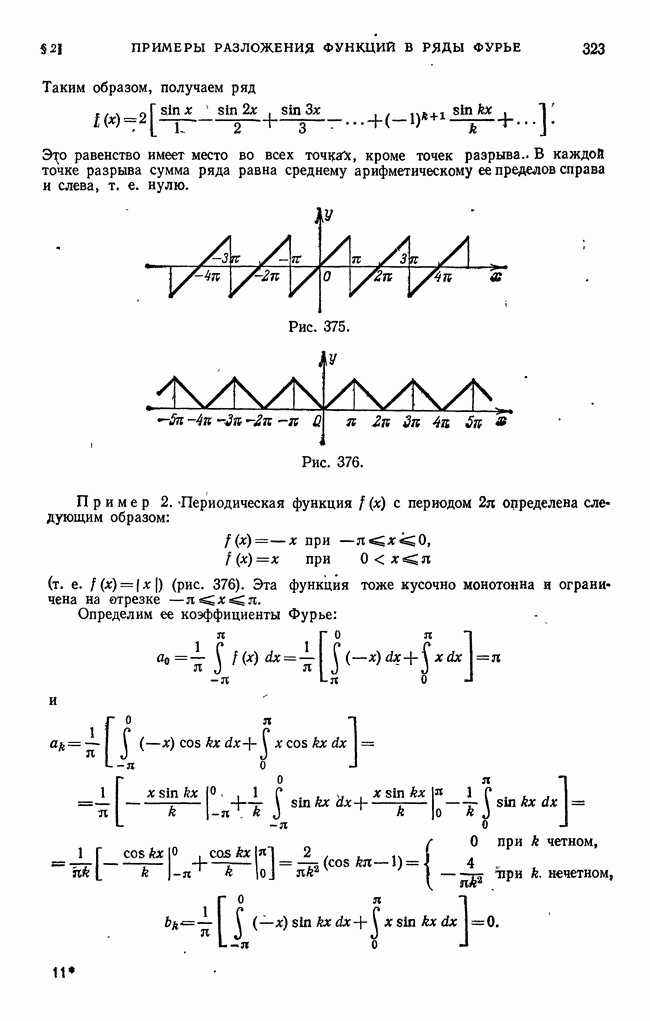
Посмотрим, какой характер имеет приближенное представление периодической функции f(x) тригонометрическими многочленами вида

где  — коэффициенты Фурье, т. е. суммой
— коэффициенты Фурье, т. е. суммой  первых членов ряда Фурье. Сделаем сначала несколько замечаний.
первых членов ряда Фурье. Сделаем сначала несколько замечаний.
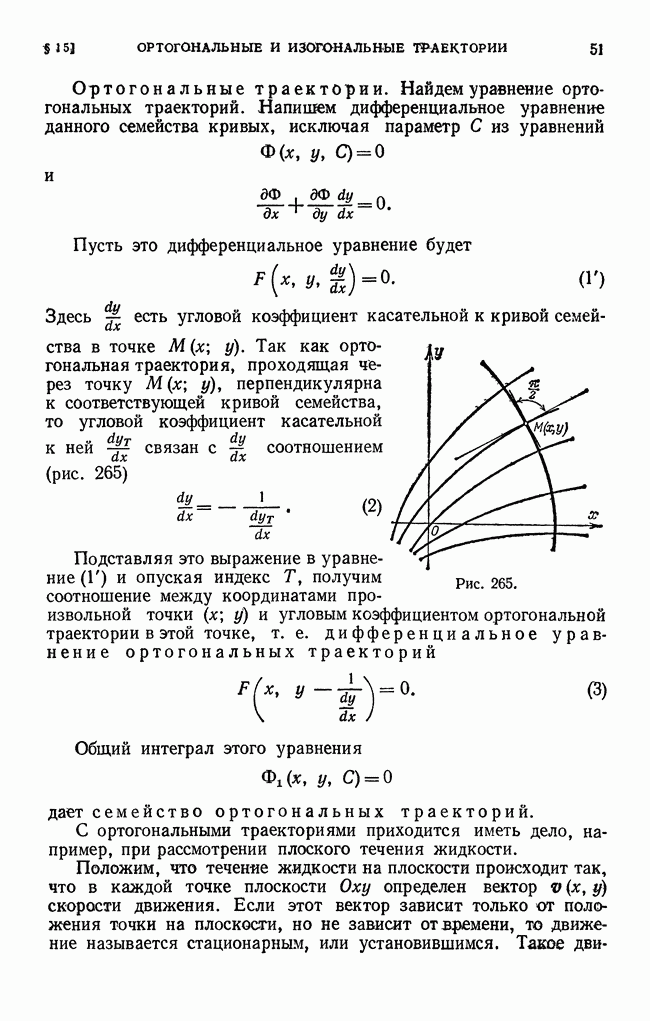
Допустим, что мы рассматриваем некоторую функцию  на отрезке
на отрезке  и хотим оценить погрешность при замене этой функции другой функцией
и хотим оценить погрешность при замене этой функции другой функцией  . Можно за меру погрешности взять
. Можно за меру погрешности взять  на отрезке
на отрезке  , т. е. так называемое наибольшее уклонение функции
, т. е. так называемое наибольшее уклонение функции  от
от  Но иногда естественнее за меру погрешности брать так называемое среднеквадратичное уклонение, которое определяется равенством
Но иногда естественнее за меру погрешности брать так называемое среднеквадратичное уклонение, которое определяется равенством

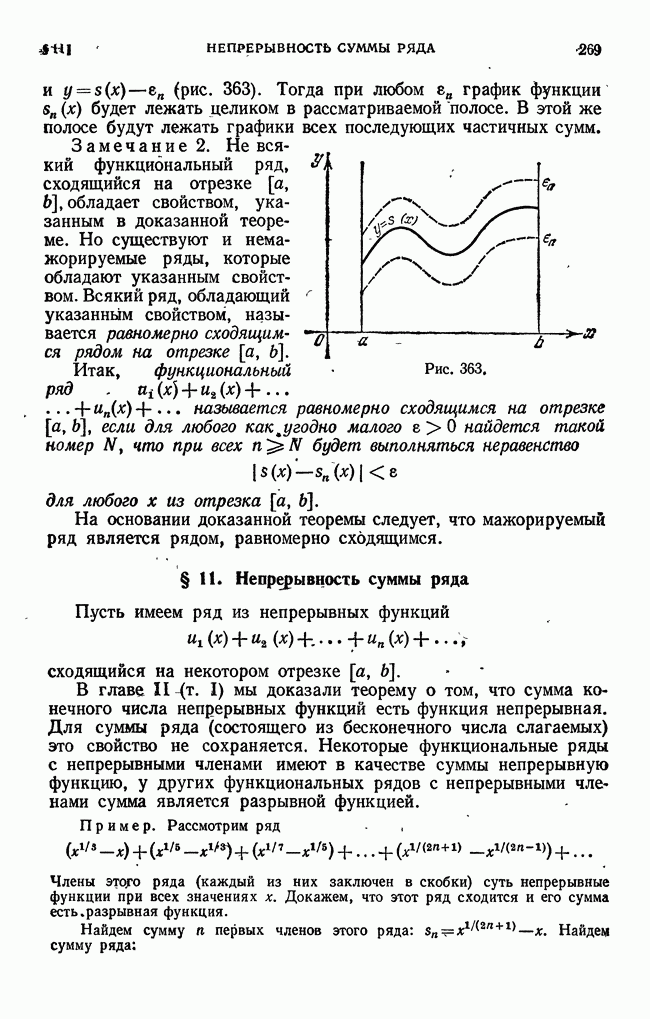
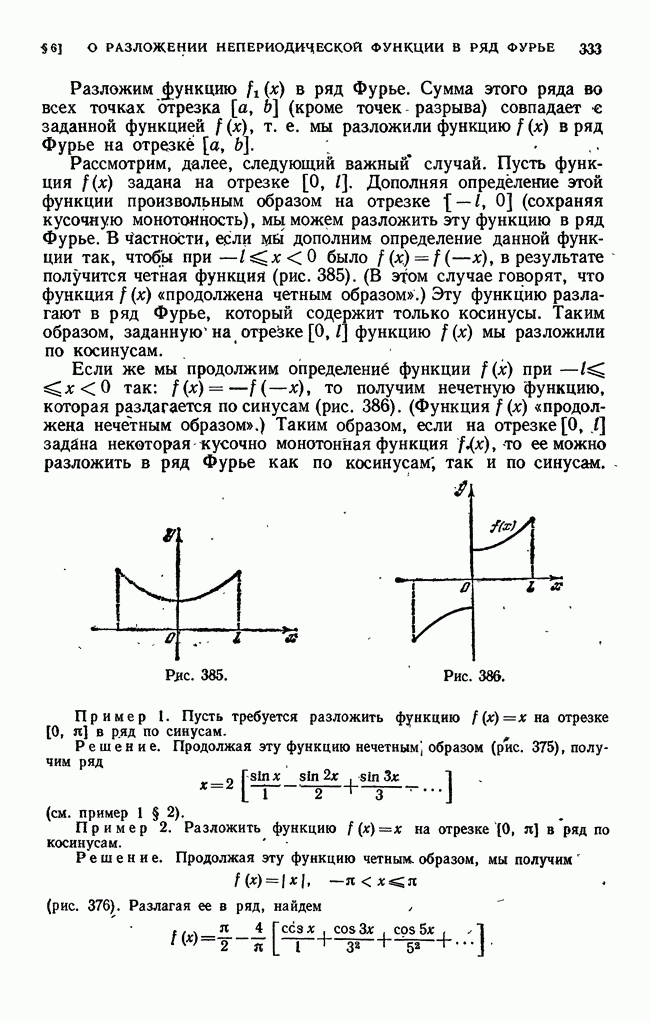
Поясним на рис. 387 различие между среднеквадратйчным уклонением и наибольшим уклонением.
Пусть сплошная линия изображает функцию  пунктирные линии изображают приближения
пунктирные линии изображают приближения  Наибольшее уклонение кривой
Наибольшее уклонение кривой  меньше, чем кривой
меньше, чем кривой  но среднеквадратичное уклонение первой кривой больше, чем второй, так как кривая
но среднеквадратичное уклонение первой кривой больше, чем второй, так как кривая  значительно отличается от кривой
значительно отличается от кривой  только на узком участке и поэтому лучше характеризует кривую
только на узком участке и поэтому лучше характеризует кривую  чем первая.
чем первая.
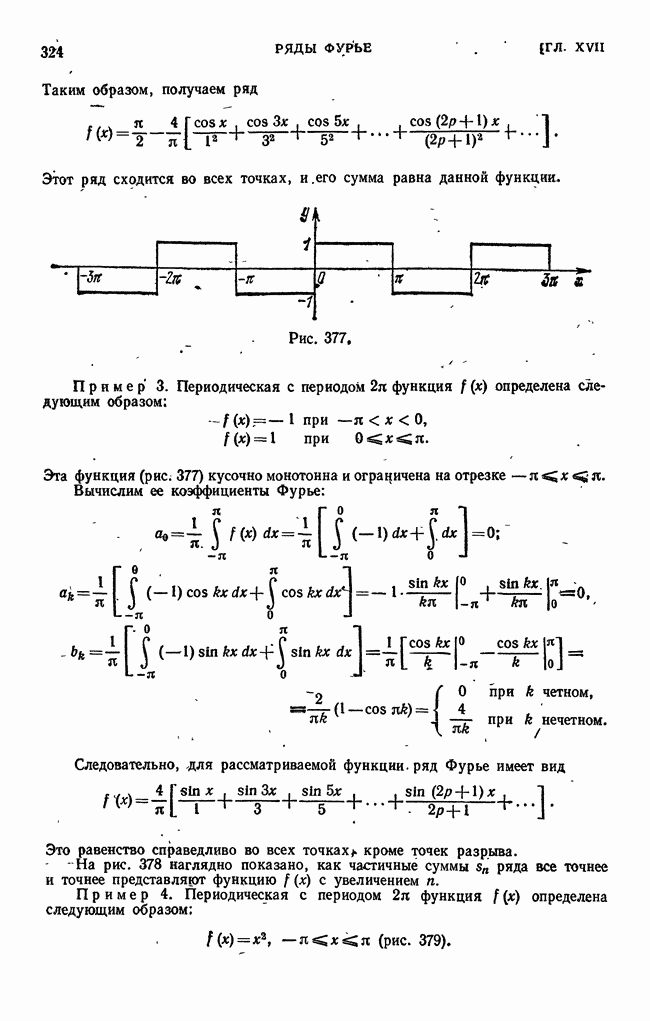
Вернемся теперь к нашей задаче.
Пусть дана периодическая с периодом  функция
функция  Среди всех тригонометрических многочленов
Среди всех тригонометрических многочленов  порядка
порядка

требуется найти путем выбора коэффициентов  тот многочлен, для которого среднеквадратичное уклонение, определяемое равенством
тот многочлен, для которого среднеквадратичное уклонение, определяемое равенством

имеет наименьшее значение.
Задача сводится к Нахождению минимума функции  переменных
переменных  .
.
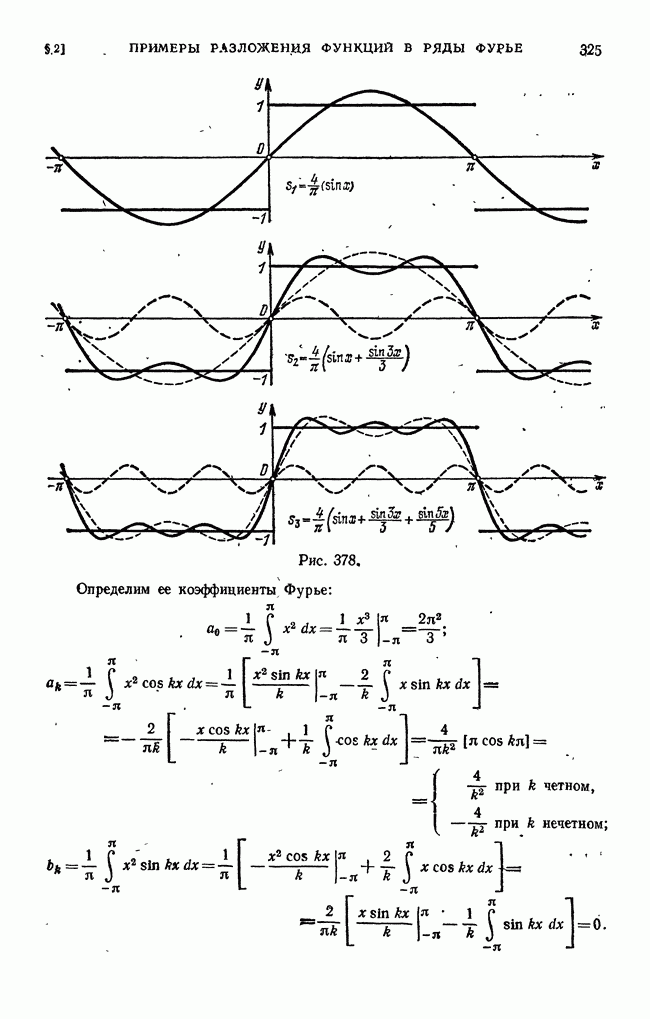
Развернув квадрат, стоящий под знаком интеграла, и интегрируя почленно, получим

Заметим, что

- коэффициенты Фурье функции f(x).
Далее, на основании формул (I) и (II) § 1 имеем: при 

при любых 

и при 

Таким образом, получаем

Прибавляя и вычитая сумму

будем иметь

Первые три слагаемых этой суммы не зависят от выбора коэффициентов  Остальные слагаемые
Остальные слагаемые

неотрицательны. Их сумма достигает наименьшего значения (равного нулю), если положить 
При таком выборе коэффициентов  тригонометрический многочлен
тригонометрический многочлен

будет меньше всего отличаться от функции  том смысле, что среднеквадратичное уклонение будет наименьшим.
том смысле, что среднеквадратичное уклонение будет наименьшим.
Таким образом, мы доказали теорему:
Среди всех тригонометрических многочленов порядка  наименьшее среднеквадратичной уклонение от функции f(x) имеет тот многочлен, коэффициенты которого суть коэффициенты Фурье функции
наименьшее среднеквадратичной уклонение от функции f(x) имеет тот многочлен, коэффициенты которого суть коэффициенты Фурье функции 
Величина наименьшего среднеквадратичного уклонения равна

Так как то при любом  имеем
имеем

Следовательно, ряд, стоящий справа, при  сходится, и мы. можем написать
сходится, и мы. можем написать 

Это соотношение называется неравенством Бесселя.
Отметим без доказательства, что для всякой ограниченной и кусочно монотонной функции среднеквадратичное уклонение, получающееся, при замене данной функции  частичной суммой ряда Фурье, стремится к нулю при
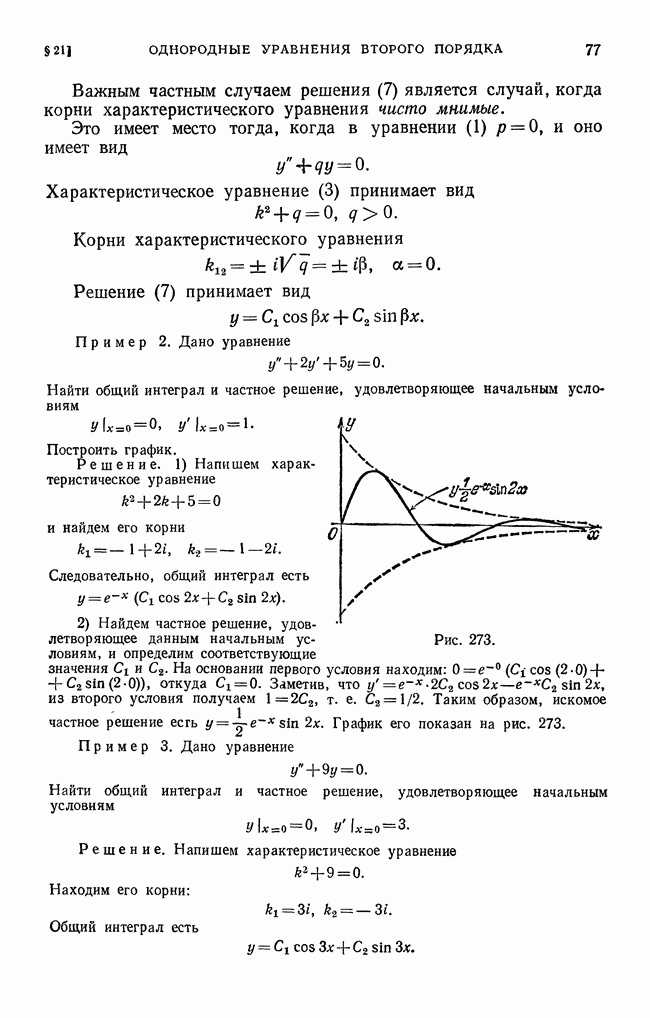
частичной суммой ряда Фурье, стремится к нулю при  при
при  Но тогда из формулы (2) вытекает равенство
Но тогда из формулы (2) вытекает равенство

которое называется равенством Ляпунова—Парсеваля. Заметим, что равенство Ляпунова—Парсеваля доказано для более широкого класса функций, чем тот, который мы здесь рассматриваем.
Из доказанного следует, что для функции, удовлетворяющей равенству Ляпунова (в частности, для всякой ограниченной
кусочно монотонной функции), соответствующий ряд Фурье дает среднеквадратичное уклонение, равное нулю.
Замечание. Установим одно свойство коэффициентов Фурье, нужное для дальнейшего. Введем сначала определение.
Функция f(x) называется кусочно непрерывной на отрезке  если она имеет конечное число точек разрыва первого рода на этом отрезке (или всюду непрерывна).
если она имеет конечное число точек разрыва первого рода на этом отрезке (или всюду непрерывна).
Докажем следующее утверждение.
Если функция f(х) кусочно непрерывна на отрезке  , то ее коэффициенты Фурье стремятся к нулю при
, то ее коэффициенты Фурье стремятся к нулю при  , т. е.
, т. е.

Доказательство. Если функция  кусочно непрерывна на отрезке
кусочно непрерывна на отрезке  , то и функция
, то и функция  также является кусочно непрерывна на этом отрезке. Тогда
также является кусочно непрерывна на этом отрезке. Тогда  существует и является конечным числом. В этом случае из неравенства Бесселя (3) следует, что ряд
существует и является конечным числом. В этом случае из неравенства Бесселя (3) следует, что ряд  сходится. Но если ряд сходится, то его общий член стремится к нулю, т. е. в данном случае
сходится. Но если ряд сходится, то его общий член стремится к нулю, т. е. в данном случае  . Отсюда непосредственно получаются равенства (4). Итак, для кусочно непрерывной и ограниченной функции справедливы равенства
. Отсюда непосредственно получаются равенства (4). Итак, для кусочно непрерывной и ограниченной функции справедливы равенства

Если функция  периодична с периодом
периодична с периодом  , то последние равенства можно переписать следующим образом (для любого а):
, то последние равенства можно переписать следующим образом (для любого а):

Заметим, что эти равенства остаются в силе, если в интегралах взять какой угодно промежуток интегрирования  т. е. интегралы
т. е. интегралы  стремятся к нулю при неограниченном возрастании
стремятся к нулю при неограниченном возрастании  , если
, если  ограниченная и кусочно непрерывная функция.
ограниченная и кусочно непрерывная функция.
Действительно, считая для определенности  рассмотрим вспомогательную функцию
рассмотрим вспомогательную функцию  периодом
периодом  определенную
определенную
следующим образом:

Тогда

Так как  есть ограниченная и кусочно непрерывная функция, то интегралы, стоящие справа, стремятся к нулю, при
есть ограниченная и кусочно непрерывная функция, то интегралы, стоящие справа, стремятся к нулю, при  Следовательно, стремятся к нулю, и интегралы, стоящие слева. Таким образом, утверждение доказано, т. е.
Следовательно, стремятся к нулю, и интегралы, стоящие слева. Таким образом, утверждение доказано, т. е.

для любых чисел  и любой кусочно непрерывной и ограниченной на
и любой кусочно непрерывной и ограниченной на  функции
функции 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА XIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. Постановка задачи. Уравнение движения тела при сопротивлении среды, пропорциональном скорости. Уравнение цепной линии
- § 2. Определения
- § 3. Дифференциальные уравнения первого порядка (общие понятия)
- § 4. Уравнения с разделенными и разделяющимися переменными. Задача о распаде радия
- § 5. Однородные уравнения первого порядка
- § 6. Уравнения, приводящиеся к однородным
- § 7. Линейные уравнения первого порядка
- § 8. Уравнение Бернулли
- § 9. Уравнение в полных дифференциалах
- § 10. Интегрирующий множитель
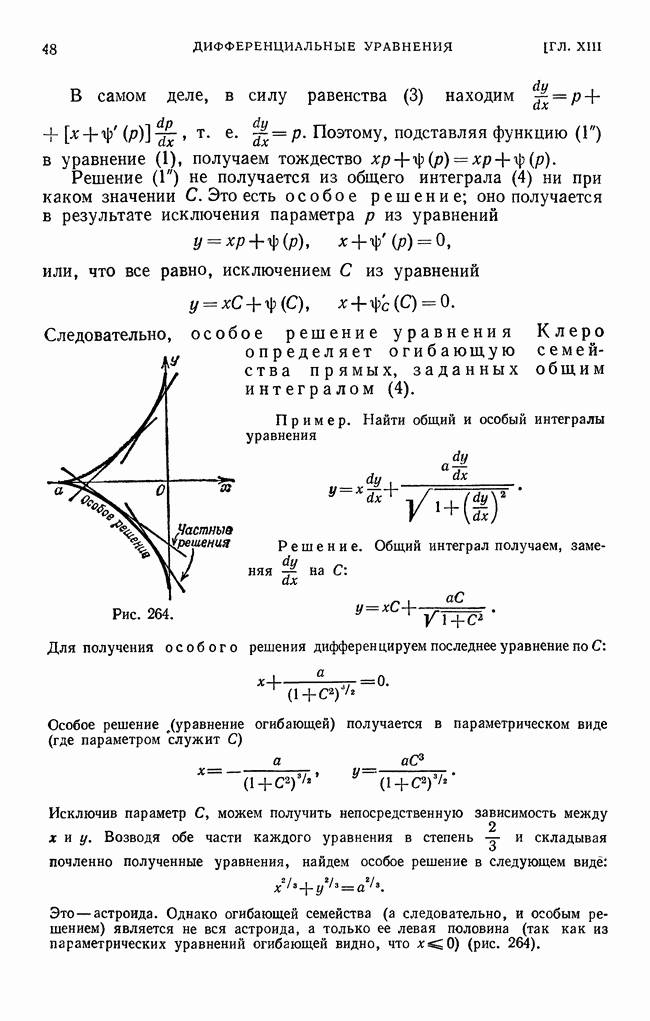
- § 11. Огибающая семейства кривых
- § 12. Особые решения дифференциального уравнения первого порядка
- § 13. Уравнение Клеро
- § 14. Уравнение Лагранжа
- § 15. Ортогональные и изогональные траектории
- § 16. Дифференциальные уравнения высших порядков (общие понятия)
- § 17. Уравнение вида y^(n) = f(x)
- § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости
- § 19. Графический метод интегрирования дифференциального уравнения второго порядка
- § 20. Линейные однородные уравнения. Определения и общие свойства
- § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- § 23. Неоднородные линейные уравнения второго порядка
- § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- § 25. Неоднородные линейные уравнения высших порядков
- § 26. Дифференциальное уравнение механических колебаний
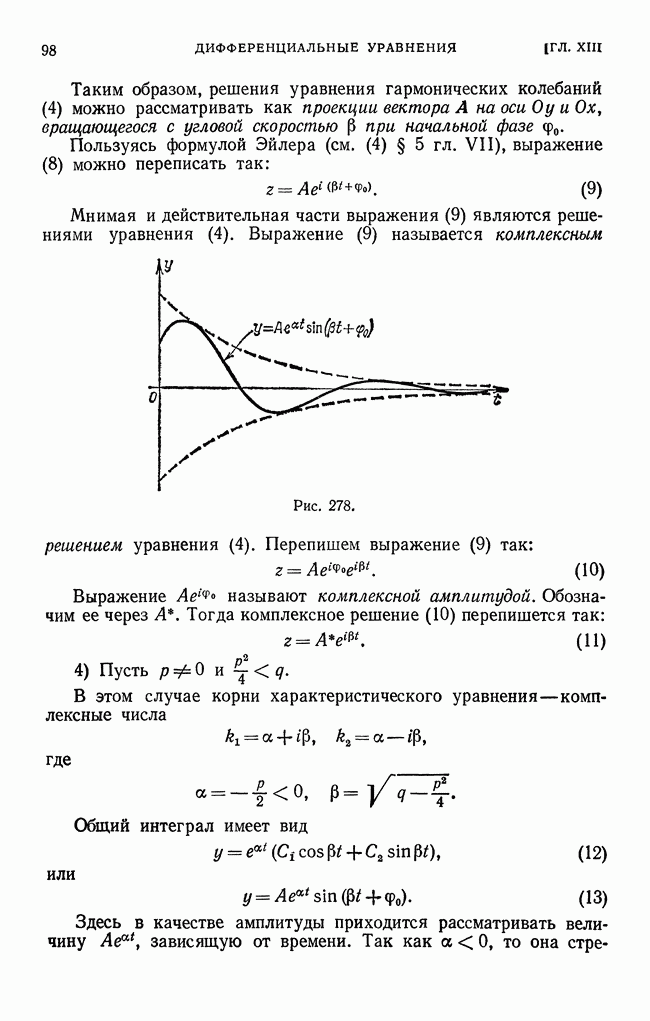
- § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний
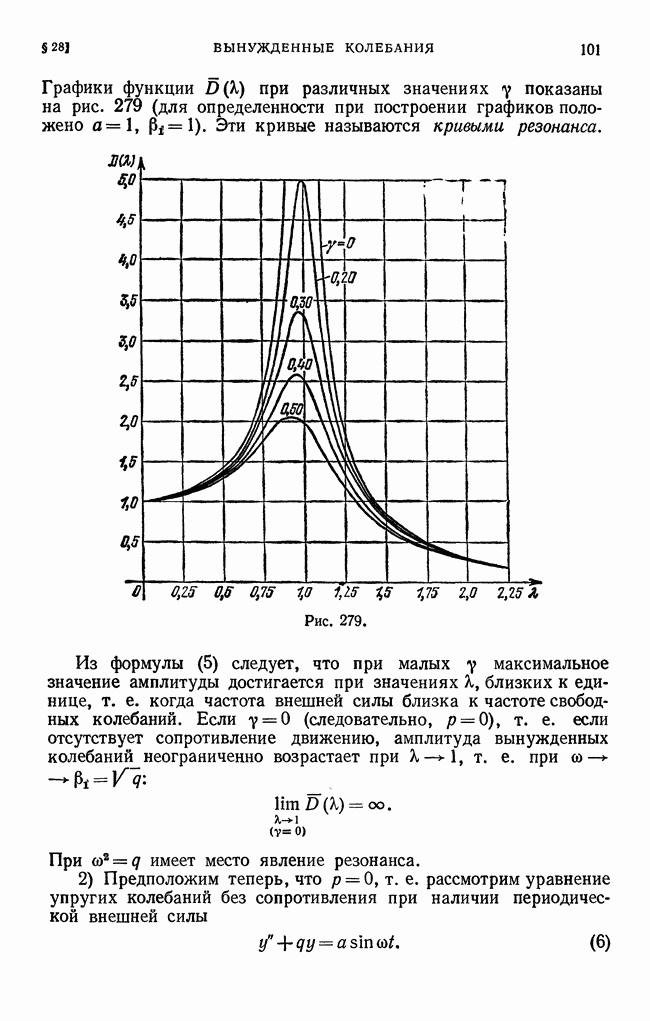
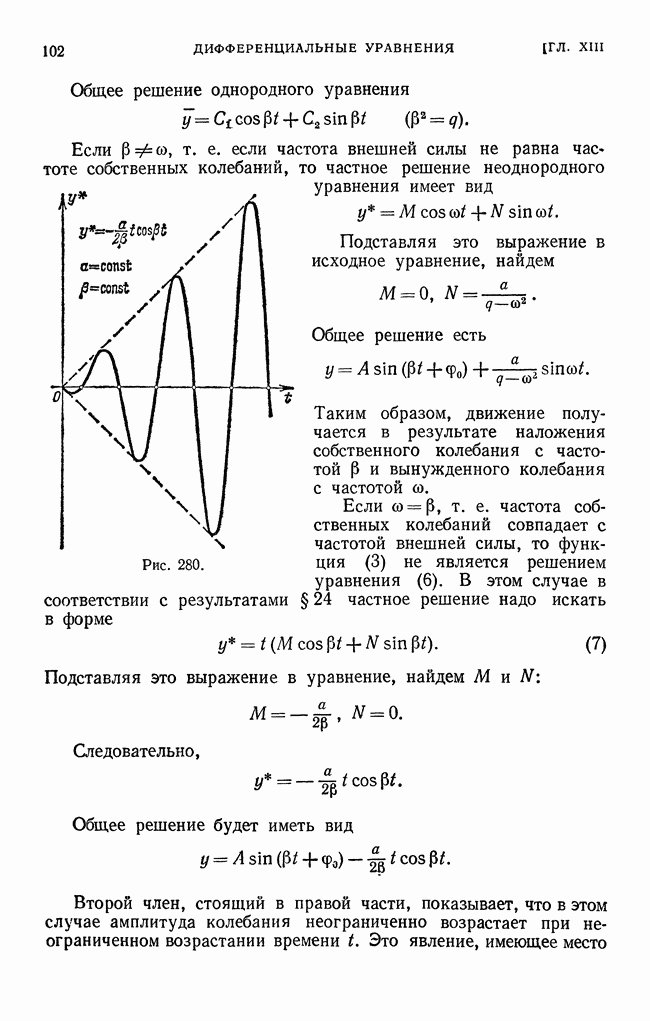
- § 28. Вынужденные колебания
- § 29. Системы обыкновенных дифференциальных уравнений
- § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
- § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса
- § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка
- Упражнения к главе XIII
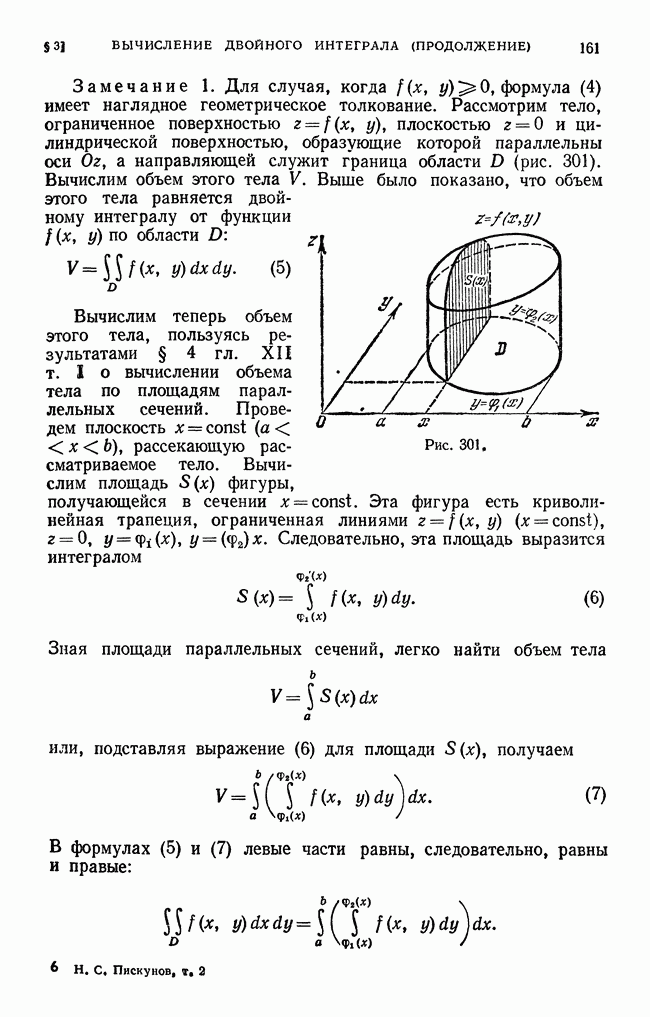
- ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ
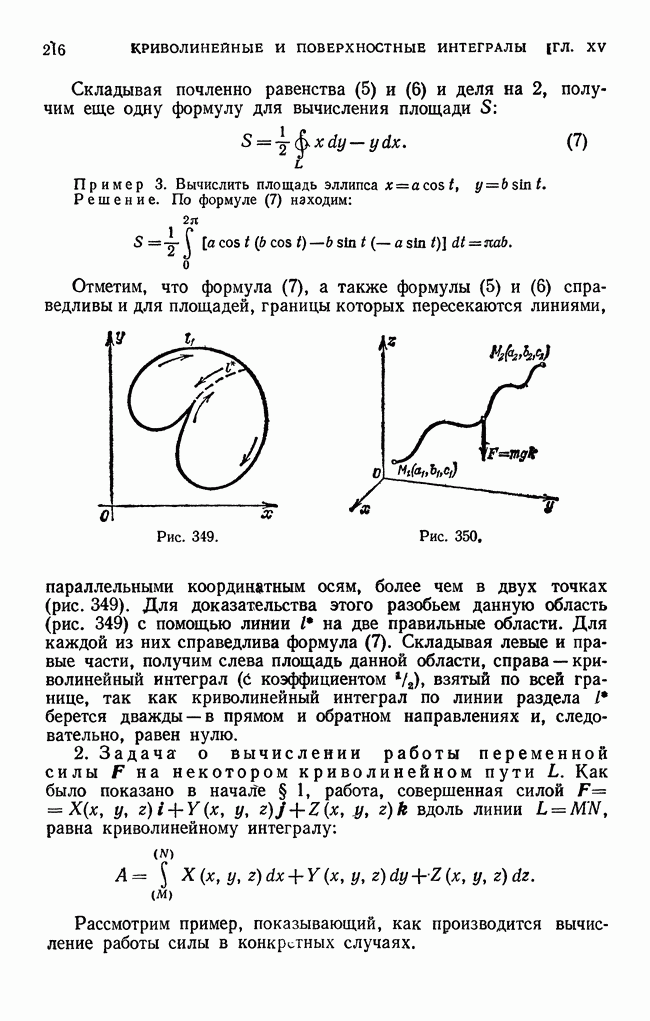
- § 2. Вычисление двойного интеграла
- § 3. Вычисление двойного интеграла (продолжение)
- § 4. Вычисление площадей и объемов с помощью двойных интегралов
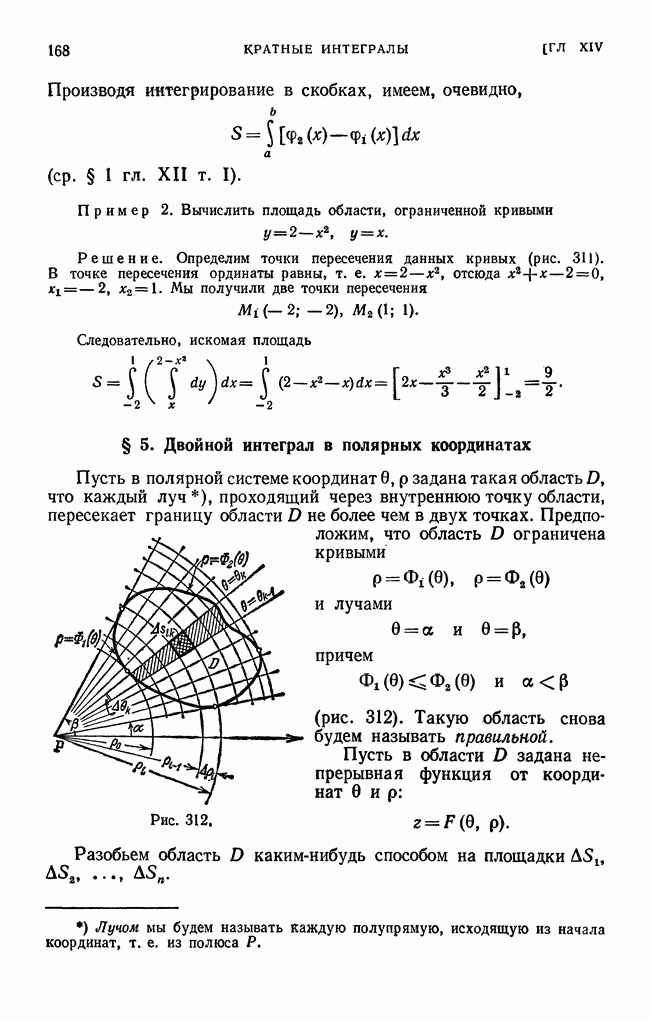
- § 5. Двойной интеграл в полярных координатах
- § 6. Замена переменных в двойном интеграле (общий случай)
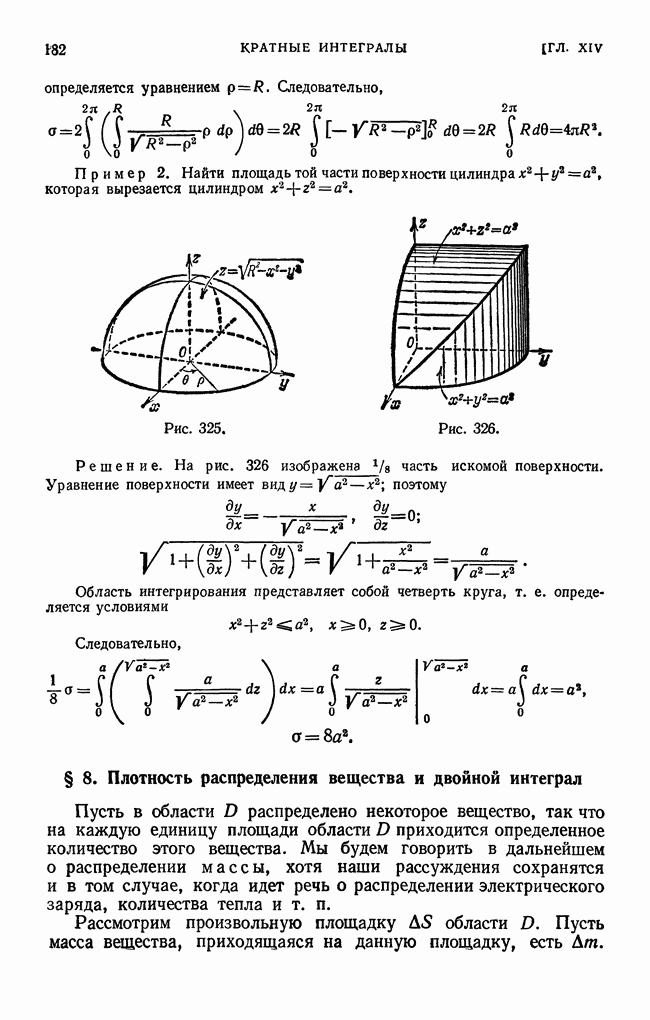
- § 7. Вычисление площади поверхности
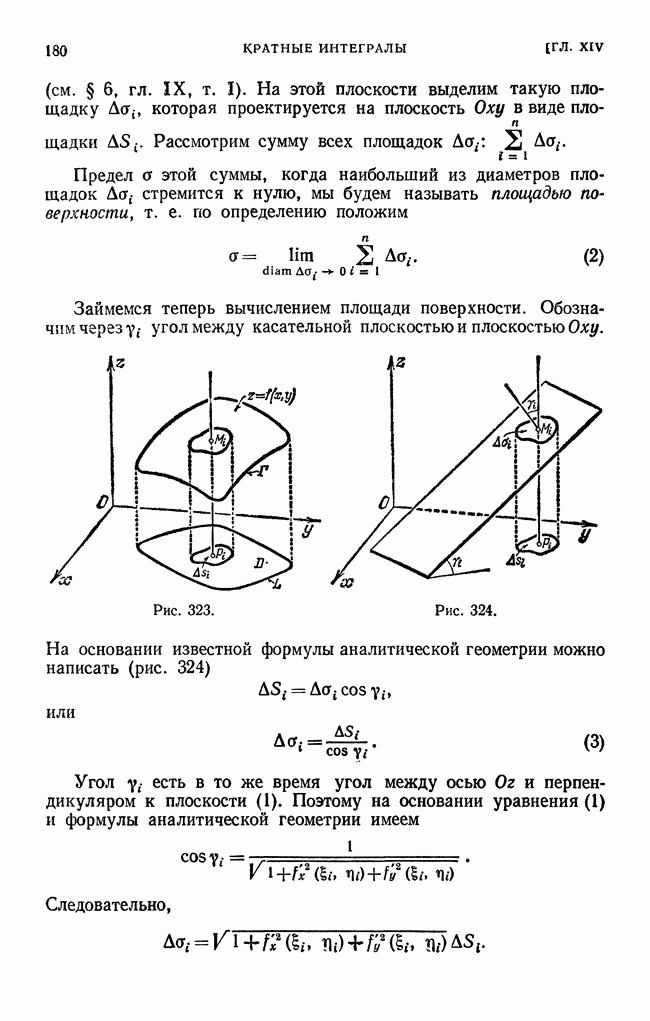
- § 9. Момент инерции площади плоской фигуры
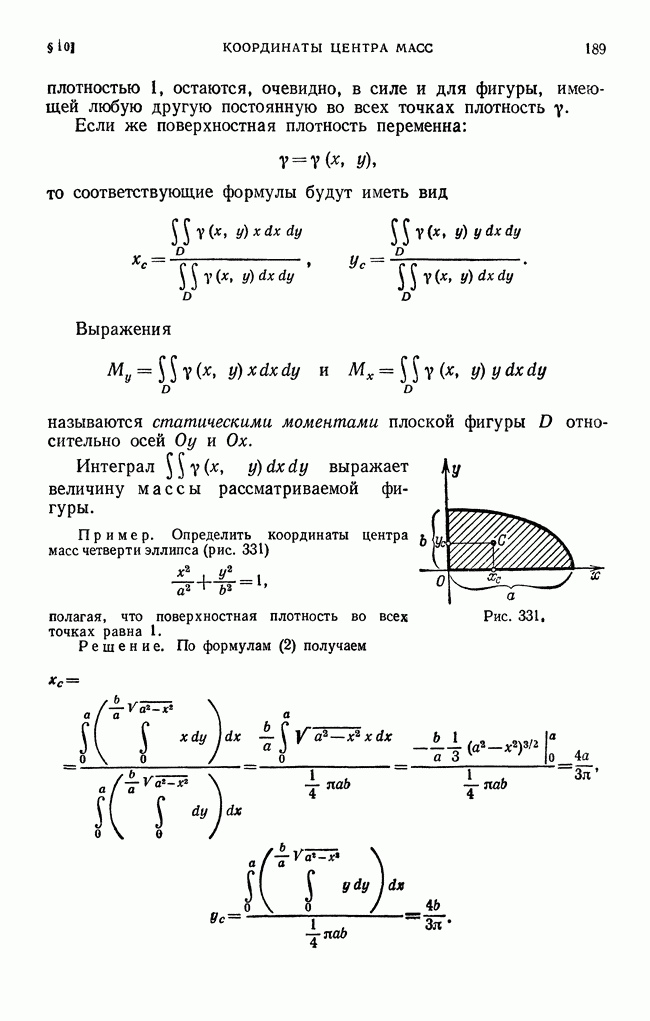
- § 10. Координаты центра масс площади плоской фигуры
- § 11. Тройной интеграл
- § 12. Вычисление тройного интеграла
- § 13. Замена переменных в тройном интеграле
- § 14. Момент инерции и координаты центра масс тела
- § 15. Вычисление интегралов, зависящих от параметра
- Упражнения к главе XIV
- ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
- § 2. Вычисление криволинейного интеграла
- § 3. Формула Грина
- § 4. Условия независимости криволинейного интеграла от пути интегрирования
- § 5. Поверхностный интеграл
- § 6. Вычисление поверхностного интеграла
- § 7. Формула Стокса
- § 9. Оператор Гамильтона. Некоторые его применения
- Упражнения к главе XV
- ГЛАВА XVI. РЯДЫ
- § 1. Ряд. Сумма ряда
- § 2. Необходимый признак сходимости ряда
- § 3. Сравнение рядов с положительными членами
- § 4. Признак Даламбера
- § 5. Признак Коши
- § 6. Интегральный признак сходимости ряда
- § 7. Знакочередующиеся ряды. Теорема Лейбница
- § 8. Знакопеременные ряды. Абсолютная и условная сходимость
- § 9. Функциональные ряды
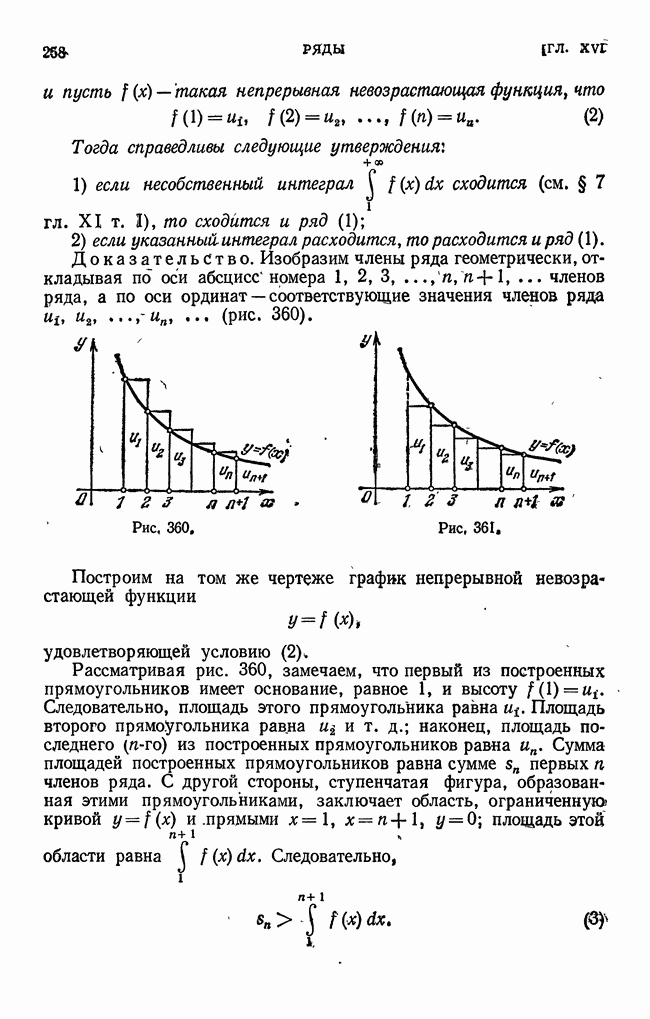
- § 10. Мажорируемые ряды
- § 11. Непрерывность суммы ряда
- § 12. Интегрирование и дифференцирование рядов
- § 13. Степенные ряды. Интервал сходимости
- § 14. Дифференцирование степенных рядов
- § 15. Ряды по степеням x-a
- § 16. Ряды Тейлора и Маклорена
- § 17. Примеры разложения функций в ряды
- § 18. Формула Эйлера
- § 19. Биномиальный ряд
- § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов
- § 21. Вычисление определенных интегралов с помощью рядов
- § 22. Интегрирование дифференциальных уравнений с помощью рядов
- § 23. Уравнение Бесселя
- § 24. Ряды с комплексными членами
- § 25. Степенные ряды с комплексной переменной
- § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций)
- § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении
- § 28. Теорема единственности решения дифференциального уравнения
- Упражнения к главе XVI
- ГЛАВА XVII. РЯДЫ ФУРЬЕ
- § 2. Примеры разложения функций в ряды Фурье
- § 3. Одно, замечание о разложении периодической функции в ряд Фурье
- § 4. Ряды Фурье для четных и нечетных функций
- § 5. Ряд Фурье для функции с периодом 2l
- § 6. О разложении непериодической функции в ряд Фурье
- § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена
- § 8. Интеграл Дирихле
- § 9. Сходимость ряда Фурье в данной точке
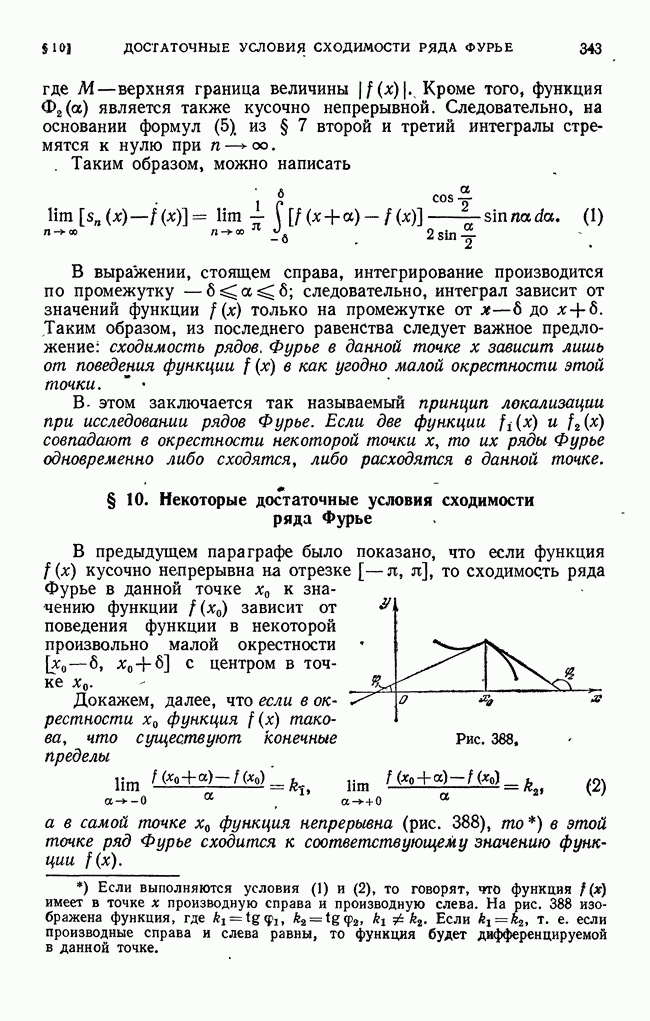
- § 10. Некоторые достаточные условия сходимости ряда Фурье
- § 11. Практический гармонический анализ
- § 12. Ряд Фурье в комплексной форме
- § 13. Интеграл Фурье
- § 14. Интеграл Фурье в комплексной форме
- § 15. Ряд Фурье по ортогональной системе функций
- § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов
- Упражнения к главе XVII
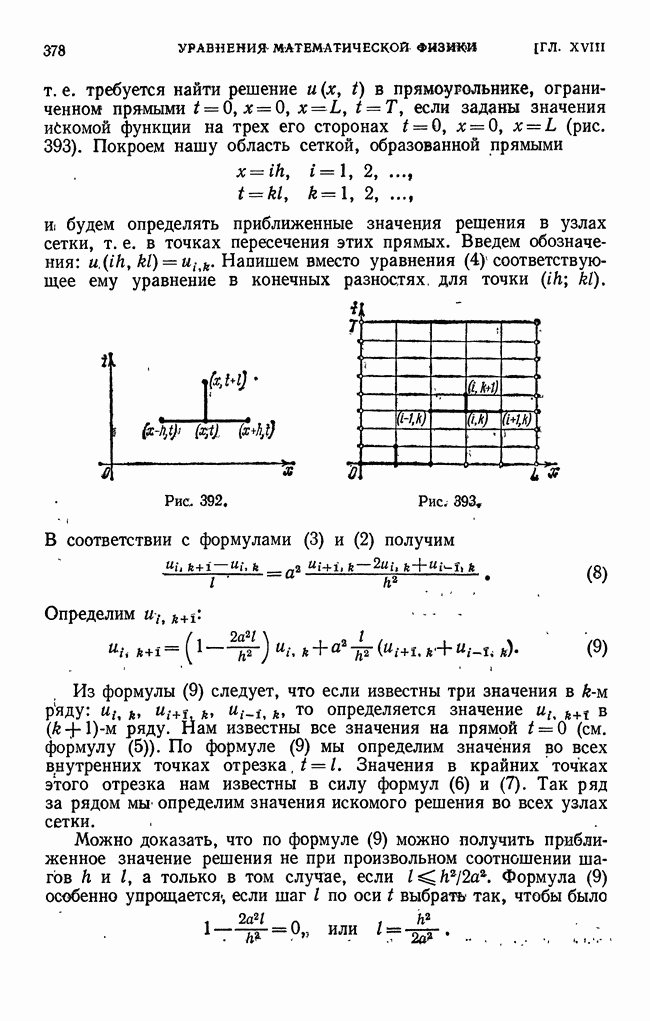
- ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Основные типы уравнений математической физики
- § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах
- § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье)
- § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи
- § 5. Распространение тепла в пространстве
- § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей
- § 7. Распространение тепла в неограниченном стержне
- § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач
- § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях
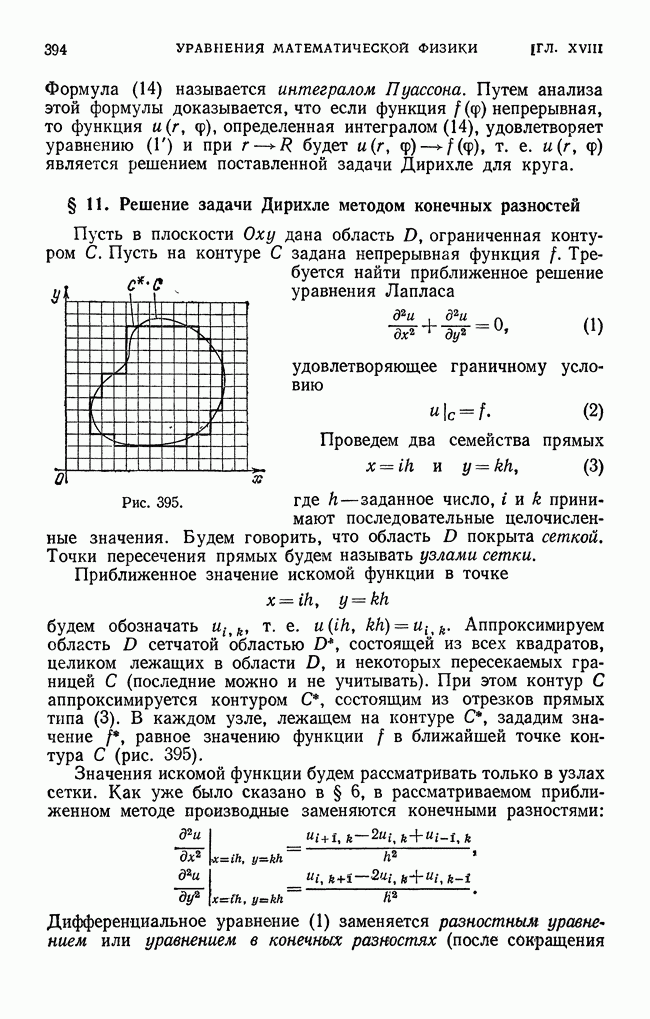
- § 10. Решение задачи Дирихле для круга
- § 11. Решение задачи Дирихле методом конечных разностей
- Упражнения к главе XVIII
- ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ
- § 1. Начальная функция и ее изображение
- § 2. Изображение функций …
- § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at
- § 4. Свойство линейности изображения
- § 5. Теорема смещения
- § 6. Изображение функций …
- § 7. Дифференцирование изображения
- § 8. Изображение производных
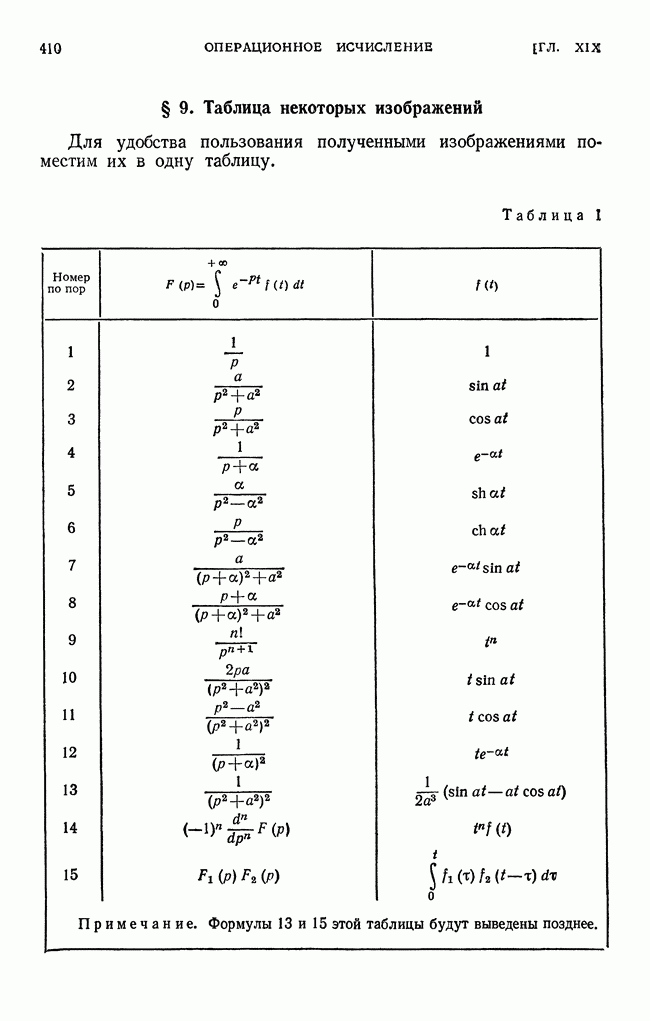
- § 9. Таблица некоторых изображений
- § 10. Вспомогательное уравнение для данного дифференциального уравнения
- § 11. Теорема разложения
- § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом
- § 13. Теорема свертывания
- § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей
- § 15. Решение дифференциального уравнения колебаний
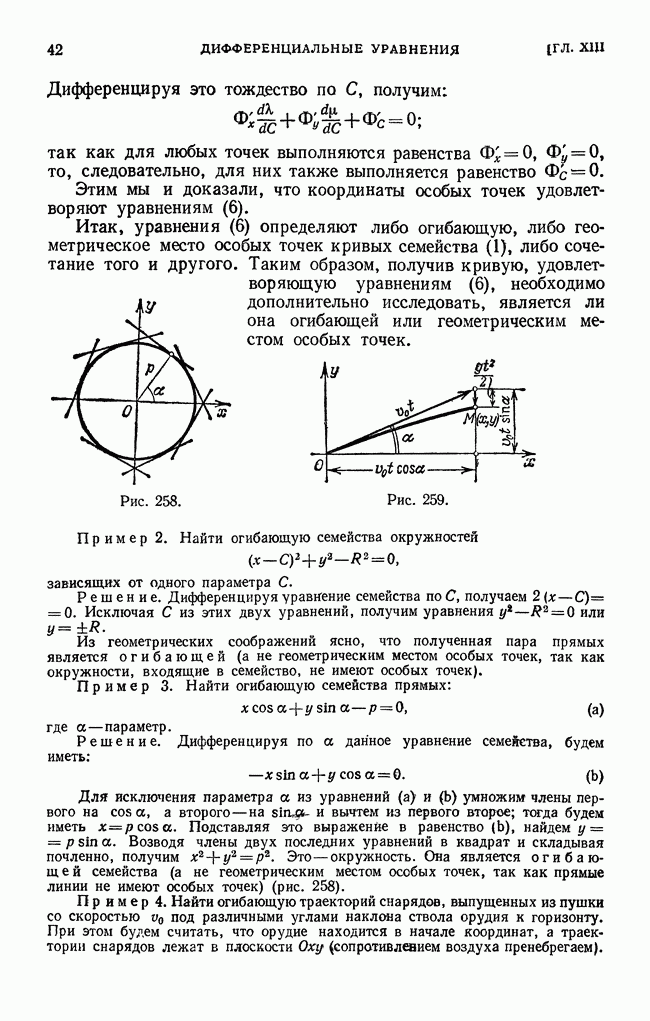
- § 16. Исследование свободных колебаний
- § 17. Исследование механических и электрических колебаний в случае периодической внешней силы
- § 18. Решение уравнения колебаний в случае резонанса
- § 19. Теорема запаздывания
- § 20. Дельта-функция и ее изображение
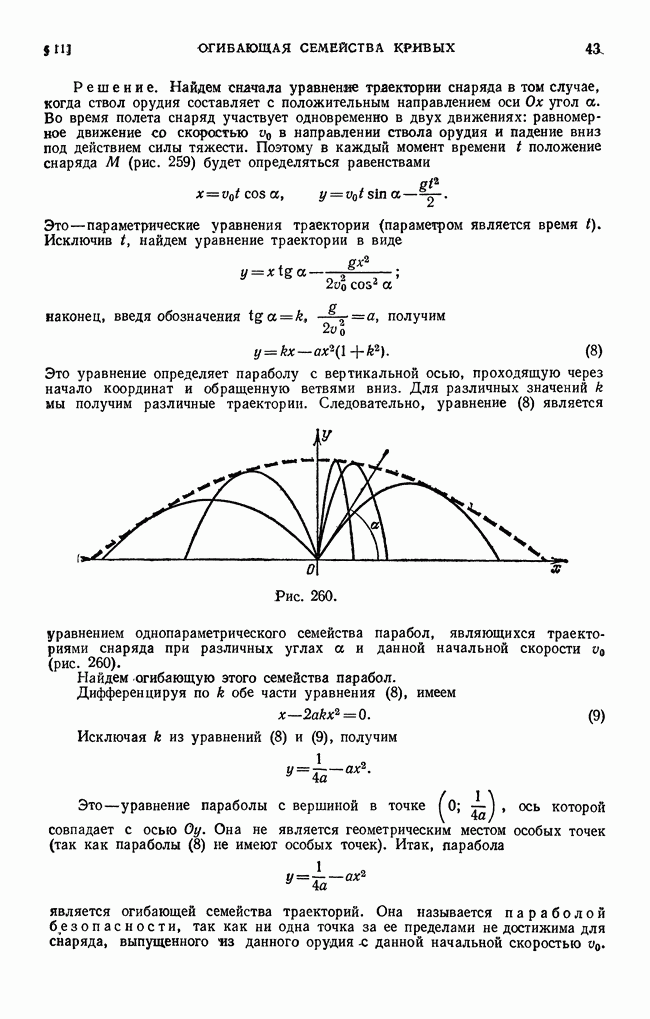
- Упражнения к главе XIX
- ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей
- § 2. Классическое определение вероятности и непосредственный подсчет вероятностей
- § 3. Сложение вероятностей. Противоположные случайные события
- § 4. Умножение вероятностей независимых событий
- § 5. Зависимые события. Условная вероятность. Полная вероятность
- § 6. Вероятность гипотез. Формула Байеса
- § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины
- § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях
- § 9. Математическое ожидание дискретной случайной величины
- § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах
- § 11. Функции от случайных величин
- § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал
- § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей
- § 14. Числовые характеристики непрерывной случайной величины
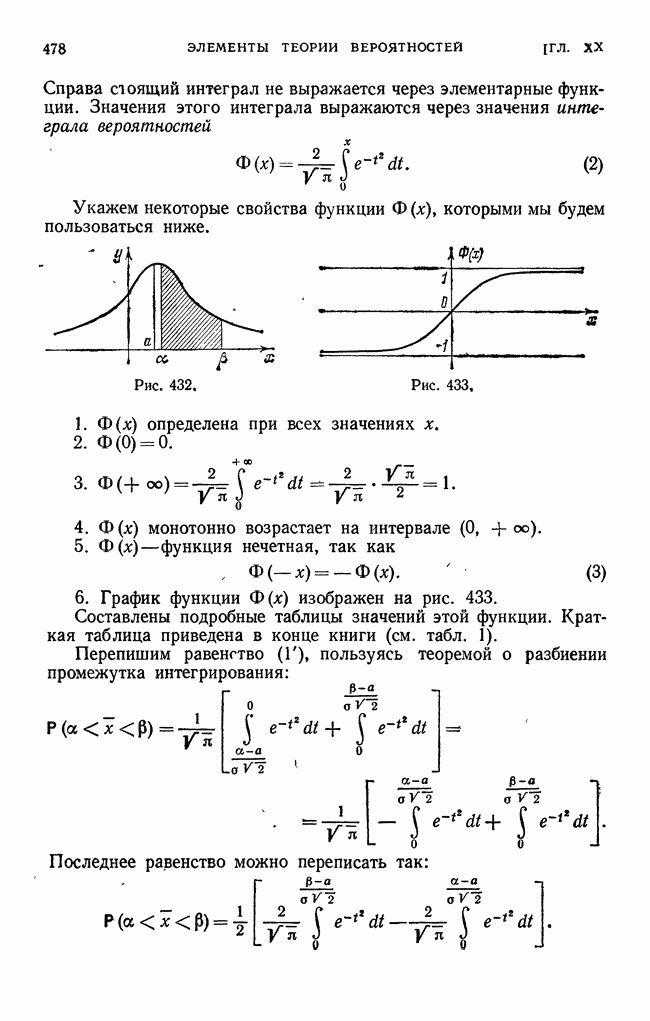
- § 15. Нормальный закон распределения. Математическое ожидание нормального распределения
- § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения
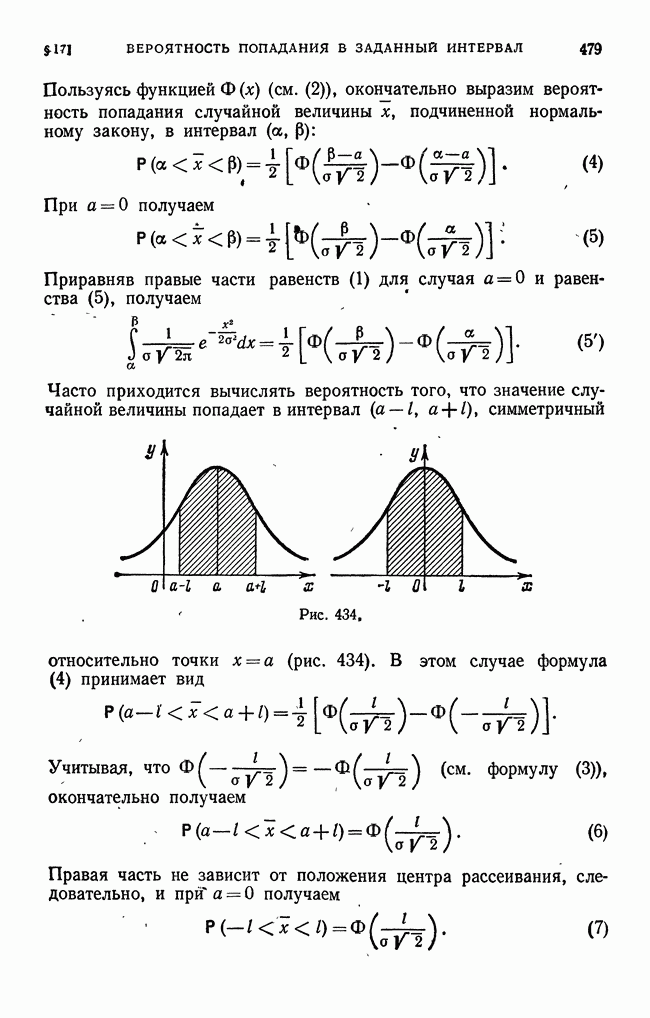
- § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона
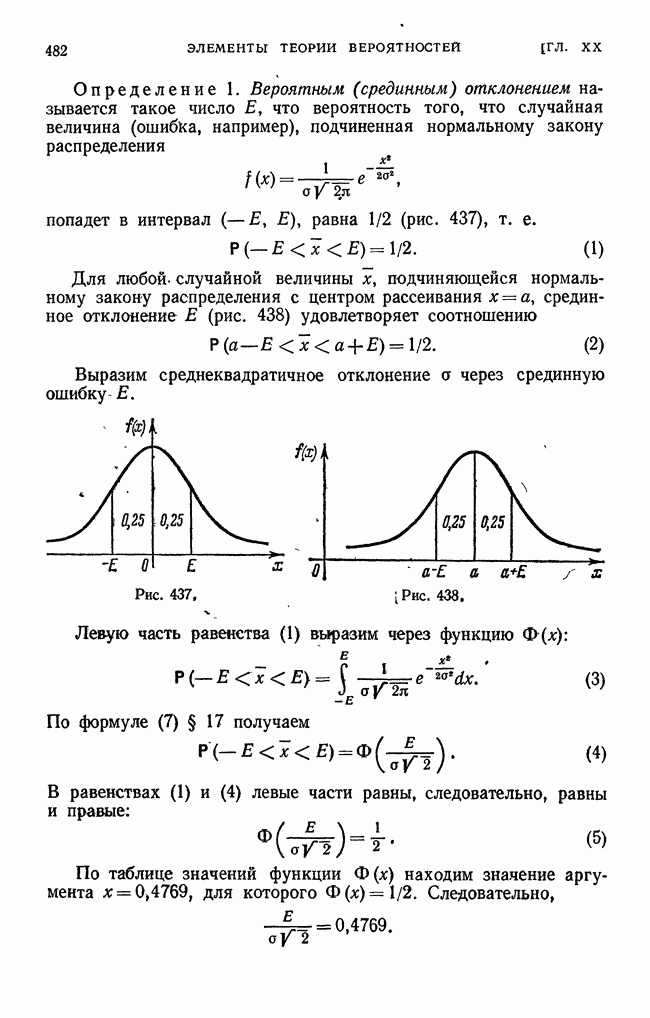
- § 18. Вероятное (срединное) отклонение или срединная ошибка
- § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа
- § 20. Правило трех сигм. Шкала вероятностей распределения ошибок
- § 21. Среднеарифметическая ошибка
- § 22. Мера точности. Соотношение между характеристиками распределения ошибок
- § 23. Двумерная случайная величина
- § 24. Нормальный закон распределения на плоскости
- § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения
- § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания
- § 27. Задачи математической статистики. Статистический материал
- § 28. Статистический ряд. Гистограмма
- § 29. Определение подходящего значения измеряемой величины
- § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа
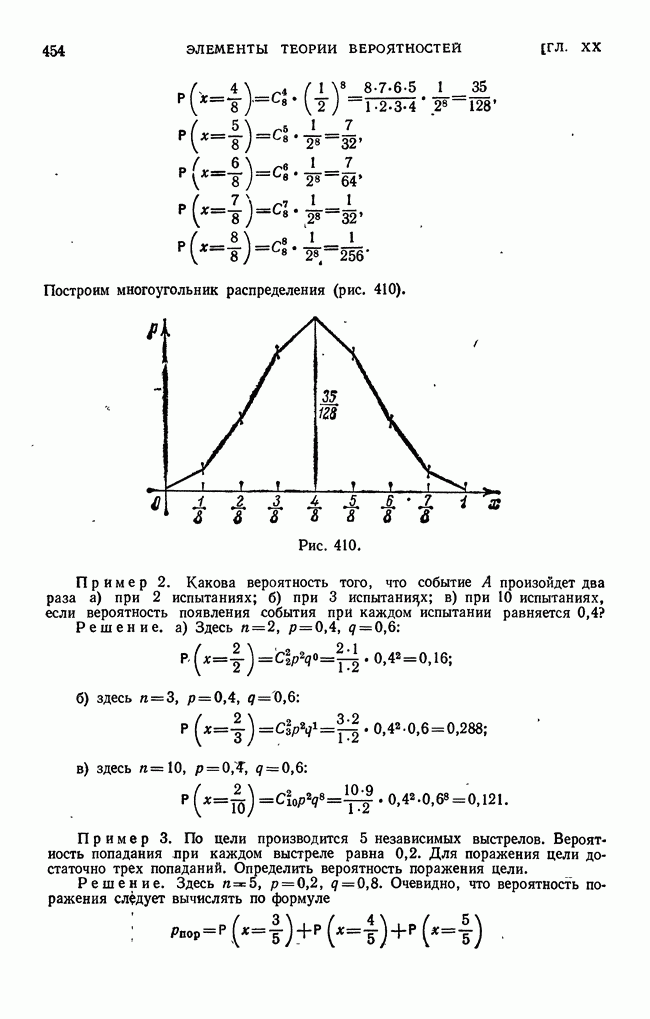
- Упражнения к главе XX
- ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. Линейные преобразования. Матрица
- § 2. Общие определения, связанные с понятием матрицы
- § 3. Обратное преобразование
- § 4. Действия над матрицами. Сложение матриц
- § 5. Преобразование вектора в другой вектор с помощью матрицы
- § 6. Обратная матрица
- § 7. Нахождение матрицы, обратной данной
- § 8. Матричная запись системы линейных уравнений
- § 9. Решение системы линейных уравнений матричным методом
- § 10. Ортогональные отображения. Ортогональные матрицы
- § 11. Собственный вектор линейного преобразования
- § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами
- § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому
- § 14. Квадратичные формы и их преобразования
- § 15. Ранг матрицы. Существование решений системы линейных уравнений
- § 16. Дифференцирование и интегрирование матриц
- § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами
- § 18. Матричная запись линейного уравнения n-го порядка
- § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи
- Упражнения к главе XXI
- ПРИЛОЖЕНИЯ