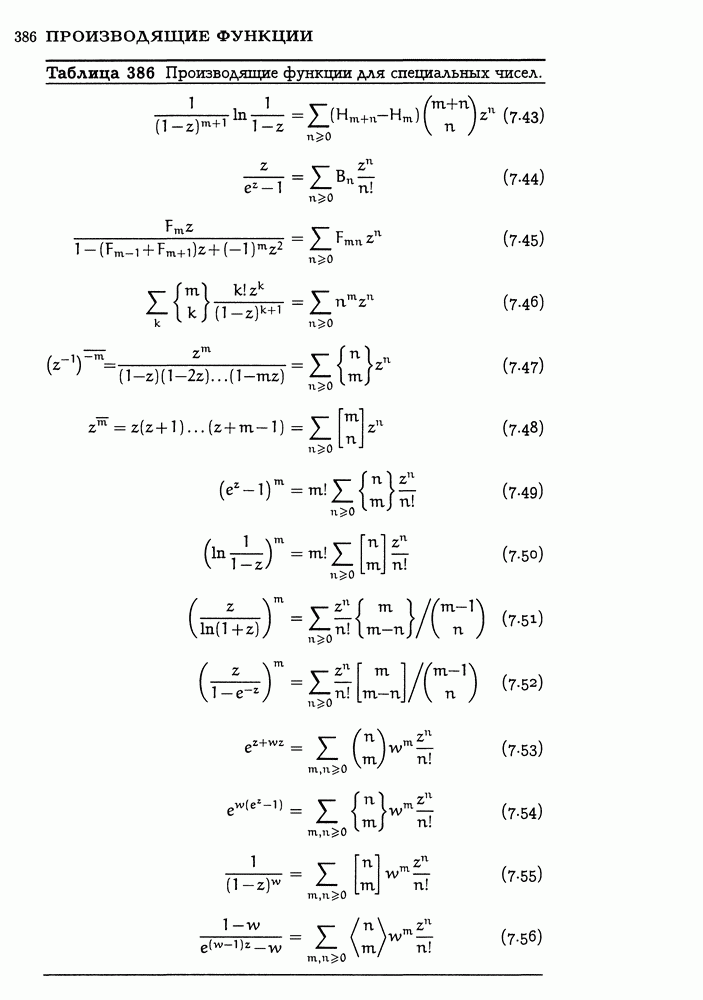2.6. ИСЧИСЛЕНИЕ КОНЕЧНОГО И БЕСКОНЕЧНОГО

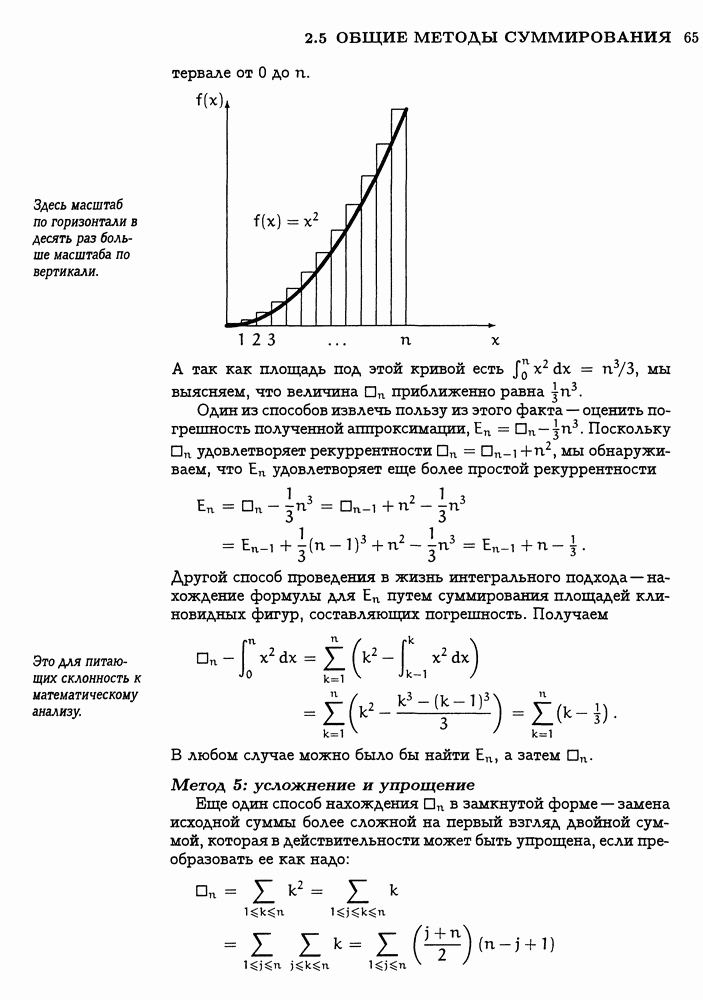
Мы изучили целый ряд способов непосредственного обращения с суммами. Теперь настала пора расширить наш кругозор, рассмотрев проблему суммирования на более высоком уровне. По аналогии с более традиционным исчислением бесконечно малых математиками разработано исчисление „конечных разностей; с помощью которого можно аккуратно и методично подойти к суммированию.

Исчисление бесконечно малых основано на свойствах дифференциального оператора определяемого как

Исчисление конечных разностей основано на свойствах разностного оператора А, определяемого как

Это конечно-разностный аналог производной, в котором мы ограничились целыми положительными значениями Н. Таким образом, — ближайшее к нулю значение, которое можно получить «в пределе» при — это при

Символы и А называются операторами, поскольку они „оперируют" с функциями, образуя новые функции: они являются функциями функций, результатом которых являются функции. Если — достаточно гладкая функция, отображающая

вещественные числа в вещественные числа, то также является функцией из вещественных чисел в вещественные числа. А если представляет собой любую функцию из вещественных чисел в вещественные числа, то таковой является и Значения функций в точке х вычисляются в соответствии с данными выше определениями.

Приступая к изучению дифференциального исчисления, мы прежде всего выясняем, как действует на степенные функции Для таких функций Неформально это можно записать, опуская как

Было бы здорово, если бы оператор А давал столь же элегантный результат; к сожалению, этого не происходит. Так,

Тем не менее, имеется некая разновидность степени; которая действительно здорово преобразуется под действием А, и именно это обстоятельство делает исчисление конечных разностей содержательным. Такие модифицированные степени х определяются по правилу

Обратите внимание на маленькую черточку под — она указывает на то, что сомножителей должны постепенно становиться все меньше и меньше. Существует, соответственно, определение, по которому сомножители становятся все больше и больше:

При имеем так как по соглашению произведение отсутствующих сомножителей принимается равным 1 (точно так же, как сумма отсутствующих слагаемых считается равной 0).

Величина называется в убывающей степени если нужно произнести это вслух; созвучно — это в возрастающей степени Эти функции называют также убывающими факториальными степенями и возрастающими факториальными степенями, поскольку они тесно связаны с факториальной функцией . В самом деле,

В математической литературе встречается ряд других обозначений для факториальных степеней, среди них -„символ Похгаммера"

для или для встречаются также обозначения типа или Тем не менее в моду входит подчеркнуто-надчеркнутое обозначение, ибо оно просто пишется, легко запоминается и избавлено от лишних скобок.

Убывающие степени особенно хороши по отношению к А:

так что исчисление конечных разностей располагает удобным в обращении правилом, под стать правилу

Это основной факториальный факт.

Оператор в исчислении бесконечно малых имеет обратный — антидифференциальный (или интегральный) оператор Основная теорема дифференциального и интегрального исчисления связывает с следующим образом:

тогда и только тогда, когда .

Здесь — неопределенный интеграл — является классом функций, производная которых есть Точно так же, оператор А имеет обратный — антиразностный (или суммирующий) оператор и в этом случае справедлива такая Основная теорема:

тогда и только тогда, когда . (2.46)

Здесь неопределенная сумма — является классом функций, разность которых есть (Заметим, что строчная соотносится с прописной А так же, как соотносится с Буква в случае неопределенных интегралов обозначает произвольную постоянную; в случае же неопределенных сумм роль играет любая функция такая, что В частности, С могла бы быть периодической функцией а — такие функции аннулируются, если мы берем от них разности (точно так же как аннулируются константы, когда мы берем от них производные). При целочисленных х функция С является константой.

Теперь мы почти подошли к кульминационному моменту. Исчисление бесконечно малых включает в себя и определенные интегралы: если то

Соответственно, исчисление конечных разностей — во всем имитирующее своего более знаменитого собрата — располагает определенными суммами: если то

Эта формула раскрывает смысл обозначения точно так же, как предыдущая формула — смысл

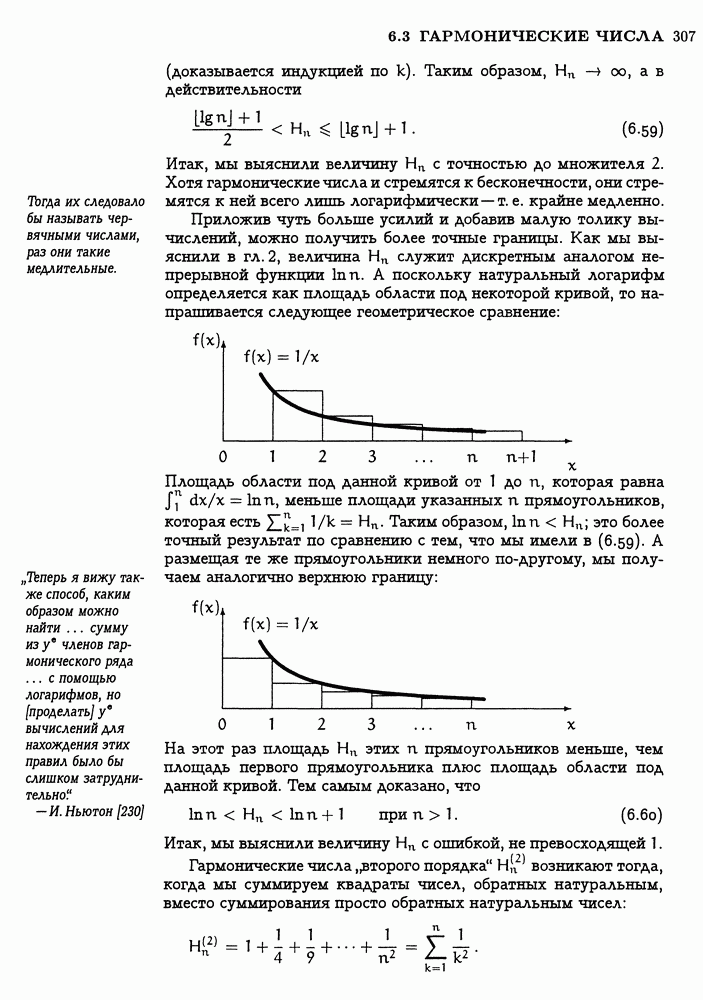
Но что же представляет собой сумма в действительности? Мы установили ее смысл по аналогии, но не по существу. Такая аналогия хороша для того, чтобы облегчить запоминание правила исчисления конечных разностей; однако подобное обозначение будет бесполезным, если мы не поймем его истинного смысла. Попробуем выяснить смысл этой суммы, рассмотрев сначала некоторые специальные случаи, исходя из того, что Если то

Далее, если то результат такой:

И еще, если к добавить 1, то

Подобные наблюдения, а также математическая индукция, позволяют выяснить точный смысл в о6щем случае, когда а и — целые числа :

Другими словами, определенная сумма — это то же самое, что и обычная сумма с пределами суммирования, но с исключенным значением верхнего предела.

Попробуем повторить этот вывод несколько иначе. Предположим, что нам дана неизвестная сумма, которая, предположительно, вычисляется в замкнутой форме, и еще предположим, что ее можно записать в виде Теория исчисления конечных разностей говорит, что ответ можно выразить в виде если только мы сможем найти неопределенную сумму или антиразностную функцию такую, что

. Один из способов понять сей принцип - выписать в развернутом виде, используя

Все члены в правой части, за исключением сокращаются, так что значением суммы является (Суммы вида часто называют телескопическими, по аналогии со складным телескопом, так как толщина стенок сложенного телескопа определяется исключительно радиусом самой большой и радиусом самой малой из труб.)

Но правило (2.48) применимо только при а; а что случится при Ну, согласно (2.47),

что аналогично соответствующему соотношению для определенного интеграла. Подобным же образом доказывается, что

— аналог соотношения для сумм. Вот это соотношение при полном параде:

для любых целых .

Скорее всего, на данном этапе некоторые начинают интересоваться: а что нам дают все эти параллели и аналогии? Ну, для начала, исчисление определенных сумм дает простой способ вычисления сумм убывающих степеней: из основных правил (2.45), (2.47) и (2.48) вытекает общее правило

Эта формула легко запоминается, поскольку она очень похожа на знакомую нам формулу

В частности, при имеем поэтому данное правило исчисления конечных разностей предоставляет простой способ запоминания того факта, что

Исчисление определенных сумм облегчается также тем обстоятельством, что суммы в промежутке зачастую оказываются проще сумм в промежутке 1 к первые из них

попросту равны в то время как последние требуют вычисления

Обычные степени также можно суммировать этим новым способом, если сперва выразить их через убывающие степени. Так,

откуда

Замена на дает еще один способ вычисления в замкнутой форме нашего старого знакомого — суммы

Вот здорово — так просто! Это действительно проще, чем любой из той уймы способов, которыми мы замучили до смерти данную сумму в предыдущем разделе. Поэтому попробуем подняться выше — от квадратов к кубам. Несложное вычисление показывает, что

(Обычные степени всегда можно обратить в факториальные и наоборот, используя числа Стирлинга, которые мы будем изучать в гл. Таким образом:

Итак, убывающие степени весьма подходят для вычисления сумм. Но обладают ли они еще какими-нибудь качествами, оправдывающими их существование? Должны ли мы обращать давно нам знакомые обычные степени в убывающие до суммирования, а затем обращать их обратно, вместо того чтобы действовать как-нибудь по-другому? Вовсе нет: зачастую можно работать непосредственно с факториальными степенями, поскольку они обладают рядом дополнительных свойств. Например, точно так же, как справедливо, что справедливо и то, что и та же самая аналогия существует между . (Эта „факториальная биномиальная теорема" доказывается в упр. 5.37.)

До сих пор мы рассматривали только убывающие степени без отрицательных показателей. Чтобы провести аналогии с обычными отрицательными степенями, нам потребуется подходящее определение при Глядя на последовательные степени

можно заметить, что для перехода от мы делим на потом — на и потом — на х. Представляется желательным (если не обязательным) затем разделить на чтобы перейти от Продолжая деление, мы получаем несколько первых убывающих степеней с отрицательными показателями,

так что в общем случае определение отрицательных убывающих степеней таково:

(Убывающие степени можно также определить и для вещественных и даже комплексных но мы отложим это до гл. 5.)

Благодаря такому определению убывающие степени обретают дополнительные замечательные свойства. Возможно, наиболее важным из них является общее правило показателей, аналогичное правилу

для обычных степеней. Его вариант для убывающих степеней:

Так,

Если бы мы определили как а не как то правило показателей (2.52) оказалось бы несправедливым в случаях типа . В действительности, можно было бы воспользоваться правилом (2.52), которое как раз и указывает, как следует определять убывающие степени с отрицательными показателями, если положить Когда какое-то существующее обозначение распространяется на большее число случаев, всегда лучше формулировать определения таким образом, чтобы общие правила оставались справедливыми.

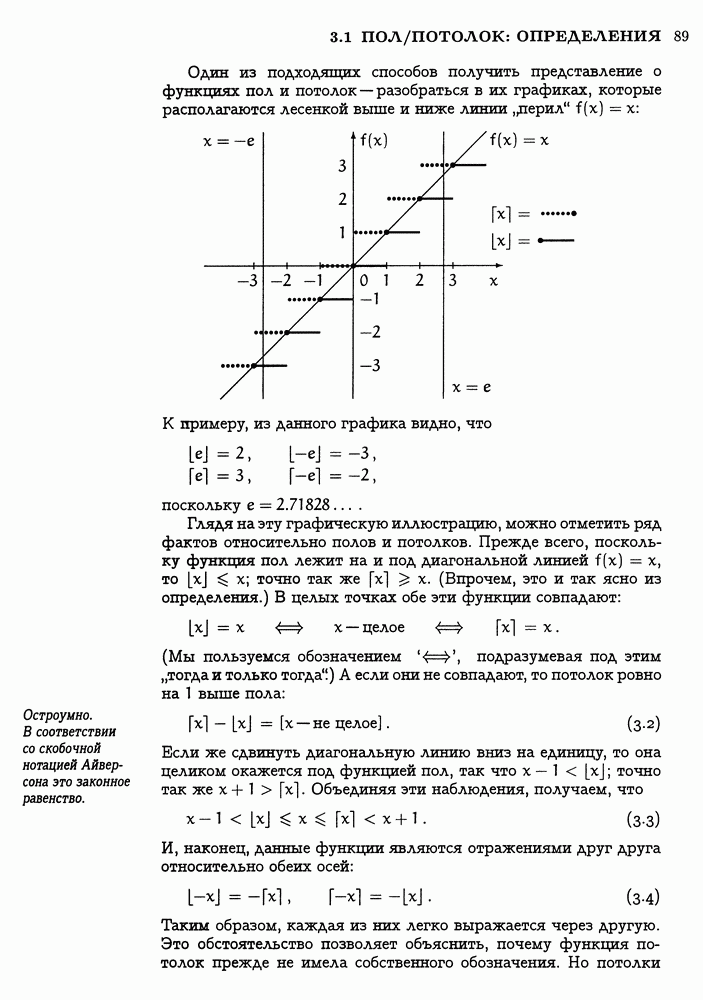
Убедимся теперь в том, что решающее разностное свойство справедливо для установленных нами по-новому убывающих степеней. Действительно ли при Если, например, то соответствующая разность

Да, все верно! Подобная проверка проходит при любом .

Следовательно, правило суммирования (2.50) остается справедливым как для отрицательных, так и для положительных убывающих степеней, до тех пор, пока не произойдет деление на нуль:

Ну, а как же быть с Вспомним, что при интегрировании при мы получаем

Нам хотелось бы иметь конечно-разностный аналог другими словами, мы хотим найти функцию такую, что

Не очень трудно видеть, что такой функцией является

когда х — целое число, а эта величина — попросту гармоническое число из (2.13). Таким образом, дискретным аналогом непрерывной функции служит (Мы определим для нецелых х только в гл. а для ближайших целей будет вполне достаточно целых х. Мы также увидим в гл. 9, что при больших х величина приближенно равна Следовательно, — не просто аналоги: обычно их значения отличаются менее чем на 1.)

Теперь можно дать полное описание сумм убывающих степеней:

Эта формула показывает, почему пресловутые „гармонические" числа очень гармонично возникают при решении дискретных задач, типа анализа задач „быстрой сортировки", тогда как так называемые „натуральные" логарифмы весьма натуральны при решении непрерывных задач.

Теперь, когда найден аналог для посмотрим, имеется ли таковой для Какая функция обладает свойством соответствующим тождеству Ответ прост:

так что мы имеем дело с простой рекуррентностью и можем принять в качестве дискретной экспоненты.

В случае произвольного с разность функции также достаточно проста, а именно,

Следовательно, антиразностью функции является если с Этот факт, вместе с основными правилами (2.47) и (2.48), дают нам компактный способ выведения общей формулы суммы геометрической прогрессии:

Всякий раз, когда мы сталкиваемся с функцией которая могла бы оказаться полезной в качестве замкнутого выражения суммы, можно вычислить ее разность — тем самым мы получаем функцию неопределенная сумма которой нам известна. Таблица 75 представляет собой начало перечня пар разность/антиразность, полезных при вычислении сумм.

Несмотря на все эти параллели между непрерывной и дискретной математикой, некоторые непрерывные понятия не имеют дискретных аналогов. К примеру, „правило цепочки" в исчислении бесконечно малых — удобное правило вычисления производной „функции от функции"; однако в исчислении конечных разностей правила, соответствующего „правилу цепочки", нет, поскольку нет подходящего выражения для В дискретном случае затруднена также замена переменных, за исключением определенных случаев, типа замены х на

Однако для есть весьма подходящее выражение, и оно обеспечивает нас правилом суммирования по частям — конечно-разностным аналогом того, что в исчислении бесконечно малых именуется „интегрированием по частям" Вспомним, что в исчислении бесконечно малых формула

приводит к правилу интегрирования по частям,

Таблица 75 Суммы и разности

после интегрирования и перестановки членов; то же самое можно проделать и в исчислении конечных разностей.

Начнем с применения разностного оператора к произведению двух функций

Эта формула может быть приведена к более удобному виду, если использовать оператор сдвига Е, определяемый как

Подставляя его вместо получаем компактное правило для разности произведения:

(Здесь Е доставляет некоторое неудобство, но зато делает это уравнение правильным.) Взяв неопределенную сумму от обеих частей этого равенства и переставив члены, мы получаем обещанное правило суммирования по частям:

Как и в исчислении бесконечно малых можно пристроить пределы суммирования ко всем трем членам, делая неопределенные суммы определенными.

Данное правило полезно, когда сумму слева вычислить труднее, чем сумму справа. Вот пример. Интеграл обычно вычисляют по частям; его дискретным аналогом является сумма с которой мы уже сталкивались в этой главе, правда, записанной в виде суммирования по частям полагаем откуда Подстановка в (2.56) дает

А теперь можно воспользоваться этим для вычисления суммы, с которой мы имели дело раньше, расставив пределы суммирования:

Вместо того чтобы использовать метод приведения, легче вычислить данную сумму таким методом, поскольку при этом не надо думать ни о чем.

Где-то посреди этой главы мы наткнулись на формулу для и сочли себя счастливыми. Но мы могли бы обнаружить нашу формулу (2.36) закономерно, если бы знали о суммировании по частям. Продемонстрируем это, взявшись вычислить даже более трудную на вид сумму На самом деле решение будет нетрудным, если исходить из аналогии с интегралом мы полагаем так что и, следовательно,

(Переходя от первой строки ко второй, мы объединили две убывающие степени используя правило показателей (2.52) с Теперь можно подключить пределы и заключить, что