| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
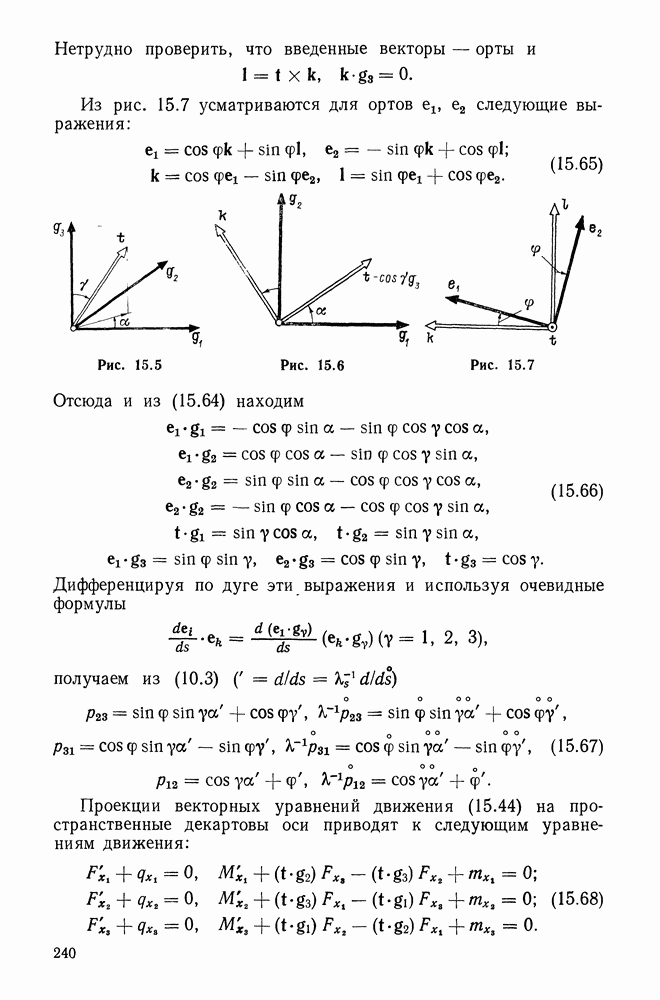
10.2. Геометрия поверхности
Пусть поверхность описывается векторным уравнением

где  криволинейные координаты. Радиус-вектор произвольной точки вблизи поверхности примем равным
криволинейные координаты. Радиус-вектор произвольной точки вблизи поверхности примем равным

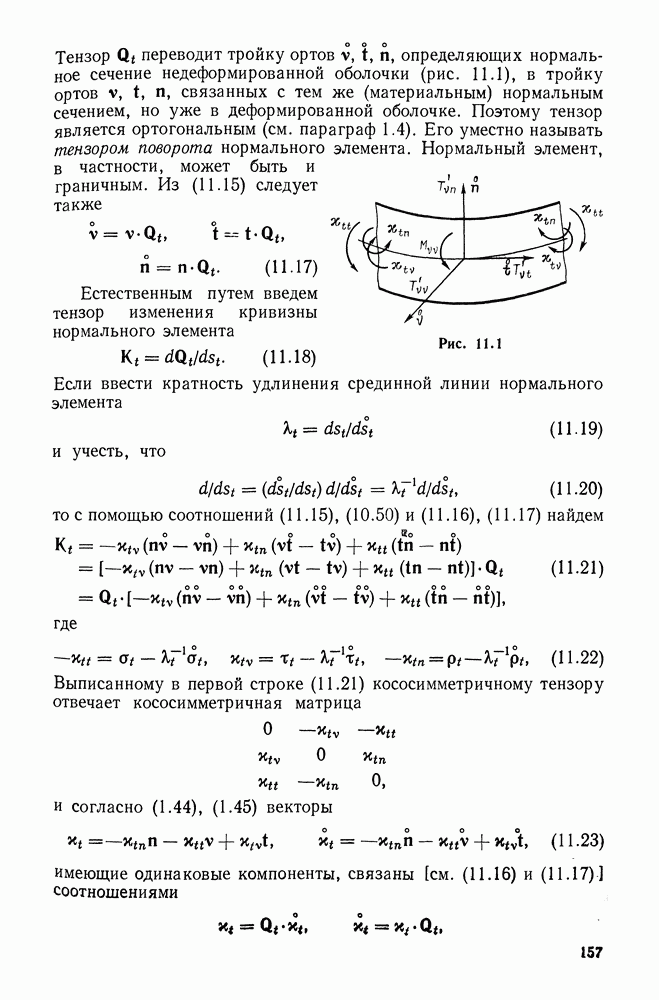
где  расстояние от точки до поверхности по нормали к последней с единичным вектором
расстояние от точки до поверхности по нормали к последней с единичным вектором  (рис. 10.2). Такую систему координат называют нормально связанной с поверхностью. Все соотношения в выбранной системе координат можно получить, заменяя в зависимостях параграфа 6.1 радиус-вектор выражением (10.9) и полагая
(рис. 10.2). Такую систему координат называют нормально связанной с поверхностью. Все соотношения в выбранной системе координат можно получить, заменяя в зависимостях параграфа 6.1 радиус-вектор выражением (10.9) и полагая 

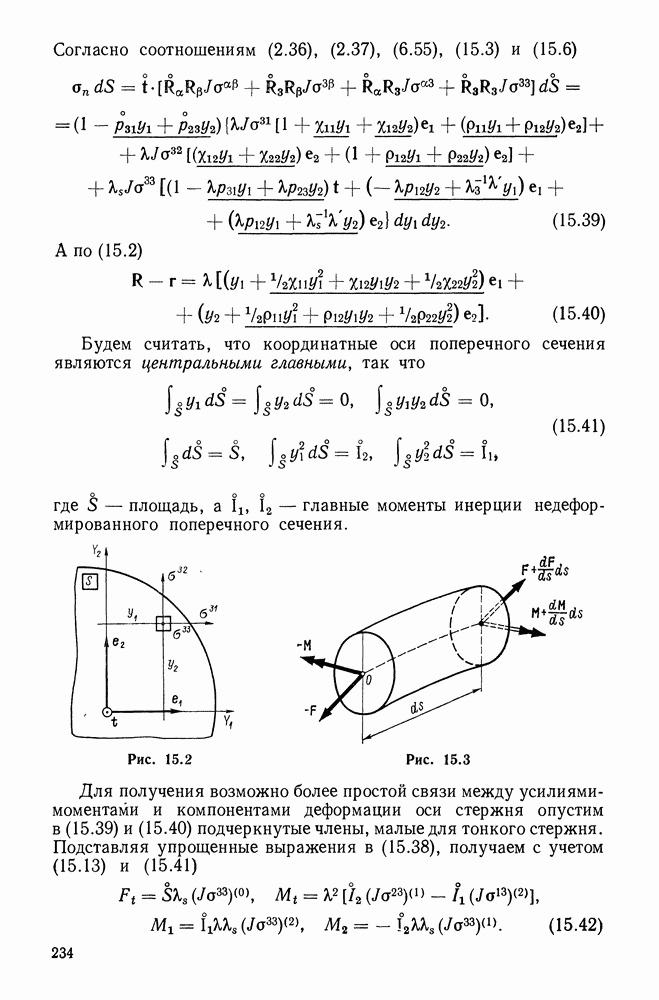
Рис. 10.2
Прежде всего из (10.9) следует

(В этой главе буквенные индексы будут принимать значения 1, 2.)
Согласно (6.9) из (10.10)

где

В дальнейшем излагаемое в этой главе будет применено к тонким оболочкам, в которых рассматриваемая поверхность является срединной (равноудаленной от верхней и нижней лицевых поверхностей). При этом

Как выяснится ниже, это сильное неравенство означает, что толщина оболочки много меньше радиусов кривизны срединной поверхности. С этим связано, что все рассматриваемые величины приближенно представимы в виде

т. е. зависимость их от  линейна. Так, из (10.11) следует
линейна. Так, из (10.11) следует

Поскольку  отсюда усматривается, что
отсюда усматривается, что  компоненты симметричного метрического тензора срединной поверхности. Как уже говорилось в параграфе
компоненты симметричного метрического тензора срединной поверхности. Как уже говорилось в параграфе  приведенные миноры элементов
приведенные миноры элементов  в определителе
в определителе  имеющем согласно (10.15) вид
имеющем согласно (10.15) вид

и, стало быть,

Согласно же (6.18), (6.23), (10.15) и (10.17)

Отнесем формулы (10.15)-(10.19) к срединной поверхности (полагая в них  При этом
При этом

Здесь  длина элемента дуги
длина элемента дуги  координатной линии поверхности,
координатной линии поверхности,  координатный угол,
координатный угол,  площадь элемента поверхности.
площадь элемента поверхности.
Соотношения (6.6), (6.9), (6.10), (6.13) на поверхности принимают вид

Поверхностный дискриминантный тензор вводится соотношениями

Из зависимостей (10.20), (10.26) следует

Перейдем к дифференцированию координатных векторов. Прежде всего согласно (6.30), (10.15)

где (см. параграф 10.4)

инварианты: гауссова и средняя кривизны поверхности.
С учетом только что полученных выражений находим при  из (6.26), (6.28)
из (6.26), (6.28)

где

поверхностные символы Кристоффеля второго рода. Из (6.37) при  находим
находим

При рассмотрении общих вопросов теорий поверхностей и оболочек широко используются поверхностные ковариантные производные:

Последняя строка показывает, что для любого инварианта (скаляра, вектора, тензора) ковариантная производная совпадает с обычной частной производной.
Из соотношений (10.30), (10.33) следует

Последние зависимости, соотношения (10.12), (10.25) и применяемое к ковариантному дифференцированию обычное правило дифференцирования произведения дают

Согласно соотношениям (10.32), (10.33)

Отсюда и вытекает первое из следующих выводимых аналогично соотношений

или согласно (10.35)

Применяя к вектору

формулы (10.30), (10.33), получаем

Можно ввести и вектор — поверхностный градиент

Пусть в пространственной прямоугольной декартовой системе координат с ортами 

Прежде всего и по (10.12)

где  координатный угол, а
координатный угол, а

Рассмотрим очевидные тождества

Используя дважды соотношения (10.30), приходим к соотношениям Кодацци


и к двум следующим:

Свертывание (суммирование) первого из них с  а второго с
а второго с  по индексу
по индексу  приводит с учетом того, что по
приводит с учетом того, что по  соотношению Гаусса
соотношению Гаусса

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
- 5.6. Законы сжимаемости сплошных эластомеров
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
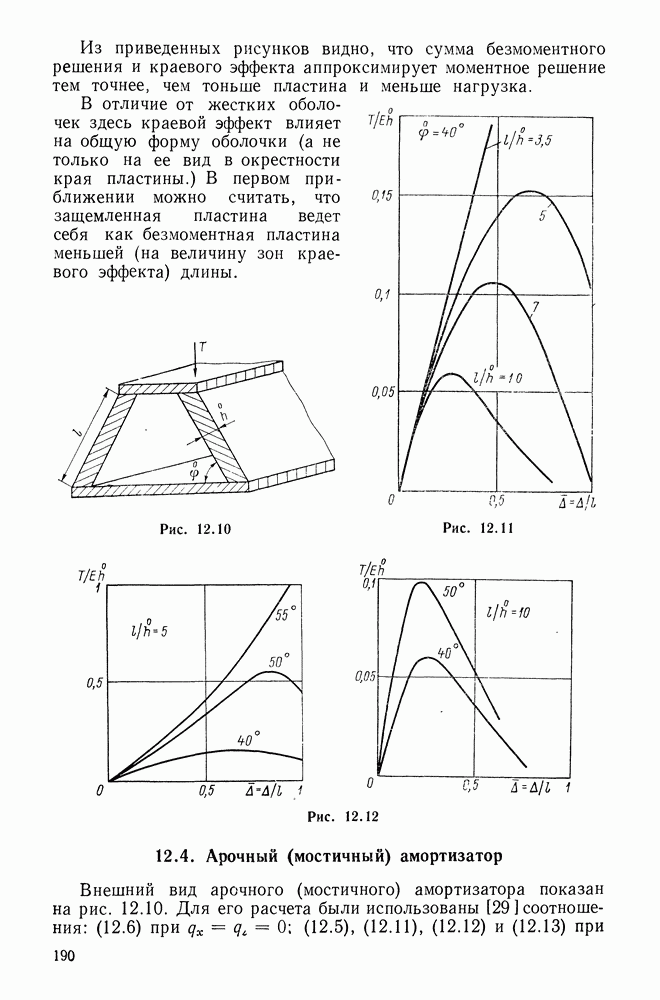
- 12.4. Арочный (мостичный) амортизатор
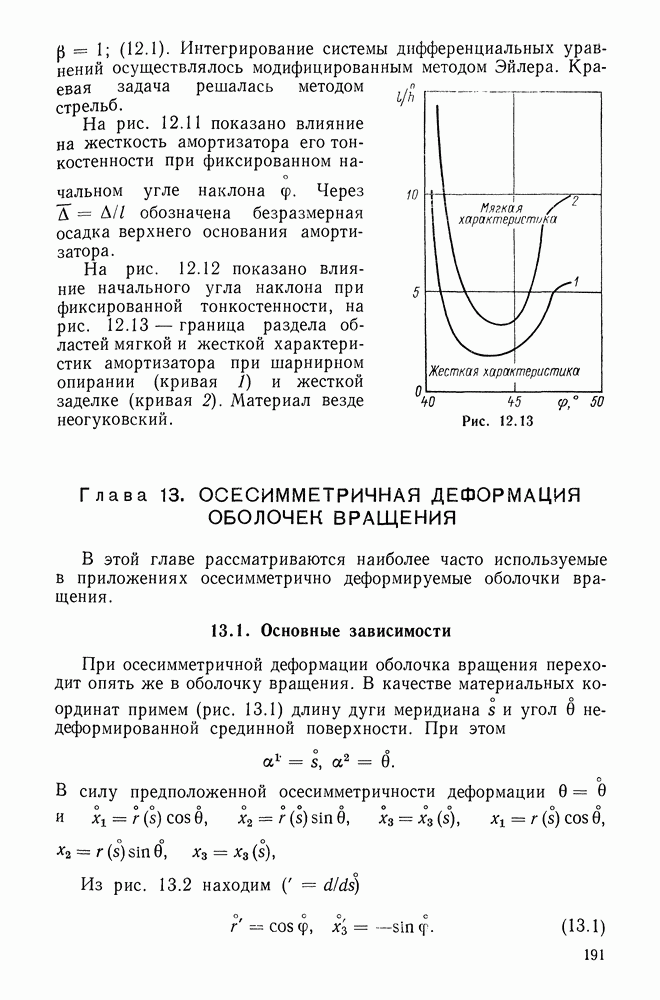
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
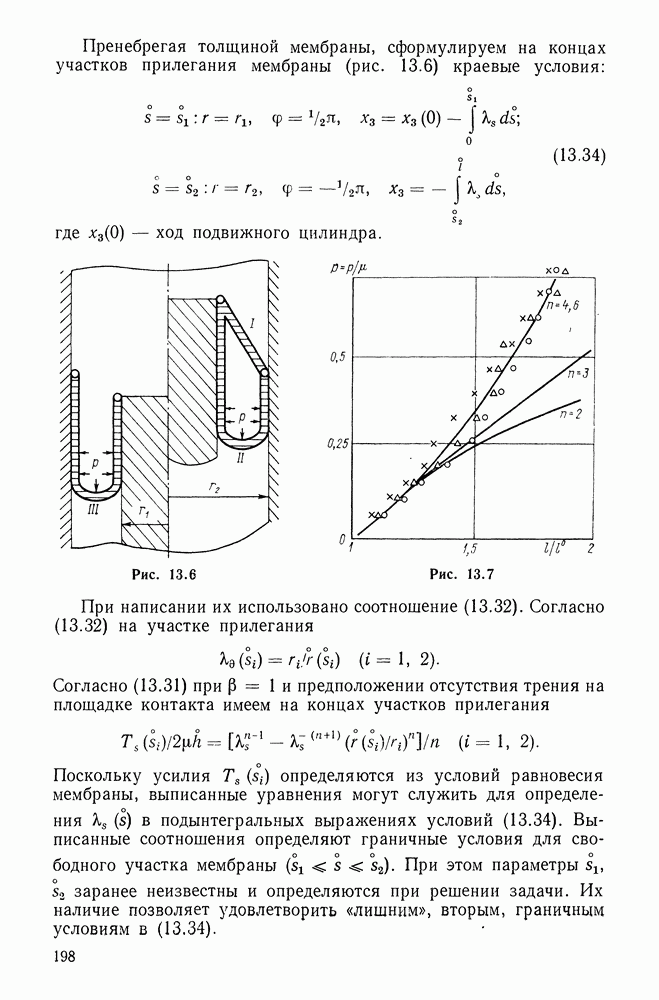
- 13.3. Перекатывающаяся мембрана
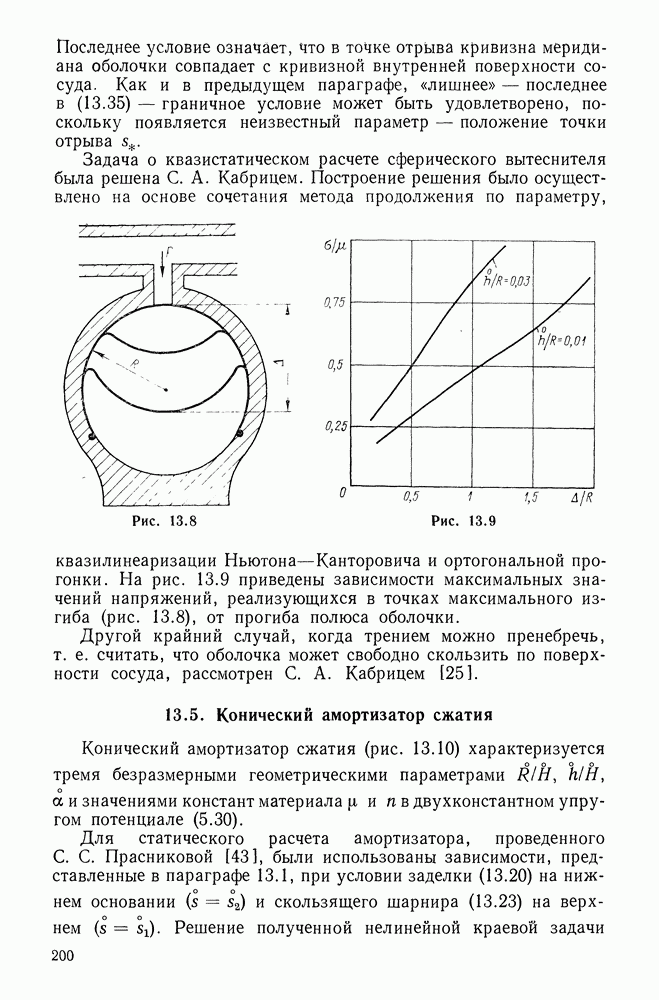
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
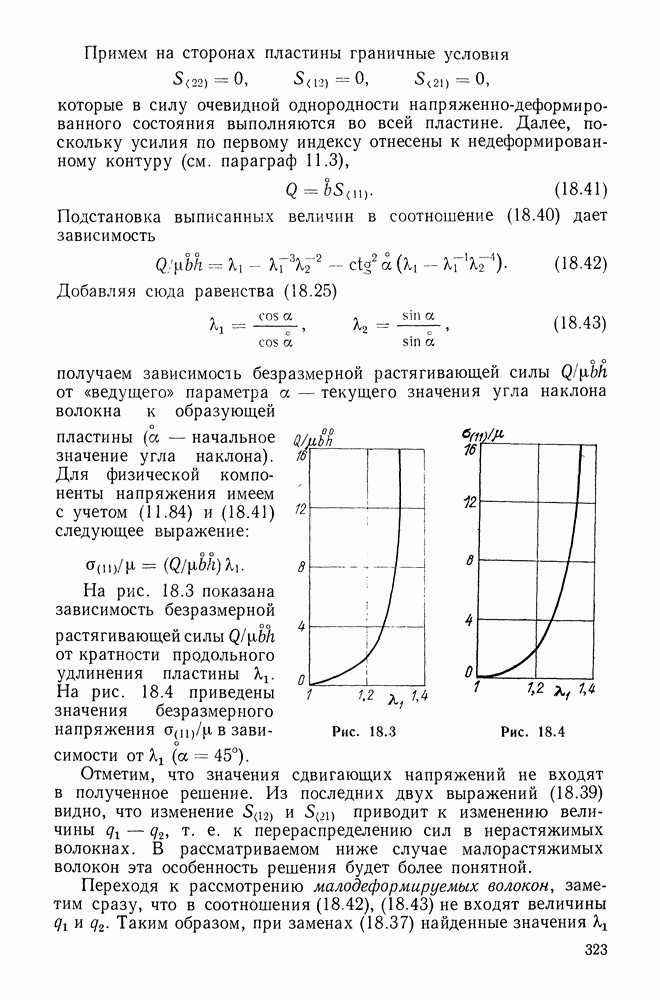
- 18.5. Растяжение армированной цилиндрической пластины
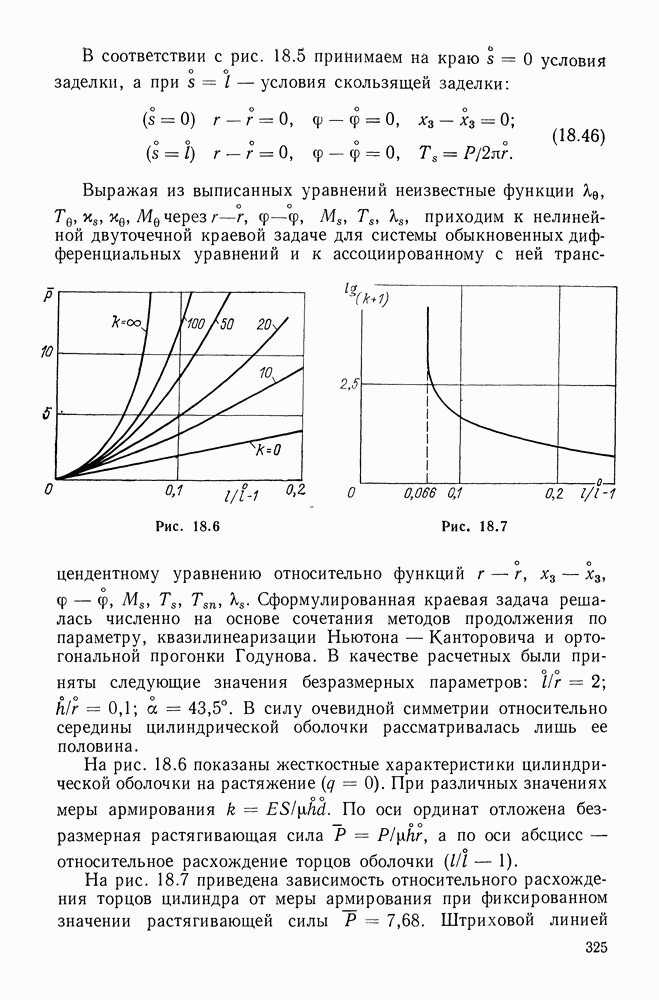
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
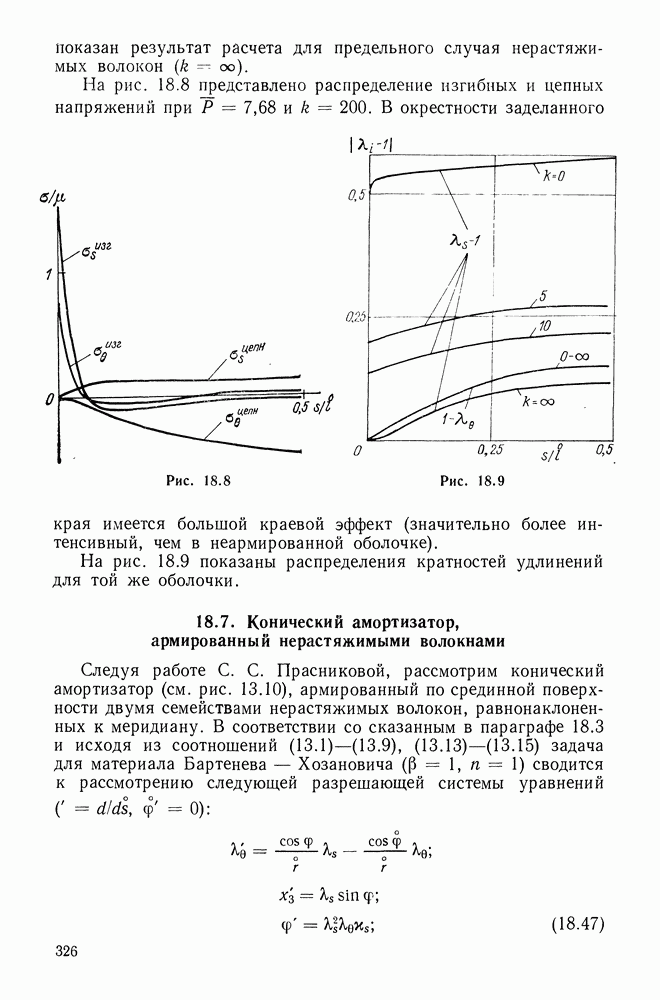
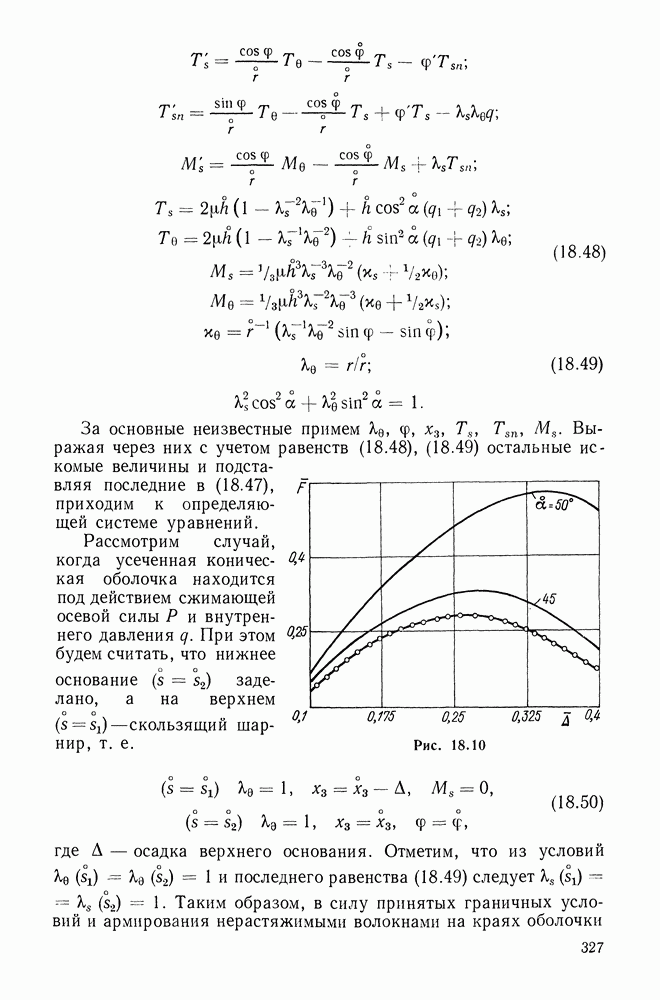
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами