| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава II. ВОЛНЫ
§ 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
Распространение колебаний в упругой среде.
Твердые, жидкие и газообразные тела больших размеров можно рассматривать как среду, состоящую из отдельных частиц, взаимодействующих между собой. Возбуждение колебаний частиц среды в одном месте вызывает вынужденные колебания соседних частиц, те, в свою очередь, возбуждают колебания следующих за ними частиц и так далее. Процесс распространения колебаний в пространстве называют волной.
При распространении волн на поверхности воды колебания происходят перпендикулярно направлению распространения волн. Волны, в которых колебания происходят перпендикулярно направлению распространения волны, называют поперечными.
Не всякие волны можно увидеть. После удара молотком по ветви камертона мы слышим звук, хотя никаких волн в воздухе не видим. Ощущение звука в наших органах слуха возникает при периодических изменениях давления воздуха.
Звуковые волны.
Рассмотрим процесс возникновения звуковой волны в воздухе. В результате быстрого смещения пластины (рис. 36) у ее поверхности происходит повышение давления воздуха на величину  и повышение его плотности на величину
и повышение его плотности на величину  Сжатый воздух расширяется и вызывает сжатие прилегающего к нему слоя воздуха. Этот процесс распространяется дальше. При распространении волны сжатия масса
Сжатый воздух расширяется и вызывает сжатие прилегающего к нему слоя воздуха. Этот процесс распространяется дальше. При распространении волны сжатия масса  воздуха, проходящего за время
воздуха, проходящего за время  через площадку
через площадку  перпендикулярно направлению распространения волны, может быть выражена так:
перпендикулярно направлению распространения волны, может быть выражена так:

где  — плотность воздуха и
— плотность воздуха и  — скорость распространения волны сжатия.
— скорость распространения волны сжатия.
Отсюда следует, что изменение импульса равно:

Это изменение импульса вызвано избыточным давлением  и равно импульсу силы
и равно импульсу силы  за тот же интервал времени
за тот же интервал времени 

Рис. 36

или

Отсюда для скорости распространения волны сжатия находим следующее выражение:

Если предположить, что сжатие воздуха происходит по изотермическому закону

то, принимая во внимание соотношения

получим:

или

Подставляя формулу (9.8) в выражение (9.4), приходим к формуле для скорости распространения волны сжатия:

В том, что проделанный вывод не содержит погрешности по физическому смыслу, можно убедиться путем проверки наименований единиц измерения величин в правой и левой частях выражения (9.9):

Таким образом, скорость распространения волны сжатия в газе прямо пропорциональна корню квадратному из давления газа  и обратно пропорциональна корню квадратному из его плотности
и обратно пропорциональна корню квадратному из его плотности  Подставив в выражение (9.9) значения давления и плотности воздуха при нормальных условиях
Подставив в выражение (9.9) значения давления и плотности воздуха при нормальных условиях  получим для скорости звука в воздухе значение:
получим для скорости звука в воздухе значение:

При экспериментальном определении скорость звука в воздухе при нормальных условиях оказалась равной  Расхождение между значениями, полученными теоретически
Расхождение между значениями, полученными теоретически
и экспериментально, Лаплас объяснил тем, что изменения давления и плотности при распространении звука в воздухе происходят очень быстро, и эти процессы следует считать адиабатными, а не изотермическими. Связь между давлением и объемом газа в адиабатном процессе определяется соотношением:

где у — постоянная величина, равная для воздуха 1,4. Из выражений (9.4) и (9.10) можно получить уточненную формулу для скорости звука:

Экспериментальные и теоретические значения скорости звука в воздухе, полученные по уточненной формуле (9.11), согласуются между собой с высокой степенью точности. По формуле (9.11) можно вычислять скорость звука не только в воздухе, но и в других газах, но для каждого газа численное значение коэффициента у имеет свое значение.
В заключение необходимо обратить внимание на то, что, хотя волны сжатия и разрежения перемещаются в газе со скоростью  никакого перемещения вещества в пространстве при этом не происходит, так как в любой точке пространства расширение периодически сменяется сжатием и направление движения частиц каждый раз изменяется на противоположное.
никакого перемещения вещества в пространстве при этом не происходит, так как в любой точке пространства расширение периодически сменяется сжатием и направление движения частиц каждый раз изменяется на противоположное.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
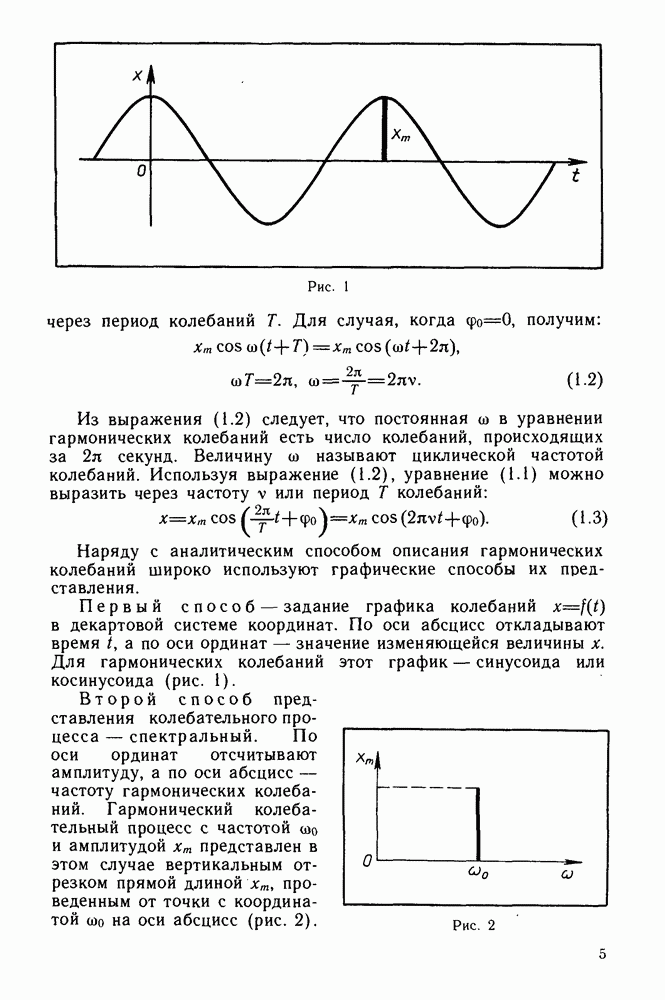
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
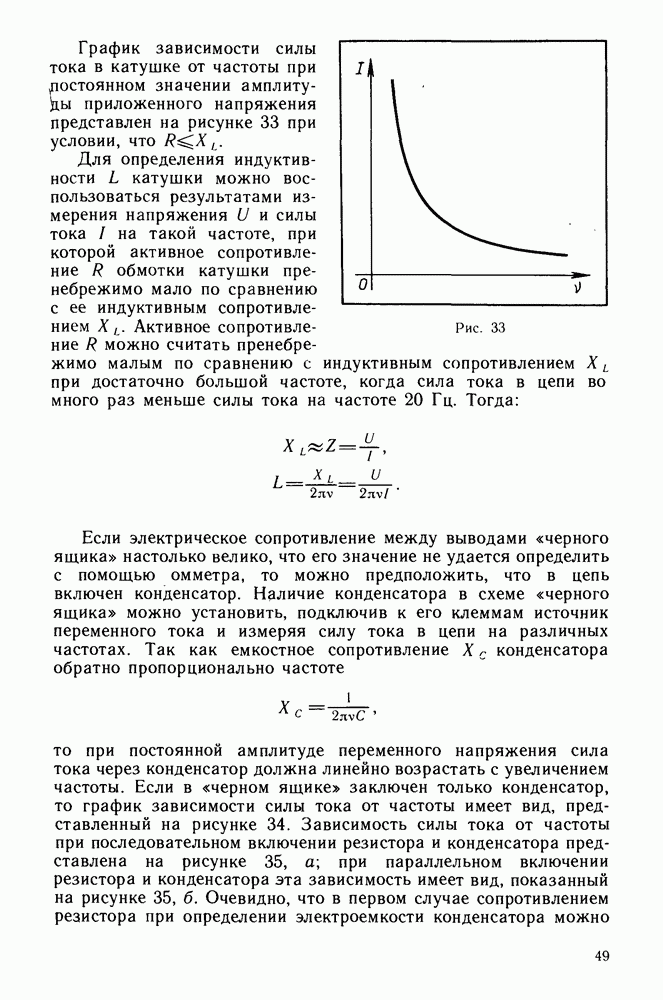
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
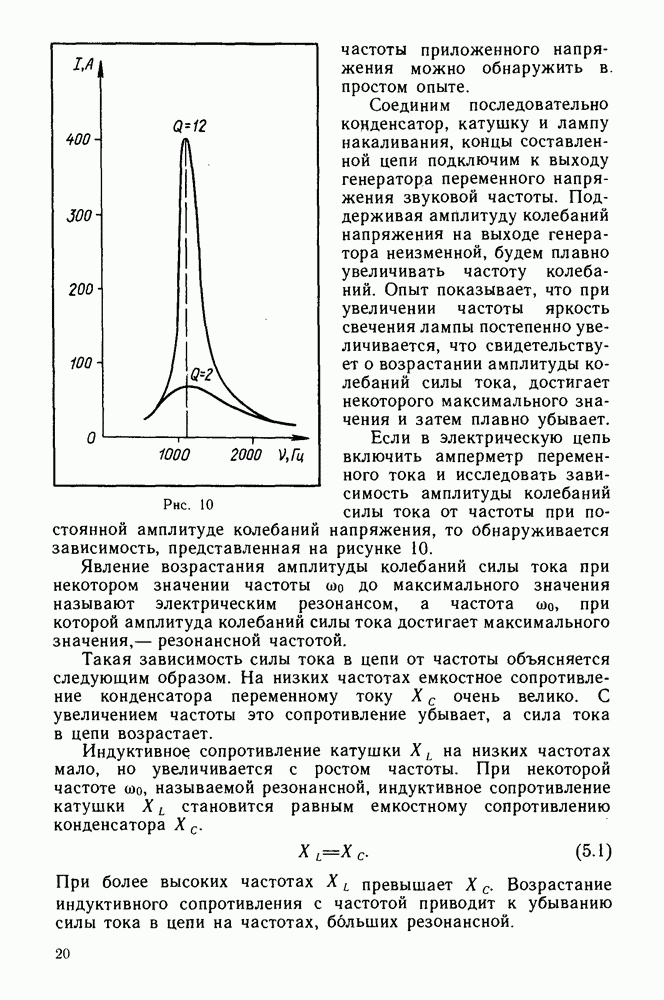
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
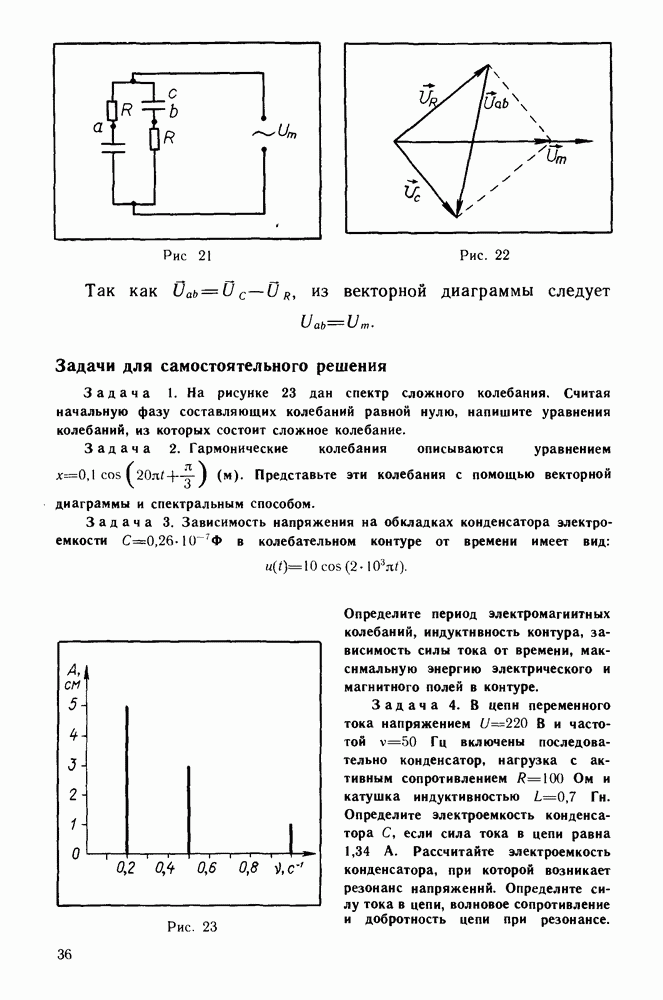
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
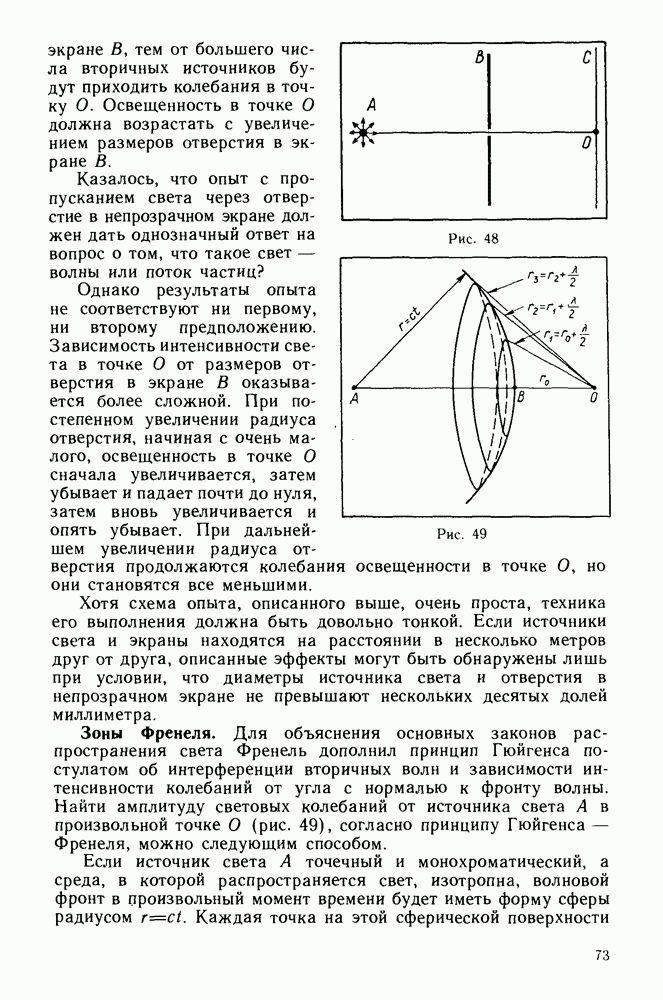
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- Принцип Ферма.
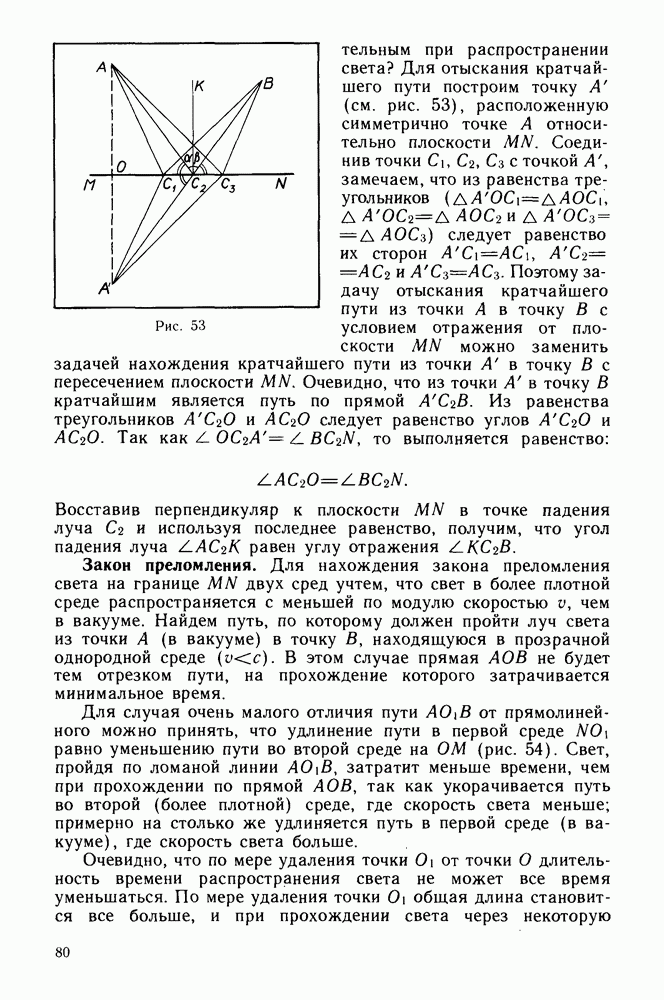
- Закон отражения света.
- Закон преломления.
- Линзы.
- Аберрация линз.
- Оптические приборы.
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
- Дифракция от круглого отверстия.
- Дифракция и разрешающая способность оптических приборов.
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
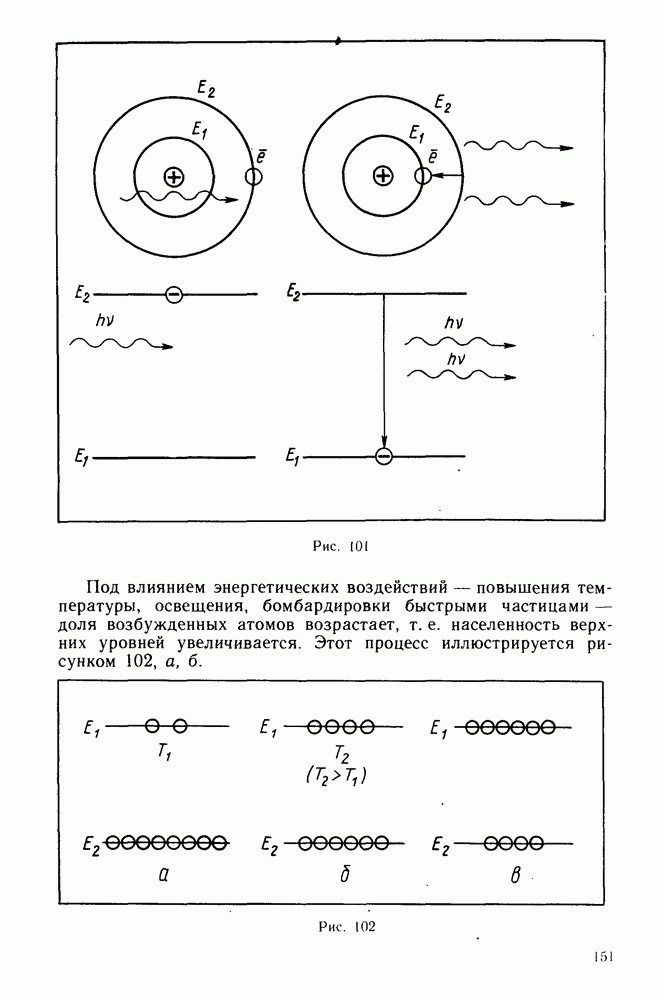
- Схема энергетических уровней.
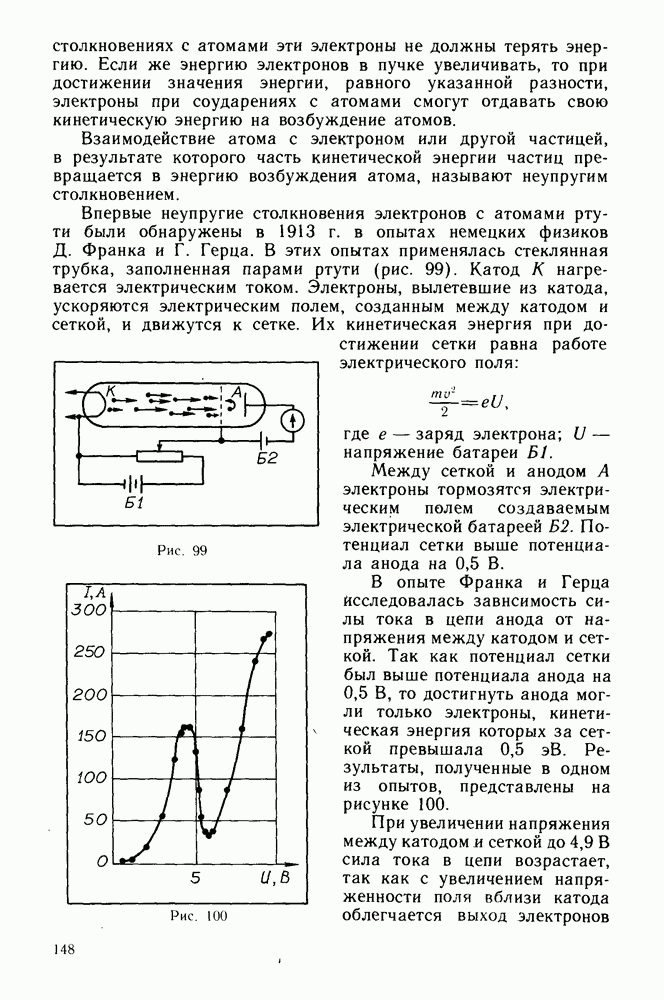
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
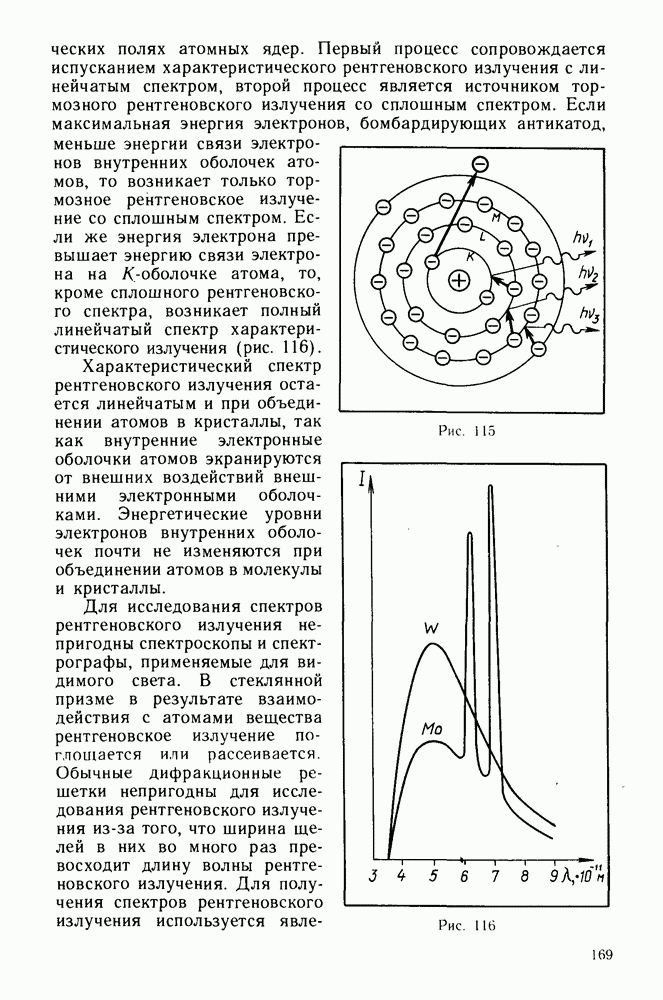
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
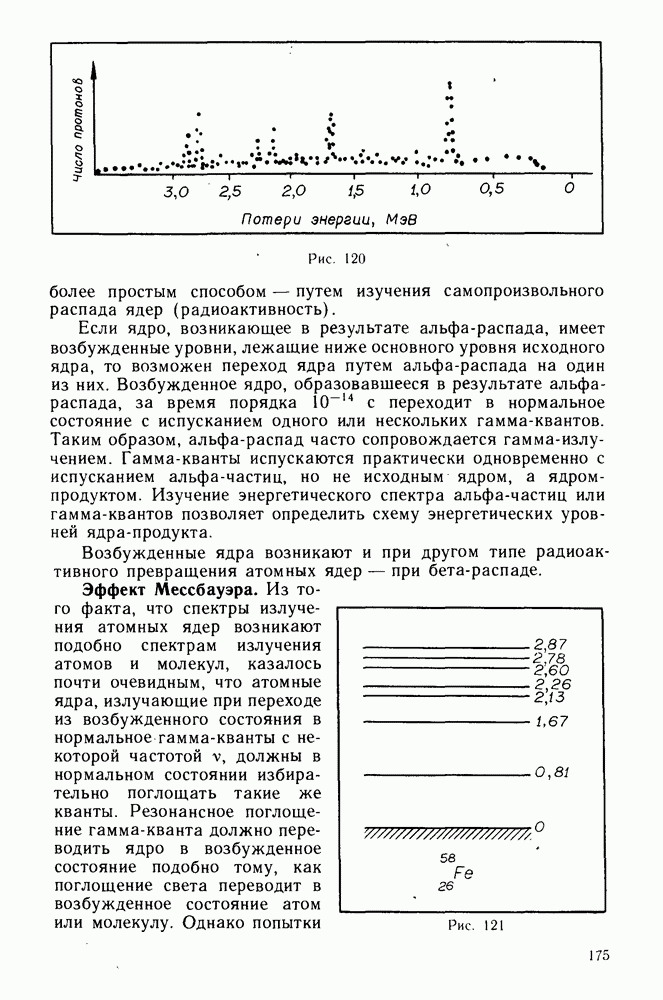
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
- Эффект Мессбауэра.
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
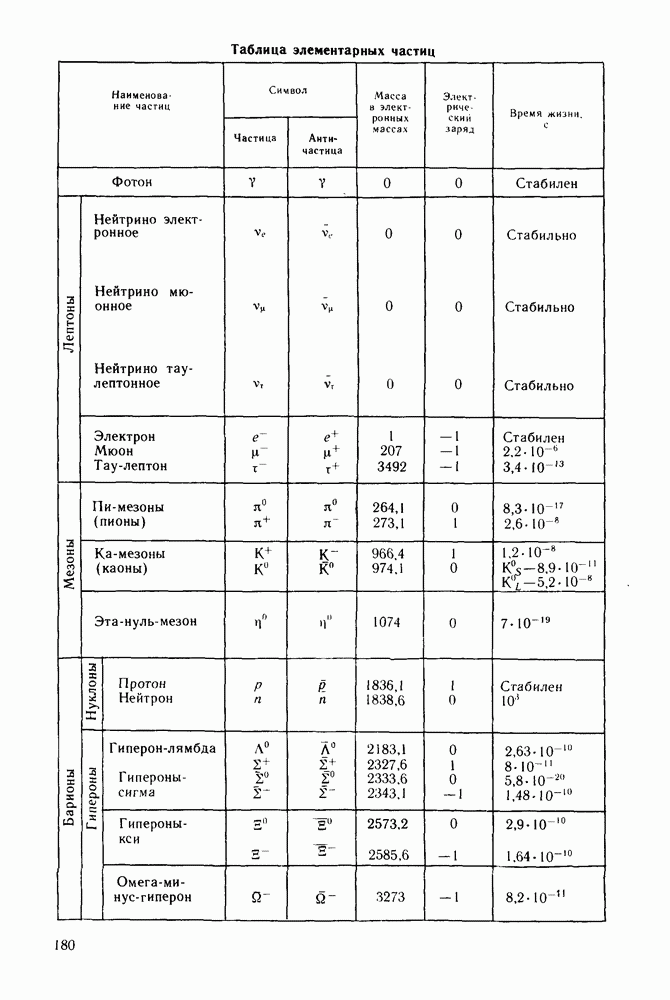
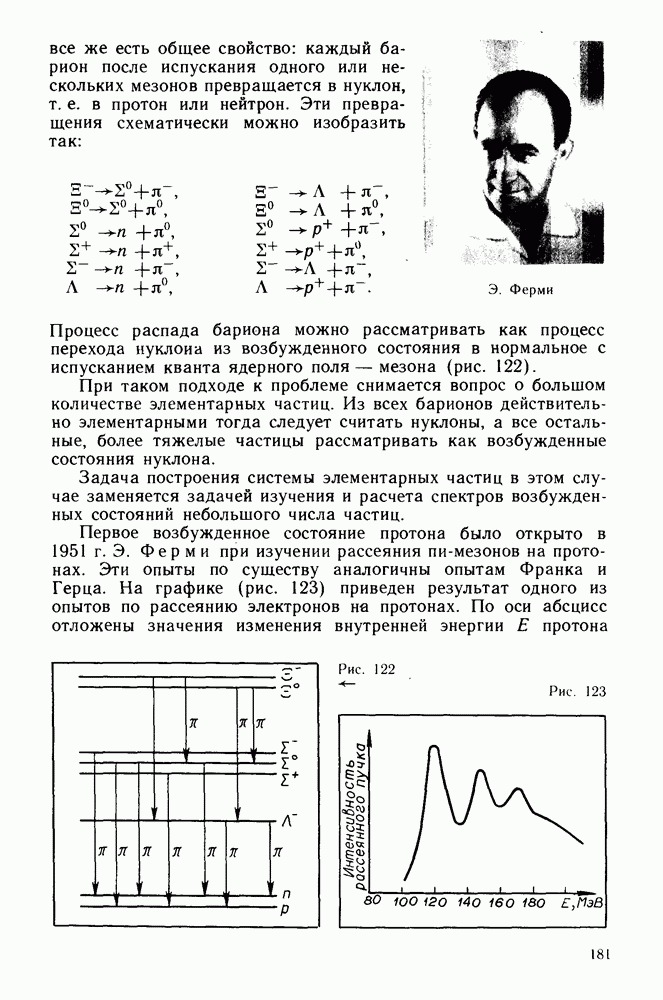
- Спектры элементарных частиц.
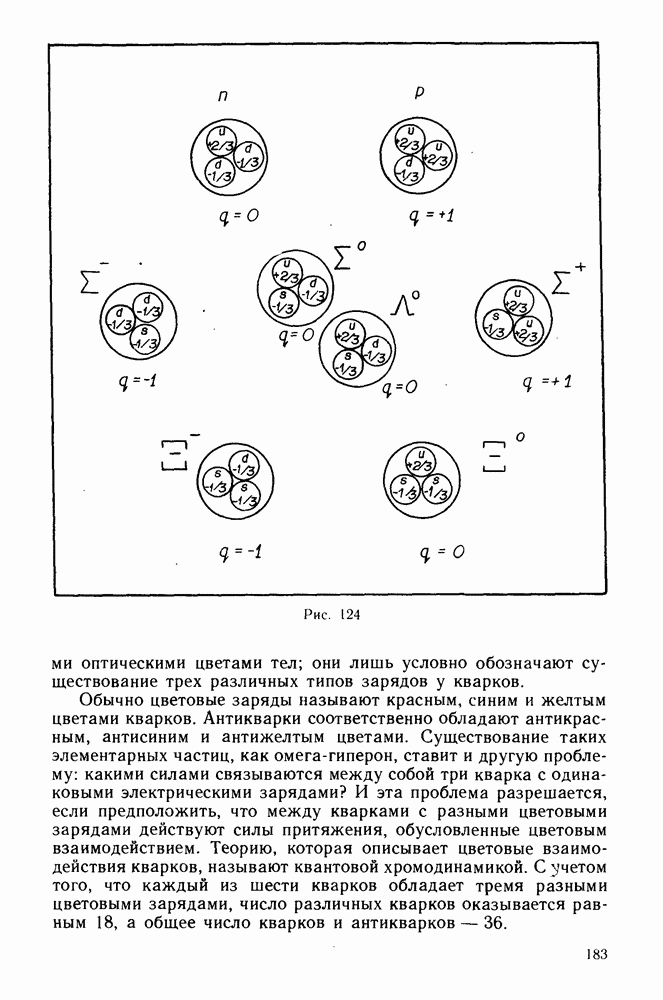
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
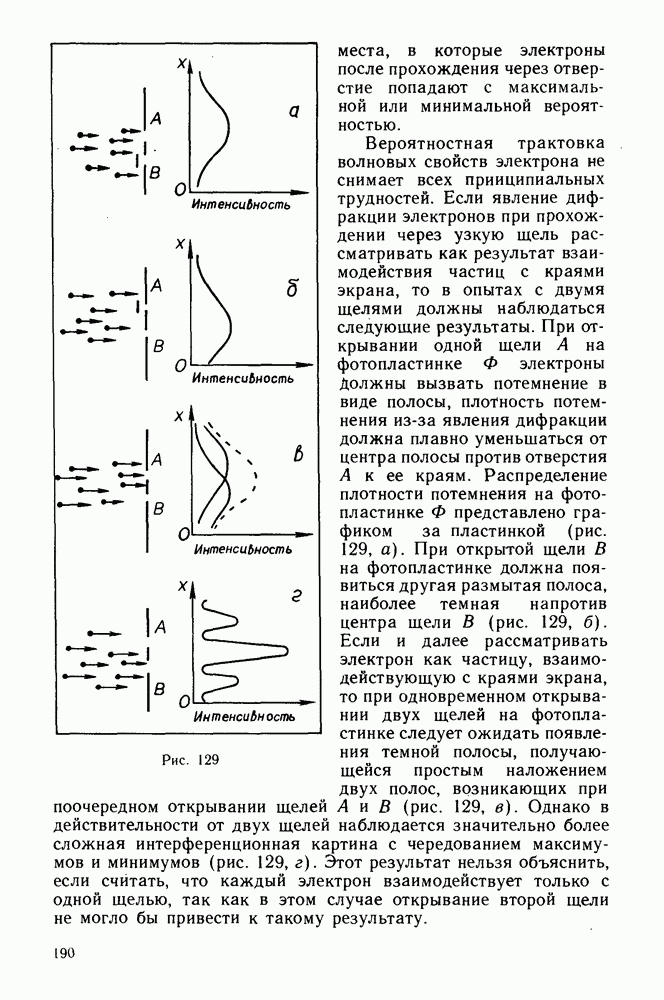
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ