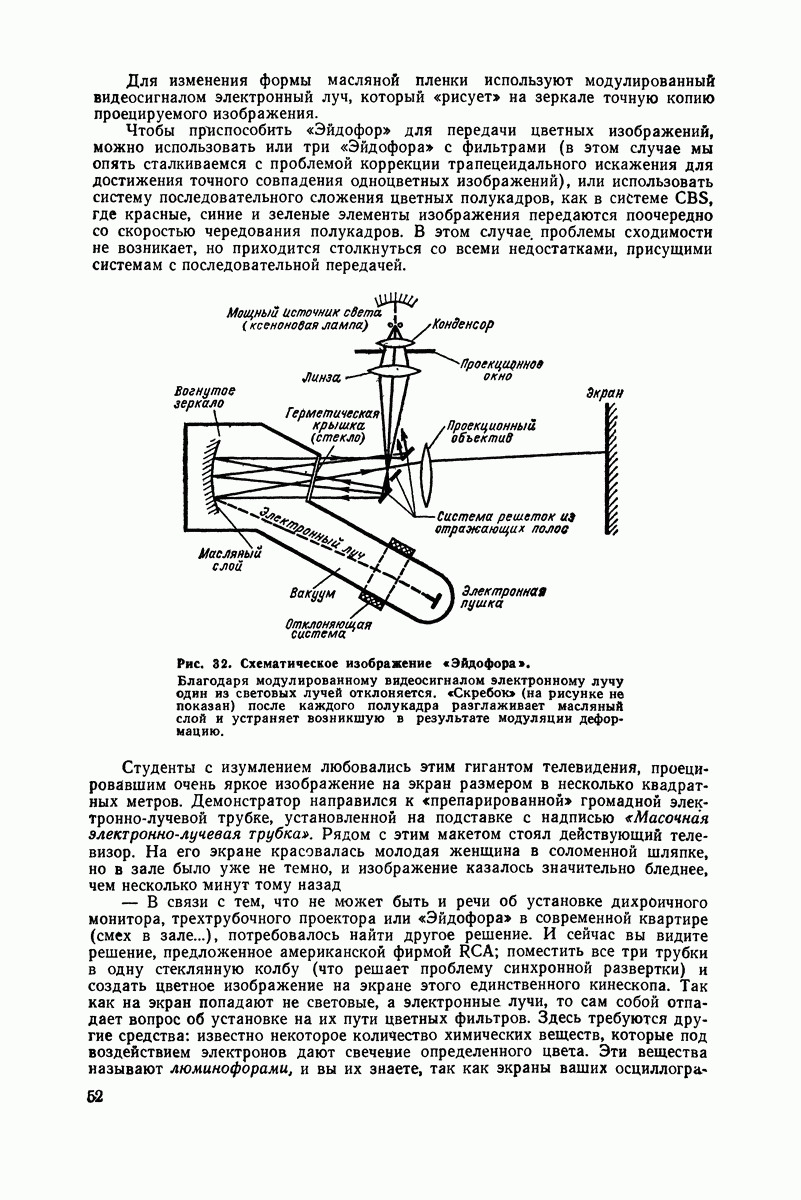
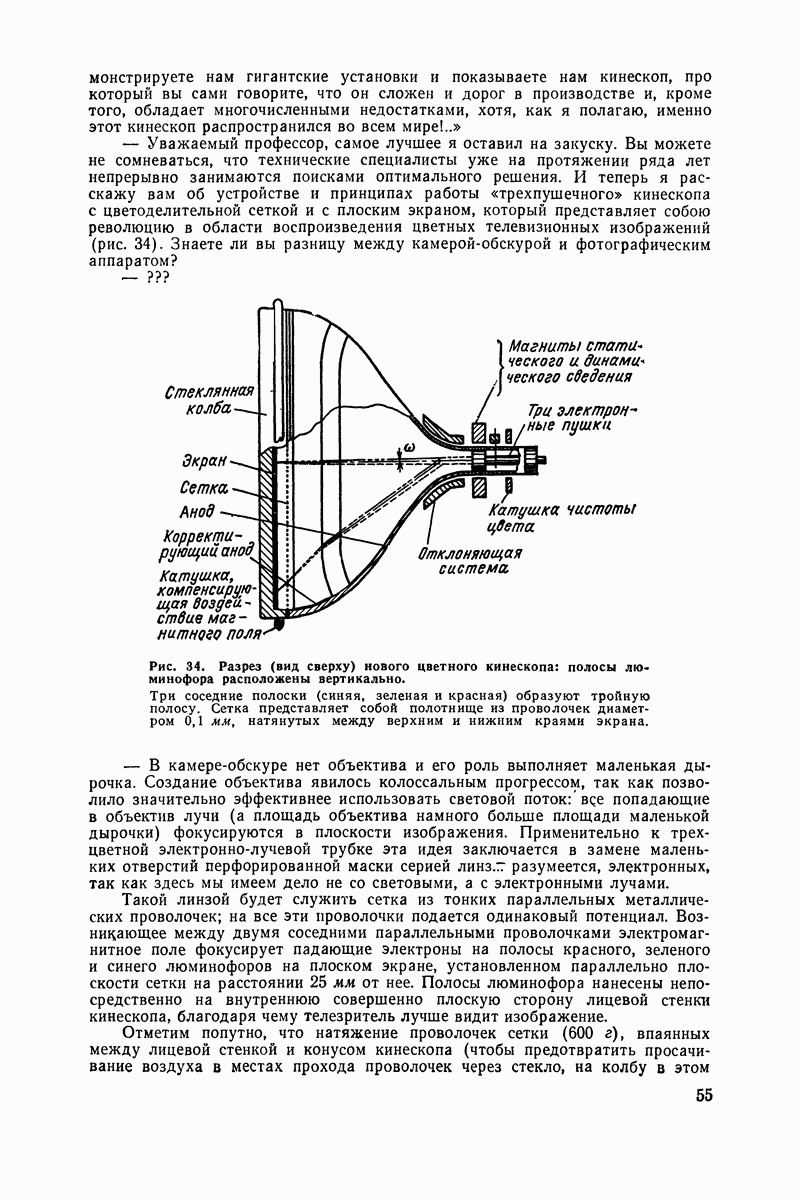
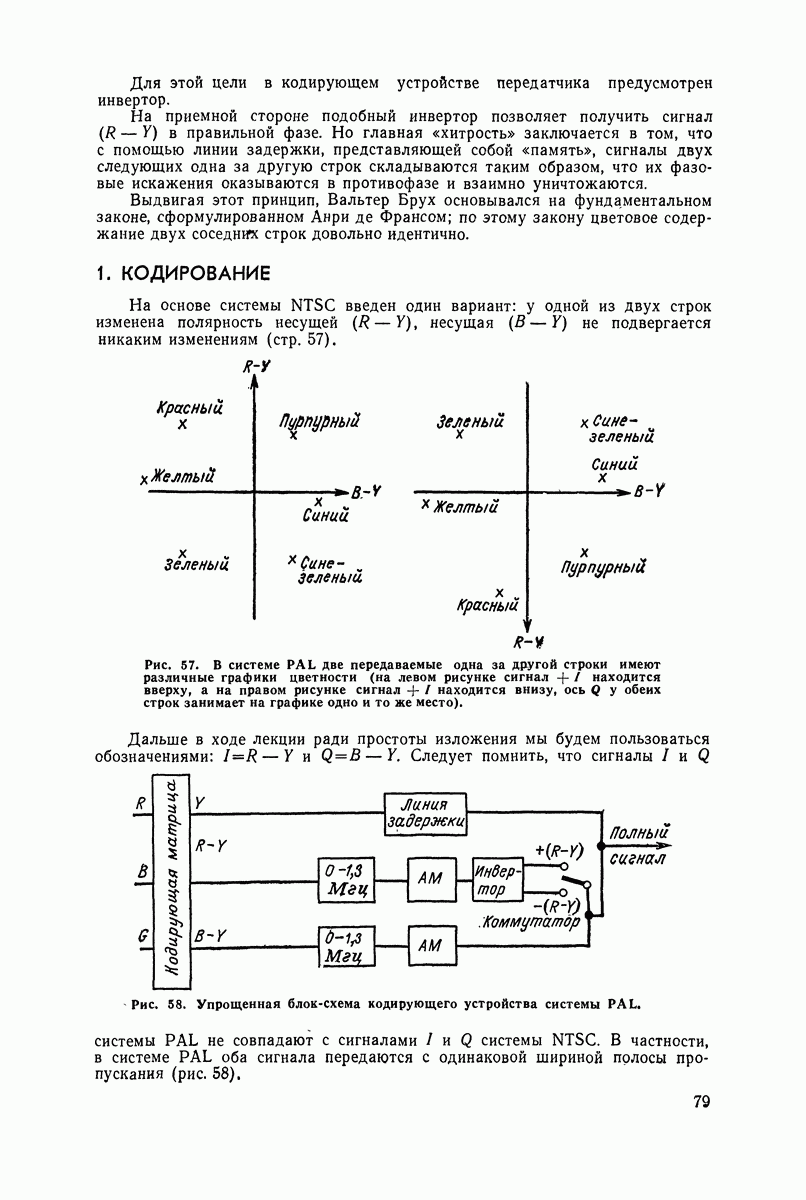
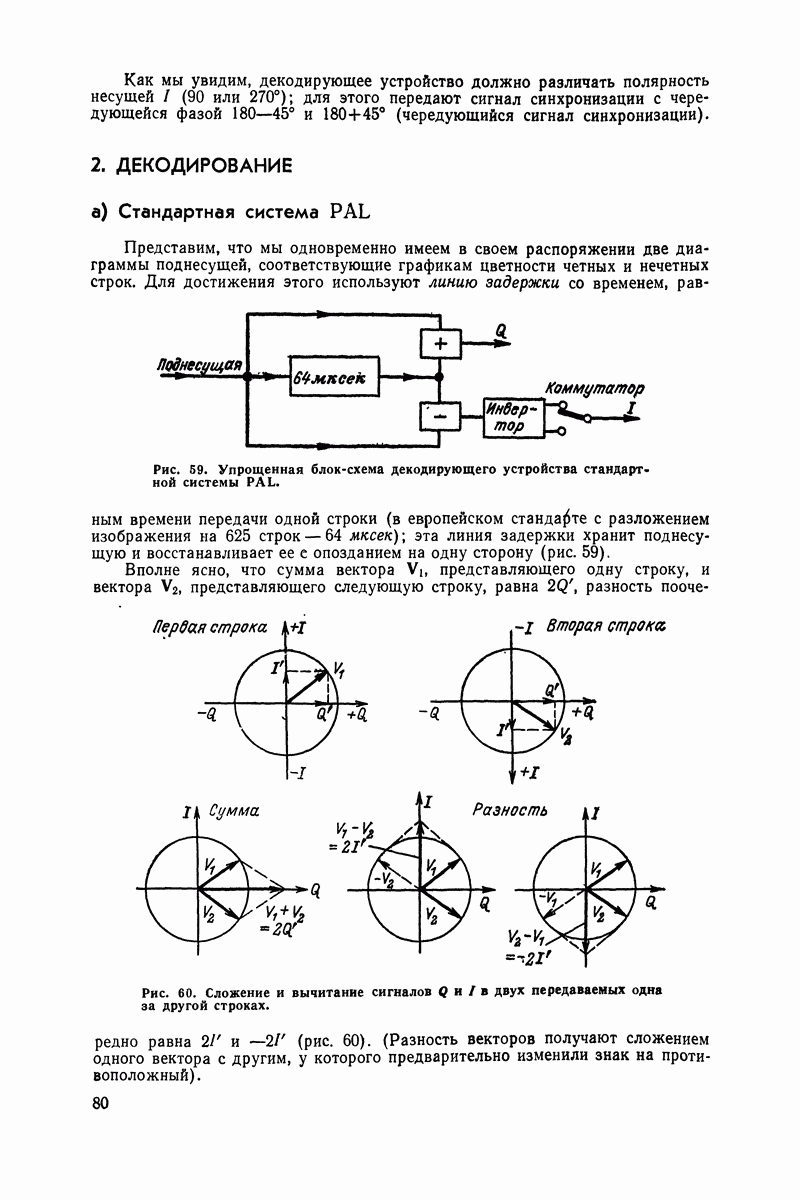
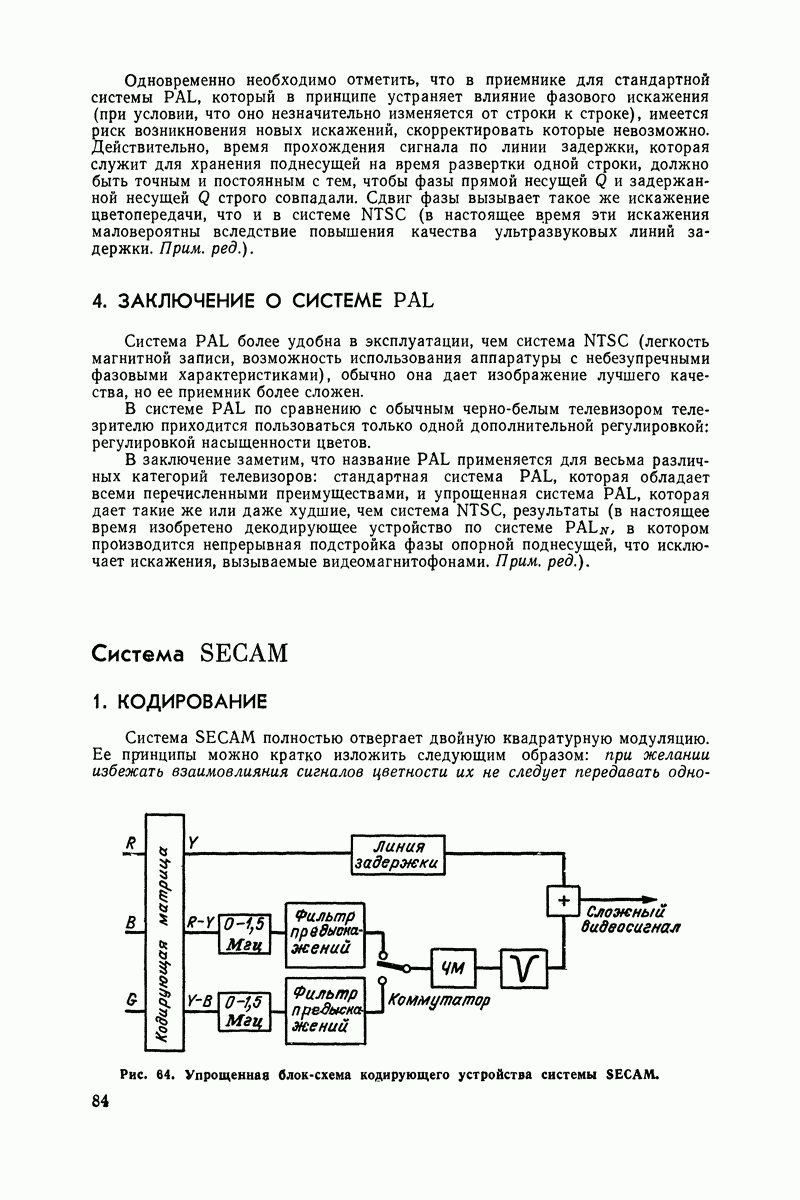
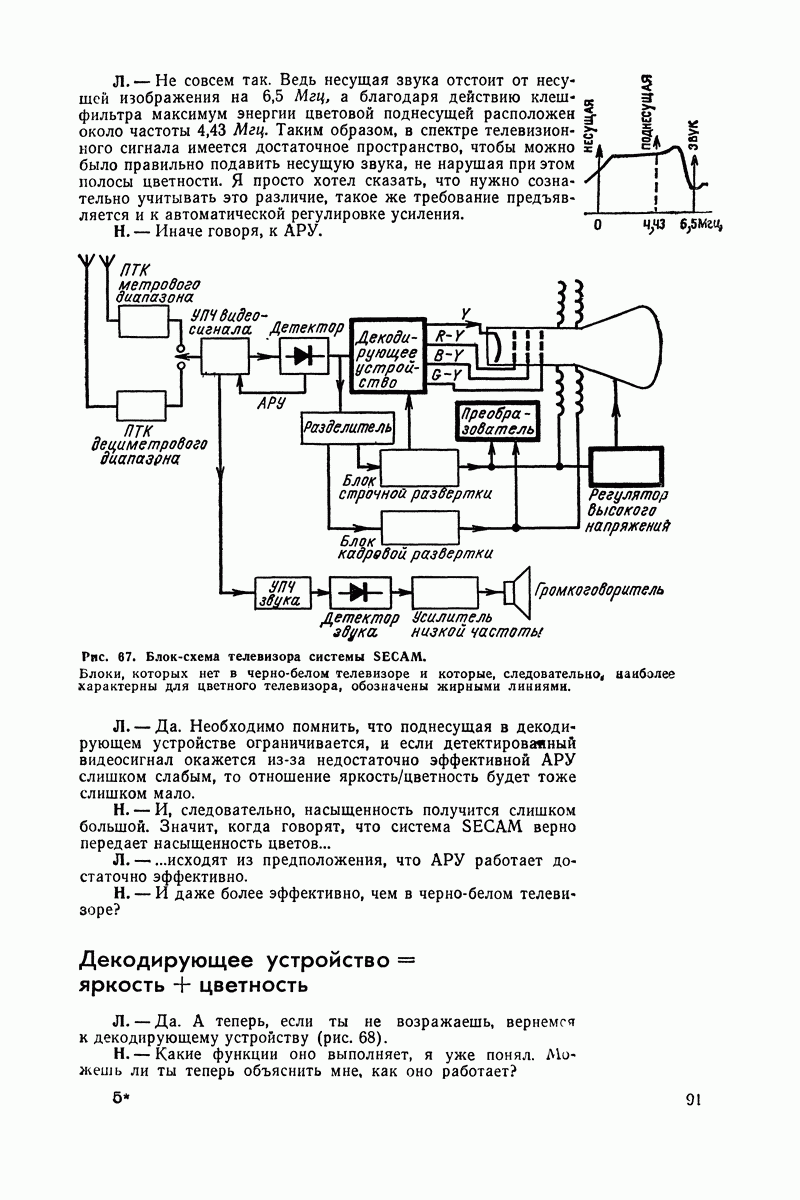
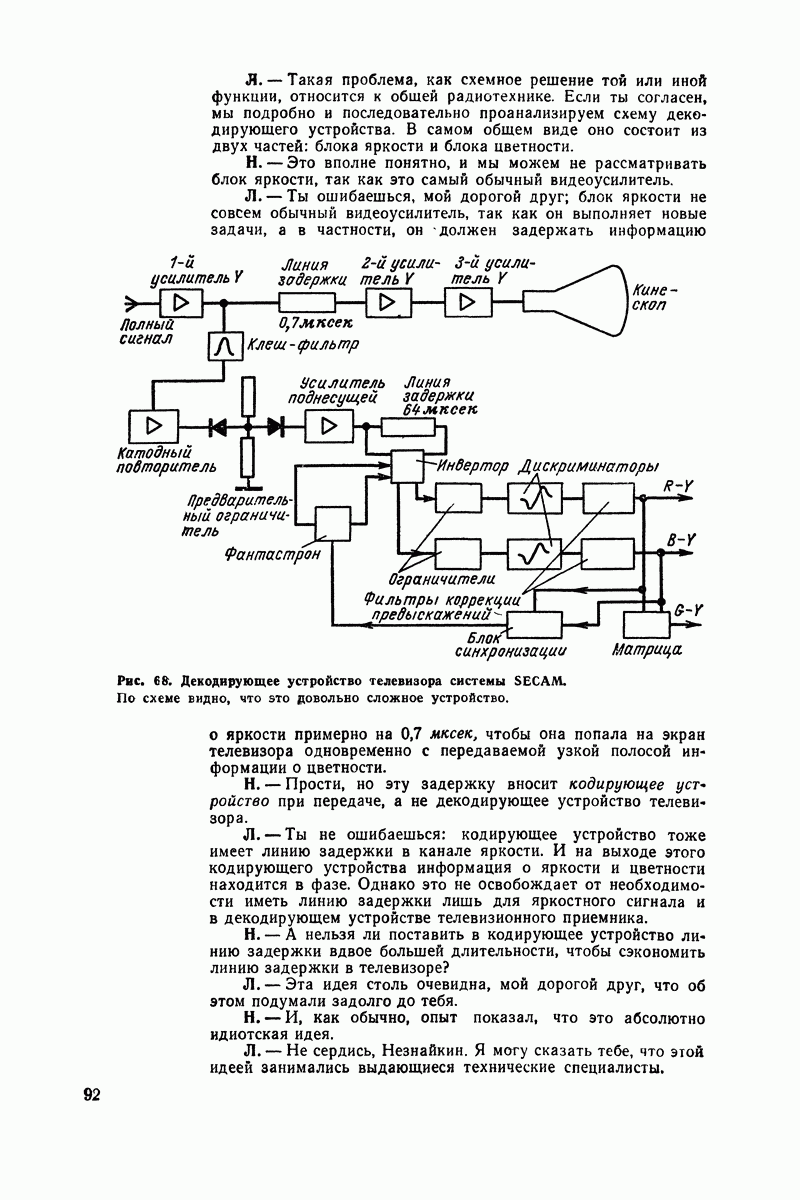
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 8
Послание Любознайкина имеет целью подготовить Незнайкина к лекции профессора Радиоля. Чтобы легче усвоить содержание предстоящей лекции, нужно знать значение векторов и уметь ими пользоваться — они полезны для сложения периодических явлений и, следовательно, для отображения различных систем модуляции. В письме разбираются следующие вопросы:
Диаграммы Френеля. Рождение синусоиды. Сложение синусоид. Сложение векторов. Метод параллелограмма. Амплитудная модуляция. Подавление несущей. Модуляция сигналами цветности.
ЧТО НУЖНО ЗНАТЬ О ВЕКТОРАХ
Любознайкин пишет Незнайкину
Дорогой мой Незнайкин!
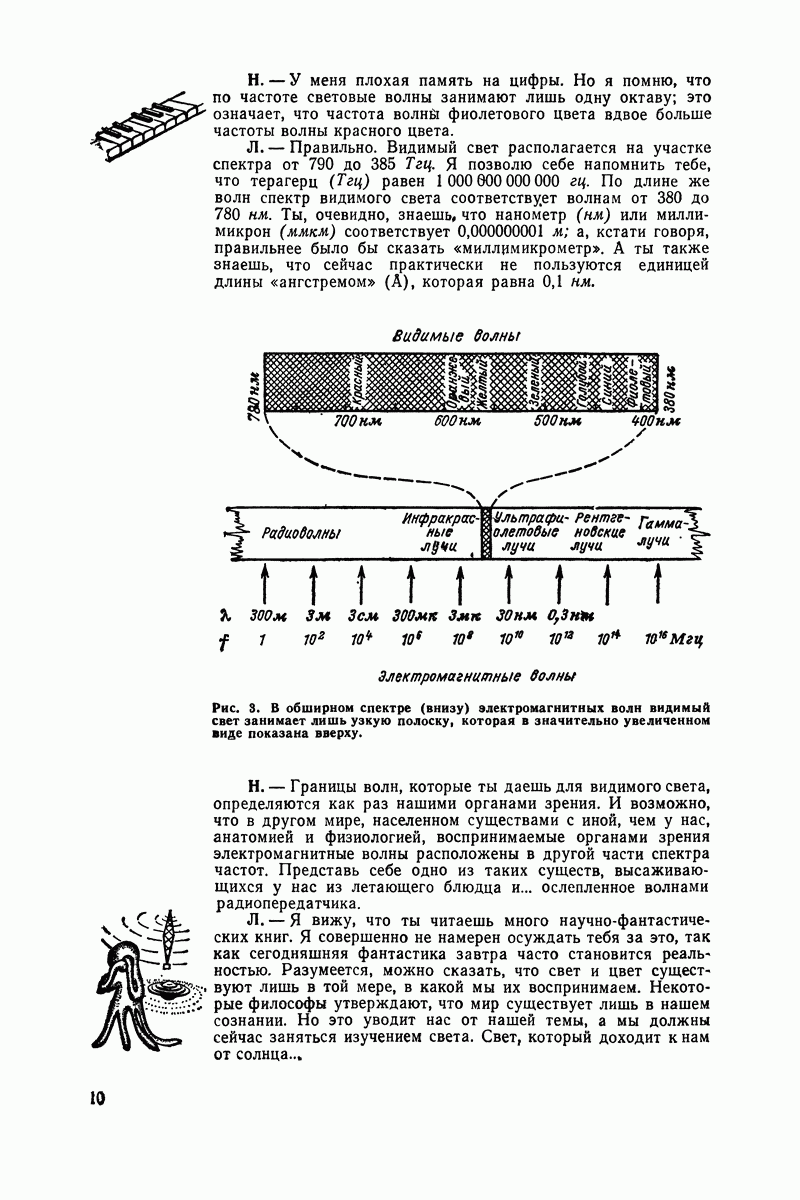
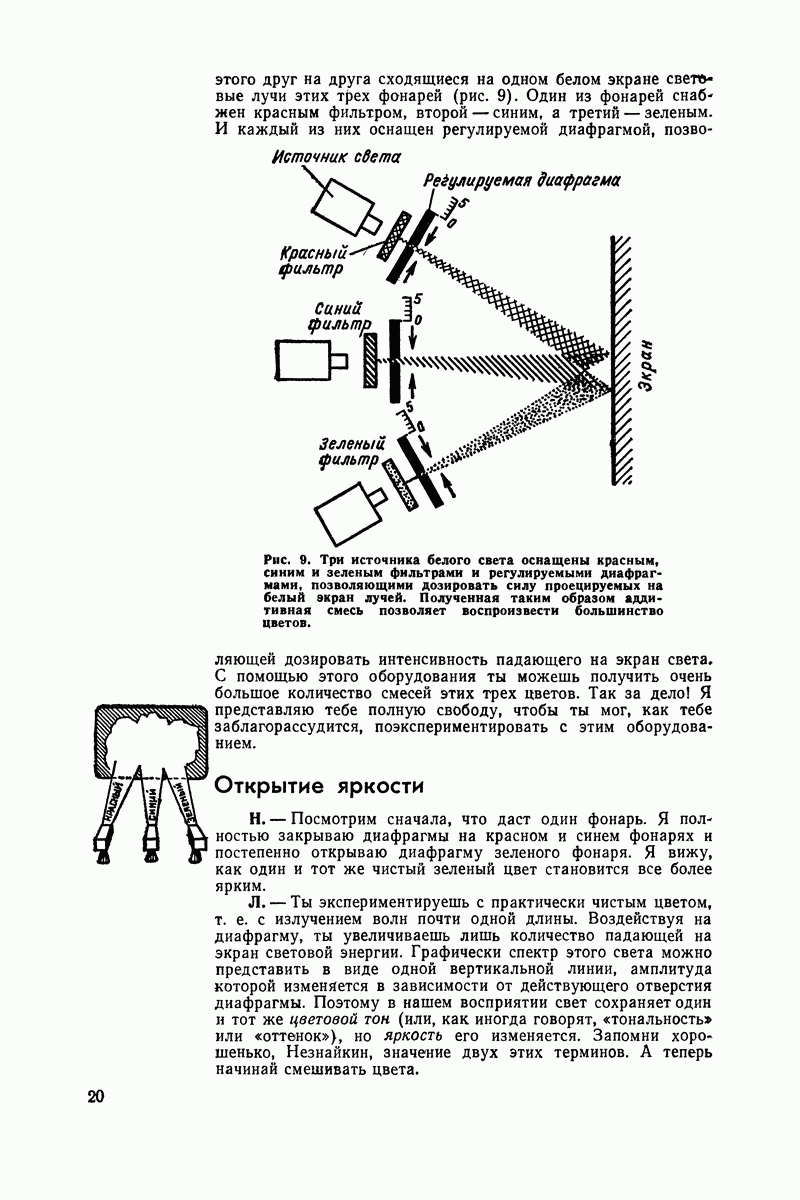
Мне сообщили, что ты намерен присутствовать на лекции моего дяди профессора Радиоля о различных системах цветного телевидения. Превосходная идея, мой друг. Ты, несомненно, знаешь, что именно мой дядя некогда вбил мне в голову основные принципы радиотехники. Я всегда был ему за это признателен, ибо его объяснения отличались удивительной ясностью.
Будут ли они такими же и для тебя? Профессор Радиоль рассчитывает свою лекцию на аудиторию специалистов по радиоэлектронике, обладающих солидными теоретическими знаниями. При изложении системы NTSC, которая лежит в основе всех других систем, он, несомненно, воспользуется диаграммами Френеля, т. е. векторным изображением периодических явлений.
Достаточно ли хорошо освоился ты с векторами и с их использованием при изучении переменных токов? Цели да, то не теряй времени на дальнейшее чтение настоящего письма.
Если же нет, то оно будет тебе полезно тем, что облегчит восприятие лекции, на которой ты собираешься присутствовать.
Рождение синусоиды
Возьмем для примера самое простое периодическое явление, которое ты хорошо знаешь, — переменный ток. Графически он изображается синусоидой. Почему?
Потому, что эта синусоида показывает величину и направление тока для каждого момента. Еще лучше: можно утверждать, что ток изменяется по синусоидальному закону, так как он наводится в витках, вращающихся в магнитном поле. Однако, как мы сейчас увидим, синусоиду можно нарисовать, приведя в равномерное вращательное движение отрезок прямой и фиксируя его проекцию на плоскости.
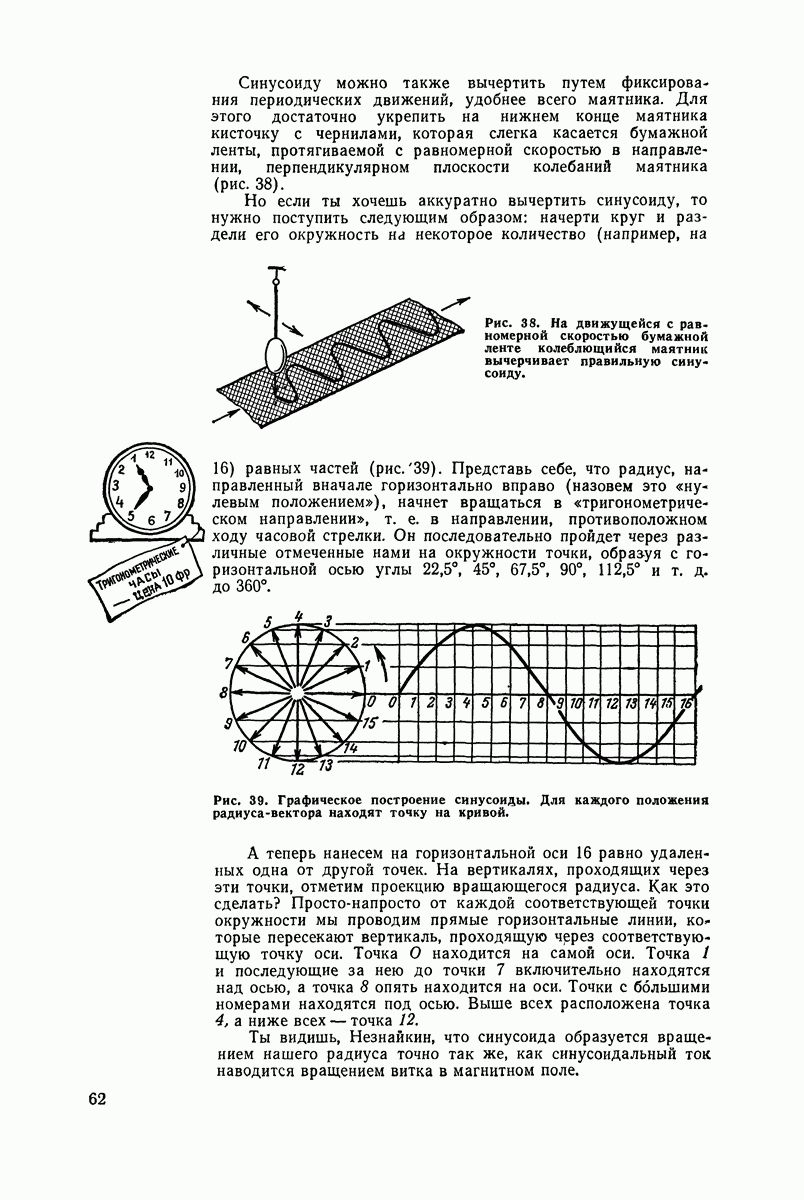
Синусоиду можно также вычертить путем фиксирования периодических движений, удобнее всего маятника. Для этого достаточно укрепить на нижнем конце маятника кисточку с чернилами, которая слегка касается бумажной ленты, протягиваемой с равномерной скоростью в направлении, перпендикулярном плоскости колебаний маятника (рис. 38).
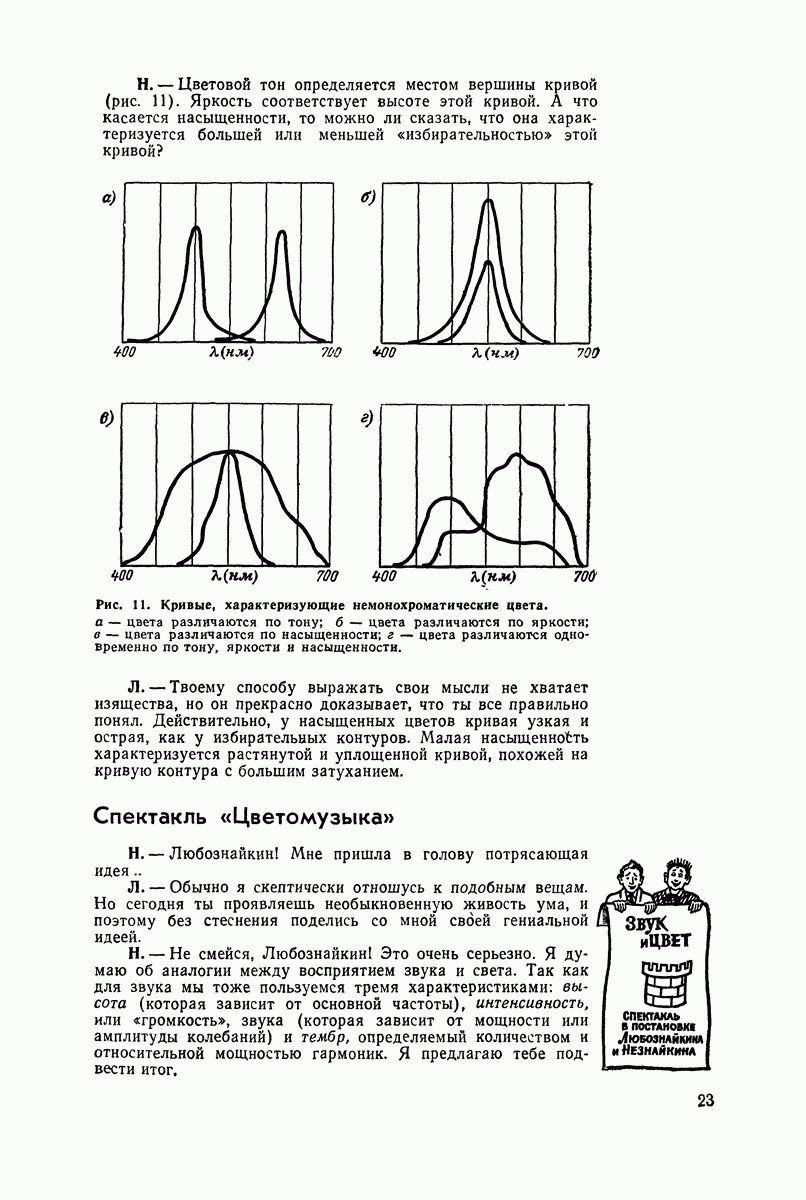
Но если ты хочешь аккуратно вычертить синусоиду, то нужно поступить следующим образом: начерти круг и раздели его окружность на некоторое количество (например, на 16) равных частей (рис. 39).

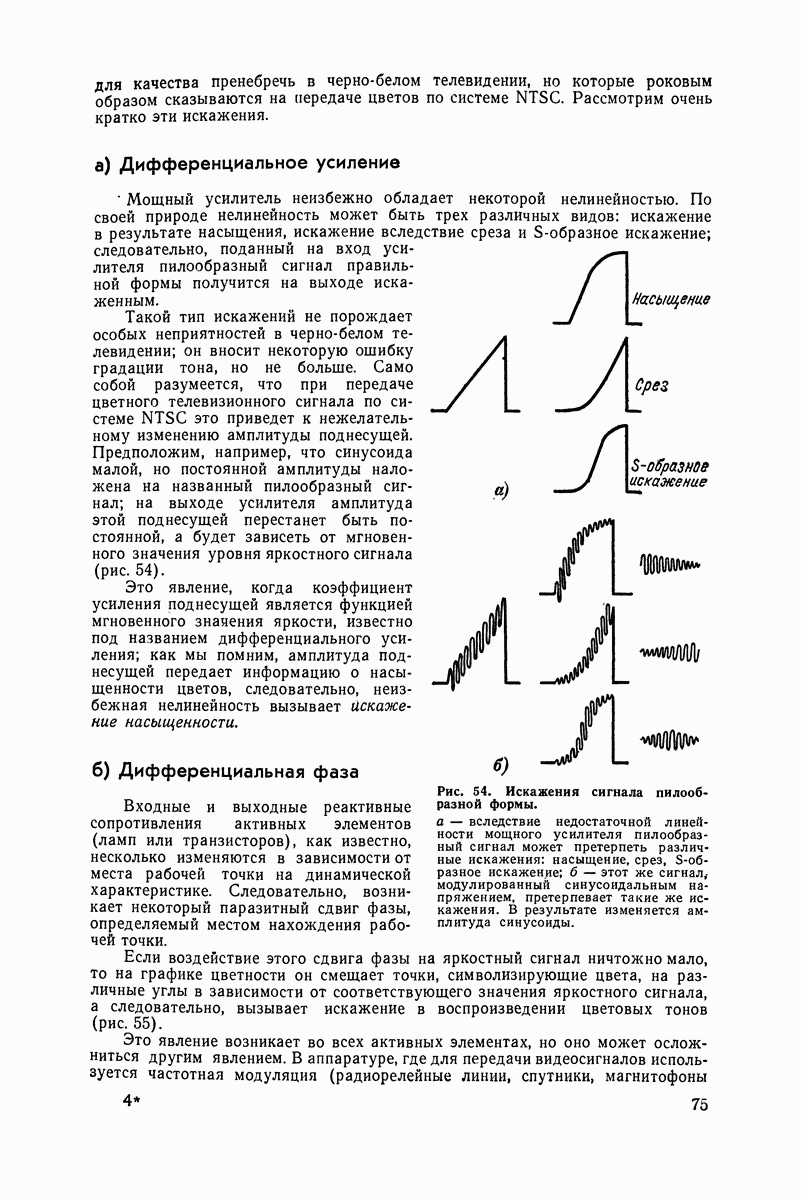
Рис. 38. На движущейся с равномерной скоростью бумажной ленте колеблющийся маятник вычерчивает правильную синусоиду.
Представь себе, что радиус, направленный вначале горизонтально вправо (назовем это «нулевым положением»), начнет вращаться в «тригонометрическом направлении», т. е. в направлении, противоположном I ходу часовой стрелки. Он последовательно пройдет через различные отмеченные нами на окружности точки, образуя с горизонтальной осью углы 22,5°, 45°, 67,5°, 90°, 112,5° и т. д. до 360°.

Рис. 39. Графическое построение синусоиды. Для каждого положения радиуса-вектора находят точку на кривой.
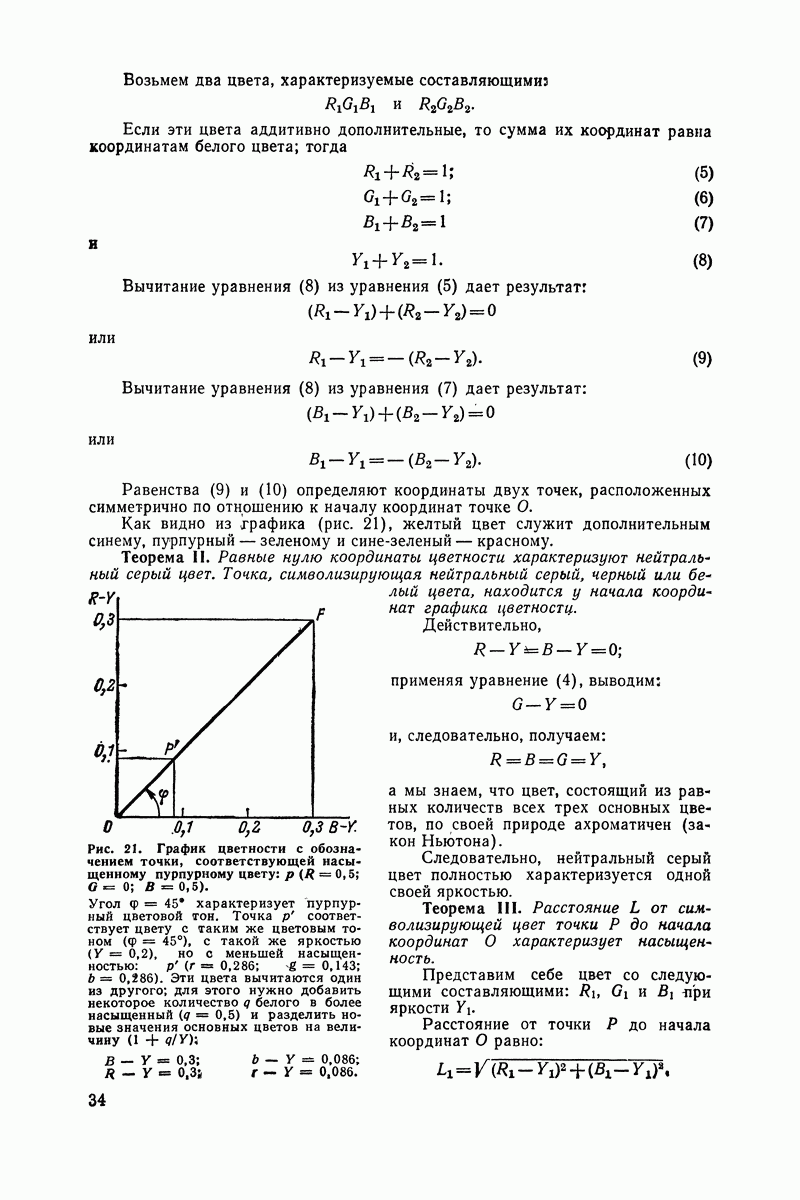
А теперь нанесем на горизонтальной оси 16 равно удаленных одна от другой точек. На вертикалях, проходящих через эти точки, отметим проекцию вращающегося радиуса. Как это сделать? Просто-напросто от каждой соответствующей точки окружности мы проводим прямые горизонтальные линии, которые пересекают вертикаль, проходящую чррез соответствующую точку оси. Точка О находится на самой оси. Точка I и последующие за нею до точки 7 включительно находятся над осью, а точка 8 опять находится на оси. Точки с большими номерами находятся под осью. Выше всех расположена точка 4, а ниже всех — точка 12.
Ты видишь, Незнайкин, что синусоида образуется вращением нашего радиуса точно так же, как синусоидальный ток наводится вращением витка в магнитном поле.
Вот что такое вектор..
Наш радиус характеризуется своими длиной и направлением. Его длина определяет амплитуду изображаемых синусоидой колебаний, а его направление определяет фазу синусоиды. Действительно, наша синусоида могла начаться не из точки О, а из любой другой точки окружности, что привело бы к смещению синусоиды вперед или назад.
Радиус, исходящий из центра круга к одной точке окружности и имеющий определенную длину, мы называем «вектором». Так можно назвать вообще любой ориентированный отрезок прямой.
Вектор полностью определен, когда известна его длина (которую называют модулем), точка, из которой он исходит, и направление, определяемое углом, который он образует с горизонтальной осью. Этот угол называется аргументом.
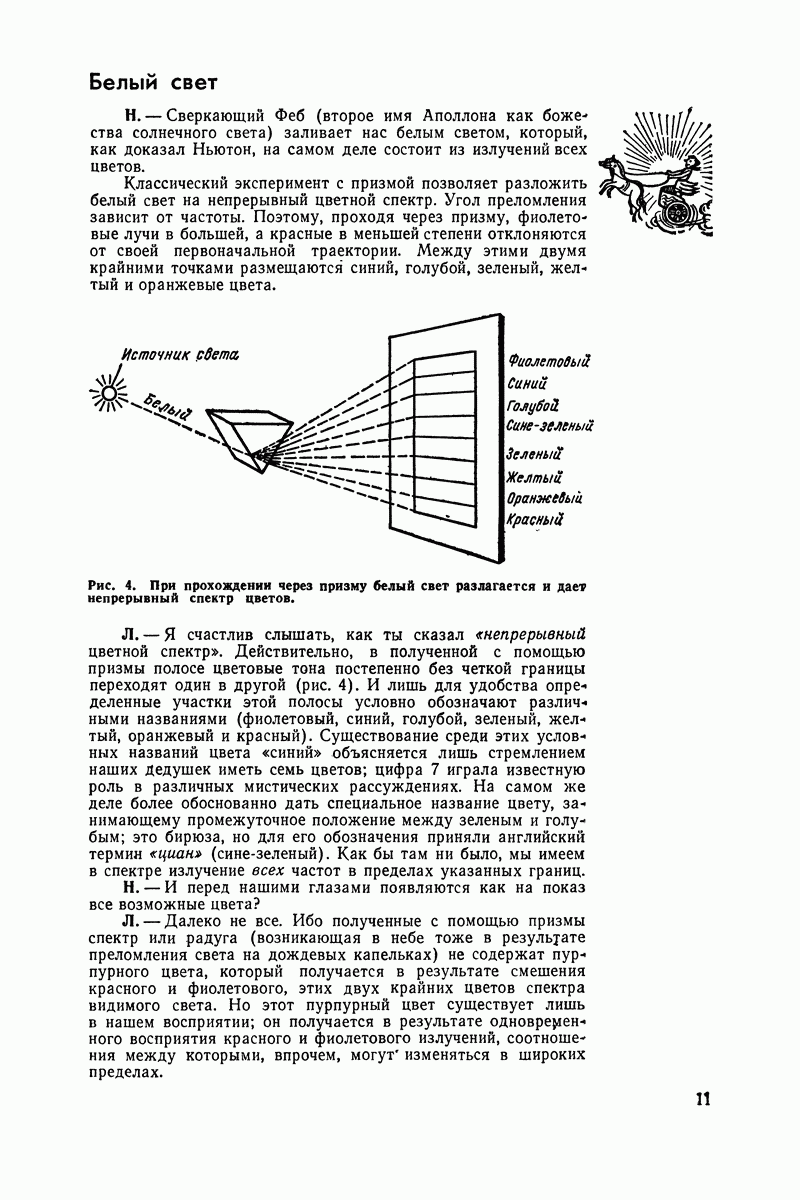
Складывать синусоиды?..
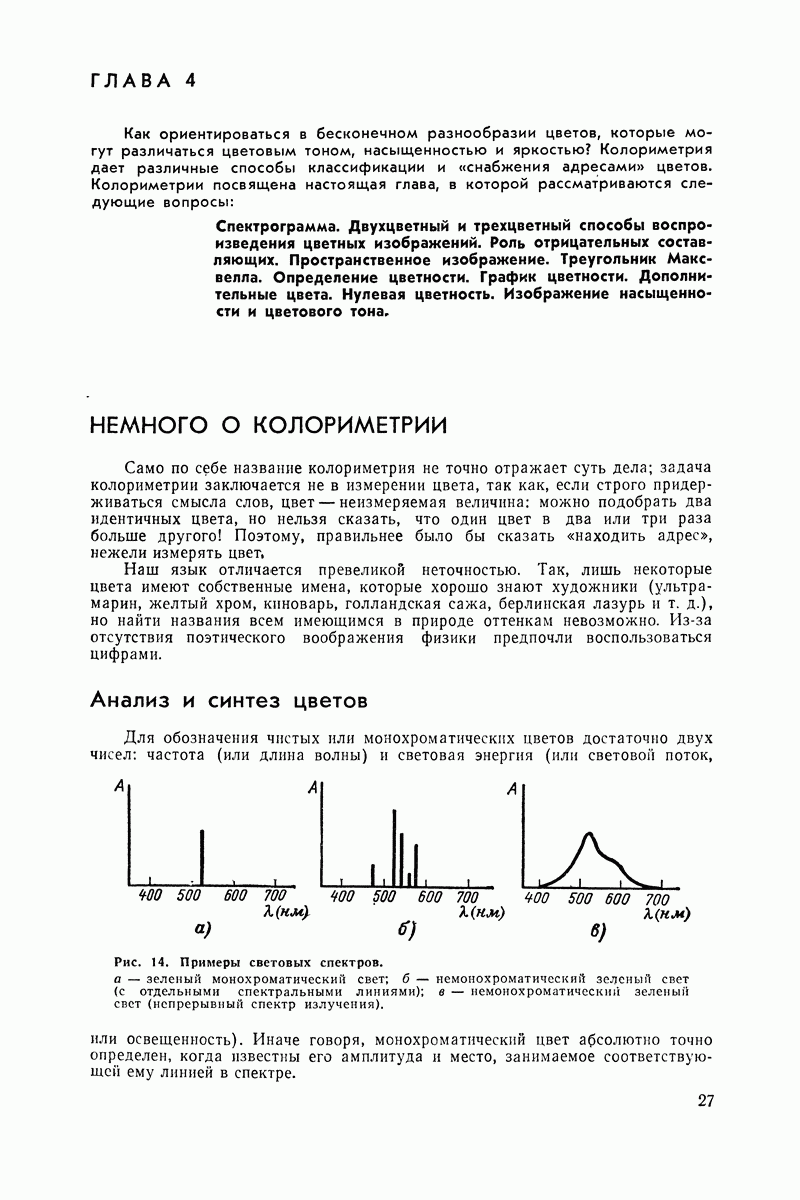
Представь теперь, Незнайкин, что мы имеем два вектора, исходящие из одной точки и вращающиеся с одной и той же скоростью, но смещенные один относительно другого (их называют «связанными»). Они порождают две синусоиды, которые тоже смещены относительно друг друга или, как говорят, «сдвинуты по фазе».

Рис. 40. Сложение двух синусоидальных колебаний с одинаковой амплитудой, но с противоположными фазами.
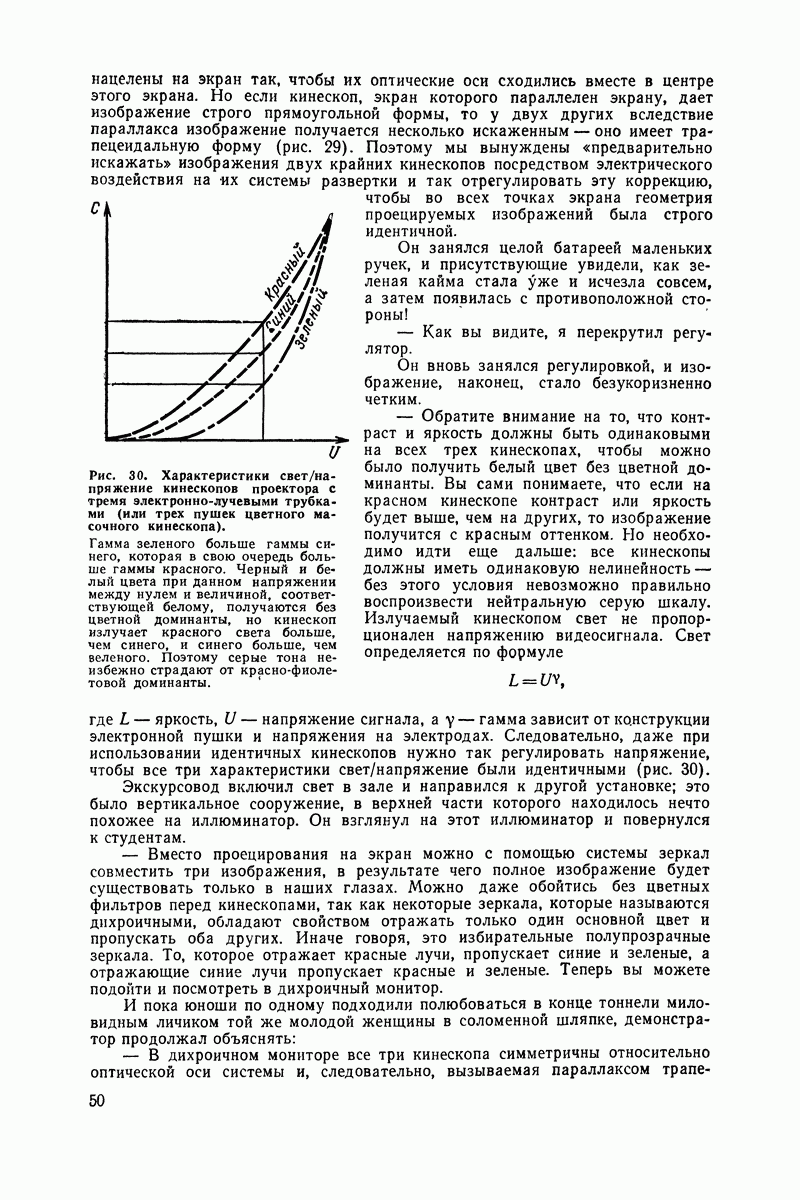
Приступим к сложению этих синусоид, чтобы определить, какой результат получится в случае наложения в одной схеме двух колебаний, изображенных этими синусоидами.

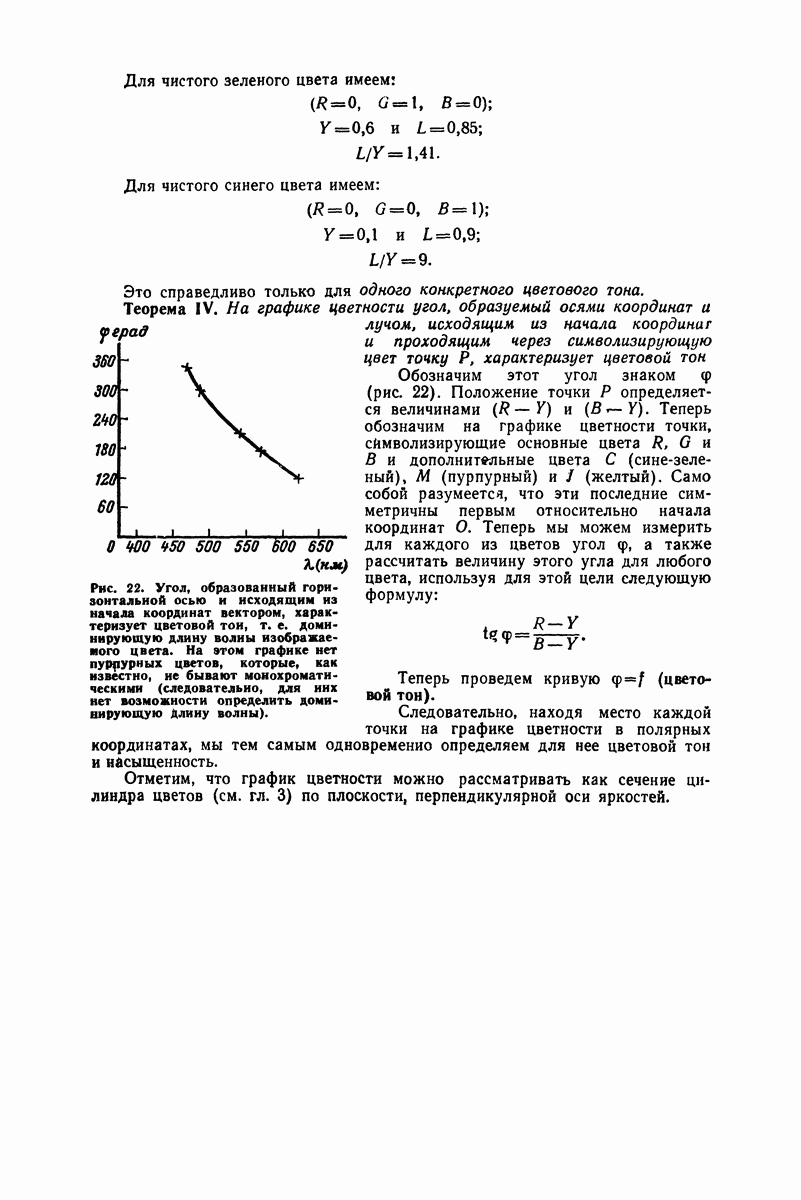
Рис. 41. Изображенные здесь колебания также находятся в противофазе, но они имеют разные амплитуды. Слагаемые синусоиды показаны пунктирными линиями, а результирующая - сплошной линией.
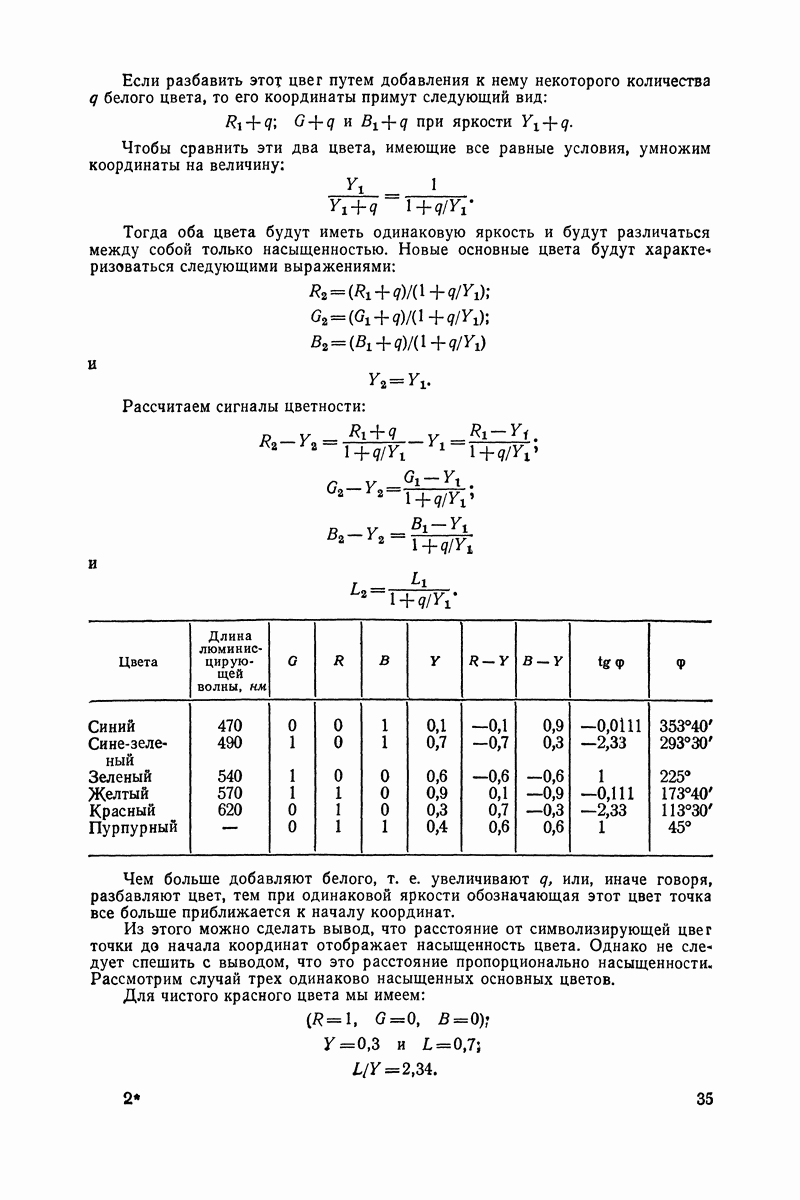
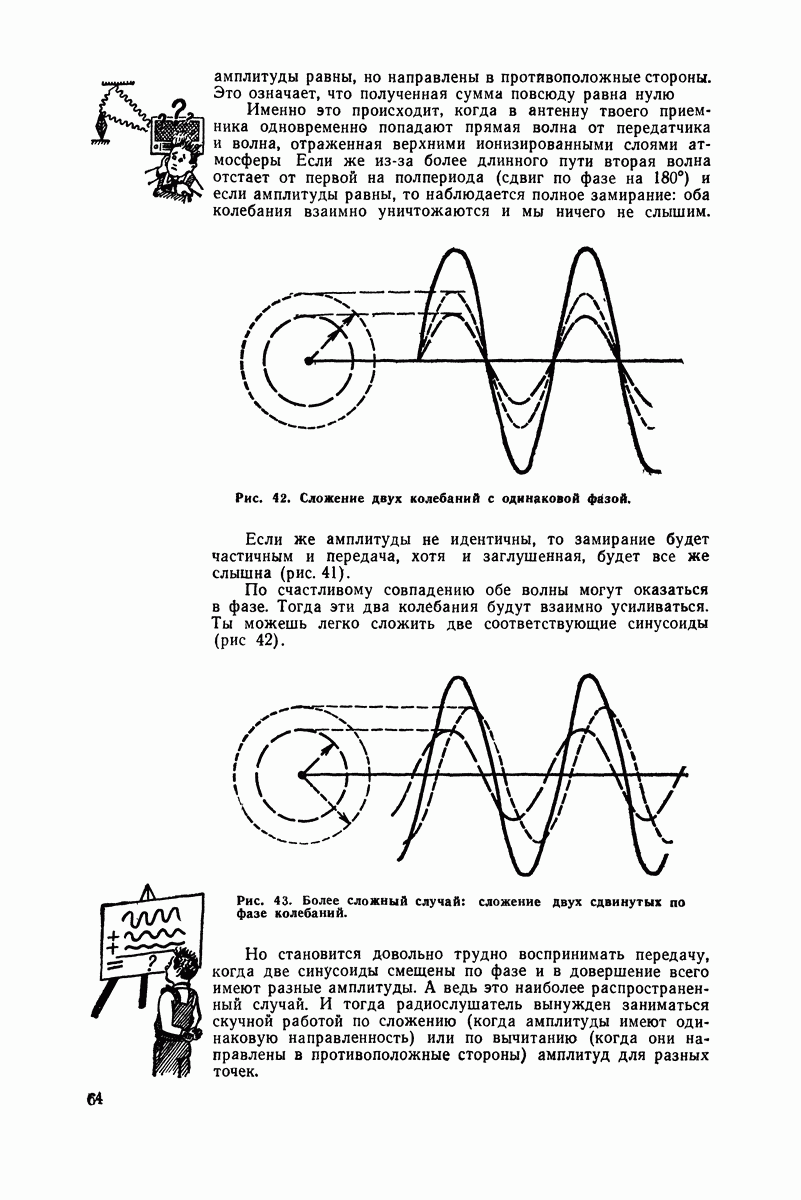
Для начала возьмем наиболее простой случай, когда два вектора имеют одинаковую длину, но направлены в разные стороны, т. е. сдвинуты на 180° (рис. 40). Мы получим две синусоиды с одинаковой амплитудой и периодом, но со смещением на 180°.
Во всех точках мгновенные значения амплитуды равны, но направлены в противоположные стороны. Это означает, что полученная сумма повсюду равна нулю
Именно это происходит, когда в антенну твоего приемника одновременно попадают прямая волна от передатчика и волна, отраженная верхними ионизированными слоями атмосферы Если же из-за более длинного пути вторая волна отстает от первой на полпериода (сдвиг по фазе на 180°) и если амплитуды равны, то наблюдается полное замирание: оба колебания взаимно уничтожаются и мы ничего не слышим.

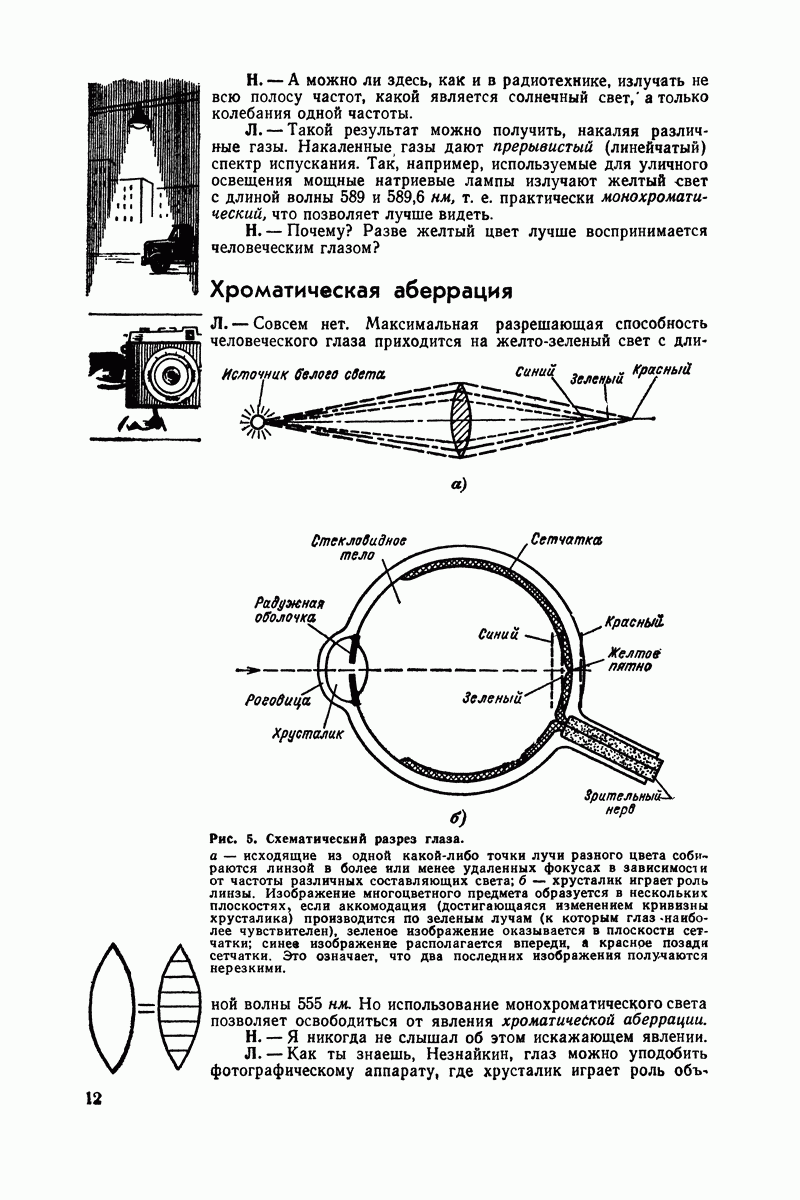
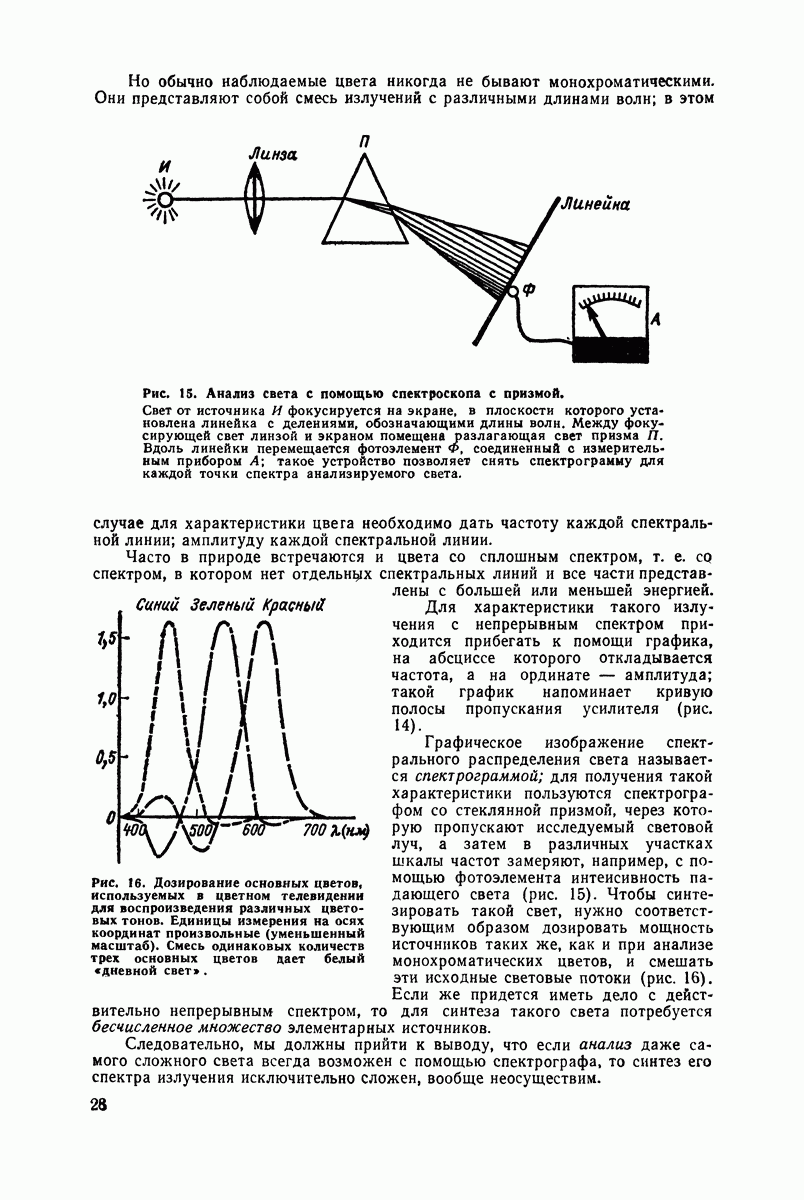
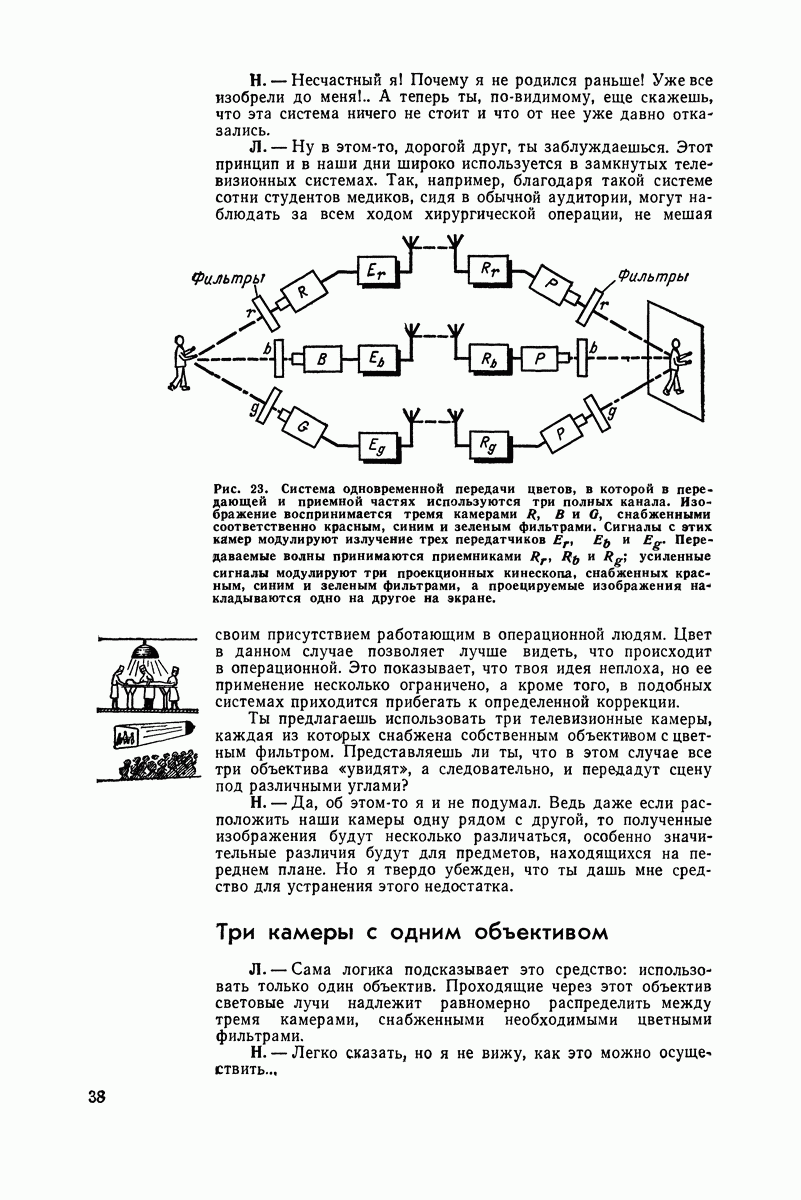
Рис. 42. Сложение двух колебаний с одинаковой фазой.
Если же амплитуды не идентичны, то замирание будет частичным и передача, хотя и заглушенная, будет все же слышна (рис. 41).
По счастливому совпадению обе волны могут оказаться в фазе. Тогда эти два колебания будут взаимно усиливаться. Ты можешь легко сложить две соответствующие синусоиды (рис 42).

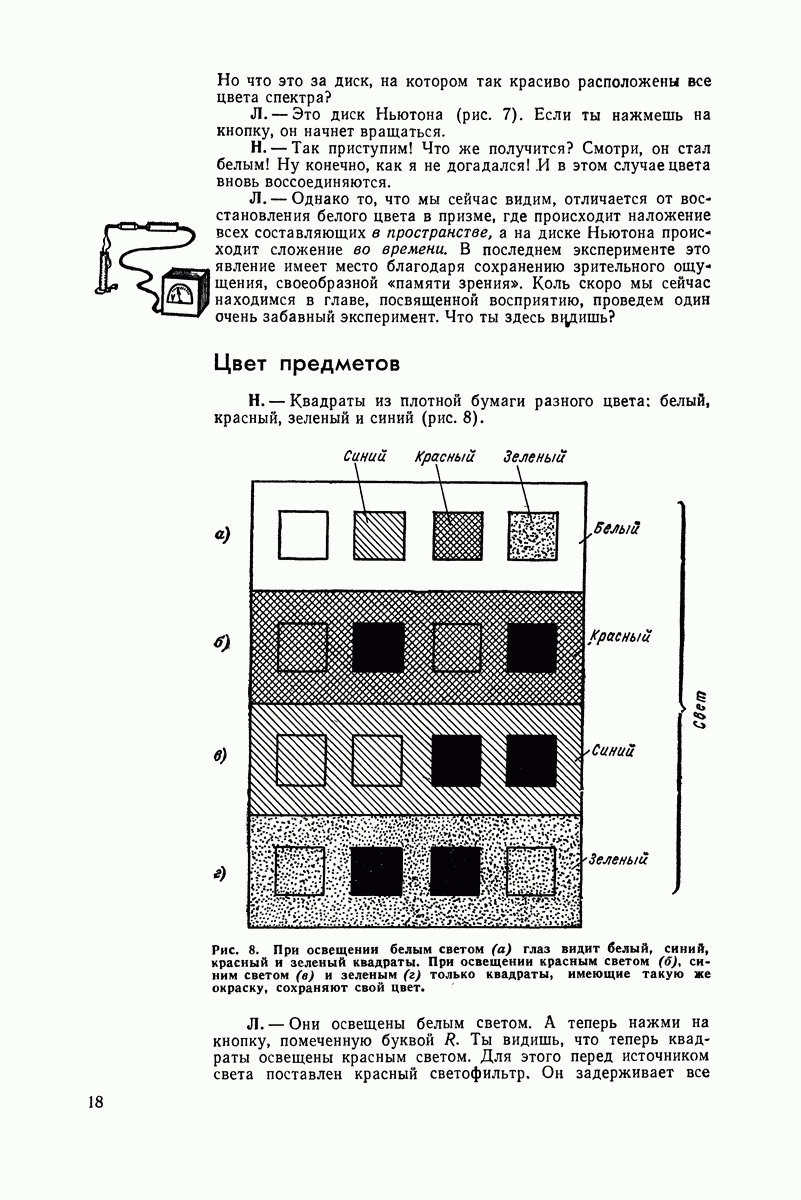
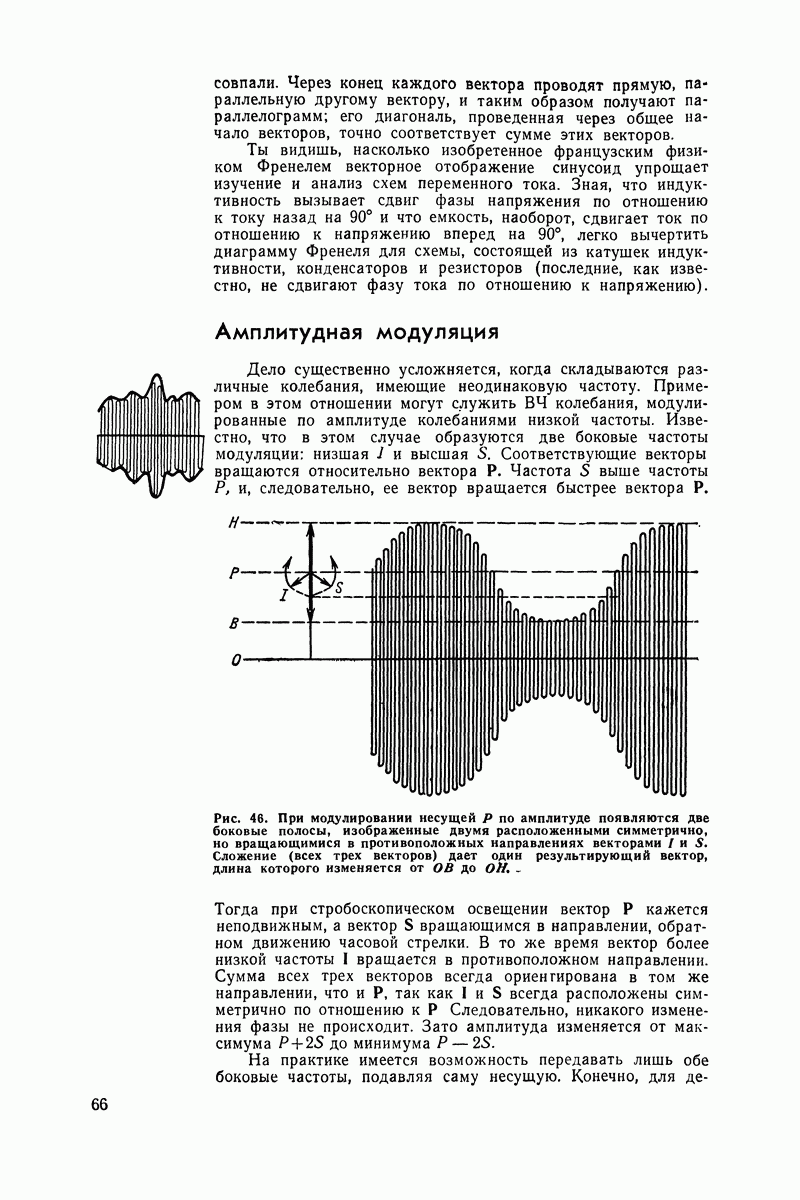
Рис. 43. Более сложный случай: сложение двух сдвинутых по фазе колебаний.
Но становится довольно трудно воспринимать передачу, когда две синусоиды смещены по фазе и в довершение всего имеют разные амплитуды. А ведь это наиболее распространенный случай. И тогда радиослушатель вынужден заниматься скучной работой по сложению (когда амплитуды имеют одинаковую направленность) или по вычитанию (когда они направлены в противоположные стороны) амплитуд для разных точек.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ РУССКОМУ ИЗДАНИЮ
- ОТ АВТОРА
- ГЛАВА 1
- ВОСШЕСТВИЕ ЦВЕТА НА ПРЕСТОЛ
- ГЛАВА 2
- ВЗГЛЯД НА ГЛАЗ
- Белый свет
- Хроматическая аберрация
- Статистические фикции
- Рациональное использование недостатков
- Анатомия и физиология глаза
- Индивидуальные и коллективные послания
- ГЛАВА 3
- ВО ДВОРЦЕ ОТКРЫТИЙ
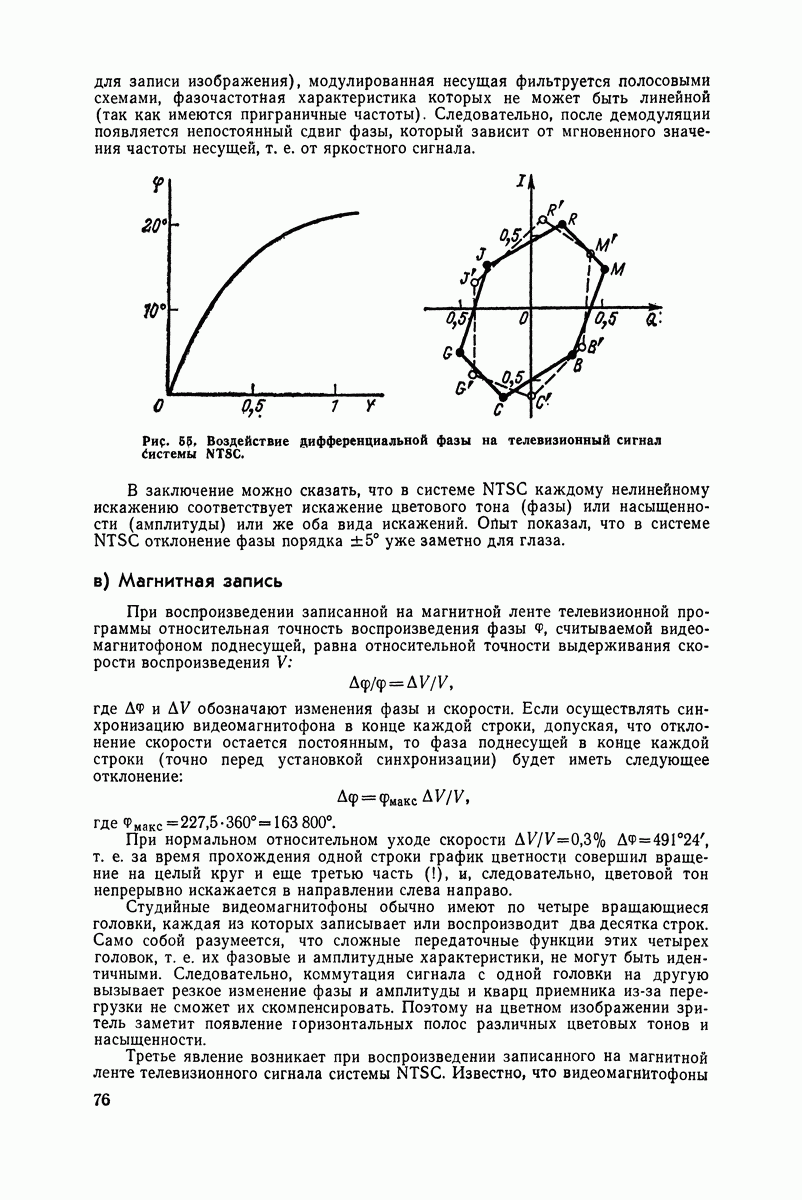
- Цвет предметов
- Вычитание цветов
- Открытие яркости
- Открытие насыщенности
- Бесконечность в кубе
- Это только иллюзия
- ГЛАВА 4
- НЕМНОГО О КОЛОРИМЕТРИИ
- Двухцветный и трехцветный способы воспроизведения цветных изображений
- Треугольник Максвелла
- Яркость и цветность — два кита цветного телевидения
- ГЛАВА 5
- ПЕРЕДАЮЩИЕ СИСТЕМЫ
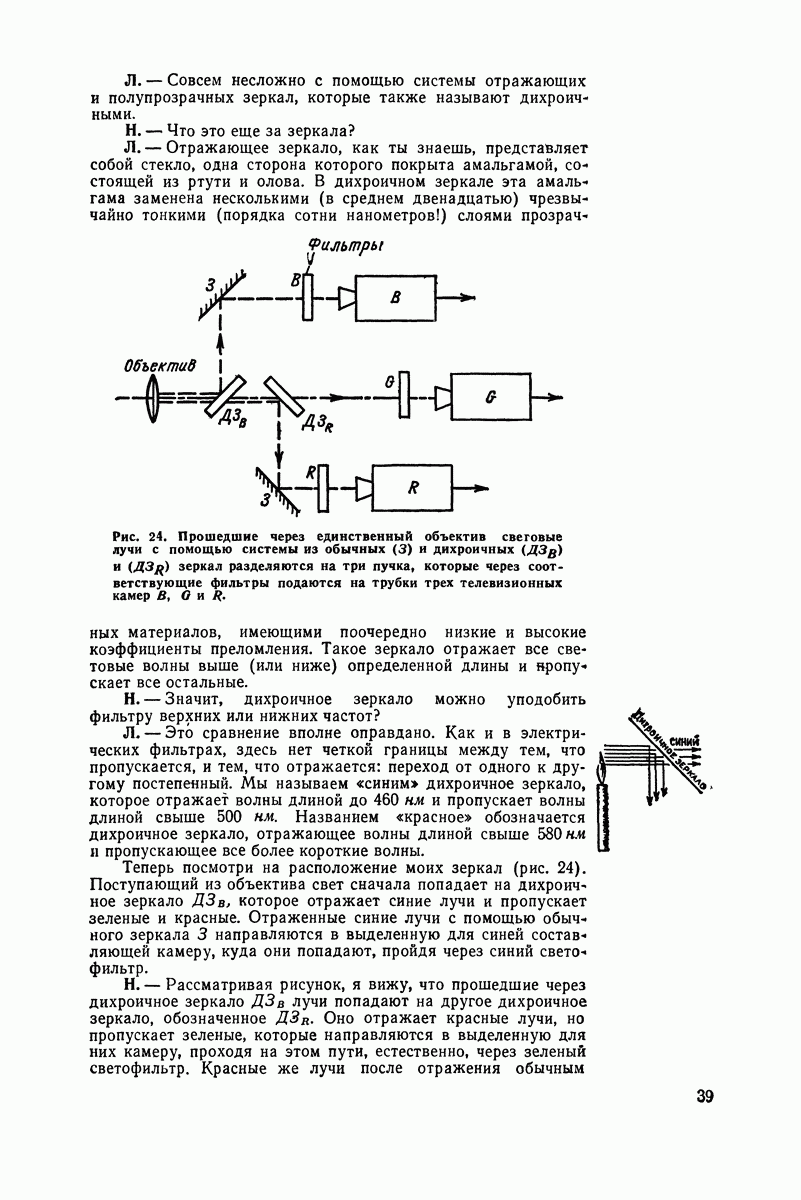
- Три камеры с одним объективом
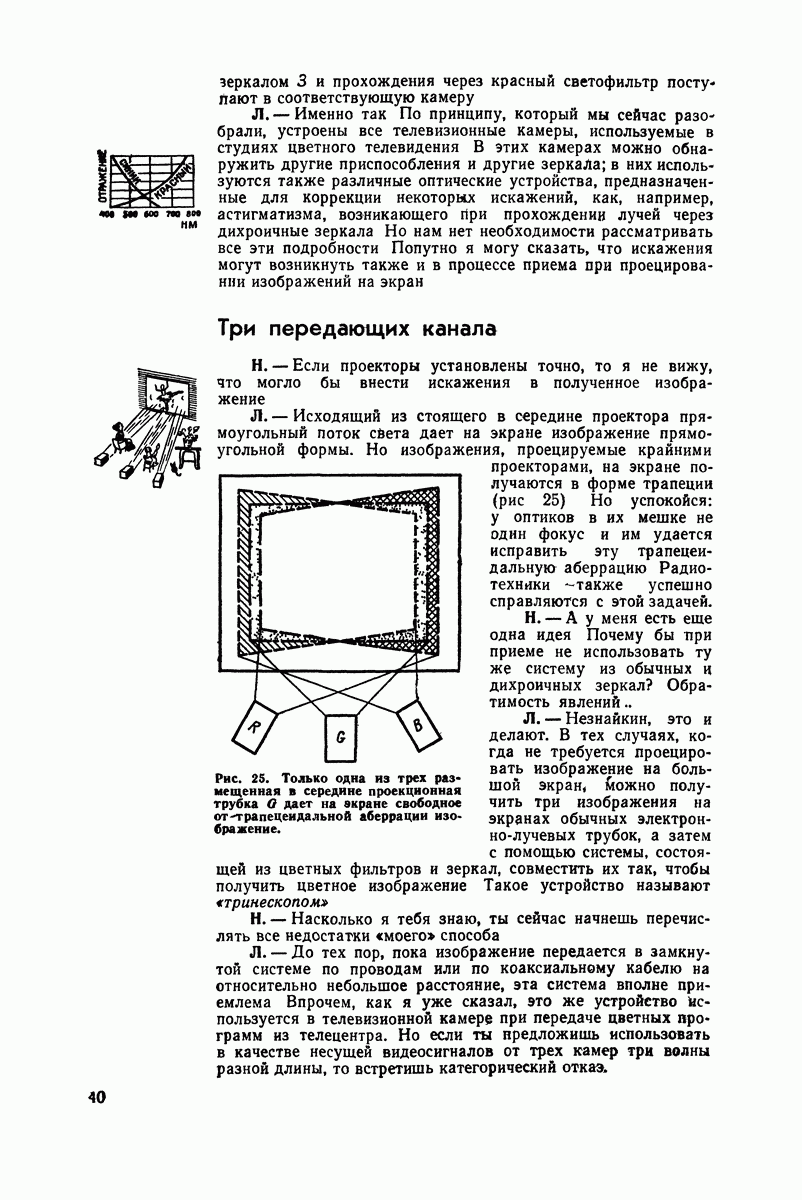
- Три передающих канала
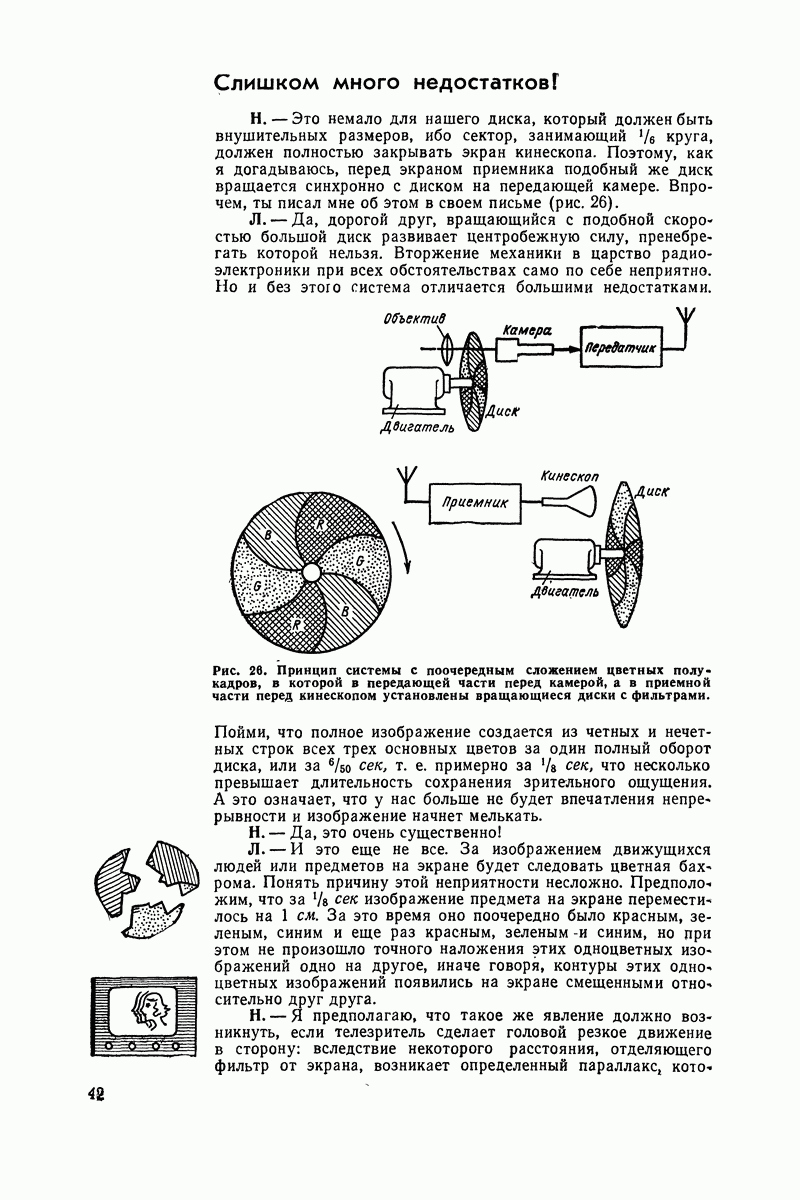
- Поочередное сложение цветных полукадров
- Слишком много недостатков!
- Условия двойной совместимости
- У Незнайкина рождается яркостная идея
- Несущая и поднесущая
- Передача цветности
- ГЛАВА 6
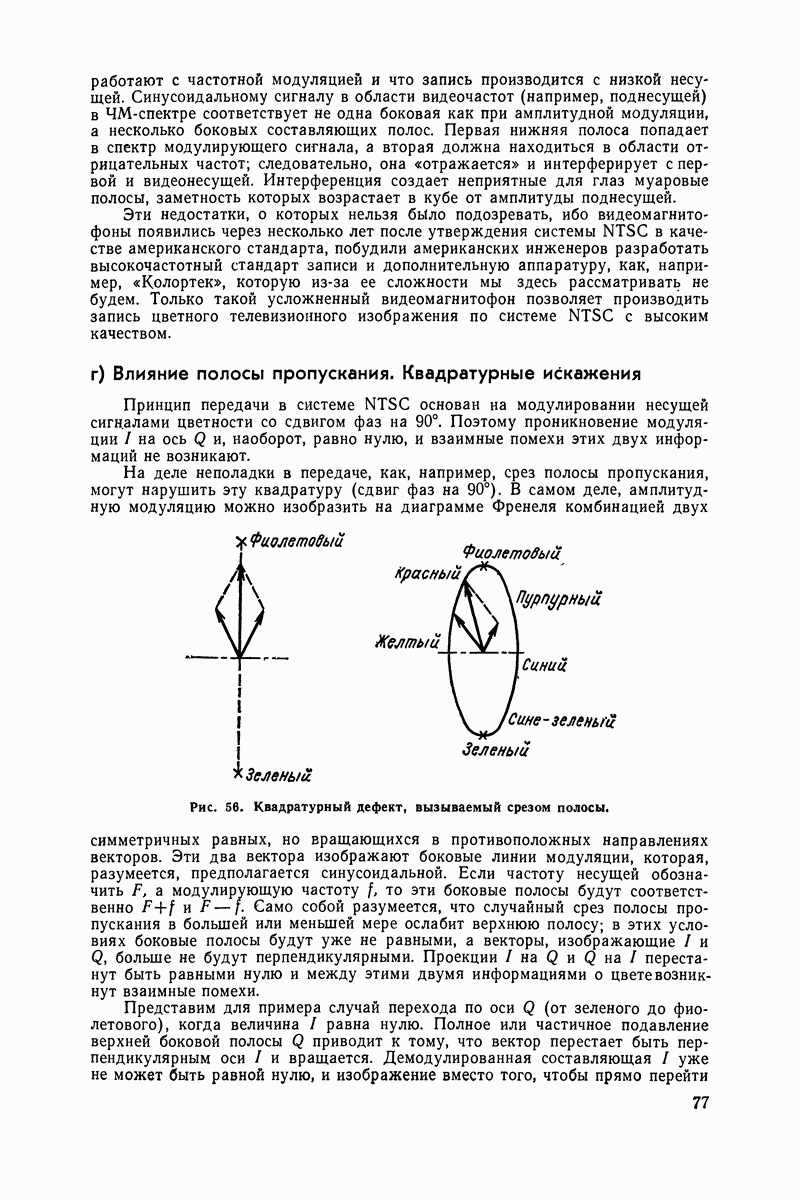
- В МУЗЕЕ ЭЛЕКТРОННО-ЛУЧЕВОЙ ТРУБКИ
- ГЛАВА 7
- НАЦИОНАЛЬНЫЙ ТЕЛЕВИЗИОННЫЙ ЦЕНТР
- Камеры
- Телевизионный кинопроектор
- ГЛАВА 8
- ЧТО НУЖНО ЗНАТЬ О ВЕКТОРАХ
- Лучше складывать векторы
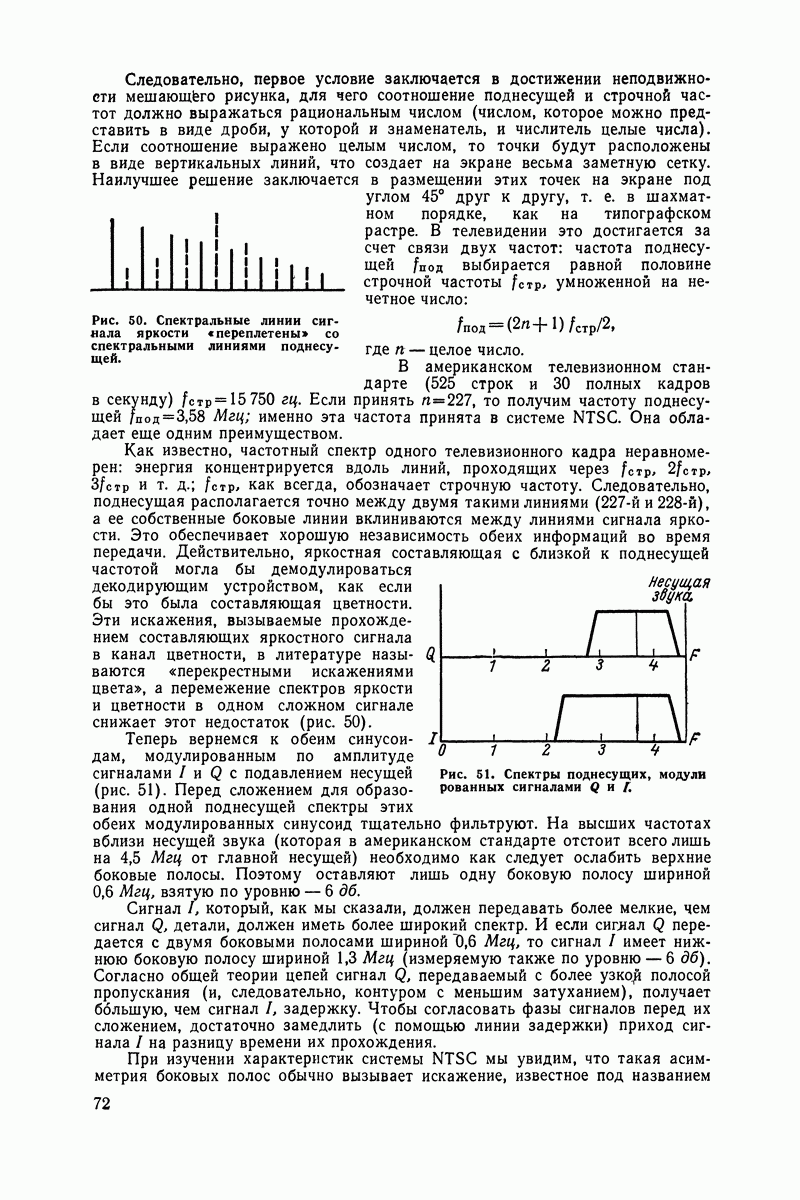
- Амплитудная модуляция
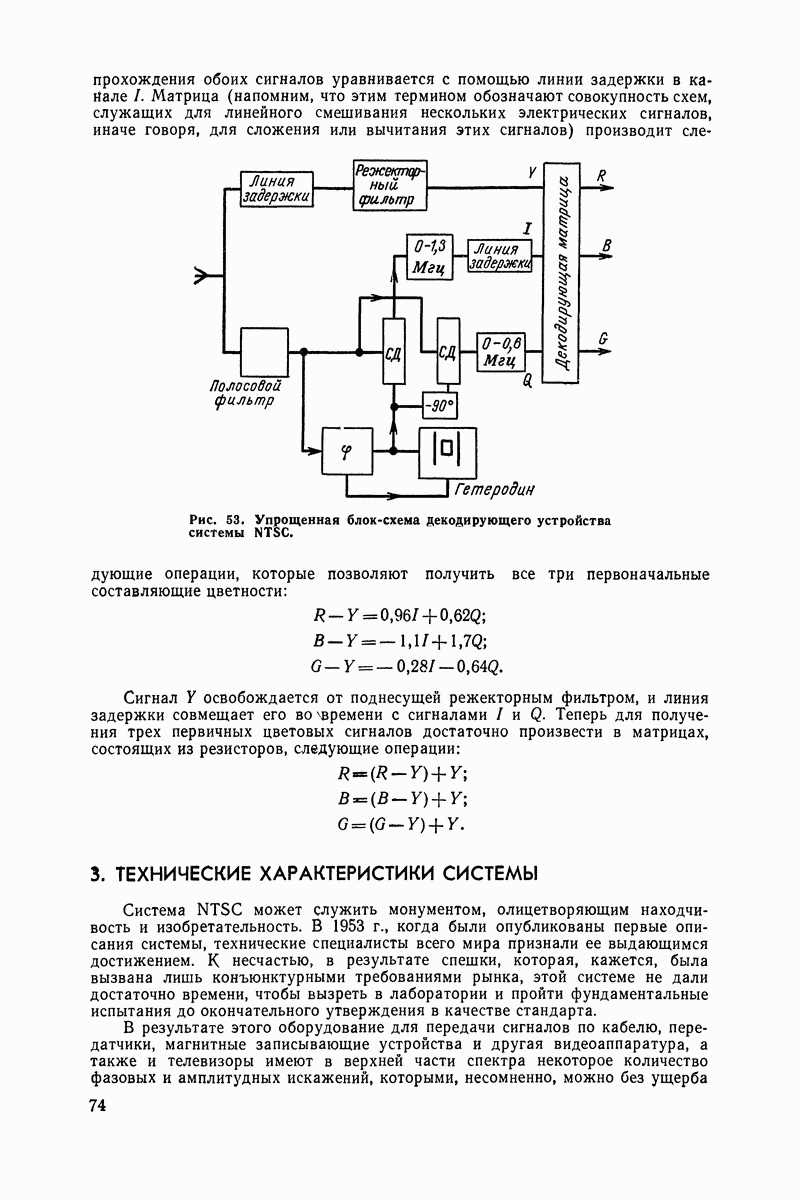
- Хитрость системы NTSC
- ГЛАВА 9
- РАЗЛИЧНЫЕ СОВМЕСТИМЫЕ СИСТЕМЫ
- Система NTSC
- Система PAL
- Система SECAM
- ГЛАВА 10
- АНАЛИЗ ТЕЛЕВИЗИОННОГО ПРИЕМНИКА СИСТЕМЫ SECAM
- Хитрости в канале яркости
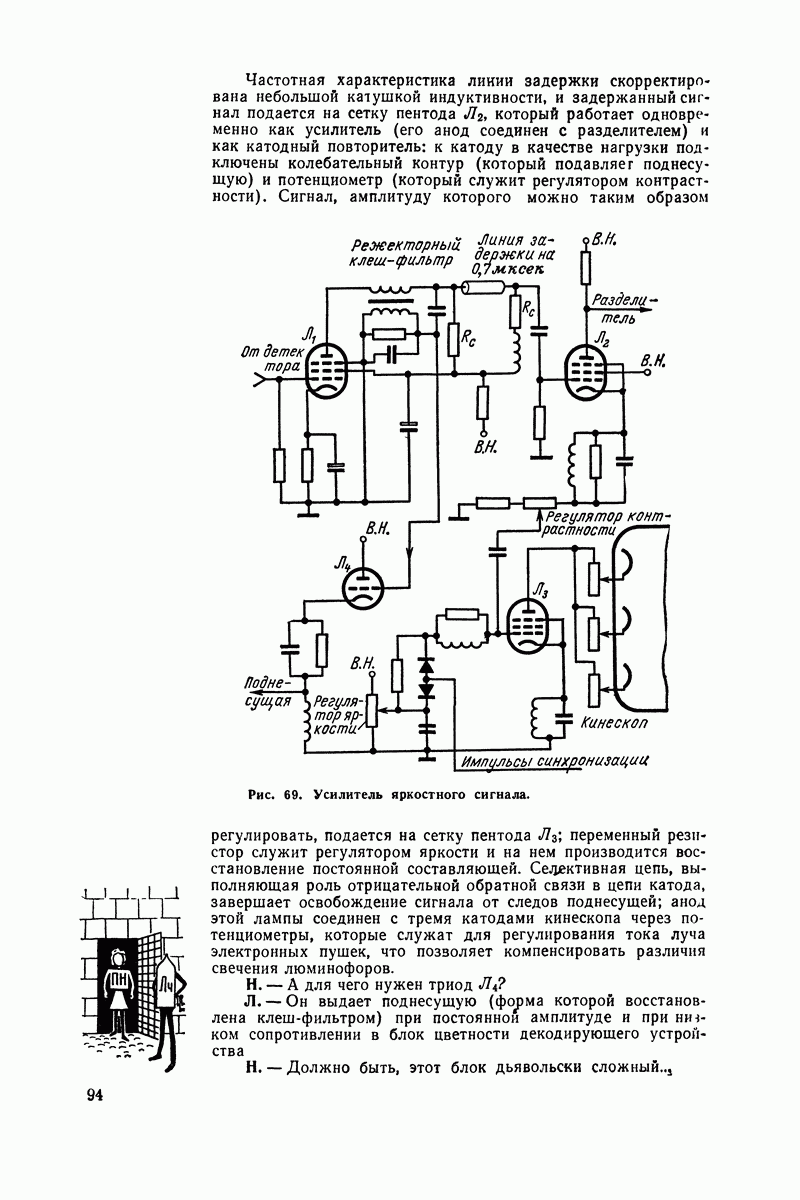
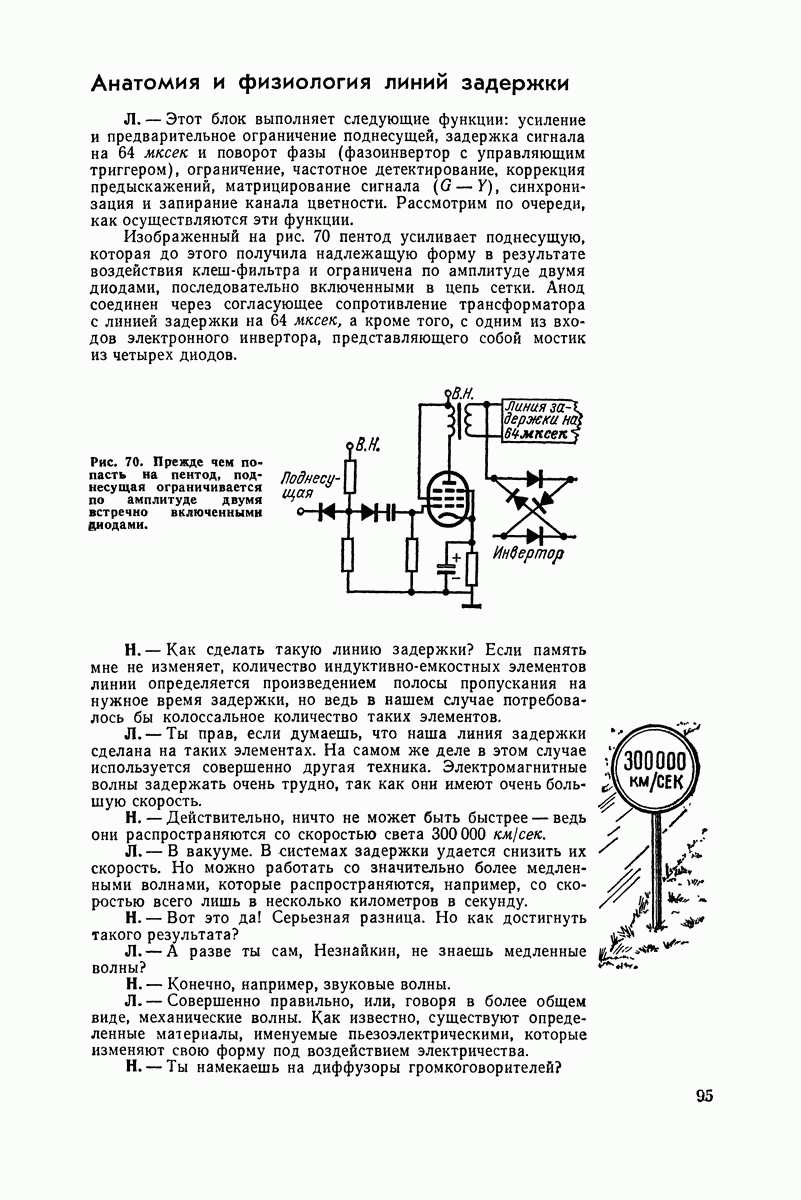
- Анатомия и физиология линий задержки
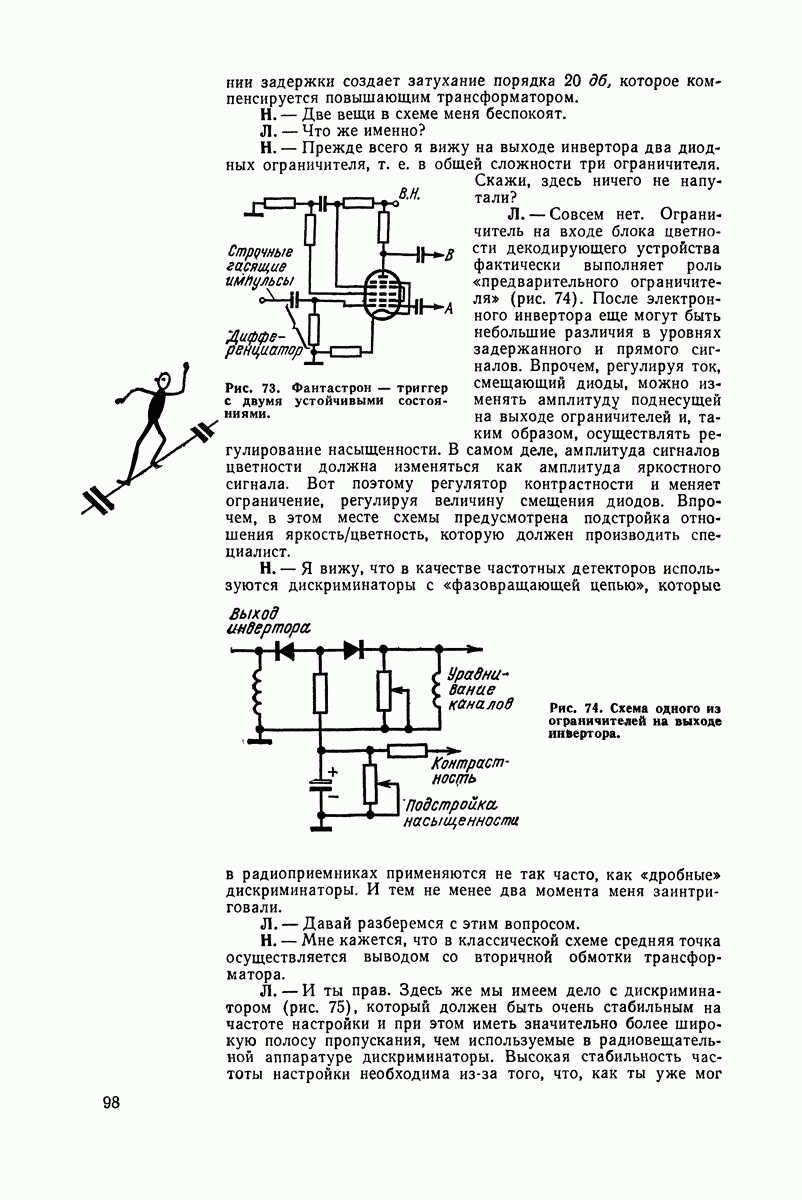
- Триггер, генератор, ограничители и дискриминаторы
- В царстве видеосигналов
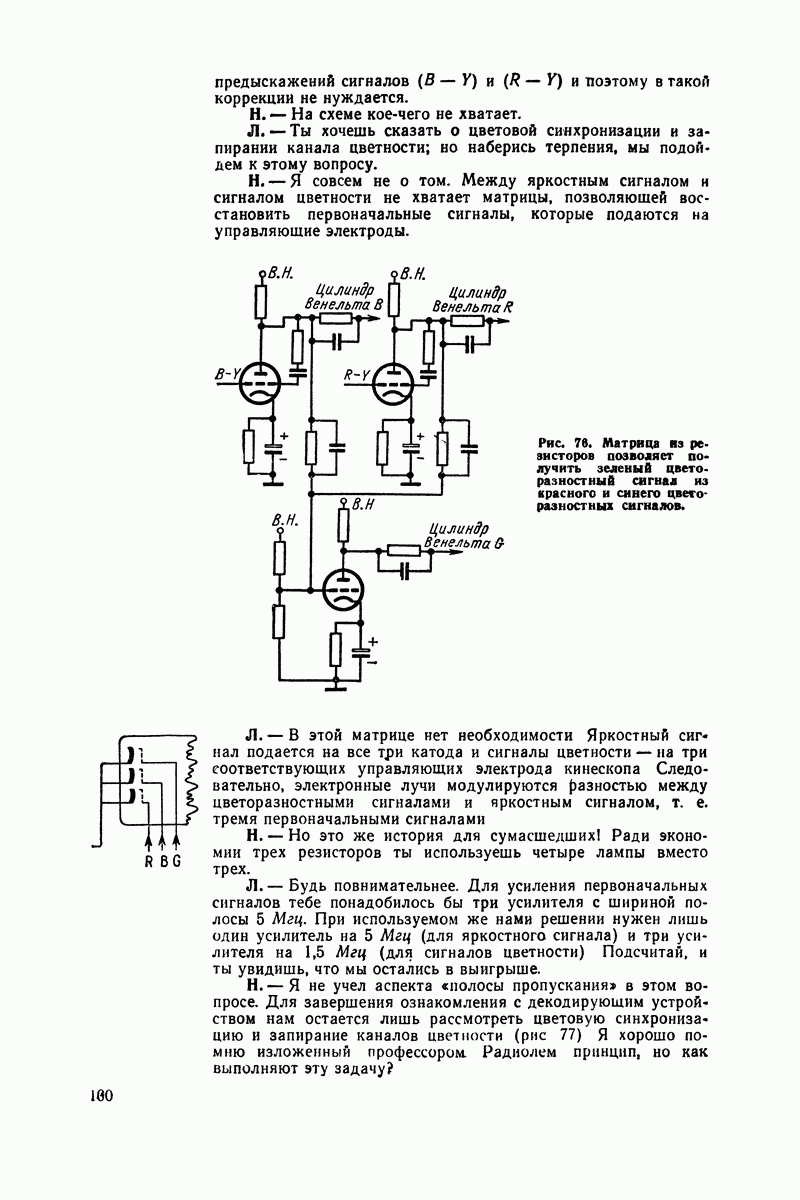
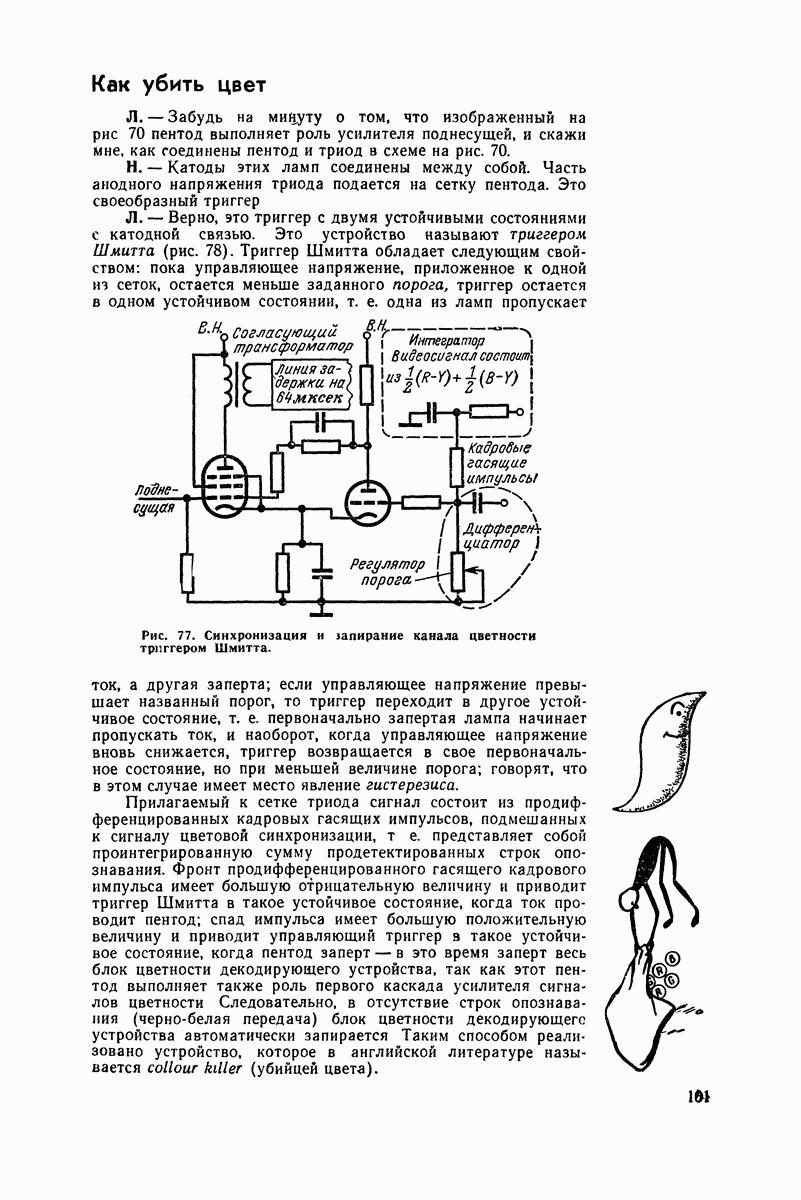
- Как убить цвет
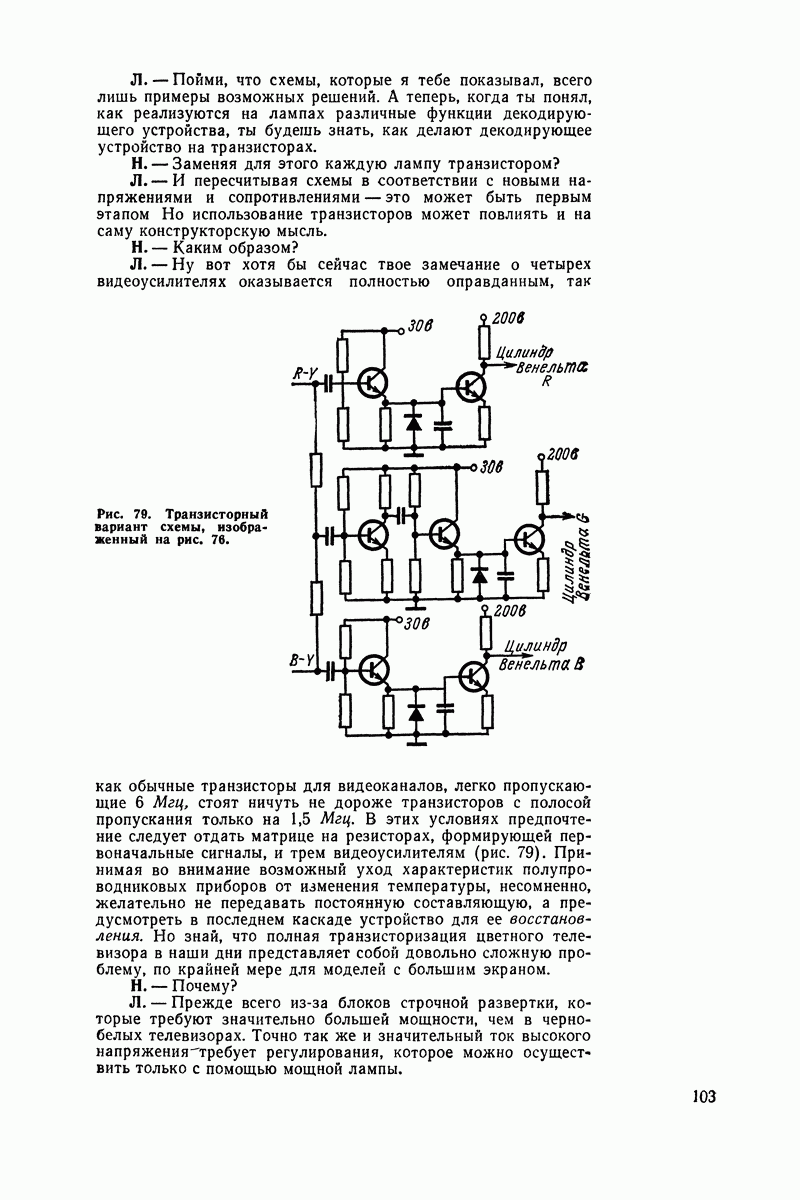
- Полупроводниковые приборы вместо вакуумных
- ГЛАВА 11
- УСТАНОВКА И РЕГУЛИРОВКА ТЕЛЕВИЗОРА. СПЕЦИАЛЬНАЯ КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА
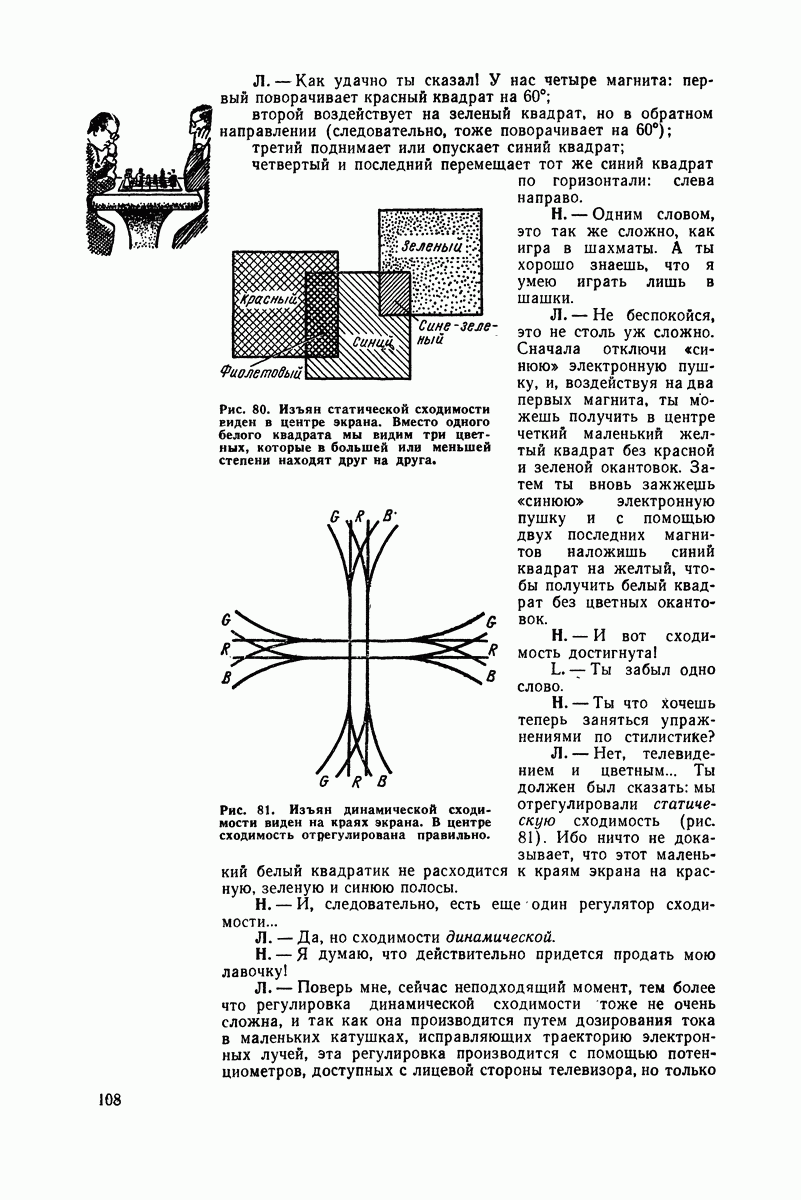
- Пять минут на регулировку цветового тона фона
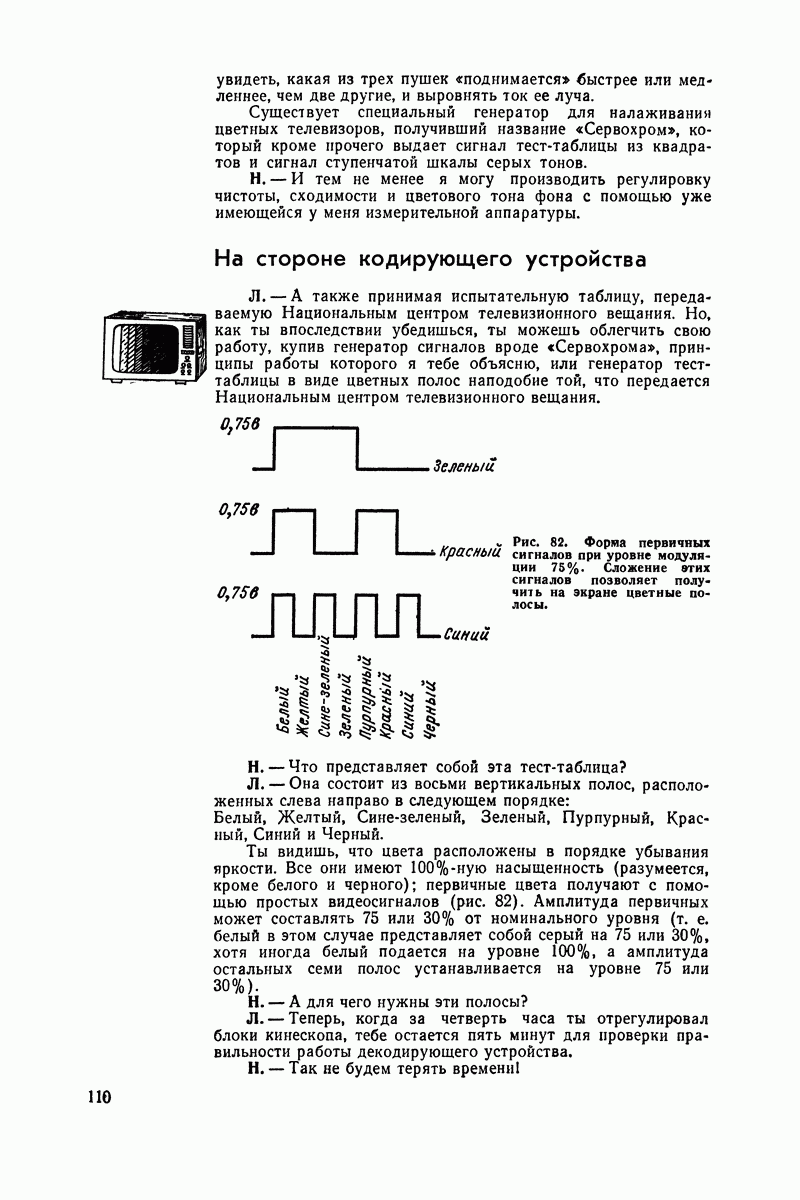
- На стороне кодирующего устройства
- Действительно универсальный генератор
- В КАЧЕСТВЕ ЗАКЛЮЧЕНИЯ
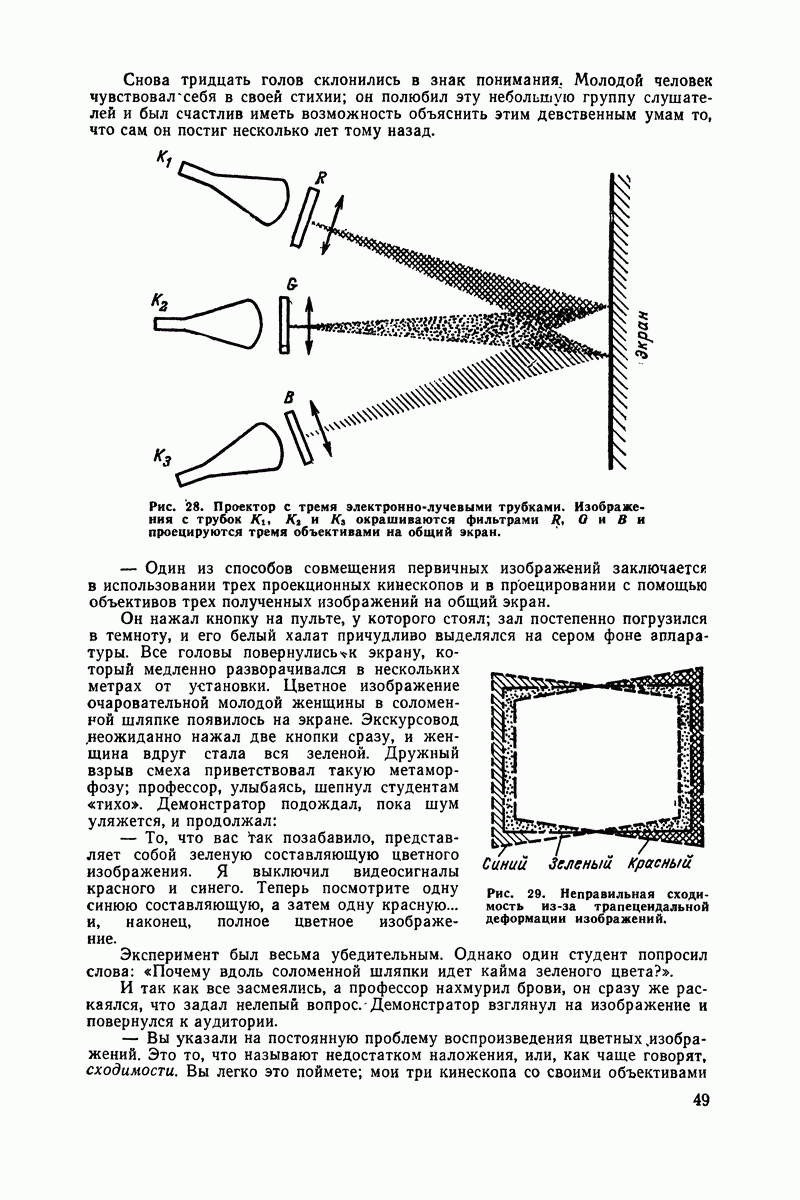
- Чудо цветного телевидения