4. МНОГОШАГОВЫЕ ПРОЦЕССЫ ПРИНЯТИЯ РЕШЕНИЙ

В качестве приложения введенных в предыдущих разделах понятий мы рассмотрим несколько основных типов задач, связанных с многошаговым принятием решений в расплывчатых условиях. Необходимо, однако, подчеркнуть, что основная задача последующего изложения — иллюстрация понятий расплывчатых целей, ограничений и решений на ряде примеров, а не развитие общей теории многошаговых процессов принятия решений, в которые тем или иным образом входит расплывчатость.

Для простоты будем предполагать, что управляемая система А является инвариантной по времени детерминированной системой с конечным числом состояний. Именно, каждое состояние в котором система А находится в момент времени принадлежит заданному конечному множеству возможных состояний при этом имеющий место в момент входной сигнал является элементом множества Эволюция системы во времени описывается уравнением состояния

в котором — заданная функция, отображающая в X. Таким образом, представляет собой последующее состояние для при входном сигнале Если является случайной функцией, — стохастическая система, состояние которой в момент характеризуется распределением вероятностей на X, условным по . Аналогично если — расплывчатая функция, то А является

расплывчатой системой [21], состояние которой в момент есть условное по расплывчатое множество, характеризуемое функцией принадлежности вида Так как подобные системы в последующих разделах рассматриваться не будут, то функция будет считаться нерасплывчатой, если только особо не оговорено противное.

Предполагается, что в каждый момент времени на входную переменную наложено расплывчатое ограничение С, являющееся расплывчатым множеством в с функцией принадлежности . Кроме того, считается, что цель — расплывчатое множество в X, определяемое функцией принадлежности , где N - время окончания процесса. Эти предположения являются общими для большинства рассматриваемых ниже задач. Предполагается, что система описывается уравнением (25), в котором — заданная неслучайная функция. Считается также, что заданы начальное состояние и фиксированное время окончания процесса Задача заключается в нахождении максимизирующего решения.

Применяя уравнение (20), можно записать решение, рассматриваемое как разложимое расплывчатое множество , в виде

где — расплывчатое множество в индуцирующее в X. Для функций принадлежности имеем

где может быть выражено как функция от путем последовательного применения соотношения

Задача сводится к нахождению последовательности входных воздействий максимизирующей в формуле (27). Как обычно в многошаговых процессах, целесообразно представить решение в виде

где — принятая «стратегия», т. е. принятое правило выбора входного воздействия в зависимости от реализовавшегося После этого для получения как так и максимизирующего (оптимального) решения можно применить метод динамического программирования. Действительно, используя (26) и (25), имеем

Если у — константа, произвольная функция аргумента то справедливо тождество

Следовательно, (28) можно переписать в виде

где

может рассматриваться как функция принадлежности расплывчатой цели в момент индуцированной заданной целью в момент

Повторяя процесс обратных итераций, получаем систему рекуррентных уравнений

которая дает решение задачи. Таким образом, максимизирующее решение получается последовательной максимизацией величин в (31), причем определяется как функция от

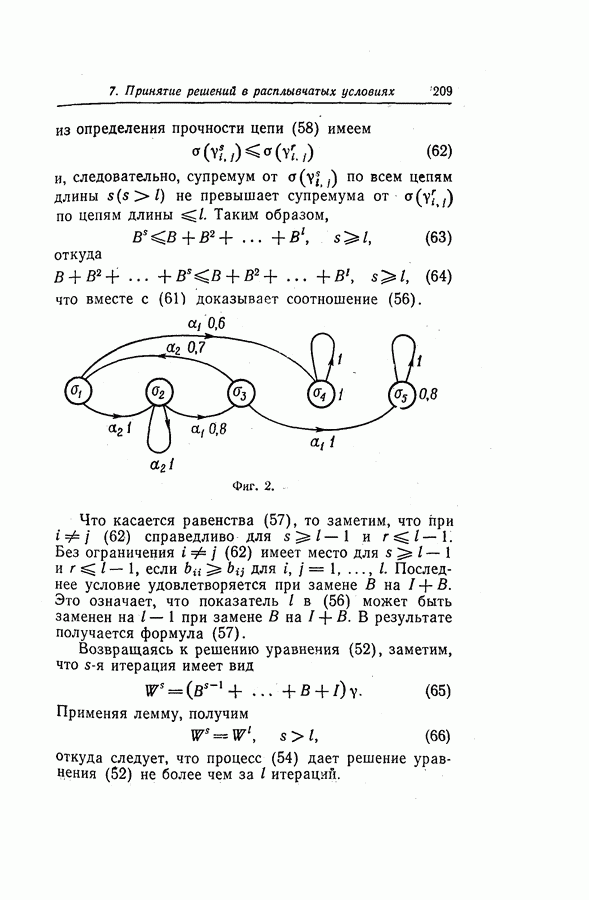
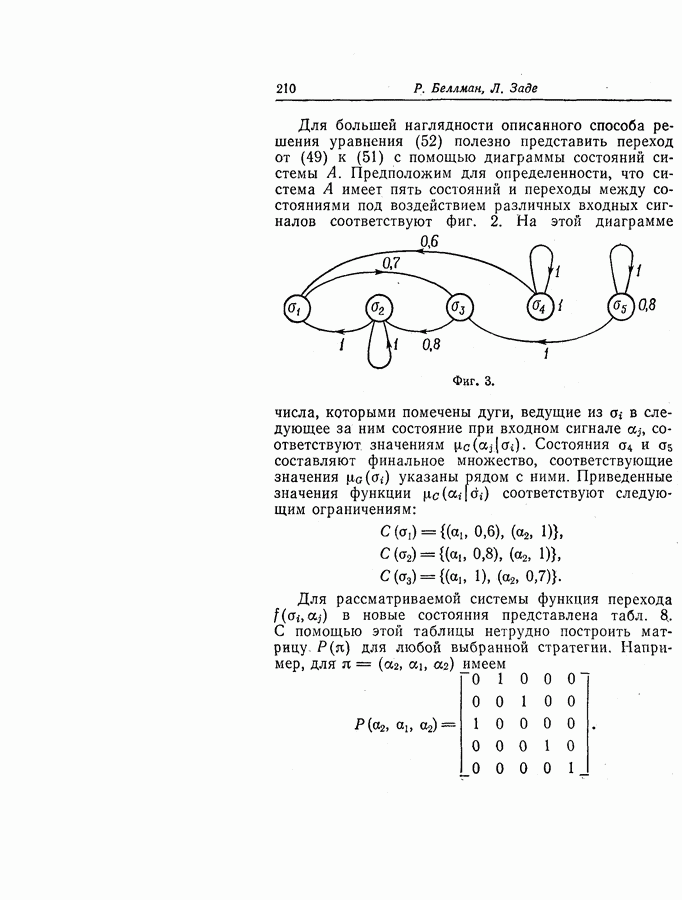
Пример. В качестве простой иллюстрации рассмотрим систему с тремя состояниями и двумя входными сигналами Пусть для простоты и расплывчатая цель в момент определяется функцией принадлежности принимающей значения

Пусть, далее, расплывчатые ограничения в моменты задаются функциями

Предположим, что таблица изменения состояний, задающая функцию в формуле (25), соответствует табл. 3. Используя (30), находим функцию принадлежности расплывчатой цели в момент

Таблица 3 (см. скан)

и соответствующее максимизирующее решение имеет вид

Аналогично для t = 0 имеем

и

Итак, если начальное состояние (в момент времени ) есть , то максимизирующим решением будет причем соответствующее значение функции принадлежности равно 0,8.

Обратимся теперь к более общему случаю многошагового процесса принятия решений, в котором управляемая система является стохастической, а цель и ограничения — расплывчатыми.