| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
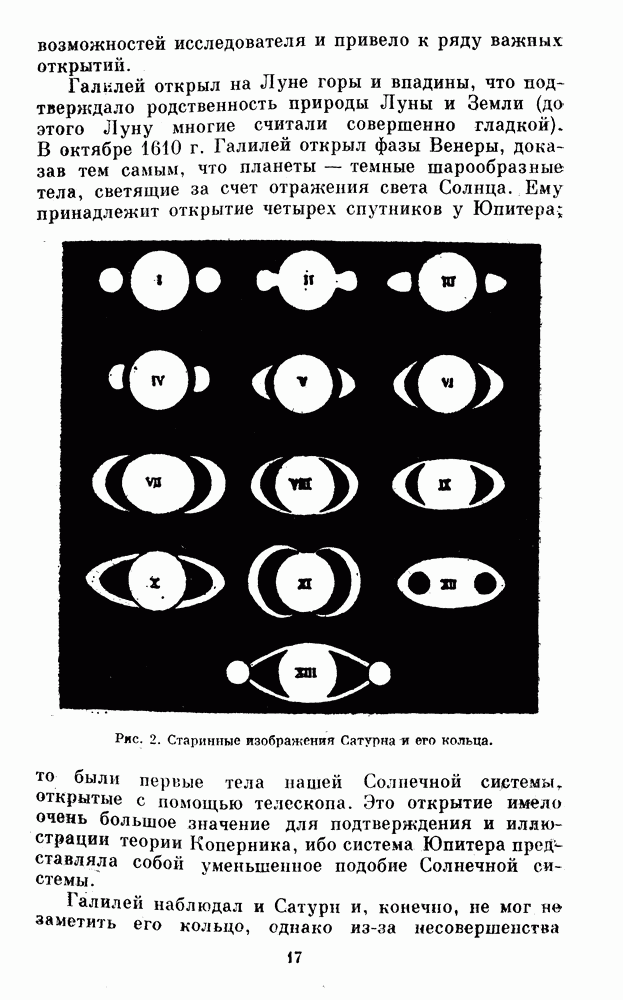
§ 34. ОБРАБОТКА НАБЛЮДЕНИЙ ФАЗ ВЕНЕРЫ
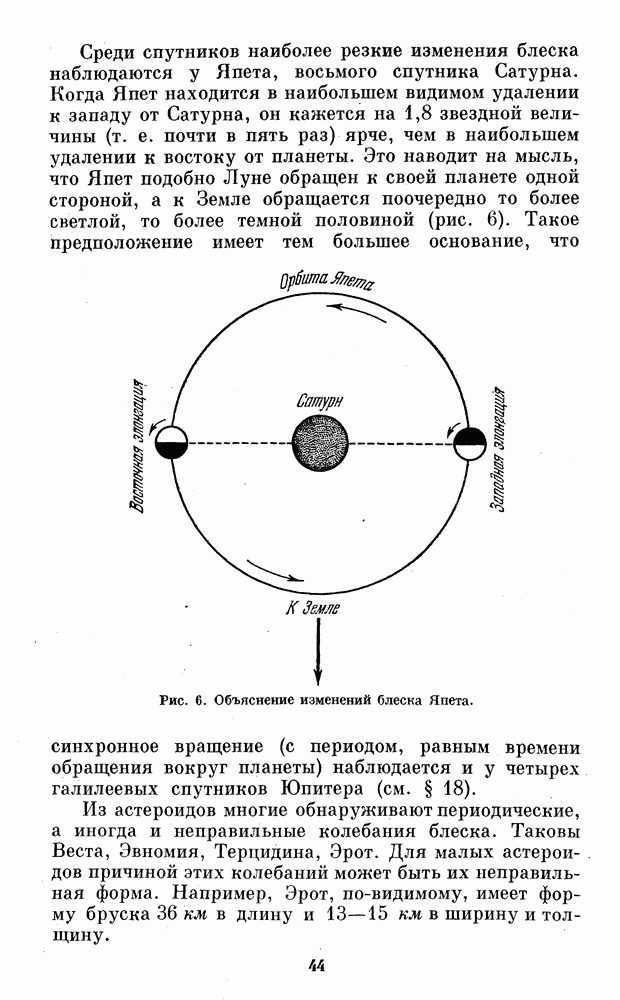
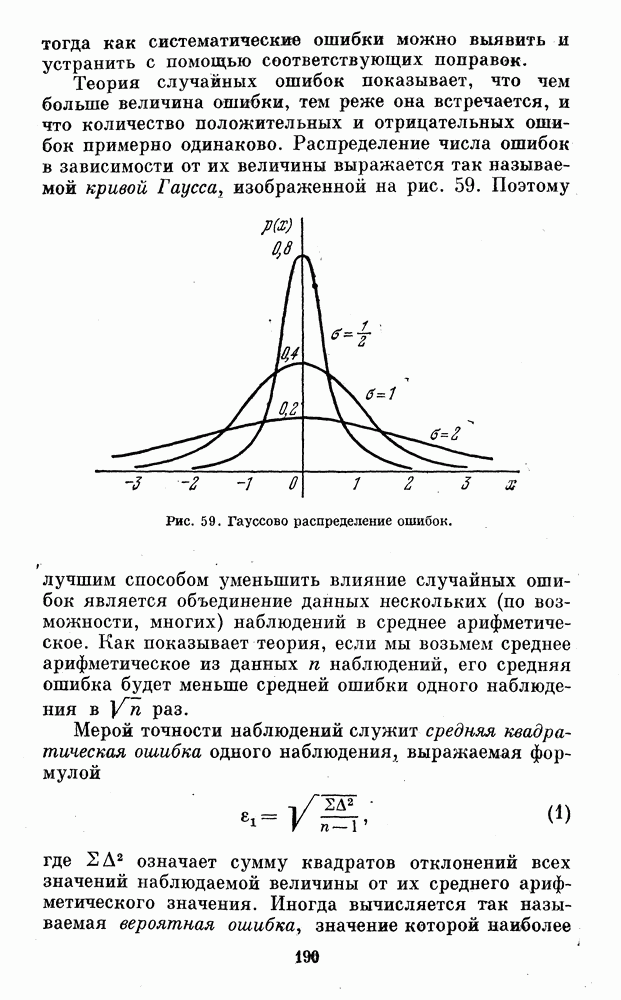
Обработка наблюдений фаз Венеры заключается в измерении наблюденной фазы, вычислении или определении из таблиц теоретической фазы и построении графика хода разности между ними в зависимости от теоретической фазы. Совершенно так же производится обработка наблюдений фаз Меркурия, Луны и искусственного шара.
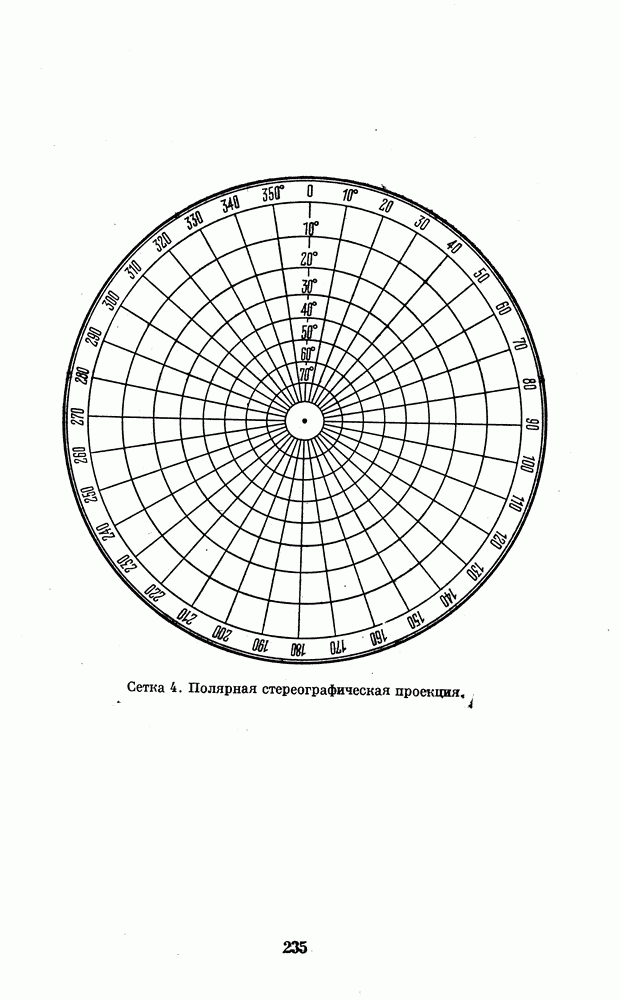
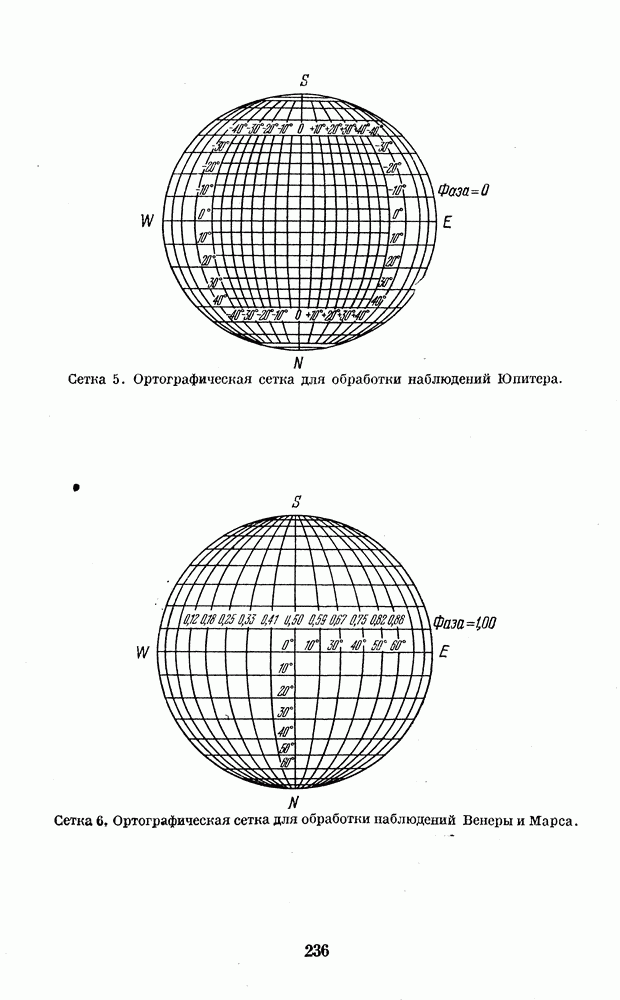
Измерение фазы на рисунке можно производить с помощью сетки. Для этого совмещаем центральный меридиан сетки с линией рогов на рисунке и отсчитываем фазу. Если диаметр планеты на рисунке отличается от стандартного (50 мм) или сетка отсутствует, фазу можно измерить без сетки с помощью хорошей линейки с миллиметровыми делениями. В этом случае измеряем наибольшую ширину серпа планеты А и диаметр диска d, после чего делим первое число на второе; частное даст нам величину фазы. Измерения при этом надо производить по возможности с точностью до ОД мм, оценивая десятые доли миллиметра на глаз.
Теоретическая фаза берется из астрономических ежегодников или календарей. В «Астрономическом Календаре» ВАГО значения фазы даются через 8 дней, поэтому для промежуточных дат придется прибегать к интерполированию. Близ нижнего соединения фаза меняется очень быстро, и интерполирование может дать слишком грубый результат. В этом случае придется вычислить фазу самому по формуле (7). Фазовый угол  вычисляется по формулам
вычисляется по формулам

Здесь  — угол элонгации планеты от Солнца,
— угол элонгации планеты от Солнца,  — угол между радиусами-векторами планеты и Земли, а и
— угол между радиусами-векторами планеты и Земли, а и  — прямое восхождение и склонение планеты,
— прямое восхождение и склонение планеты,  — то же для Солнца, X и
— то же для Солнца, X и  — гелиоцентрические долготы планеты и Земли,
— гелиоцентрические долготы планеты и Земли,  — гелиоцентрическая широта планеты. Гелиоцентрические координаты планет, в том числе Земли, также приводятся в наших астрономических календарях.
— гелиоцентрическая широта планеты. Гелиоцентрические координаты планет, в том числе Земли, также приводятся в наших астрономических календарях.
Далее для каждого наблюдения составляются разности  (наблюденная фаза минус вычисленная). Их значения наносятся на график, где по оси абсцисс отложены значения
(наблюденная фаза минус вычисленная). Их значения наносятся на график, где по оси абсцисс отложены значения  (пример дан на рис. 61, стр. 199). Такие графики рекомендуется составлять отдельно для каждого наблюдателя (при достаточном числе наблюдений), а также по возможности выделять (хотя бы условными знаками) дневные, сумеречные и ночные наблюдения. В этом случае дневными считаются наблюдения, сделанные до захода (или после восхода) Солнца, сумеречными — наблюдения, сделанные во время гражданских и астрономических сумерек. Наблюдать Венеру ночью удается редко, в периоды наилучшей видимости планеты.
(пример дан на рис. 61, стр. 199). Такие графики рекомендуется составлять отдельно для каждого наблюдателя (при достаточном числе наблюдений), а также по возможности выделять (хотя бы условными знаками) дневные, сумеречные и ночные наблюдения. В этом случае дневными считаются наблюдения, сделанные до захода (или после восхода) Солнца, сумеречными — наблюдения, сделанные во время гражданских и астрономических сумерек. Наблюдать Венеру ночью удается редко, в периоды наилучшей видимости планеты.
На довольно большом диапазоне фаз  полученные разности ДФ можно представить уравнением прямой линии
полученные разности ДФ можно представить уравнением прямой линии

где а — величина отклонения наблюденной фазы от теоретической при фазе 0,5, а А: — угловой коэффициент прямой. Величины а и к находятся по способу Коши следующим образом.
Допустим, что мы имеем ряд значений ДФ для соответствующих им значений 

Составляем ряд условных уравнений типа  подставляя в них значения
подставляя в них значения  (а и k являются неизвестными):
(а и k являются неизвестными):

Разделив произвольным образом все наши условные уравнения на две равные группы, мы складываем почленно левые и правые части каждой группы, в результате чего получаем два уравнения с двумя неизвестным которые и решаем совместно:

Полученное уравнение будет выглядеть так:

В области малых фаз  и больших фаз
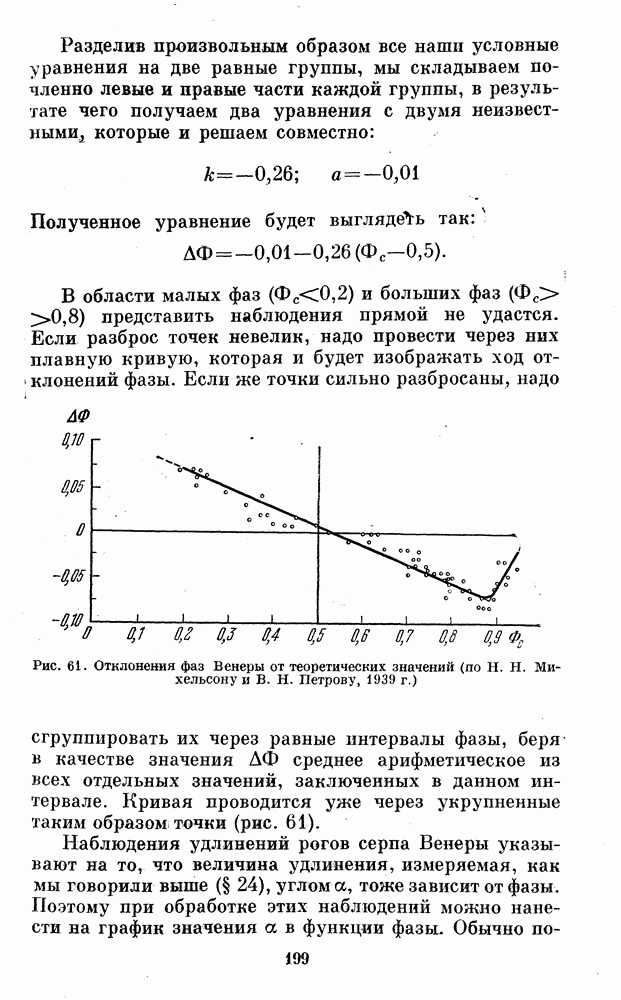
и больших фаз  представить наблюдения прямой не удастся. Если разброс точек невелик, надо провести через них плавную кривую, которая и будет изображать ход
представить наблюдения прямой не удастся. Если разброс точек невелик, надо провести через них плавную кривую, которая и будет изображать ход  клонений фазы.
клонений фазы.

Рис. 61. Отклонения фаз Венеры от теоретических значений (по Н. Н. Михельсону и В. Н. Петрову, 1939 г.)
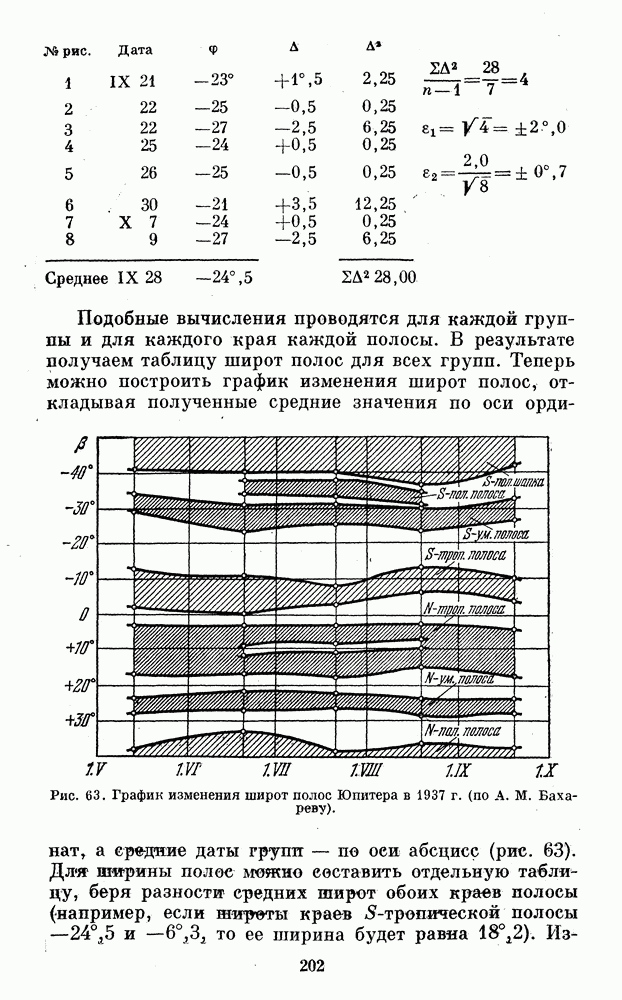
Если же точки сильно разбросаны, надо сгруппировать их через равные интервалы фазы, беря в качестве значения ДФ среднее арифметическое из всех отдельных значений, заключенных в данном интервале. Кривая проводится уже через укрупненные таким образом точки (рис. 61).
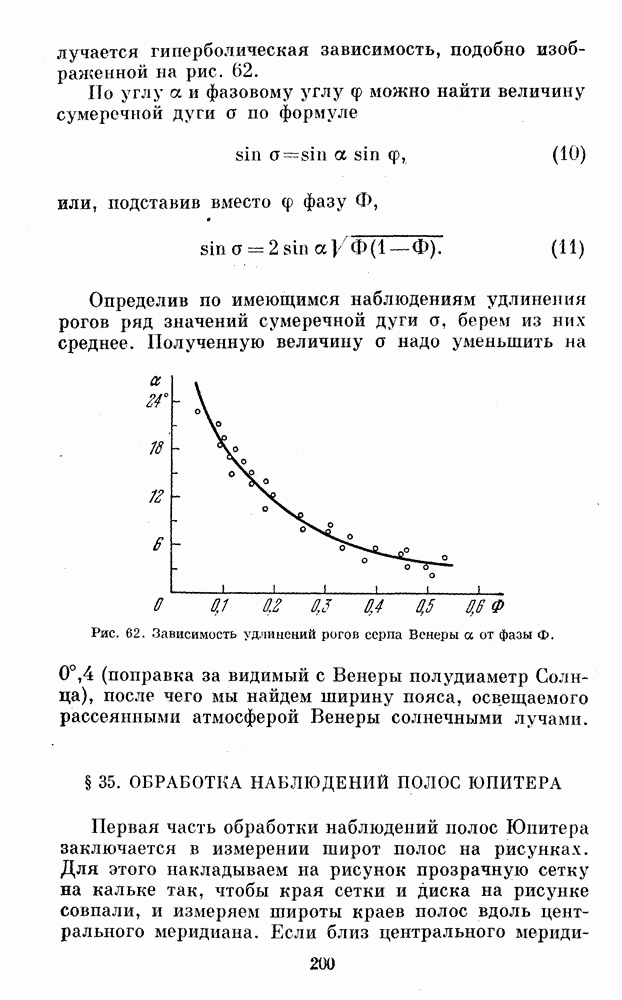
Наблюдения удлинений рогов серпа Венеры указывают на то, что величина удлинения, измеряемая, как мы говорили выше (§ 24), углом а, тоже зависит от фазы. Поэтому при обработке этих наблюдений можно нанести на график значения а в функции фазы.
Обычно получается гиперболическая зависимость, подобно изображенной на рис. 62.
По углу а и фазовому углу  можно найти величину сумеречной дуги
можно найти величину сумеречной дуги  по формуле
по формуле
 (10)
(10)
или, подставив вместо  фазу Ф,
фазу Ф,

Определив по имеющимся наблюдениям удлинения рогов ряд значений сумеречной дуги а, берем из них среднее.

Рис. 62. Зависимость удлинений рогов серпа Венеры а от фазы Ф.
Полученную величину а надо уменьшить на  (поправка за видимый с Венеры полудиаметр Солнца), после чего мы найдем ширину пояса, освещаемого рассеянными атмосферой Венеры солнечными лучами.
(поправка за видимый с Венеры полудиаметр Солнца), после чего мы найдем ширину пояса, освещаемого рассеянными атмосферой Венеры солнечными лучами.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редакционной коллегий серии книг «БИБЛИОТЕКА ЛЮБИТЕЛЯ АСТРОНОМИИ»
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОБЩИЕ СВЕДЕНИЯ О ПЛАНЕТАХ
- § 1. ЧТО ТАКОЕ ПЛАНЕТЫ
- § 2. ИСТОРИЧЕСКИЙ ОЧЕРК РАЗВИТИЯ ЗНАНИЙ О ПЛАНЕТАХ
- § 3. ОБЗОР СОЛНЕЧНОЙ СИСТЕМЫ
- ГЛАВА II. МЕТОДЫ ИССЛЕДОВАНИЯ ПЛАНЕТ
- § 4. ОПРЕДЕЛЕНИЕ МАСС И ДИАМЕТРОВ ПЛАНЕТ
- § 5. НАБЛЮДЕНИЯ ПОВЕРХНОСТЕЙ ПЛАНЕТ В ТЕЛЕСКОП
- § 6. ФОТОГРАФИРОВАНИЕ ПЛАНЕТ
- § 7. ФОТОМЕТРИЯ
- § 8. РАДИОМЕТРИЧЕСКИЕ НАБЛЮДЕНИЯ
- § 9. СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 10. РАДИОАСТРОНОМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
- § 11. РАДИОЛОКАЦИЯ ПЛАНЕТ
- § 12. ИССЛЕДОВАНИЕ ПЛАНЕТ КОСМИЧЕСКИМИ АППАРАТАМИ
- ГЛАВА III. РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ ПЛАНЕТ
- § 13. МЕРКУРИЙ
- § 14. ВЕНЕРА
- § 15. МАРС
- § 16. ЮПИТЕР, САТУРН, УРАН И НЕПТУН
- § 17. ПЛУТОН
- § 18. СПУТНИКИ ПЛАНЕТ И АСТЕРОИДЫ
- § 19. ВНУТРЕННЕЕ СТРОЕНИЕ ПЛАНЕТ
- ГЛАВА IV. НАБЛЮДЕНИЯ ПЛАНЕТ
- § 20. ЦЕЛИ И ЗАДАЧИ ЛЮБИТЕЛЬСКИХ НАБЛЮДЕНИЙ
- § 21. ОБЩИЕ ПРАВИЛА НАБЛЮДЕНИЙ
- § 22. УСЛОВИЯ НАБЛЮДЕНИЙ
- § 23. ИНСТРУМЕНТЫ И ПРИБОРЫ
- § 24. НАБЛЮДЕНИЯ ВЕНЕРЫ
- § 25. НАБЛЮДЕНИЯ МАРСА
- § 26. НАБЛЮДЕНИЯ ЮПИТЕРА
- § 27. НАБЛЮДЕНИЯ САТУРНА И ЕГО КОЛЬЦА
- § 28. НАБЛЮДЕНИЯ ОСТАЛЬНЫХ ПЛАНЕТ
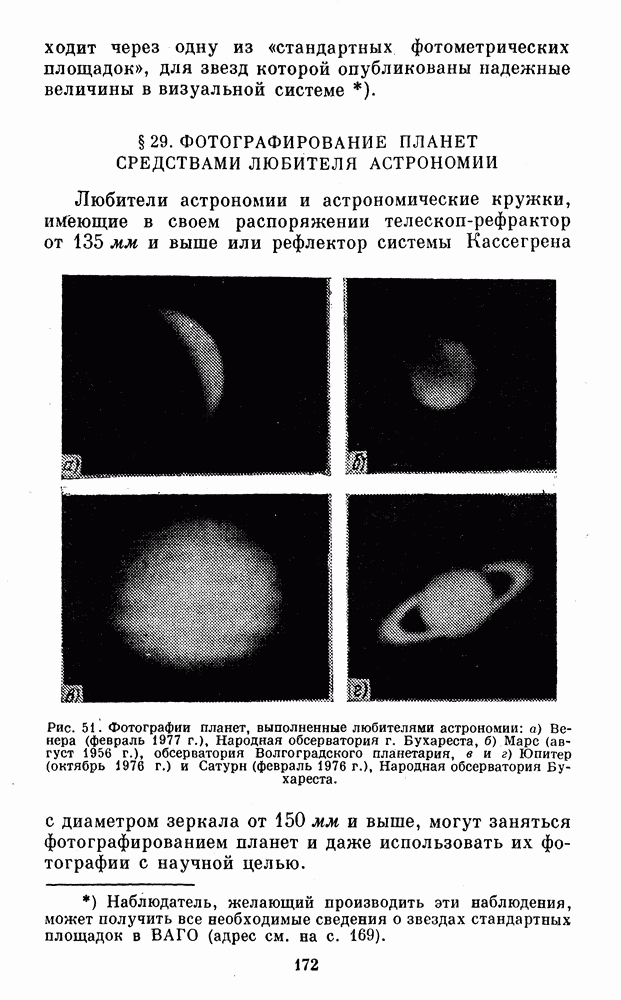
- § 29. ФОТОГРАФИРОВАНИЕ ПЛАНЕТ СРЕДСТВАМИ ЛЮБИТЕЛЯ АСТРОНОМИИ
- § 30. ФОТОЭЛЕКТРИЧЕСКАЯ ФОТОМЕТРИЯ ПЛАНЕТ
- ГЛАВА V. ОБРАБОТКА НАБЛЮДЕНИЙ
- § 31. ЧТО ТАКОЕ ОБРАБОТКА НАБЛЮДЕНИЙ
- § 32. ОШИБКИ НАБЛЮДЕНИЙ
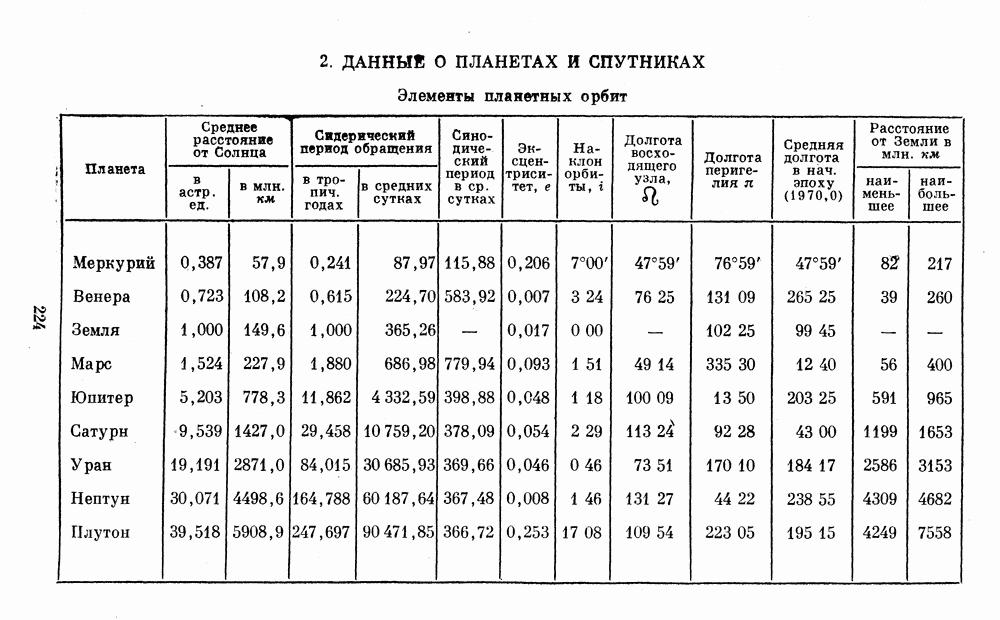
- § 33. ЭЛЕМЕНТЫ ПЛАНЕТНЫХ ОРБИТ И ЭФЕМЕРИДЫ
- § 34. ОБРАБОТКА НАБЛЮДЕНИЙ ФАЗ ВЕНЕРЫ
- § 35. ОБРАБОТКА НАБЛЮДЕНИЙ ПОЛОС ЮПИТЕРА
- § 36. СОСТАВЛЕНИЕ КАРТ ПЛАНЕТ
- § 37. ОПРЕДЕЛЕНИЕ ПЕРИОДА ВРАЩЕНИЯ ПЛАНЕТЫ
- § 38. ОБРАБОТКА ФОТОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ
- § 39. ОРГАНИЗАЦИЯ И ПРОГРАММА РАБОТЫ
- ПРИЛОЖЕНИЯ
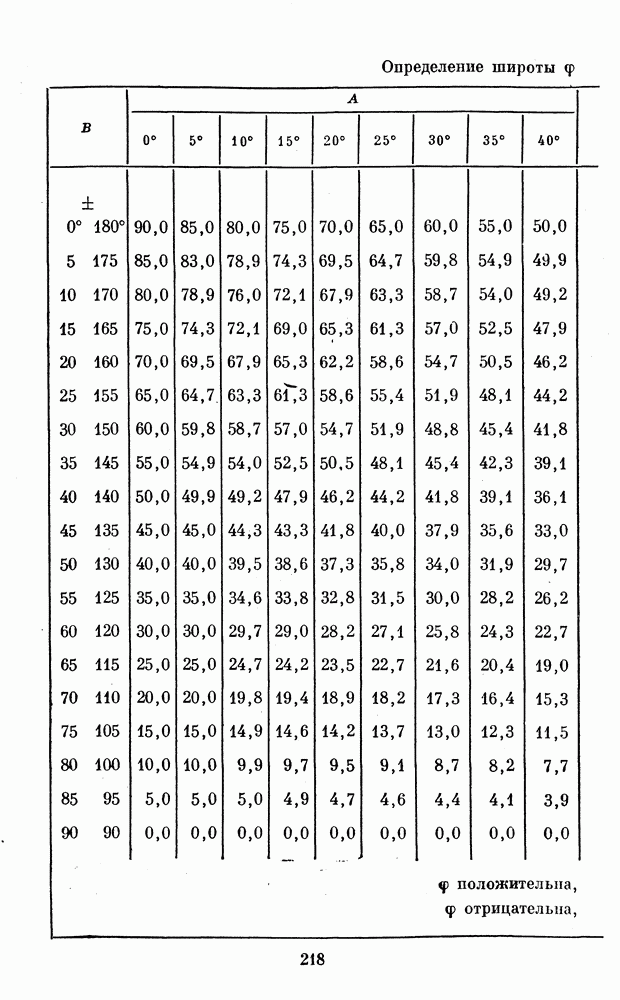
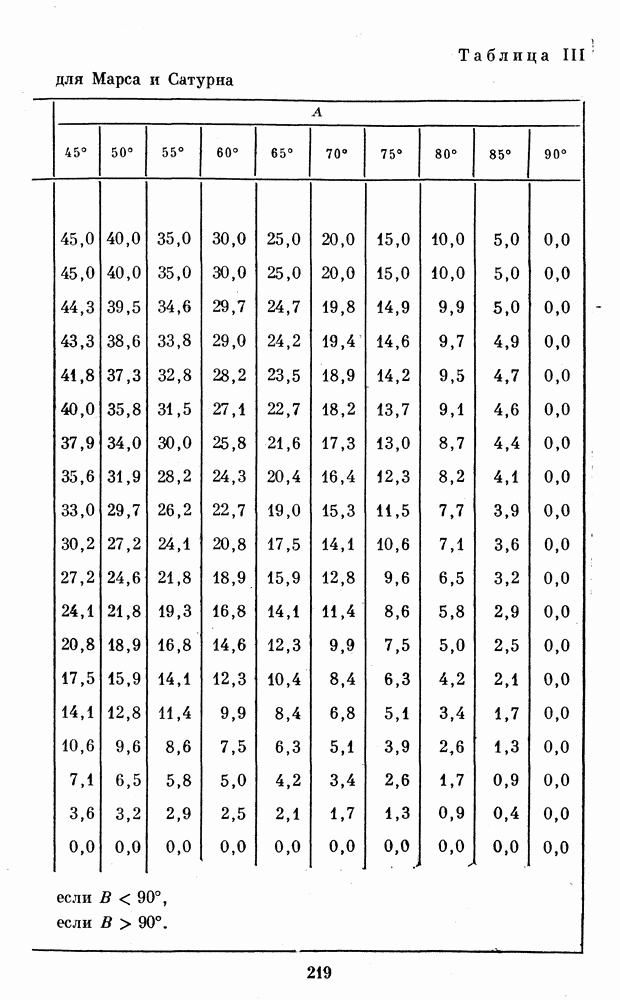
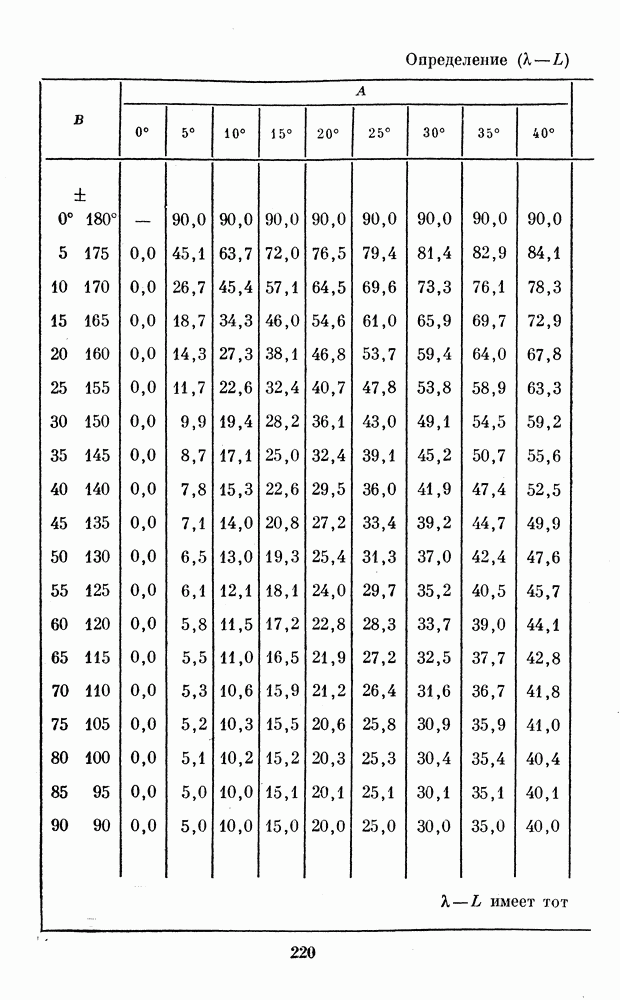
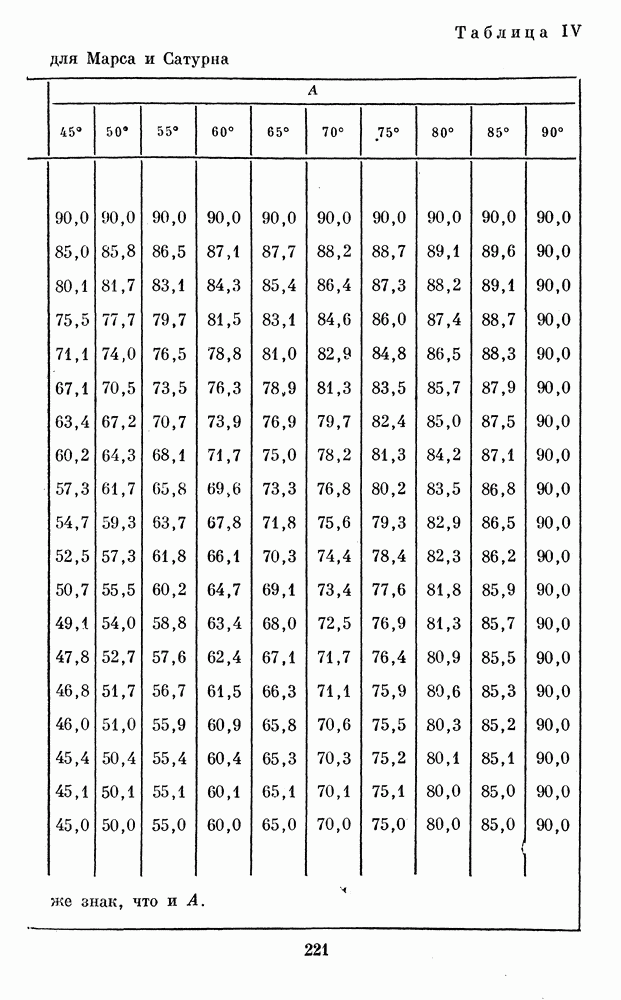
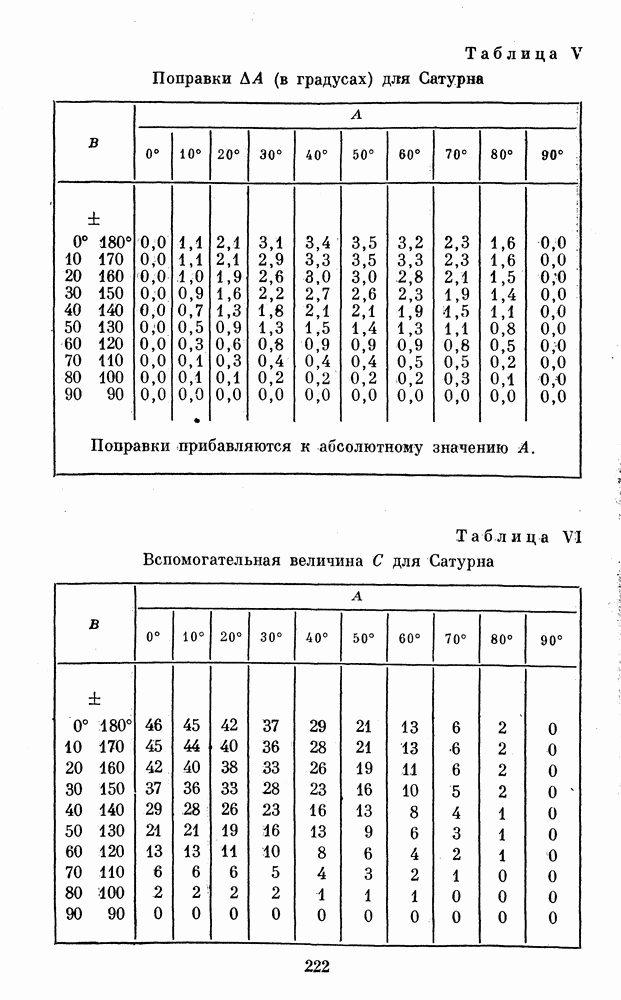
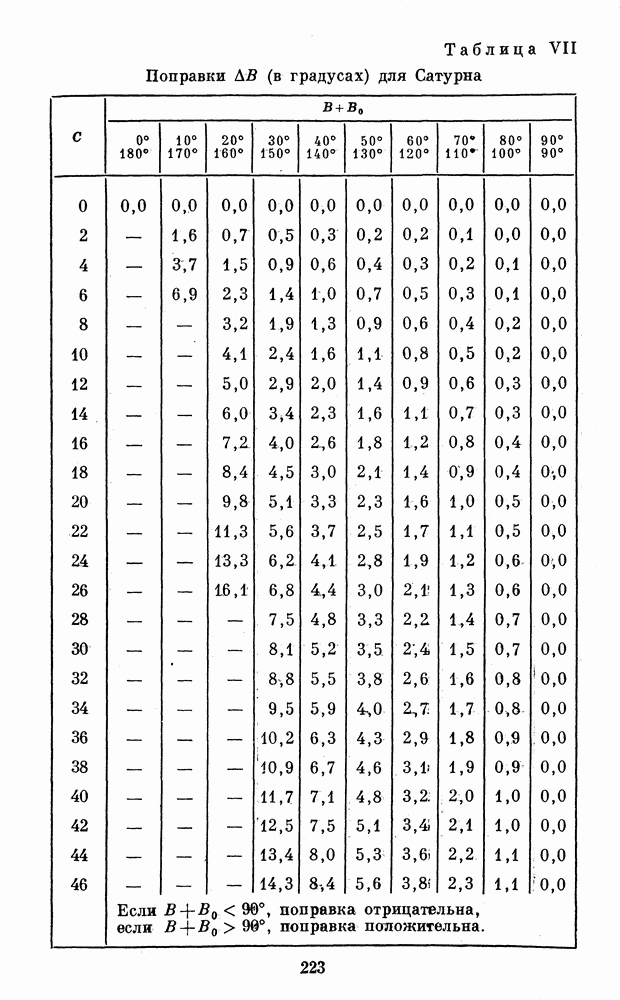
- 1. ТАБЛИЦЫ ДЛЯ ОБРАБОТКИ РИСУНКОВ ПЛАНЕТ
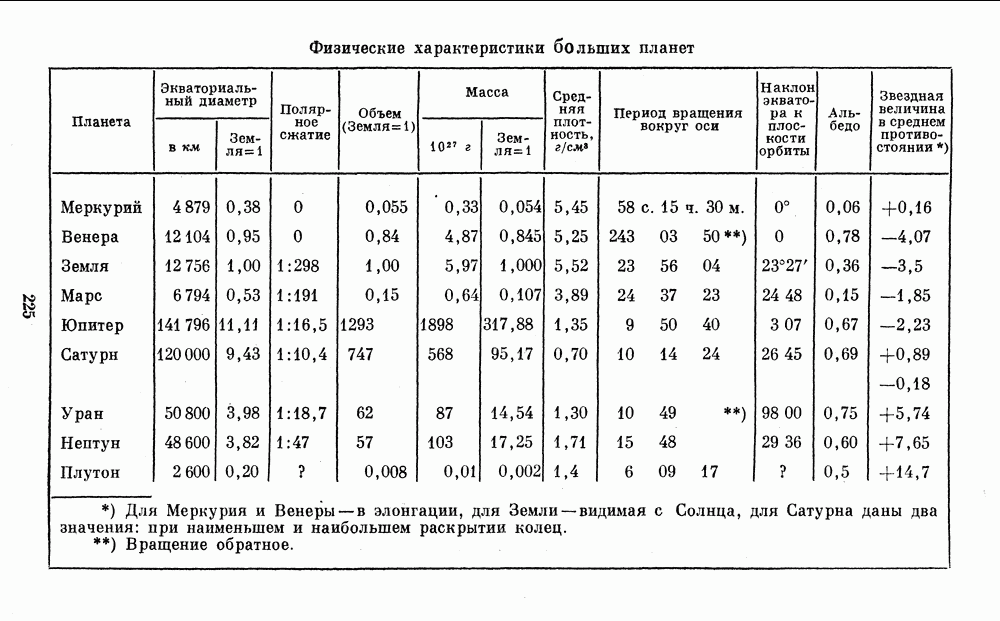
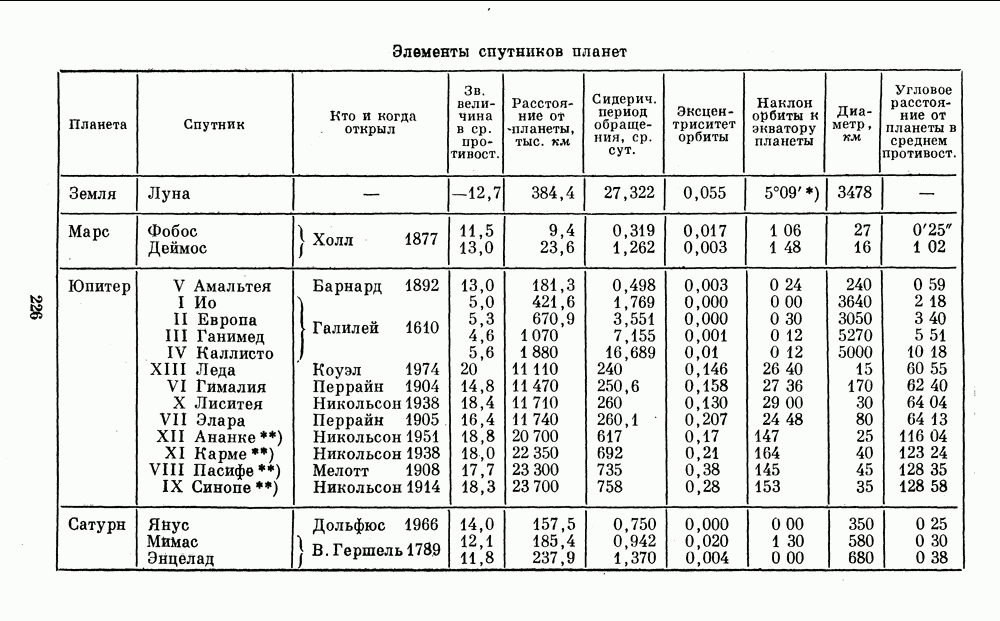
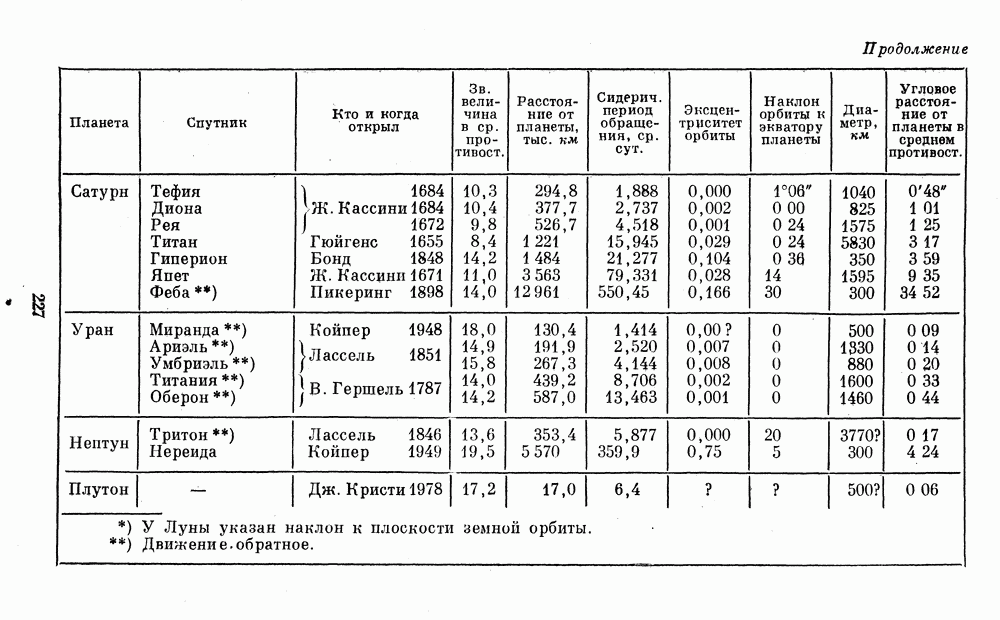
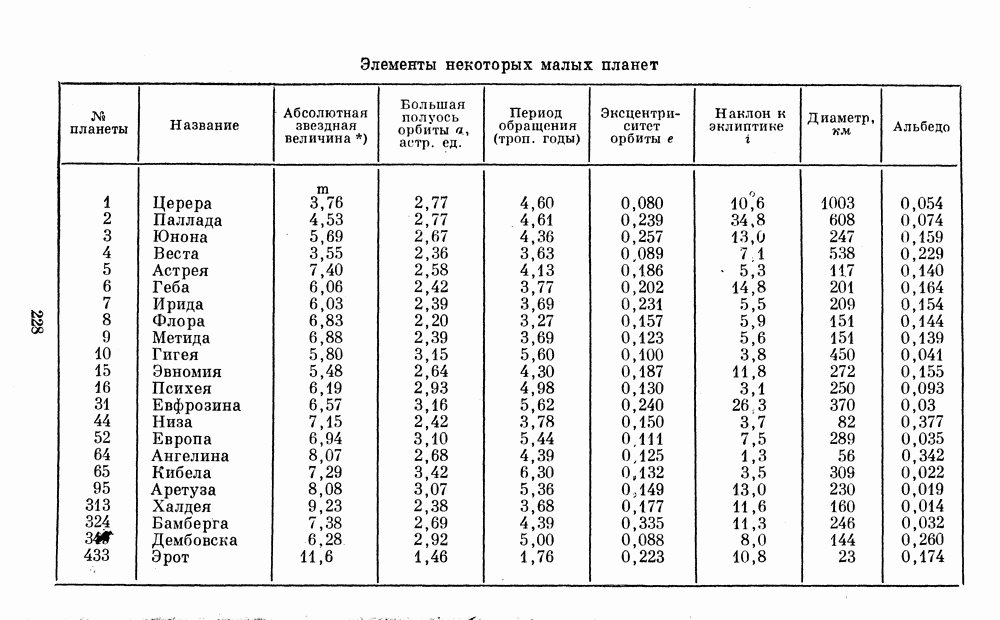
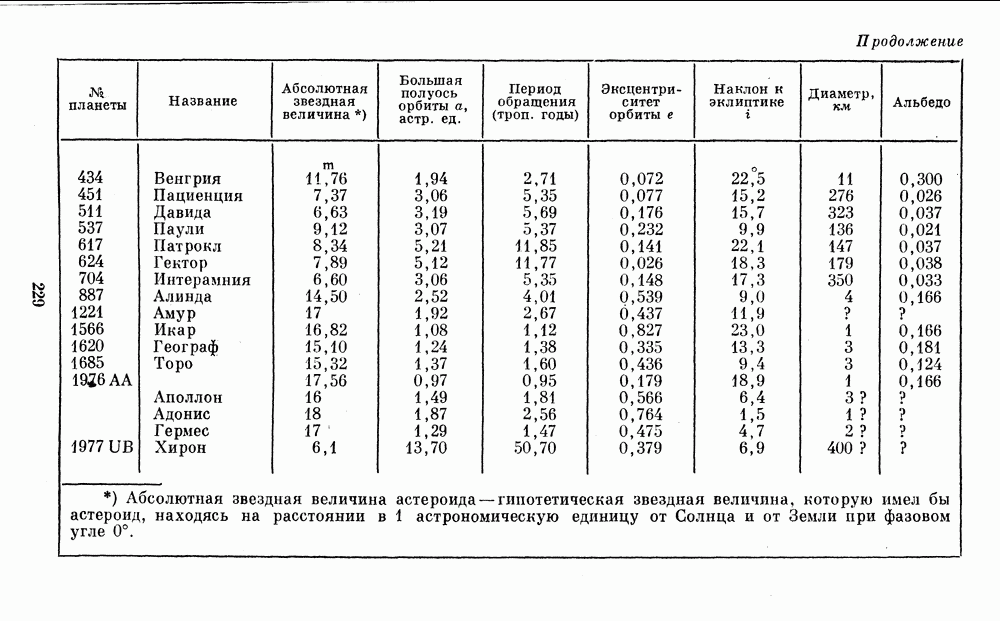
- 2. ДАННЫЕ О ПЛАНЕТАХ И СПУТНИКАХ
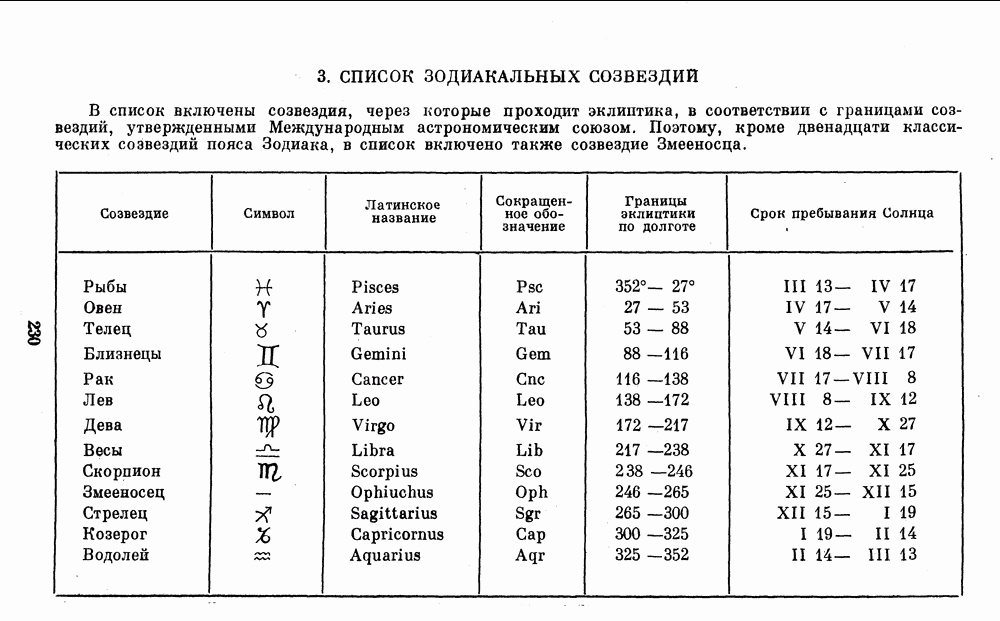
- 3. СПИСОК ЗОДИАКАЛЬНЫХ СОЗВЕЗДИЙ
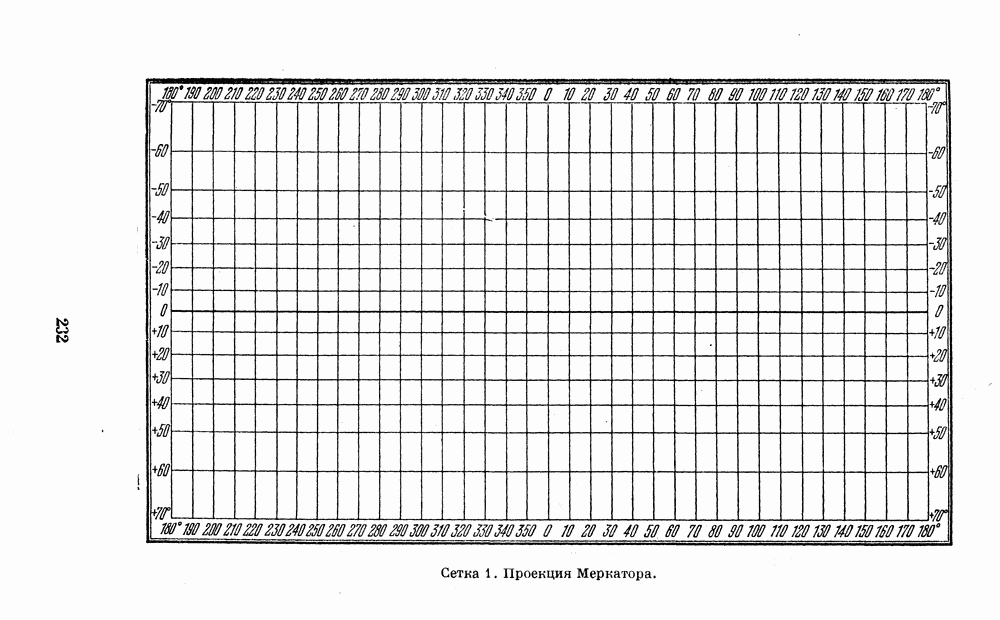
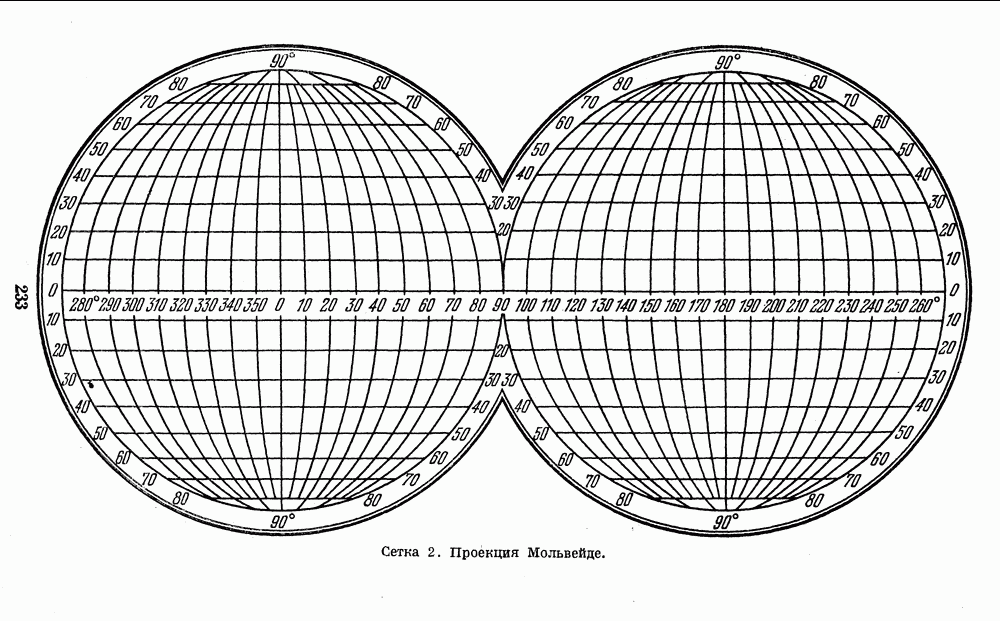
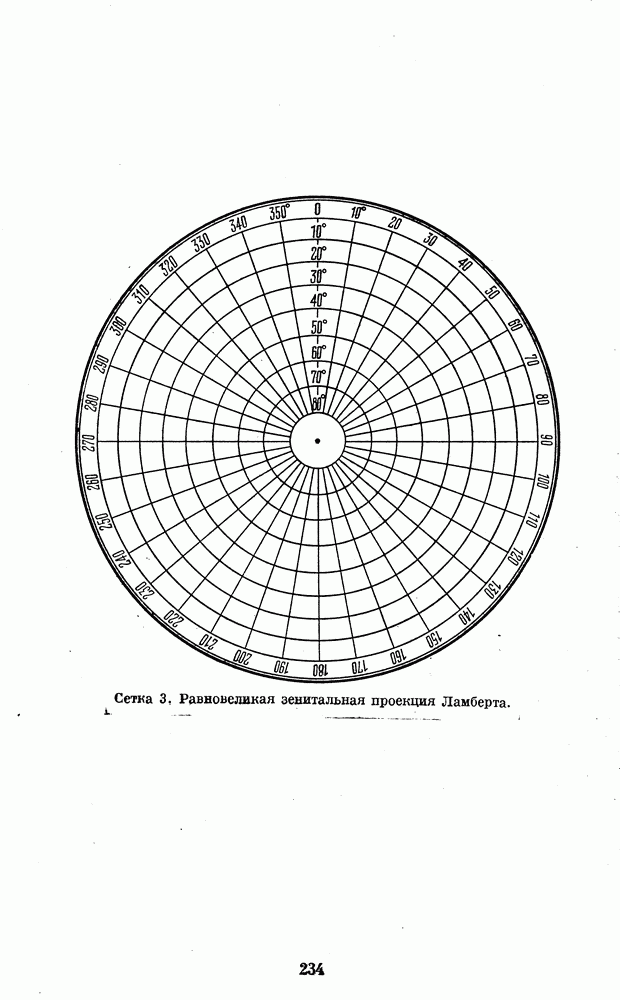
- 4. КООРДИНАТНЫЕ СЕТКИ ДЛЯ ПОСТРОЕНИЯ КАРТ ПЛАНЕТ
- ЛИТЕРАТУРА