| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА II. МЕТОДЫ ИССЛЕДОВАНИЯ ПЛАНЕТ
§ 4. ОПРЕДЕЛЕНИЕ МАСС И ДИАМЕТРОВ ПЛАНЕТ
При изучении планет с физической точки зрения прежде всего необходимо знать их размеры и массу. Зная то и другое, можно легко вычислить и среднюю плотность планеты.
Определение масс планет, имеющих спутники, производится на основании III закона Кеплера в его точной форме. Если М — масса Солнца,  — массы планеты и спутника,
— массы планеты и спутника,  — периоды обращения планеты вокруг Солнца и спутника вокруг планеты,
— периоды обращения планеты вокруг Солнца и спутника вокруг планеты,  — большие полуоси их орбит, то III закон Кеплера можно написать в таком виде:
— большие полуоси их орбит, то III закон Кеплера можно написать в таком виде:

Поскольку массы планет во много раз меньше массы Солнца, а массы спутников, как правило, ничтожны по сравнению с массами планет, мы можем пренебречь вторыми слагаемыми в скобках и получить отношение масс планеты и Солнца:

Зная массу Земли, мы по этой формуле можем найти массу Солнца, а затем и тех планет, у которых имеются спутники.
Определение масс планет, не имеющих спутников, а также масс самих спутников и астероидов представляет собой более трудную задачу.
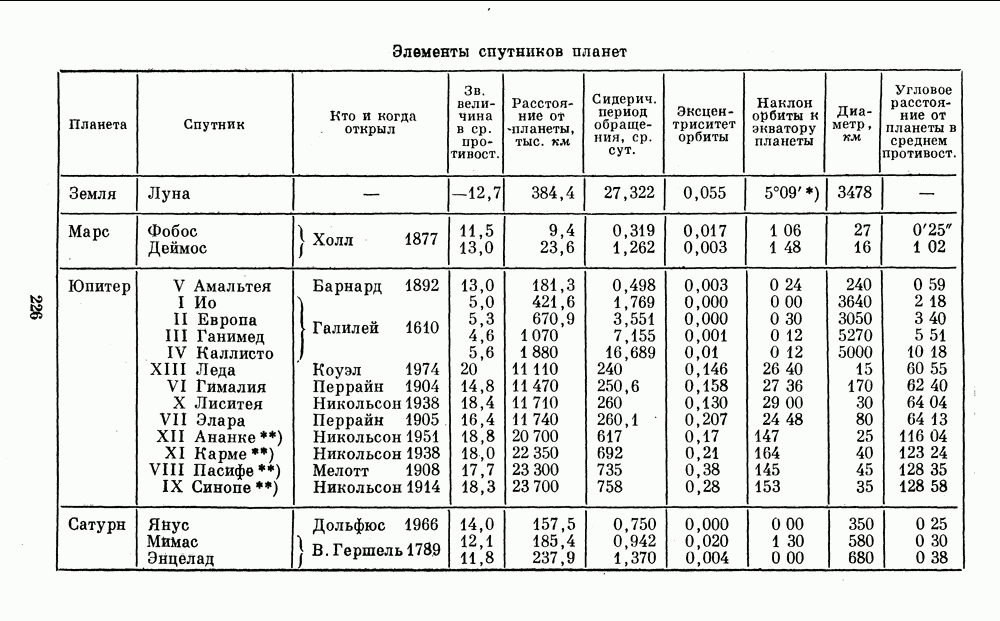
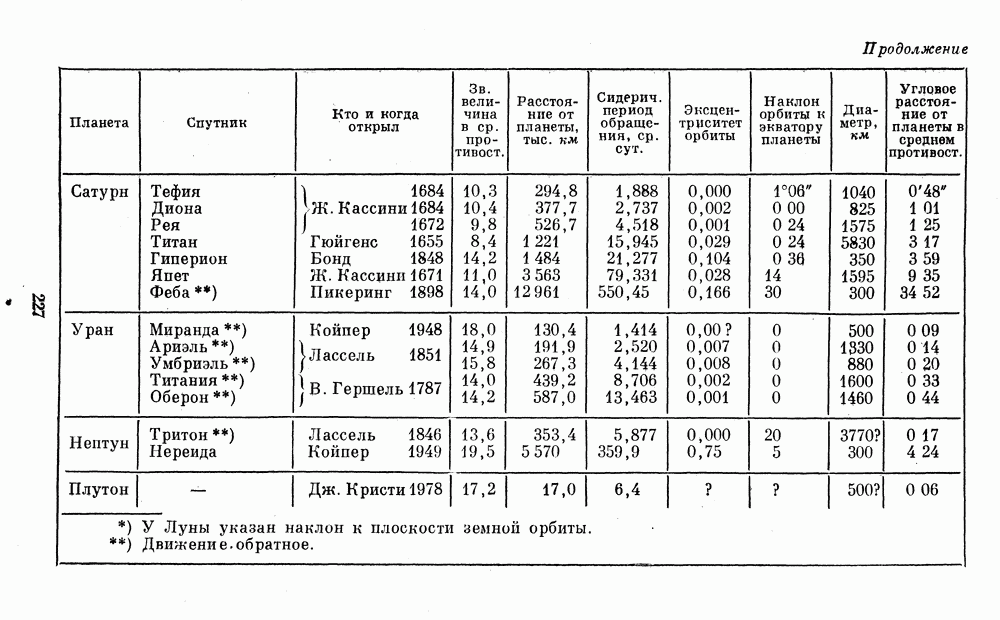
Массы Меркурия и Венеры были первоначальна определены по тем возмущениям, которые они вызывают в движении других планет. Полеты к этим планетам космических аппаратов позволили существенно уточнить значения их масс по их воздействию на траекторию аппарата. Масса Плутона до последнего времени была известна лишь весьма приблизительно, и лишь недавно, после открытия спутника Плутона, ее удалось уточнить. Масса Луны была найдена по воздействию на Землю, под влиянием которого Земля описывает маленький эллипс вокруг их общего центра тяжести. Массы крупных спутников Юпитера можно определить по их взаимным возмущениям. Для остальных спутников, а также для астероидов приходится делать только приближенную оценку массы и диаметра по их блеску (см. § 7).
Линейный диаметр планеты легко определить, зная расстояние и измерив ее угловой диаметр. Так как угловые диаметры планет очень малы (меньше 1), мы можем написать:

где  — расстояние планеты от Земли, d" — ее угловой диаметр, выраженный в секундах дуги, D — линейный диаметр.
— расстояние планеты от Земли, d" — ее угловой диаметр, выраженный в секундах дуги, D — линейный диаметр.
Измерение угловых диаметров планет производится с помощью специального измерительного прибора — микрометра, помещаемого в фокусе телескопа; Наиболее употребительным является нитяной микрометр. Устройство его таково. На неподвижной рамке укреплены перпендикулярно друг к другу две тонкие нити. Вдоль рамки, в направлении горизонтальной нити, может перемещаться другая рамка с вертикальной нитью, параллельной вертикальной неподвижной нити. Движение этой нити осуществляется с помощью микрометрического винта, один оборот которого передвигает рамку на строго определенную величину (на так называемый шаг винта).
Для измерения углового диаметра планет микрометр поворачивается так, чтобы направление горизонтальной нити соответствовало измеряемому диаметру, поскольку у планет имеющих значительное сжатие, видимые диаметры, полярный и экваториальный, заметно отличаются друг от друга.
Точность измерения у длиннофокусных телескопов доходит до сотых долей секунды дуги.
С помощью нитяного микрометра измеряются не только угловые диаметры всех планет, имеющих видимые диски, но и их полярное сжатие, величина фазы, а также положение темных полос на Юпитере, протяженность полярных шапок Марса и т. д.
Другим прибором, применяемым для измерений угловых диаметров и фаз планет, является гелиометр. Он представляет собой телескоп-рефрактор, объектив которого распилен по диаметру пополам, причем обе половинки могут раздвигаться с помощью микрометрического винта вдоль их общего диаметра. Кроме того, вся система может поворачиваться вокруг оптической оси телескопа.
При раздвигании обеих половин объектива в окуляре вместо одного изображения планеты возникают два. Вращая микрометрический винт, можно добиться того, чтобы оба изображения планеты касались друг друга. Тогда, очевидно, одно из них будет смещено относительно другого как раз на величину углового диаметра планеты. Зная цену оборота винта гелиометра и произведя отсчет, мы получим нужную нам величину.
Понятно что гелиометр сложнее нитяного микрометра, так как требует специальной оптики, тогда как последний может быть приспособлен к любому телескопу. Кроме того, необходимость распиловки объектива гелиометра ограничивает его возможные размеры. Однако точность, с которой можно выполнять измерения, у гелиометра выше.
Измерения угловых диаметров планет можно производить и по фотопластинкам. В этом случае применяются лабораторные измерительные приборы, главными частями которых являются: столик, на который кладется пластинка, два микрометрических винта, перемещающих ее по двум взаимно перпендикулярным направлениям, и микроскоп для рассматривания планетных дисков, имеющих подчас очень малые размеры.
Чтобы перевести измеренные на пластинке величины в угловые единицы, надо знать масштаб снимка.
Если снимок получен в фокусе объектива, то его масштаб определяется соотношением

т. е. 1" на снимке имеет длину, равную 1/206 265 фокусного расстояния объектива. Для объектива с фокусным расстоянием 2 м это будет всего лишь 0,001 мм, а для самого длиннофокусного в мире рефрактора Йеркской обсерватории — около ОД мм.
Если фотографирование производится с дополнительным увеличением, например, при помощи окуляра, то нужно определить постоянную увеличительной системы, т. е. узнать, во сколько раз она увеличивает изображение. Эта величина дается формулой

где  — фокусное расстояние окуляра, а г — его расстояние от пластинки при фотографировании. Надо сказать, что получение снимков планет с большим увеличением (более 10 раз) ограничивается уменьшением освещенности изображения (см. ниже § 6).
— фокусное расстояние окуляра, а г — его расстояние от пластинки при фотографировании. Надо сказать, что получение снимков планет с большим увеличением (более 10 раз) ограничивается уменьшением освещенности изображения (см. ниже § 6).
При серьезных работах вместо обычных окуляров для увеличения размеров изображения используют специальные оптические системы. Например, можно применить вогнутую (рассеивающую) линзу (линзу Барлоу), которая уменьшает угол схождения лучей и тем самым как бы увеличивает фокусное расстояние объектива, а стало быть, и размеры изображения планеты. Следует отметить, что вообще диски планет на фотографиях весьма невелики. Так, например, на снимках Марса, полученных в 1909 г. Г. А. Тиховым с 30-дюймовым рефрактором Пулковской обсерватории (F=14 м), диаметр изображения планеты равен примерно 1,5 мм. При использовании увеличительной системы даже со столь крупными телескопами можно получить диск Марса размером в 8—10 мм, а диск Юпитера — до 15 мм.
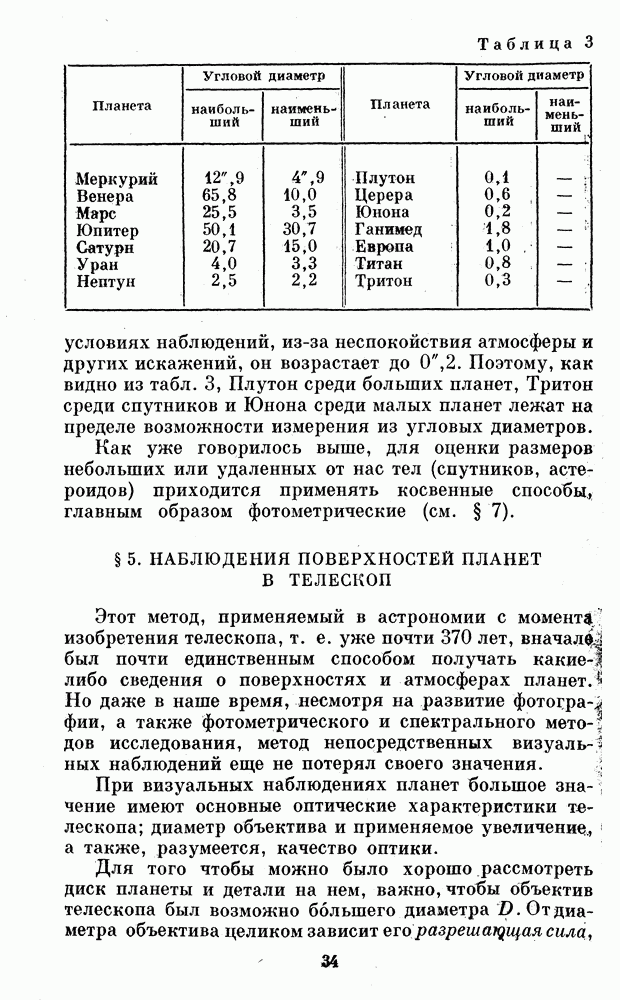
В таблице 3 даны угловые диаметры планет и некоторых спутников при их наименьшем и наибольшем расстоянии от Земли.
Для крупнейшего в мире рефрактора предел точности измерений теоретически равен  но в реальных условиях наблюдений, из-за неспокойствия атмосферы и других искажений, он возрастает до
но в реальных условиях наблюдений, из-за неспокойствия атмосферы и других искажений, он возрастает до 
Таблица 3

Поэтому, как видно из табл. 3, Плутон среди больших планет, Тритон среди спутников и Юнона среди малых планет лежат на пределе возможности измерения из угловых диаметров.
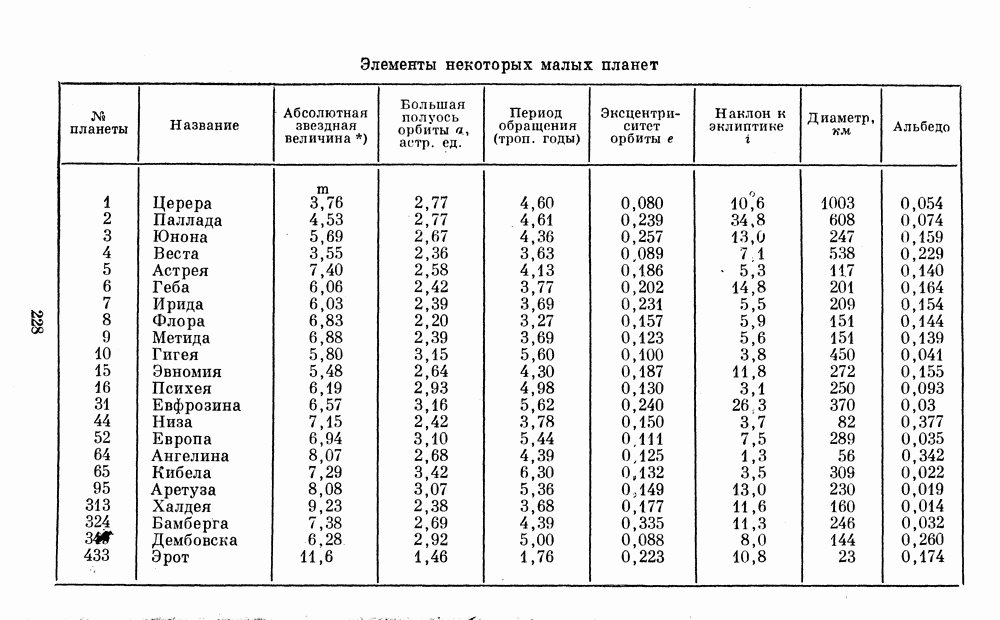
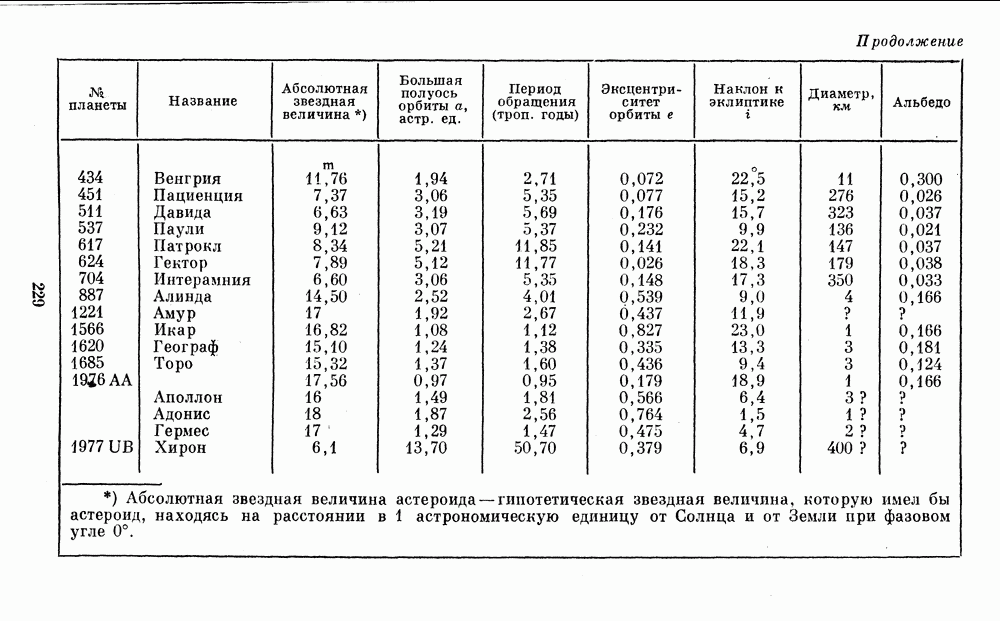
Как уже говорилось выше, для оценки размеров небольших или удаленных от нас тел (спутников, астероидов) приходится применять косвенные способы, главным образом фотометрические (см. § 7).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редакционной коллегий серии книг «БИБЛИОТЕКА ЛЮБИТЕЛЯ АСТРОНОМИИ»
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОБЩИЕ СВЕДЕНИЯ О ПЛАНЕТАХ
- § 1. ЧТО ТАКОЕ ПЛАНЕТЫ
- § 2. ИСТОРИЧЕСКИЙ ОЧЕРК РАЗВИТИЯ ЗНАНИЙ О ПЛАНЕТАХ
- § 3. ОБЗОР СОЛНЕЧНОЙ СИСТЕМЫ
- ГЛАВА II. МЕТОДЫ ИССЛЕДОВАНИЯ ПЛАНЕТ
- § 4. ОПРЕДЕЛЕНИЕ МАСС И ДИАМЕТРОВ ПЛАНЕТ
- § 5. НАБЛЮДЕНИЯ ПОВЕРХНОСТЕЙ ПЛАНЕТ В ТЕЛЕСКОП
- § 6. ФОТОГРАФИРОВАНИЕ ПЛАНЕТ
- § 7. ФОТОМЕТРИЯ
- § 8. РАДИОМЕТРИЧЕСКИЕ НАБЛЮДЕНИЯ
- § 9. СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 10. РАДИОАСТРОНОМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
- § 11. РАДИОЛОКАЦИЯ ПЛАНЕТ
- § 12. ИССЛЕДОВАНИЕ ПЛАНЕТ КОСМИЧЕСКИМИ АППАРАТАМИ
- ГЛАВА III. РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ ПЛАНЕТ
- § 13. МЕРКУРИЙ
- § 14. ВЕНЕРА
- § 15. МАРС
- § 16. ЮПИТЕР, САТУРН, УРАН И НЕПТУН
- § 17. ПЛУТОН
- § 18. СПУТНИКИ ПЛАНЕТ И АСТЕРОИДЫ
- § 19. ВНУТРЕННЕЕ СТРОЕНИЕ ПЛАНЕТ
- ГЛАВА IV. НАБЛЮДЕНИЯ ПЛАНЕТ
- § 20. ЦЕЛИ И ЗАДАЧИ ЛЮБИТЕЛЬСКИХ НАБЛЮДЕНИЙ
- § 21. ОБЩИЕ ПРАВИЛА НАБЛЮДЕНИЙ
- § 22. УСЛОВИЯ НАБЛЮДЕНИЙ
- § 23. ИНСТРУМЕНТЫ И ПРИБОРЫ
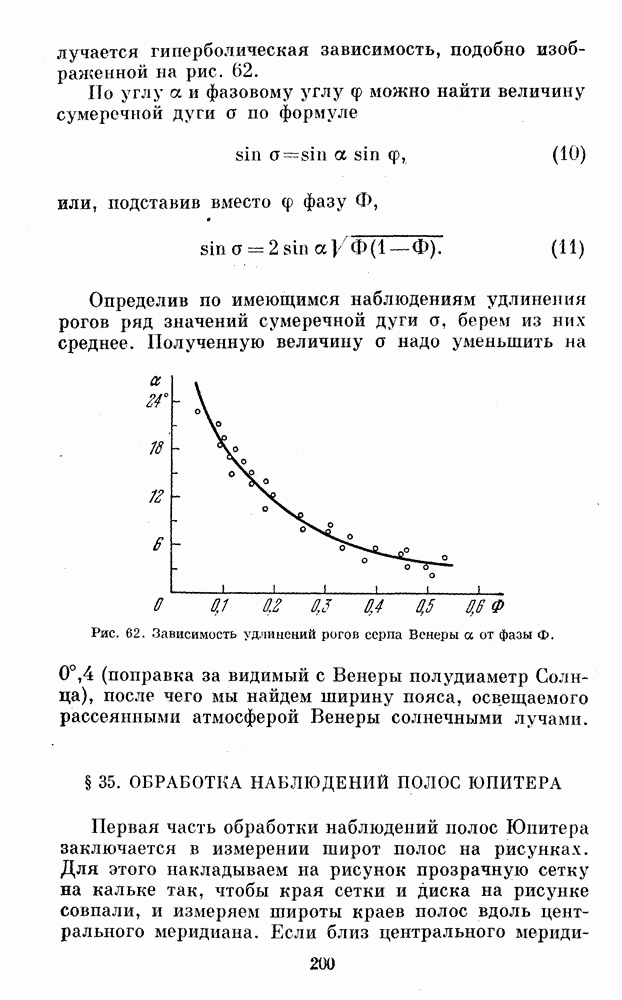
- § 24. НАБЛЮДЕНИЯ ВЕНЕРЫ
- § 25. НАБЛЮДЕНИЯ МАРСА
- § 26. НАБЛЮДЕНИЯ ЮПИТЕРА
- § 27. НАБЛЮДЕНИЯ САТУРНА И ЕГО КОЛЬЦА
- § 28. НАБЛЮДЕНИЯ ОСТАЛЬНЫХ ПЛАНЕТ
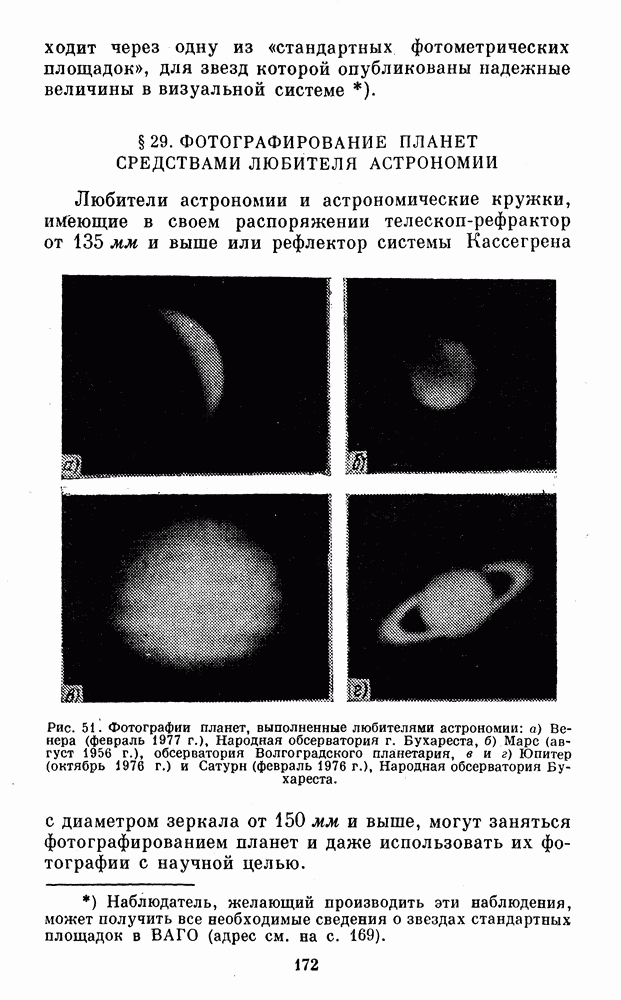
- § 29. ФОТОГРАФИРОВАНИЕ ПЛАНЕТ СРЕДСТВАМИ ЛЮБИТЕЛЯ АСТРОНОМИИ
- § 30. ФОТОЭЛЕКТРИЧЕСКАЯ ФОТОМЕТРИЯ ПЛАНЕТ
- ГЛАВА V. ОБРАБОТКА НАБЛЮДЕНИЙ
- § 31. ЧТО ТАКОЕ ОБРАБОТКА НАБЛЮДЕНИЙ
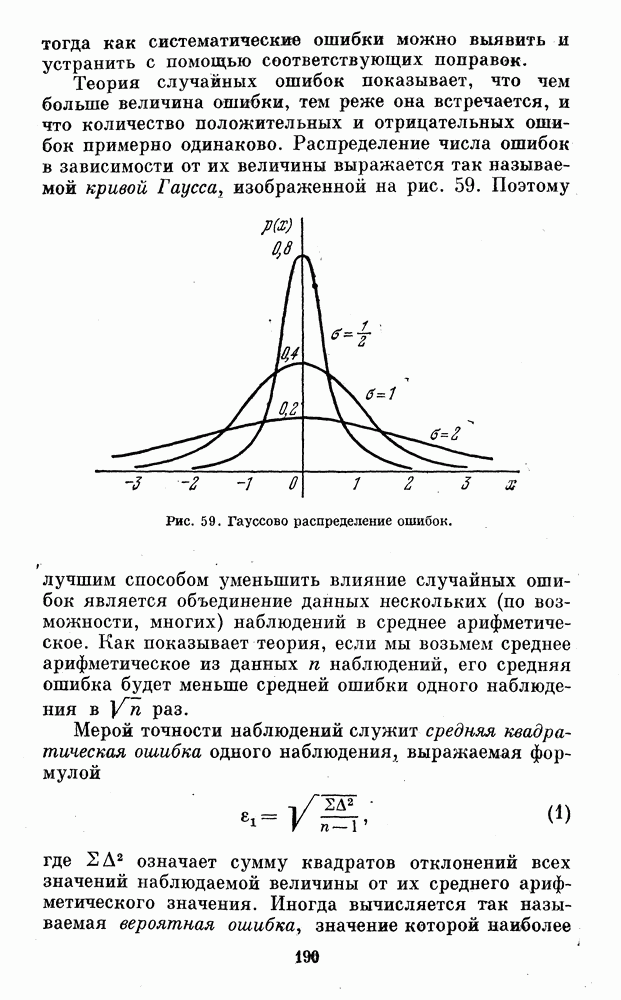
- § 32. ОШИБКИ НАБЛЮДЕНИЙ
- § 33. ЭЛЕМЕНТЫ ПЛАНЕТНЫХ ОРБИТ И ЭФЕМЕРИДЫ
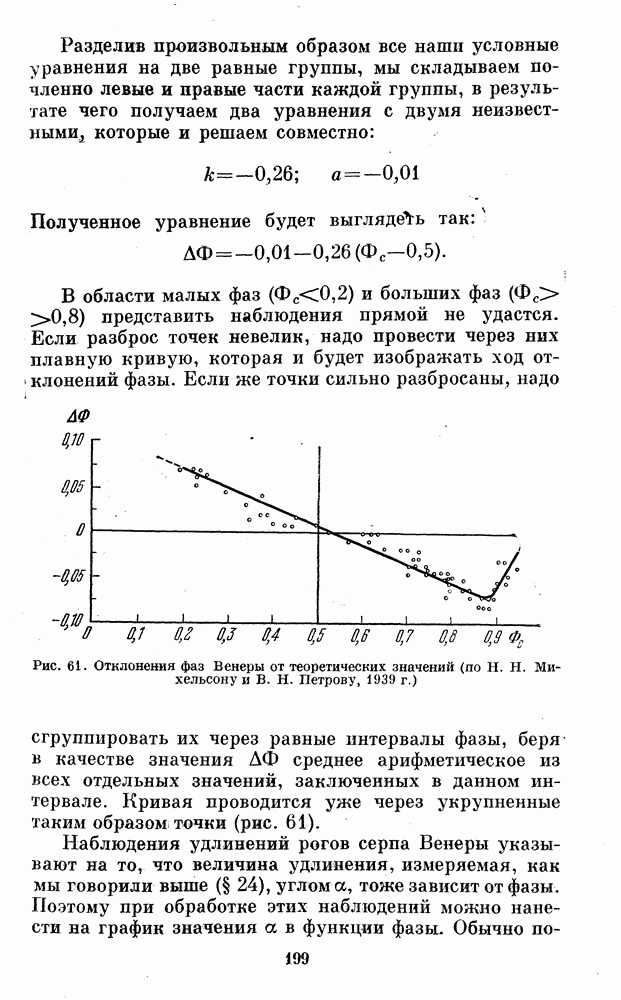
- § 34. ОБРАБОТКА НАБЛЮДЕНИЙ ФАЗ ВЕНЕРЫ
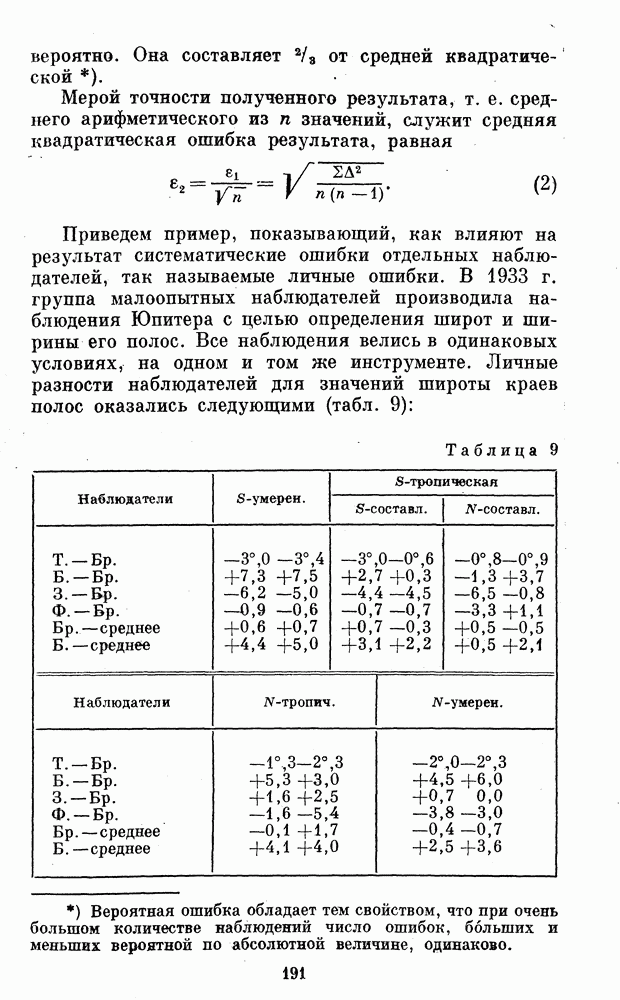
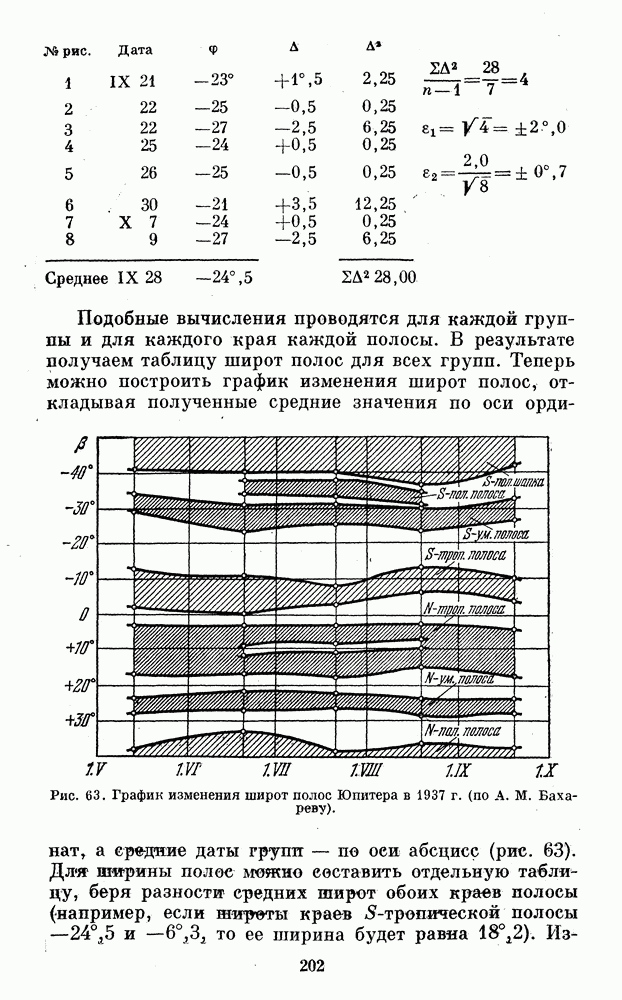
- § 35. ОБРАБОТКА НАБЛЮДЕНИЙ ПОЛОС ЮПИТЕРА
- § 36. СОСТАВЛЕНИЕ КАРТ ПЛАНЕТ
- § 37. ОПРЕДЕЛЕНИЕ ПЕРИОДА ВРАЩЕНИЯ ПЛАНЕТЫ
- § 38. ОБРАБОТКА ФОТОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ
- § 39. ОРГАНИЗАЦИЯ И ПРОГРАММА РАБОТЫ
- ПРИЛОЖЕНИЯ
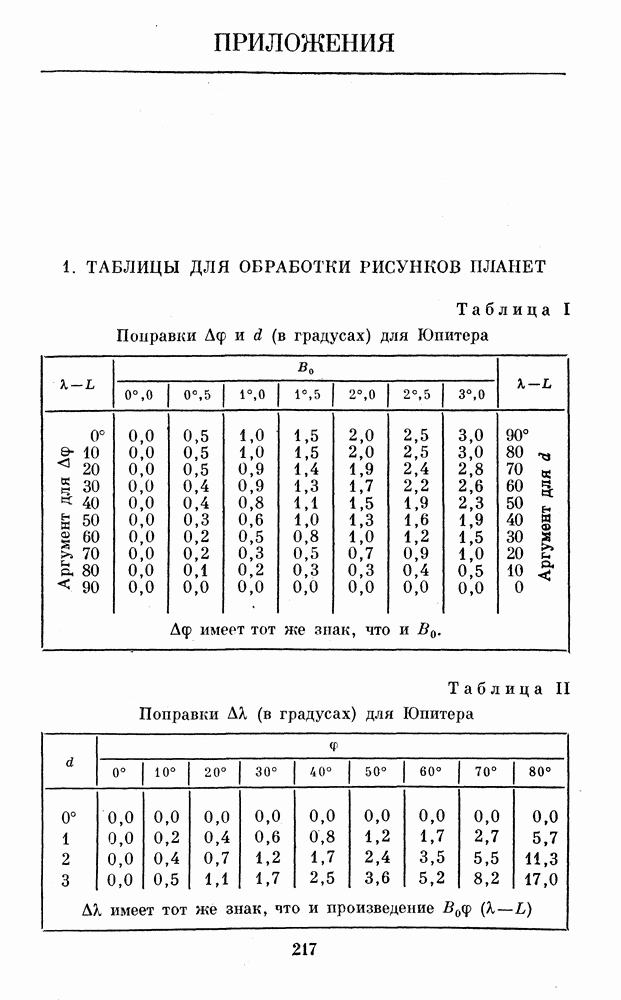
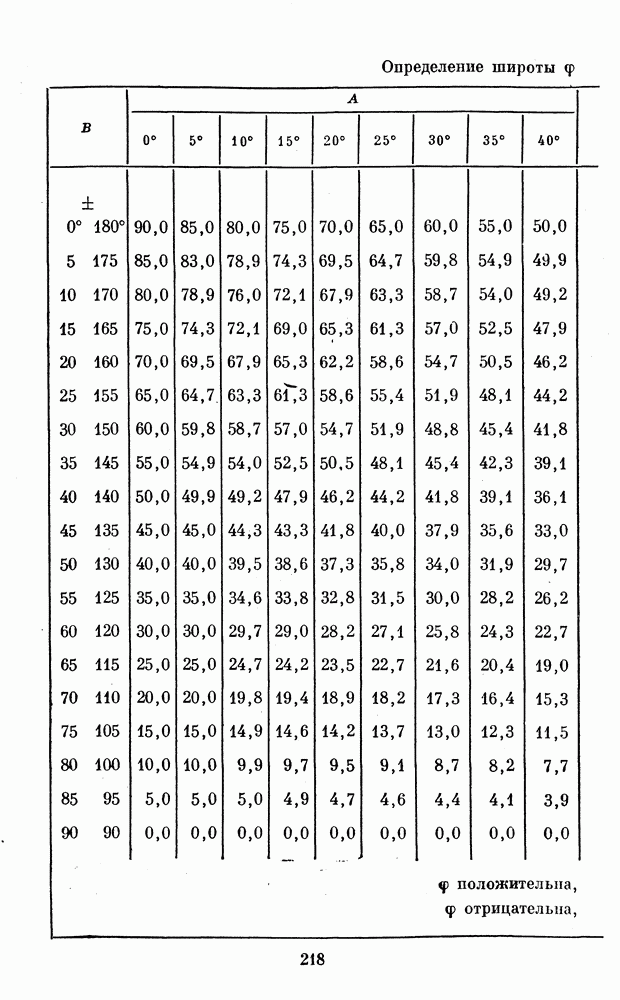
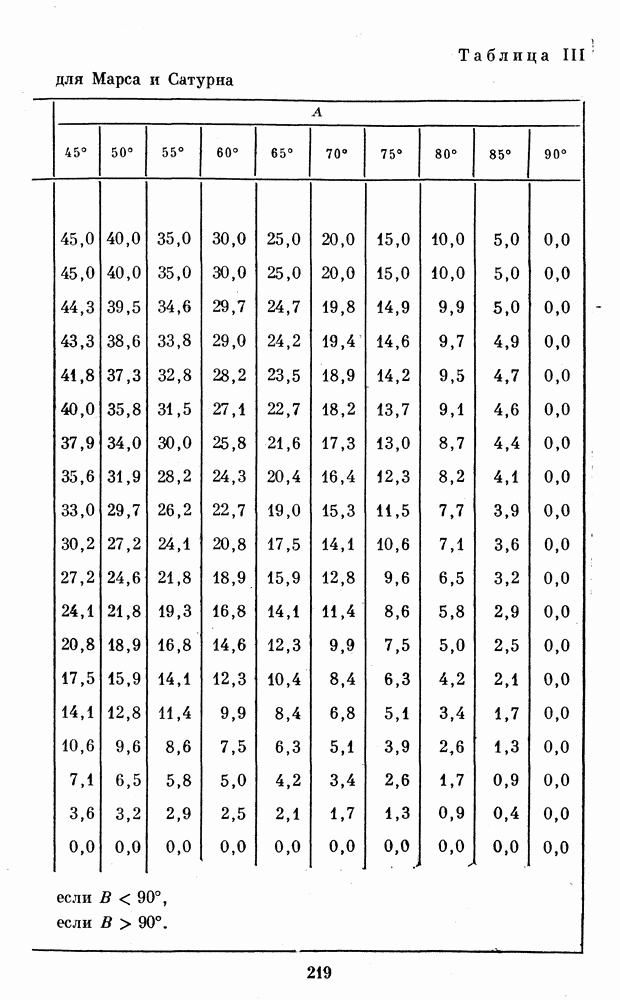
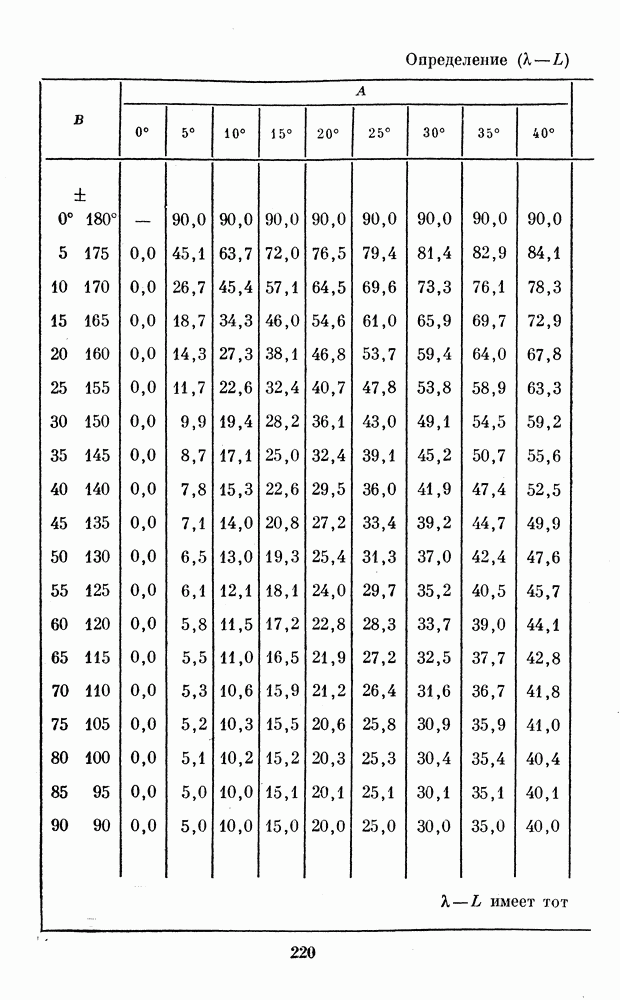
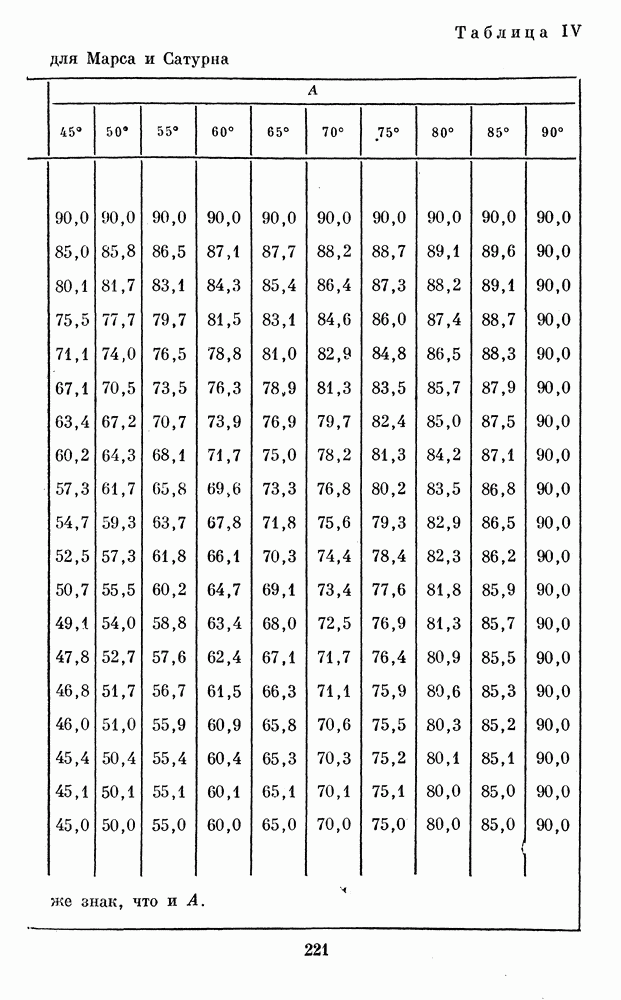
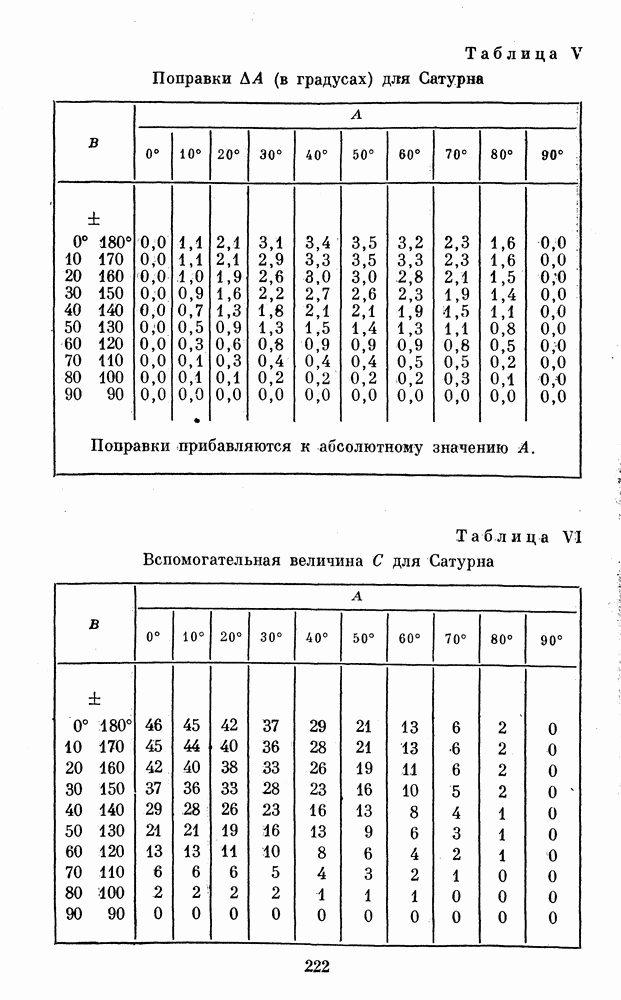
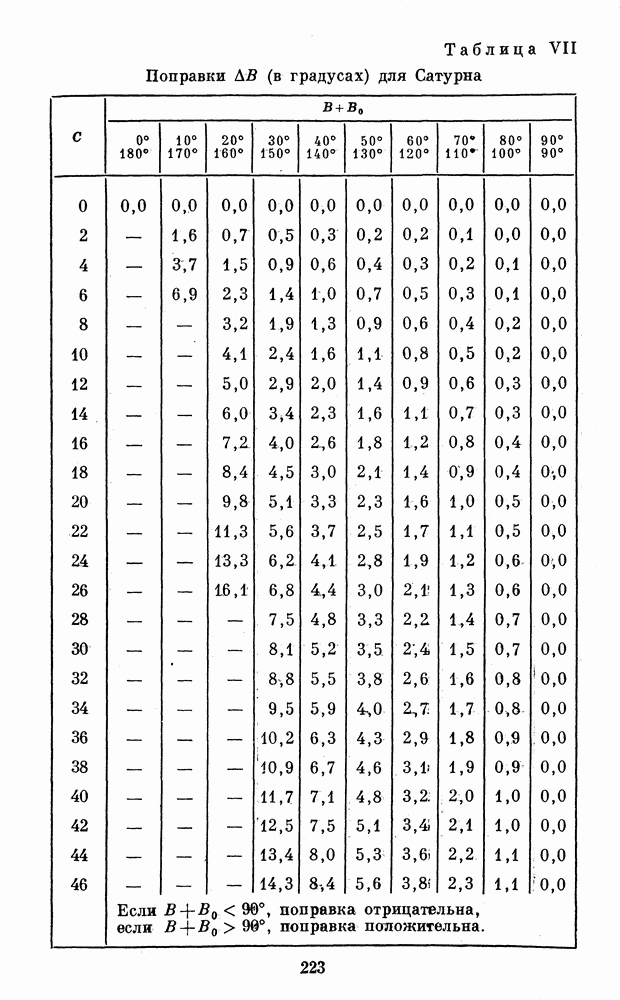
- 1. ТАБЛИЦЫ ДЛЯ ОБРАБОТКИ РИСУНКОВ ПЛАНЕТ
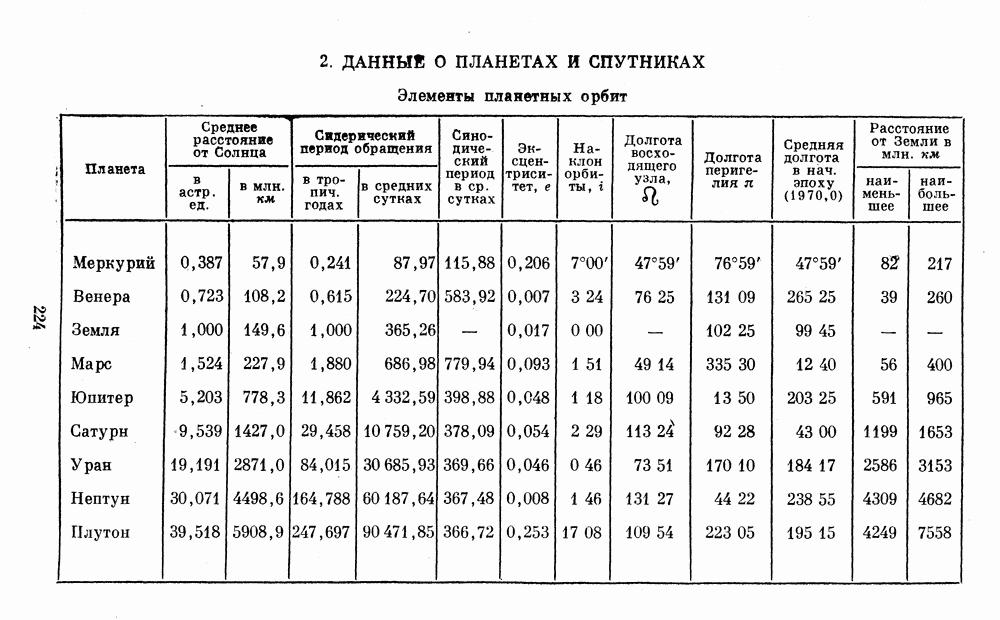
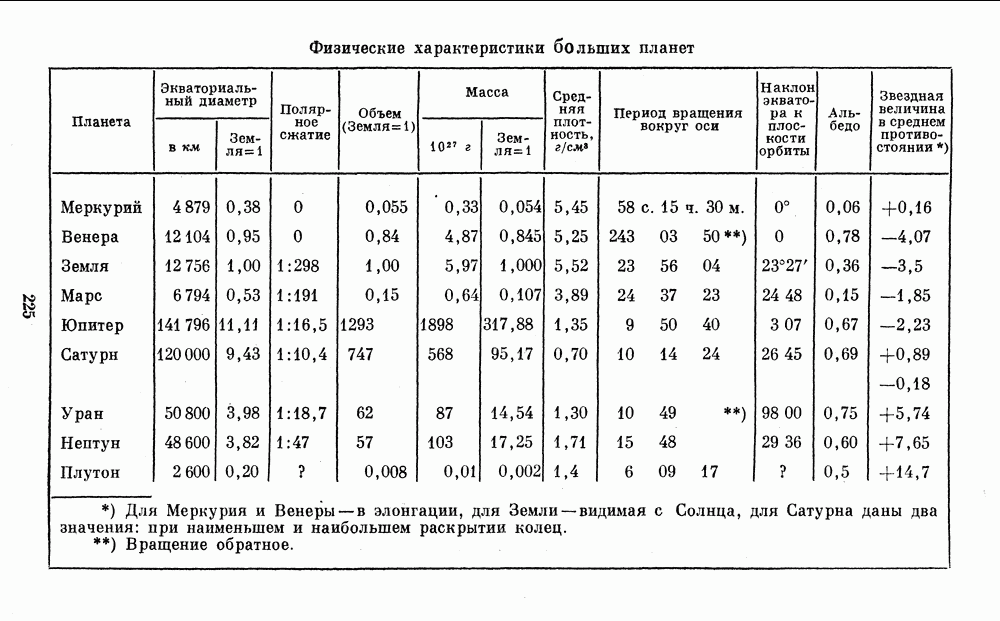
- 2. ДАННЫЕ О ПЛАНЕТАХ И СПУТНИКАХ
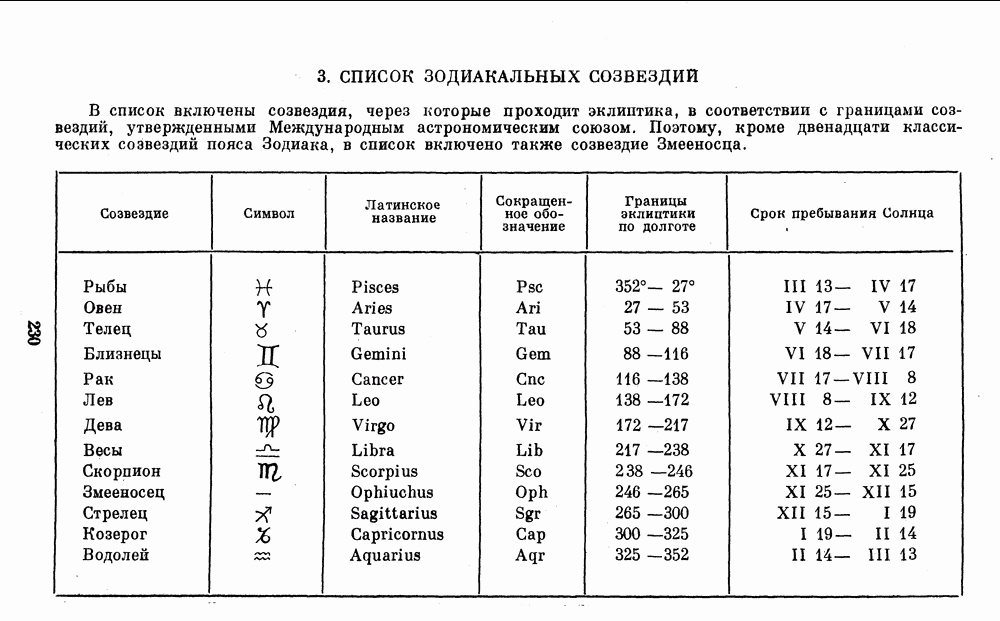
- 3. СПИСОК ЗОДИАКАЛЬНЫХ СОЗВЕЗДИЙ
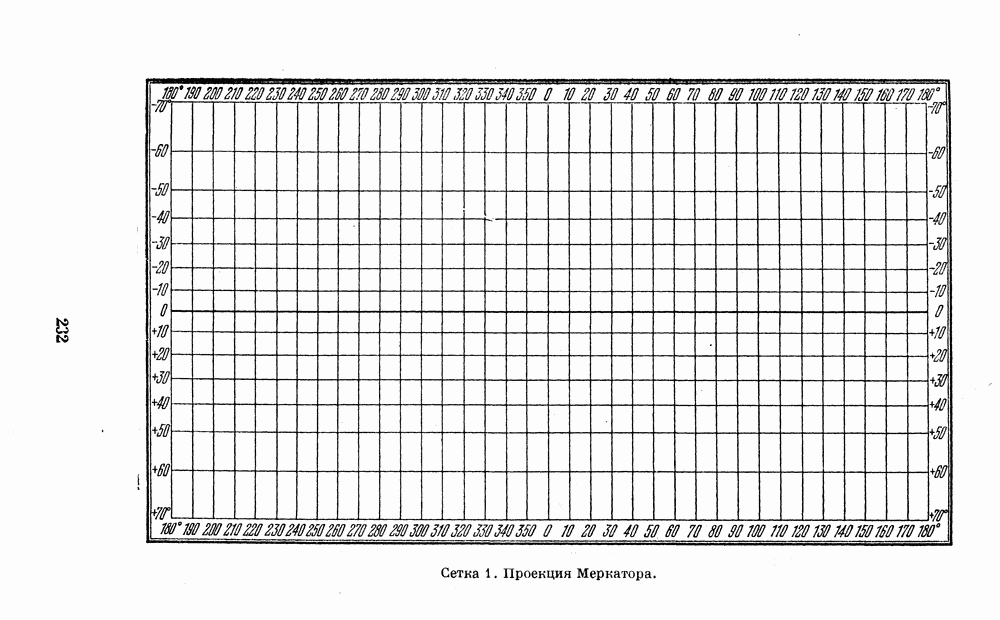
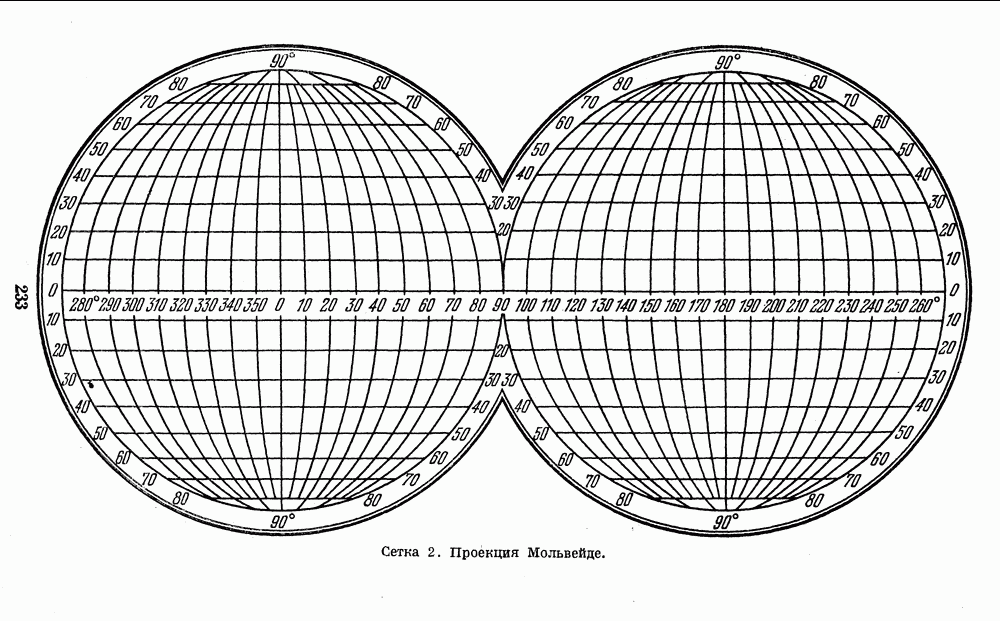
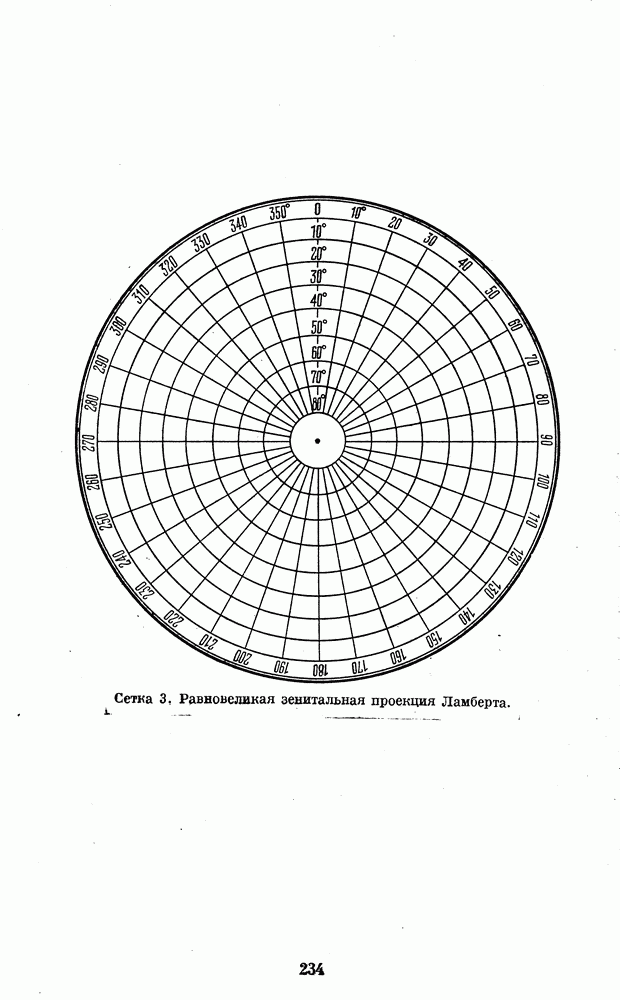
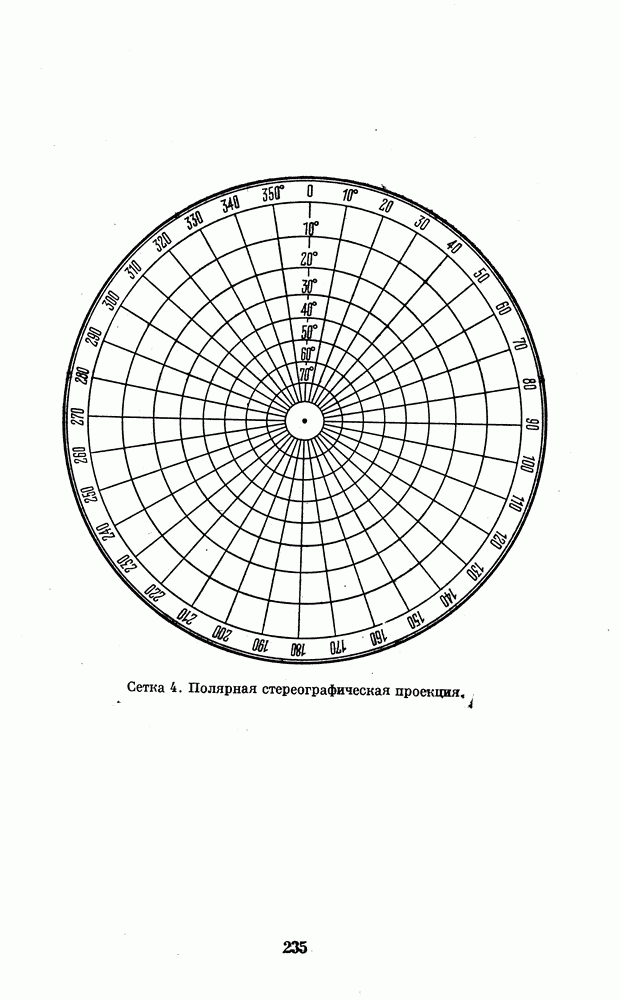
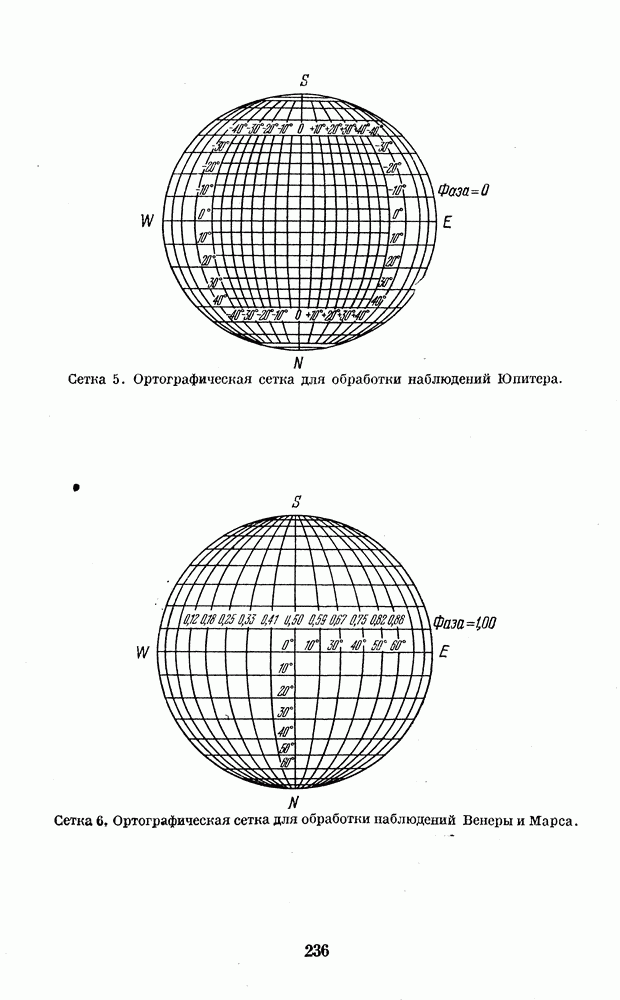
- 4. КООРДИНАТНЫЕ СЕТКИ ДЛЯ ПОСТРОЕНИЯ КАРТ ПЛАНЕТ
- ЛИТЕРАТУРА