| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
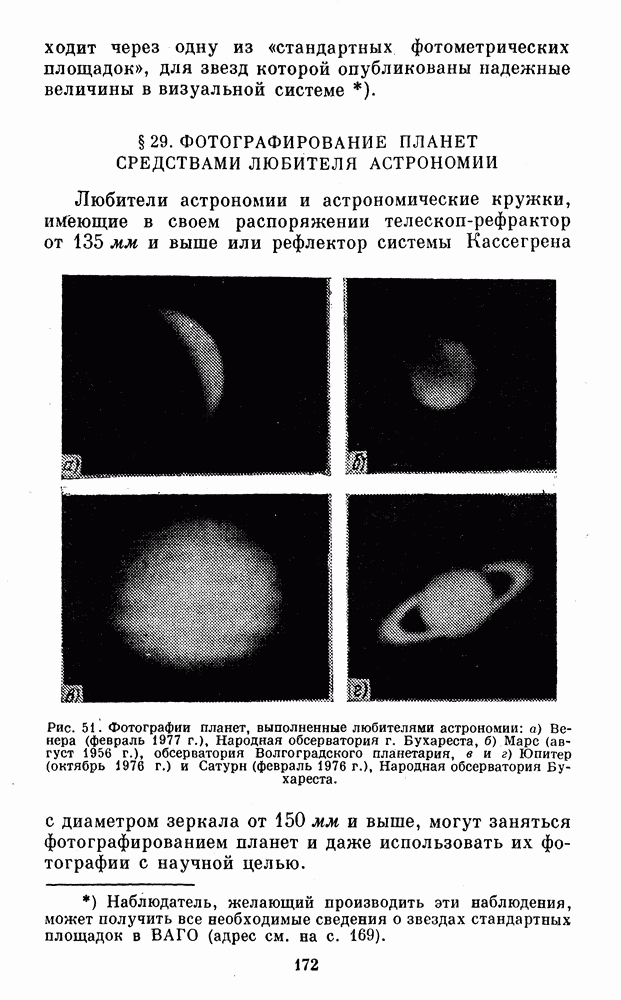
§ 36. СОСТАВЛЕНИЕ КАРТ ПЛАНЕТ
Карты планет, так же как и географические карты, имеют целью дать изображение поверхности планеты на плоскости в определенном масштабе.
Перенесение шаровой, а тем более эллипсоидальной поверхности на плоскость — не простая задача, ибо поверхность шара нельзя развернуть на плоскость, как поверхность цилиндра или конуса. Для изображения поверхности шара на плоскости приходится прибегать к различного рода картографическим проекциям, при которых неизбежны различные искажения, т. е. нарушение подобия между отдельными частями поверхности планеты и их изображениями на карте.
Различные виды проекций применяются в зависимости от их свойств и характера вносимых искажений, в соответствии с той целью, для которой составляется карта.
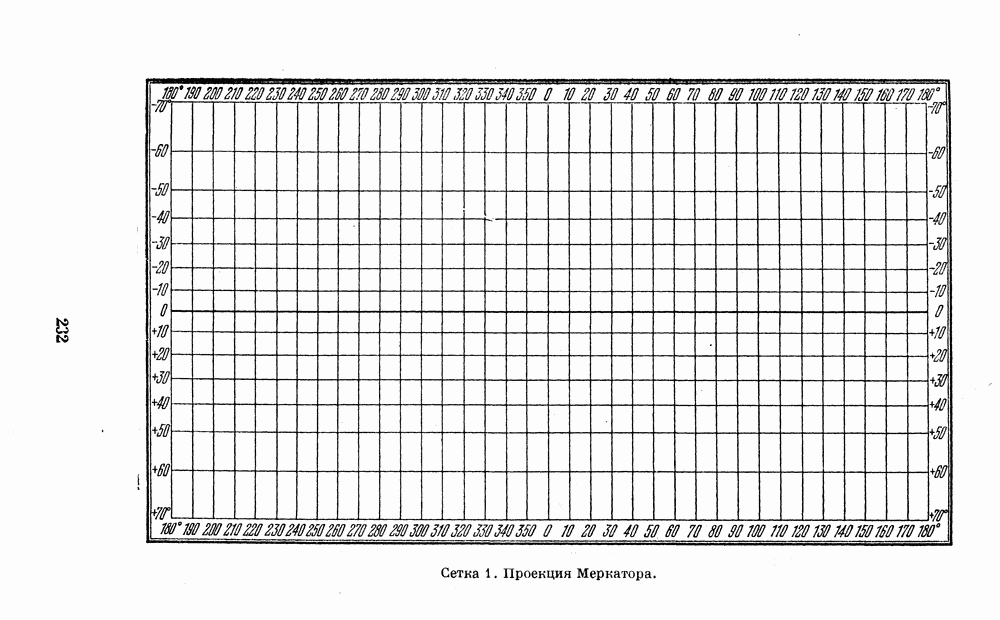
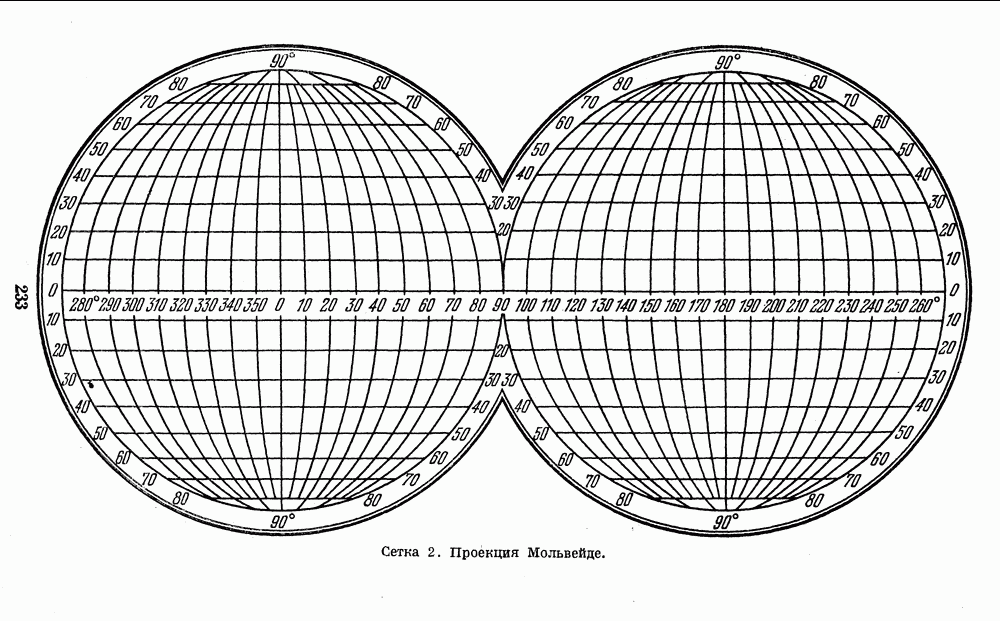
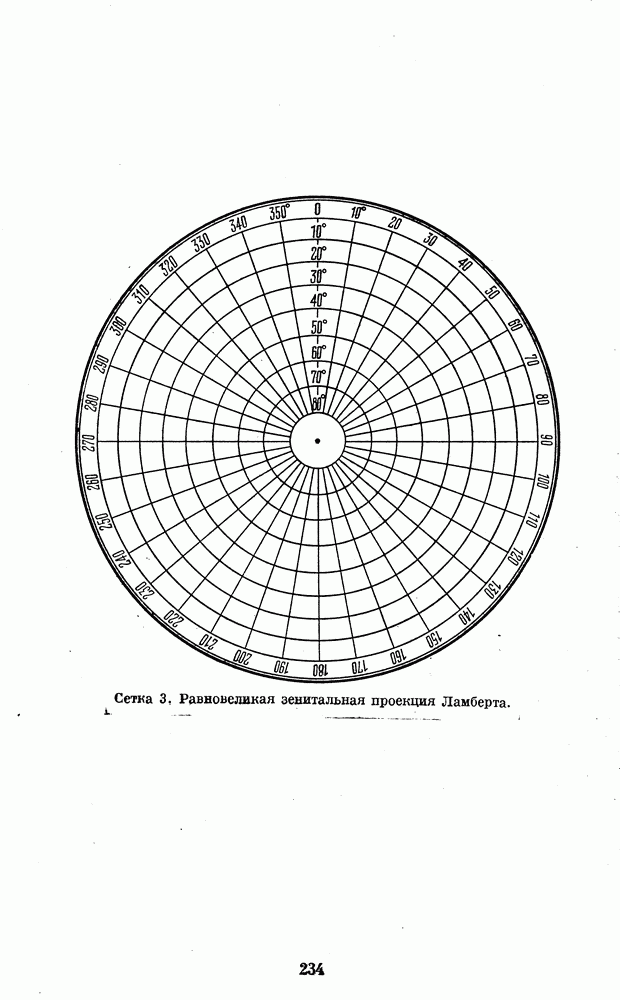
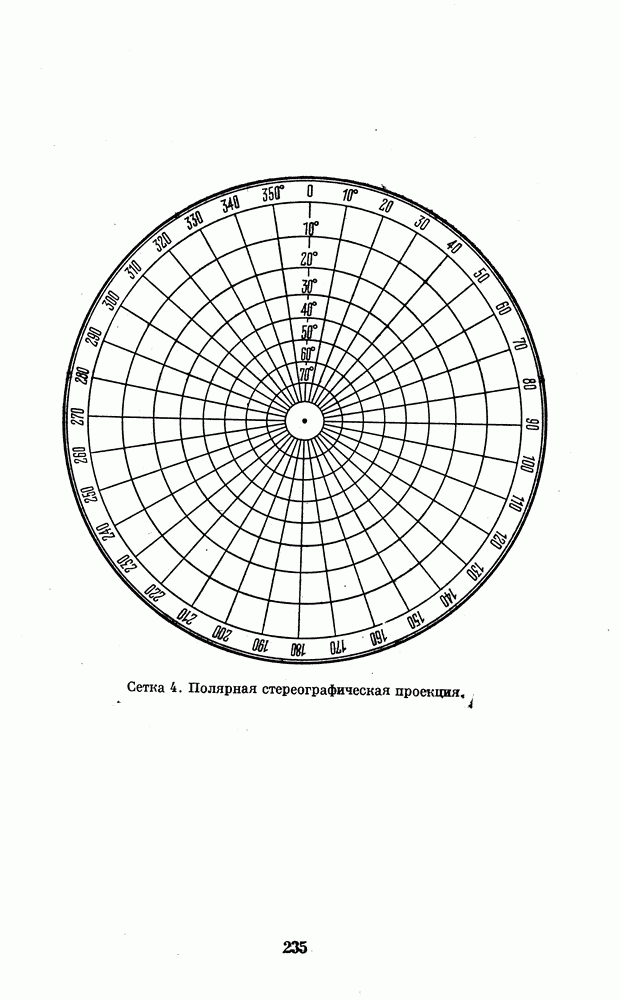
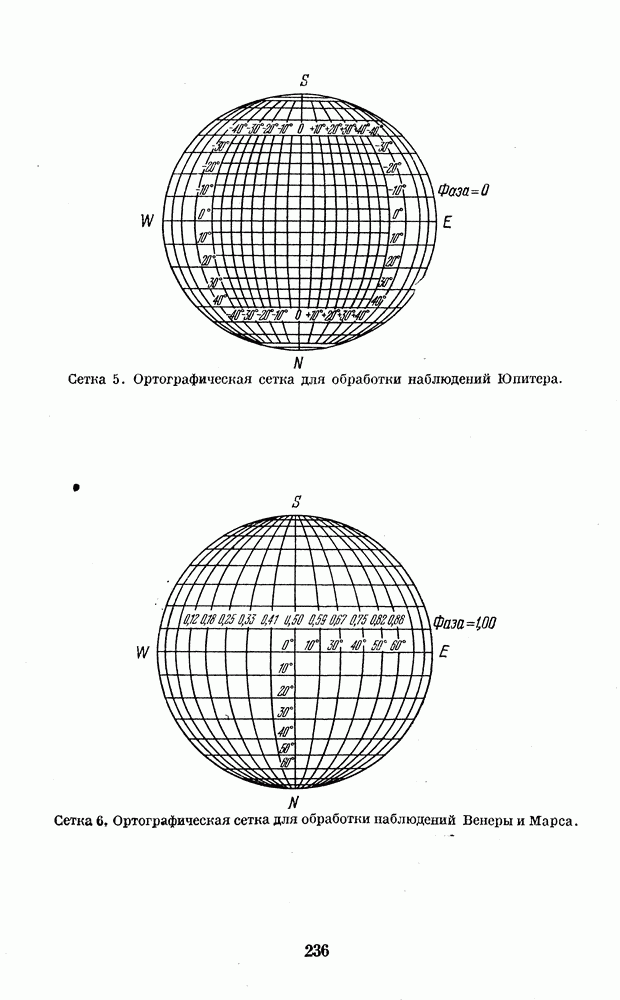
В основном их можно разделить на две группы: конформные, т. е. сохраняющие подобные формы деталей поверхности планеты, и равновеликие, т. е. сохраняющие правильное отношение их площадей. Подробнее о принципах, лежащих в основе различных картографических проекций, можно прочитать в книгах по картографии и картоведению. Некоторые из них указаны в списке литературы в конце книги. Кроме того, в Приложении 4 приведены сетки координат для построения карт планет в наиболее употребительных в планетоведении картографических проекциях с необходимыми пояснениями.
Перейдем к практическим приемам составления карт планет. Для Юпитера, на поверхности которого происходят быстрые изменения, карты составляются для сравнительно коротких промежутков времени (1 — 2 месяца). Такой метод обработки получил название метода коротких сроков.
Построение карты Юпитера представляет собой сравнительно несложную задачу.
Прежде всего измеряются долготы деталей, изображенных на рисунках, по отношению к центральному меридиану. Если деталь невелика, можно делать измерение для ее центра, если же она имеет значительную протяженность по долготе, то измеряются долготы ее крайних точек. Все измерения производятся с помощью сетки, подобно измерениям широт полос. Поскольку обычно детали связаны с полосами, их широты измерять почти не приходится; это оказывается необходимым лишь в отдельных случаях.
Чтобы перейти от относительных долгот к абсолютным, нужно вычислить долготу центрального меридиана для момента наблюдений в I и II системах (см. § 33). Все необходимые, данные для этого даются в астрономических календарях, а само вычисление производится путем линейного интерполирования. После того как получена долгота центрального меридиана, нужно прибавить к ней измеренные по сетке долготы деталей, расположенных к востоку от центрального меридиана (на рисунке справа), и вычесть долготы деталей, расположенных к западу (т. е. слева). Таким образом мы получим список деталей в порядке их наблюдения с указанием долгот. Рекомендуется такие списки делать отдельно для каждой полосы и зоны.
Когда все долготы деталей известны и составлен их список, приступаем к отождествлению деталей. Многие детали могут оказаться на нескольких рисунках, особенно если они сделаны в один и тот же день. Сравнивая долготы деталей одного типа (например, темных пятен), выбираем те из них, у которых долготы совпадают или отличаются не более чем на 10°. Чем больше интервал времени между наблюдениями, тем больше допустимая разность долгот. В сомнительных случаях надо сравнить рисунки. Если деталь наблюдалась близко к краю диска, ошибка определения долготы обычно бывает весьма велика, и наблюдение при обработке отбрасывается.
Когда отождествление закончено, составляется окончательный каталог деталей, куда вносятся лишь те детали, которые наблюдались не менее двух раз (т. е. имеются на двух и более рисунках). В каталоге нужно указывать период видимости детали, ее интенсивность, цвет, долготу для середины периода видимости и собственное движение по долготе.
Собственное движение у деталей имеет место, если их период вращения не совпадает с принятым периодом вращения соответствующей системы (для I системы 9 ч. 50 м. 30 с., для II системы 9 ч. 55 м. 41 с.).
Для определения собственного движения составляем условные уравнения, определяющие долготу детали  в данный момент Т через долготу
в данный момент Т через долготу  в начальный момент
в начальный момент  . Эти уравнения имеют следующий вид:
. Эти уравнения имеют следующий вид:

Решая по способу Коши, находим начальную долготу и собственное движение к в градусах за сутки.
Для некоторых деталей, в том числе для Красного пятна, значение к не остается постоянным. Тогда, нанеся долготы детали на график в функции времени, мы можем разбить весь период видимости детали на несколько частей, внутри которых к сохраняет примерно одинаковое значение., и вычислить его для каждой части отдельно.
После этого можно нанести полосы и детали на карту. Для этого проще всего приготовить так называемую квадратную сетку, в которой меридианы и параллели изображаются прямыми линиями.

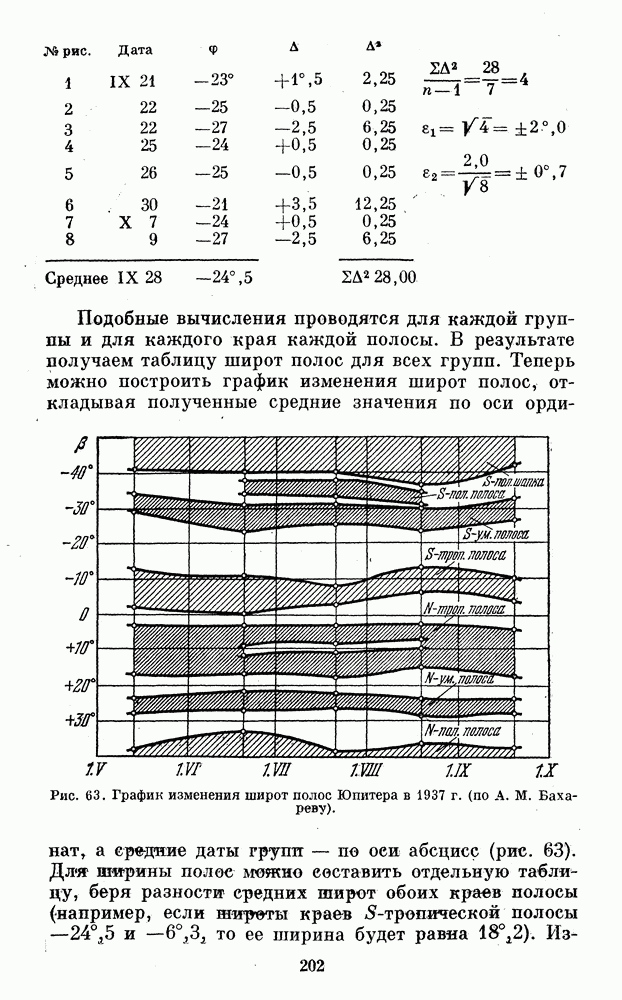
Рис. 64. Карта Юпитера, составленная на 1 августа 1950 г. В. Марголиной по любительским наблюдениям.
Удобно принять за масштаб 1° в 1 мм. На большом листе миллиметровой бумаги сначала чертим экватор в виде прямой линии длиной 36 см. Ту же длину будут иметь и параллели, которые проводятся параллельно экватору на расстоянии 1 см одна от другой.
Меридианы будут прямыми линиями, перпендикулярными к параллелям, также проведенными через 1 см. Длина каждого из них — 18 см (180°), по 9 см к северу и к югу от акватора. Сетка такого типа хорошо передает контуры деталей в экваториальной зоне; чем ближе к полюсу, тем больше искажения, поскольку на сетке все параллели имеют одинаковую длину, в то время как в действительности их длина убывает с широтой.
Начертив сетку, наносим сперва контуры полос по значениям широт их краев. Затем по сделанному каталогу наносим детали по их долготам, прибегая для передачи вида детали к наиболее удачным рисункам, на которых она изображена. Очертив контуры, производим тушовку, стремясь правильно передать интенсивность деталей и полос. Пример такой карты Юпитера представлен на рис. 64. Юг на ней находится вверху, а север — внизу, как на телескопических изображениях планеты.
Прежде чем наносить полосы и детали на карту, надо учесть наклон оси планеты к картинной плоскости, равный иовиографической широте центра диска  Для Юпитера угол
Для Юпитера угол  никогда не превышает
никогда не превышает  величина его дается на каждый год в «Астрономическом Календаре» ВАГО. Поскольку измерение широт полос производится обычно у центрального меридиана, достаточно прибавить к измеренным величинам значение
величина его дается на каждый год в «Астрономическом Календаре» ВАГО. Поскольку измерение широт полос производится обычно у центрального меридиана, достаточно прибавить к измеренным величинам значение  (которое может быть положительным или отрицательным). Более точно поправки широты и долготы определяются по формулам
(которое может быть положительным или отрицательным). Более точно поправки широты и долготы определяются по формулам

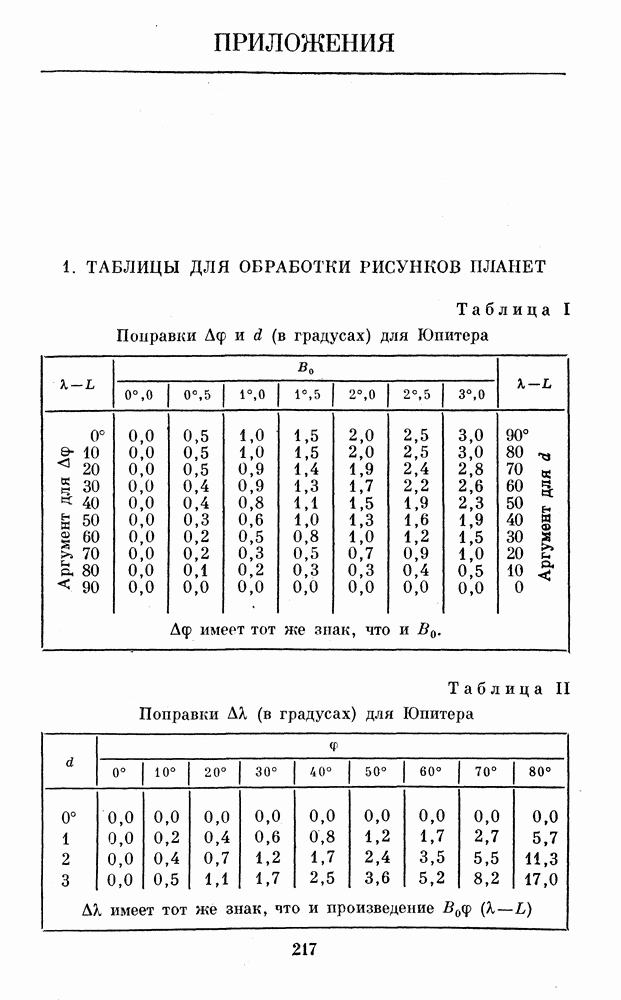
где L — долгота центрального меридиана. Эти поправки можно найти с помощью табл. I и II Приложения 1. В табл. I даны значения  по аргументу
по аргументу  а из табл. II по d и
а из табл. II по d и  находится
находится 
При измерении координат деталей на рисунках Марса нужно прежде всего найти направление проекции оси планеты на плоскость рисунка. Для этого используем отмеченное на рисунке направление суточной параллели (см. § 25).
Проведем через центр диска перпевдикуляр к этому направлению — это будет круг склонения центра диска Марса. Затем, взяв из ежегодника значение угла Р между проекцией оси и кругом склонения, откладываем этот угол на рисунке (он считается положительным к востоку) и получаем нужное нам направление проекции оси планеты.
При составлении карт Марса и Сатурна некоторое затруднение представляет большой наклон оси планеты к картинной плоскости, который может достигать 25° для Марса и 28° для Сатурна.

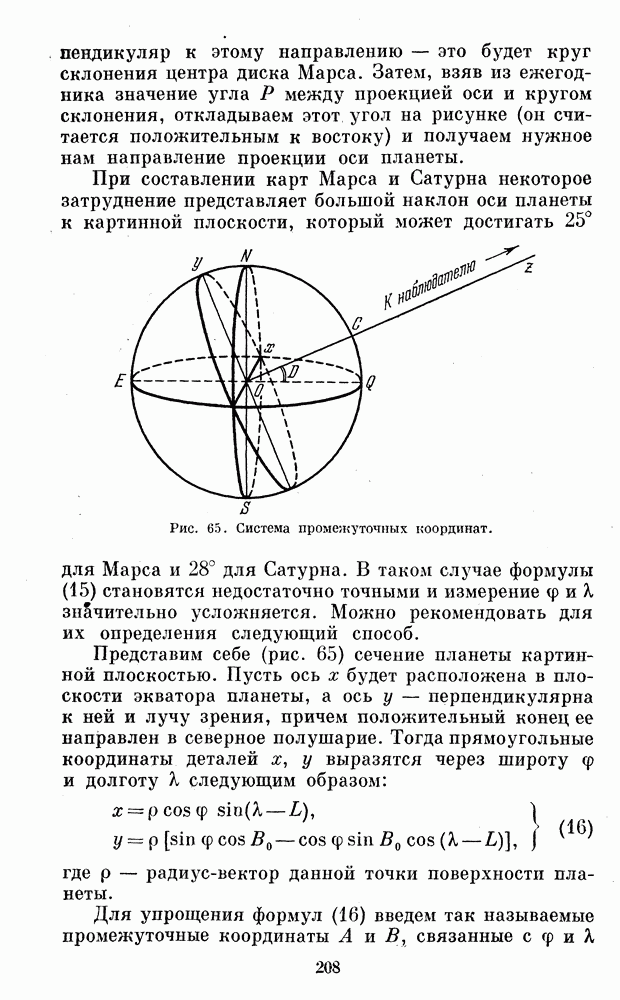
Рис. 65. Система промежуточных координат.
В таком случае формулы (15) становятся недостаточно точными и измерение  и X значительно усложняется. Можно рекомендовать для их определения следующий способ.
и X значительно усложняется. Можно рекомендовать для их определения следующий способ.
Представим себе (рис. 65) сечение планеты картинной плоскостью. Пусть ось  будет расположена в плоскости экватора планеты, а ось у — перпендикулярна к ней и лучу зрения, причем положительный конец ее направлен в северное полушарие. Тогда прямоугольные координаты деталей
будет расположена в плоскости экватора планеты, а ось у — перпендикулярна к ней и лучу зрения, причем положительный конец ее направлен в северное полушарие. Тогда прямоугольные координаты деталей  у выразятся через широту
у выразятся через широту  и долготу X следующим образом:
и долготу X следующим образом:

где  — радиус-вектор данной точки поверхности планеты.
— радиус-вектор данной точки поверхности планеты.
Для упрощения формул (16) введем так называемые промежуточные координаты А и  связанные с
связанные с  следующими формулами:
следующими формулами:

Подставляя (17) в (16), получим

Теперь, если мы измерим на нашем рисунке координаты  и у каждой детали, можно из формул (18) определить А и
и у каждой детали, можно из формул (18) определить А и  а именно:
а именно:

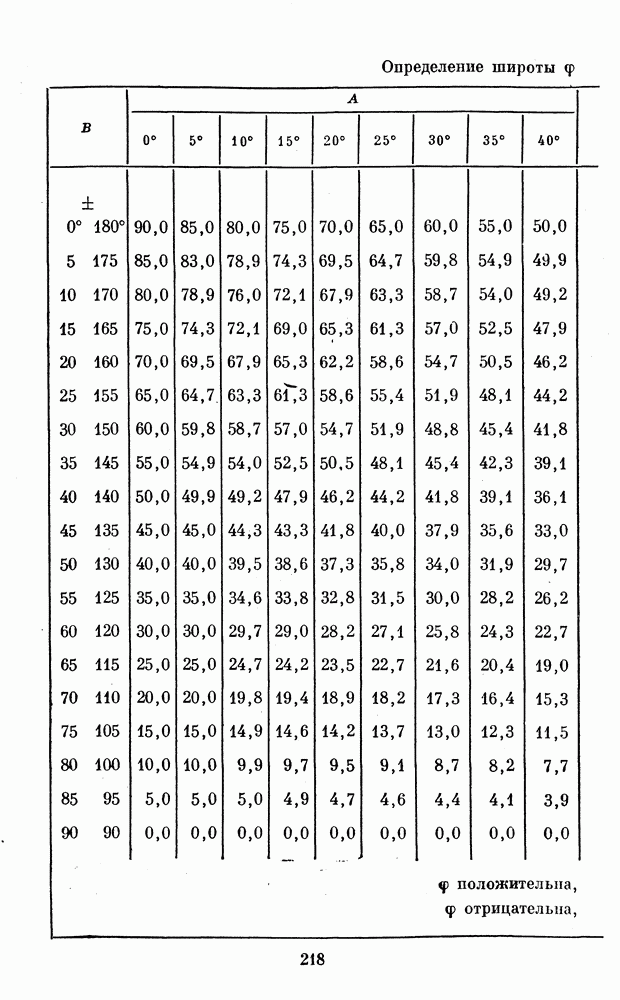
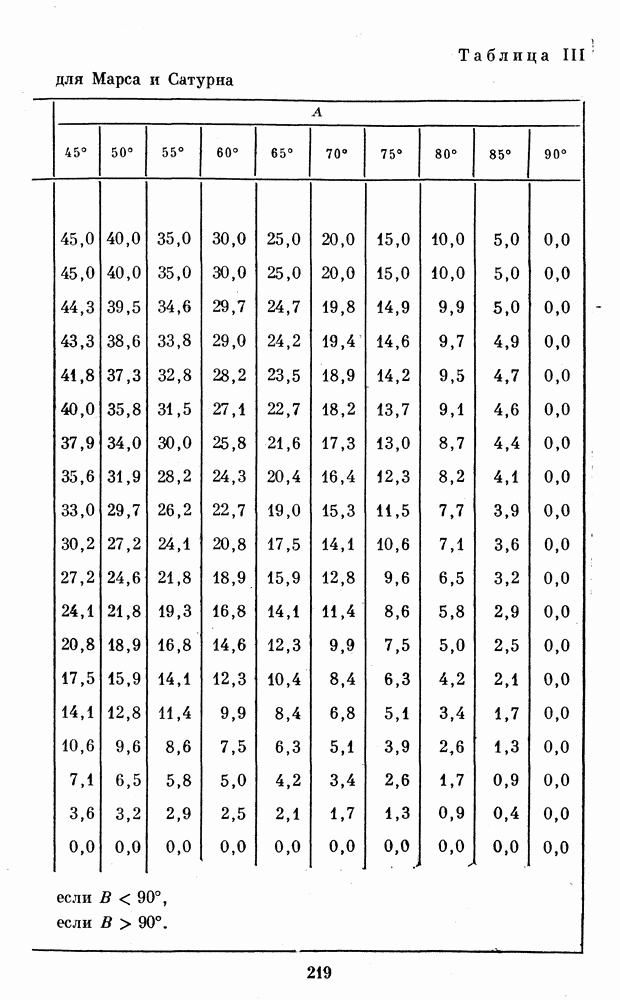
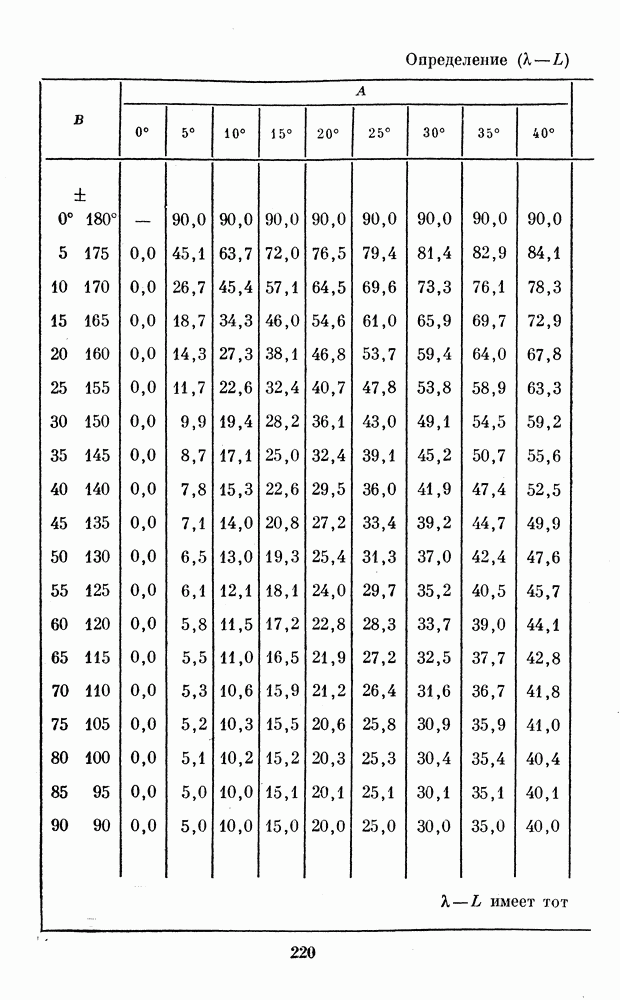
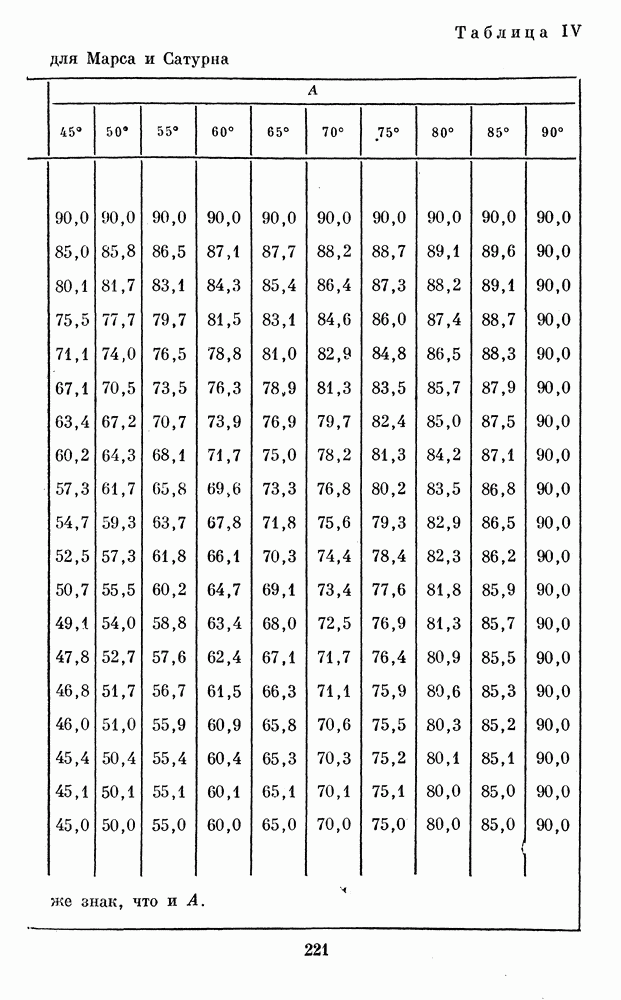
После этого по А и В с помощью формул (17) можно найти  Для облегчения этого в Приложении 1 приведены табл. III и IV.
Для облегчения этого в Приложении 1 приведены табл. III и IV.
Нетрудно сообразить, что промежуточные координаты А и В вполне аналогичны планетографическим координатам  и к, но их система повернута по отношению к
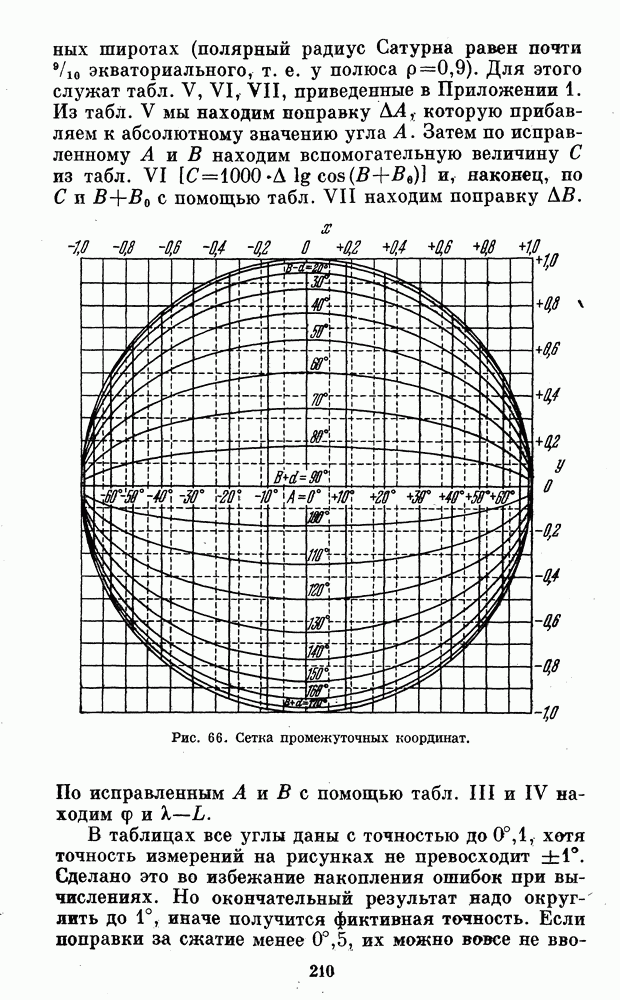
и к, но их система повернута по отношению к  и к на 90°. «Полюсы» промежуточных координат расположены на экваторе планеты, а «экватор» этой системы совпадает с центральным меридианом планеты (рис. 66). «Долготы» В отсчитываются от северного полюса планеты к центру диска, причем на северном конце центрального меридиана
и к на 90°. «Полюсы» промежуточных координат расположены на экваторе планеты, а «экватор» этой системы совпадает с центральным меридианом планеты (рис. 66). «Долготы» В отсчитываются от северного полюса планеты к центру диска, причем на северном конце центрального меридиана  и на южном
и на южном 
Благодаря такому соотношению мы можем не измерять  а просто наложить прозрачную сетку на рисунок, повернув ее на 90° так, чтобы экватор сетки совпал с центральным меридианом на рисунке планеты, причем северный полюс сетки, обозначенный буквой
а просто наложить прозрачную сетку на рисунок, повернув ее на 90° так, чтобы экватор сетки совпал с центральным меридианом на рисунке планеты, причем северный полюс сетки, обозначенный буквой  был бы слева. Измеряем затем
был бы слева. Измеряем затем  — широты и долготы, указанные на сетке). Зная
— широты и долготы, указанные на сетке). Зная  находим
находим  после чего из табл. III и IV по известным А и В находим
после чего из табл. III и IV по известным А и В находим 
Для Марса, форма которого мало отличается от шара, можно положить  Однако для Сатурна, имеющего значительное сжатие (1 : 9,7), требуется еще ввести поправки за различие радиусов-векторов
Однако для Сатурна, имеющего значительное сжатие (1 : 9,7), требуется еще ввести поправки за различие радиусов-векторов  разных широтах (полярный радиус Сатурна равен почти
разных широтах (полярный радиус Сатурна равен почти  экваториального, т. е. у полюса
экваториального, т. е. у полюса  ).
).
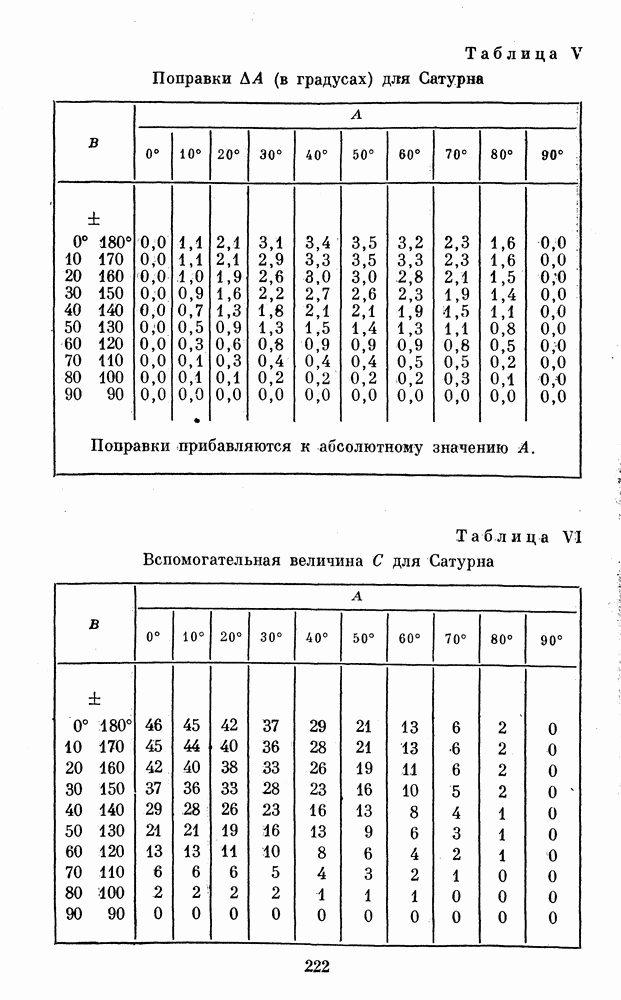
Для этого служат табл. V, VI, VII, приведенные в Приложении 1. Из табл. V мы находим поправку  которую прибавляем к абсолютному значению угла А. Затем по исправленному А и В находим вспомогательную величину С из табл. VI
которую прибавляем к абсолютному значению угла А. Затем по исправленному А и В находим вспомогательную величину С из табл. VI  и, наконец, по
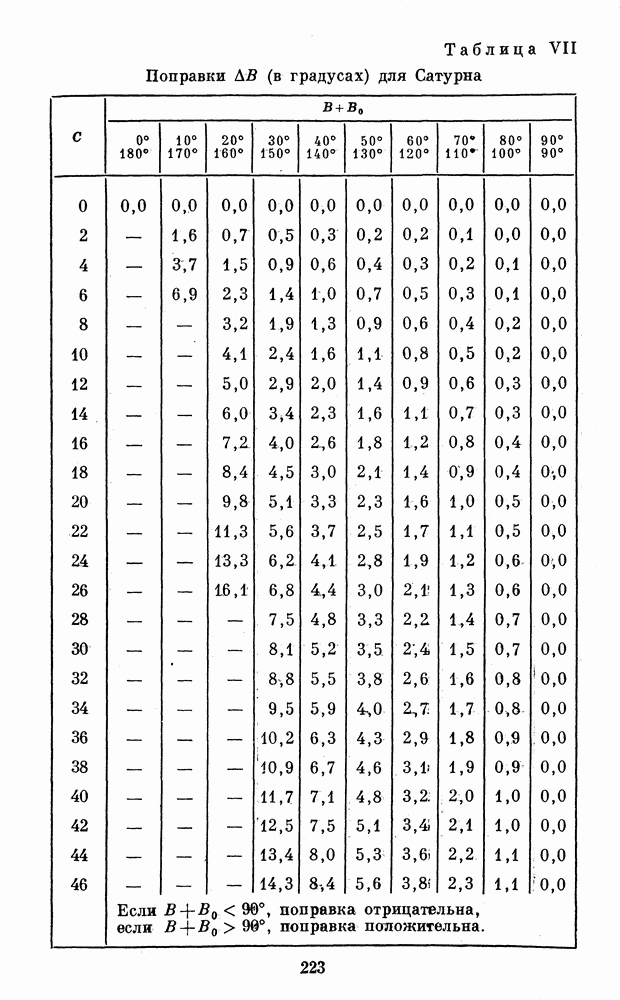
и, наконец, по  с помощью табл. VII находим поправку
с помощью табл. VII находим поправку 

Рис. 66. Сетка промежуточных координат.
По исправленным А и В с помощью табл. III и IV находим 
В таблицах все углы даны с точностью до  хотя точность измерений на рисунках не превосходит ±1°. Сделано это во избежание накопления ошибок при вычислениях. Но окончательный результат надо округлить до 1°, иначе получится фиктивная точность. Если поправки за сжатие менее
хотя точность измерений на рисунках не превосходит ±1°. Сделано это во избежание накопления ошибок при вычислениях. Но окончательный результат надо округлить до 1°, иначе получится фиктивная точность. Если поправки за сжатие менее  их можно вовсе не вводить.
их можно вовсе не вводить.
На Сатурне детали наблюдаются довольно редко, и поэтому такую процедуру придется применять лишь иногда.
Пример. На рисунке Сатурна, сделанном 26 апреля 4978 г., измерены промежуточные координаты детали:  Требуется определить
Требуется определить 
Из «Астрономического Календаря» на 1978 г. находим для 26 апреля  (к Земле обращен южный конец оси пданеты), откуда
(к Земле обращен южный конец оси пданеты), откуда  По табл. V находим
По табл. V находим  значит,
значит,  . С этим значением из табл. VI находим
. С этим значением из табл. VI находим  а из табл. VII
а из табл. VII  По
По  из табл. III и IV находим окончательно
из табл. III и IV находим окончательно 
Поверхность Марса изображается в виде планисфер — двух полушарий. Сетку для построения такой карты можно скопировать из географического атласа, где встречаются карты земных полушарий в различном масштабе (а также и в различных проекциях). Полярные области Марса вместе с имеющейся полярной шапкой удобно изобразить в виде так называемой полярной проекции. В центре такой планисферы помещается полюс, меридианы имеют вид прямых линий, расходящихся радиусами от полюса под равными углами, а параллели и экватор представляются концентрическими окружностями. В географических атласах в такой проекции даются карты Арктики и Антарктики  Для полярной области составляется несколько карт, отделенных друг от друга 20-30-дневными интервалами. Протяженность полярной шапки измеряется дугой меридиана, закрытой шапкой (если на разных меридианах шапка имеет различное протяжение, то берется среднее значение). Приведем для примера результаты наблюдений Н. П. Барабашова, произведенных в 1924 г.
Для полярной области составляется несколько карт, отделенных друг от друга 20-30-дневными интервалами. Протяженность полярной шапки измеряется дугой меридиана, закрытой шапкой (если на разных меридианах шапка имеет различное протяжение, то берется среднее значение). Приведем для примера результаты наблюдений Н. П. Барабашова, произведенных в 1924 г.

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редакционной коллегий серии книг «БИБЛИОТЕКА ЛЮБИТЕЛЯ АСТРОНОМИИ»
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОБЩИЕ СВЕДЕНИЯ О ПЛАНЕТАХ
- § 1. ЧТО ТАКОЕ ПЛАНЕТЫ
- § 2. ИСТОРИЧЕСКИЙ ОЧЕРК РАЗВИТИЯ ЗНАНИЙ О ПЛАНЕТАХ
- § 3. ОБЗОР СОЛНЕЧНОЙ СИСТЕМЫ
- ГЛАВА II. МЕТОДЫ ИССЛЕДОВАНИЯ ПЛАНЕТ
- § 4. ОПРЕДЕЛЕНИЕ МАСС И ДИАМЕТРОВ ПЛАНЕТ
- § 5. НАБЛЮДЕНИЯ ПОВЕРХНОСТЕЙ ПЛАНЕТ В ТЕЛЕСКОП
- § 6. ФОТОГРАФИРОВАНИЕ ПЛАНЕТ
- § 7. ФОТОМЕТРИЯ
- § 8. РАДИОМЕТРИЧЕСКИЕ НАБЛЮДЕНИЯ
- § 9. СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 10. РАДИОАСТРОНОМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
- § 11. РАДИОЛОКАЦИЯ ПЛАНЕТ
- § 12. ИССЛЕДОВАНИЕ ПЛАНЕТ КОСМИЧЕСКИМИ АППАРАТАМИ
- ГЛАВА III. РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ ПЛАНЕТ
- § 13. МЕРКУРИЙ
- § 14. ВЕНЕРА
- § 15. МАРС
- § 16. ЮПИТЕР, САТУРН, УРАН И НЕПТУН
- § 17. ПЛУТОН
- § 18. СПУТНИКИ ПЛАНЕТ И АСТЕРОИДЫ
- § 19. ВНУТРЕННЕЕ СТРОЕНИЕ ПЛАНЕТ
- ГЛАВА IV. НАБЛЮДЕНИЯ ПЛАНЕТ
- § 20. ЦЕЛИ И ЗАДАЧИ ЛЮБИТЕЛЬСКИХ НАБЛЮДЕНИЙ
- § 21. ОБЩИЕ ПРАВИЛА НАБЛЮДЕНИЙ
- § 22. УСЛОВИЯ НАБЛЮДЕНИЙ
- § 23. ИНСТРУМЕНТЫ И ПРИБОРЫ
- § 24. НАБЛЮДЕНИЯ ВЕНЕРЫ
- § 25. НАБЛЮДЕНИЯ МАРСА
- § 26. НАБЛЮДЕНИЯ ЮПИТЕРА
- § 27. НАБЛЮДЕНИЯ САТУРНА И ЕГО КОЛЬЦА
- § 28. НАБЛЮДЕНИЯ ОСТАЛЬНЫХ ПЛАНЕТ
- § 29. ФОТОГРАФИРОВАНИЕ ПЛАНЕТ СРЕДСТВАМИ ЛЮБИТЕЛЯ АСТРОНОМИИ
- § 30. ФОТОЭЛЕКТРИЧЕСКАЯ ФОТОМЕТРИЯ ПЛАНЕТ
- ГЛАВА V. ОБРАБОТКА НАБЛЮДЕНИЙ
- § 31. ЧТО ТАКОЕ ОБРАБОТКА НАБЛЮДЕНИЙ
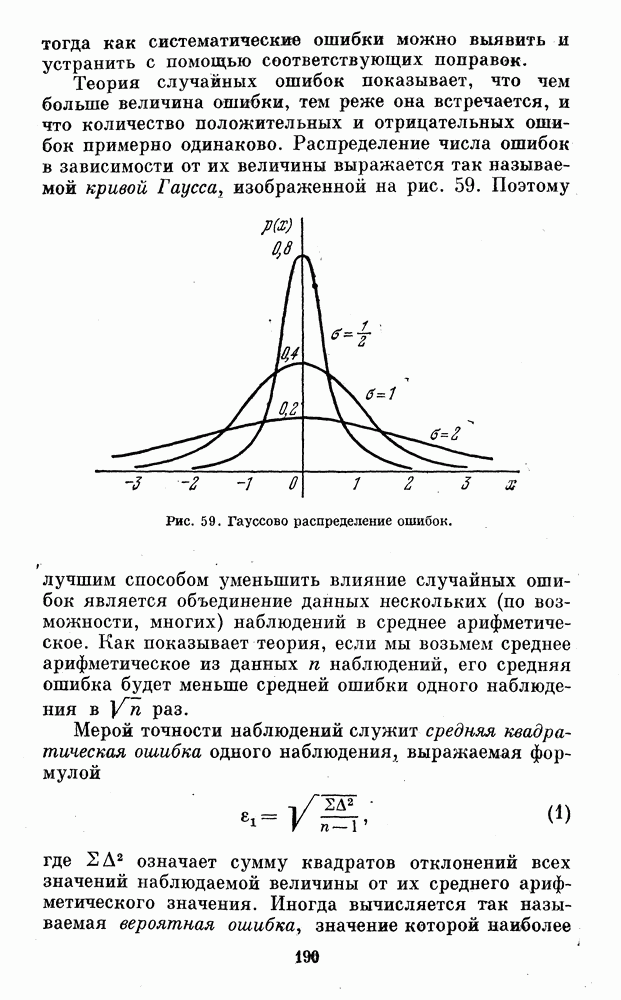
- § 32. ОШИБКИ НАБЛЮДЕНИЙ
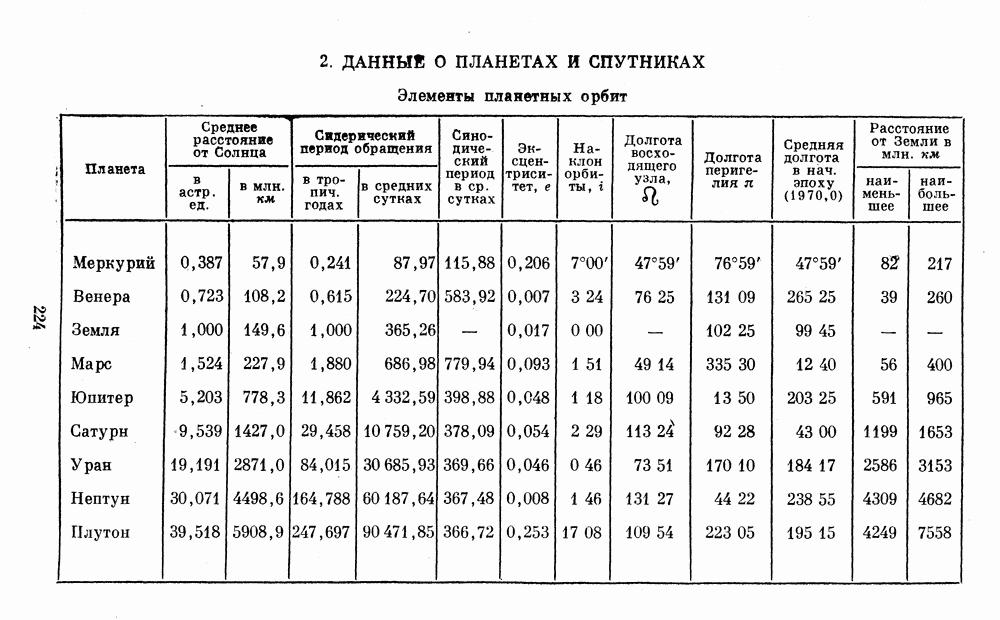
- § 33. ЭЛЕМЕНТЫ ПЛАНЕТНЫХ ОРБИТ И ЭФЕМЕРИДЫ
- § 34. ОБРАБОТКА НАБЛЮДЕНИЙ ФАЗ ВЕНЕРЫ
- § 35. ОБРАБОТКА НАБЛЮДЕНИЙ ПОЛОС ЮПИТЕРА
- § 36. СОСТАВЛЕНИЕ КАРТ ПЛАНЕТ
- § 37. ОПРЕДЕЛЕНИЕ ПЕРИОДА ВРАЩЕНИЯ ПЛАНЕТЫ
- § 38. ОБРАБОТКА ФОТОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ
- § 39. ОРГАНИЗАЦИЯ И ПРОГРАММА РАБОТЫ
- ПРИЛОЖЕНИЯ
- 1. ТАБЛИЦЫ ДЛЯ ОБРАБОТКИ РИСУНКОВ ПЛАНЕТ
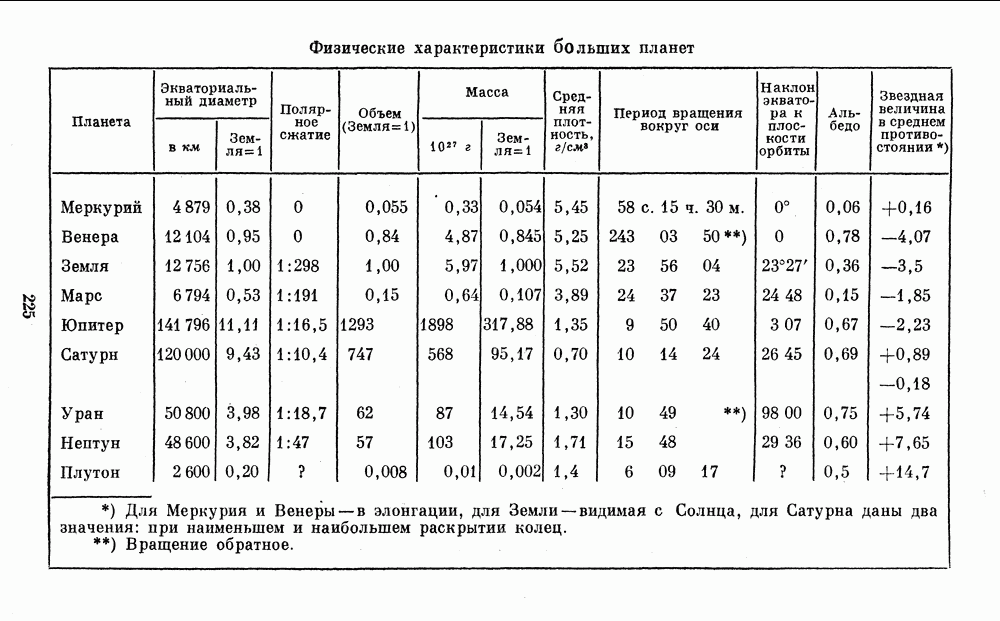
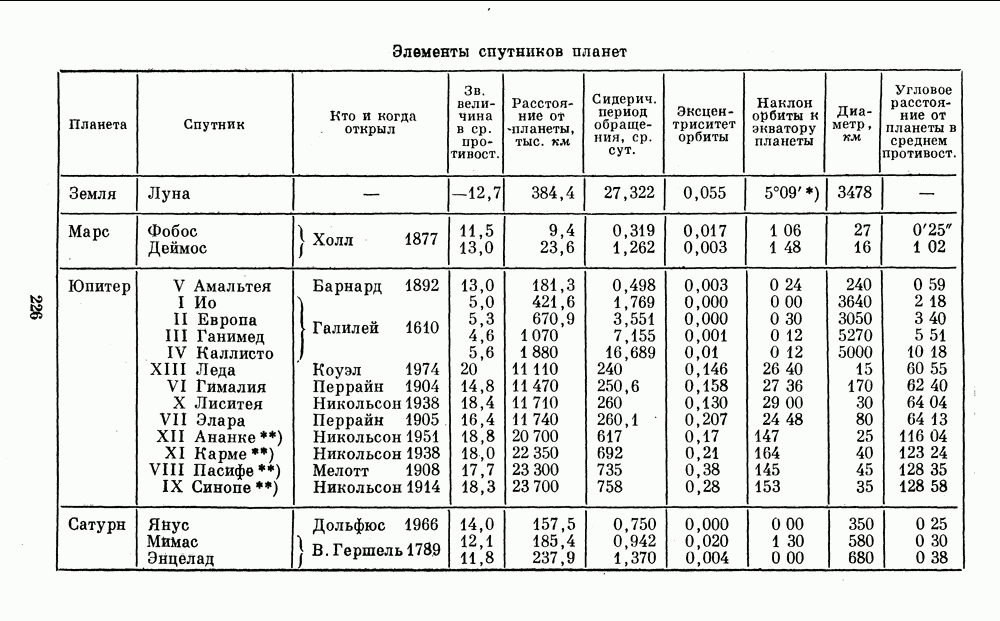
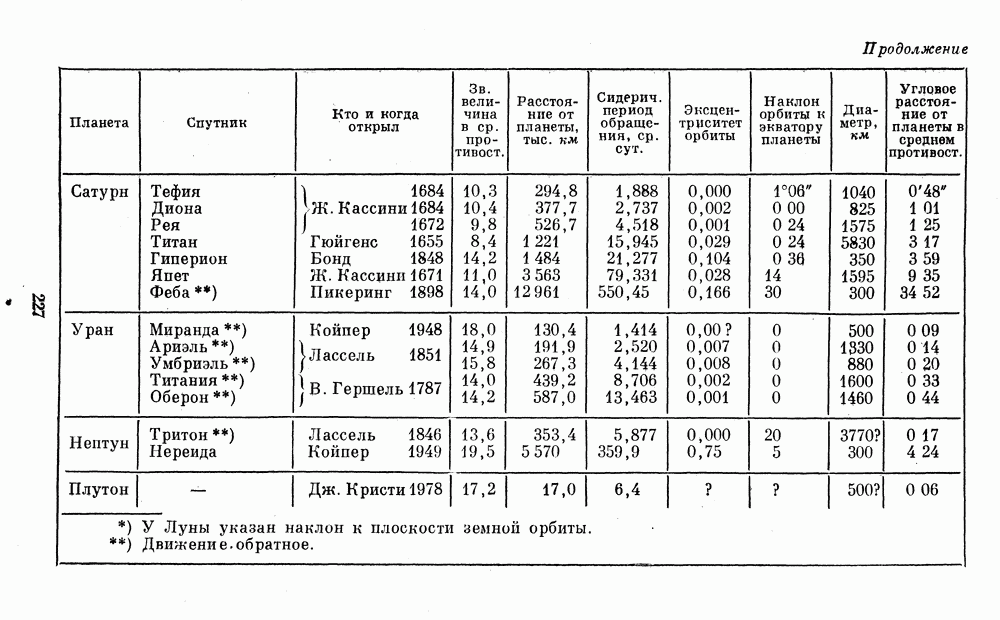
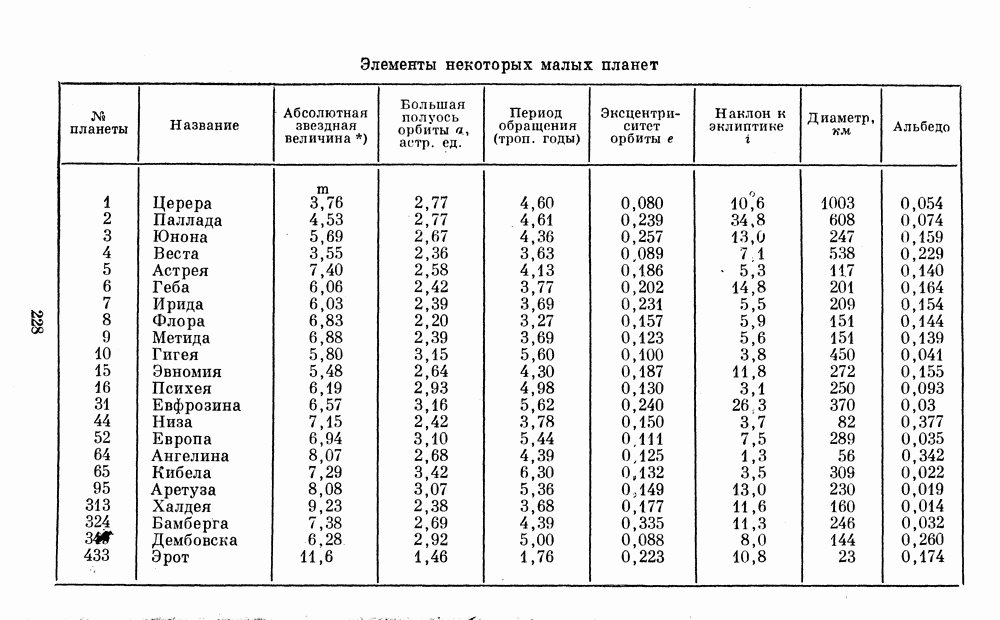
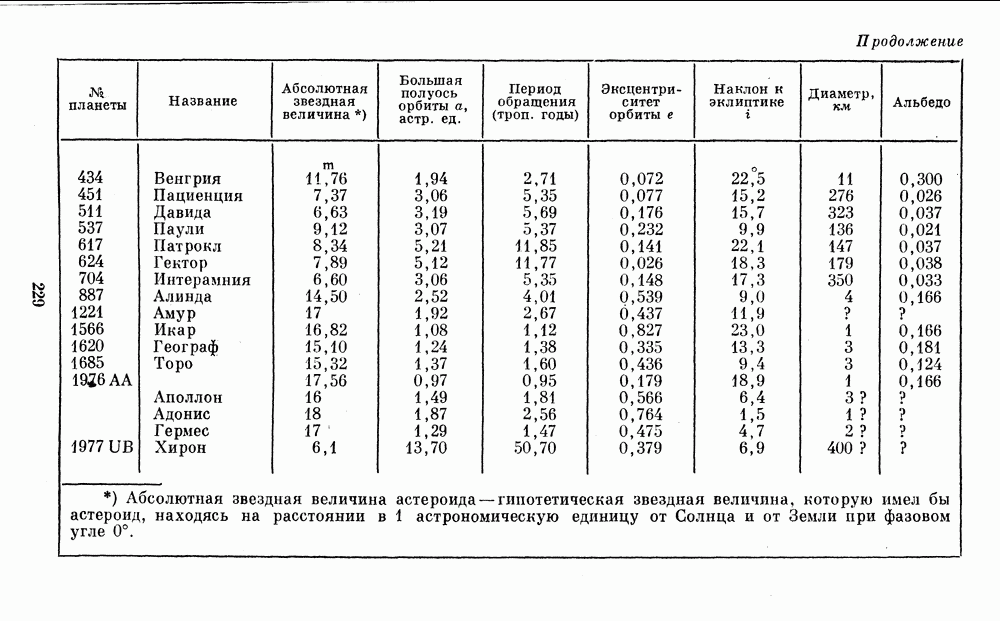
- 2. ДАННЫЕ О ПЛАНЕТАХ И СПУТНИКАХ
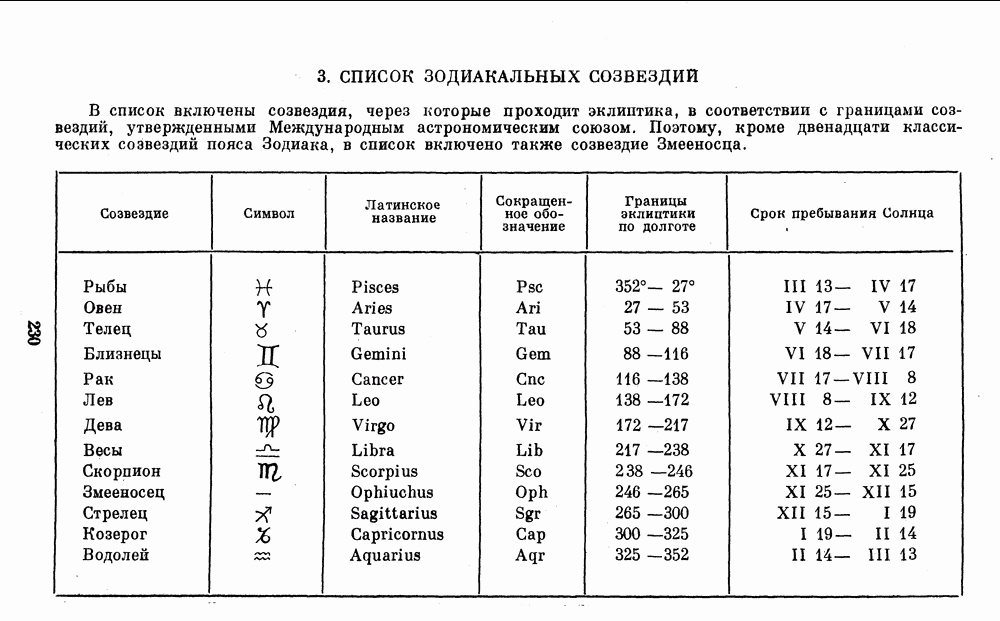
- 3. СПИСОК ЗОДИАКАЛЬНЫХ СОЗВЕЗДИЙ
- 4. КООРДИНАТНЫЕ СЕТКИ ДЛЯ ПОСТРОЕНИЯ КАРТ ПЛАНЕТ
- ЛИТЕРАТУРА