2.2. Динамические ошибки систем управления

            Точность систем управления является важнейшим показателем их качества. Чем выше точность, тем выше качество системы. Однако предъявление повышенных требований к точности вызывает неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная точность может привести к несоответствию характеристик системы условиям функционирования и необходимости ее повторной разработки. Поэтому на этапе проектирования системы должно быть проведено тщательное обоснование требуемых показателей точности.

            В этом разделе рассматриваются методы определения ошибок, возникающих при работе систем управления с детерминированными входными воздействиями. Вначале анализируются ошибки систем в переходном режиме. Затем особое внимание уделено простым способам расчета ошибок систем в установившемся режиме. Будет показано, что все системы управления можно разделить по величине установившихся ошибок на системы без памяти, так называемые статические системы, и системы, обладающие памятью, – астатические системы управления.

Типовые входные воздействия

            Для оценки качества работы систем управления рассматривают их поведение при некоторых типовых воздействиях. Обычно такими воздействиями служат следующие три основные вида функций:

а) ступенчатое воздействие:          g(t) = 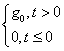 ,            g(p) = ;

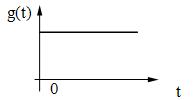
б) линейное воздействие:      g(t) = t ,   t > 0 ;           ;

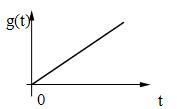
в) квадратичное воздействие:  /2 ,    t > 0 ;    g(p) = .

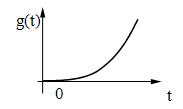
            В некоторых случаях рассматривают обобщенное полиномиальное воздействие:

,   t  >  0.

            Ступенчатое воздействие является одним из простейших, но именно с его помощью определяется ряд важных свойств систем управления, связанных с видом переходного процесса. Линейное и квадратичное воздействия часто бывают связаны с задачами слежения за координатами движущегося объекта. Тогда линейное воздействие соответствует движению объекта с постоянной скоростью; квадратичное - движению объекта с постоянным ускорением.

            Переходные процессы при типовых воздействиях можно построить следующим   образом.  Пусть  задана  передаточная  функция  замкнутой   системы  управления W(p). Тогда

x(p) = W(p) g(p),

где g(p) – изображение соответствующего воздействия.

            Например, если    , то        и для  g(t) = g0  получим  .

            С помощью вычетов или по таблицам находим обратное преобразование Лапласа и получаем вид переходного процесса x(t) для заданного входного воздействия:

,

где Res x(p) – вычет функции x(p) в  точке a.

            Обычно реакция системы на ступенчатое воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.

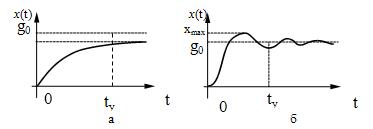
Рис. 21.

Переходный процесс, как правило, характеризуют двумя параметрами – длительностью переходного процесса (временем установления) и величиной перерегулирования.

            Под временем установления tу понимают временной интервал, по истечении которого отклонение |x(t) - xуст | выходного процесса от установившегося значения  xуст не превышает     определенную величину, например, 0,1gо.  Время установления является важным параметром САУ, позволяющим оценить ее быстродействие. Величину tу  можно оценить приближенно по амплитудно-частотной характеристике системы. При заданной частоте среза . Для оценки качества системы используется также величина перерегулирования, определяемая соотношением  .

В зависимости от характера собственных колебаний системы переходный процесс в ней может быть колебательным, как это показано на рис. 21, б, или плавным гладким, называемым апериодическим (рис. 21,а). Если корни характеристического уравнения системы действительны, то переходный процесс в ней апериодический.  В случае комплексных корней характеристического уравнения собственные колебания устойчивой системы управления являются затухающими гармоническими и переходный процесс в системе имеет колебательный характер.

            При малом запасе устойчивости САУ ее собственные колебания затухают медленно, и перерегулирование в переходном режиме получается значительным. Как следствие, величина перерегулирования может служить  мерой запаса устойчивости системы. Для многих систем запас устойчивости считается достаточным, если величина перерегулирования   .

Установившийся режим

            При проектировании систем управления часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной или бесконечно большой величиной.

            Очень важно,  что величина установившейся ошибки  может быть легко найдена с помощью теоремы о предельном значении оригинала: .

            При использовании этой теоремы нужно выразить величину ошибки e (p)  через g(p).  Для этого рассмотрим  структурную схему замкнутой системы управления (рис. 22).

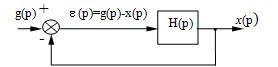
Рис. 22

            Очевидно, e (p) = g(p) - x(p) = g(p) - H(p)e(p).  Отсюда    или  e (p) = He(p)g(p) , где He(p) =  называется передаточной функцией системы управления от входного воздействия g(p) к ошибке слежения e(p). Таким образом, величину установившейся ошибки можно найти с помощью следующего соотношения:

,

где He(p) = 1/(1+H(p));   g(p) -  изображение типового входного воздействия.

            Пример 1.   Рассмотрим систему управления, в составе которой нет интеграторов, например,

                   .

            Найдем  величину  установившейся   ошибки   при   ступенчатом  входном  воздействии g(t) = g0, t ³ 0. В этом случае

.

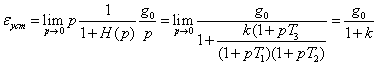            Предположим  теперь, что  входное воздействие изменяется линейно t    или   .

            Тогда   . Соответствующие входные воздействия и переходные процессы можно представить графиками на рис. 23,а и б.

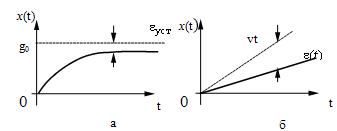
Рис. 23

            Пример 2. Рассмотрим теперь систему, содержащую один интегратор. Типичным примером может быть система сервопривода (рис. 6) с   .

            Для ступенчатого воздействия g(t) = g0    или  g(p) =  получим

.

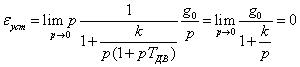При линейном входном воздействии

.

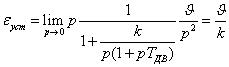Такие процессы можно проиллюстрировать соответствующими кривыми на рис.24, а и б.

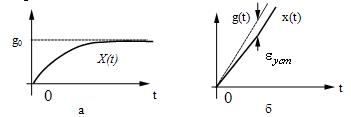
Рис. 24

            Пример 3.  Рассмотрим систему с двумя интеграторами. Пусть, например,  . При ступенчатом воздействии .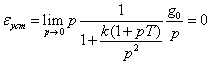

            При линейном     .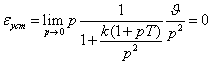

            Наконец, если входное воздействие квадратичное  g(t) = at2/2  (g(p) = a/p3), то     

.

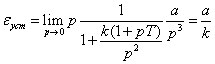            Таким образом, в системе с двумя интеграторами может осуществляться слежение за квадратичным входным воздействием при конечной величине установившейся ошибки. Например, можно следить за координатами объекта, движущегося с постоянным ускорением.

Статические и астатические системы управления

            Анализ рассмотренных примеров показывает, что системы управления, содержащие интегрирующие звенья, выгодно отличаются от систем без интеграторов. По этому признаку все системы делятся на статические системы, не  содержащие интегрирующих звеньев, и астатические системы, которые содержат интеграторы. Системы с одним интегратором называются системами с астатизмом первого порядка. Системы с двумя интеграторами – системами с астатизмом второго порядка и т.д.

            Для статических систем даже при неизменяющемся воздействии g(t) = g0  установившаяся ошибка имеет конечную величину  g(t) = g0 . В системах с астатизмом первого порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно изменяющемся  воздействии  . Наконец, в системах с астатизмом второго порядка ненулевая установившаяся ошибка появляется только при квадратичных входных воздействиях   g(t) = at2 /2 и составляет величину   eуст = a/k.

            Какие же физические причины лежат в основе таких свойств астатических систем управления?

            Рассмотрим систему управления с астатизмом второго порядка (рис. 25)

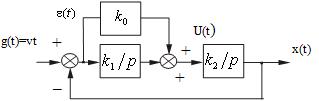
Рис. 25

            Пусть входной сигнал системы управления изменяется линейно:  t. Как было установлено, в такой системе установившаяся ошибка равна нулю, т.е. e (t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если  x(t) = t , то на входе второго интегратора должен быть сигнал .  Действительно, при нулевом рассогласовании  e (t) =0  в системе с интеграторами возможно существование ненулевого выходного сигнала первого интегратора  .  Первый интегратор после окончания переходного процесса «запоминает»  скорость  изменения входного воздействия и в дальнейшем работа системы управления осуществляется по «памяти». Таким образом, физическим объяснением такого значительного различия статических и астатических систем является наличие памяти у астатических систем управления.

* * *

            Итак, существуют простые возможности определения важнейшего показателя систем управления – величины их динамических ошибок. Детальный анализ  переходных процессов в системах управления обычно выполняют  с помощью моделирования на ПЭВМ. Вместе с тем величины установившихся ошибок легко находятся аналитически. При этом астатические системы управления, т.е. системы с интеграторами, имеют существенно лучшие показатели качества по сравнению со статическими системами.