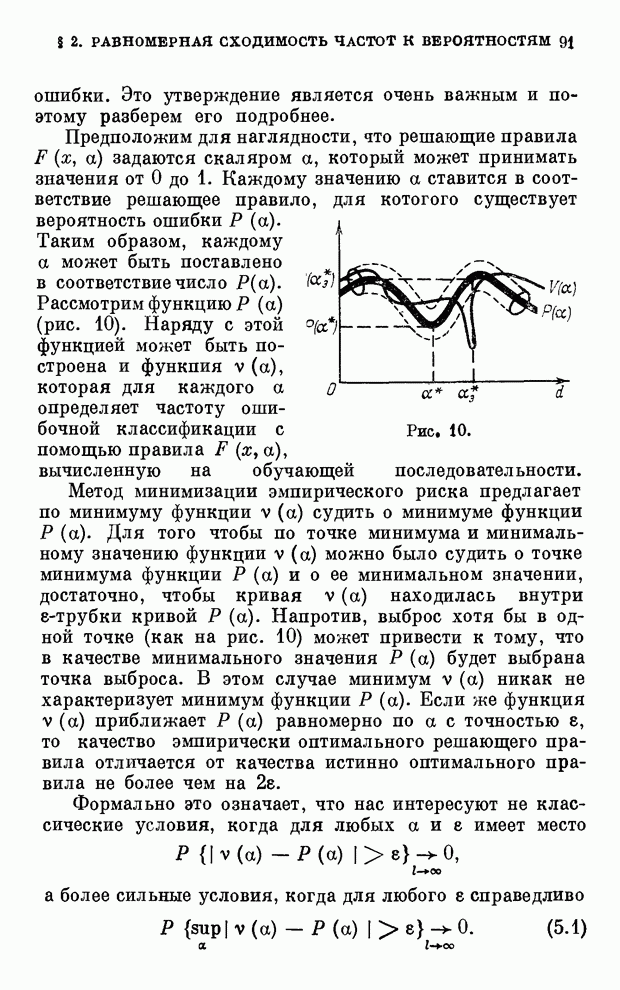
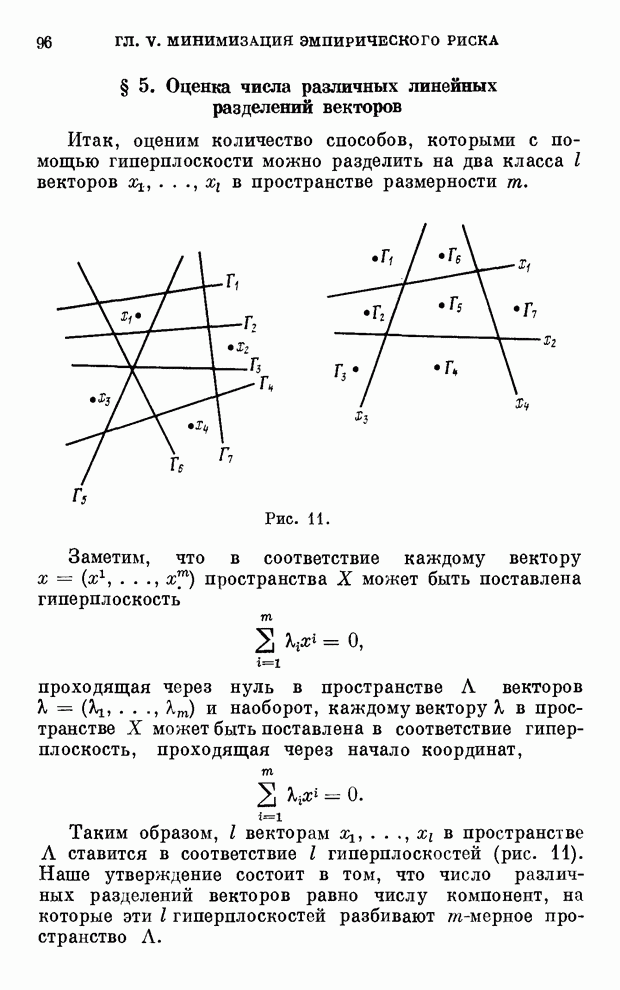
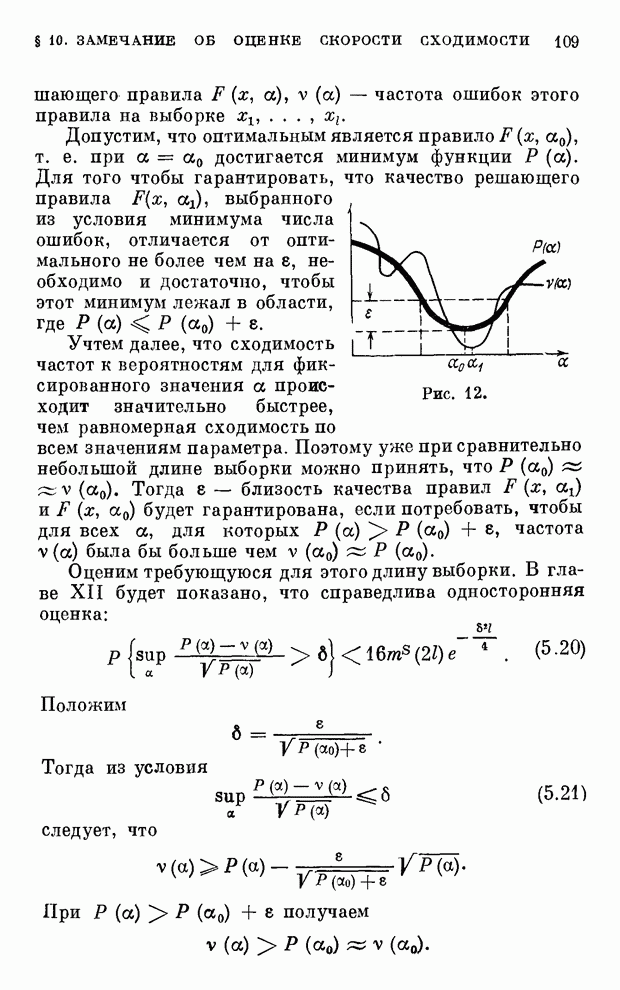
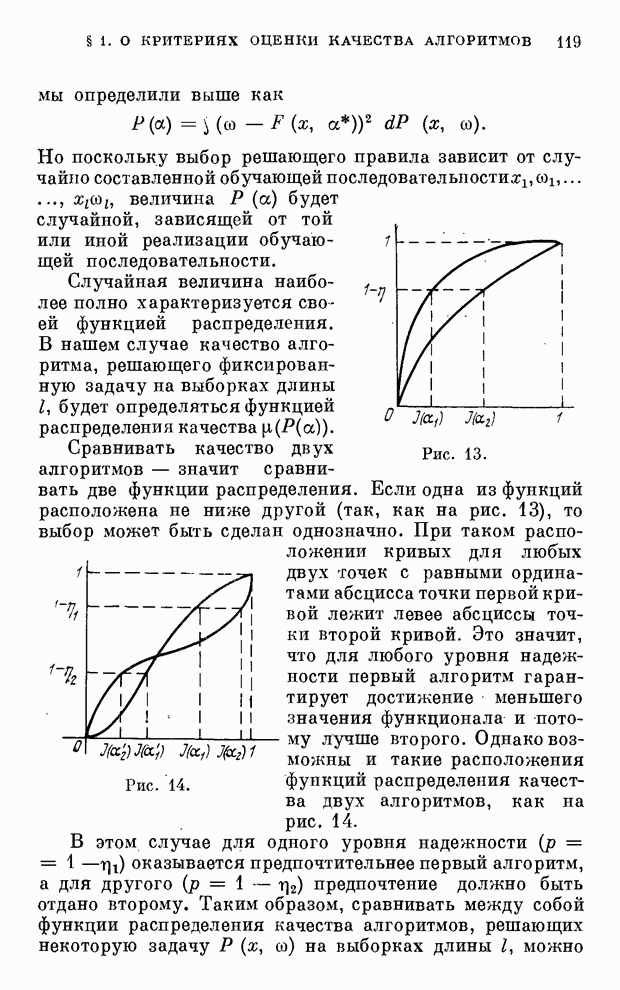
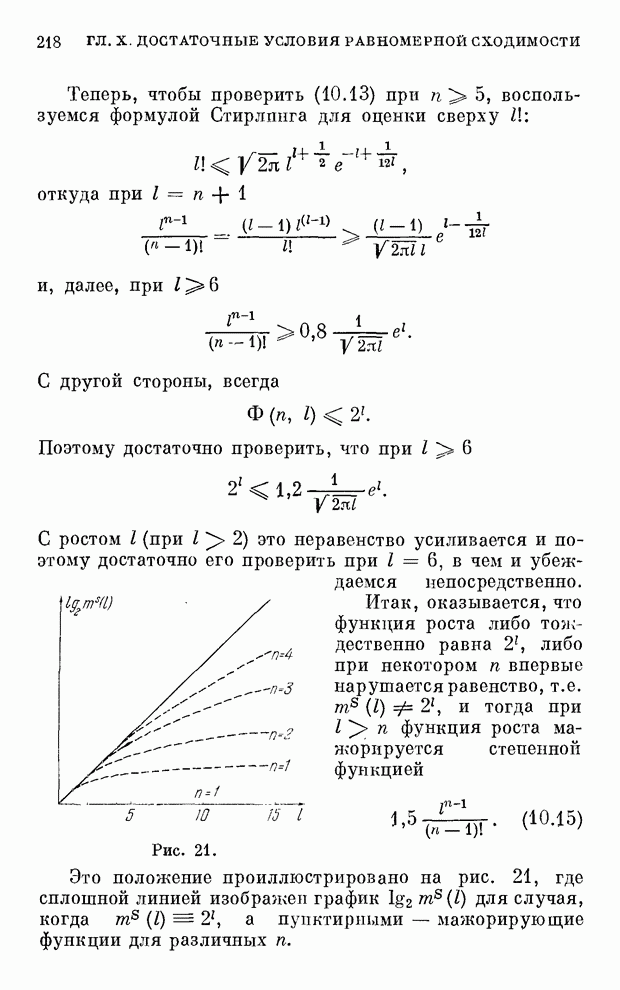
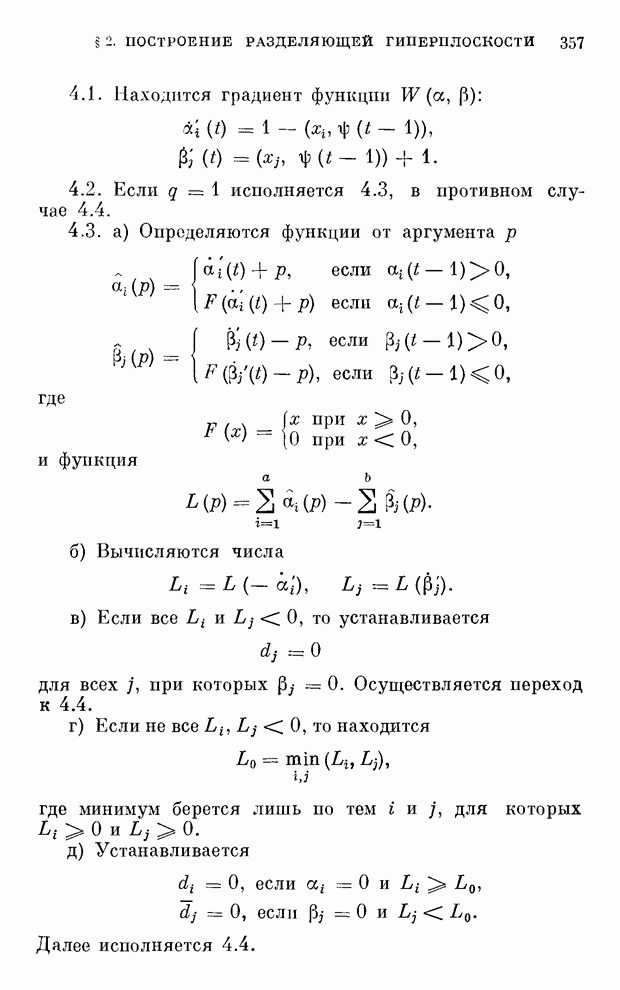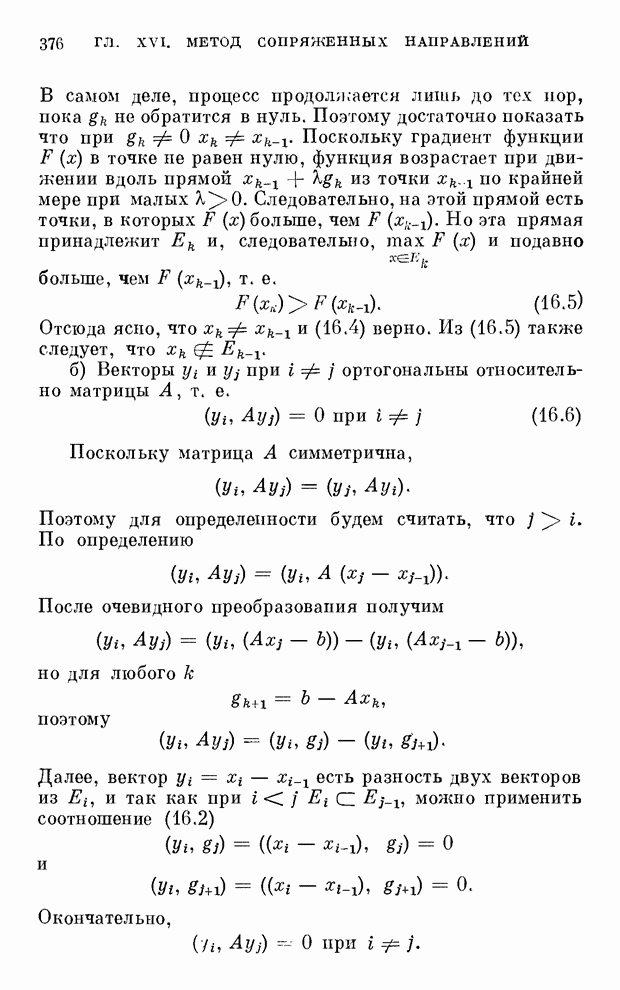| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
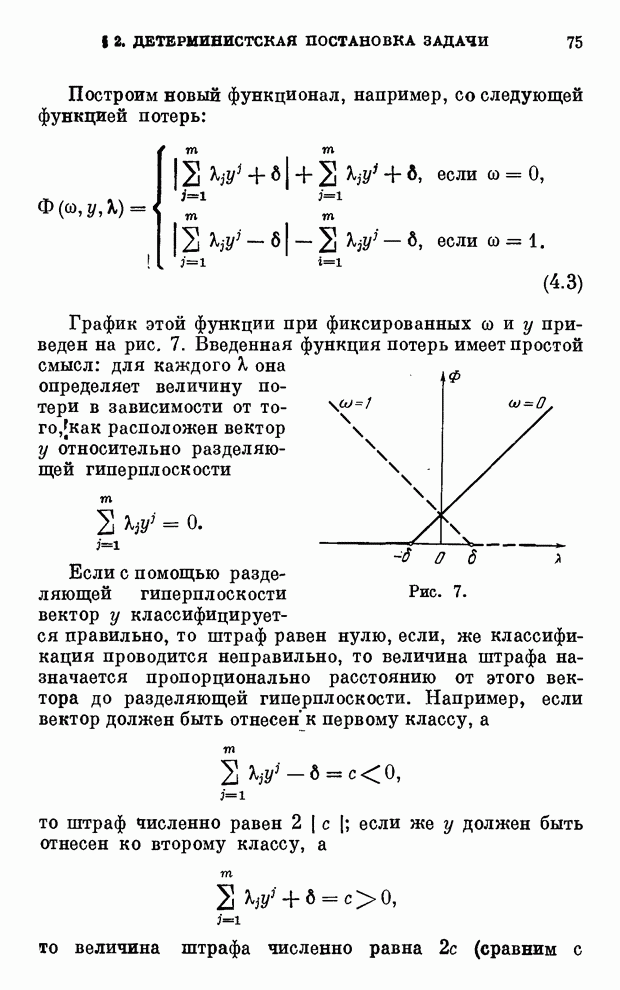
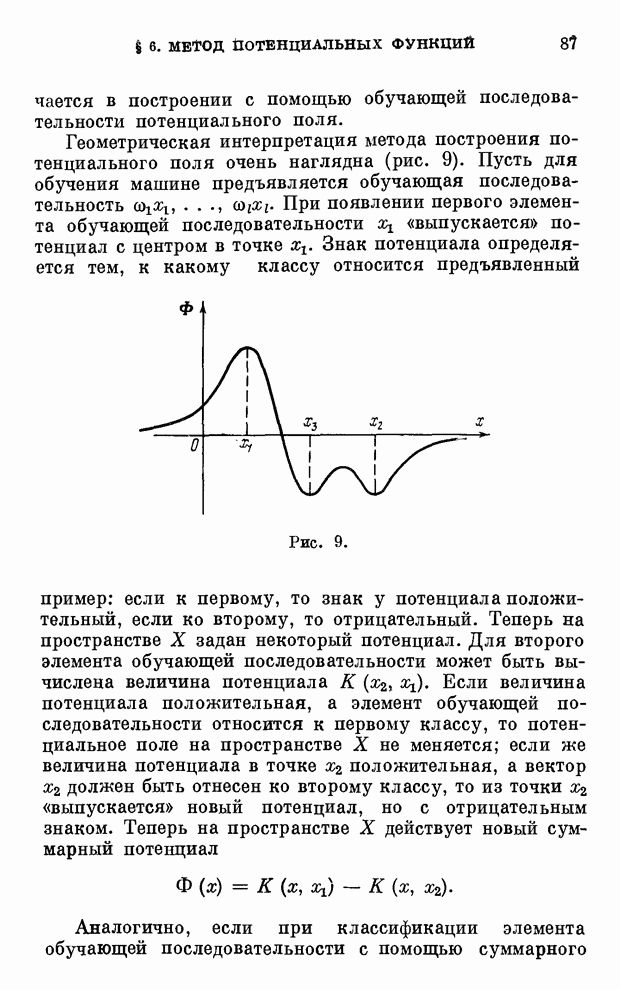
§ 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
Алгоритм ОП-4 предназначен для поиска минимальной
размерности, в котором множества векторов обучающей последовательности могут
быть разделены гиперплоскостью так, чтобы расстояние между выпуклыми оболочками
множеств было больше ![]() .
.
Так же как и две предыдущие
задачи, эта задача в принципе может быть точно решена, однако точное ее решение
сопряжено с необходимостью организации полного перебора по всем возможным
подпространствам исходного пространства. Для достаточно большой размерности
исходного пространства ![]() такой перебор неприемлем и поэтому, так
же как и в предыдущих случаях, конструктивное решение задачи сопряжено с заменой
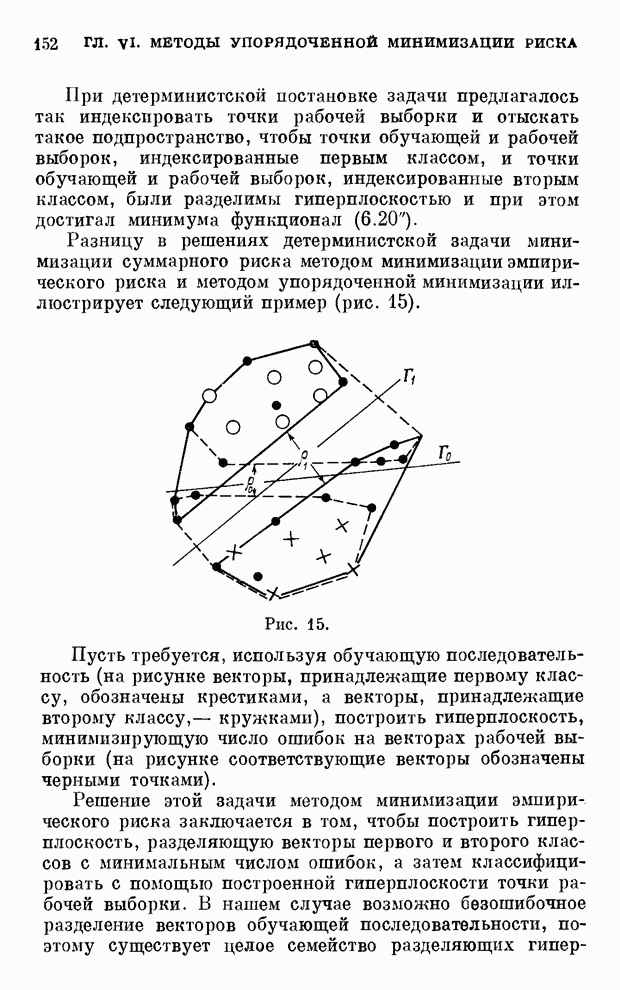
полного перебора эвристической схемой поиска решения.
такой перебор неприемлем и поэтому, так
же как и в предыдущих случаях, конструктивное решение задачи сопряжено с заменой
полного перебора эвристической схемой поиска решения.
Примем все тот же эвристический прием поиска решения: из множества признаков исключаем «наименее информативный признак»; затем из оставшегося множества опять исключаем наименее информативный признак и т. д. Процесс исключения признаков будем продолжать до тех пор, пока не выяснится, что множество векторов обучающей последовательности не может быть разделено на два класса.
Таким образом, поиск минимального
подпространства определяется введенным понятием «наименее информативный
признак». Определим его следующим образом. Пусть в пространстве ![]() (
(![]() признаков) заданы два
множества векторов обучающей последовательности – множество векторов
признаков) заданы два
множества векторов обучающей последовательности – множество векторов ![]() и множество векторов
и множество векторов
![]() . В
пространстве
. В
пространстве ![]() могут
быть построены выпуклая оболочка множества
могут
быть построены выпуклая оболочка множества ![]() и выпуклая оболочка множества
и выпуклая оболочка множества ![]() . Пусть расстояние
между выпуклыми оболочками будет
. Пусть расстояние
между выпуклыми оболочками будет ![]() .
.
Рассмотрим теперь пространство ![]() , образованное
, образованное ![]() признаком (исключен
признак
признаком (исключен
признак ![]() ).
В этом пространстве могут быть построены выпуклые оболочки множеств
).
В этом пространстве могут быть построены выпуклые оболочки множеств ![]() и
и ![]() (векторы
(векторы ![]() и
и ![]() суть проекции
векторов
суть проекции
векторов ![]() и
и
![]() на
подпространство
на
подпространство ![]() )
и вычислено расстояние между выпуклыми оболочками. Пусть оно равно
)
и вычислено расстояние между выпуклыми оболочками. Пусть оно равно ![]() . Если расстояние
между оболочками больше
. Если расстояние
между оболочками больше ![]() , то будем считать, что в этом
пространстве возможно построение разделяющей гиперплоскости, в противном случае
будем полагать, что разделение гиперплоскостью векторов
, то будем считать, что в этом
пространстве возможно построение разделяющей гиперплоскости, в противном случае
будем полагать, что разделение гиперплоскостью векторов ![]() и
и ![]() невозможно.
невозможно.
Рассмотрим теперь величину ![]() . Эта величина
показывает, насколько уменьшится расстояние между выпуклыми оболочками векторов
в пространстве
. Эта величина
показывает, насколько уменьшится расстояние между выпуклыми оболочками векторов
в пространстве ![]() (с
исключением
(с
исключением ![]() -го
признака). Будем считать тот признак наименее информативным, с удалением
которого расстояние между выпуклыми оболочками уменьшается на минимальную
величину.
-го
признака). Будем считать тот признак наименее информативным, с удалением
которого расстояние между выпуклыми оболочками уменьшается на минимальную
величину.
Таким образом, для того чтобы
организовать поиск подпространства минимальной размерности, в котором возможно
разделение двух множеств векторов обучающей последовательности по предложенной
эвристической схеме, надо уметь определять расстояния между выпуклыми
оболочками двух множеств векторов. В этом случае, для того чтобы исключить один
из ![]() признаков
(или установить, что исключение невозможно), надо определить расстояние между
выпуклыми оболочками в
признаков
(или установить, что исключение невозможно), надо определить расстояние между
выпуклыми оболочками в ![]() -мерном подпространстве. Определить
расстояние между выпуклыми оболочками можно с помощью программы ОП-1 (где
ищется оптимальная разделяющая гиперплоскость).
-мерном подпространстве. Определить
расстояние между выпуклыми оболочками можно с помощью программы ОП-1 (где
ищется оптимальная разделяющая гиперплоскость).
Расстояние между выпуклыми оболочками определяется по формуле
![]() ,
,
где
![]() –
обобщенный портрет, соответствующий оптимальному
–
обобщенный портрет, соответствующий оптимальному ![]() . Однако, даже несмотря на то, что для
поиска «наименее информативного признака» происходит
. Однако, даже несмотря на то, что для
поиска «наименее информативного признака» происходит ![]() раз вычислять расстояние
между выпуклыми оболочками, такой способ исключения признака не является
чрезмерно трудоемким.
раз вычислять расстояние
между выпуклыми оболочками, такой способ исключения признака не является
чрезмерно трудоемким.
Удобно проводить поиск наименее информативного из признаков по следующей схеме.
Сначала в пространстве ![]() (
(![]() признаков) строится
оптимальная разделяющая гиперплоскость и определяется расстояние между выпуклыми
оболочками двух множеств (это делается с помощью соответствующей модификации
программы ОП-1). Пусть
признаков) строится
оптимальная разделяющая гиперплоскость и определяется расстояние между выпуклыми
оболочками двух множеств (это делается с помощью соответствующей модификации
программы ОП-1). Пусть ![]() – найденный обобщенный портрет,
– найденный обобщенный портрет, ![]() ;
; ![]() – соответствующие
коэффициенты разложения вектора
– соответствующие
коэффициенты разложения вектора ![]() по информативным векторам обучающей
последовательности.
по информативным векторам обучающей
последовательности.
Спроектируем вектор ![]() и векторы обучающей
последовательности на подпространство
и векторы обучающей
последовательности на подпространство ![]() . Для этого достаточно в те разряды
ячеек, где записаны значения
. Для этого достаточно в те разряды
ячеек, где записаны значения ![]() -й координаты вектора
-й координаты вектора ![]() и векторов
и векторов ![]() , заслать нули.
, заслать нули.
Затем построим оптимальную
разделяющую гиперплоскость в подпространстве ![]() (также с помощью ОП-1). Однако за
начальные условия следует брать не
(также с помощью ОП-1). Однако за
начальные условия следует брать не ![]() , а те значения
, а те значения ![]() и
и ![]() , которые были найдены при
построении разделяющей гиперплоскости в пространстве размерности
, которые были найдены при
построении разделяющей гиперплоскости в пространстве размерности ![]() . При таких начальных
условиях отыскание вектора произойдет значительно быстрее.
. При таких начальных
условиях отыскание вектора произойдет значительно быстрее.
Программа ОП-4 использует как составную часть программу ОП-1.
Алгоритм ОП-5 используется для поиска
минимальной размерности, в котором разделяющая гиперплоскость делит обучающую
последовательность, совершая не более ![]() ошибок (
ошибок (![]() – параметр алгоритма). Структура
алгоритма ОП-5 аналогична структуре алгоритма ОП-4. Разница заключается лишь в
том, что алгоритм ОП-4 прекращает поиск соответствующего подпространства, когда
выясняется, что построение разделяющей гиперплоскости становится невозможным, в
то время как алгоритм ОП-5 исключает
– параметр алгоритма). Структура
алгоритма ОП-5 аналогична структуре алгоритма ОП-4. Разница заключается лишь в
том, что алгоритм ОП-4 прекращает поиск соответствующего подпространства, когда
выясняется, что построение разделяющей гиперплоскости становится невозможным, в
то время как алгоритм ОП-5 исключает ![]() векторов, «препятствующих» построению
разделяющей гиперплоскости, и только после этого прекращает поиск минимального
подпространства.
векторов, «препятствующих» построению
разделяющей гиперплоскости, и только после этого прекращает поиск минимального
подпространства.
В соответствии с этим алгоритм ОП-5 использует в качестве составной части не алгоритм ОП-1, а ОП-2.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
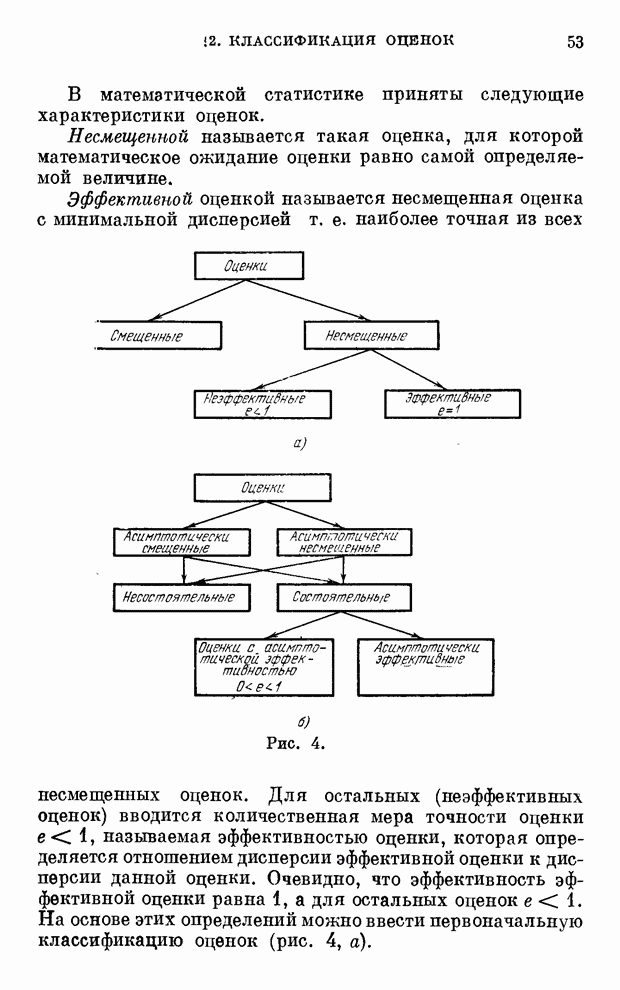
- § 2. Классификация оценок
- § 3. Метод максимума правдоподобия
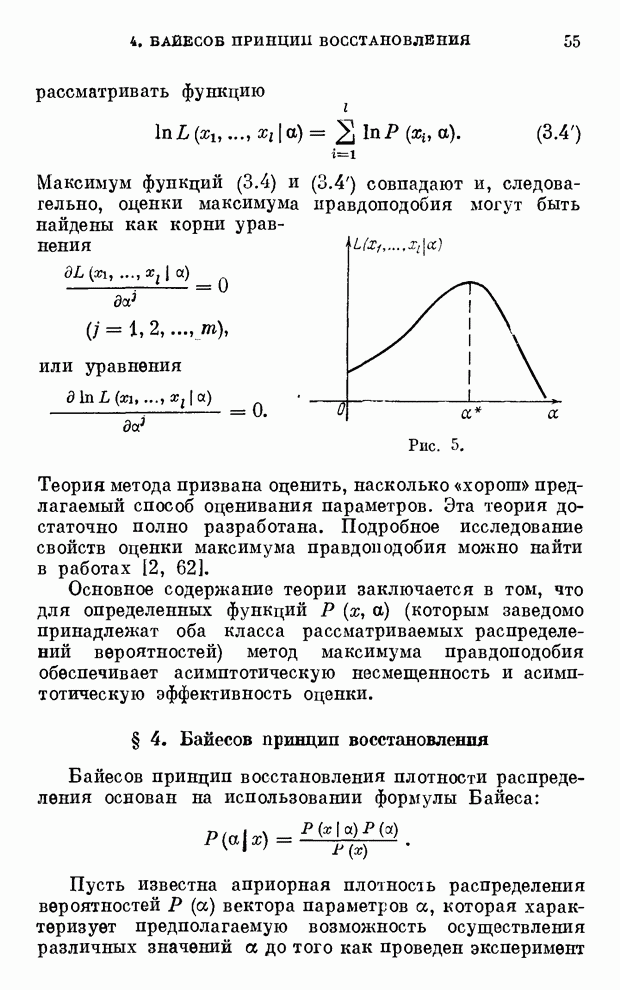
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА