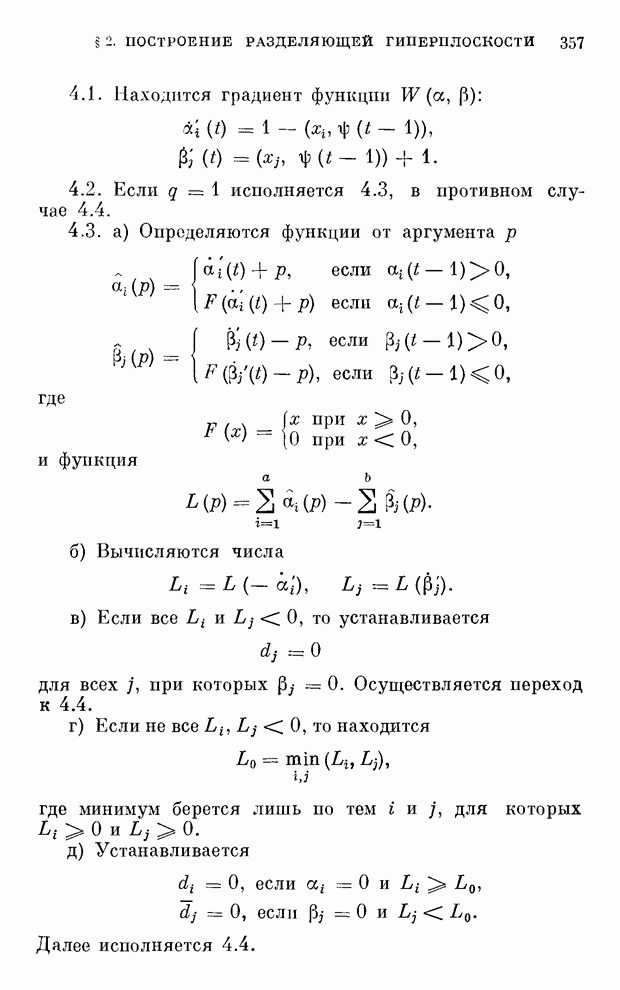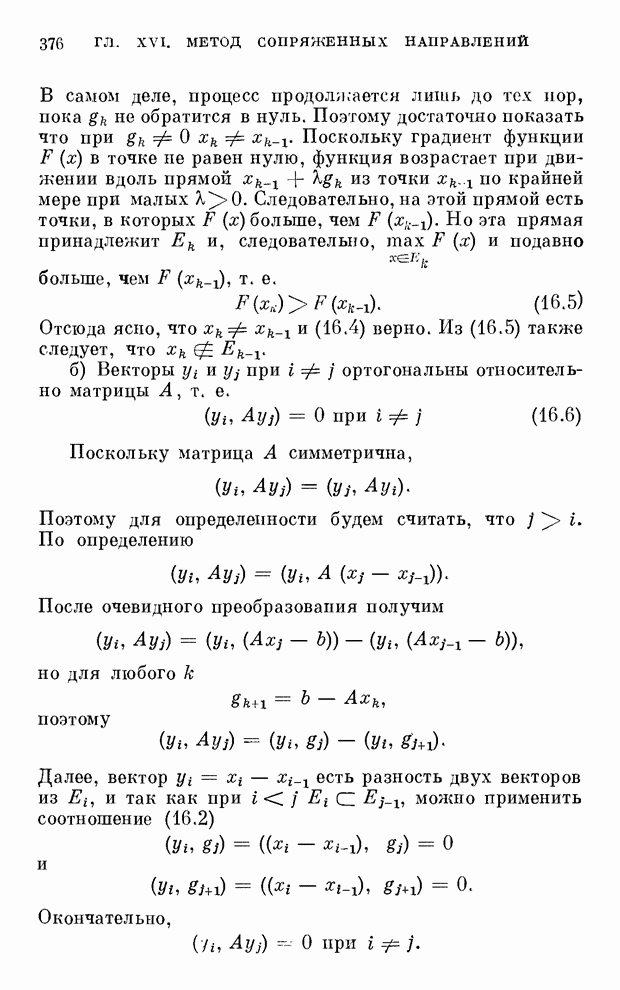| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
Почему же оценки, полученные для детерминистского и стохастического вариантов постановки задачи, так сильно различаются.
Объяснение этому частично дано в
предыдущем параграфе, где формулы (5.3), (5.10) и (5.13), (5.18) определяют
скорости равномерной сходимости частот появления событий к их вероятностям по
различным классам событий ![]() .
.
В детерминистском варианте
постановки учитываются только те события исходного множества событий ![]() , частоты которых
равны нулю. Обозначим этот подкласс
, частоты которых
равны нулю. Обозначим этот подкласс ![]() . В стохастическом варианте задачи
уклонение оценивалось для всех событий исходного класса событий
. В стохастическом варианте задачи
уклонение оценивалось для всех событий исходного класса событий ![]() .
.
Формально этот факт находит свое
отражение в структуре формул, задающих оценку равномерной сходимости, (5.10),
(5.18). Правая часть неравенств (5.10), (5.18) состоит из двух сомножителей.
Первый сомножитель характеризует емкость класса событий (он идентичен, как в
случае (5.10), так и в (5.18)), второй сомножитель оценивает вероятность
уложиться в заданное уклонение ![]() частоты от вероятности для любого
события заданного класса (в детерминистской постановке этот класс есть
частоты от вероятности для любого
события заданного класса (в детерминистской постановке этот класс есть ![]() , в стохастической –
этот класс совпадает с
, в стохастической –
этот класс совпадает с ![]() ).
).
Оказывается, удается существенно
по-разному оценить этот второй сомножитель. Так как при стохастическом варианте
постановки априори не известны никакие характеристики вероятностей событий
класса ![]() , то
оценка уклонения частоты от вероятности для любого события
, то
оценка уклонения частоты от вероятности для любого события ![]() , принадлежащего
, принадлежащего ![]() , производится в
условиях наиболее неблагоприятного случая, когда
, производится в
условиях наиболее неблагоприятного случая, когда ![]() . Поэтому возможна лишь оценка (5.10).
. Поэтому возможна лишь оценка (5.10).
Для детерминистского варианта
постановки наиболее неблагоприятное событие в классе ![]() то, для которого
то, для которого ![]() . Для оценки уклонения
частоты от вероятности этого события возможна более тонкая оценка (5.14).
. Для оценки уклонения
частоты от вероятности этого события возможна более тонкая оценка (5.14).
Таким образом, оценки, полученные
для детерминистского и стохастического вариантов постановки задачи, различаются
так, как различаются оценки уклонения частот от вероятностей в двух событиях: в
событии ![]() ,
для которого
,
для которого ![]() близко
к нулю, и в событии
близко
к нулю, и в событии ![]() для
которого
для
которого ![]() близко
к
близко
к ![]() .
.
Это обстоятельство заставляет внимательно отнестись к тем требованиям, которые предъявляются к величинам уклонения частот от вероятностей.
В задаче обучения распознаванию
образов можно ослабить требования к характеру сходимости: разумно требовать не
равномерного отклонения частот от вероятностей для всех событий, а разрешить
большее уклонение для тех событий, которым соответствует вероятность, близкая
к ![]() , и меньшее
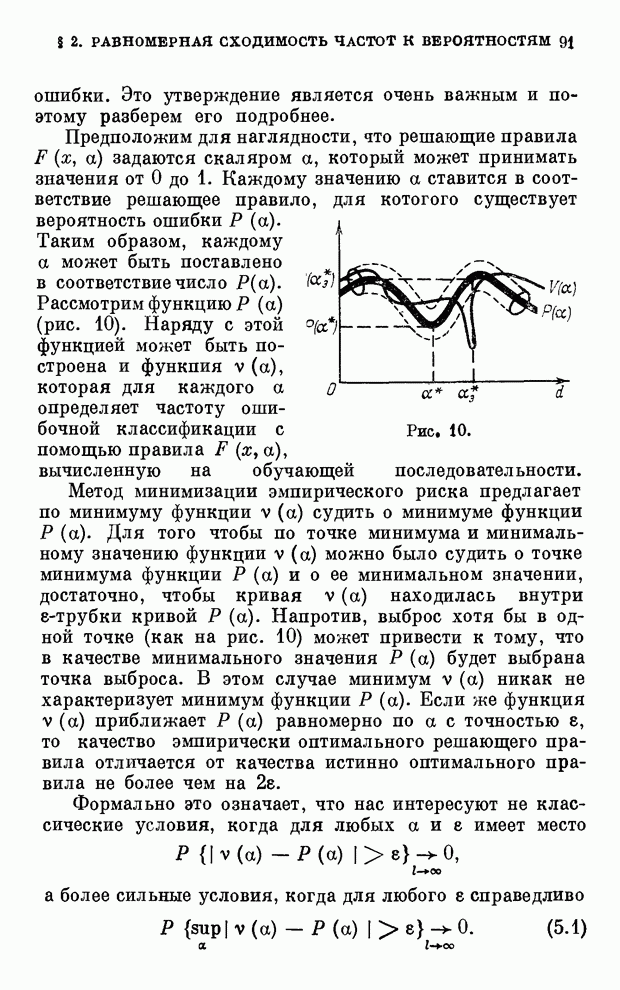
для событий с вероятностями, близкими к нулю. Рассмотрим снова функции
, и меньшее
для событий с вероятностями, близкими к нулю. Рассмотрим снова функции ![]() и
и ![]() (рис. 12), где
(рис. 12), где ![]() – вероятность ошибки
для решающего правила
– вероятность ошибки
для решающего правила ![]() ,
, ![]() – частота ошибок этого правила на
выборке
– частота ошибок этого правила на
выборке ![]() .
.

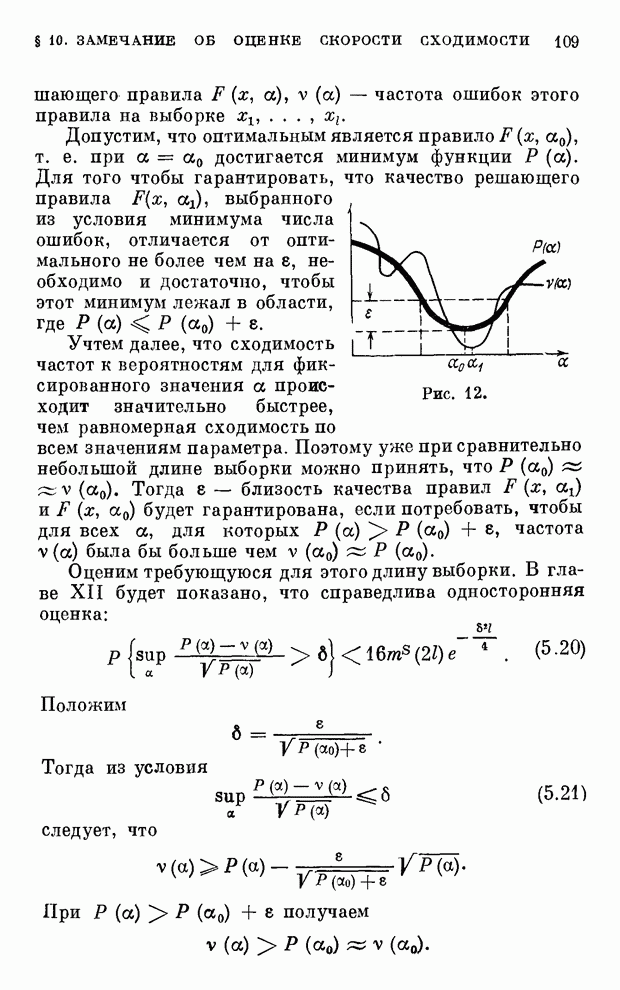
Рис. 12.
Допустим, что оптимальным
является правило ![]() ,
т. е. при
,
т. е. при ![]() достигается
минимум функции
достигается
минимум функции ![]() .
Для того чтобы гарантировать, что качество решающего правила
.
Для того чтобы гарантировать, что качество решающего правила ![]() , выбранного из
условия минимума числа ошибок, отличается от оптимального не более чем на
, выбранного из
условия минимума числа ошибок, отличается от оптимального не более чем на ![]() , необходимо и
достаточно, чтобы этот минимум лежал в области, где
, необходимо и
достаточно, чтобы этот минимум лежал в области, где ![]() .
.
Учтем далее, что сходимость
частот к вероятностям для фиксированного значения ![]() происходит значительно быстрее, чем
равномерная сходимость по всем значениям параметра. Поэтому уже при
сравнительно небольшой длине выборки можно принять, что
происходит значительно быстрее, чем
равномерная сходимость по всем значениям параметра. Поэтому уже при
сравнительно небольшой длине выборки можно принять, что ![]() . Тогда
. Тогда ![]() – близость качества правил
– близость качества правил ![]() и
и ![]() будет гарантирована, если
потребовать, чтобы для всех
будет гарантирована, если
потребовать, чтобы для всех ![]() , для которых
, для которых ![]() , частота
, частота ![]() была бы больше чем
была бы больше чем ![]() .
.
Оценим требующуюся для этого длину выборки. В главе XII будет показано, что справедлива односторонняя оценка:
 . (5.20)
. (5.20)
Положим
 .
.
Тогда из условия
 (5.21)
(5.21)
следует, что
 .
.
При
![]() получаем
получаем
![]() .
.
Таким образом, условия (5.21)
достаточно для ![]() -близости
эмпирически оптимального решающего правила к истинно оптимальному. Подставляя
значение
-близости
эмпирически оптимального решающего правила к истинно оптимальному. Подставляя
значение ![]() в
(5.20), получаем
в
(5.20), получаем
 . (5.22)
. (5.22)
В детерминистском случае ![]() и мы получаем оценку,
близкую к (5.18), а при
и мы получаем оценку,
близкую к (5.18), а при ![]() – оценку, близкую к (5.10).
– оценку, близкую к (5.10).
Результаты главы XII позволяют
получить и другую оценку качества решающего правила. Допустим, что выполняется
(5.21). Тогда, разрешая (5.21) относительно ![]() , получим
, получим
 . (5.22')
. (5.22')
Потребуем теперь, чтобы (5.21)
выполнялось для всех ![]() с вероятностью, превышающей
с вероятностью, превышающей ![]() . Для этого достаточно
правую часть (5.20) приравнять
. Для этого достаточно
правую часть (5.20) приравнять ![]() :
:
![]() .
.
Разрешая это уравнение
относительно ![]() и
подставляя найденное значение в (5.22'), получаем окончательно
и
подставляя найденное значение в (5.22'), получаем окончательно

![]() .
.
При
![]()

 . (5.23)
. (5.23)
Как и раньше, примем, что в точке
![]()
![]() .
.
Заметим,
что для эмпирически оптимального ![]() справедливо
справедливо
![]() .
.
Тогда
с вероятностью ![]()

 . (5.23')
. (5.23')
Используя (5.22), можно получить
оценку длины обучающей последовательности, которая в одном предельном случае
(при ![]() )
совпадает с оценкой (5.19), а в другом предельном случае
)
совпадает с оценкой (5.19), а в другом предельном случае ![]() – с оценкой (5.12). Для этого
достаточно правую часть неравенства (5.22) приравнять
– с оценкой (5.12). Для этого
достаточно правую часть неравенства (5.22) приравнять ![]() и разрешить относительно
и разрешить относительно ![]() . Получаем
. Получаем
![]() .
.
В этой главе были приведены качественные оценки длины обучающей последовательности. Строгие оценки получены в главе XIII. Однако при использовании оценок важно не столько их конкретное выражение (ведь оценки получены в предположении наиболее неблагоприятных условий), сколько структура связи основных параметров
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
- § 2. Классификация оценок
- § 3. Метод максимума правдоподобия
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА