2. Преобразование Адамара

Самым простым унитарным преобразованием является преобразование Адамара. Матрица  для случая двух случайных величин будет иметь вид:

.

Если из элементов матрицы  составить базисные вектора , , то они будут характеризовать поворот ортогональной системы координат на 45° относительно единичного базиса.

Если случайные величины  и  имеют корреляционную зависимость , то проекция вектора  на базисный вектор  будет, в среднем, больше, чем проекция этого же вектора на базисный вектор . Благодаря этому информация будет сосредотачиваться в первом коэффициенте преобразования. Второй коэффициент служит для уточнения представления вектора  в новом базисе.

Рассмотрим подробнее процесс разложения вектора  по базисным векторам Адамара. Проекция  представляет собой удвоенное среднее значение элементов вектора , проекция  - удвоенную разность между средним значением и элементом  (рис. 2).

Рис. 2. Графическое представление проекций

Выполним восстановление вектора  по первому коэффициенту  с помощью обратной матрицы , получим:

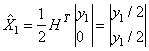.                                              (5)

Из выражения (5) видно, что восстановленный вектор  представляет собой средние значения элементов  и , что соответствует «грубому» приближению вектора , без наличия мелких деталей.

Рассмотрим теперь восстановление того же вектора по коэффициенту , получим:

.                             (6)

Анализ выражения (6) показывает, что вектор  описывает только мелкие детали вектора . При этом можно заметить, что сумма  даст исходный вектор , что соответствует восстановлению по обоим коэффициентам разложения.

При увеличении размерности пространства большая часть информации будет сосредоточена в малом числе коэффициентов

Матрицу Адамара размерности 4х4 элементов легко построить из матрицы Адамара  размерностью 2х2 элемента:

,

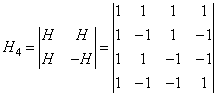Пользуясь данным соотношением можно построить матрицу Адамара любой размерности , где  - любое целое положительное число.

Анализ изображений выполняется на основе разделимого преобразования:

.

Так как матрица  представляет собой оператор ортогонального преобразования, то обратное преобразование из  в  запишется в виде

.

Восстановление изображения  по неполному числу коэффициентов разложения, также как и для случая двух случайных величин, будет приводить к похожим эффектам сглаживания и выделения мелких деталей. При этом возникают ошибки восстановления , которым можно поставить в соответствие некоторую функцию потерь . Значение этой функции будет характеризовать качество восстановления. На практике часто используют квадратичную функцию потерь

.                                  (7)

Так как  носит случайный характер, то значение  также является случайной величиной. При этом желательно, чтобы , в среднем, была минимальна. Для этого перепишем выражение (7) в виде

,                (8)

где  - знак математического ожидания. Найдем базисные вектора, минимизирующие (8).