9. Выполнение вейвлет-преобразования на основе лифтинговой схемы

Любое ВП можно эффективно выполнить с помощью лифтинговой схемы. Пусть задан вектор . Рассмотрим его разложение по базисным функциям Хаара. Первый высокочастотный коэффициент

,                                                  (26)

низкочастотный

.                                           (27)

Анализ выражений (26) и (27) показывает, что величину  можно интерпретировать как ошибку оценивания элемента . Величина  представляет высокочастотные составляющие и вычисляется путем прибавления вейвлет-коэффициента  к элементу . Таким образом, вектор  можно разбить на оцениваемые элементы  и наблюдения  Перепишем выражения (26) и (27) в виде

,                                        (28)

.

При этом коэффициенты низкочастотного вейвлет-фильтра . Лучших результатов сглаживания элементов  можно получить если положить

.  (29)

В этом случае коэффициенты низкочастотного фильтра  и высокочастотного . Если коэффициенты  и  записать в матрицу преобразования , то можно вычислять данное ВП с помощью выражений (21)-(24). При этом матрица обратного преобразования .

Рассмотрим этап восстановления сигнала по вейвлет-коэффициентам  и низкочастотной составляющей . Также будем полагать, что  и . Из выражений (28) и (29) следует, что

,

,

при . Объединение восстановленных четных и нечетных элементов даст исходный вектор .

При анализе двумерных сигналов на основе лифтинговой схемы выполняется разделимое преобразование. Пусть имеется изображение , размером  элементов. Требуется выполнить ВП с коэффициентами вейвлет-фильтров  и . Тогда для каждой строки  можно вычислить вейвлет-коэффициенты согласно выражениям (28) и (29):

,

,                         (30)

при . Таким образом, получили две матрицы  и  размерностью . Так как преобразование является разделимым, то для вычисленных  и  выполняются аналогичные операции применительно к столбцам:

,

,                           (31)

,

при . В результате получаем четыре матрицы размером . Здесь , ,  представляют собой высокочастотные составляющие (детали изображения), а  - низкочастотную, представляющая уменьшенную в четыре раза и сглаженную копию исходного изображения. Выражения (30), (31) можно рекуррентно повторять для низкочастотных составляющих . На практике обычно выполняют 4-5 итераций.

Рассмотрим алгоритм обратного ВП. В соответствии с выражением (31) имеем:

,

,

,                    (32)

при . Объединение четных и нечетных строк даст матрицы  и  размером  элементов. Окончательно из выражения (30) имеем:

,

,                                 (33)

при . Выражения (32) и (33) определяют обратное двумерное ВП на основе лифтинговой схемы с  и . В общем случае для произвольных  и  прямое ВП на основе лифтинговой схемы можно записать в виде

                                                    (34)

где  - оператор разбиения последовательности  на наблюдения  и оцениваемые элементы ;  - оператор оценивания элементов  на основе наблюдений ;  - оператор обновления. Схема обратного преобразования будет иметь вид

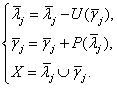                                                    (35)

Выражения (34) и (35) описывают один шаг ВП на основе лифтинговой схемы.