| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
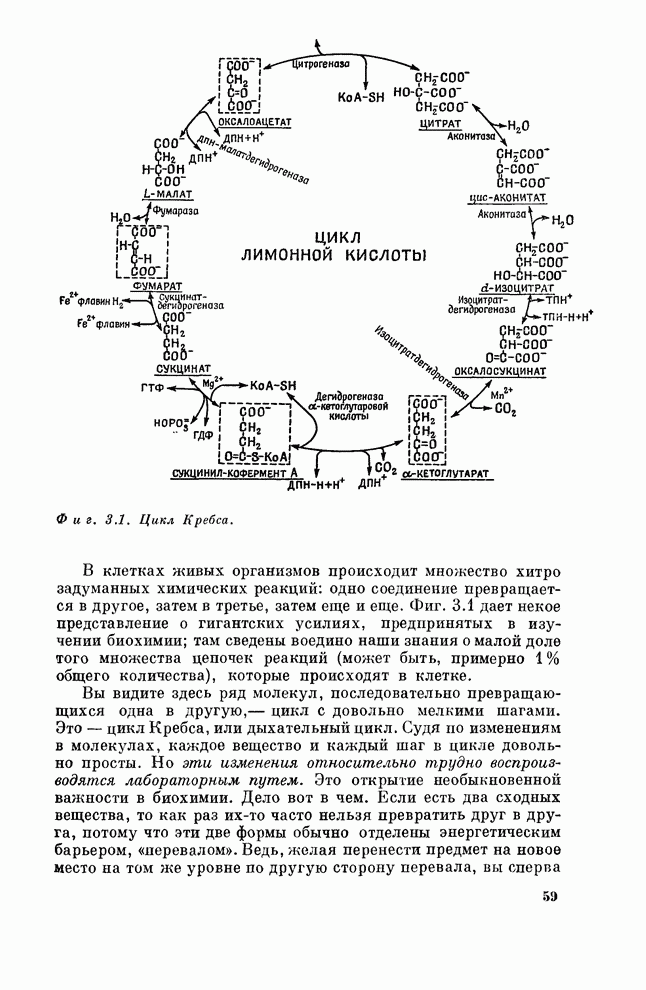
§ 2. Флуктуации
Теперь мне бы хотелось несколько подробнее показать, как
можно использовать идею вероятности, чтобы ответить на вопрос: сколько же в
самом деле я ожидаю выпадений «орла», если подбрасываю монету ![]() раз? Однако,
прежде чем ответить на него, давайте посмотрим, что все-таки дает нам такой «эксперимент».
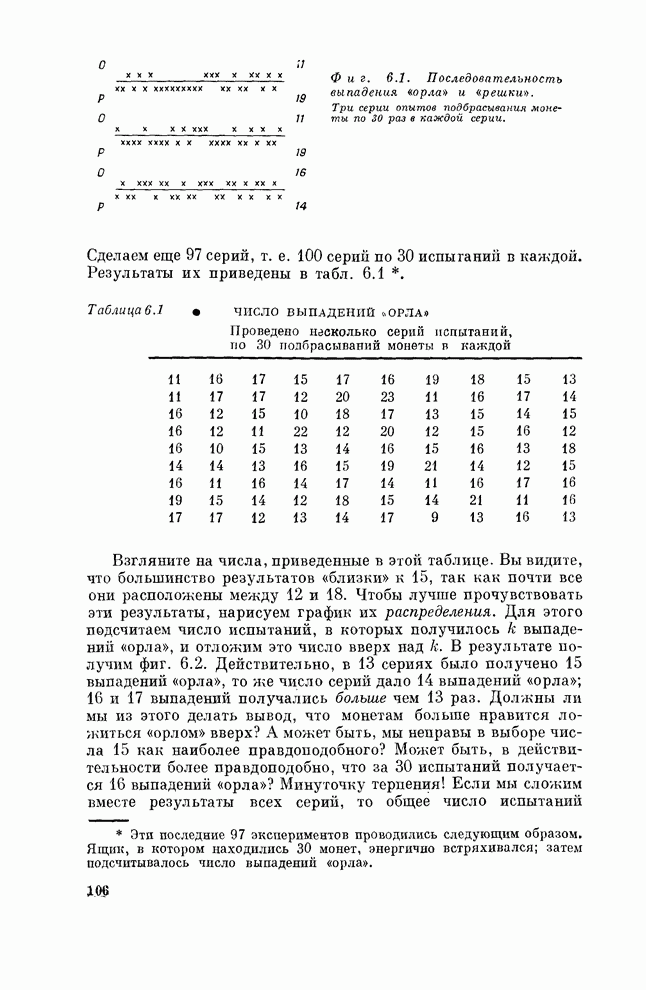
На фиг. 6.1 показаны результаты, полученные в первых трех сериях испытаний по
30 испытаний в каждой. Последовательности выпадений «орла» и «решки» показаны в
том порядке, как это происходило. В первый раз получилось 11 выпадений «орла»,
во второй — тоже 11, а в третий — 16. Можно ли на этом основании подозревать,
что монета была «нечестной»? Или, может быть, мы ошиблись, приняв 15 за
наиболее вероятное число выпадений «орла» в каждой серии испытаний?
раз? Однако,
прежде чем ответить на него, давайте посмотрим, что все-таки дает нам такой «эксперимент».
На фиг. 6.1 показаны результаты, полученные в первых трех сериях испытаний по
30 испытаний в каждой. Последовательности выпадений «орла» и «решки» показаны в
том порядке, как это происходило. В первый раз получилось 11 выпадений «орла»,
во второй — тоже 11, а в третий — 16. Можно ли на этом основании подозревать,
что монета была «нечестной»? Или, может быть, мы ошиблись, приняв 15 за
наиболее вероятное число выпадений «орла» в каждой серии испытаний?

Фигура 6.1. Последовательность выпадения «орла» и «решки». Три серии опытов подбрасывания монеты по 30 раз в каждой серии.
Сделаем еще 97 серий, т. е. 100 серий по 30 испытаний в каждой. Результаты их приведены в табл. 6.1
Таблица 6.1 Число выпадений «орла»
|
Проведено несколько серий испытаний, по 30 подбрасываний монеты в каждой |
|||||||||
|
11 |
16 |
17 |
15 |
17 |
16 |
19 |
18 |
15 |
13 |
|
11 |
17 |
17 |
12 |
20 |
23 |
11 |
16 |
17 |
14 |
|
16 |
12 |
15 |
10 |
18 |
17 |
13 |
15 |
14 |
15 |
|
16 |
12 |
11 |
22 |
12 |
20 |
12 |
15 |
16 |
12 |
|
16 |
10 |
15 |
13 |
14 |
16 |
15 |
16 |
13 |
18 |
|
14 |
14 |
13 |
16 |
15 |
19 |
21 |
14 |
12 |
15 |
|
16 |
11 |
16 |
14 |
17 |
14 |
11 |
16 |
17 |
16 |
|
19 |
15 |
14 |
12 |
18 |
15 |
14 |
21 |
11 |
16 |
|
17 |
17 |
12 |
13 |
14 |
17 |
9 |
13 |
16 |
13 |
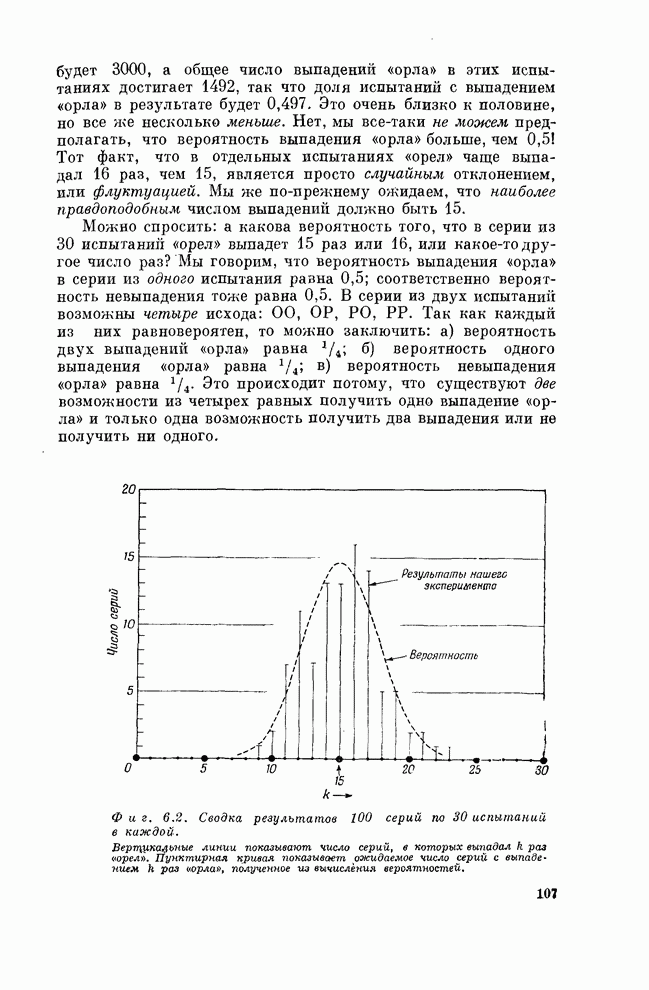
Взгляните на числа, приведенные в этой таблице. Вы
видите, что большинство результатов «близки» к 15, так как почти все они
расположены между 12 и 18. Чтобы лучше прочувствовать эти результаты, нарисуем
график их распределения. Для этого подсчитаем число испытании, в которых
получилось ![]() выпадений
«орла», и отложим это число вверх над
выпадений
«орла», и отложим это число вверх над ![]() . В результате получим фиг. 6.2.
Действительно, в 13 сериях было получено 15 выпадений «орла», то же число серий
дало 14 выпадений «орла»; 16 и 17 выпадений получались больше чем 13 раз.
Должны ли мы из этого делать вывод, что монетам больше нравится ложиться «орлом»
вверх? А может быть, мы неправы в выборе числа 15 как наиболее правдоподобного?
Может быть, в действительности более правдоподобно, что за 30 испытаний
получается 10 выпадений «орла»? Минуточку терпения! Если мы сложим вместе
результаты всех серий, то общее число испытаний будет 3000, а общее число
выпадении «орла» в этих испытаниях достигает 1492, так что доля испытаний с
выпадением «орла» в результате будет 0,497. Это очень близко к половине, но все
же несколько меньше. Нет, мы все-таки не можем предполагать, что вероятность
выпадения «орла» больше, чем 0,5! Тот факт, что в отдельных испытаниях «орел»
чаще выпадал 10 раз, чем 15, является просто случайным отклонением, или флуктуацией.
Мы же по-прежнему ожидаем, что наиболее правдоподобным числом выпадении должно
быть 15.
. В результате получим фиг. 6.2.
Действительно, в 13 сериях было получено 15 выпадений «орла», то же число серий
дало 14 выпадений «орла»; 16 и 17 выпадений получались больше чем 13 раз.
Должны ли мы из этого делать вывод, что монетам больше нравится ложиться «орлом»
вверх? А может быть, мы неправы в выборе числа 15 как наиболее правдоподобного?
Может быть, в действительности более правдоподобно, что за 30 испытаний
получается 10 выпадений «орла»? Минуточку терпения! Если мы сложим вместе
результаты всех серий, то общее число испытаний будет 3000, а общее число
выпадении «орла» в этих испытаниях достигает 1492, так что доля испытаний с
выпадением «орла» в результате будет 0,497. Это очень близко к половине, но все
же несколько меньше. Нет, мы все-таки не можем предполагать, что вероятность
выпадения «орла» больше, чем 0,5! Тот факт, что в отдельных испытаниях «орел»
чаще выпадал 10 раз, чем 15, является просто случайным отклонением, или флуктуацией.
Мы же по-прежнему ожидаем, что наиболее правдоподобным числом выпадении должно
быть 15.
Можно спросить: а какова вероятность того, что в серии
из 30 испытании «орел» выпадет 15 раз или 16, или какое-то другое число раз? Мы
говорим, что вероятность выпадения «орла» в серии из одного испытания равна
0,5; соответственно вероятность невыпадения тоже равна 0,5. В серии из двух
испытании возможны четыре исхода: ОО, ОР, РО, РР. Так как каждый из них
равновероятен, то можно заключить: а) вероятность двух выпадений «орла» равна ![]() ; б) вероятность
одного выпадения «орла» равна
; б) вероятность
одного выпадения «орла» равна ![]() ; в) вероятность невыпадения «орла»
равна
; в) вероятность невыпадения «орла»
равна ![]() .
Это происходит потому, что существуют две возможности из четырех равных
получить одно выпадение «орла» и только одна возможность получить два выпадения
или не получить ни одного.
.
Это происходит потому, что существуют две возможности из четырех равных
получить одно выпадение «орла» и только одна возможность получить два выпадения
или не получить ни одного.

Фигура 6.2. Сводка результатов 100 серий по
30 испытаний в каждой. Вертикальные линии показывают число серий, в которых
выпадал ![]() раз
«орел», пунктирная кривая показывает ожидаемое число серий с выпадением
раз
«орел», пунктирная кривая показывает ожидаемое число серий с выпадением ![]() раз «орла»,
полученное из вычисления вероятностей.
раз «орла»,
полученное из вычисления вероятностей.

Фигура 6.3. Диаграмма, иллюстрирующая число различных возможностей получения 0, 1, 2 и 3 выпадений «орла» в серии из трех испытаний
Рассмотрим теперь серию из трех испытаний. Третье
испытание с равной вероятностью может дать либо «орел», либо «решку», поэтому
существует только один способ получения трех выпадений «орла»: мы должны получить
два выпадения «орла» в двух первых испытаниях и затем выпадение «орла» в последнем.
Однако получить два выпадения «орла» можно уже тремя способами: после двух
выпадении «орла» может выпасть «решка» и еще два способа — после одного
выпадения «орла» в первых двух испытаниях выпадет «орел» в третьем. Так что
число равновероятных способов получить 3, 2, 1 и 0 выпадений «орла» будет
соответственно равно 1, 3, 3 и 1; полное лее число всех возможных способов
равно 8. Таким образом, получаются следующие вероятности: ![]() .
.
Эти результаты удобно записать в виде диаграммы (фиг.
6.3). Ясно, что эту диаграмму можно продолжить, если мы интересуемся еще
большим числом испытании. На фиг. 6.4 приведена аналогичная диаграмма для шести
испытании. Число «способов», соответствующих каждой точке диаграммы,— это просто
число различных «путей» (т. е., попросту говоря, последовательность выпадения
«орла» и «решки»), которыми можно прийти в эту точку из начальной, не
возвращаясь при этом назад, а высота этой точки дает общее число выпадений
«орла». Этот набор чисел известен под названием треугольника Паскаля, а сами
числа называются биномиальными коэффициентами, поскольку они появляются при
разложении выражения ![]() . Обычно эти числа на нашей диаграмме
обозначаются символом
. Обычно эти числа на нашей диаграмме
обозначаются символом ![]() или
или ![]() (число сочетаний из
(число сочетаний из ![]() по
по ![]() ), где
), где ![]() — полное число испытаний,
а
— полное число испытаний,
а ![]() —
число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно
вычислять по формуле
—
число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно
вычислять по формуле
![]() (6.4)
(6.4)
где символ ![]() ,
называемый «
,
называемый «![]() -факториалом», обозначает
произведение всех целых чисел от 1 до
-факториалом», обозначает
произведение всех целых чисел от 1 до ![]() , т. е.
, т. е. ![]() .
.

Фигура 6.4. Диаграмма, подобная изображенной на фиг. 6.3, для серии из шести испытаний.
Теперь уже все готово для того, чтобы с помощью
выражения (6.1) подсчитать вероятность ![]() выпадения
выпадения ![]() раз «орла» в серии из
раз «орла» в серии из ![]() испытаний. Полное
число всех возможностей будет
испытаний. Полное
число всех возможностей будет ![]() (поскольку в каждом испытании
возможны два исхода), а число равновероятных комбинаций, в которых выпадет «орел»,
будет
(поскольку в каждом испытании
возможны два исхода), а число равновероятных комбинаций, в которых выпадет «орел»,
будет ![]() ,
так что
,
так что
 (6.5)
(6.5)
Поскольку ![]() — доля тех серий испытаний, в которых
выпадение «орла» ожидается
— доля тех серий испытаний, в которых
выпадение «орла» ожидается ![]() раз, то из ста серий
раз, то из ста серий ![]() выпадений «орла»
ожидается
выпадений «орла»
ожидается ![]() раз.
Пунктирная кривая на фиг. 6.2 проведена как раз через точки функции
раз.
Пунктирная кривая на фиг. 6.2 проведена как раз через точки функции ![]() . Видите, мы ожидали
получить 15 выпадений «орла» в 14 или 15 сериях испытаний, а получили только в
13. Мы ожидали получить 16 выпадений «орла» в 13 или 14 сериях испытаний, а получили
в 16. Но такие флуктуации вполне допускаются «правилами игры».
. Видите, мы ожидали
получить 15 выпадений «орла» в 14 или 15 сериях испытаний, а получили только в
13. Мы ожидали получить 16 выпадений «орла» в 13 или 14 сериях испытаний, а получили
в 16. Но такие флуктуации вполне допускаются «правилами игры».
Использованный здесь метод можно применять и в более общей
ситуации, где в каждом единичном испытании возможны только два исхода, которые
давайте обозначим через В (выигрыш) и П (проигрыш). Вообще говоря, вероятности
В и П в каждом отдельном испытании могут быть разными. Пусть ![]() , например, будет
вероятностью результата В. Тогда
, например, будет
вероятностью результата В. Тогда ![]() (вероятность результата П) должна
быть равна
(вероятность результата П) должна
быть равна ![]() .
В серии из
.
В серии из ![]() испытаний
вероятность того, что результат В получится
испытаний
вероятность того, что результат В получится ![]() раз, равна
раз, равна
![]() . (6.6)
. (6.6)
Эта функция вероятностей называется биномиальным законом распределения вероятности.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
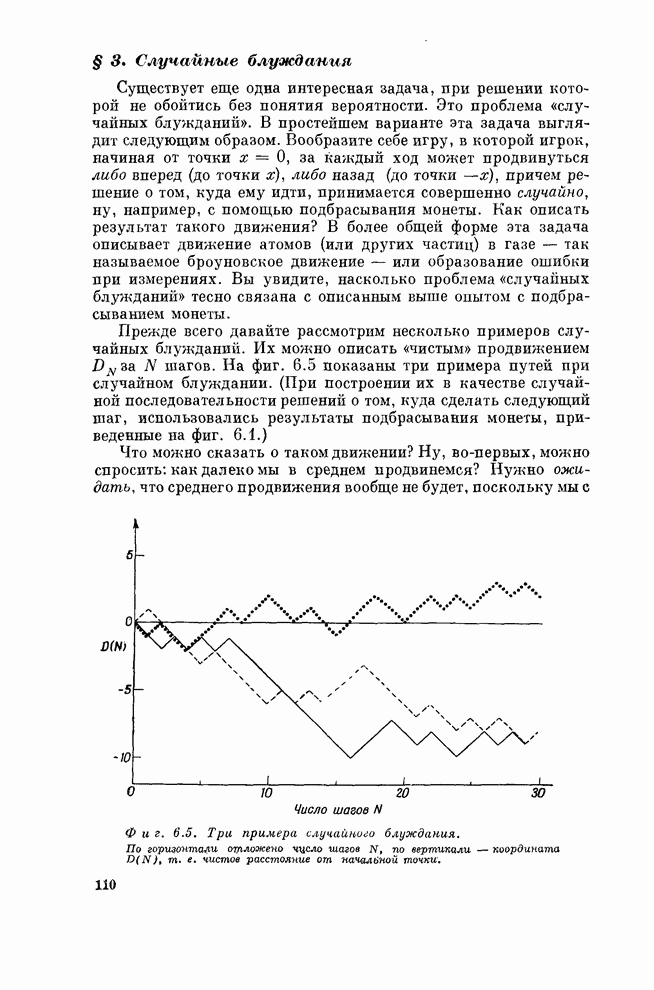
- § 3. Случайные блуждания
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
- § 5. Численное решение уравнений
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля