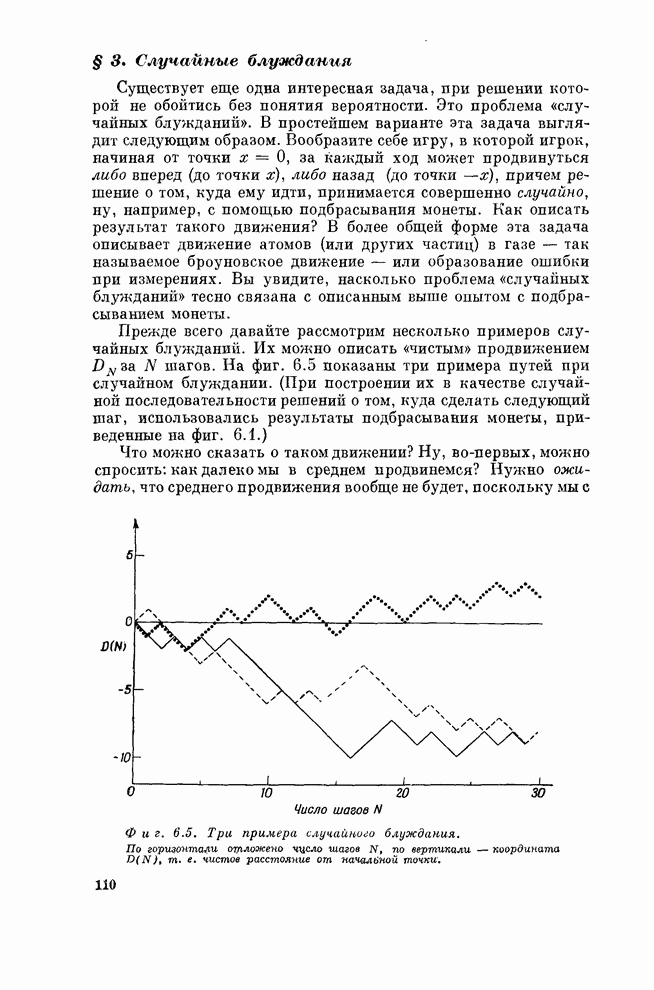
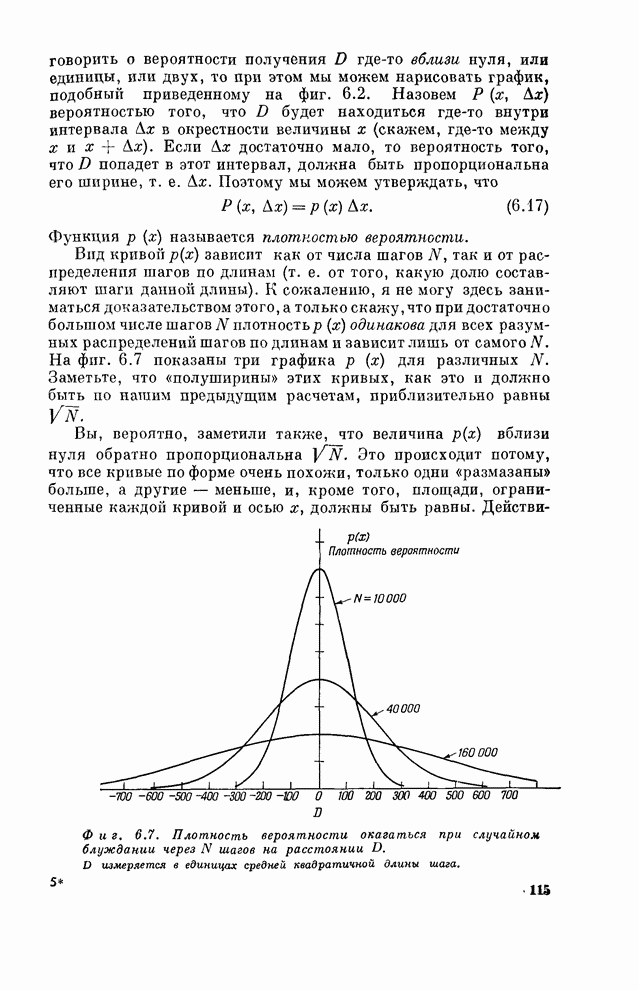
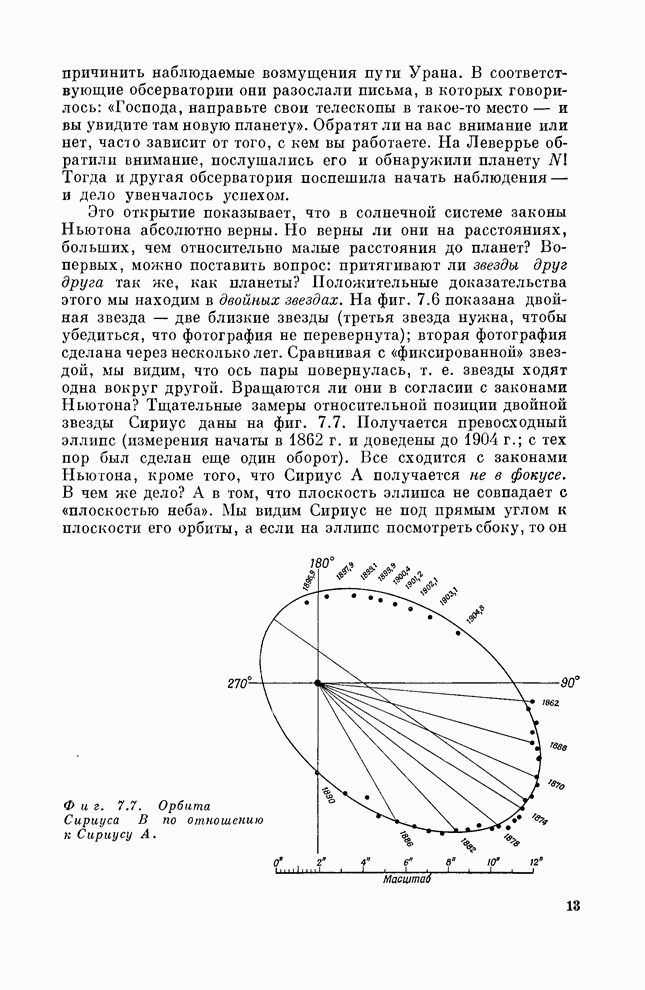
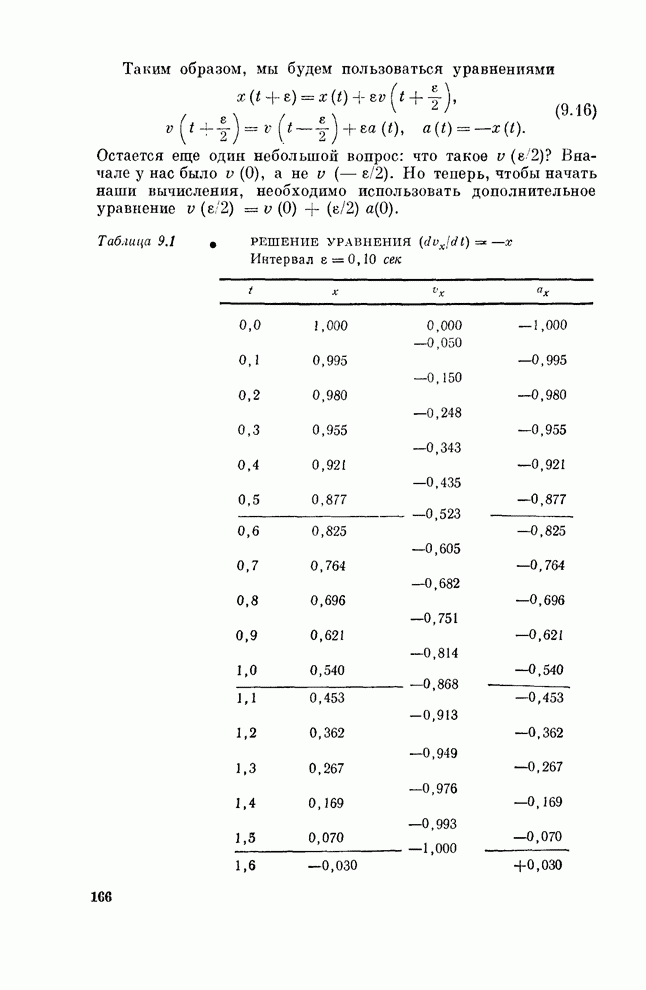
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
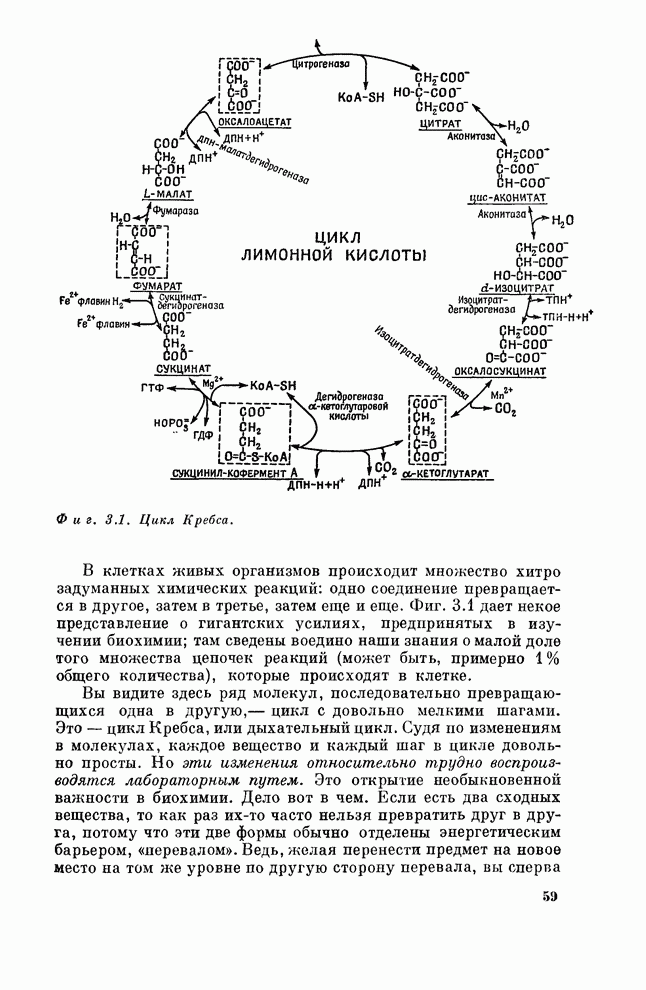
§ 4. Поле тяготения больших тел
Теперь
рассчитаем поля, встречающиеся во многих физических задачах, когда речь идет о распределении
масс. Мы пока не рассматривали распределения масс, а занимались только
отдельными частицами. Но интересно рассчитать и поля, образуемые более чем
одной частицей. Для начала найдем силу притяжения со стороны плоского пласта
вещества бесконечной протяженности. Сила притяжения единичной массы в данной
точке ![]() (фиг.
13.5), конечно, направлена к плоскости. Расстояние от точки до плоскости есть
(фиг.
13.5), конечно, направлена к плоскости. Расстояние от точки до плоскости есть ![]() , а масса единицы
площади этой плоскости есть
, а масса единицы
площади этой плоскости есть ![]() .
.

Фигура 13.5. Сила притяжения материальной точки материальной плоскостью.
Пусть ![]() будет постоянной:
слой однороден. Какой же величины поло
будет постоянной:
слой однороден. Какой же величины поло ![]() создается массой
создается массой ![]() , удаленной от
, удаленной от ![]() не ближе, чем на
не ближе, чем на ![]() , и не дальше, чем
на
, и не дальше, чем
на ![]() (
(![]() — это точка
плоскости, ближайшая к
— это точка
плоскости, ближайшая к ![]() )? Ответ:
)? Ответ: ![]() . Но оно, это поле,
направлено вдоль
. Но оно, это поле,
направлено вдоль ![]() , а мы понимаем, что из трех
составляющих
, а мы понимаем, что из трех
составляющих ![]() после
сложения всех
после
сложения всех ![]() должна
остаться лишь
должна
остаться лишь ![]() составляющая.
составляющая.
Она равна
![]() .
.
Все массы ![]() , которые находятся на
одном и том же расстоянии
, которые находятся на
одном и том же расстоянии ![]() от
от ![]() , дадут одно и то же значение
, дадут одно и то же значение ![]() , так что за
, так что за ![]() можно сразу
принять массу всего кольца между
можно сразу
принять массу всего кольца между ![]() и
и ![]() , т. е.
, т. е. ![]() (
(![]() — это площадь кольца радиусом
— это площадь кольца радиусом ![]() и шириной
и шириной ![]() при
при ![]() ). Итак,
). Итак,
![]() .
.
Но ![]() из-за того, что
из-за того, что ![]() . Поэтому
. Поэтому
 . (13.17)
. (13.17)
Стало
быть, сила не зависит от расстояния ![]() ! Почему? Не ошиблись ли мы? Казалось
бы, чем дальше от плоскости, тем сила слабее. Но нет! Если точка находится
вплотную к плоскости, то большая часть вещества притягивает ее под неудачными
углами, а если вдалеке, то у большей части вещества притяжение направлено
прямее к плоскости. На любом расстоянии самая «влиятельная» часть плоскости
лежит в некотором конусе. С удалением сила ослабляется обратно пропорционально
квадрату расстояния, но в том же конусе под тем же углом оказывается больше
вещества, а рост количества вещества тоже пропорционален квадрату расстояния!
Этот анализ может быть сделан более строгим, если заметить, что дифференциал
вклада любого данного конуса не зависит от расстояния в результате
противоположных изменений напряженности поля данной массы и количества самой
этой массы (с ростом расстояния). Впрочем, на самом деле сила не постоянна, ибо
на другой стороне плоскости она меняет знак.
! Почему? Не ошиблись ли мы? Казалось
бы, чем дальше от плоскости, тем сила слабее. Но нет! Если точка находится
вплотную к плоскости, то большая часть вещества притягивает ее под неудачными
углами, а если вдалеке, то у большей части вещества притяжение направлено
прямее к плоскости. На любом расстоянии самая «влиятельная» часть плоскости
лежит в некотором конусе. С удалением сила ослабляется обратно пропорционально
квадрату расстояния, но в том же конусе под тем же углом оказывается больше
вещества, а рост количества вещества тоже пропорционален квадрату расстояния!
Этот анализ может быть сделан более строгим, если заметить, что дифференциал
вклада любого данного конуса не зависит от расстояния в результате
противоположных изменений напряженности поля данной массы и количества самой
этой массы (с ростом расстояния). Впрочем, на самом деле сила не постоянна, ибо
на другой стороне плоскости она меняет знак.
Мы
решили, кстати, и задачу по электричеству: мы доказали, что у заряженной
пластины, каждая единица площади которой несет заряд ![]() , электрическое поле равно
, электрическое поле равно ![]() и направлено от
пластины, если она заряжена положительно, и к ней, если она заряжена
отрицательно. Чтобы доказать это, надо просто вспомнить, что в законе тяготения
и направлено от
пластины, если она заряжена положительно, и к ней, если она заряжена
отрицательно. Чтобы доказать это, надо просто вспомнить, что в законе тяготения
![]() играет
ту же роль, что
играет
ту же роль, что ![]() в
электричестве.
в
электричестве.
А теперь
пусть имеются две пластины, одна с положительным зарядом ![]() , а другая с отрицательным
, а другая с отрицательным ![]() (на единицу
площади), и пусть промежуток между ними равен
(на единицу
площади), и пусть промежуток между ними равен ![]() . Каково поле этих пластин? Снаружи
пластин поле равно нулю. Отчего? Оттого, что одна из них отталкивает, а другая
притягивает и у обеих сила не зависит от расстояния, значит, силы всюду
уничтожаются! А вот поле между пластинами вдвое больше, чем поле одной
пластины, направлено оно от положительной пластины к отрицательной и равно
. Каково поле этих пластин? Снаружи
пластин поле равно нулю. Отчего? Оттого, что одна из них отталкивает, а другая
притягивает и у обеих сила не зависит от расстояния, значит, силы всюду
уничтожаются! А вот поле между пластинами вдвое больше, чем поле одной
пластины, направлено оно от положительной пластины к отрицательной и равно ![]() .
.
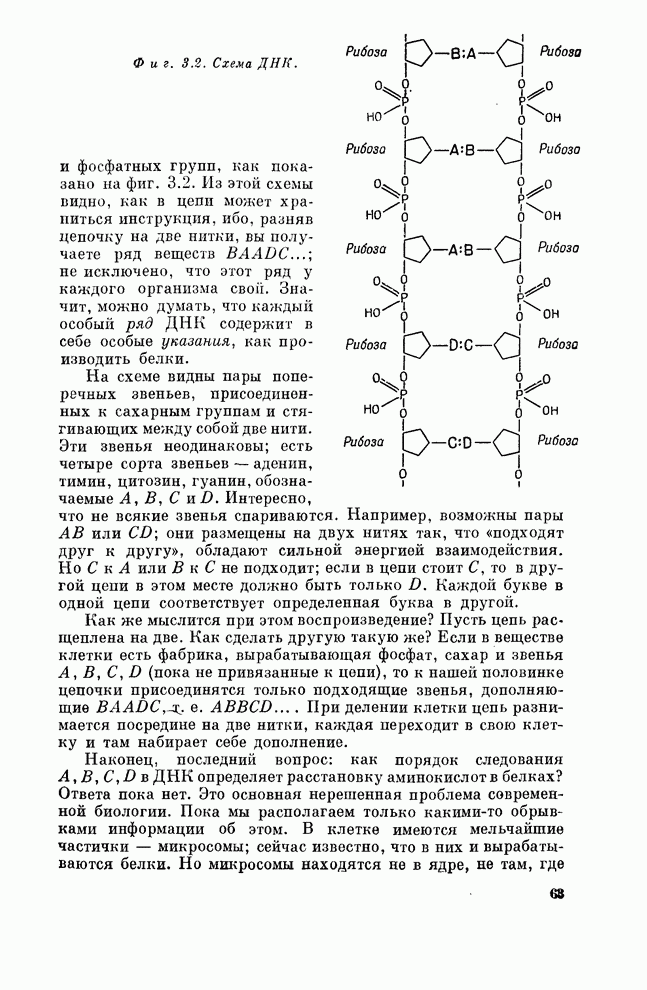
Перейдем теперь к еще более интересному и важному вопросу; впрочем, мы давно уже ответили на него, предположив, что сила притяжения Земли в точке на ее поверхности или над нею такая же, как если бы вся масса Земли сосредоточилась в ее центре. Справедливость этого предположения не очевидна: ведь когда мы находимся у самой земли, какая-то часть ее массы очень к нам близка, а другая далека и т. д. Когда мы складываем действие всех таких масс, то кажется чудом, что в конце концов сила сводится к тому, что вся Земля сжалась в одну точку, стянулась к своему центру!
Мы
теперь покажем, что это чудо обыкновенное; чтобы продемонстрировать это,
разобьем Землю на тонкие сферические слои. Пусть вся масса сферы равна ![]() . Давайте
рассчитаем потенциальную энергию частицы массы
. Давайте
рассчитаем потенциальную энергию частицы массы ![]() на расстоянии
на расстоянии ![]() от центра сферы (фиг.
13.6). Мы увидим, что потенциальная энергия как раз такая, как если бы масса
от центра сферы (фиг.
13.6). Мы увидим, что потенциальная энергия как раз такая, как если бы масса ![]() сферы вся
собралась в ее центре. (Легче иметь дело с потенциальной энергией чем с
напряженностью поля: не нужно думать об углах, а просто складывать
потенциальные энергии всех частей сферы.) Нарежем сферу на узкие пояски, и
пусть
сферы вся
собралась в ее центре. (Легче иметь дело с потенциальной энергией чем с
напряженностью поля: не нужно думать об углах, а просто складывать
потенциальные энергии всех частей сферы.) Нарежем сферу на узкие пояски, и
пусть ![]() —
расстояние плоскости пояска от центра сферы; тогда вся масса пояска толщиной
—
расстояние плоскости пояска от центра сферы; тогда вся масса пояска толщиной ![]() находится на
одном и том же расстоянии
находится на
одном и том же расстоянии ![]() от точки
от точки ![]() , а потенциальная энергия
притяжения этого пояска равна
, а потенциальная энергия
притяжения этого пояска равна ![]() . Сколько же массы содержится в
пояске
. Сколько же массы содержится в
пояске ![]() ?
Вот сколько:
?
Вот сколько:
![]() ,
,
где ![]() — поверхностная
плотность массы. (Вообще площадь поверхности шарового пояса пропорциональна его
высоте.) Поэтому потенциальная энергия притяжения массы
— поверхностная
плотность массы. (Вообще площадь поверхности шарового пояса пропорциональна его
высоте.) Поэтому потенциальная энергия притяжения массы ![]() есть
есть
![]() .
.
Но мы видим, что
![]() .
.
Значит, или
![]() ,
,
или
![]() .
.
Поэтому
![]()
и получается
 . (13.18)
. (13.18)

Фигура 13.6. Тонкий сферический слой масс (или зарядов).
Стало
быть, для тонкого слоя потенциальная энергия массы ![]() внешней по отношению к
слою, такова, как если бы масса слоя собралась в его центре. Землю же можно
представить в виде ряда таких слоев, и притяжение каждого из слоев зависит
только от его массы; сложив их, получим всю массу планеты; значит, и вся Земля
действует так, словно все ее вещество находится в ее центре!
внешней по отношению к
слою, такова, как если бы масса слоя собралась в его центре. Землю же можно
представить в виде ряда таких слоев, и притяжение каждого из слоев зависит
только от его массы; сложив их, получим всю массу планеты; значит, и вся Земля
действует так, словно все ее вещество находится в ее центре!
Но
посмотрим, что произойдет, если точка ![]() окажется внутри слоя. Проделывая те
же расчеты вплоть до интегрирования, мы получим разность двух значений
окажется внутри слоя. Проделывая те
же расчеты вплоть до интегрирования, мы получим разность двух значений ![]() , но уже в другой
форме:
, но уже в другой
форме: ![]() ?
(двойное расстояние от
?
(двойное расстояние от ![]() до центра). Другими словами, теперь
до центра). Другими словами, теперь ![]() становится равной
становится равной
![]() , что не
зависит от
, что не
зависит от ![]() ,
т. е. точка
,
т. е. точка ![]() всюду
внутри сферы обладает одной и той же энергией тяготения. А значит, на нее не
действует никакая сила, и не нужно никакой работы, чтобы двигать ее внутри.
Когда потенциальная энергия тела всюду, в любой точке внутри сферы, одинакова,
то на тело не действует никакая сила. Внутри сферы тело не испытывает действия
сил, сила действует только снаружи.
всюду
внутри сферы обладает одной и той же энергией тяготения. А значит, на нее не
действует никакая сила, и не нужно никакой работы, чтобы двигать ее внутри.
Когда потенциальная энергия тела всюду, в любой точке внутри сферы, одинакова,
то на тело не действует никакая сила. Внутри сферы тело не испытывает действия
сил, сила действует только снаружи.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
- § 3. Случайные блуждания
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
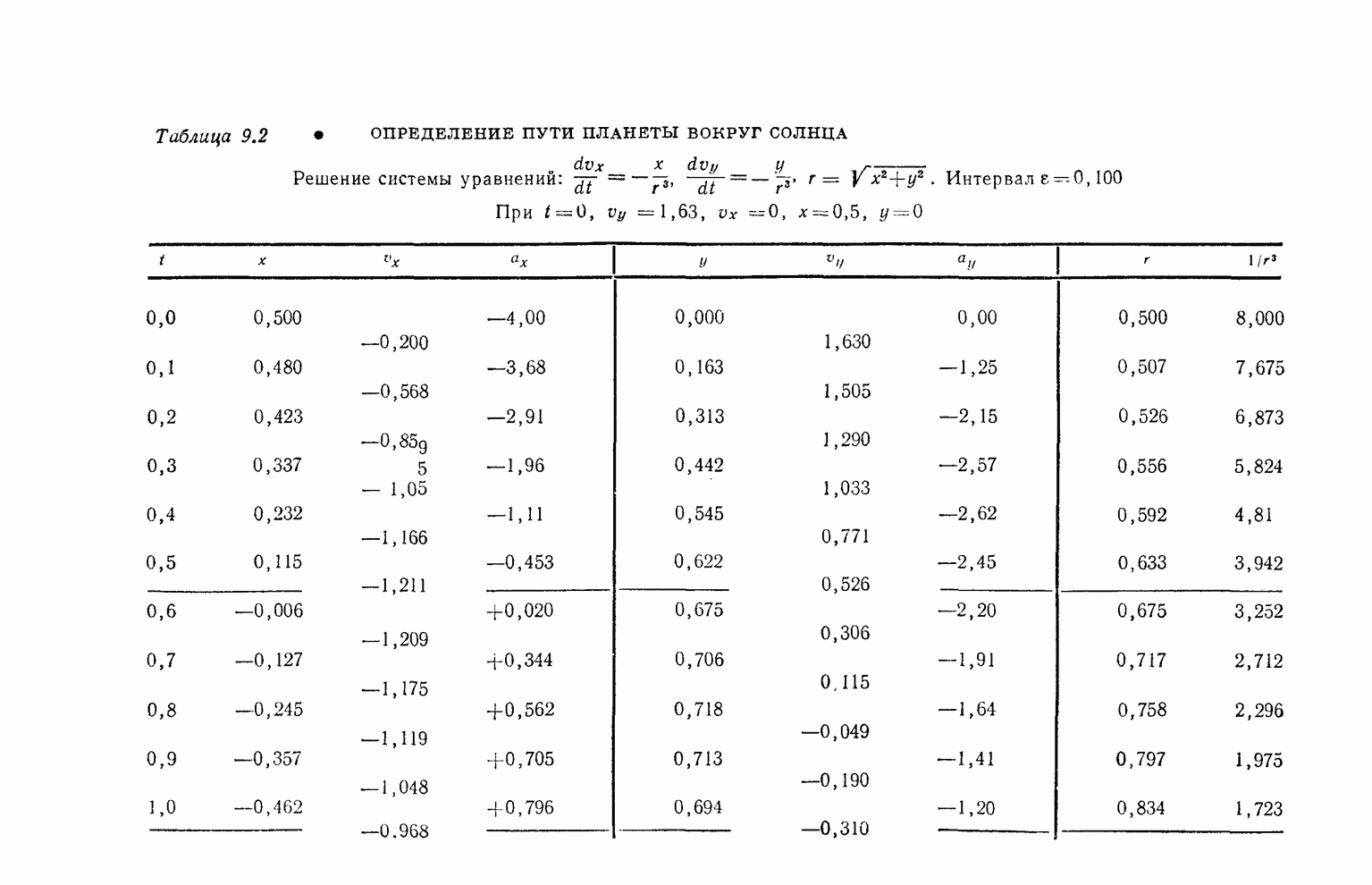
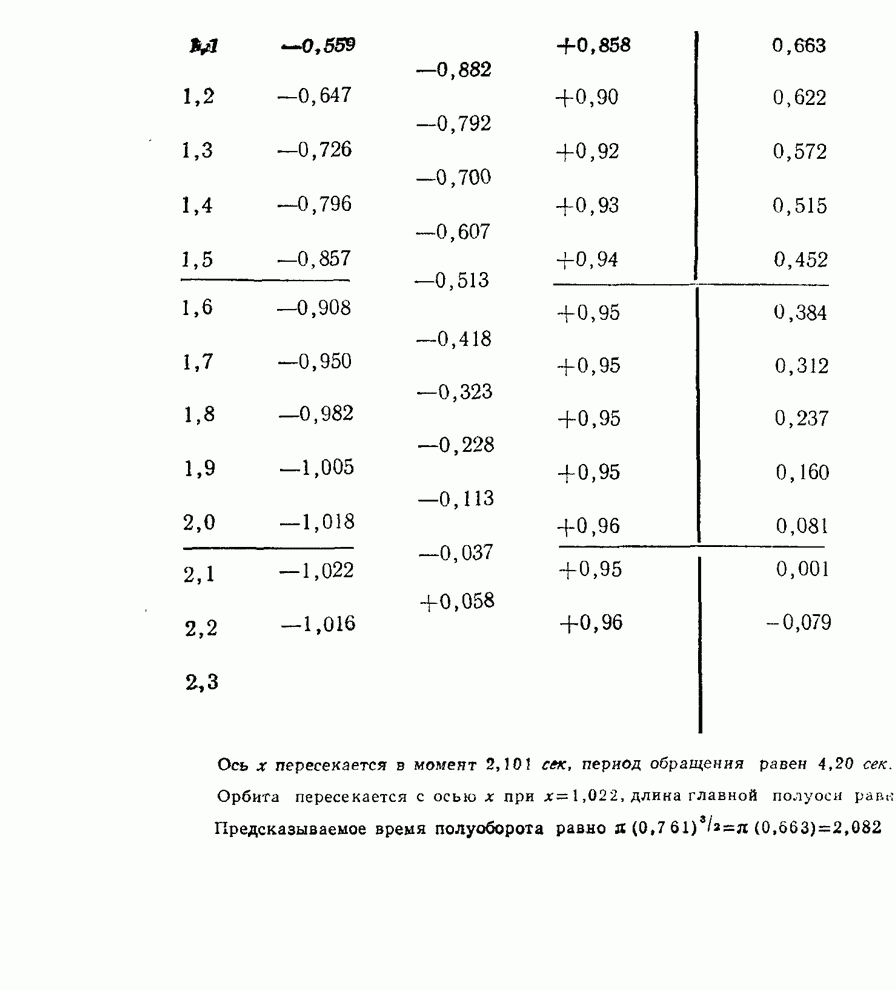
- § 5. Численное решение уравнений
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля