| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Скорость как производная
Процедура, которую мы только что выполнили, настолько
часто встречается в математике, что для величин ![]() и
и ![]() было придумано специальное
обозначение:
было придумано специальное
обозначение: ![]() обозначается
как
обозначается
как ![]() , а
, а ![]() — как
— как ![]() . Величина
. Величина ![]() означает
«небольшой добавок к
означает
«небольшой добавок к ![]() », причем подразумевается, что этот
добавок можно делать меньше. Значок
», причем подразумевается, что этот
добавок можно делать меньше. Значок ![]() ни в коем случае не означает
умножение на какую-то величину, точно так же как
ни в коем случае не означает
умножение на какую-то величину, точно так же как ![]() не означает
не означает ![]() . Это просто некоторый добавок
ко времени, причем значок
. Это просто некоторый добавок
ко времени, причем значок ![]() напоминает нам о его особом характере.
Ну, а если
напоминает нам о его особом характере.
Ну, а если ![]() не
множитель, то его нельзя сократить в отношении
не
множитель, то его нельзя сократить в отношении ![]() . Это все равно, что в выражении
. Это все равно, что в выражении ![]() сократить все
буквы и получить
сократить все
буквы и получить ![]() . В этих новых обозначениях скорость
равна пределу отношения
. В этих новых обозначениях скорость
равна пределу отношения ![]() при
при ![]() , стремящемся к нулю, т. е.
, стремящемся к нулю, т. е.
![]() (8.5)
(8.5)
Это по существу формула (8.3), но теперь яснее видно, что здесь все изменяется, а, кроме того, она напоминает, какие именно величины изменяются.
Существует еще один закон, который выполняется с хорошей
точностью. Он гласит: изменение расстояния равно скорости, умноженной на
интервал времени, за которое это изменение произошло, т. е. ![]() . Это правило строго
справедливо только тогда, когда скорость не изменяется в течение интервала
. Это правило строго
справедливо только тогда, когда скорость не изменяется в течение интервала ![]() , а это, вообще
говоря, происходит, только когда
, а это, вообще
говоря, происходит, только когда ![]() достаточно мало. В таких случаях
обычно пишут
достаточно мало. В таких случаях
обычно пишут ![]() ,
где под
,
где под ![]() подразумевают
интервал времени
подразумевают
интервал времени ![]() при условии, что он сколь угодно
мал. Если интервал
при условии, что он сколь угодно
мал. Если интервал ![]() достаточно велик, то скорость за это
время может измениться и выражение
достаточно велик, то скорость за это
время может измениться и выражение ![]() будет уже приближенным. Однако если
мы пишем
будет уже приближенным. Однако если
мы пишем ![]() ,
то при этом подразумевается, что интервал времени неограниченно мал и в этом
смысле выражение
,
то при этом подразумевается, что интервал времени неограниченно мал и в этом
смысле выражение ![]() точное. В новых обозначениях выражение
(8.5) имеет вид
точное. В новых обозначениях выражение
(8.5) имеет вид
![]() .
.
Величина ![]() называется «производной
называется «производной ![]() по
по ![]() » (такое название
напоминает о том, что изменяется), а сложный процесс нахождения производной
называется, кроме того, дифференцированием. Если же
» (такое название
напоминает о том, что изменяется), а сложный процесс нахождения производной
называется, кроме того, дифференцированием. Если же ![]() и
и ![]() появляются отдельно, а не
в виде отношения
появляются отдельно, а не
в виде отношения ![]() , то они носят названия дифференциалов.
Чтобы получше познакомить вас с новой терминологией, скажу еще, что в
предыдущем параграфе мы нашли производную от функции
, то они носят названия дифференциалов.
Чтобы получше познакомить вас с новой терминологией, скажу еще, что в
предыдущем параграфе мы нашли производную от функции ![]() , или просто производную от
, или просто производную от
![]() . Она
оказалась равной
. Она
оказалась равной ![]() . Когда вы больше привыкнете к новым
словам, вам станет более понятна сама мысль. Для тренировки давайте найдем
производную более сложной функции. Рассмотрим выражение
. Когда вы больше привыкнете к новым
словам, вам станет более понятна сама мысль. Для тренировки давайте найдем
производную более сложной функции. Рассмотрим выражение ![]() , которое может описывать
движение точки. Буквы
, которое может описывать
движение точки. Буквы ![]() так же как и в обычном квадратном
уравнении, обозначают постоянные числа. Нам нужно найти скорость движения,
описываемого этой формулой в любой момент времени
так же как и в обычном квадратном
уравнении, обозначают постоянные числа. Нам нужно найти скорость движения,
описываемого этой формулой в любой момент времени ![]() . Рассмотрим для этого момент
. Рассмотрим для этого момент ![]() , причем к
, причем к ![]() прибавится некоторая
добавка
прибавится некоторая
добавка ![]() ,
и найдем, как выражается
,
и найдем, как выражается ![]() через
через ![]() Поскольку
Поскольку
![]()
а
![]()
то
![]() .
.
Но нам нужна не сама величина ![]() , а отношение
, а отношение ![]() . После деления на
. После деления на
![]() получим
выражение
получим
выражение
![]() ,
,
которое после устремления ![]() к нулю превратится в
к нулю превратится в
![]() .
.
В этом состоит процесс взятия производной, или
дифференцирования функций. На самом деле он несколько легче, чем это кажется на
первый взгляд. Заметьте, что если в разложениях, подобных предыдущим, встречаются
члены, пропорциональные ![]() или
или ![]() или еще более высоким степеням, то
их можно сразу вычеркнуть, поскольку они все равно обратятся в нуль, когда в
конце мы будем
или еще более высоким степеням, то
их можно сразу вычеркнуть, поскольку они все равно обратятся в нуль, когда в
конце мы будем ![]() устремлять
к нулю. После небольшой тренировки вы сразу будете видеть, что нужно оставлять,
а что сразу отбрасывать. Существует много правил и формул для дифференцирования
различных видов функций. Их можно либо запомнить, либо пользоваться
специальными таблицами. Небольшой список таких правил приводится в табл. 8.3.
устремлять
к нулю. После небольшой тренировки вы сразу будете видеть, что нужно оставлять,
а что сразу отбрасывать. Существует много правил и формул для дифференцирования
различных видов функций. Их можно либо запомнить, либо пользоваться
специальными таблицами. Небольшой список таких правил приводится в табл. 8.3.
Таблица 8.3. Некоторые производные
![]() - произвольные функции
- произвольные функции
![]() — произвольнее постоянные.
— произвольнее постоянные.
|
Функция |
Производная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
- § 3. Случайные блуждания
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
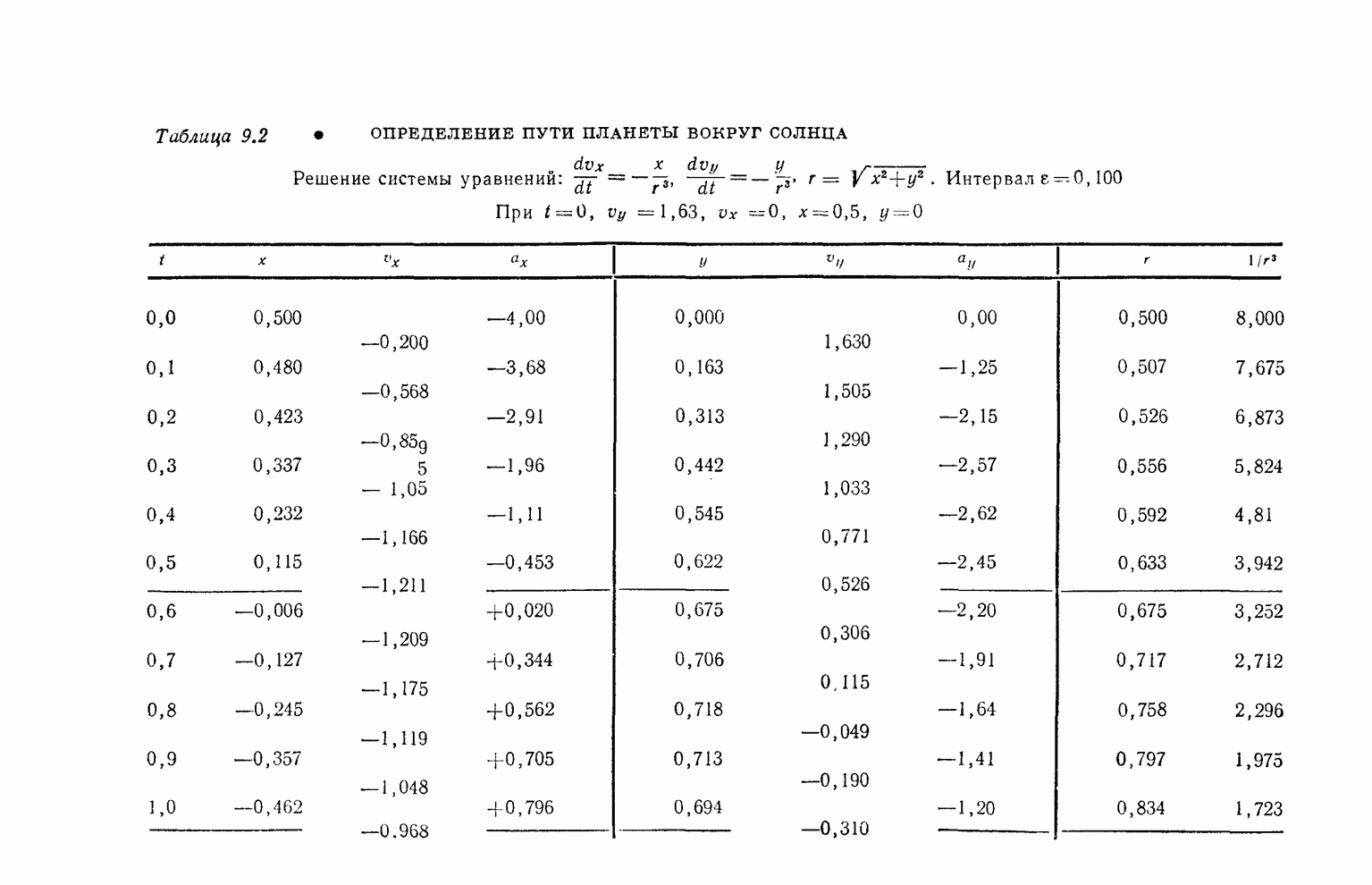
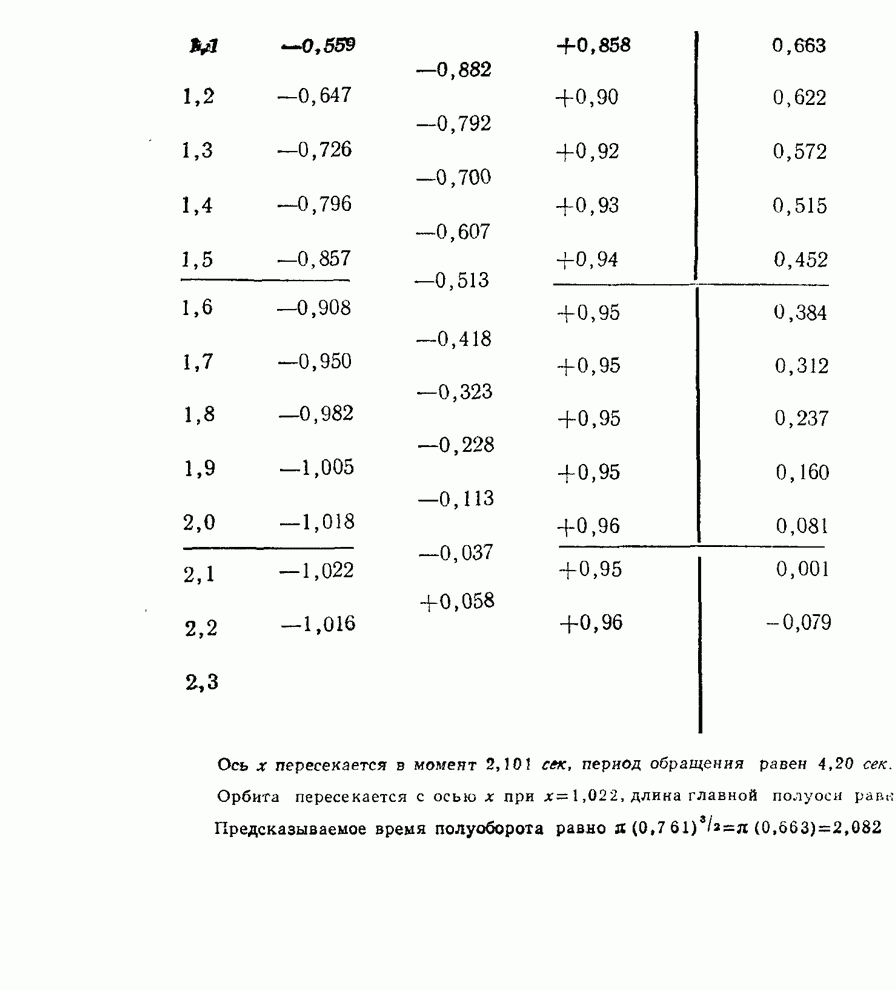
- § 5. Численное решение уравнений
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля