| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Консервативные силы
В
природе существуют силы, скажем сила тяжести, обладающие замечательным
свойством — «консервативностью» (никаких политических идей, ничего
двусмысленного в этом понятии нет). Когда мы подсчитываем, какую работу
выполняет сила, двигая тело от одной точки к другой, то вообще работа зависит
от траектории; но в особых случаях эта зависимость пропадает. Если работа не
зависит от траектории, мы говорим, что сила консервативна. Иными словами, если
интеграл от произведения силы на приращения смещений между точками ![]() и
и ![]() (фиг. 14.2) один
раз вычислен вдоль кривой
(фиг. 14.2) один
раз вычислен вдоль кривой ![]() , а другой — вдоль кривой
, а другой — вдоль кривой ![]() , и оба раза
получается одинаковое количество джоулей, и если это выполнено для любой кривой,
соединяющей эту пару точек, и если это же справедливо для любой пари точек, то
говорят, что сила консервативна. В таких обстоятельствах интеграл работы между
точками
, и оба раза
получается одинаковое количество джоулей, и если это выполнено для любой кривой,
соединяющей эту пару точек, и если это же справедливо для любой пари точек, то
говорят, что сила консервативна. В таких обстоятельствах интеграл работы между
точками ![]() и
и
![]() можно
легко подсчитать и дать для него формулу. А в других случаях это не так просто:
нужно задавать еще форму кривой; но когда работа не зависит от кривой, то,
ясное дело, остается только зависимость от положений точек
можно
легко подсчитать и дать для него формулу. А в других случаях это не так просто:
нужно задавать еще форму кривой; но когда работа не зависит от кривой, то,
ясное дело, остается только зависимость от положений точек ![]() и
и ![]() .
.

Фигура 14.2. Возможные пути, соединяющие две точки в поле сил.
Чтобы доказать это, рассмотрим фиг.
14.2. Фиксируем произвольную точку ![]() . Криволинейный интеграл работы на
участке
. Криволинейный интеграл работы на
участке ![]() можно
вычислить, разбив его на две части: работу на участке
можно
вычислить, разбив его на две части: работу на участке ![]() и работу на участке
и работу на участке ![]() , потому что
сейчас у нас всюду консервативные силы, и по какому пути ни пойти, значение
работы одно и то же. Работа перемещения из точки
, потому что
сейчас у нас всюду консервативные силы, и по какому пути ни пойти, значение
работы одно и то же. Работа перемещения из точки ![]() в любую точку пространства является
функцией положения конечной точки. Она зависит и от
в любую точку пространства является
функцией положения конечной точки. Она зависит и от ![]() , но мы во всем дальнейшем
анализе точку
, но мы во всем дальнейшем
анализе точку ![]() закрепим,
так что работа перемещения тела от точки
закрепим,
так что работа перемещения тела от точки ![]() к точке
к точке ![]() будет некоторой функцией
положения точки
будет некоторой функцией
положения точки ![]() .
Она зависит от того, где находится точка
.
Она зависит от того, где находится точка ![]() ; если переместить тело в другую
точку, ответ будет другой.
; если переместить тело в другую
точку, ответ будет другой.
Обозначим
эту функцию положения через ![]() ; желая отметить, что речь идет
именно о точке
; желая отметить, что речь идет
именно о точке ![]() с
координатами
с
координатами ![]() ,
мы будем просто писать
,
мы будем просто писать ![]() , сокращая обозначение
, сокращая обозначение ![]() . Работу
перемещения из точки
. Работу
перемещения из точки ![]() в точку
в точку ![]() можно написать, обратив
направление интегрирования (переменив знаки всех
можно написать, обратив
направление интегрирования (переменив знаки всех ![]() ). Другими словами, работа на участке
). Другими словами, работа на участке
![]() равна
работе на участке
равна
работе на участке ![]() со знаком минус:
со знаком минус:
 .
.
Значит,
работа на участке ![]() есть
есть ![]() участке
участке ![]() есть
есть ![]() . Поэтому интеграл от
. Поэтому интеграл от ![]() до
до ![]() равен
равен ![]() плюс [
плюс [![]() назад], т. в.
назад], т. в. ![]() :
:
 ,
,
 . (14.1)
. (14.1)
Величина
![]() называется
изменением потенциальной энергии, а
называется
изменением потенциальной энергии, а ![]() можно назвать потенциальной
энергией. Мы будем говорит, что когда предмет находится в положении
можно назвать потенциальной
энергией. Мы будем говорит, что когда предмет находится в положении ![]() , то он обладает
потенциальной энергией
, то он обладает
потенциальной энергией ![]() , а в положении
, а в положении ![]() — потенциальной энергией
— потенциальной энергией ![]() . Когда он
находится в положении
. Когда он
находится в положении ![]() , его потенциальная энергия равна
нулю. Если бы вместо
, его потенциальная энергия равна
нулю. Если бы вместо ![]() взять любую другую точку
взять любую другую точку ![]() , то оказалось бы
(это предоставляется доказать вам самим), что потенциальная энергия всех точек
изменилась бы только на постоянную добавку. Так как сохранение энергии зависит
только от изменений ее, то эта добавочная постоянная никакого значения не
имеет. Вот поэтому точка
, то оказалось бы
(это предоставляется доказать вам самим), что потенциальная энергия всех точек
изменилась бы только на постоянную добавку. Так как сохранение энергии зависит
только от изменений ее, то эта добавочная постоянная никакого значения не
имеет. Вот поэтому точка ![]() произвольна.
произвольна.
Итак, у
нас имеются два утверждения: 1) работа, выполняемая силой, равна изменению
кинетической энергии системы, но 2) математически для консервативных сил
выполненная работа равна минус изменению функции ![]() называемой потенциальной энергией.
Как следствие этих утверждений возникает еще одно: если действуют только консервативные
силы, сумма потенциальной
называемой потенциальной энергией.
Как следствие этих утверждений возникает еще одно: если действуют только консервативные
силы, сумма потенциальной ![]() и кинетической
и кинетической ![]() энергий остается
постоянной:
энергий остается
постоянной:
![]() . (14.2)
. (14.2)
Рассмотрим формулу потенциальной энергии для ряда случаев. Если поле тяготения однородно, если мы не поднимаемся до высот, сравнимых с радиусом Земли, то сила постоянна и направлена вертикально, а работа равна просто произведению силы на расстояние по вертикали. Стало быть,
![]() , (14.3)
, (14.3)
и за
точку ![]() с
нулевой потенциальной энергией можно принять любую точку на поверхности
с
нулевой потенциальной энергией можно принять любую точку на поверхности ![]() . Но можно также
говорить, что потенциальная энергия равна
. Но можно также
говорить, что потенциальная энергия равна ![]() , если нам так уж этого хочется! Все
результаты в нашем анализе останутся теми же, кроме того что потенциальная
энергия на поверхности
, если нам так уж этого хочется! Все
результаты в нашем анализе останутся теми же, кроме того что потенциальная
энергия на поверхности ![]() будет равна
будет равна ![]() . Разницы никакой, ведь в
расчет надо принимать только разности потенциальных энергий.
. Разницы никакой, ведь в
расчет надо принимать только разности потенциальных энергий.
Энергия,
необходимая для сжатия пружины на расстояние ![]() от точки равновесия, равна
от точки равновесия, равна
![]() , (14.4)
, (14.4)
и нуль
потенциальной энергии приходится на точку ![]() , т. е. на равновесное состояние
пружины. И здесь тоже мы можем добавить любую константу.
, т. е. на равновесное состояние
пружины. И здесь тоже мы можем добавить любую константу.
Потенциальная
энергия тяготения точечных масс ![]() и
и ![]() на расстоянии
на расстоянии ![]() друг от друга равна
друг от друга равна
![]() . (14.5)
. (14.5)
Константа здесь выбрана так, чтобы потенциал исчезал на бесконечности. Конечно, эту же формулу можно применить и к электрическим зарядам, поскольку закон один и тот же:
![]() . (14.6)
. (14.6)
Давайте теперь поработаем с одной из этих формул, посмотрим, поняли ли мы их смысл.
Вопрос: С какой скоростью должна отправиться ракета с Земли, чтобы покинуть ее?
Ответ: Сумма кинетической и потенциальной
энергий должна быть постоянной; покинуть Землю — значит удалиться от нее на
миллионы километров; если у ракеты только-только хватает сил, чтобы покинуть
Землю, то надо предположить, что там, вдалеке, ее скорость будет равна нулю и
что на бесконечности она будет едва-едва двигаться. Пусть ![]() — радиус Земли, а
— радиус Земли, а ![]() — ее масса.
Кинетическая плюс потенциальная энергии первоначально были равны
— ее масса.
Кинетическая плюс потенциальная энергии первоначально были равны ![]() . В конце
движения эти обе энергии должны сравниться. Кинетическую энергию в конце движения
мы считаем нулевой, потому что тело еле движется (почти с нулевой скоростью), а
потенциальная энергия равна величине
. В конце
движения эти обе энергии должны сравниться. Кинетическую энергию в конце движения
мы считаем нулевой, потому что тело еле движется (почти с нулевой скоростью), а
потенциальная энергия равна величине ![]() , деленной на бесконечность, т. е.
опять нулевая. Значит, с одной стороны стоит разность двух нулей; поэтому
квадрат скорости должен быть равен
, деленной на бесконечность, т. е.
опять нулевая. Значит, с одной стороны стоит разность двух нулей; поэтому
квадрат скорости должен быть равен ![]() . Но
. Но ![]() это как раз то, что называют
ускорением силы тяжести
это как раз то, что называют
ускорением силы тяжести ![]() . Итак,
. Итак,
![]() .
.
С какой
скоростью должен двигаться искусственный спутник, чтобы не падать на Землю? Мы
когда-то решали эту задачу и получили ![]() . Значит, чтобы покинуть Землю, нужна
скорость, в
. Значит, чтобы покинуть Землю, нужна
скорость, в ![]() большая,
чем скорость вращения спутника вокруг Земли. Иными словами, чтобы улететь с
Земли, нужно вдвое больше энергии (энергия пропорциональна квадрату скорости),
чем чтобы облететь вокруг нее. Поэтому исторически сначала были совершены
облеты искусственных спутников вокруг Земли, для чего понадобились скорости
около
большая,
чем скорость вращения спутника вокруг Земли. Иными словами, чтобы улететь с
Земли, нужно вдвое больше энергии (энергия пропорциональна квадрату скорости),
чем чтобы облететь вокруг нее. Поэтому исторически сначала были совершены
облеты искусственных спутников вокруг Земли, для чего понадобились скорости
около ![]() . И
только потом космические корабли были заброшены в мировое пространство; для
этого потребовалось уже вдвое больше энергии, т. е. скорости около
. И
только потом космические корабли были заброшены в мировое пространство; для
этого потребовалось уже вдвое больше энергии, т. е. скорости около ![]() .
.
Продолжим
теперь наш обзор характеристик потенциальной энергии. Давайте рассмотрим
взаимодействие двух молекул или двух атомов, например двух атомов кислорода.
Когда они находятся далеко друг от друга, они притягиваются с силой, обратно
пропорциональной седьмой степени расстояния, а при тесном сближении они сильно
отталкиваются. Проинтегрировав минус седьмую степень расстояния, чтобы получить
работу, мы увидим, что потенциальная энергия ![]() (функция расстояния между атомами
кислорода) изменяется как минус шестая степень расстояния (на больших
расстояниях).
(функция расстояния между атомами
кислорода) изменяется как минус шестая степень расстояния (на больших
расстояниях).
Если мы
чертим некую кривую потенциальной энергии ![]() (фиг. 14.3), то при больших
(фиг. 14.3), то при больших ![]() она выглядит как
она выглядит как ![]() , а при достаточно
малых
, а при достаточно
малых ![]() достигает
минимума. Минимум потенциальной энергии в точке
достигает
минимума. Минимум потенциальной энергии в точке ![]() означает, что если мы сдвинемся от
нее на малое расстояние, на очень малое расстояние, то произведенная работа, равная
изменению потенциальной энергии на этом промежутке, почти равна нулю, потому
что на донышке кривой энергия почти не меняется. Значит, в этой точке сила
равна нулю, и это есть точка равновесия. Условие равновесия можно высказать и
иначе: для удаления из точки равновесия в любую сторону нужно затратить работу.
Когда два атома кислорода расположены так, что никакой энергии из их силы
взаимодействия больше выжать нельзя, то они находятся в наинизшем
энергетическом состоянии и промежуток между ними равен
означает, что если мы сдвинемся от
нее на малое расстояние, на очень малое расстояние, то произведенная работа, равная
изменению потенциальной энергии на этом промежутке, почти равна нулю, потому
что на донышке кривой энергия почти не меняется. Значит, в этой точке сила
равна нулю, и это есть точка равновесия. Условие равновесия можно высказать и
иначе: для удаления из точки равновесия в любую сторону нужно затратить работу.
Когда два атома кислорода расположены так, что никакой энергии из их силы
взаимодействия больше выжать нельзя, то они находятся в наинизшем
энергетическом состоянии и промежуток между ними равен ![]() . Так выглядит молекула кислорода, когда она но нагрета. При
нагревании атомы колеблются и расходятся; их можно и совсем развести, но для
этого нужно определенное количество работы или энергии, равное разности
потенциальных энергий в точках
. Так выглядит молекула кислорода, когда она но нагрета. При
нагревании атомы колеблются и расходятся; их можно и совсем развести, но для
этого нужно определенное количество работы или энергии, равное разности
потенциальных энергий в точках ![]() и
и ![]() . При попытке сблизить атомы энергия
быстро возрастает вследствие их взаимного отталкивания.
. При попытке сблизить атомы энергия
быстро возрастает вследствие их взаимного отталкивания.

Фигура 14.3. Потенциальная энергия взаимодействия двух атомов как функция расстояния между ними.
Почему мы говорим о потенциальной энергии? Потому что идея силы не очень пригодна для квантовой механики, тем более естественна идея энергии. Когда мы рассматриваем более сложные взаимодействия: ядерного вещества, молекул и т. д., то, хотя понятия силы и скорости «рассасываются» и исчезают, оказывается, что понятие энергии все же остается. Поэтому в книгах по квантовой механике мы находим кривые потенциальной энергии, но очень редко увидим график силы взаимодействия двух молекул, потому что те, кто изучает эти явления, больше уже привыкли думать об энергии, чем о силе.
Заметим еще, что, когда на тело одновременно действуют несколько консервативных сил, потенциальная энергия тела есть сумма потенциальных энергий от каждой силы. Это то, что мы утверждали и раньше, потому что, когда сила представляется векторной суммой сил, работа, производимая ею, равна сумме работ, производимых отдельными силами; поэтому ее можно представить как изменения потенциальных энергий от каждой силы но отдельности. Значит, общая потенциальная энергия равна сумме всех частей.
Мы можем
обобщить это на случай системы многих тел, как, например, Юпитера, Сатурна,
Урана и т. д. или атомов кислорода, азота, углерода и т. д., взаимодействующих
друг с другом попарно, причем силы взаимодействия каждой пары консервативны. В
таких условиях кинетическая энергия всей системы есть просто сумма кинетических
энергий всех отдельных атомов, или планет, или частиц, а потенциальная энергия
системы есть сумма потенциальных энергий взаимодействия отдельных пар,
рассчитанных в предположении, что других частиц нет. (На самом деле для
молекулярных сил это неверно, и формула получается несколько сложнее; для
ньютонова тяготения это определенно справедливо, а для молекулярных сил годится
лишь как приближение» Можно, конечно, говорить о потенциальной энергии
молекулярных сил, но она иногда оказывается более сложной функцией положений
атомов, чем простая сумма попарных взаимодействий.) Поэтому потенциальная
энергия в частном случае тяготения представляется суммой по всем парам ![]() и
и ![]() членов
членов ![]() [как было
показано в уравнении (13.14)]. Уравнение (13.14) выражает математически
следующее предложение: общая потенциальная плюс общая кинетическая энергии не
меняются со временем. Пусть себе различные планеты вращаются, обращаются и
покачиваются, все равно если подсчитать общую потенциальную и общую
кинетическую энергии, то окажется, что их сумма всегда остается постоянной.
[как было
показано в уравнении (13.14)]. Уравнение (13.14) выражает математически
следующее предложение: общая потенциальная плюс общая кинетическая энергии не
меняются со временем. Пусть себе различные планеты вращаются, обращаются и
покачиваются, все равно если подсчитать общую потенциальную и общую
кинетическую энергии, то окажется, что их сумма всегда остается постоянной.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
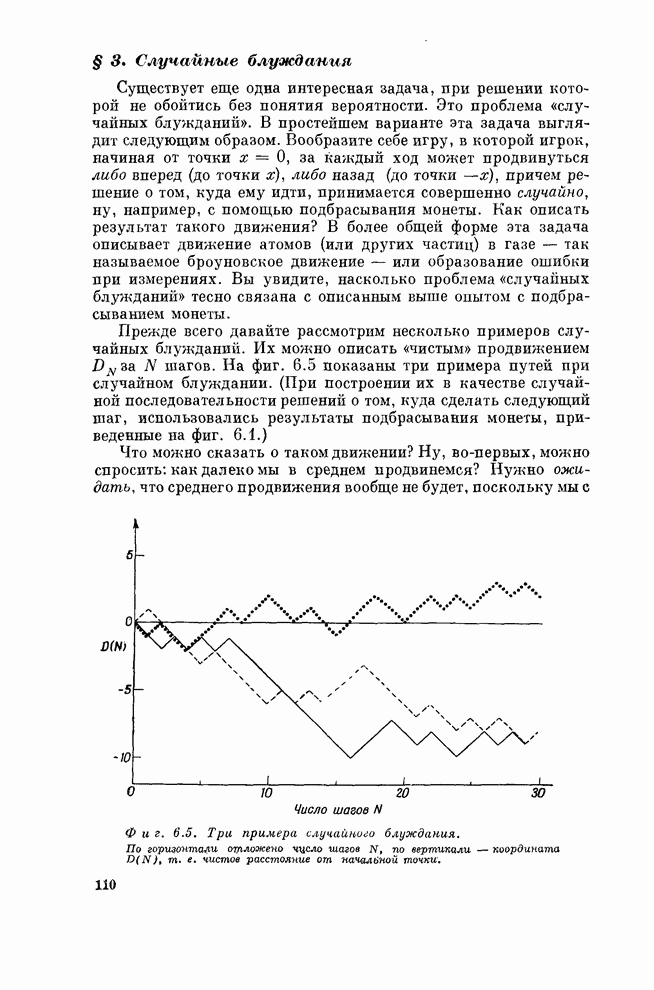
- § 3. Случайные блуждания
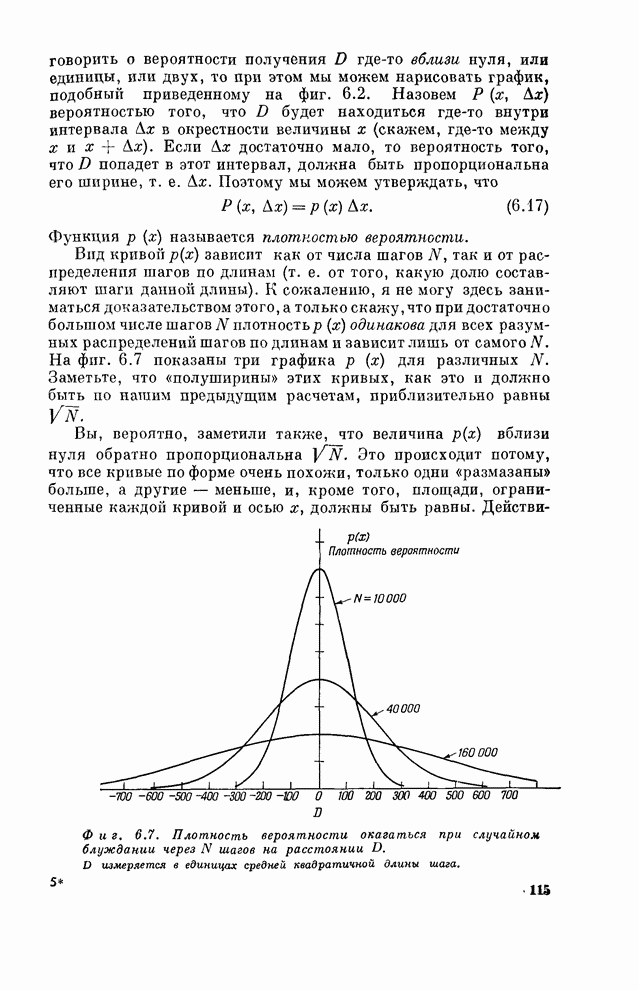
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
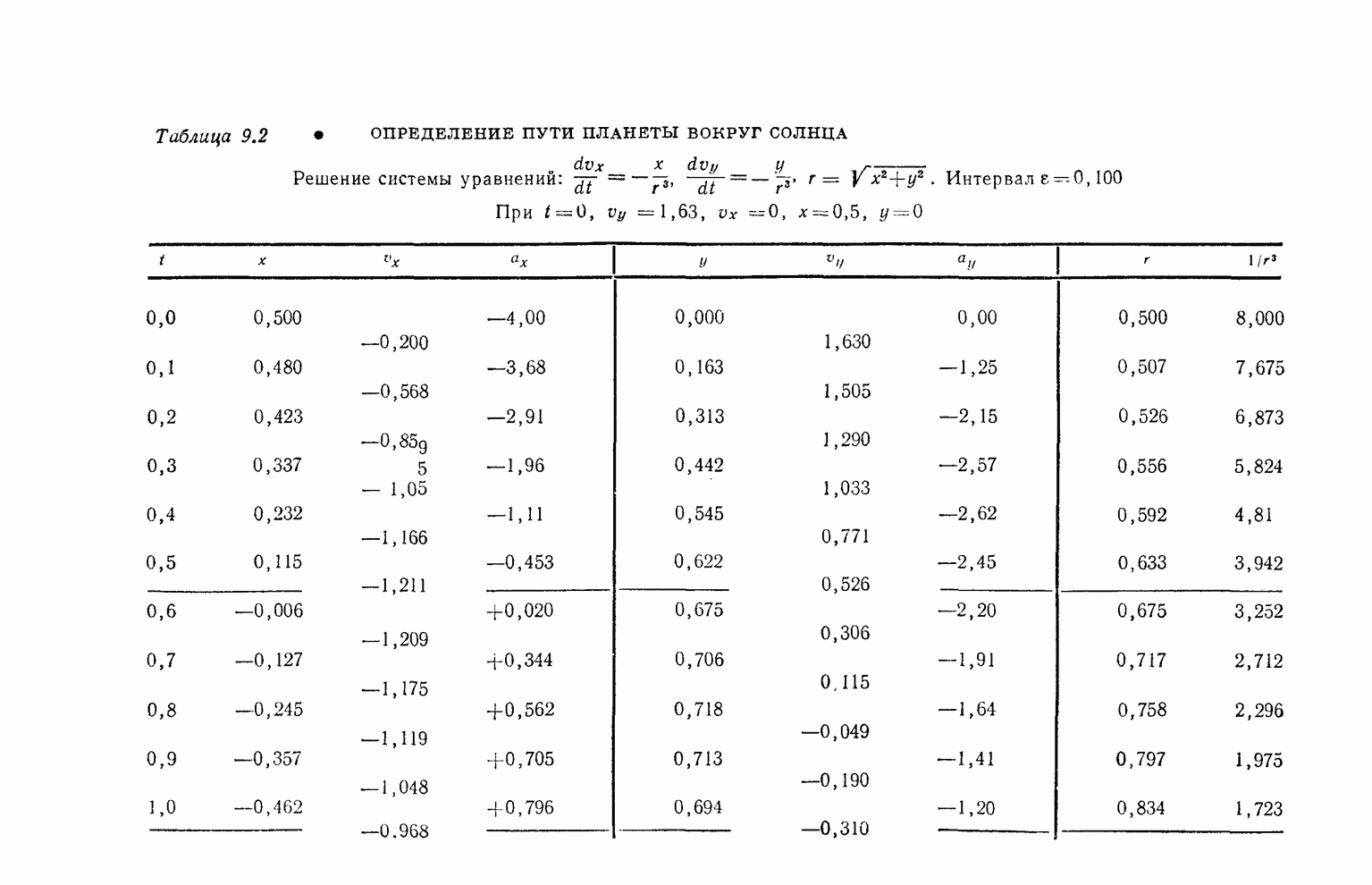
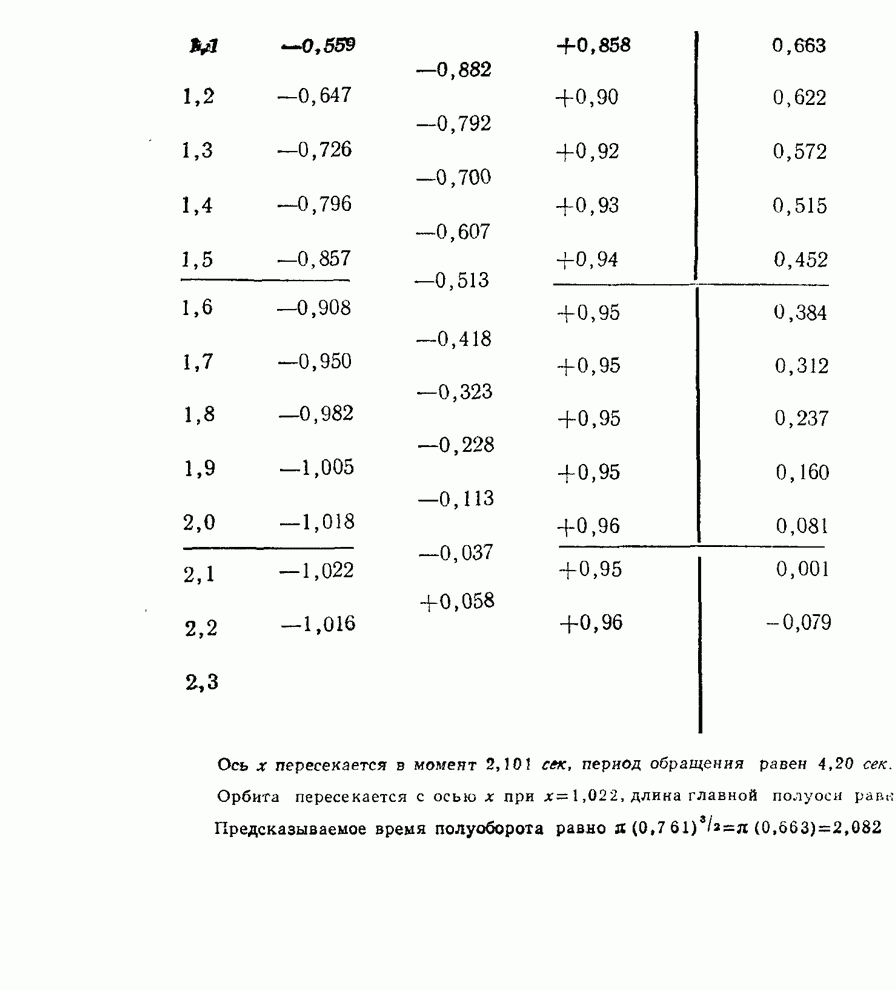
- § 5. Численное решение уравнений
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля