| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.6. Векторный фильтр Калмана
Возможности применения рассматриваемых методов калмановской фильтрации значительно расширяются при переходе к многомерным системам. Вместе с тем для получения основных уравнений рекуррентного оценивания векторных СП достаточно повторить преобразования, уже выполненные при выводе алгоритма (2.35). Поэтому остановимся лишь на некоторых особенностях синтеза многомерного фильтра.
Для описания ![]() -мерной информационной СП воспользуемся
векторным авторегрессионным уравнением (1.48):
-мерной информационной СП воспользуемся
векторным авторегрессионным уравнением (1.48): ![]() .
.
Оценка СП ![]() производится на основе анализа
последовательности
производится на основе анализа
последовательности ![]() - мерных наблюдений
- мерных наблюдений
![]() (2.38)
(2.38)
где ![]() -матрица;
-матрица;
![]() -мерная
некоррелированная гауссовская СП с нулевым средним и
-мерная
некоррелированная гауссовская СП с нулевым средним и ![]() .
.
Записывая рекуррентную процедуру формирования оценки в виде
![]() аналогичном
(2.33), найдем следующее выражение для ошибки фильтрации
аналогичном
(2.33), найдем следующее выражение для ошибки фильтрации ![]() , где
, где ![]() – единичная диагональная
матрица. Оптимизация оценки связана с поиском матриц
– единичная диагональная
матрица. Оптимизация оценки связана с поиском матриц ![]() , для которых минимальна
ковариационная матрица
, для которых минимальна
ковариационная матрица ![]() ошибок фильтрации:
ошибок фильтрации:
![]() , (2.39)
, (2.39)
где ![]() -матрица;
-матрица;
![]() . Анализ
(2.39) показывает, что наилучшим является выбор
. Анализ
(2.39) показывает, что наилучшим является выбор ![]() . Обозначая минимальное значение
. Обозначая минимальное значение ![]() через
через ![]() , можно записать
уравнение для рекуррентной оценки CП в виде:
, можно записать
уравнение для рекуррентной оценки CП в виде:
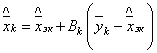 , (2.40)
, (2.40)
![]() ,
,
где ![]()
![]() .
.
Применение алгоритма (2.40) предполагает нахождение
обратной матрицы ![]() размером
размером
![]() на каждом
шаге фильтрации. В некоторых случаях удобно использовать другую форму
представления коэффициентов
на каждом
шаге фильтрации. В некоторых случаях удобно использовать другую форму
представления коэффициентов
![]() , (2.41)
, (2.41)
для которой размер обращаемой матрицы составляет ![]() элементов. С помощью
непосредственной подстановки нетрудно убедиться в тождественности вычислений
матриц
элементов. С помощью
непосредственной подстановки нетрудно убедиться в тождественности вычислений
матриц ![]() и
и ![]() по формулам (2.40) и
(2.41).
по формулам (2.40) и
(2.41).
Полученные результаты (2.40), (2.41) обобщают алгоритм фильтрации
(2.35), (2.36) скалярной последовательности. Сравнение этих выражений
показывает, что структура фильтра Калмана и наиболее существенные
особенности процесса рекуррентного оценивания сохраняются и в многомерном
случае. В частности, разность 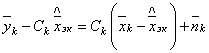 следует рассматривать как векторный сигнал
ошибки, который взвешивается с учетом соотношения элементов ковариационных
матриц ошибок фильтрации
следует рассматривать как векторный сигнал
ошибки, который взвешивается с учетом соотношения элементов ковариационных
матриц ошибок фильтрации ![]() и помехи
и помехи ![]() и добавляется к прогнозированному
значению
и добавляется к прогнозированному
значению ![]() оцениваемого
оцениваемого
![]() -мерного
параметра
-мерного
параметра![]() .
.
В заключение рассмотрим задачу рекуррентного оценивания
изменяющегося параметра ![]() , заданного уравнениями
, заданного уравнениями
![]() , (2.42)
, (2.42)
аналогичными (2.32). При этой оценка параметра ![]() осуществляется на основе
наблюдений
осуществляется на основе
наблюдений ![]() .
Для решения поставленной задачи введем вектор информационных параметров
.
Для решения поставленной задачи введем вектор информационных параметров ![]() и запишем модель
наблюдений в виде:
и запишем модель
наблюдений в виде: ![]() ,
где
,
где ![]() .
Уравнения (2.42) также представим в векторной форме
.
Уравнения (2.42) также представим в векторной форме ![]() , где
, где ![]() ;
; ![]() ;
; 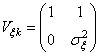 .
.
Введенные обозначения дают возможность применить формулы (2.40)
для построения алгоритма фильтрации CП ![]() . Раскрывая векторные обозначения в (2.40),
можно представить рекуррентные оценки параметров в виде:
. Раскрывая векторные обозначения в (2.40),
можно представить рекуррентные оценки параметров в виде:
![]() ,
,
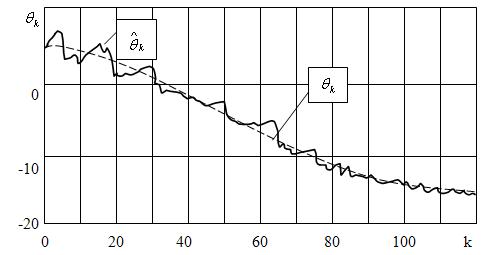
Рис. 2.7. Реализации случайных последовательностей
где ![]() и
и
![]() – элементы
ковариационной матрицы ошибок
– элементы
ковариационной матрицы ошибок 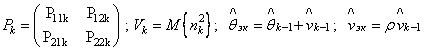 . Характерные реализации СП
. Характерные реализации СП ![]() и
и ![]() , полученные с помощью вычислений
по найденным формулам при
, полученные с помощью вычислений
по найденным формулам при ![]() , приведены на рис. 2.7. По мере увеличения
количества шагов оценивания
, приведены на рис. 2.7. По мере увеличения
количества шагов оценивания ![]() дисперсии ошибок фильтрации (2.40) убывают
так же, как и в одномерном случае (рис.2.5,а), стремясь к некоторым
предельным значениям.
дисперсии ошибок фильтрации (2.40) убывают
так же, как и в одномерном случае (рис.2.5,а), стремясь к некоторым
предельным значениям.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1.2. Случайные величины
- 1.2. Случайные величины
- 1.3. Системы случайных величин
- 1.3. Системы случайных величин
- 1.4. Функции случайных аргументов
- 1.4. Функции случайных аргументов
- 1.5. Марковские последовательности
- 1.5. Марковские последовательности
- 2. Оценивание параметров сигналов
- 2. Оценивание параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.3. Метод моментов
- 2.3. Метод моментов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.5. Скалярный фильтр Калмана
- 2.5. Скалярный фильтр Калмана
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.2. Критерий Байеса
- 3.2. Критерий Байеса
- 3.3. Критерий Неймана-Пирсона
- 3.3. Критерий Неймана-Пирсона
- 3.4. Вычисление вероятностей ошибок
- 3.4. Вычисление вероятностей ошибок
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- Список литературы
- Список литературы
