| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Метод моментов
При неизвестных параметрах ![]() начальные моменты распределения являются
функциями
начальные моменты распределения являются
функциями ![]() :
:
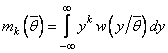 .
.
Вместе с тем, на основе наблюдений ![]() могут быть найдены выборочные начальные
моменты
могут быть найдены выборочные начальные
моменты ![]() -го
порядка
-го
порядка
![]() ,
,
которые служат состоятельными оценками моментов распределения ![]() .
.
Метод моментов заключается в приравнивании ![]() выборочных моментов
к соответствующим моментам распределения и нахождении оценок неизвестных
параметров из системы уравнений:
выборочных моментов
к соответствующим моментам распределения и нахождении оценок неизвестных
параметров из системы уравнений:
![]() .
.
Кроме начальных моментов, для оценок параметров могут использоваться центральные моменты распределения и выборочные центральные моменты:
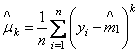 .
.
Для некоторых распределений, например, нормального или
экспоненциального, оценки параметров, найденные с помощью метода моментов,
совпадают с соответствующими ОМП. Вместе с тем имеются многочисленные
задачи, в которых метод моментов приводит к худшим по точности оценкам, чем
метод максимального правдоподобия. Характерным примером является оценка
параметра ![]() равномерного
распределения
равномерного
распределения ![]() .
Для нахождения этой оценки на основе метода моментов приравняем
математическое ожидание (первый начальный момент)
.
Для нахождения этой оценки на основе метода моментов приравняем
математическое ожидание (первый начальный момент) ![]() и выборочное среднее
и выборочное среднее ![]() . В результате получаем
несмещенную оценку
. В результате получаем
несмещенную оценку ![]() с
дисперсией
с
дисперсией 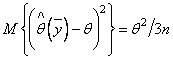 .
Заметим, что найденное значение в
.
Заметим, что найденное значение в ![]() раз больше дисперсии (2.27) оценки
максимального правдоподобия. Приведенный результат подчеркивает
целесообразность поиска эффективных оценок с помощью метода максимального
правдоподобия. Однако встречаются примеры, где решение уравнений правдоподобия
найти не удается, но можно получить хорошие оценки по методу моментов.
Рассмотрим два таких примера.
раз больше дисперсии (2.27) оценки
максимального правдоподобия. Приведенный результат подчеркивает
целесообразность поиска эффективных оценок с помощью метода максимального
правдоподобия. Однако встречаются примеры, где решение уравнений правдоподобия
найти не удается, но можно получить хорошие оценки по методу моментов.
Рассмотрим два таких примера.
Пусть требуется оценить параметры ![]() и
и ![]() гамма-распределения (табл. 1.1).
Приравнивая моменты распределения
гамма-распределения (табл. 1.1).
Приравнивая моменты распределения ![]() и
и ![]() к первому
к первому ![]() и второму
и второму ![]() выборочным моментам, получаем
следующие оценки параметров по методу моментов:
выборочным моментам, получаем
следующие оценки параметров по методу моментов:
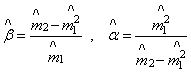 .
.
Проанализируем теперь возможности решения более сложной
задачи оценки двух параметров ![]() и
и ![]() распределения Вейбулла (табл. 1.1).
Как следует из табл.1.1, после приравнивания моментов распределения
распределения Вейбулла (табл. 1.1).
Как следует из табл.1.1, после приравнивания моментов распределения ![]() и
и ![]() к выборочным
к выборочным ![]() и
и ![]() получается система двух уравнений
относительно неизвестных оценок параметров
получается система двух уравнений
относительно неизвестных оценок параметров ![]() и
и ![]() , аналитическое решение которой не
представляется возможным.
, аналитическое решение которой не
представляется возможным.
Попытаемся подобрать функциональное преобразование
выборочных значений ![]() ,
приводящее к упрощению поставленной задачи оценивания. Заметим,
что двухпараметрический класс вейбулловских СВ
,
приводящее к упрощению поставленной задачи оценивания. Заметим,
что двухпараметрический класс вейбулловских СВ ![]() может быть получен с помощью
нелинейного преобразования
может быть получен с помощью
нелинейного преобразования ![]() СВ
СВ ![]() с экспоненциальным законом распределения:
с экспоненциальным законом распределения: ![]() . Такое преобразование
упрощается, если рассматривать прологарифмированные данные эксперимента, т.е.
ввести СВ
. Такое преобразование
упрощается, если рассматривать прологарифмированные данные эксперимента, т.е.
ввести СВ ![]() и
соответствующие наблюдения
и
соответствующие наблюдения ![]() . Но самое главное, что моменты
распределения
. Но самое главное, что моменты
распределения ![]() оказываются
довольно простыми функциями неизвестных параметров
оказываются
довольно простыми функциями неизвестных параметров ![]() и
и![]() . Действительно,
. Действительно,
![]() ;
;
![]() .
.
Используя таблицы интегралов [25], запишем:
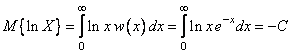 ,
,
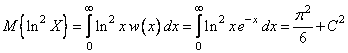 ,
,
где ![]() –
постоянная Эйлера [25]. С учетом приведенных табличных интегралов получаем
следующие выражения для моментов распределения логарифмов наблюдений:
–
постоянная Эйлера [25]. С учетом приведенных табличных интегралов получаем
следующие выражения для моментов распределения логарифмов наблюдений: ![]() .
.
Оценки ![]() теперь могут быть легко найдены из
системы двух уравнений
теперь могут быть легко найдены из
системы двух уравнений ![]() , где
, где ![]() и
и 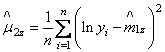 – выборочные моменты. После элементарных
преобразований решение системы уравнений для оценок параметров распределения
Вейбулла запишется в виде:
– выборочные моменты. После элементарных
преобразований решение системы уравнений для оценок параметров распределения
Вейбулла запишется в виде:
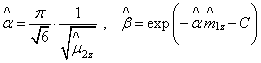 .
.
Полученные оценки могут использоваться, например, при построении классификатора типа помех в радиолокационном приемнике, поскольку распределение Вейбулла описывает широкий класс возможных помех в виде собственного шума приемника, отражений от местных предметов, гидрометеоров и др.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1.2. Случайные величины
- 1.2. Случайные величины
- 1.3. Системы случайных величин
- 1.3. Системы случайных величин
- 1.4. Функции случайных аргументов
- 1.4. Функции случайных аргументов
- 1.5. Марковские последовательности
- 1.5. Марковские последовательности
- 2. Оценивание параметров сигналов
- 2. Оценивание параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.3. Метод моментов
- 2.3. Метод моментов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.5. Скалярный фильтр Калмана
- 2.5. Скалярный фильтр Калмана
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.2. Критерий Байеса
- 3.2. Критерий Байеса
- 3.3. Критерий Неймана-Пирсона
- 3.3. Критерий Неймана-Пирсона
- 3.4. Вычисление вероятностей ошибок
- 3.4. Вычисление вероятностей ошибок
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- Список литературы
- Список литературы
