| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.38. Цифровые фильтры
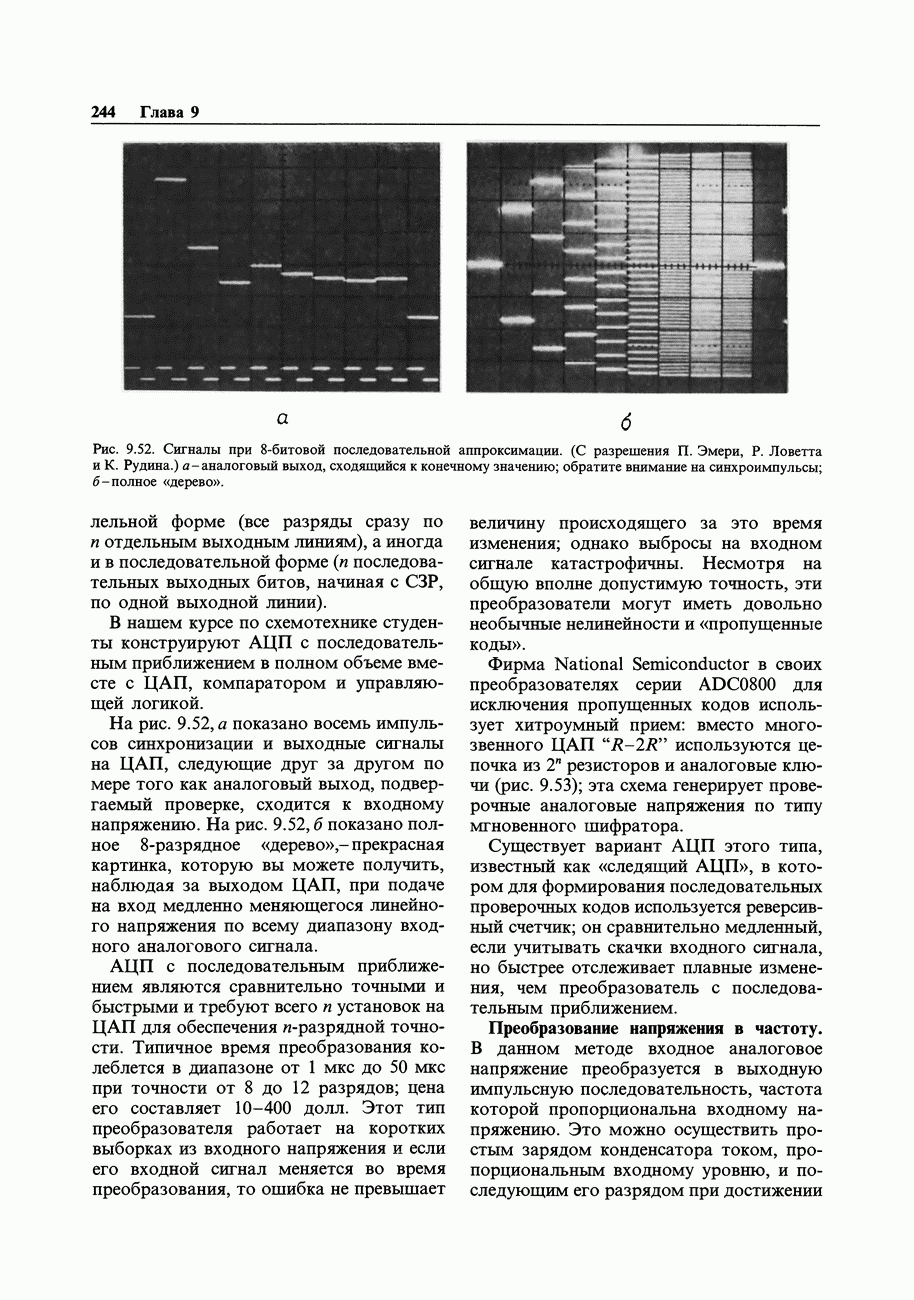
Последний пример затронул интересную тему цифровой фильтрации, в данном случае формирование НЧ-сигнала путем взвешенного суммирования 32 значений псевдослучайной последовательности, каждое из которых соответствует уровню напряжения 0 или  . На вход такого «фильтра» поступают сигналы, которые могут иметь только два уровня напряжения. Вообще говоря, то же самое можно сделать с аналоговым сигналом на входе, образуя взвешенную сумму его значений
. На вход такого «фильтра» поступают сигналы, которые могут иметь только два уровня напряжения. Вообще говоря, то же самое можно сделать с аналоговым сигналом на входе, образуя взвешенную сумму его значений  , распределенных во времени через равные интервалы
, распределенных во времени через равные интервалы

Здесь  являются дискретными выборками из входного сигнала,
являются дискретными выборками из входного сигнала,  - весовые коэффициенты, а
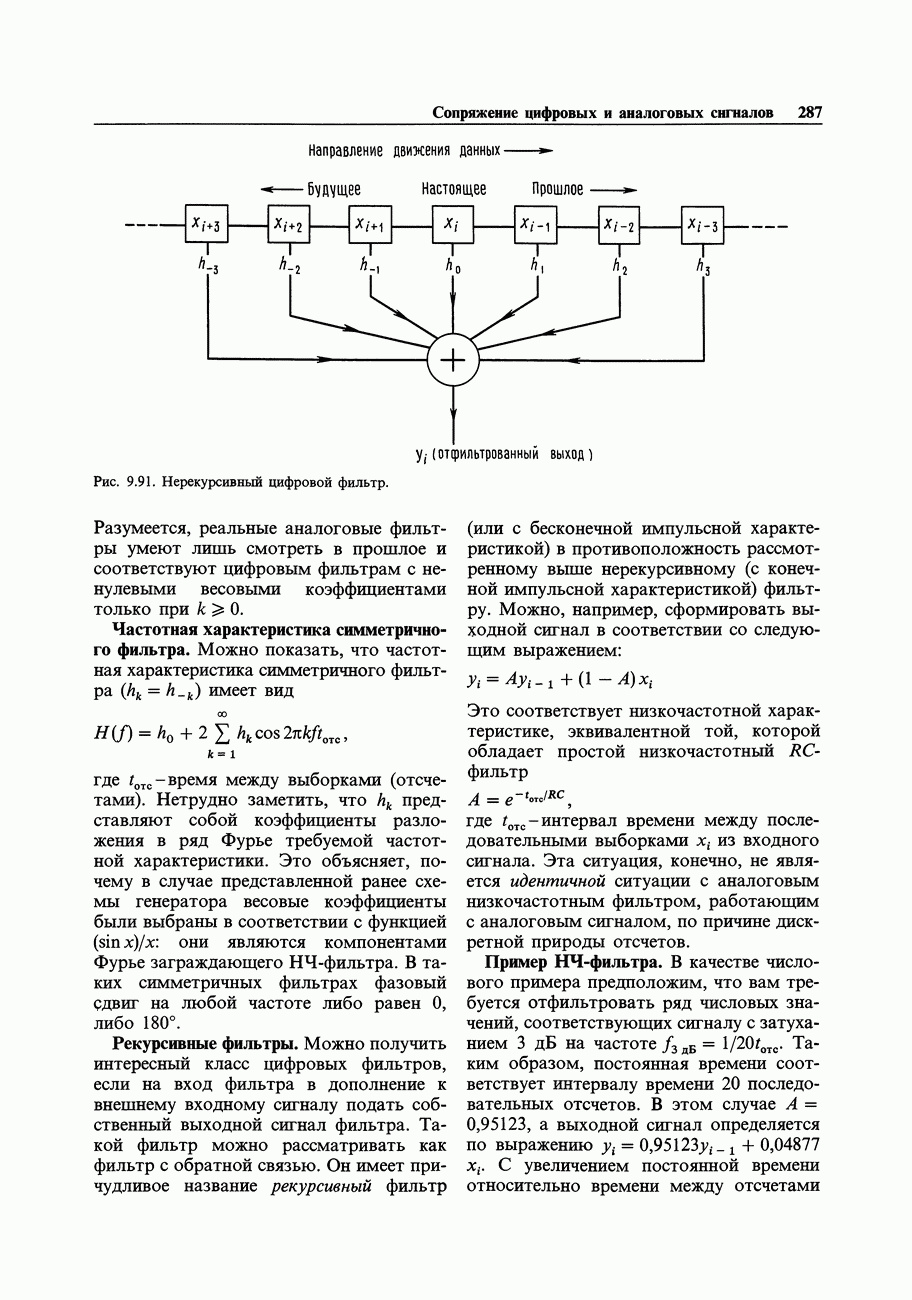
- весовые коэффициенты, а  - значения выходного сигнала. В реальных условиях цифровой фильтр будет суммировать только конечное множество входных значений, как, например, в генераторе шума, где было использовано 32 члена. На рис. 9.91 схематично показано, как это происходит.
- значения выходного сигнала. В реальных условиях цифровой фильтр будет суммировать только конечное множество входных значений, как, например, в генераторе шума, где было использовано 32 члена. На рис. 9.91 схематично показано, как это происходит.
Заметьте, что такой фильтр может обладать интересным свойством симметричности во времени, т. е. усреднением прошлого и будушего для того, чтобы сформировать текущее значение выхода.

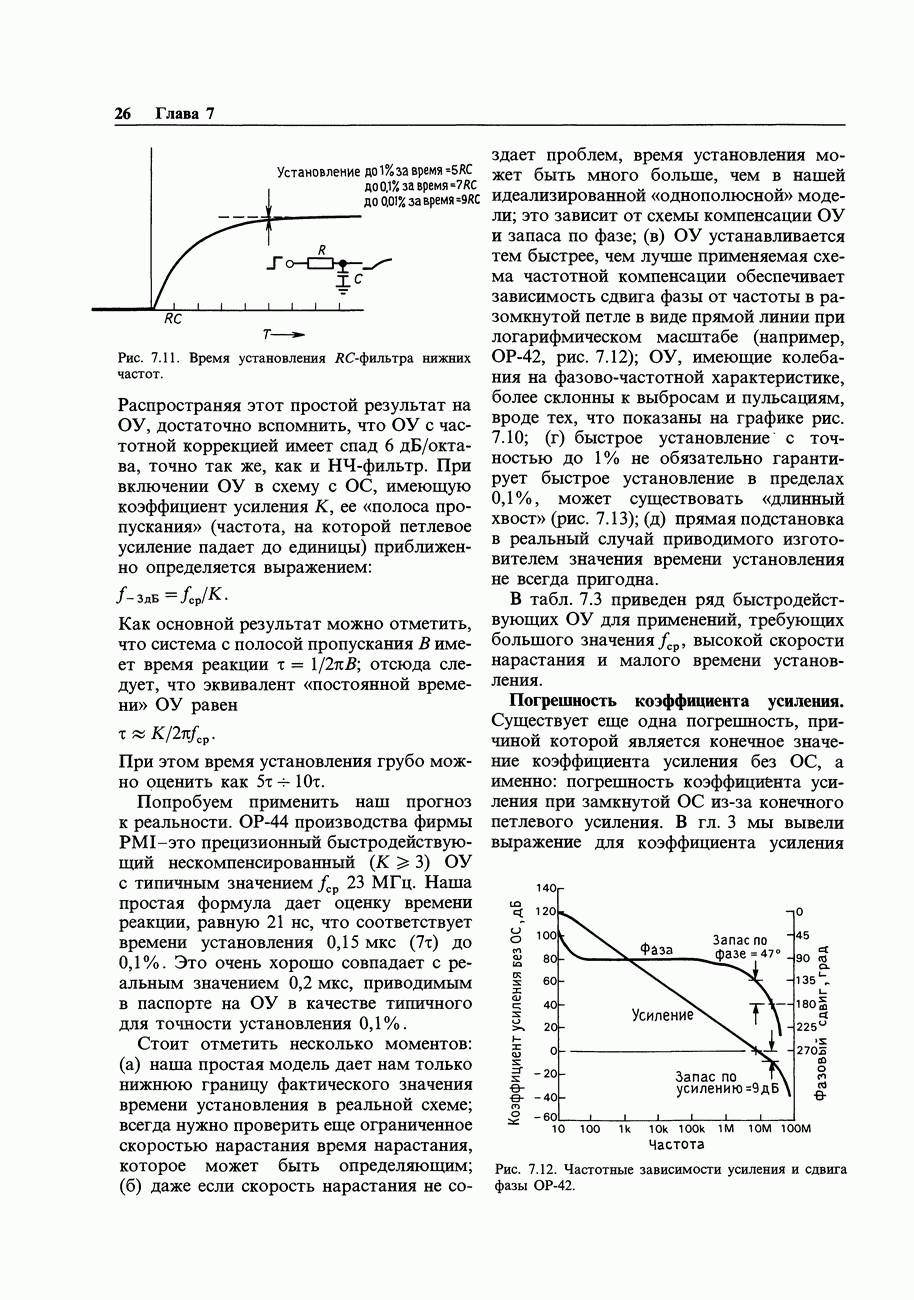
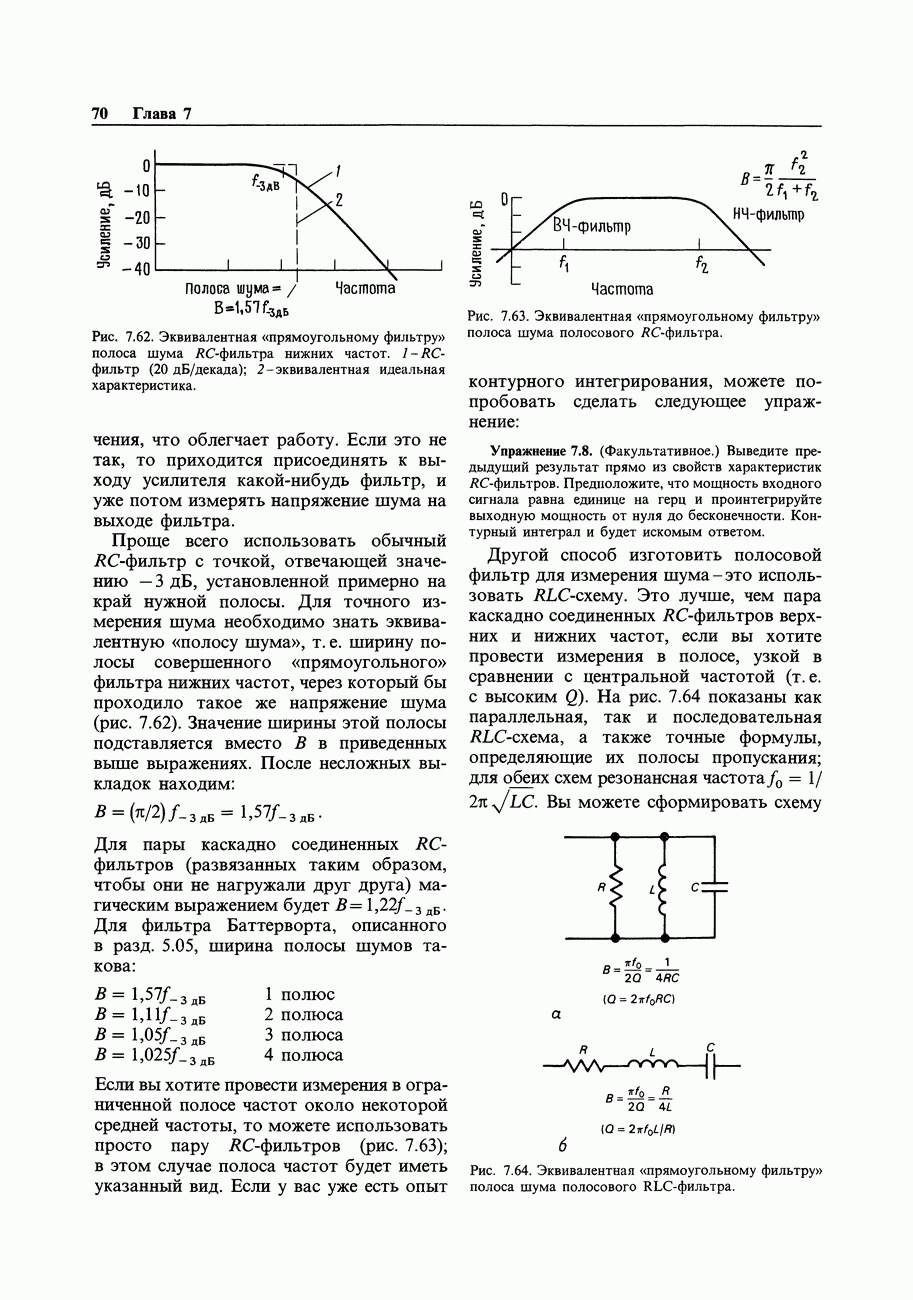
Рис. 9.91. Нерекурсивный цифровой фильтр.
Разумеется, реальные аналоговые фильтры умеют лишь смотреть в прошлое и соответствуют цифровым фильтрам с ненулевыми весовыми коэффициентами только при  .
.
Частотная характеристика симметричного фильтра.
Можно показать, что частотная характеристика симметричного фильтра имеет вид 00
имеет вид 00

где  - время между выборками (отсчетами). Нетрудно заметить, что
- время между выборками (отсчетами). Нетрудно заметить, что  представляют собой коэффициенты разложения в ряд Фурье требуемой частотной характеристики. Это объясняет, почему в случае представленной ранее схемы генератора весовые коэффициенты были выбраны в соответствии с функцией
представляют собой коэффициенты разложения в ряд Фурье требуемой частотной характеристики. Это объясняет, почему в случае представленной ранее схемы генератора весовые коэффициенты были выбраны в соответствии с функцией  они являются компонентами Фурье заграждающего НЧ-фильтра. В таких симметричных фильтрах фазовый Сдвиг на любой частоте либо равен 0, либо 180°.
они являются компонентами Фурье заграждающего НЧ-фильтра. В таких симметричных фильтрах фазовый Сдвиг на любой частоте либо равен 0, либо 180°.
Рекурсивные фильтры.
Можно получить интересный класс цифровых фильтров, если на вход фильтра в дополнение к внешнему входному сигналу подать собственный выходной сигнал фильтра. Такой фильтр можно рассматривать как фильтр с обратной связью. Он имеет причудливое название рекурсивный фильтр (или с бесконечной импульсной характеристикой) в противоположность рассмотренному выше нерекурсивному (с конечной импульсной характеристикой) фильтру. Можно, например, сформировать выходной сигнал в соответствии со следующим выражением:
Это соответствует низкочастотной характеристике, эквивалентной той, которой обладает простой низкочастотный  -фильтр
-фильтр

где  - интервал времени между последовательными выборками X; из входного сигнала. Эта ситуация, конечно, не является идентичной ситуации с аналоговым низкочастотным фильтром, работающим с аналоговым сигналом, по причине дискретной природы отсчетов.
- интервал времени между последовательными выборками X; из входного сигнала. Эта ситуация, конечно, не является идентичной ситуации с аналоговым низкочастотным фильтром, работающим с аналоговым сигналом, по причине дискретной природы отсчетов.
Пример НЧ-фильтра.
В качестве числового примера предположим, что вам требуется отфильтровать ряд числовых значений, соответствующих сигналу с затуханием 3 дБ на частоте . Таким образом, постоянная времени соответствует интервалу времени 20 последовательных отсчетов. В этом случае
. Таким образом, постоянная времени соответствует интервалу времени 20 последовательных отсчетов. В этом случае  а выходной сигнал определяется по выражению
а выходной сигнал определяется по выражению  .
.

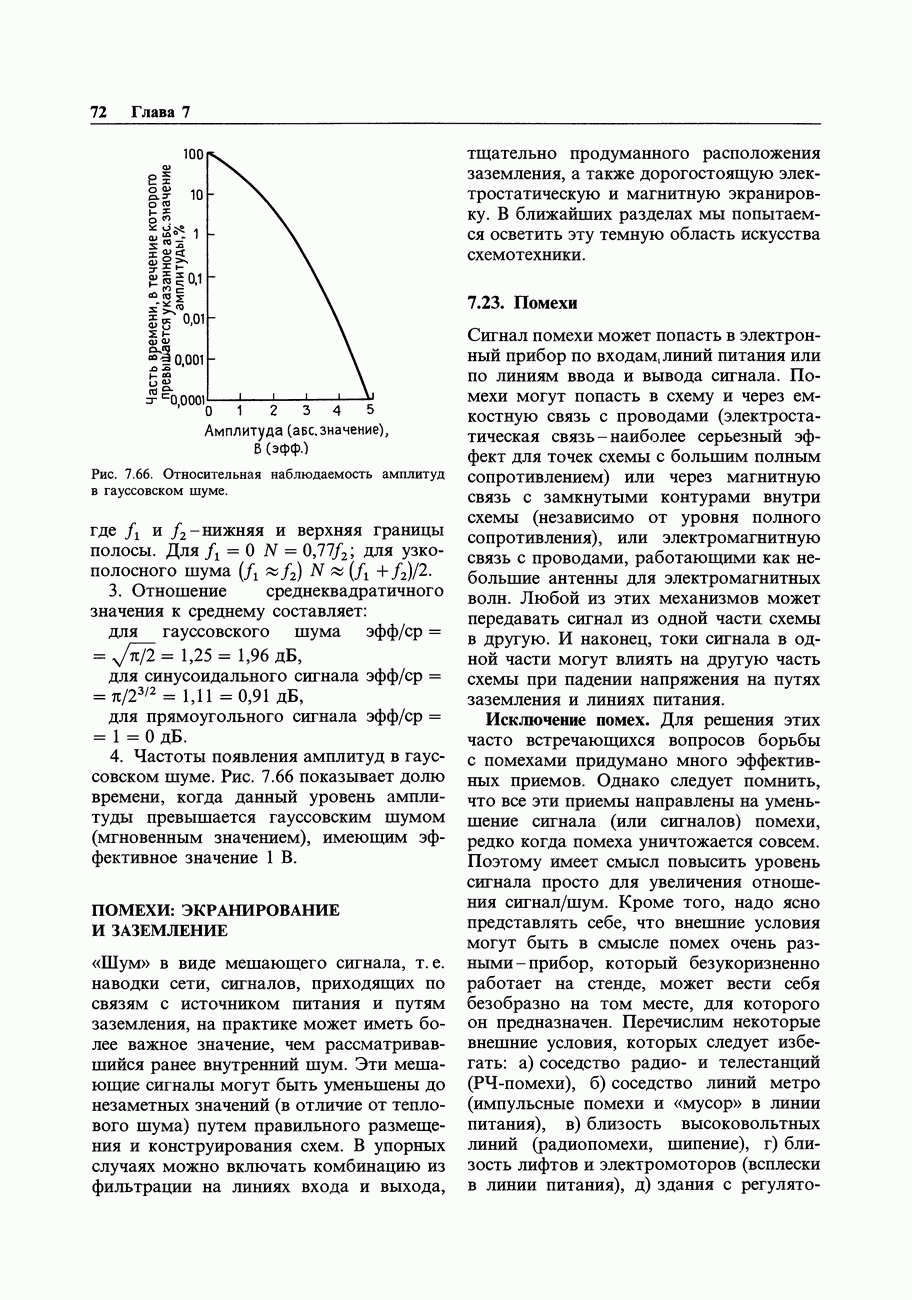
Рис. 9.92. Рекурсивный фильтр на коммутируемых конденсаторах.
С увеличением постоянной времени относительно времени между отсчетами  приближение к реальному НЧ-фильтру улучшается.
приближение к реальному НЧ-фильтру улучшается.
Для обработки данных уже представленных в виде дискретных отсчетов, как, например, массив данных в компьютере, вы, возможно, предпочтете использовать такой фильтр. Рекурсивный фильтр при этом будет реализовываться с помощью однократного прохода по данным с тривиальной арифметической обработкой. Программа НЧ-фильтра на языке Фортран будет выглядеть следующим образом:

где X - матрица данных,  -интервал времени между отсчетами (т. е.
-интервал времени между отсчетами (т. е.  ), а ТС - выбранная постоянная времени фильтра. Эта маленькая программа осуществляет фильтрацию на месте, т. е. она заменяет первоначальные данные отфильтрованными. Можно, конечно, создавать из отфильтрованных данных отдельный массив.
), а ТС - выбранная постоянная времени фильтра. Эта маленькая программа осуществляет фильтрацию на месте, т. е. она заменяет первоначальные данные отфильтрованными. Можно, конечно, создавать из отфильтрованных данных отдельный массив.
НЧ-фильтр с коммутацией.
Такой же фильтр можно построить аппаратным путем, используя схему, показанную на рис. 9.92. Ключи на полевых транзисторах коммутируются с некоторой тактовой частотой, периодически заряжая конденсатор
коммутируются с некоторой тактовой частотой, периодически заряжая конденсатор  до входного напряжения и затем передавая его заряд на конденсатор
до входного напряжения и затем передавая его заряд на конденсатор  . Если
. Если  имеет напряжение
имеет напряжение  заряжается до входного уровня
заряжается до входного уровня  , то при подключении
, то при подключении  напряжение на обоих конденсаторах будет определяться соотношением
напряжение на обоих конденсаторах будет определяться соотношением  , что эквивалентно рассмотренному ранее рекурсивному фильтру при
, что эквивалентно рассмотренному ранее рекурсивному фильтру при

Приравнивая эти коэффициенты к заданному ранее значению А, получим

Упражнение 9.8. Покажите, что этот результат правилен.
Этот фильтр практичен во всех отношениях и обладает одной привлекательной особенностью - электронной настройкой посредством тактовой частоты  . В обычных схемах используются КМОП-ключи, а емкость
. В обычных схемах используются КМОП-ключи, а емкость  берется много больше
берется много больше  . Поэтому сигнал переключения должен быть несимметричным и большую часть времени тратить на замыкание
. Поэтому сигнал переключения должен быть несимметричным и большую часть времени тратить на замыкание  .
.
Приведенная схема представляет собой простой пример фильтра с коммутацией; в этот класс фильтров входят фильтры, выполненные на матрицах коммутируемых конденсаторов. Они имеют периодическую частотную характеристику, что делает их удобными для использования в качестве гребенчатых и узкополосных режекторных фильтров.
Для всех фильтров классического типа (Баттерворта, Чебышева и т.п.) можно построить их приближенные дискретные аналоги в форме ВЧ, НЧ, полосовых и заграждающих фильтров, как симметричных во времени, так и с истинным временем запаздывания. Такие фильтры очень удобны при обработке квантованных данных, перед которыми, безусловно, большое будущее.
В настоящее время выпускают большое число недорогих ИМС фильтров с коммутируемыми конденсаторами. ИМС  фирмы National, например, является
фирмы National, например, является  -звенным НЧ-фильтром Баттерворта, размещенным в корпусе
-звенным НЧ-фильтром Баттерворта, размещенным в корпусе  он не требует внешних компонентов и работает от одного источника питания с напряжением от
он не требует внешних компонентов и работает от одного источника питания с напряжением от  до
до  . Частота среза фильтра (0,1 Гц мин. и
. Частота среза фильтра (0,1 Гц мин. и  макс.) устанавливается с помощью внешней тактовой частоты
макс.) устанавливается с помощью внешней тактовой частоты  . ИМС
. ИМС  («универсальные фильтры с коммутируемыми конденсаторами») работают несколько иначе.
(«универсальные фильтры с коммутируемыми конденсаторами») работают несколько иначе.

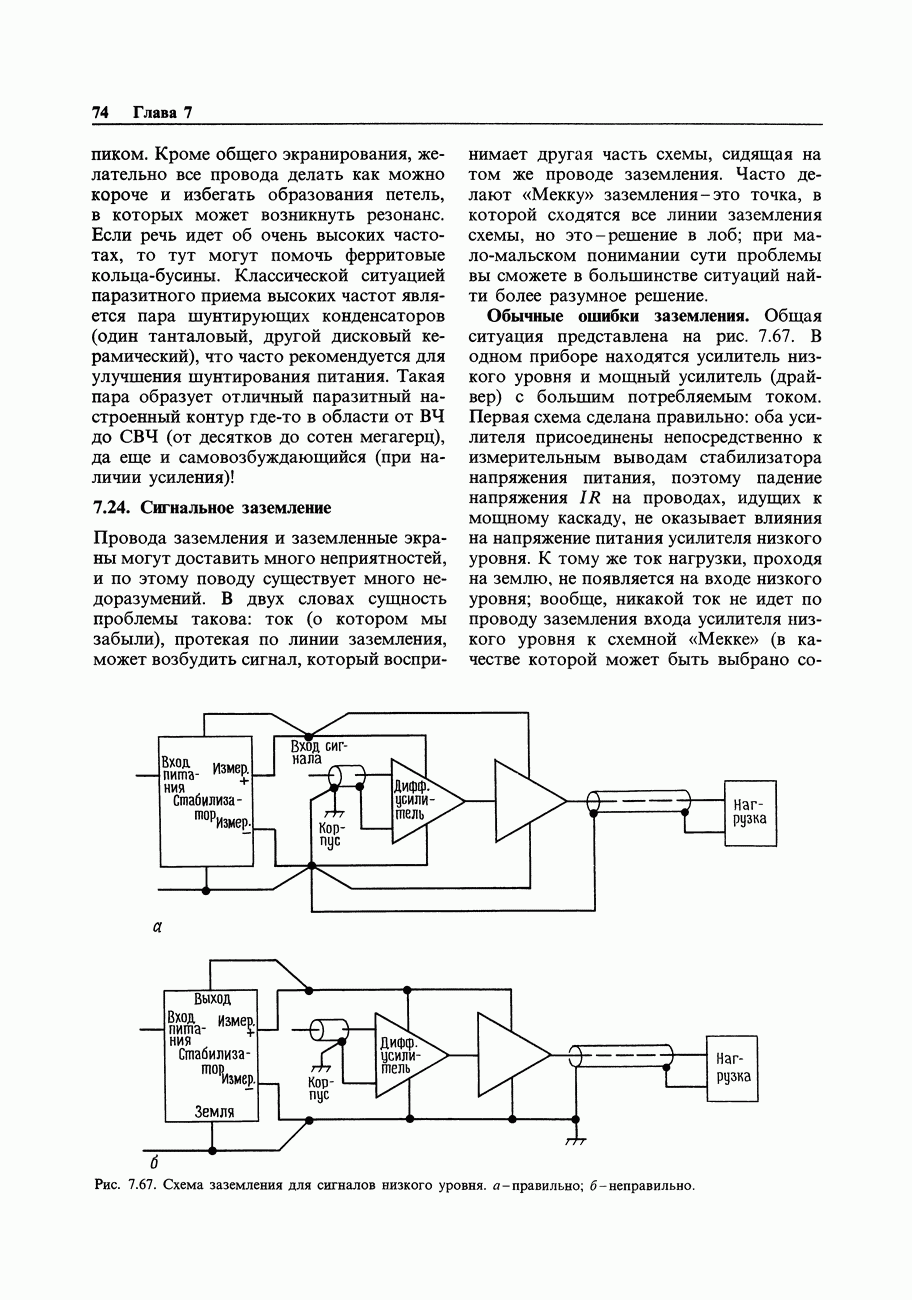
Рис. 9.93. Цифровой генератор синусоидальных сигналов.
С помощью внешних резисторов устанавливаются тип фильтра (ВЧ, НЧ, полосовой, заграждающий) и характеристика фильтра (Баттерворта, Чебышева и т. п.), а с помощью тактовой частоты, как и раньше, устанавливается частота среза. Другими изготовителями фильтров с коммутируемыми конденсаторами являются фирмы American Microsystems (AMI), Linear Technology (LTC) и Reticon. Фирма LTC как всегда использовала несколько хитроумных приемов для улучшения технических характеристик. Ее фильтры  похожи на
похожи на  , но являются
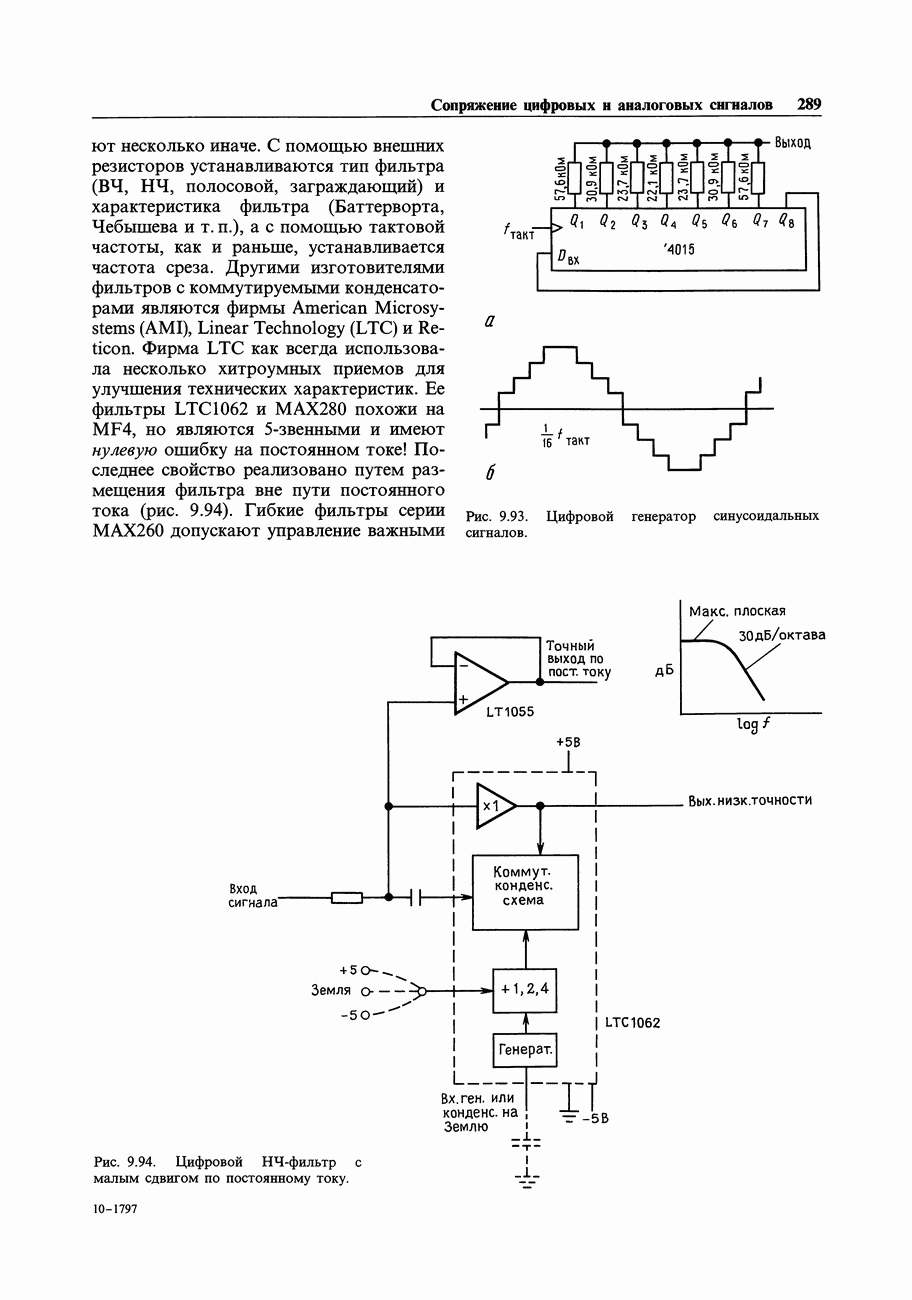
, но являются  -звенными и имеют нулевую ошибку на постоянном токе! Последнее свойство реализовано путем размещения фильтра вне пути постоянного тока (рис. 9.94). Гибкие фильтры серии
-звенными и имеют нулевую ошибку на постоянном токе! Последнее свойство реализовано путем размещения фильтра вне пути постоянного тока (рис. 9.94). Гибкие фильтры серии  допускают управление важными параметрами фильтра от микропроцессора.
допускают управление важными параметрами фильтра от микропроцессора.

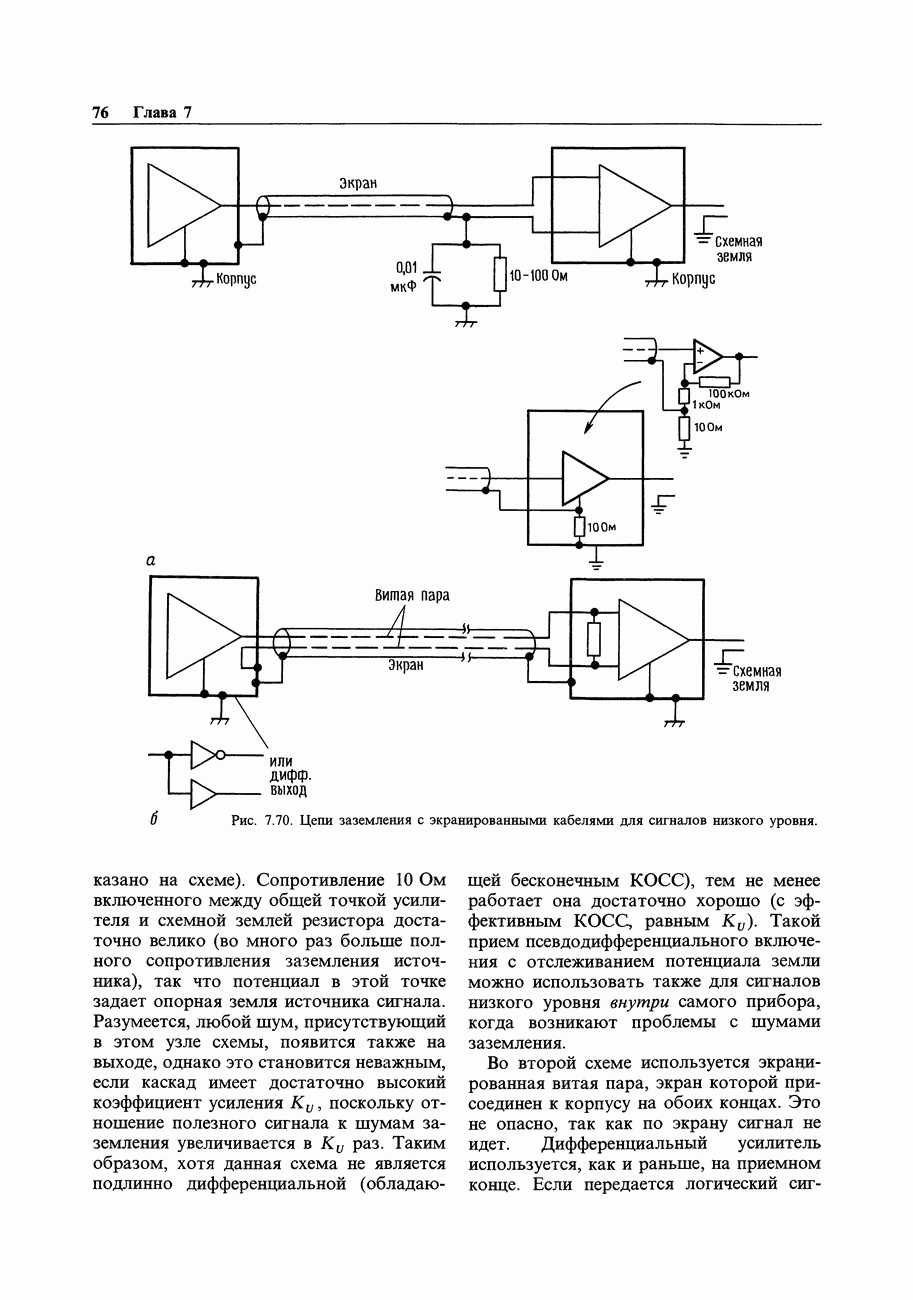
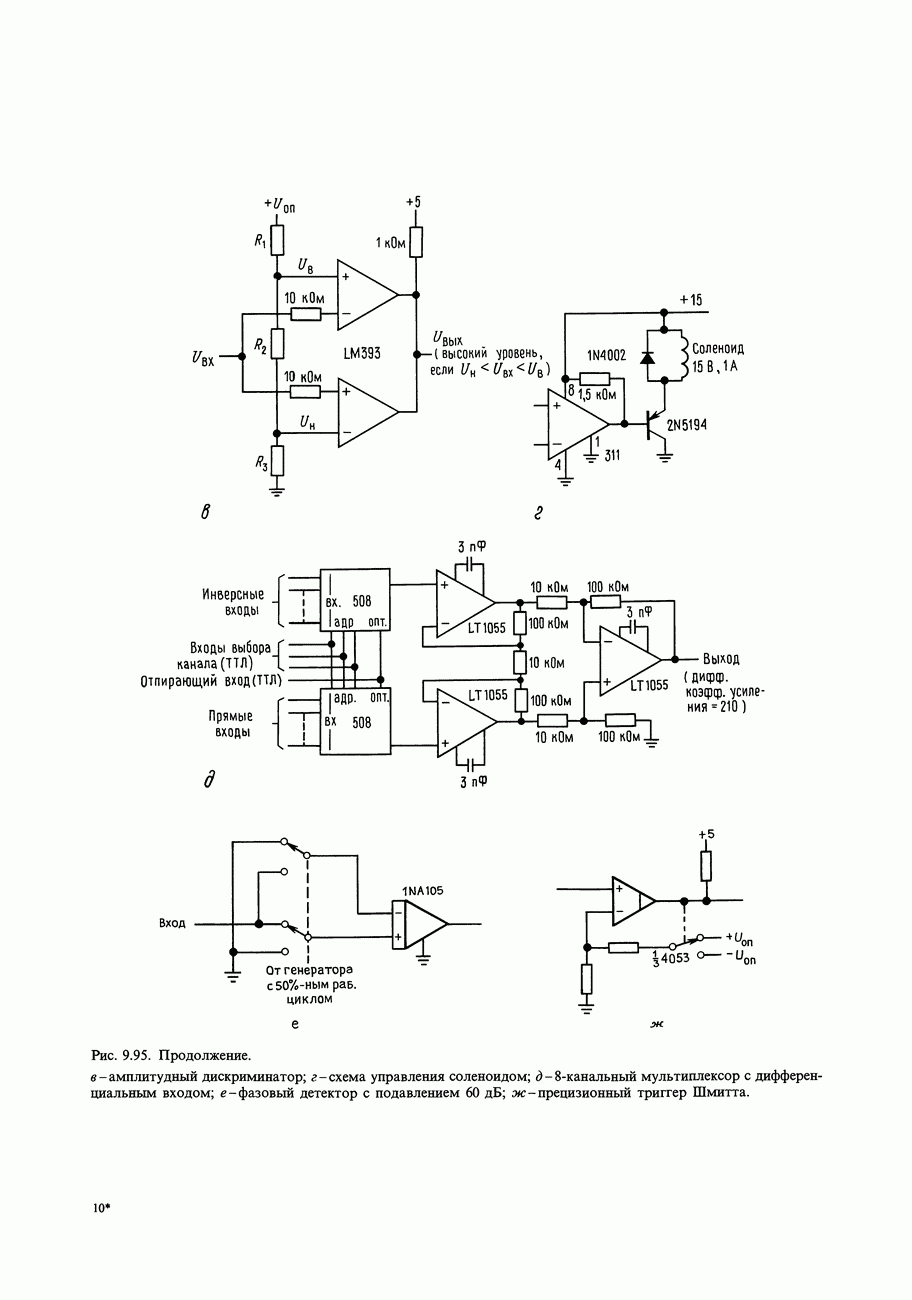
Рис. 9.94. Цифровой НЧ-фильтр с малым сдвигом по постоянному току.

Рис. 9.95. а - преобразователь отрицательных уровней в уровни ТТЛ; б - управление нагрузкой; подключенной на землю;
Вообще говоря, такие фильтры с коммутируемыми конденсаторами работают только на верхнем конце звукового диапазона. В них также наблюдается существенное проникновение тактовой частоты на выход обычно в пределах  . Это ограничивает их динамический диапазон в тех применениях, где тактовая частота находится внутри полосы пропускания (например, ВЧ-фильтры). Они могут иметь значительный шум, ограничивающий динамический диапазон до 80 дБ и менее (сравните со 140 дБ и выше для хорошего операционного усилителя). С другой (положительной) стороны, фильтры на коммутируемых конденсаторах просты в применении и позволяют осуществлять эффективную настройку (с помощью тактовой частоты). Фильтры такого типа широко используют в модемах (при передаче данных по телефонным линиям) и в других областях связи. См. разд. 5.11.
. Это ограничивает их динамический диапазон в тех применениях, где тактовая частота находится внутри полосы пропускания (например, ВЧ-фильтры). Они могут иметь значительный шум, ограничивающий динамический диапазон до 80 дБ и менее (сравните со 140 дБ и выше для хорошего операционного усилителя). С другой (положительной) стороны, фильтры на коммутируемых конденсаторах просты в применении и позволяют осуществлять эффективную настройку (с помощью тактовой частоты). Фильтры такого типа широко используют в модемах (при передаче данных по телефонным линиям) и в других областях связи. См. разд. 5.11.
Формирование синусоидальных колебаний цифровым способом.
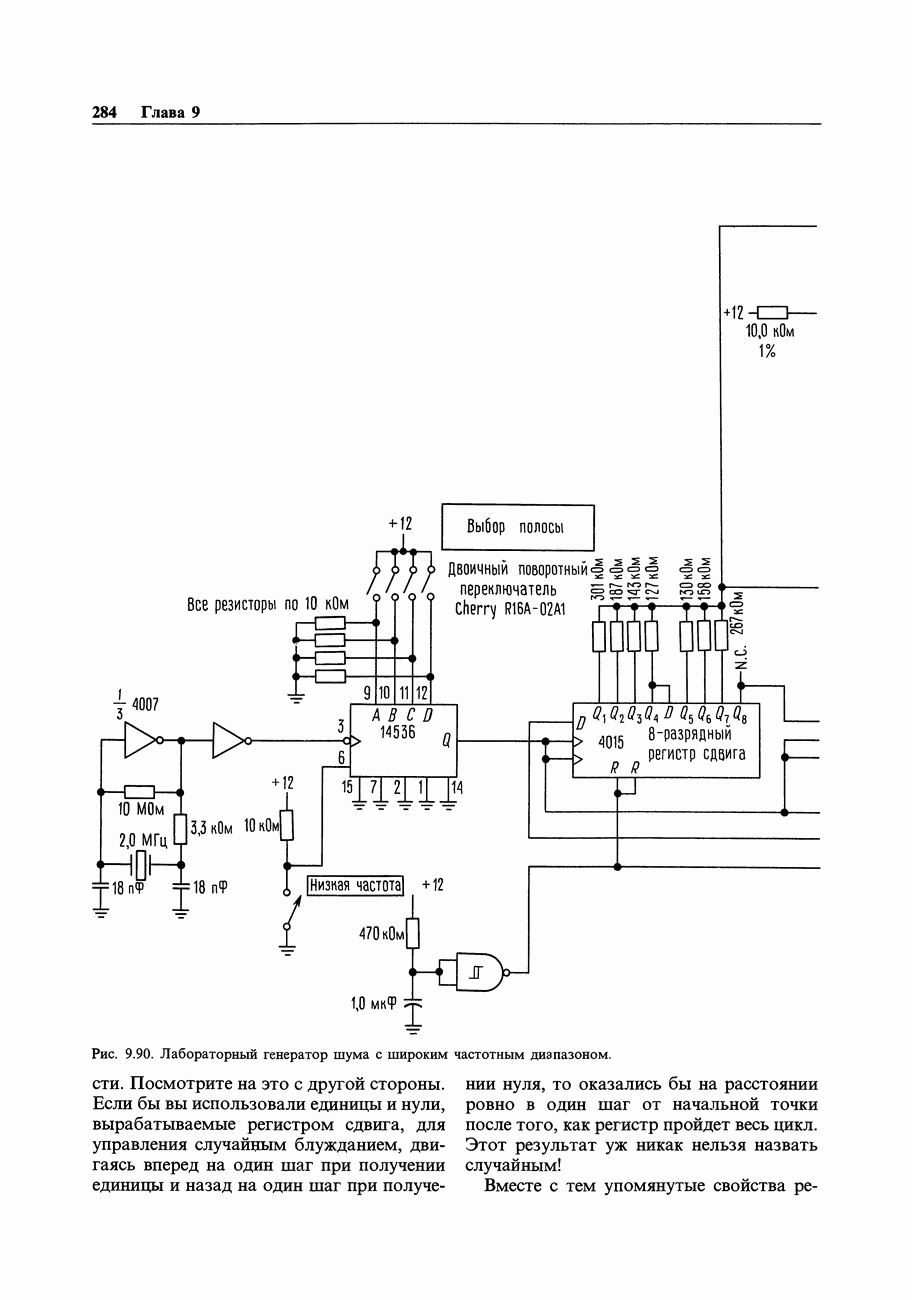
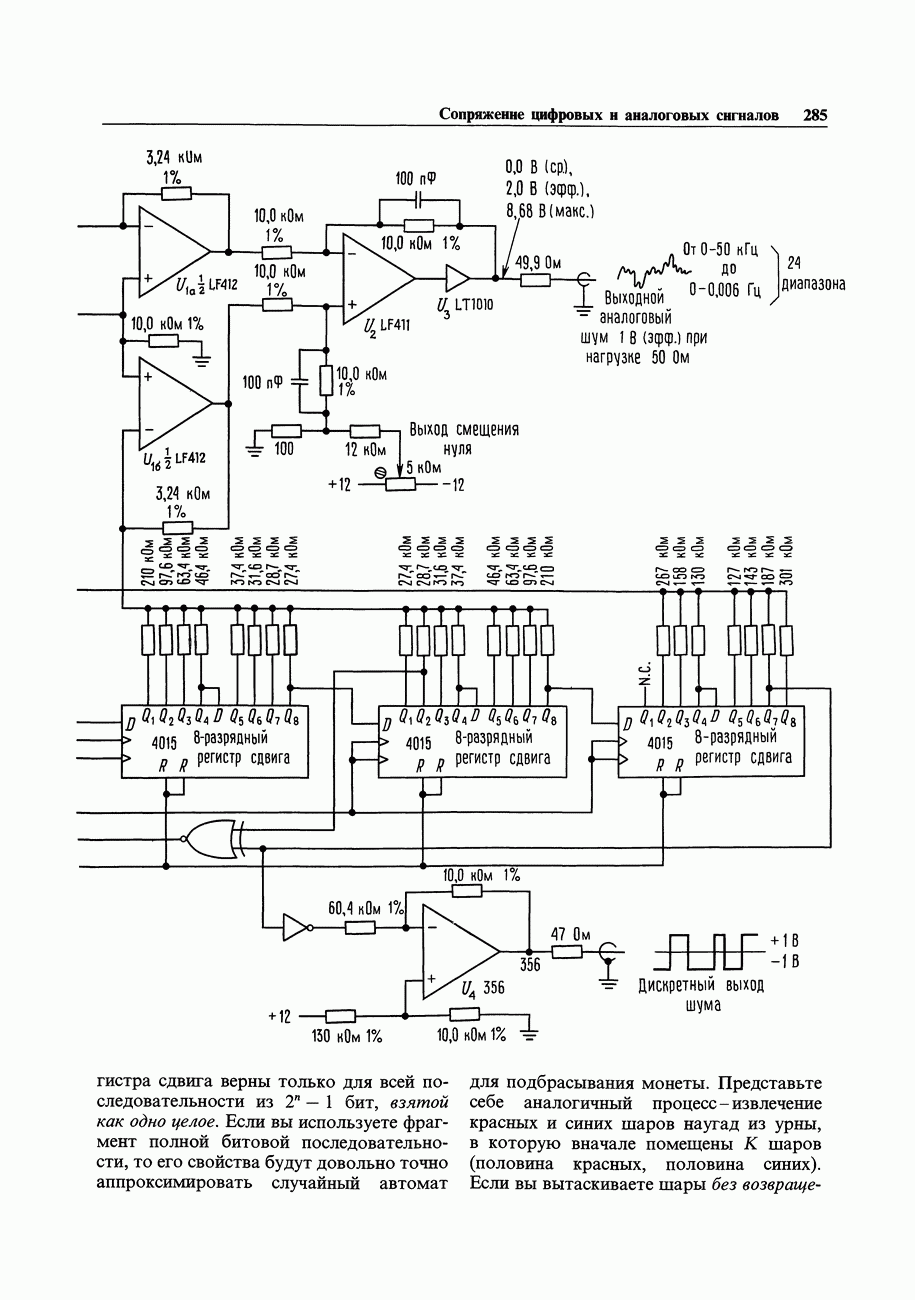
С нерекурсивной цифровой фильтрацией связан интересный способ синтеза синусоидальных колебаний с использованием взвешенных сумм сигналов с выходов счетчика Джонсона (кольцевой счетчик с коэффициентом пересчета, вдвое превышающим число разрядов). Схема на рис. 9.93 показывает способ реализации такого генератора. ИМС 4015 представляет собой -разрядный регистр сдвига с параллельным выходом. Подавая на вход инвертированный сигнал с последнего разряда, можно организовать счетчик Джонсона, который будет проходить через 16 состояний (в общем случае
-разрядный регистр сдвига с параллельным выходом. Подавая на вход инвертированный сигнал с последнего разряда, можно организовать счетчик Джонсона, который будет проходить через 16 состояний (в общем случае  состояний для
состояний для  -разрядного регистра сдвига). Начиная с состояния «все нули», происходит заполнение счетчика слева направо «1» (марш
-разрядного регистра сдвига). Начиная с состояния «все нули», происходит заполнение счетчика слева направо «1» (марш  ) до полного заполнения всеми единицами, затем начинается марш «0» и т.д. Показанное на рисунке взвешивание формирует
) до полного заполнения всеми единицами, затем начинается марш «0» и т.д. Показанное на рисунке взвешивание формирует  -уровневое приближение к синусоидальному колебанию с частотой, равной 1/16 тактовой частоты, и с первым ненулевым членом искажения на
-уровневое приближение к синусоидальному колебанию с частотой, равной 1/16 тактовой частоты, и с первым ненулевым членом искажения на  гармонике, имеющей затухание 24 дБ.
гармонике, имеющей затухание 24 дБ.
| << Предыдущий параграф | Следующий параграф >> |
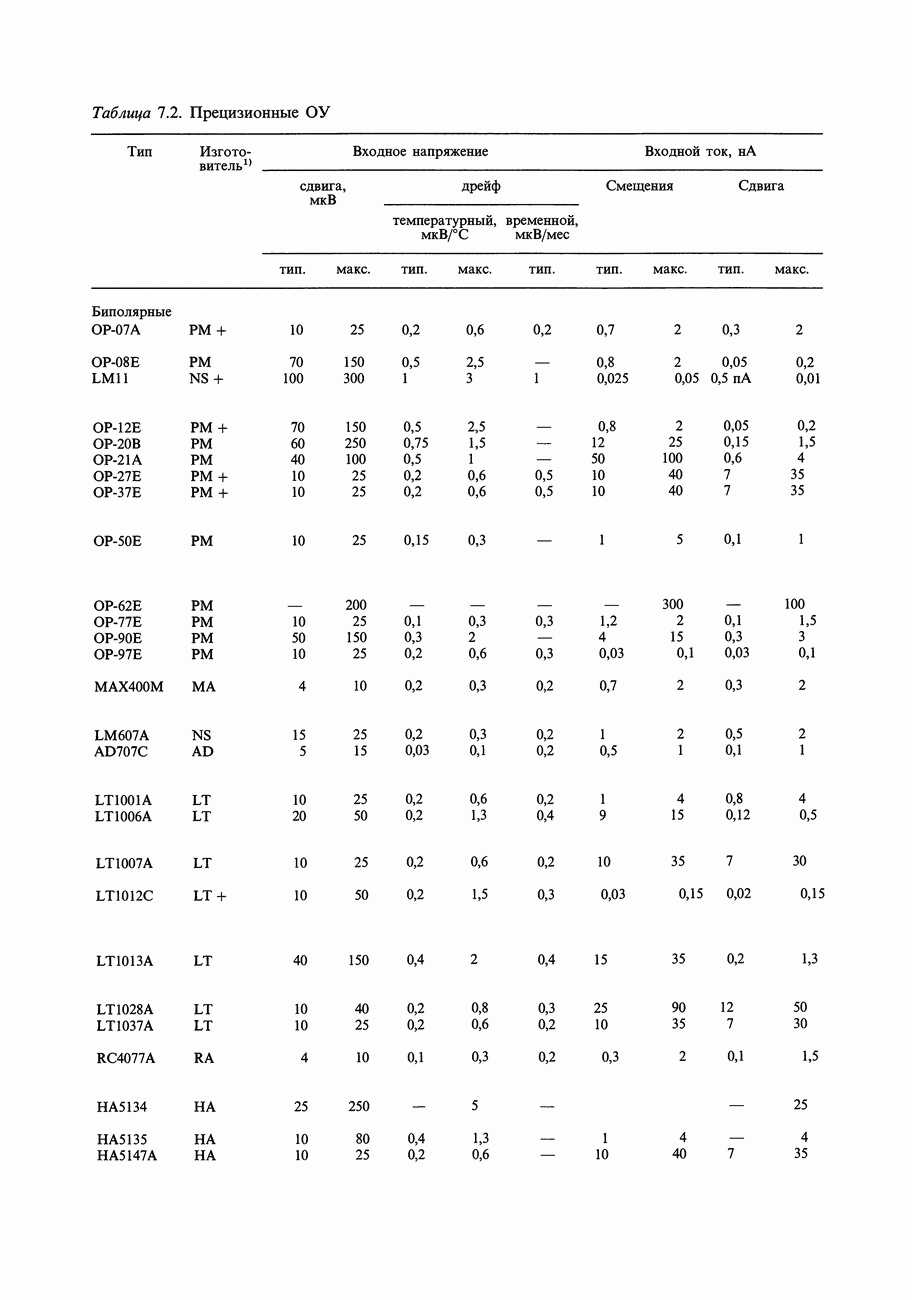
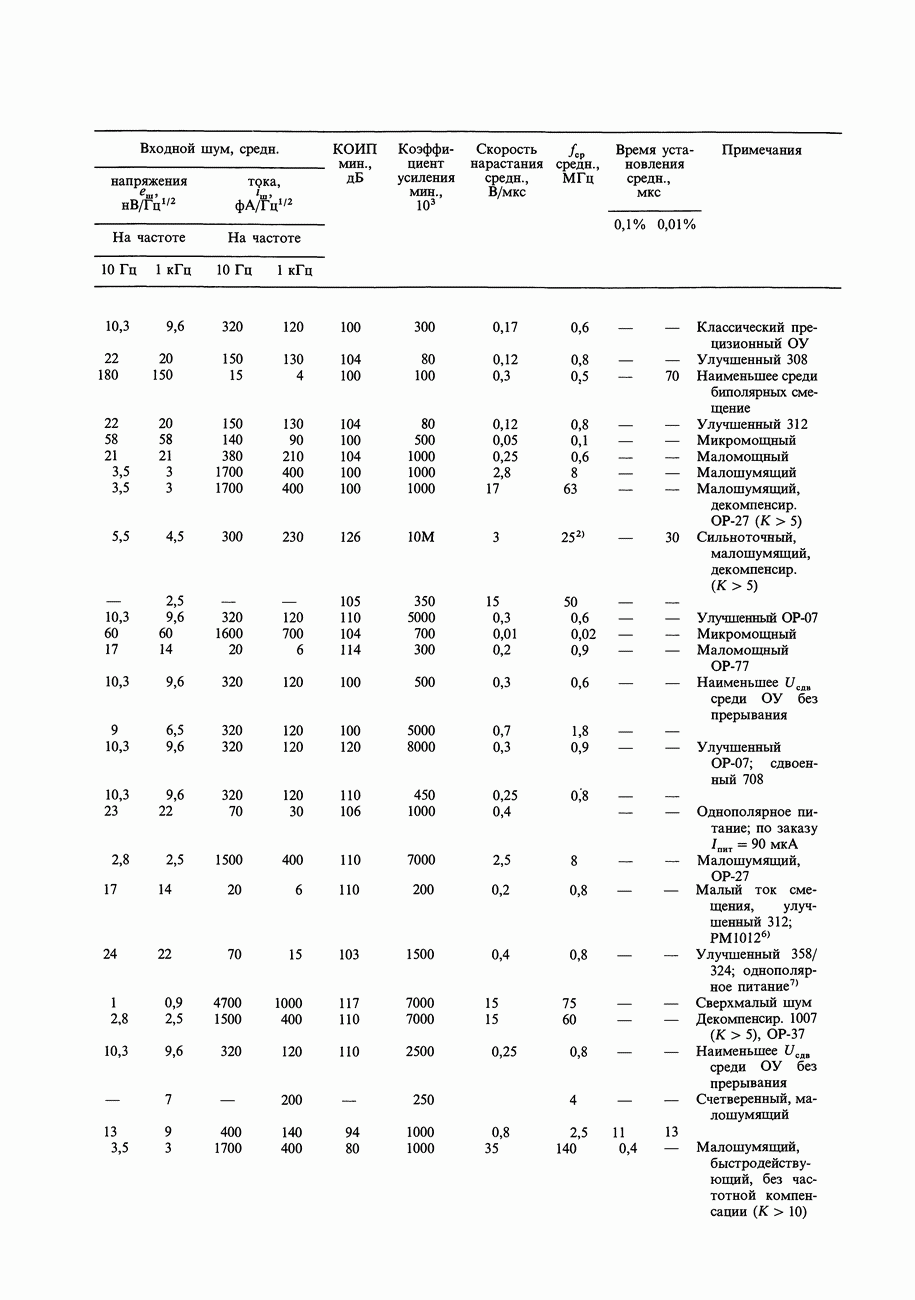
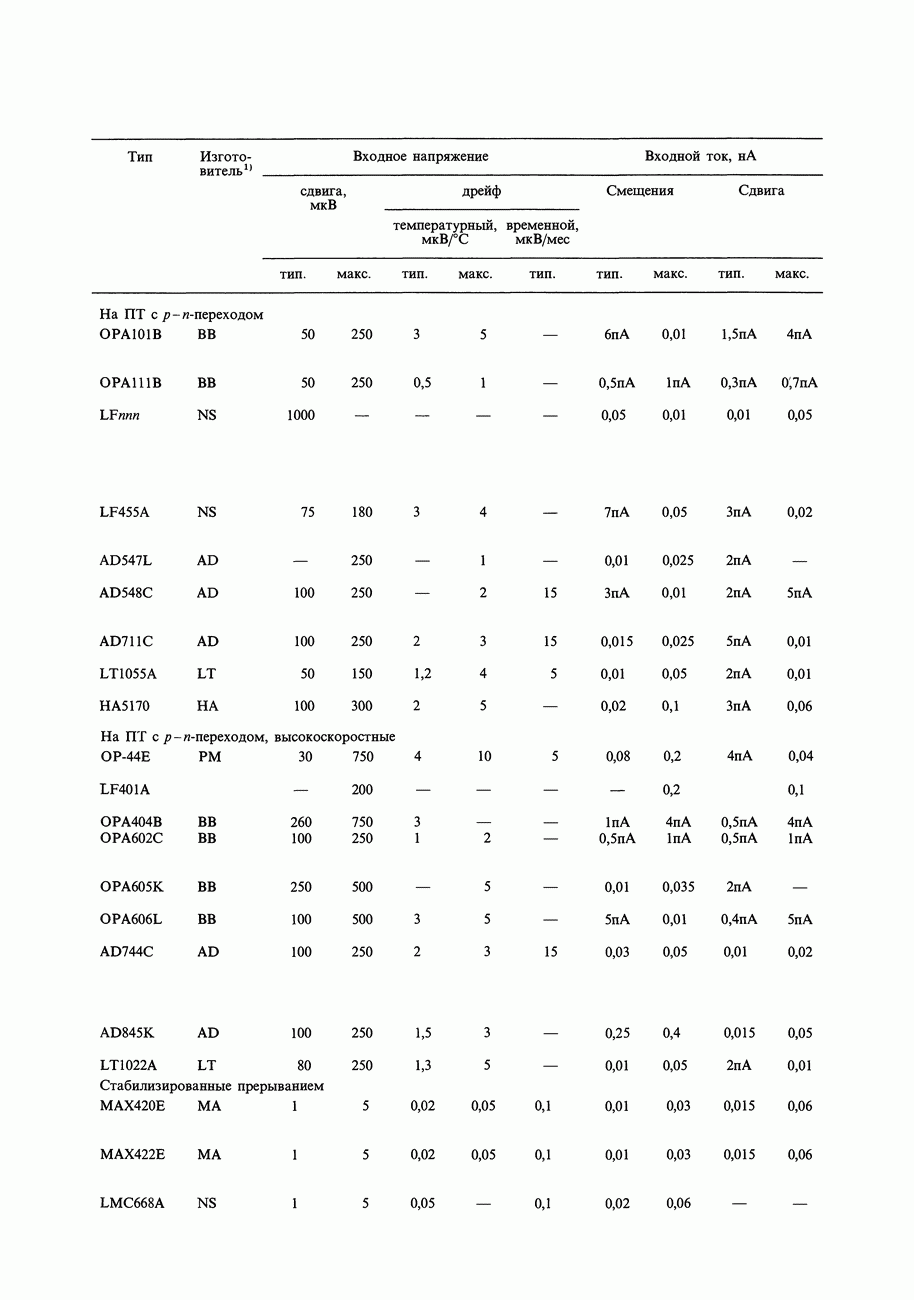
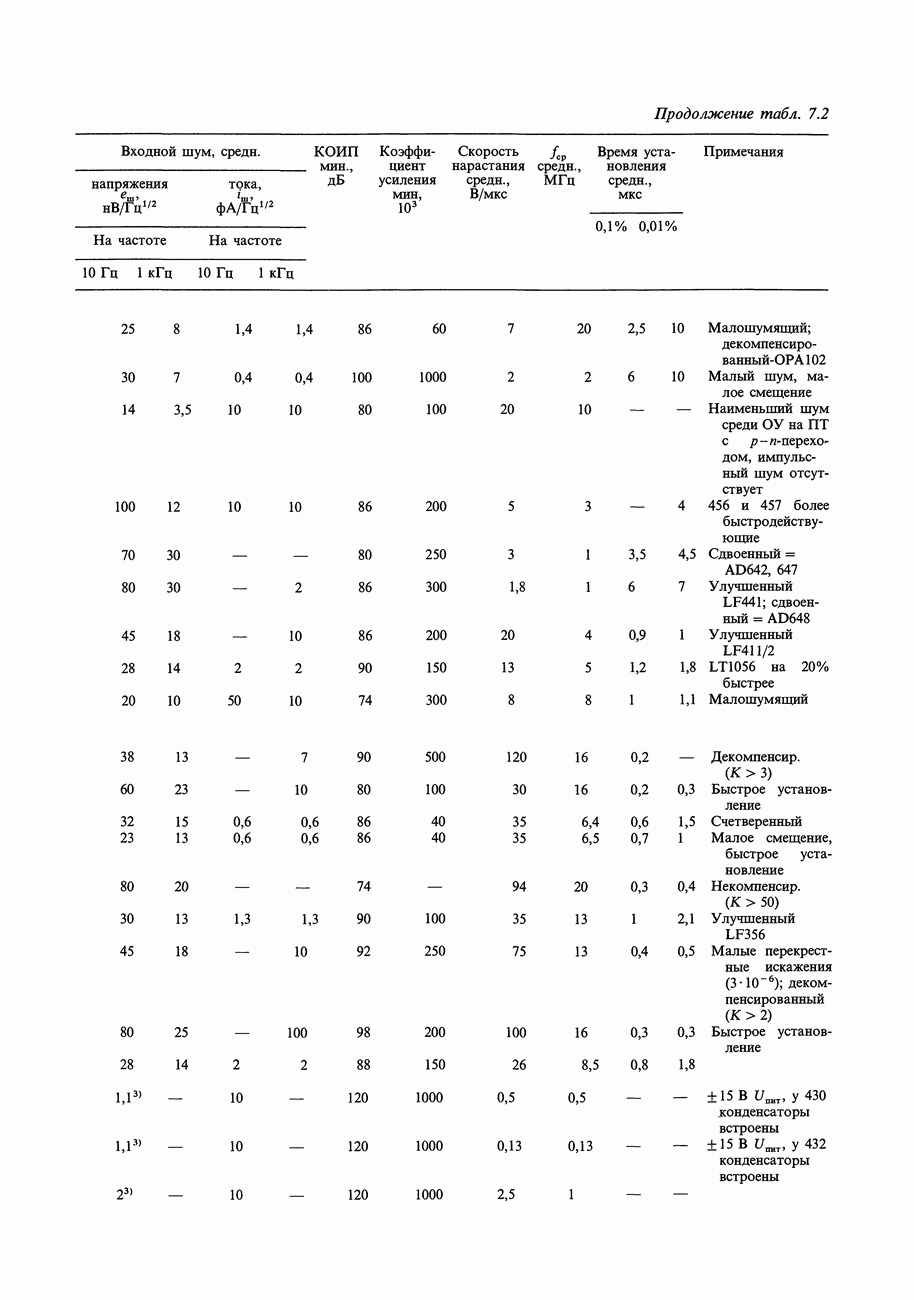
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
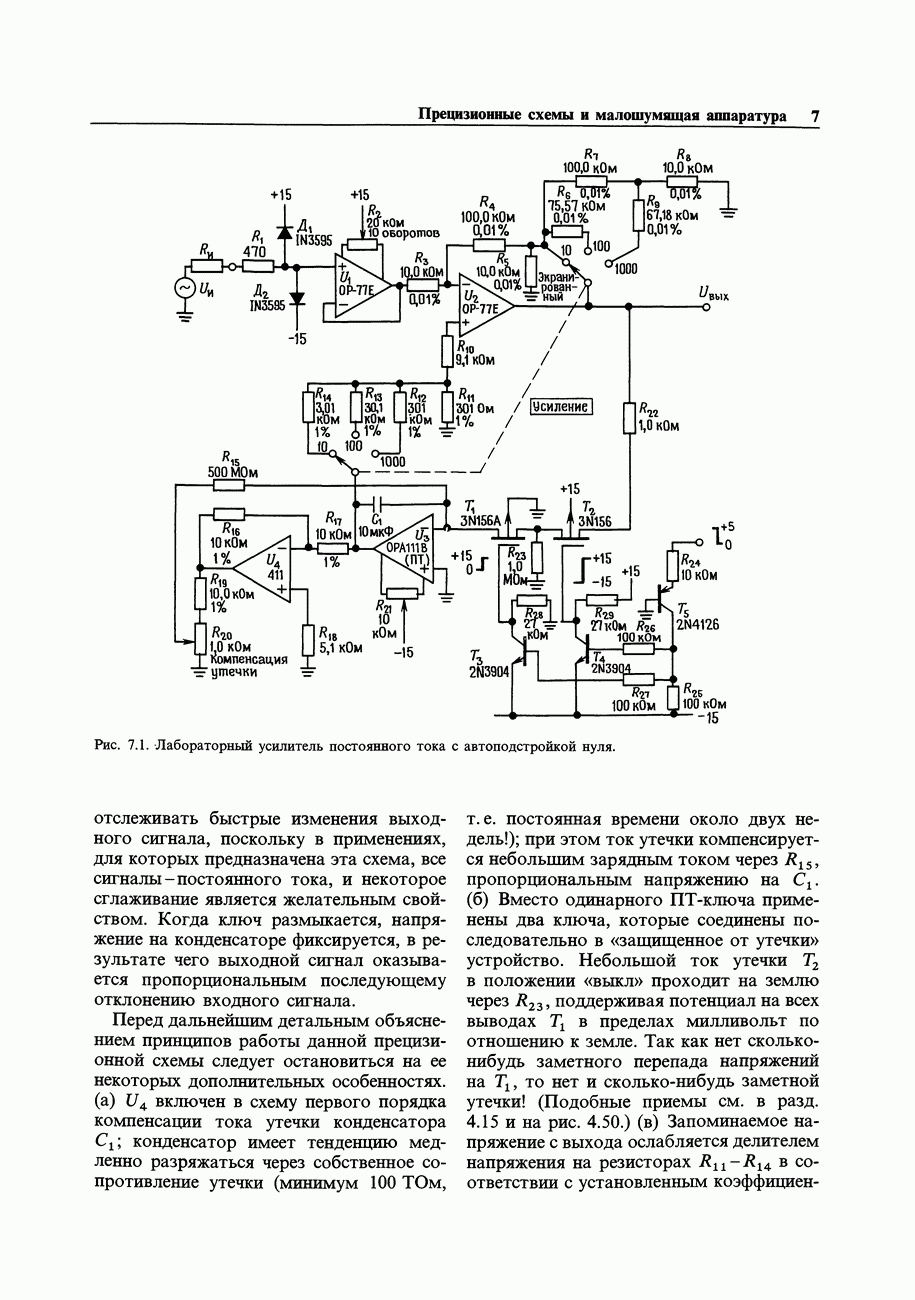
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
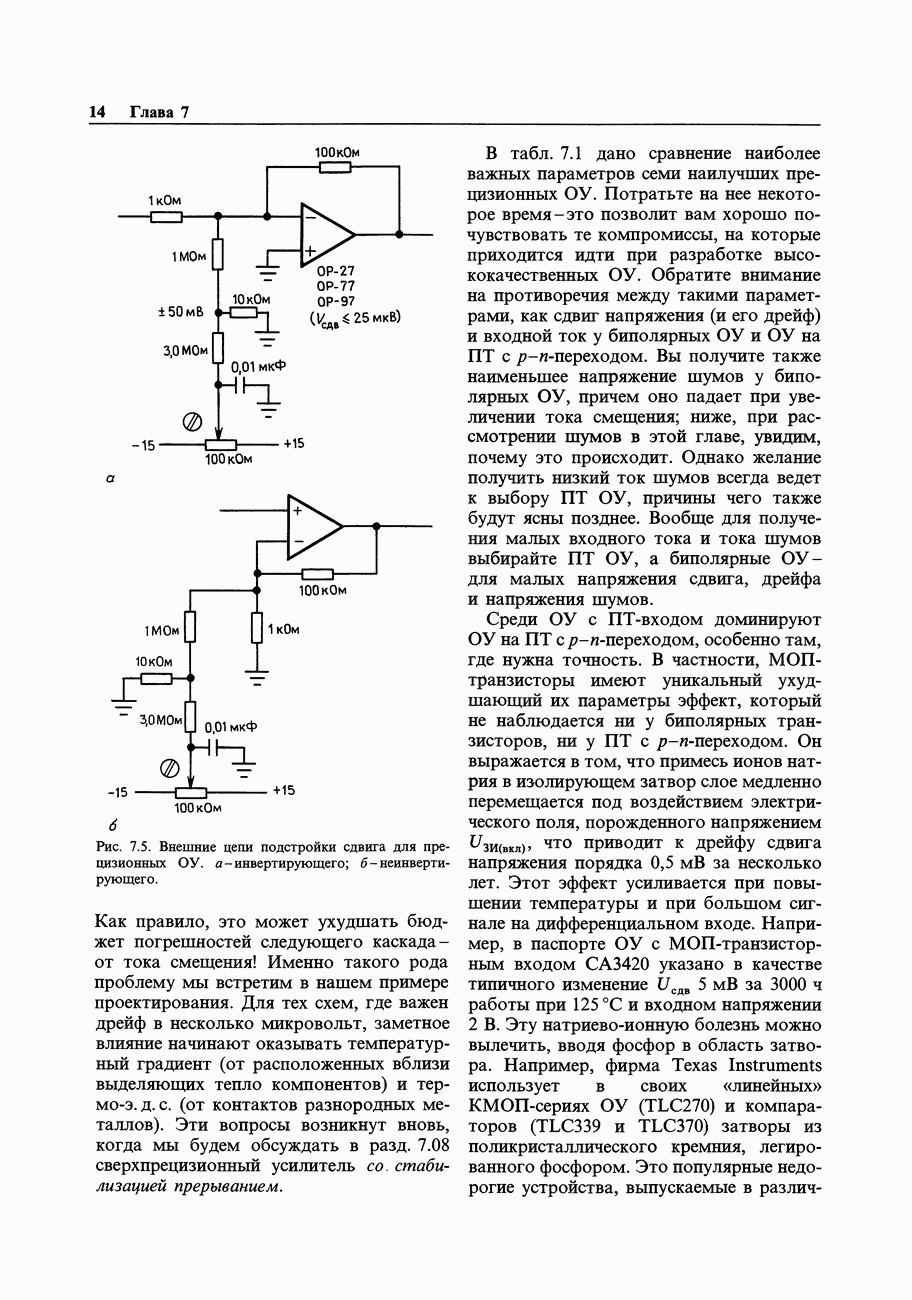
- 7.05. Погрешности внешних цепей
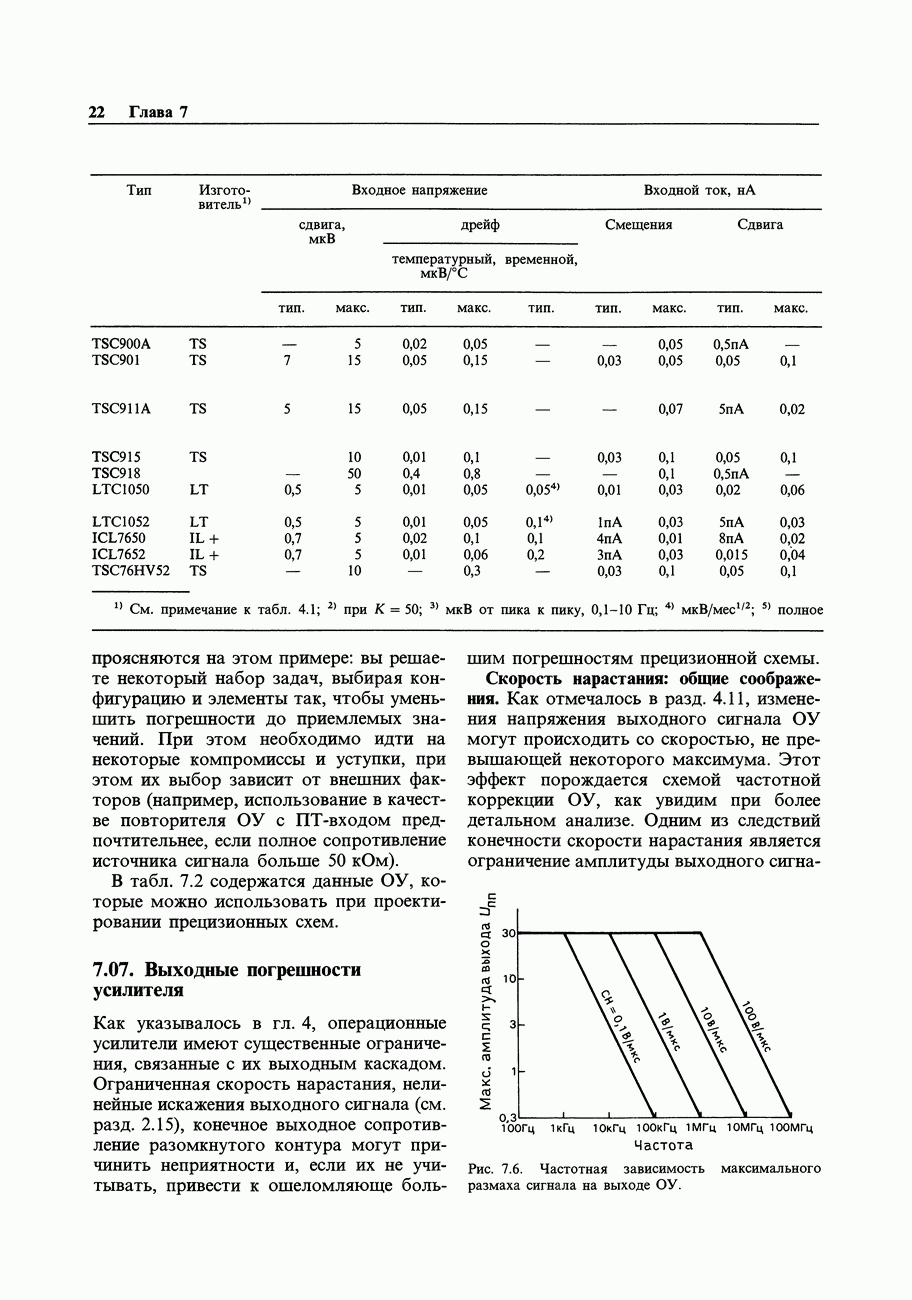
- 7.06. Входные погрешности усилителя
- 7.07. Выходные погрешности усилителя
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
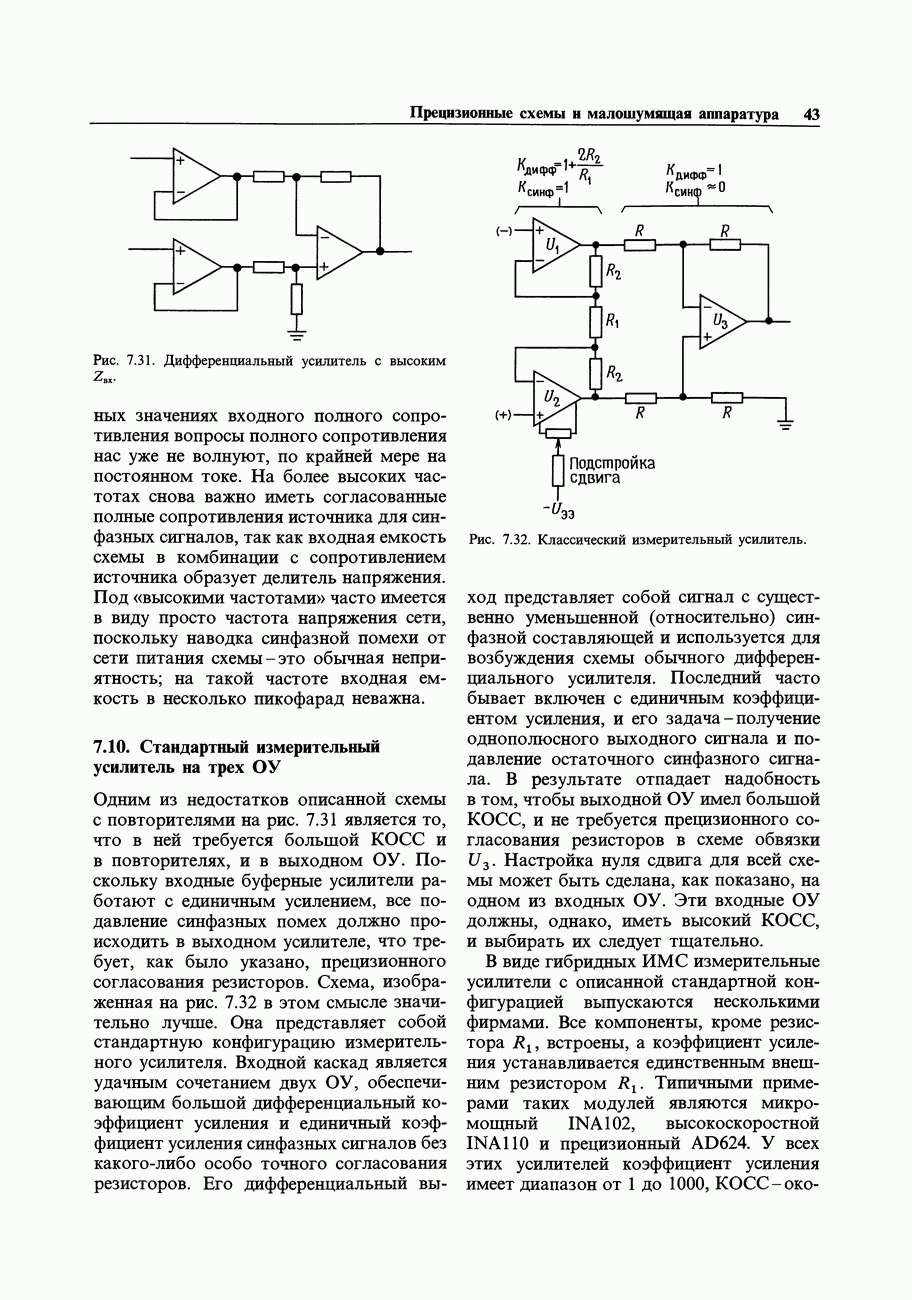
- 7.09. Простой разностный усилитель
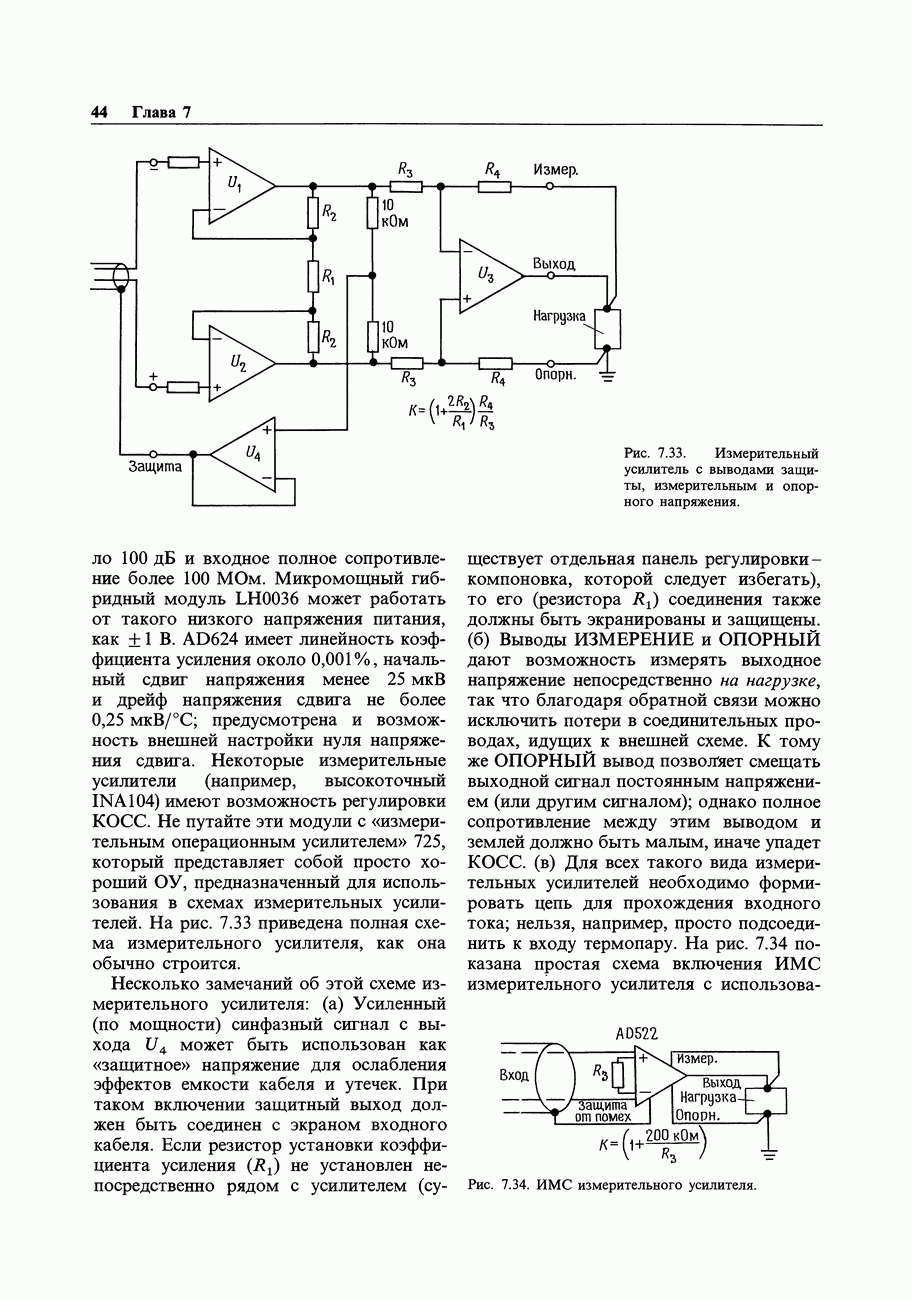
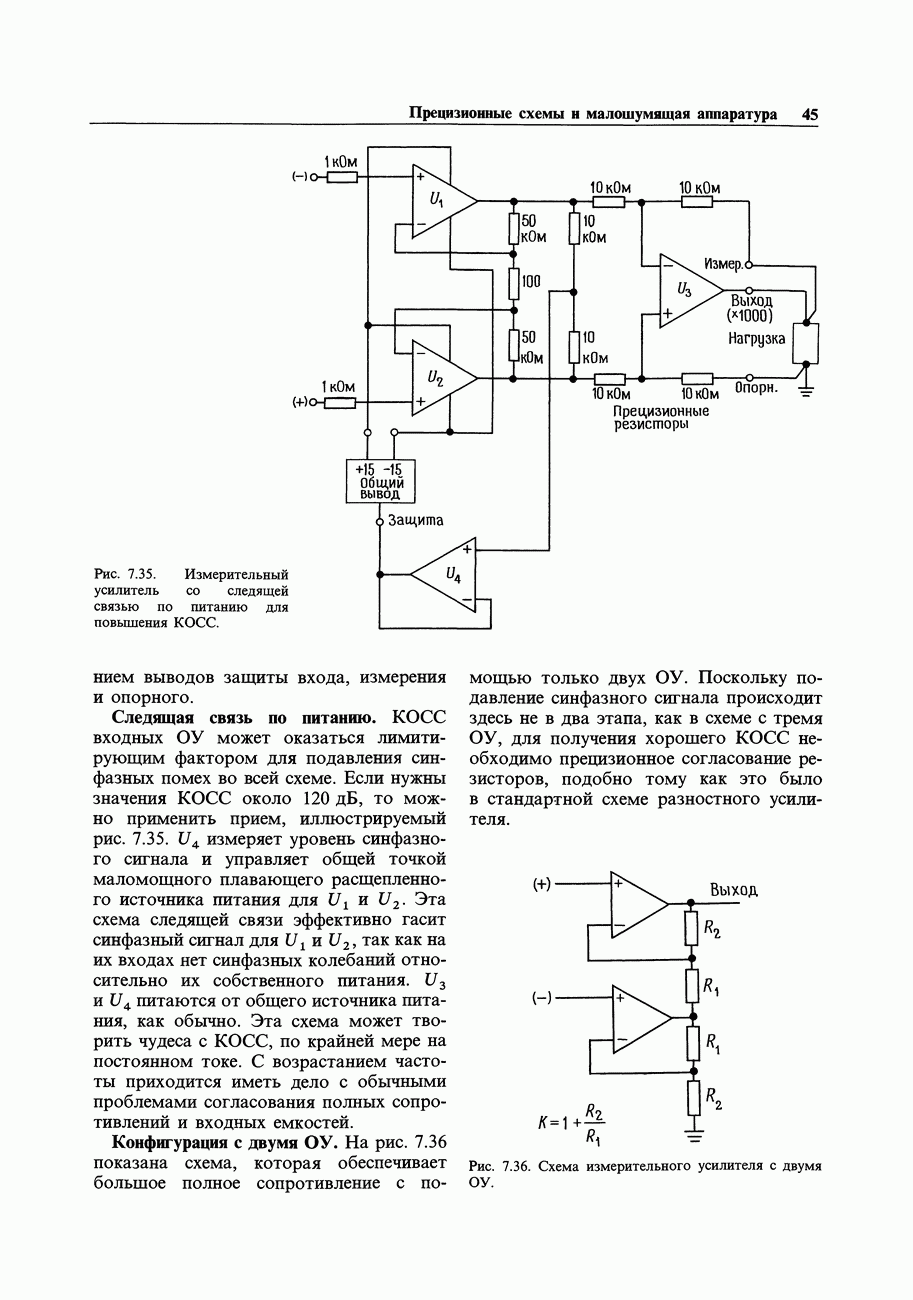
- 7.10. Стандартный измерительный усилитель на трех ОУ
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
- 7.12. Отношение сигнал/шум и коэффициент шума
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
- 7.15. Шум ПТ
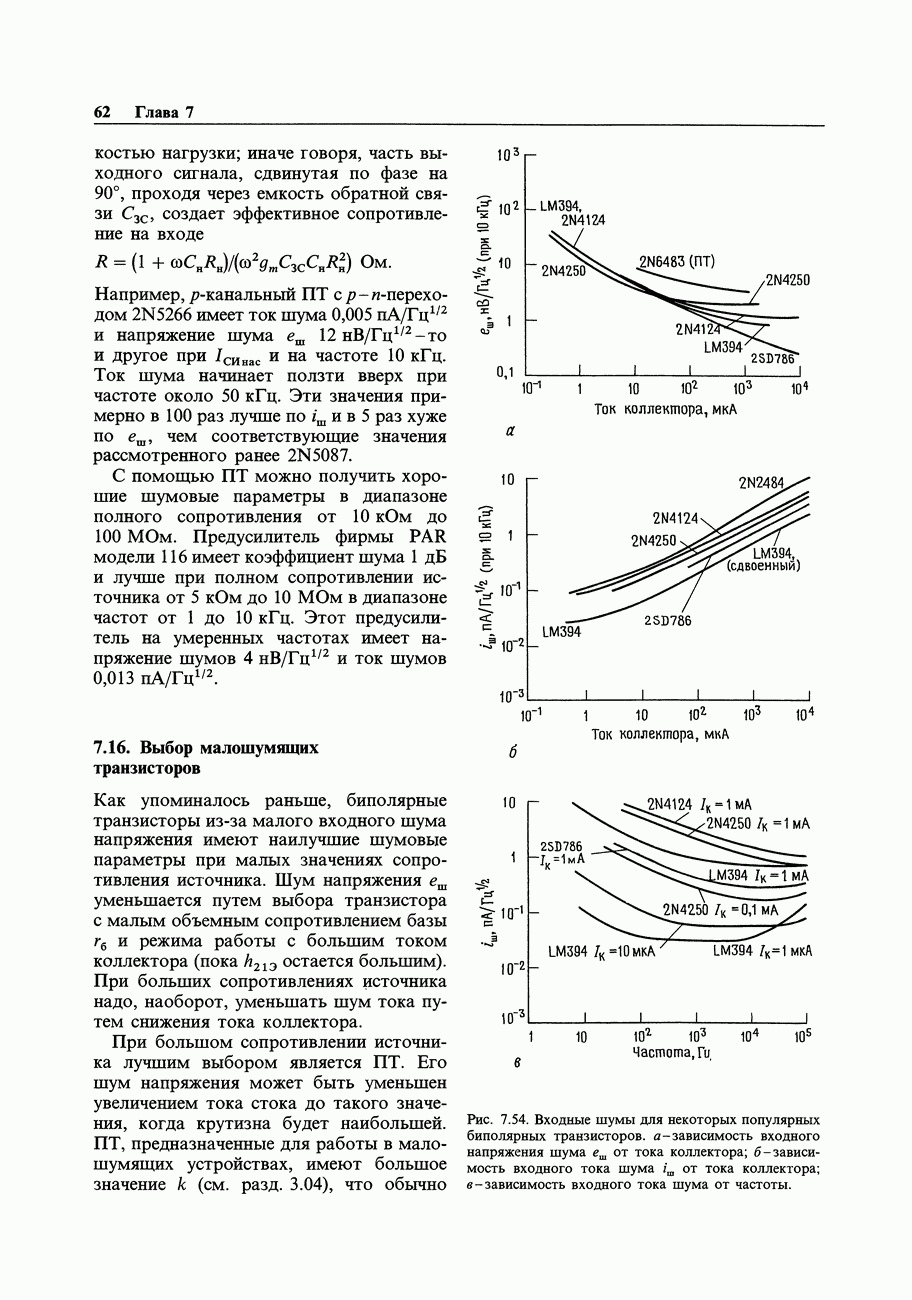
- 7.16. Выбор малошумящих транзисторов
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
- 7.18. Измерение без источника шума
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
- 7.22. Попурри на тему шумов
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
- 7.23. Помехи
- 7.24. Сигнальное заземление
- 7.25. Межприборное заземление
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
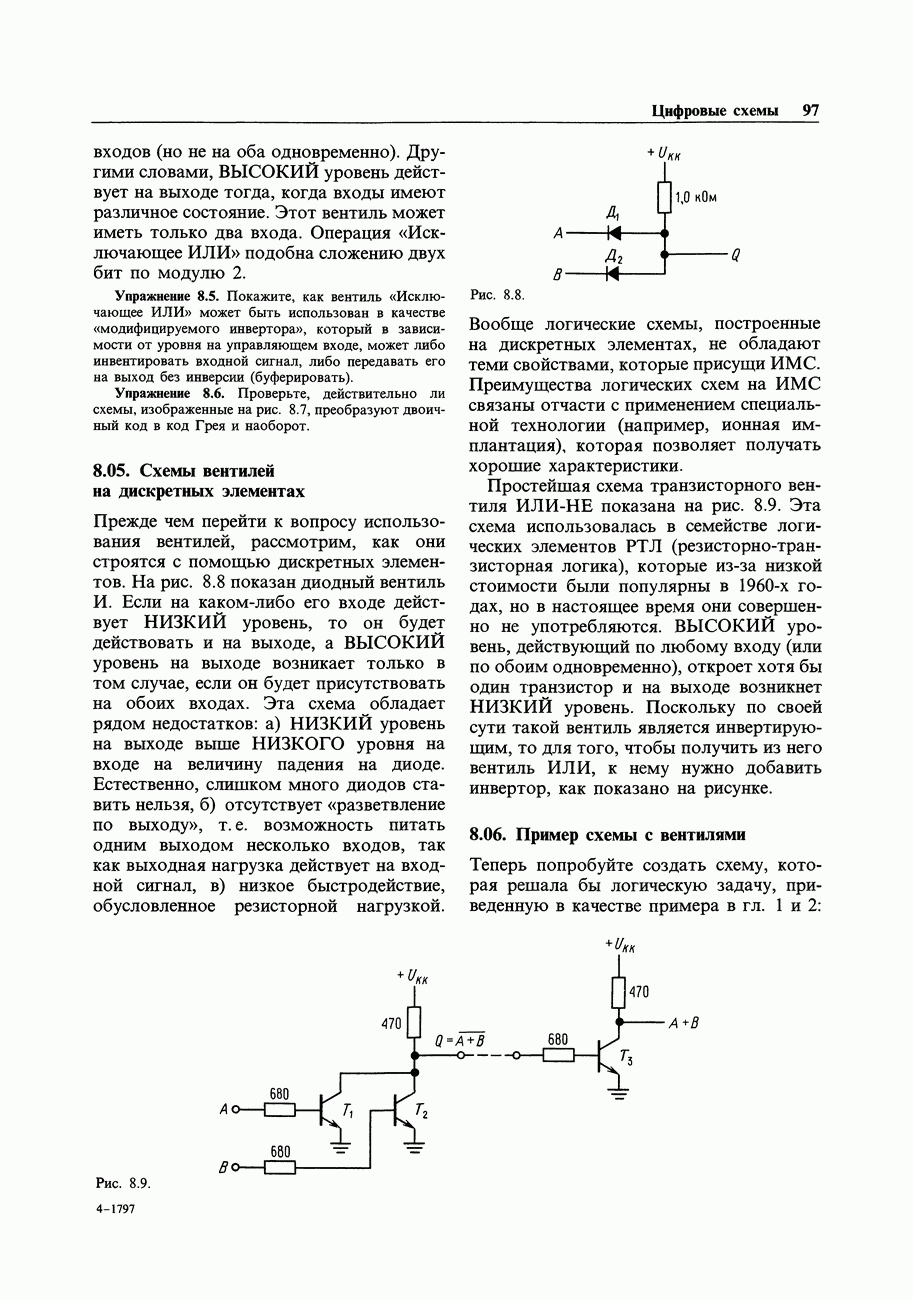
- 8.04. Вентили и таблицы истинности
- 8.05. Схемы вентилей на дискретных элементах
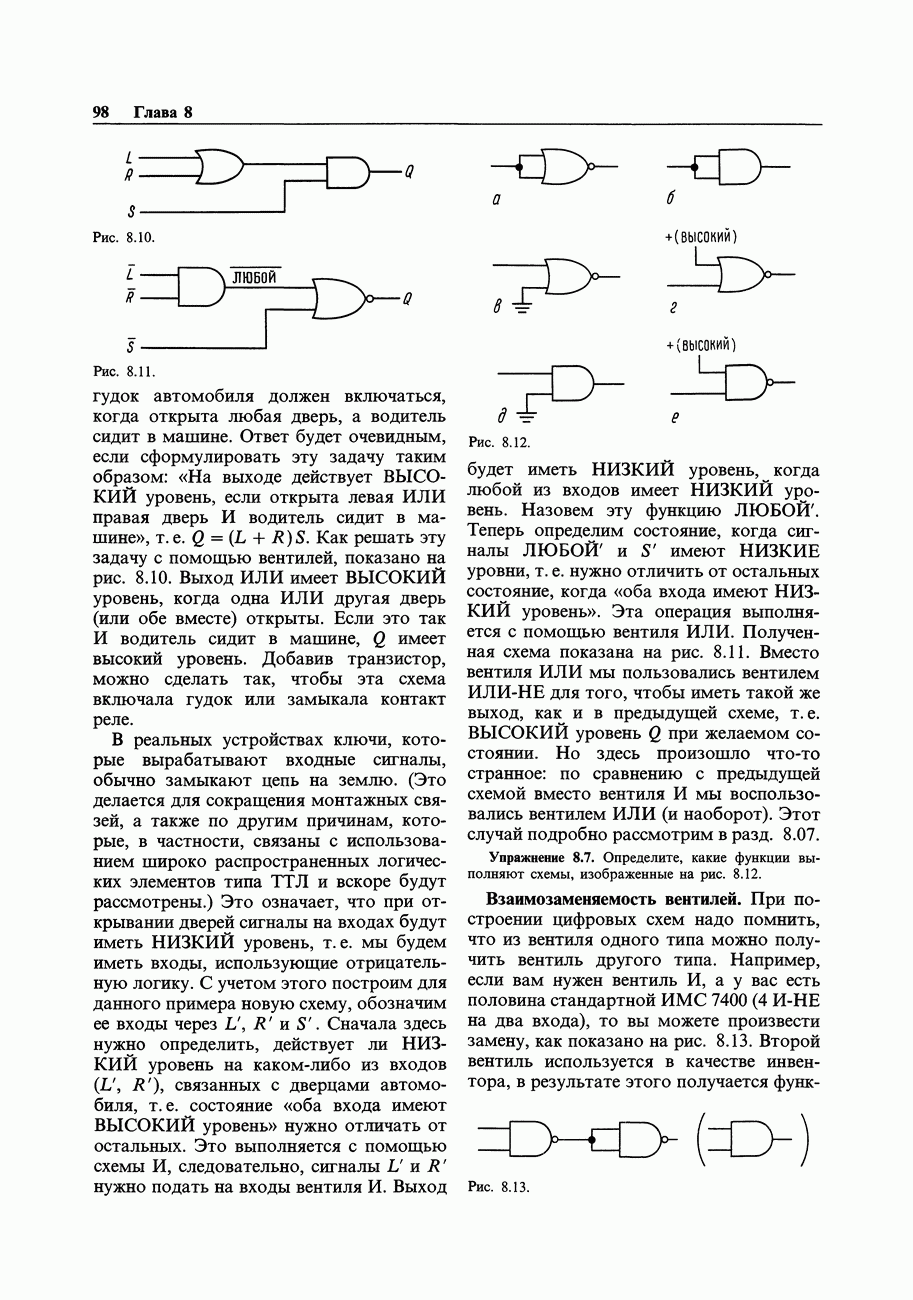
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
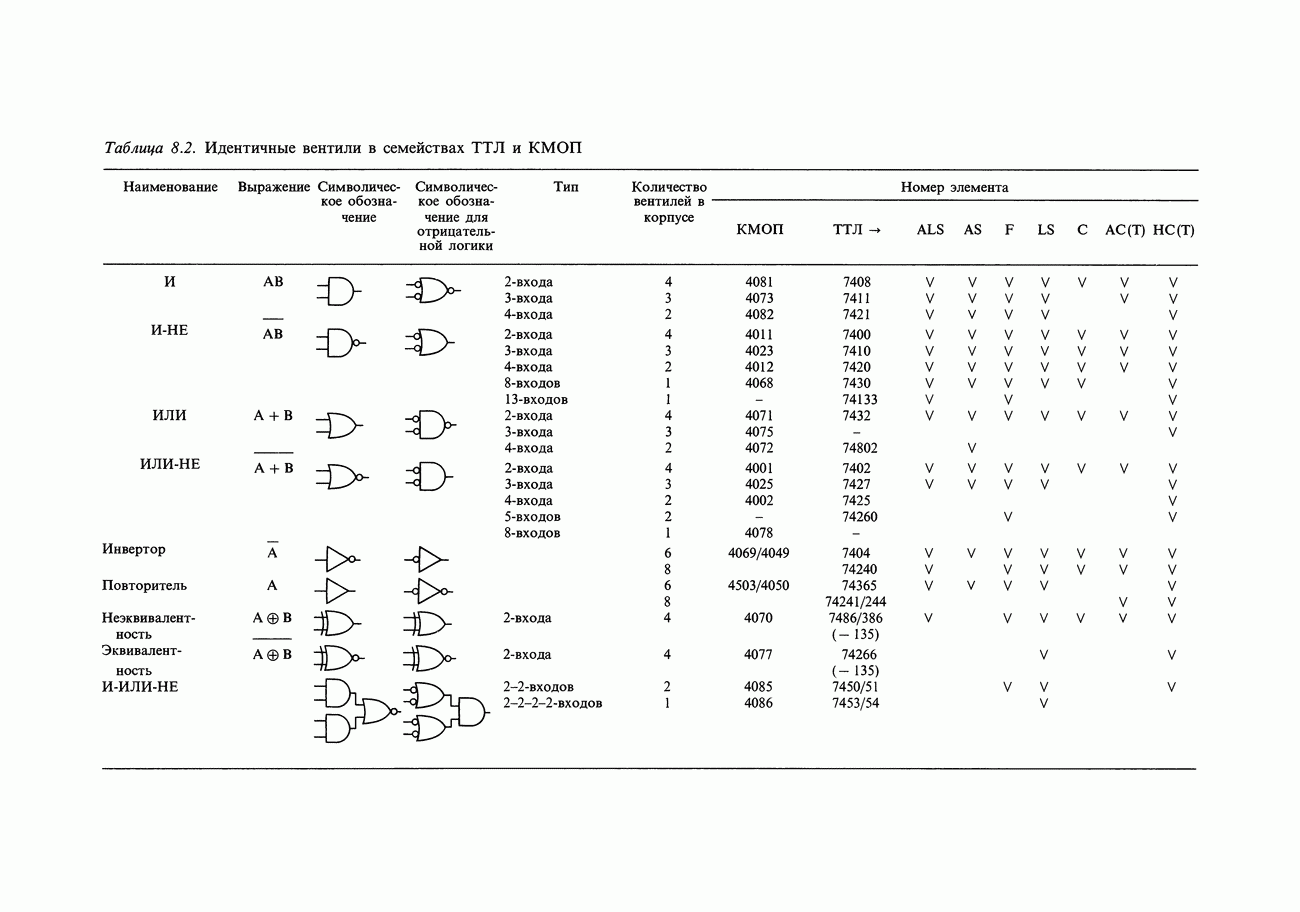
- 8.08. Каталог идентичных вентилей
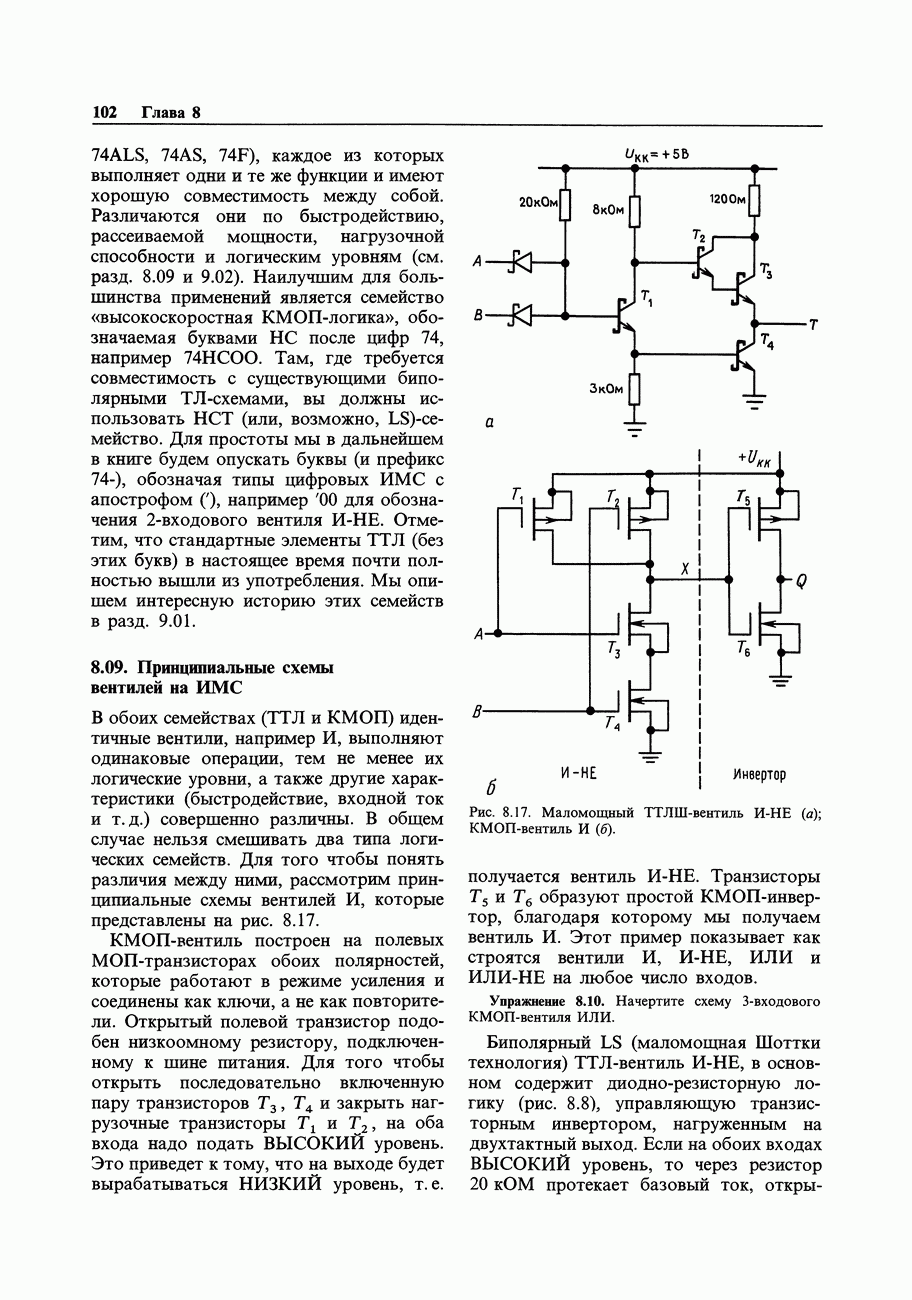
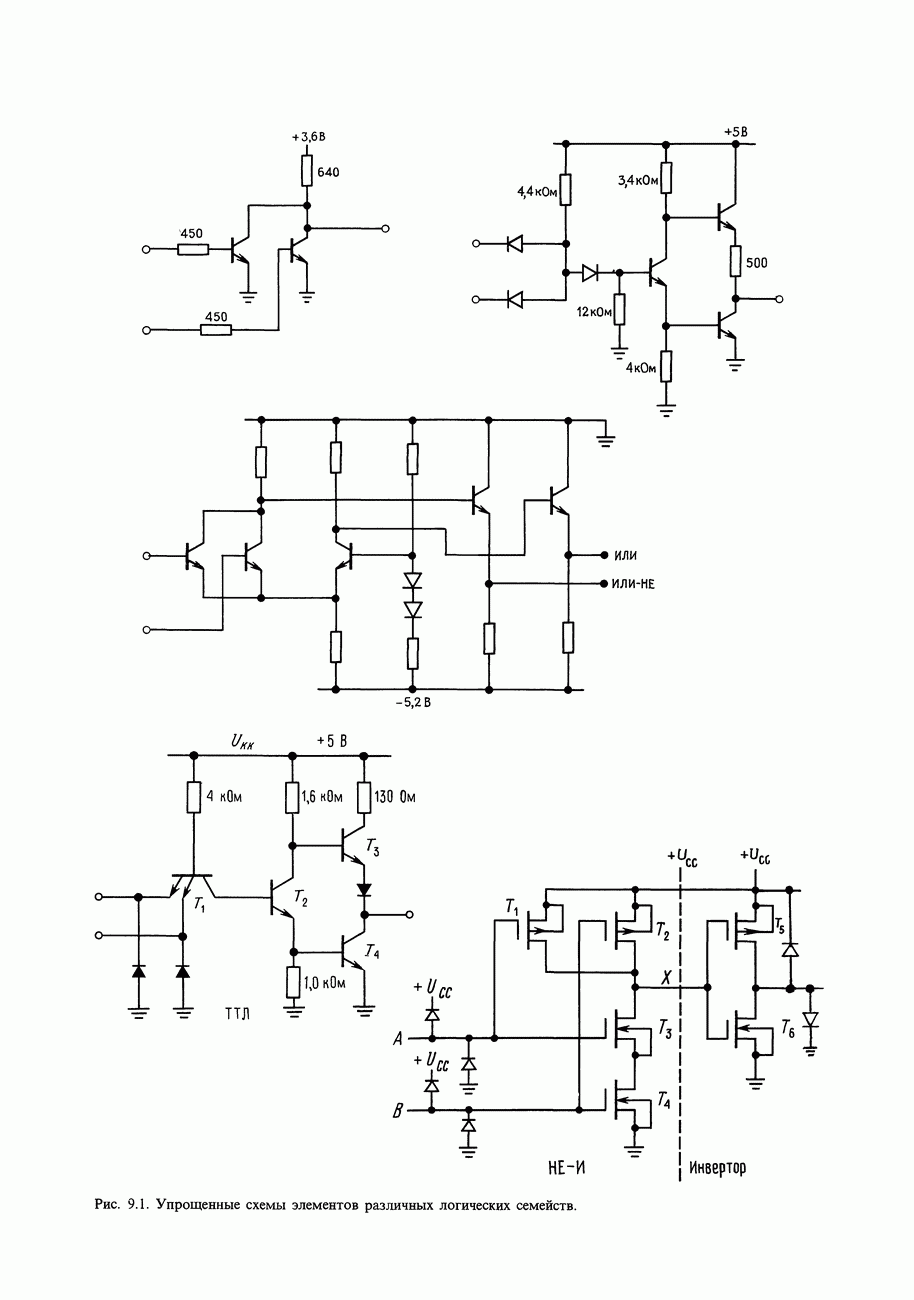
- 8.09. Принципиальные схемы вентилей на ИМС
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
- 8.16. Устройства с памятью: триггеры
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
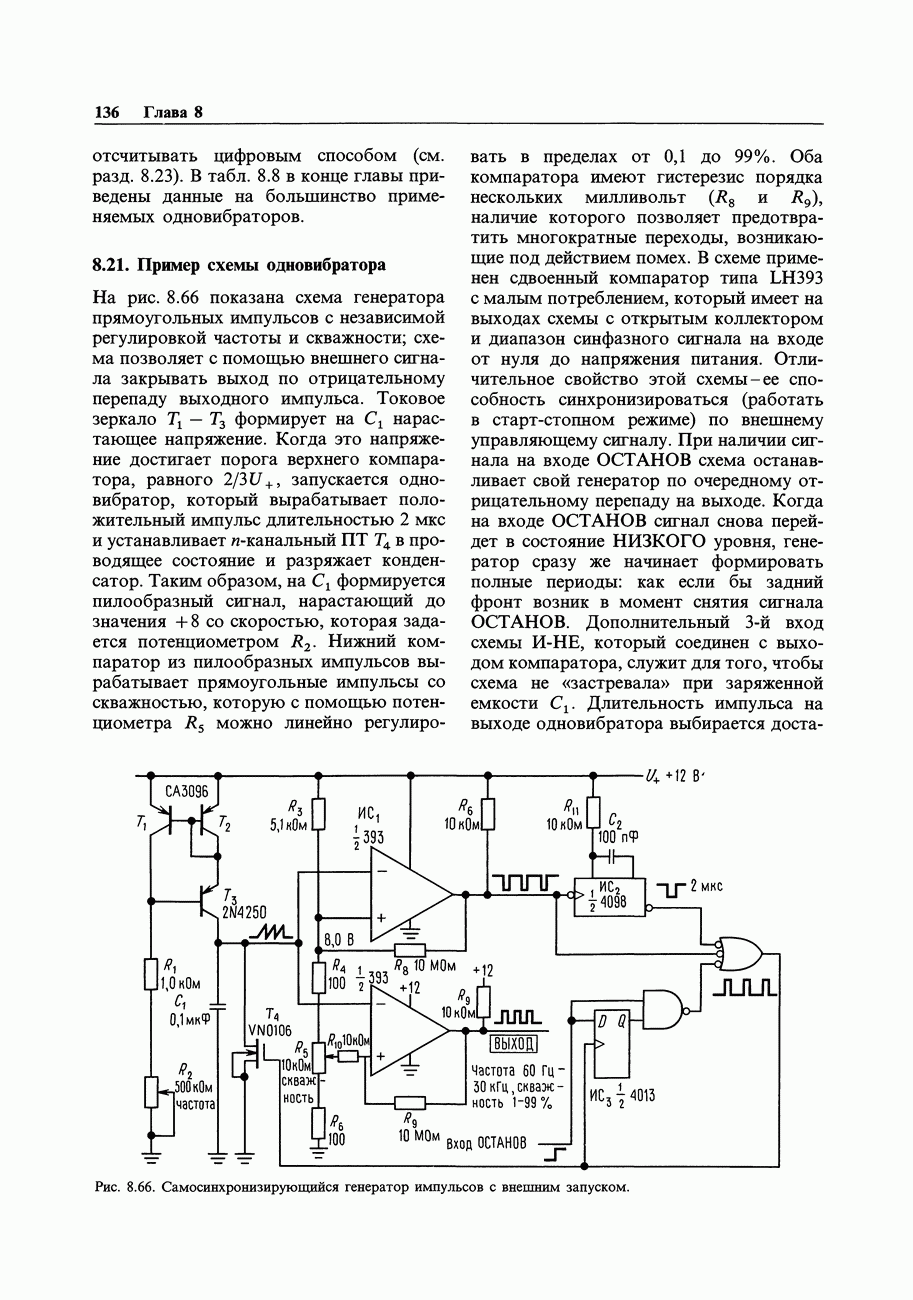
- 8.20. Характеристики одновибраторов
- 8.21. Пример схемы одновибратора
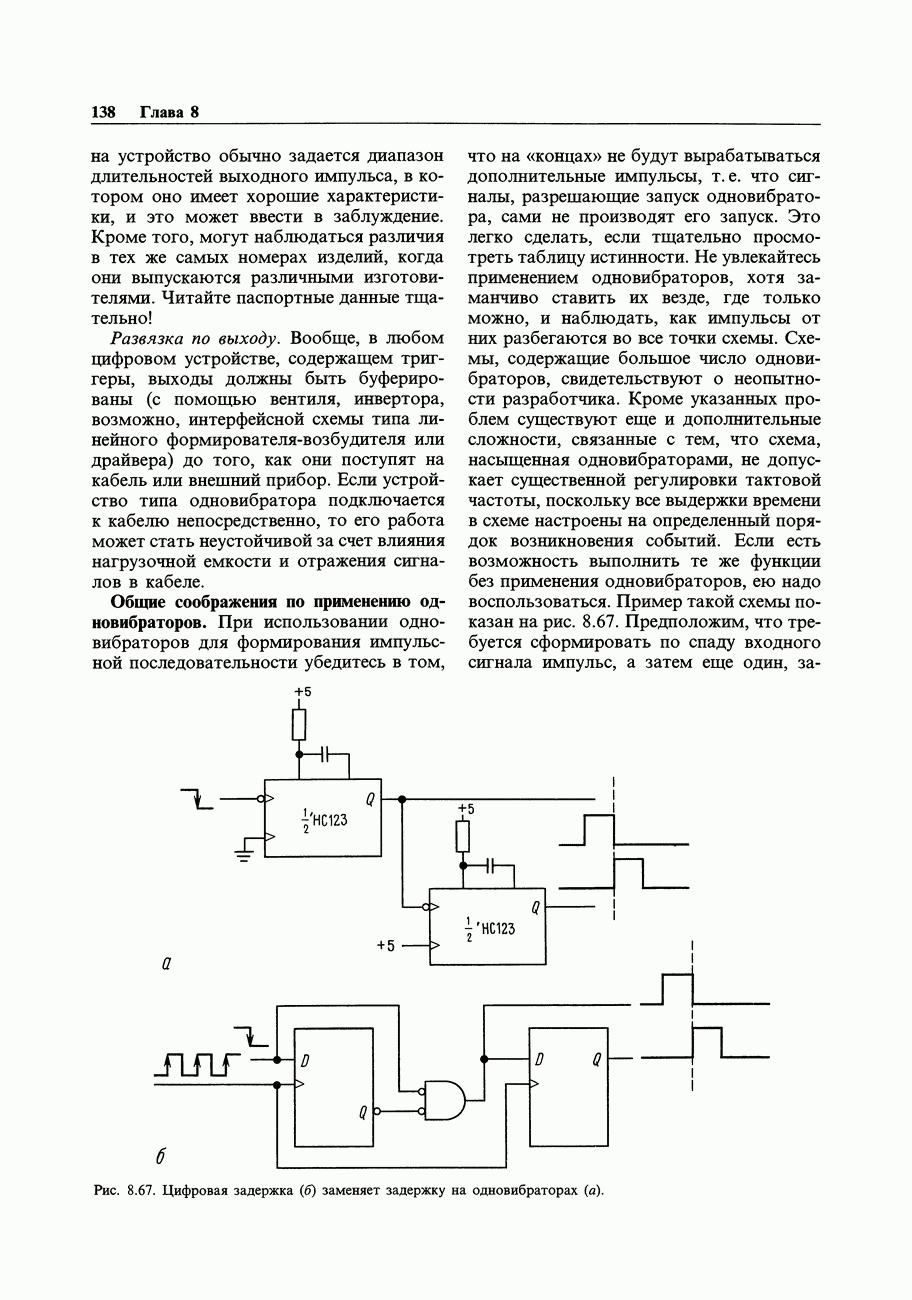
- 8.22. Предостережения относительно одновибраторов
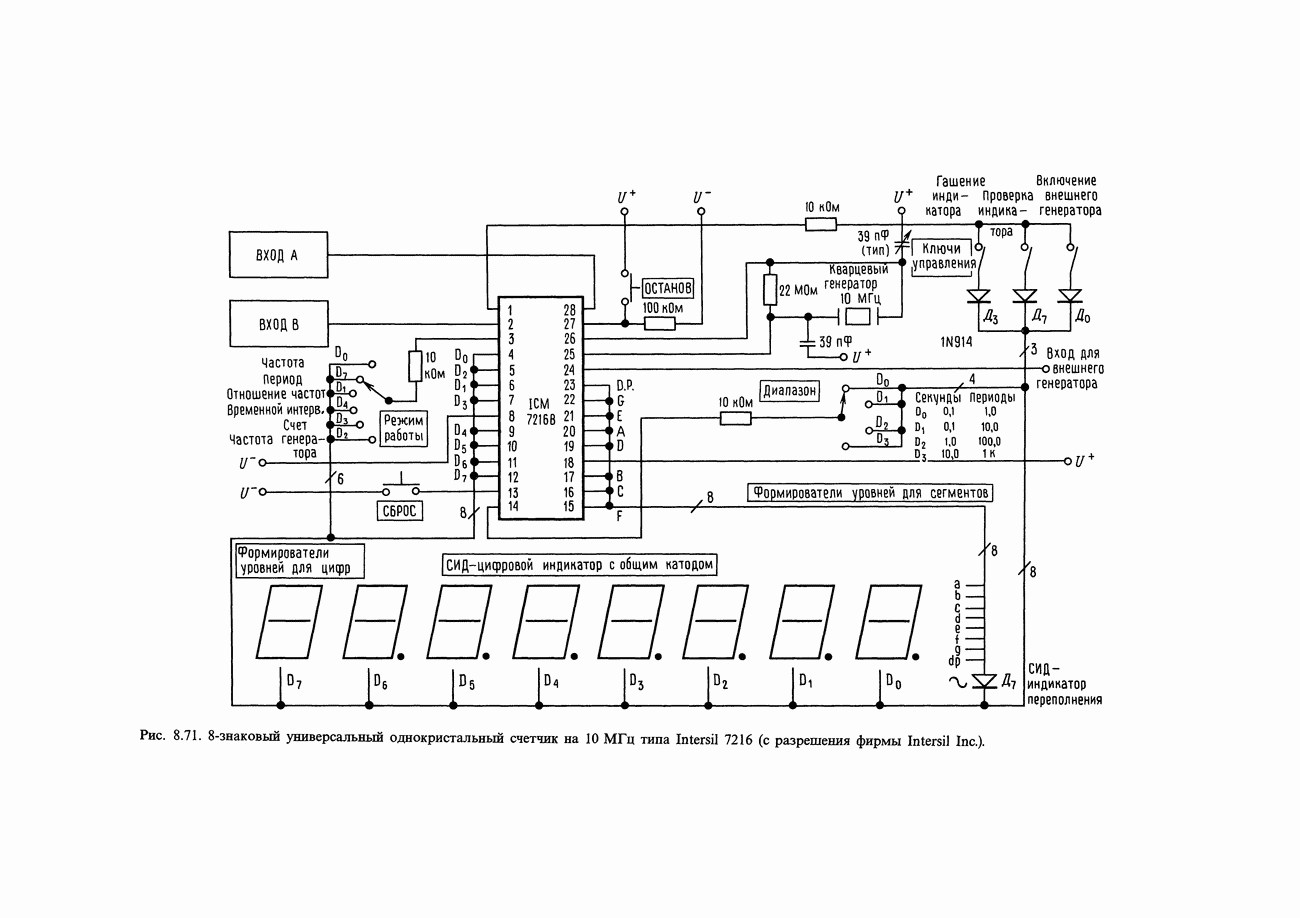
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
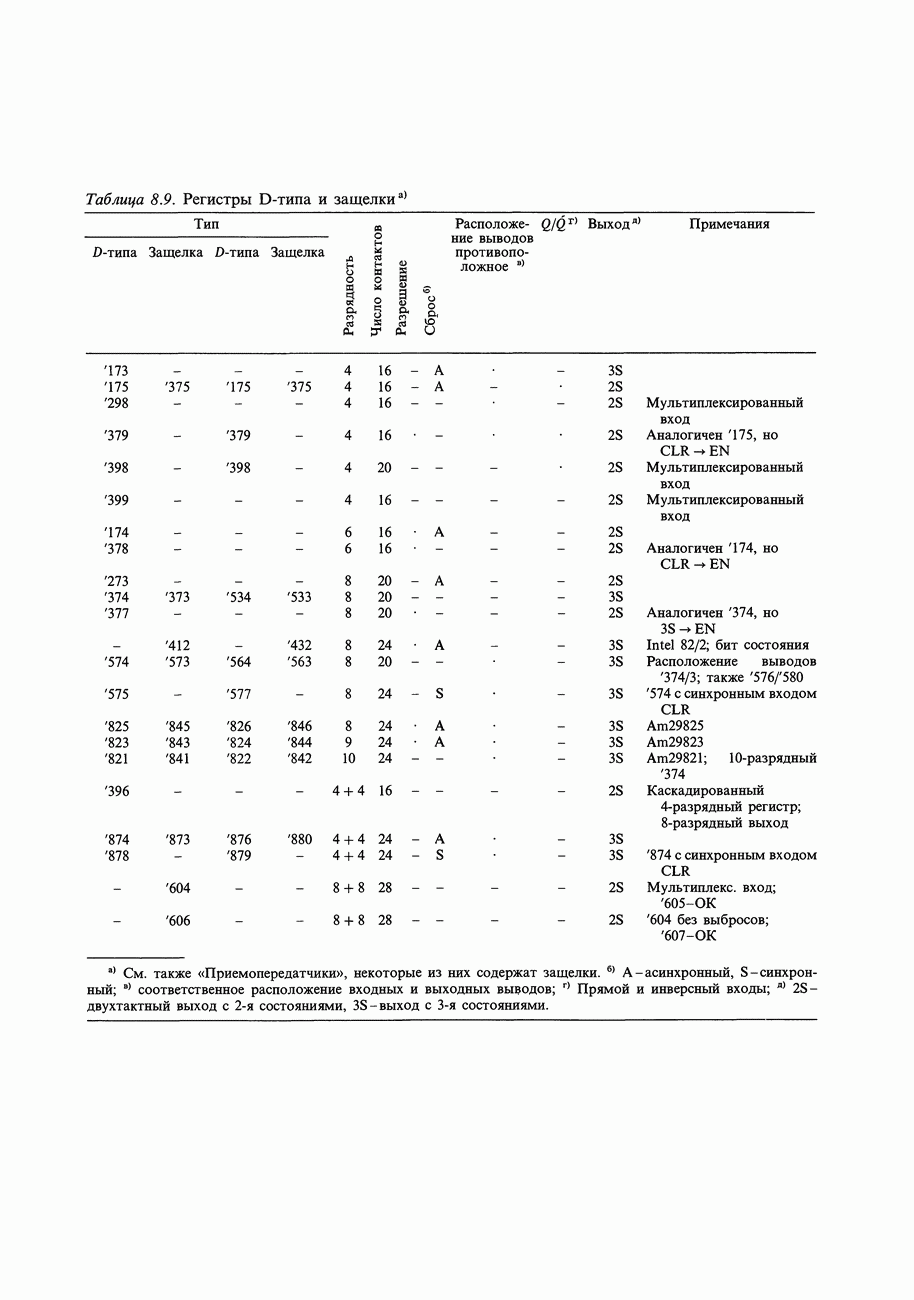
- 8.24. Фиксирующие схемы-защелки и регистры
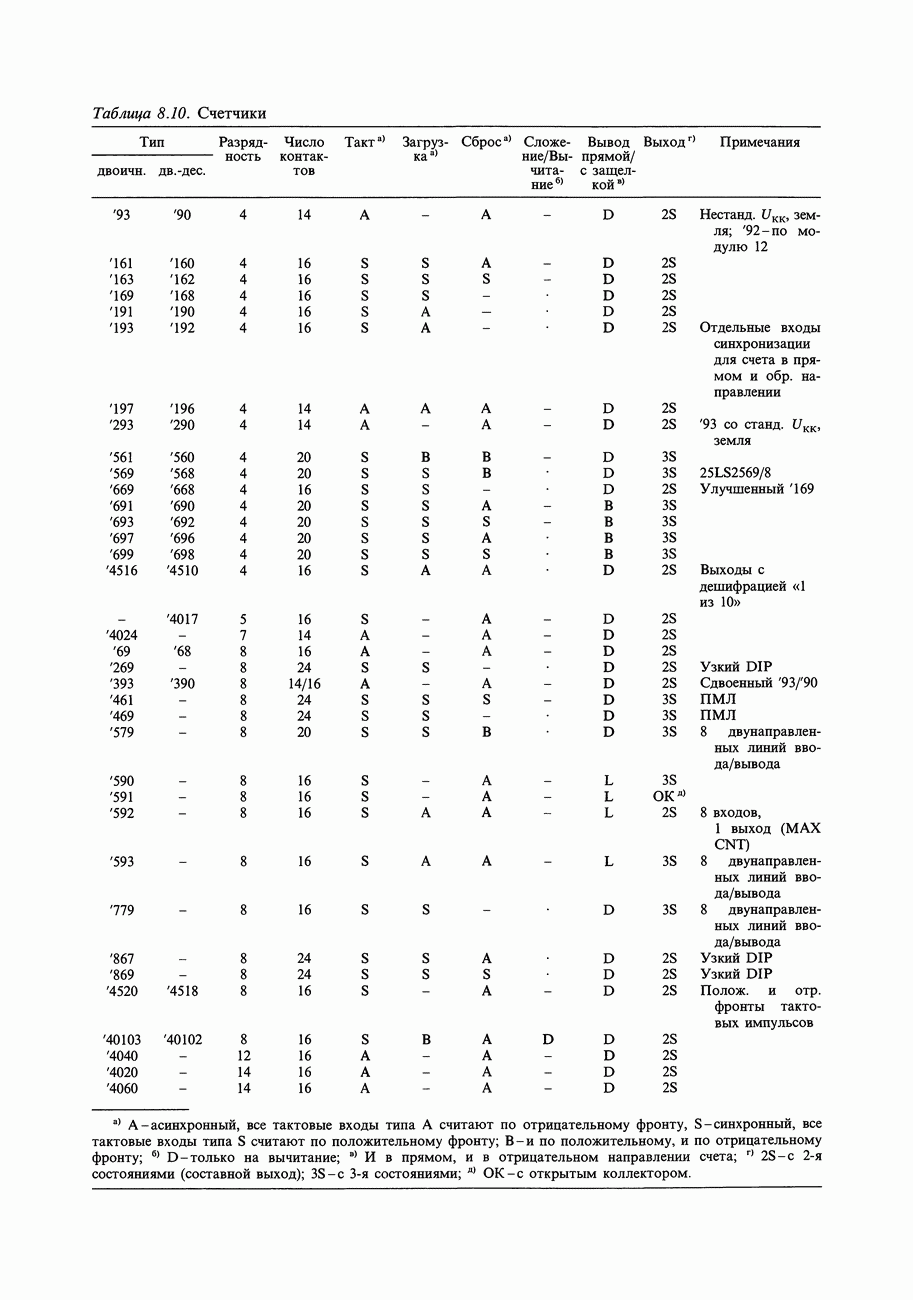
- 8.25. Счетчики
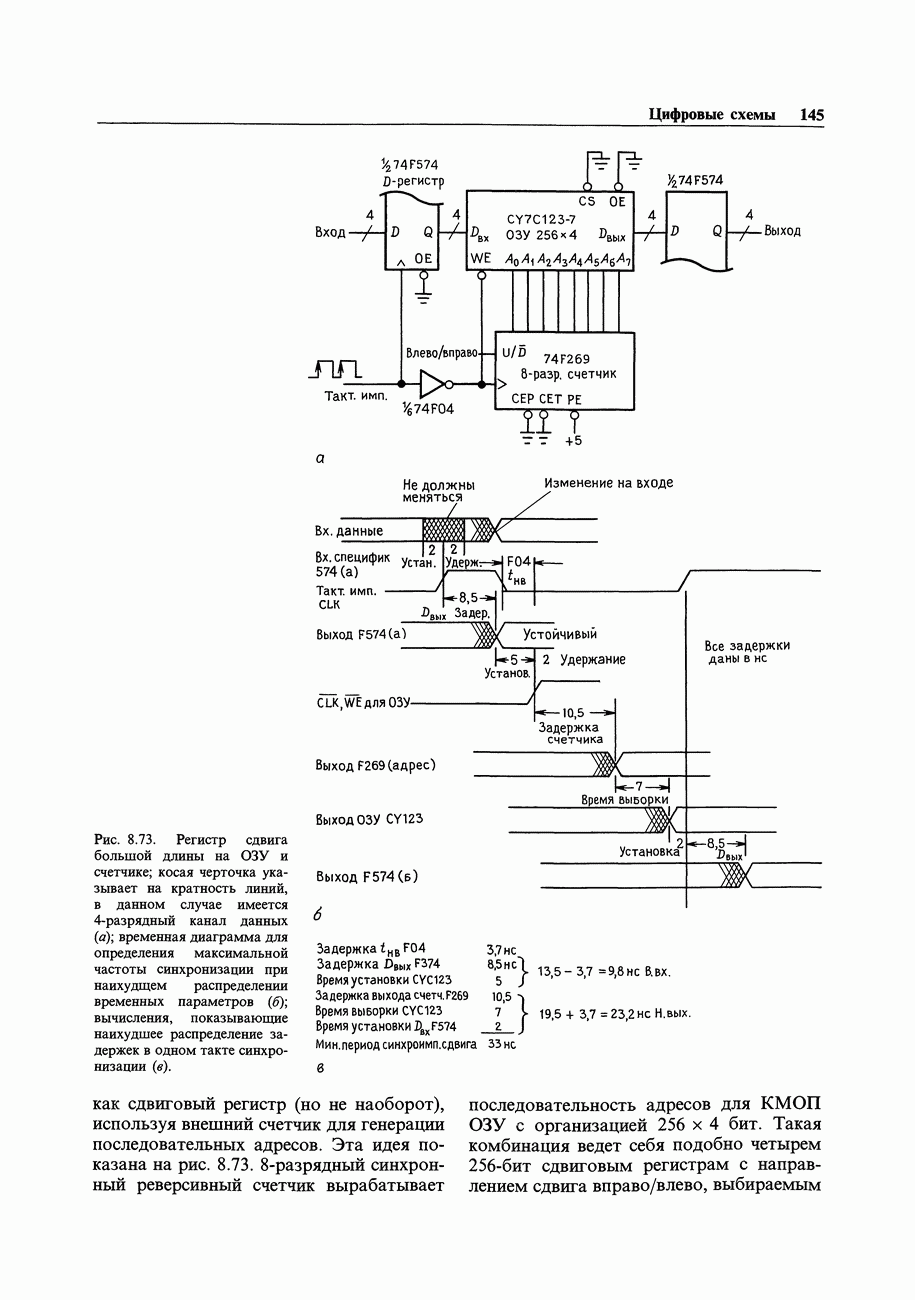
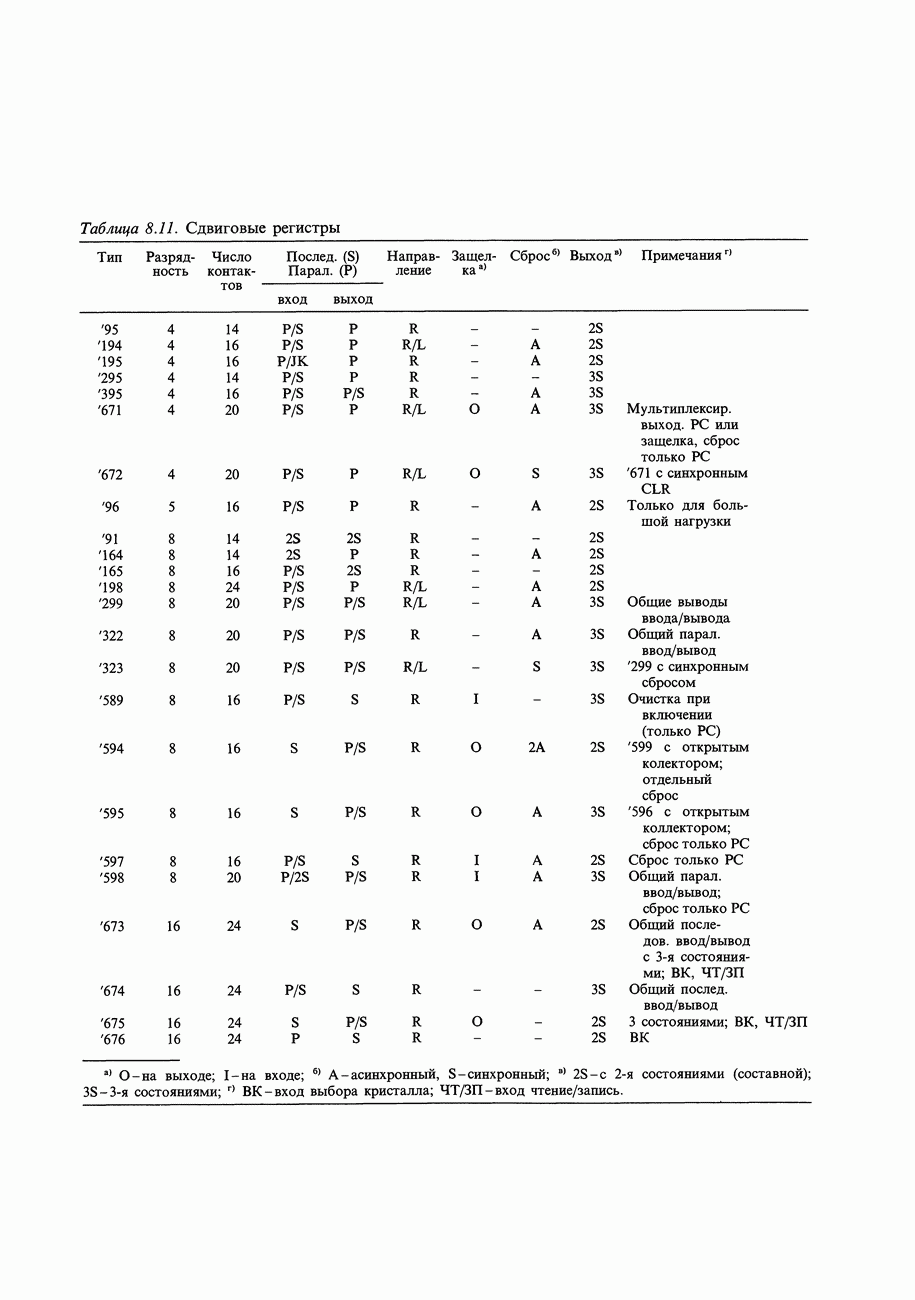
- 8.26. Регистры сдвига
- 8.27. Последовательностные ПМЛ
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
- 8.29. Счетчик по модулю n
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
- 8.31. Привод звездного телескопа
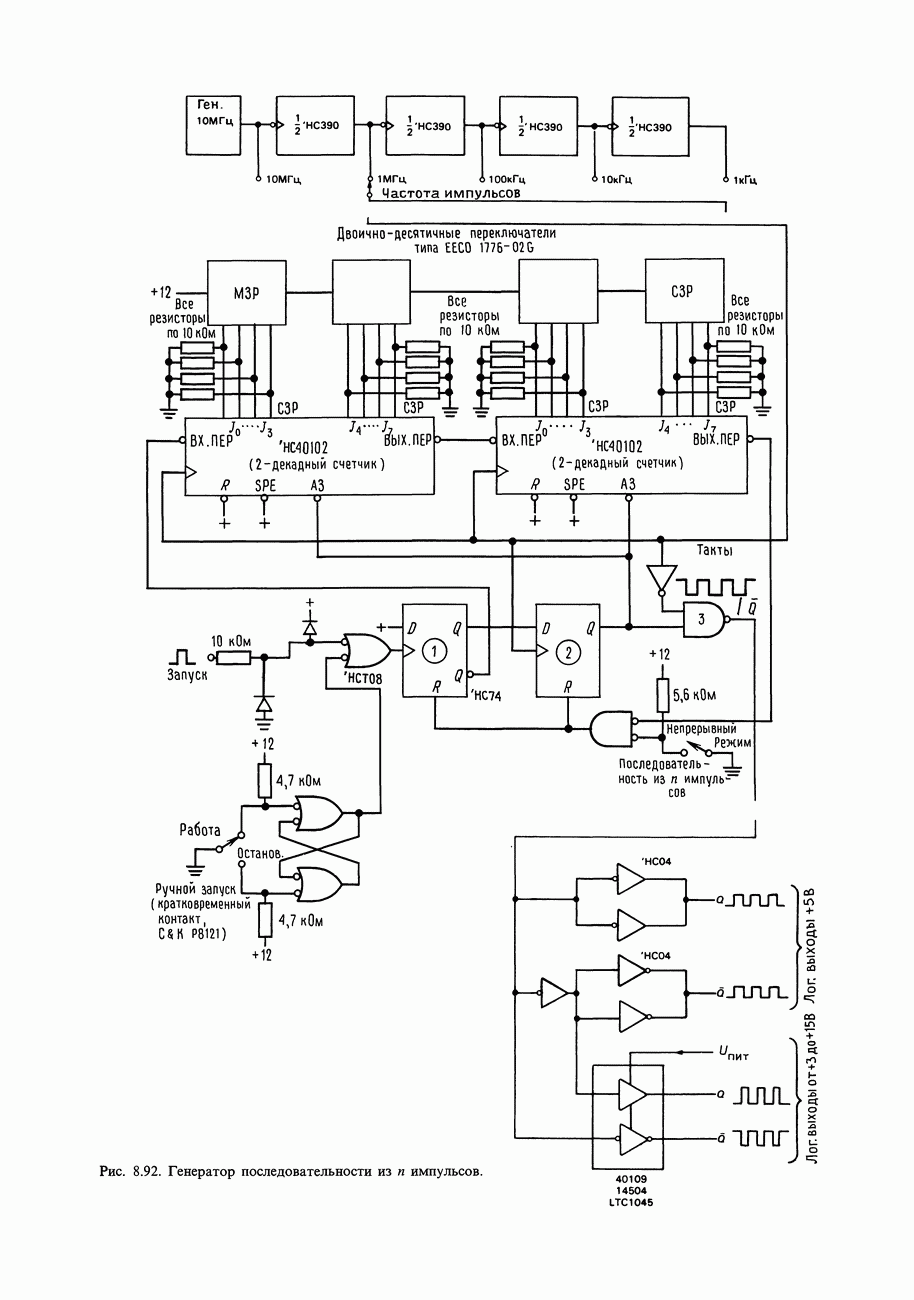
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
- 8.35. Прирожденные недостатки ТТЛ и КМОП
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
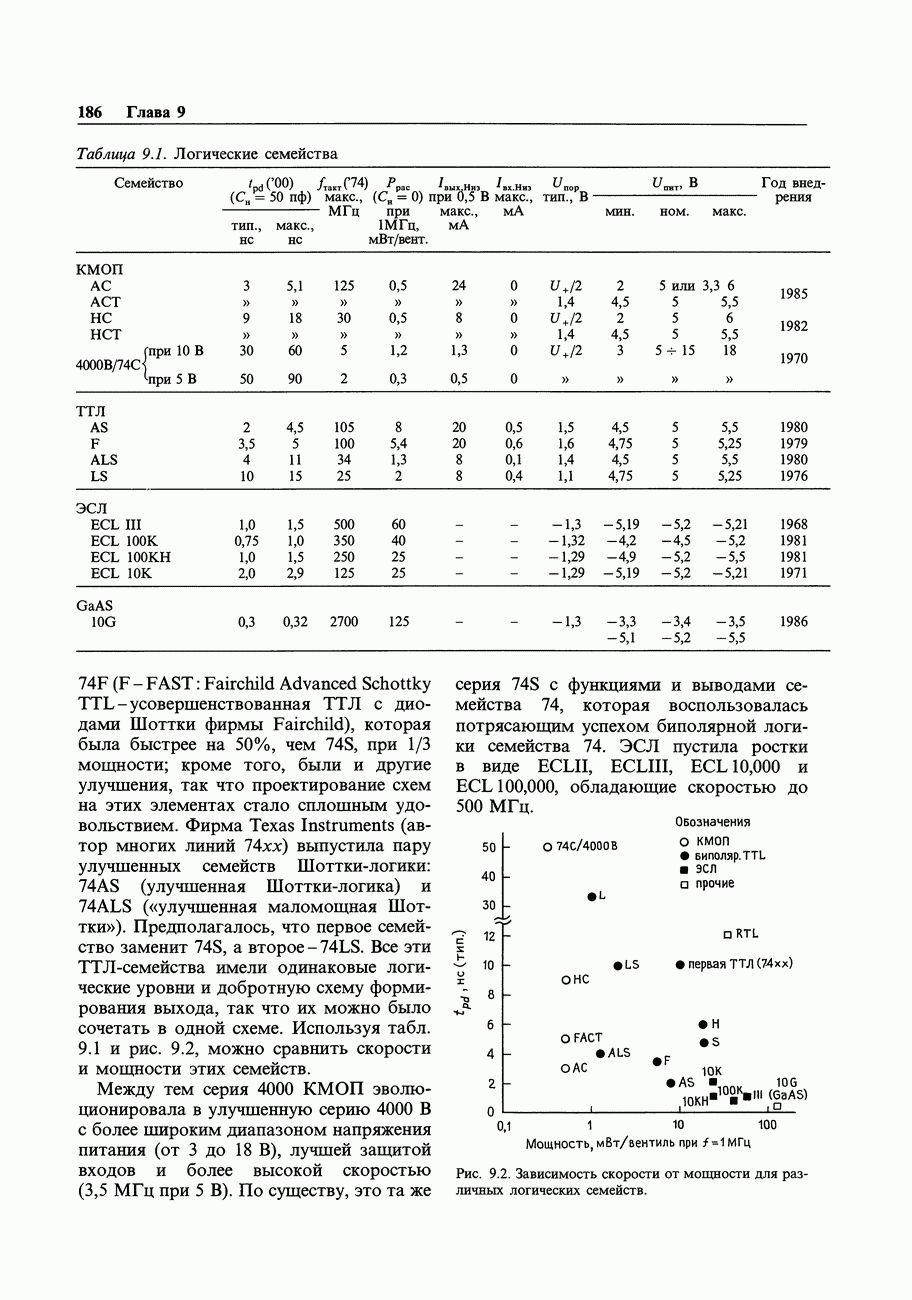
- 9.01. Хронология логических семейств
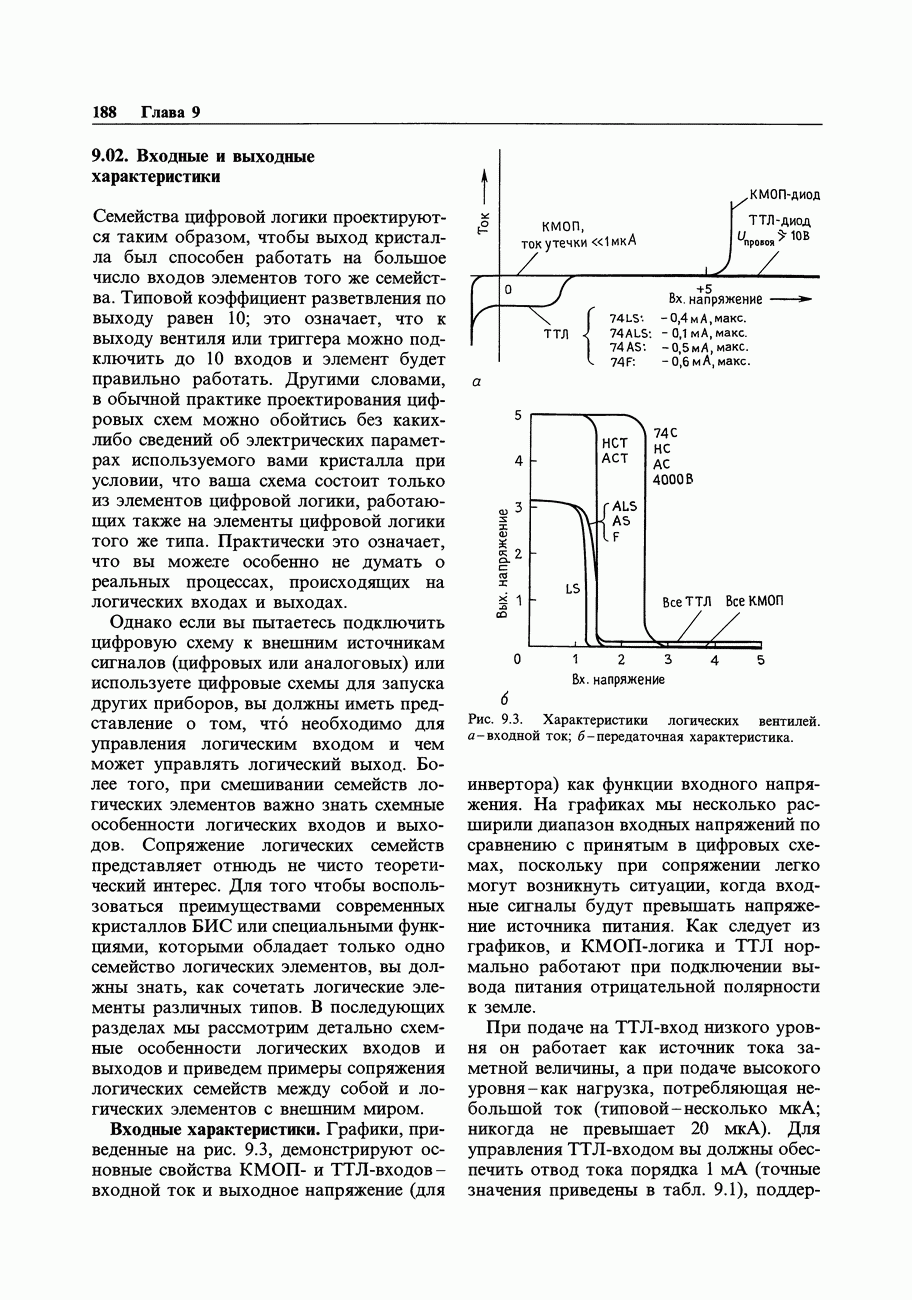
- 9.02. Входные и выходные характеристики
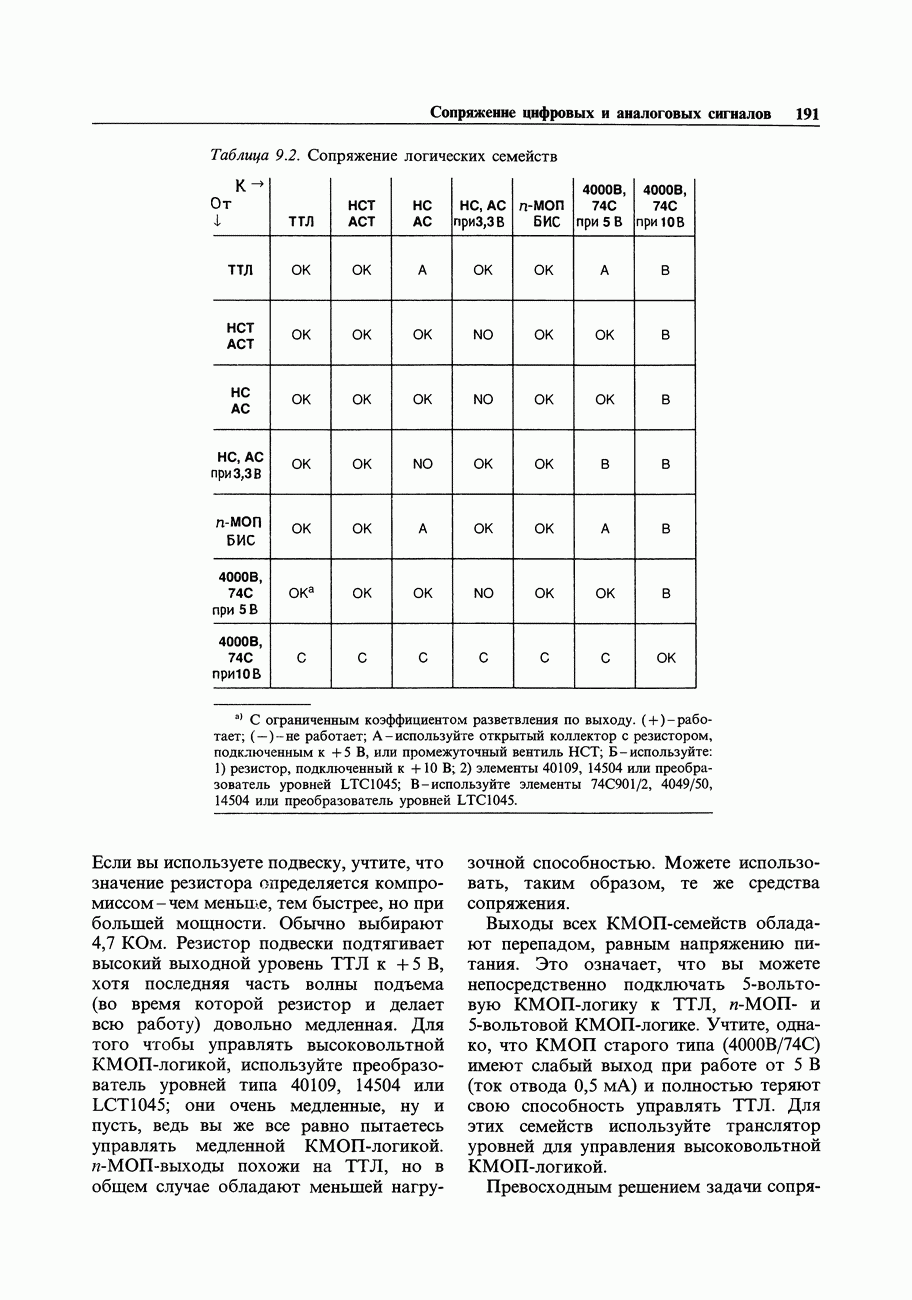
- 9.03. Сопряжение логических семейств
- 9.04. Управление КМОП-и ТТЛ-входами
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
- 9.07. Компараторы
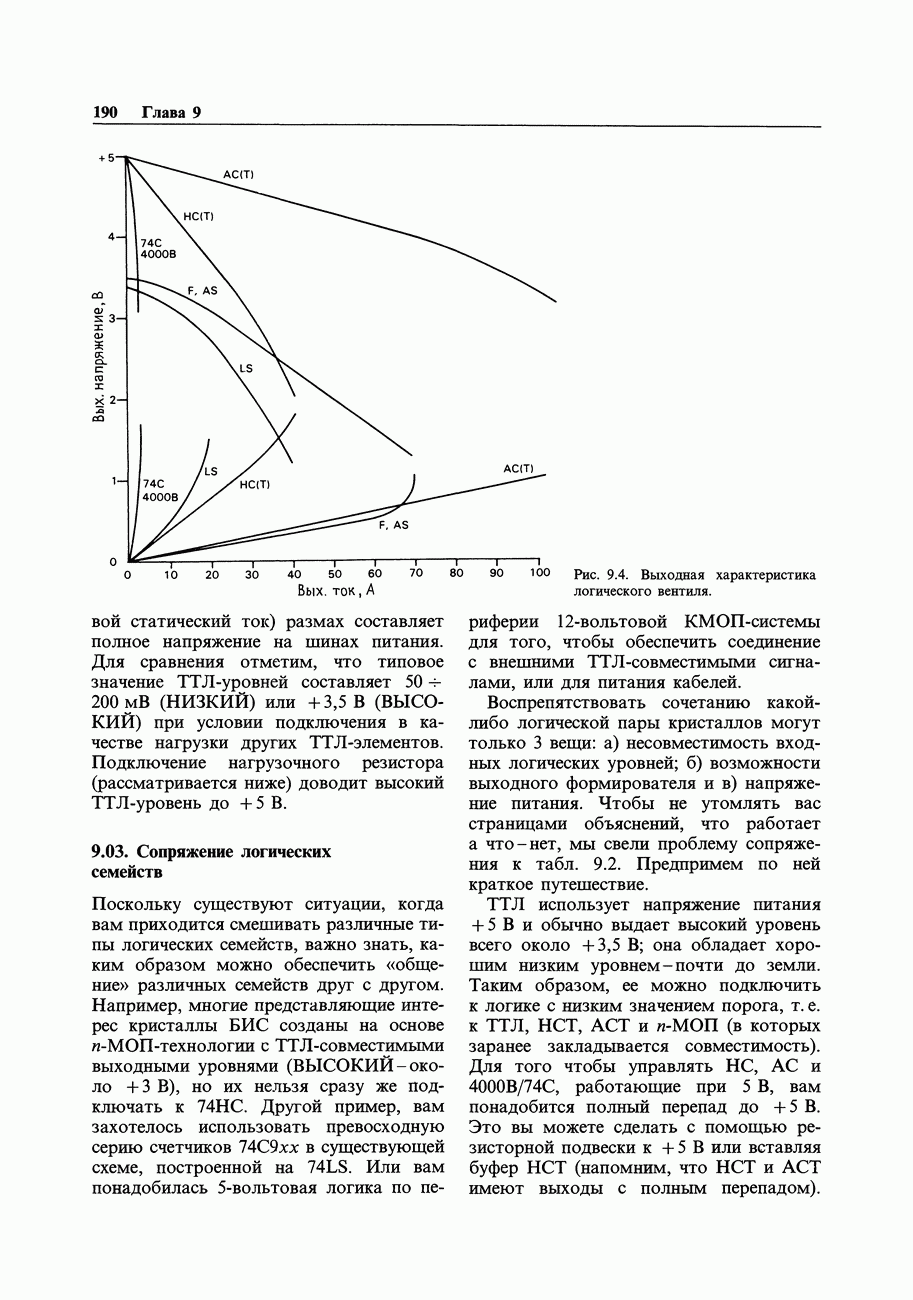
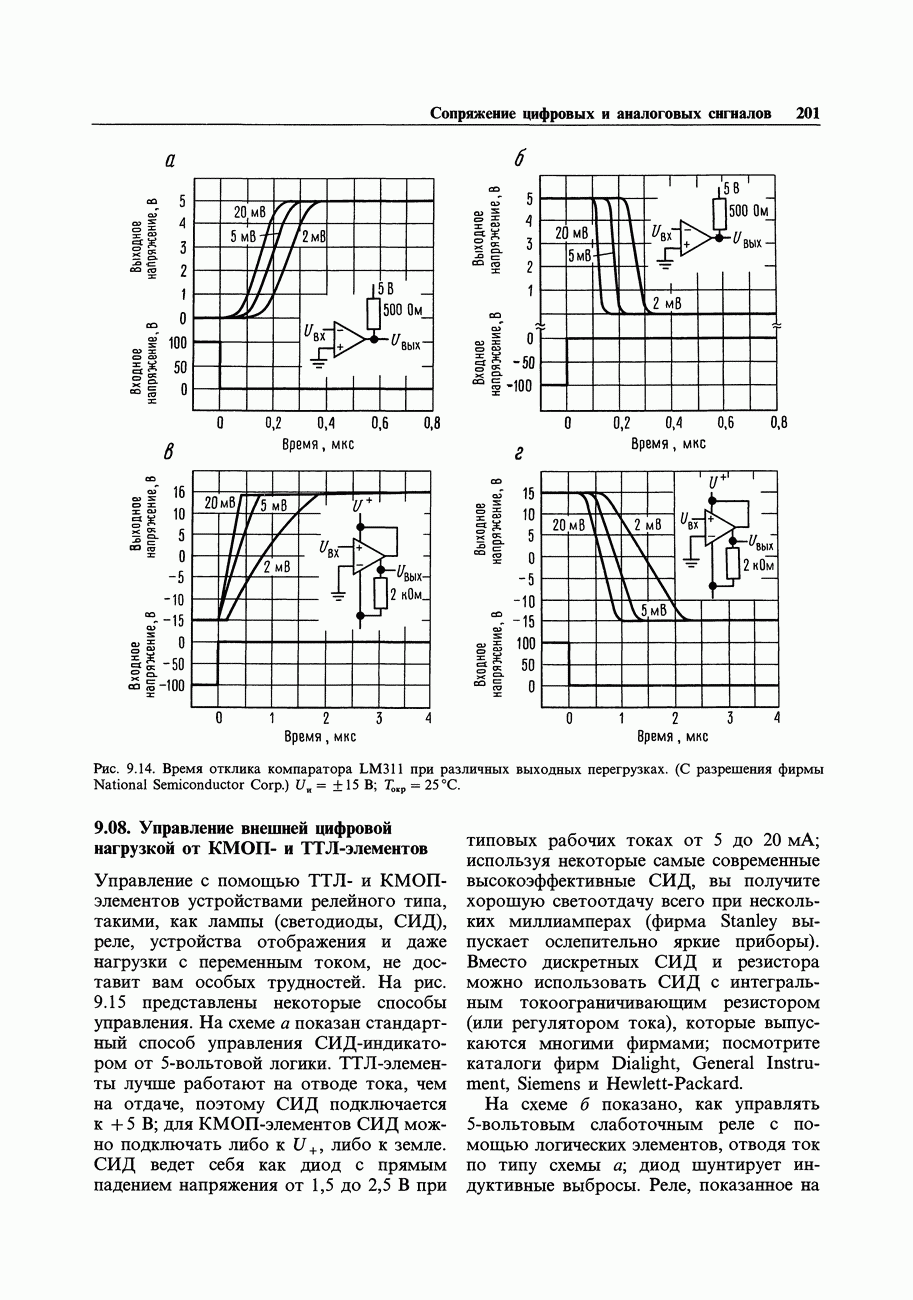
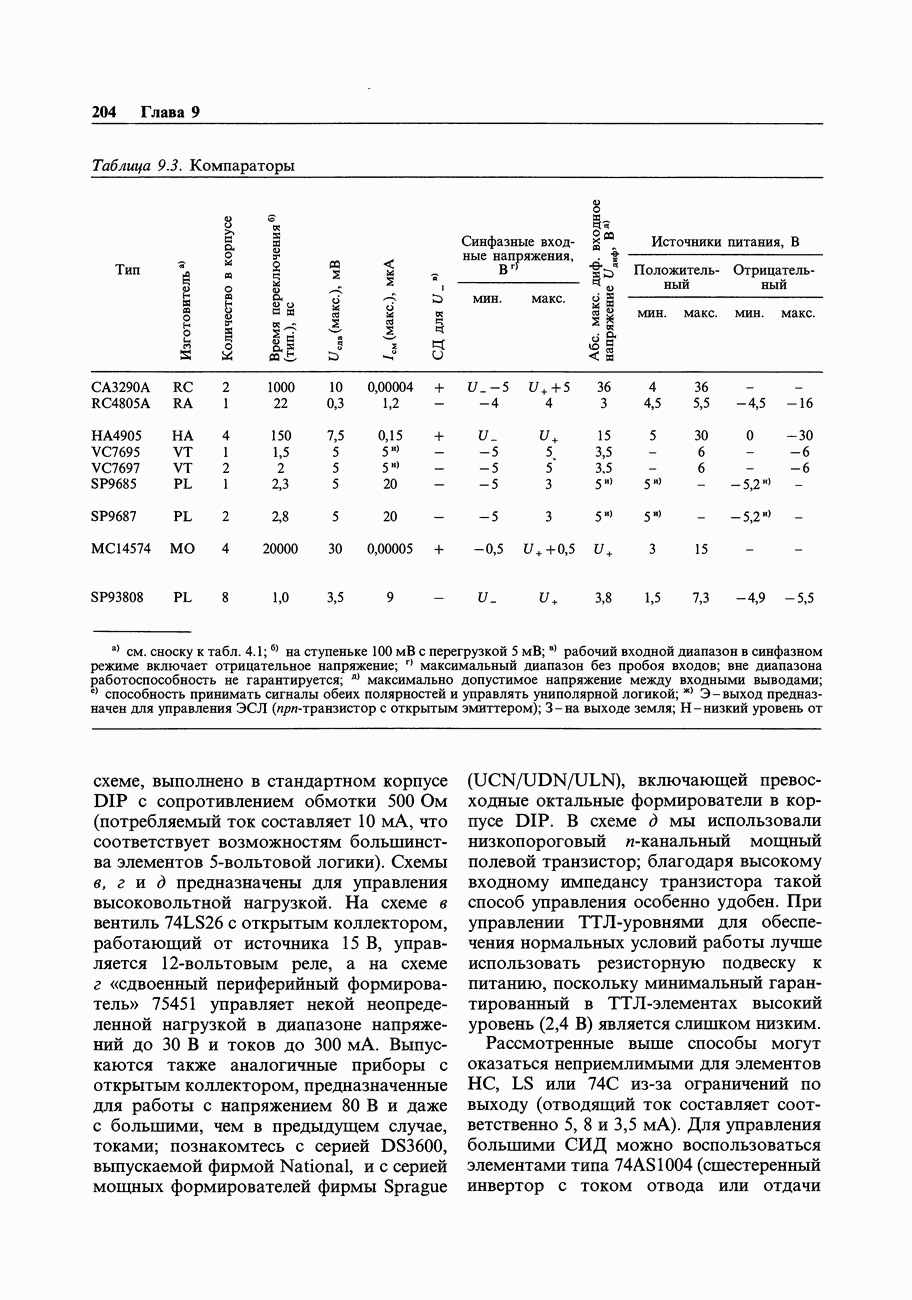
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
- 9.09. Сопряжение n-МОП БИС
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
- 9.14. Кабельные связи
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
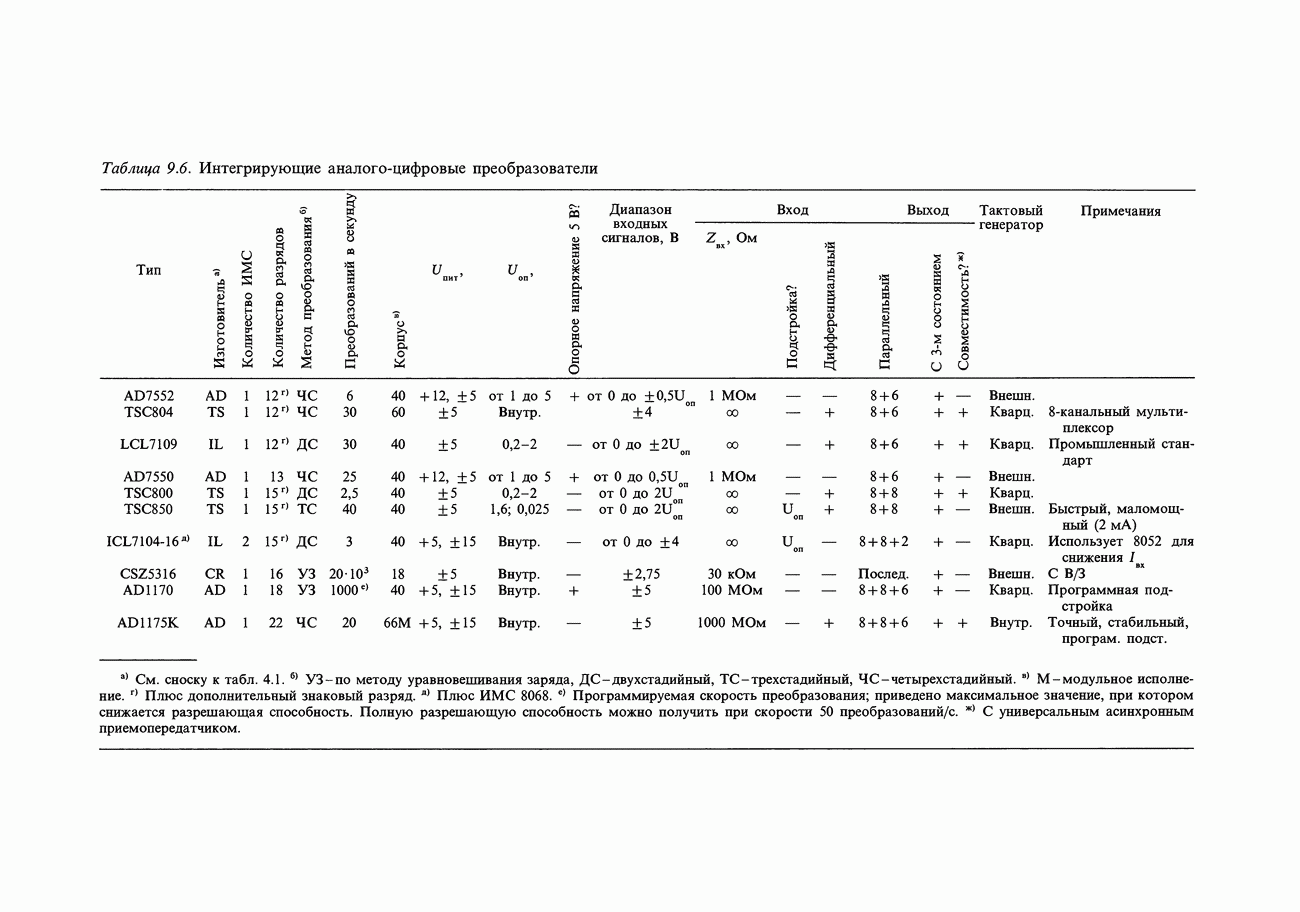
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
- 9.19. Выбор ЦАП
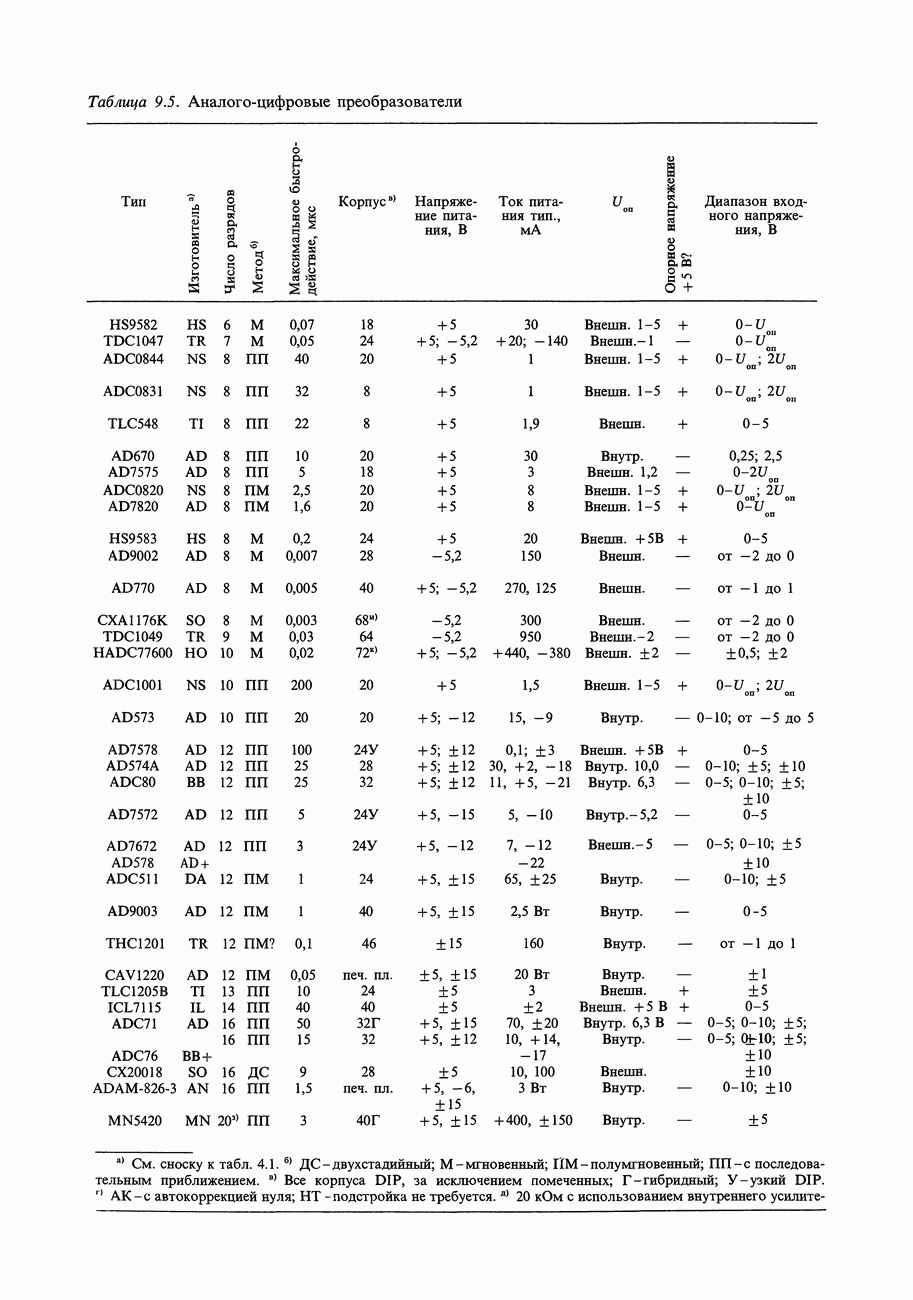
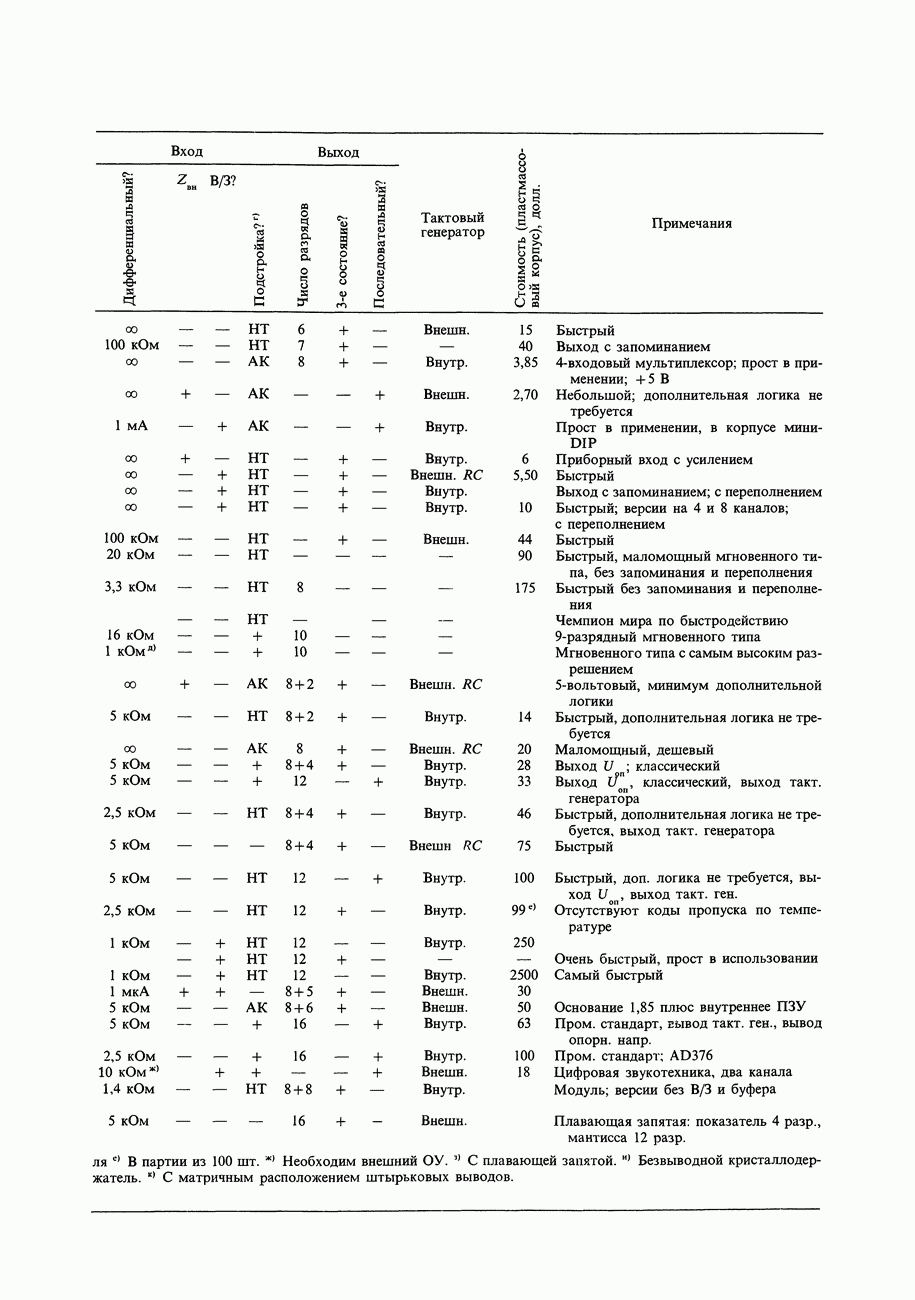
- 9.20. Аналого-цифровые преобразователи
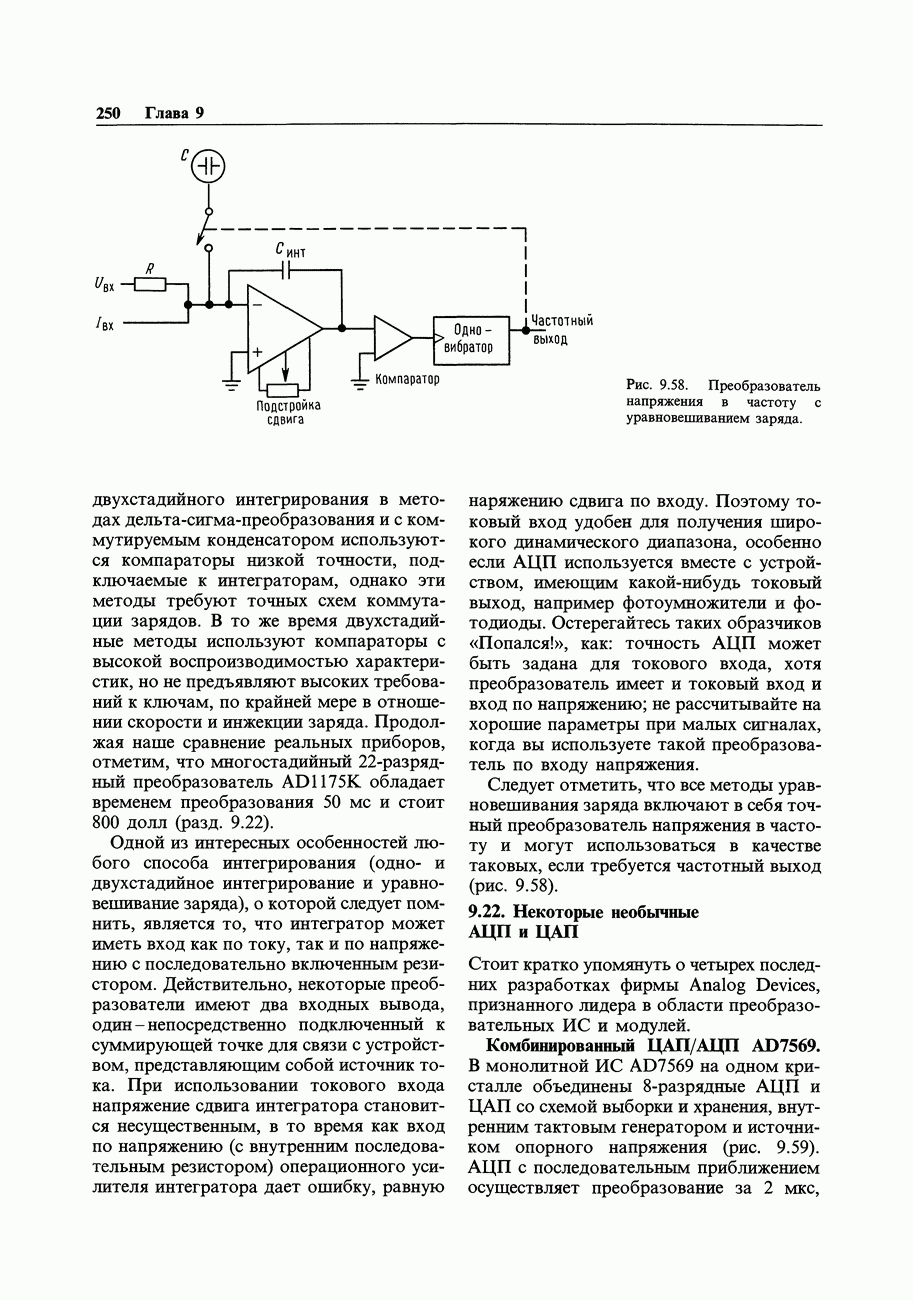
- 9.21. Методы уравновешивания заряда
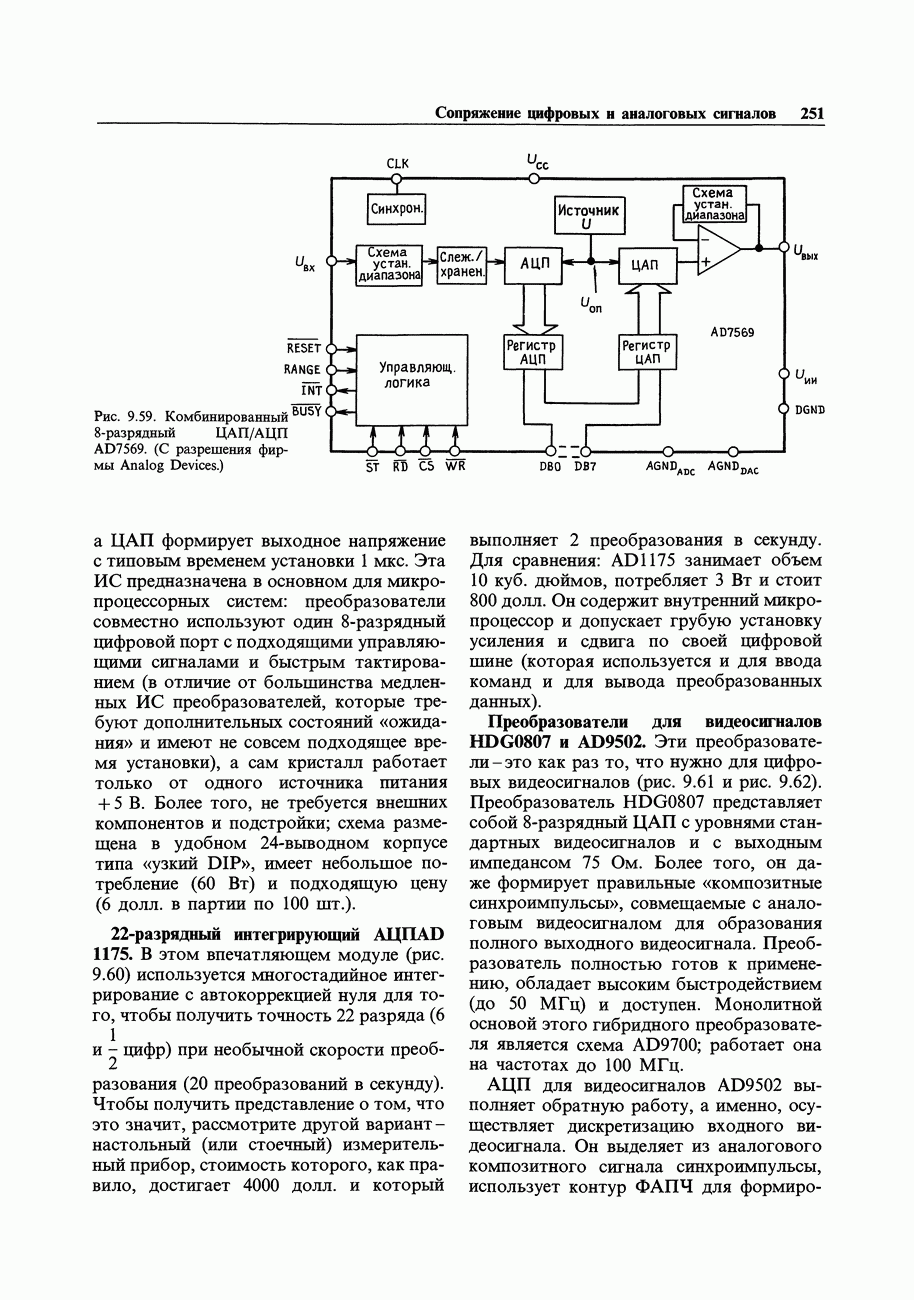
- 9.22. Некоторые необычные АЦП и ЦАП
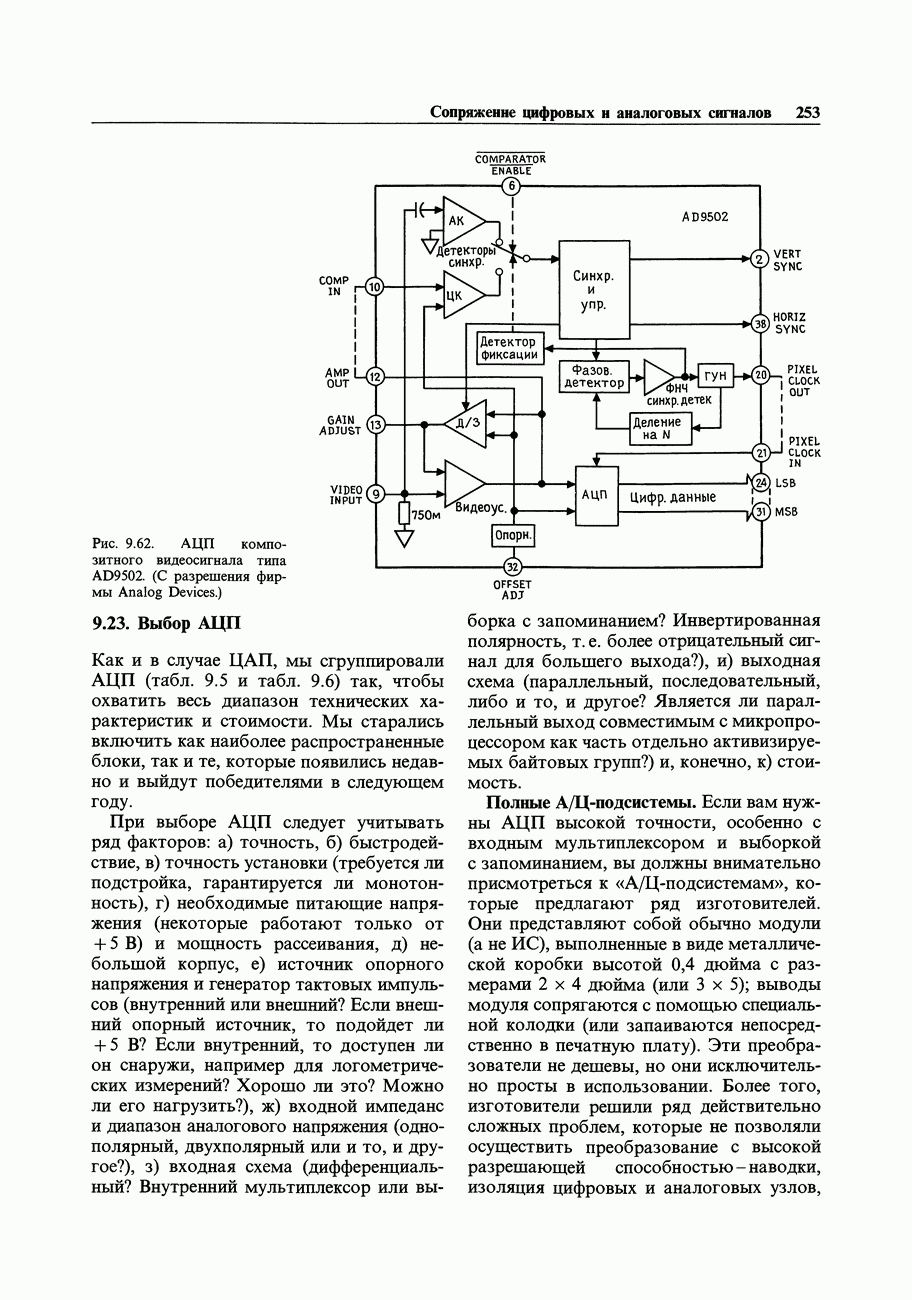
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
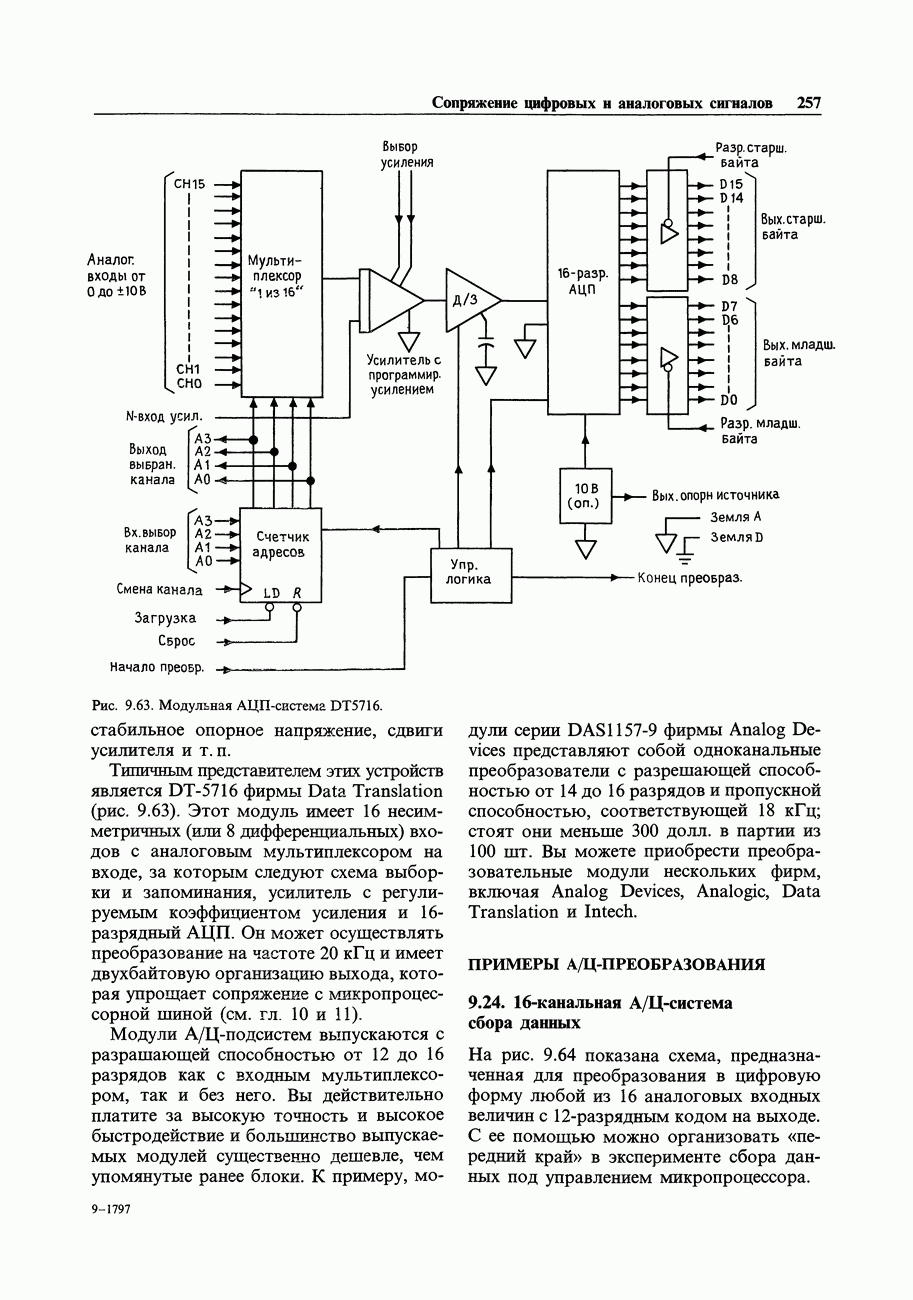
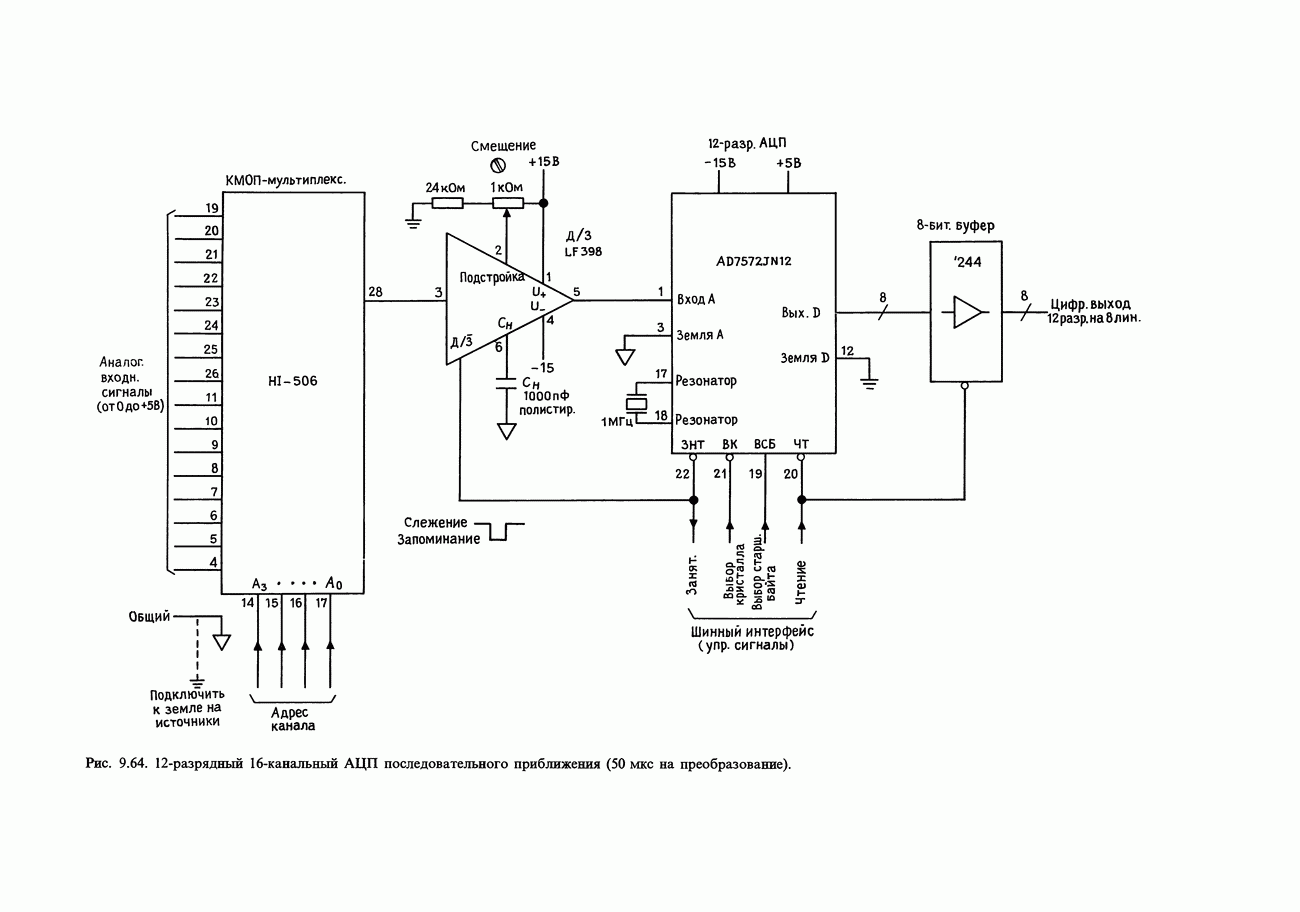
- 9.24. 16-канальная А/Ц-система сбора данных
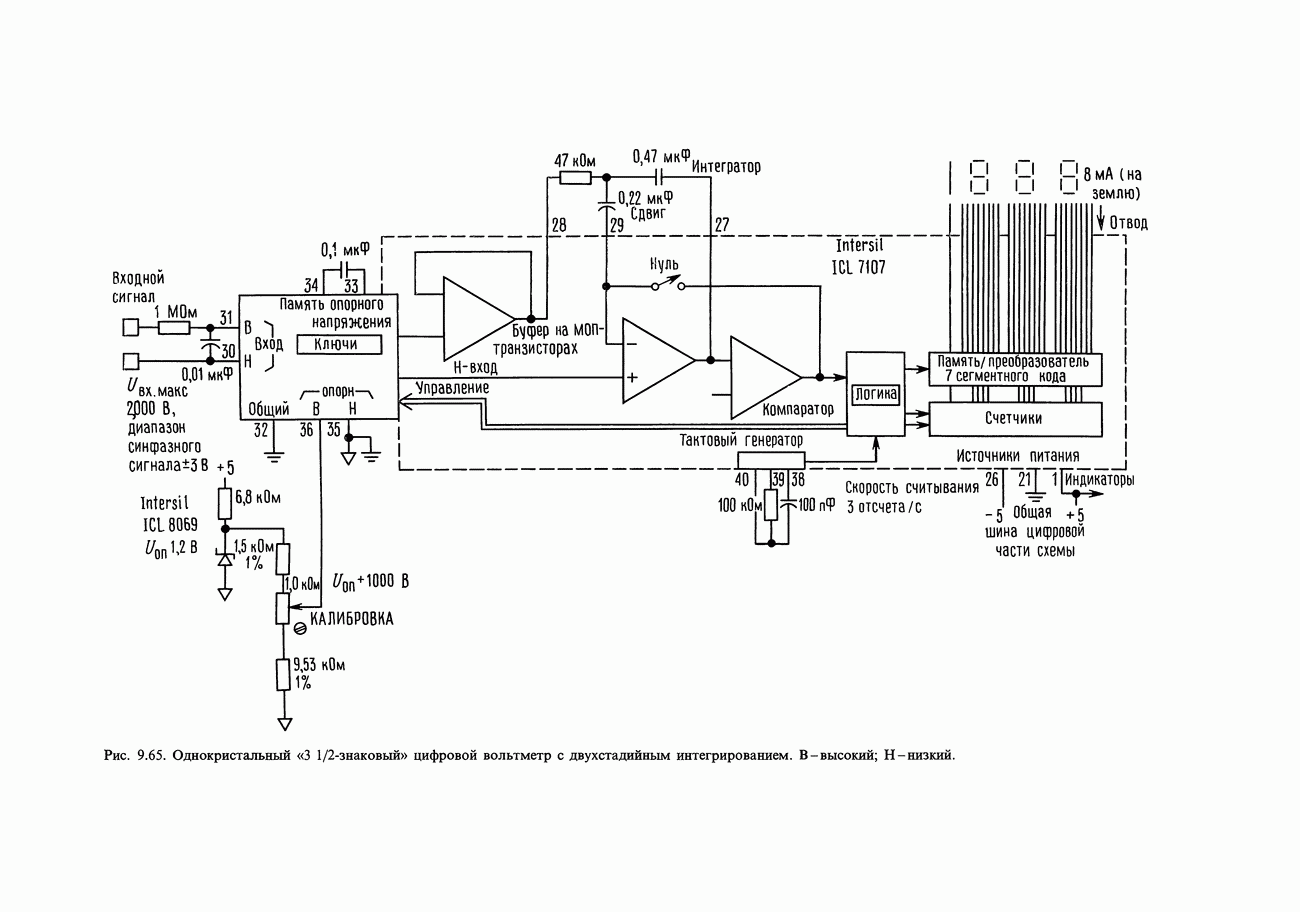
- 9.25. 3 1/2 — знаковый цифровой вольтметр
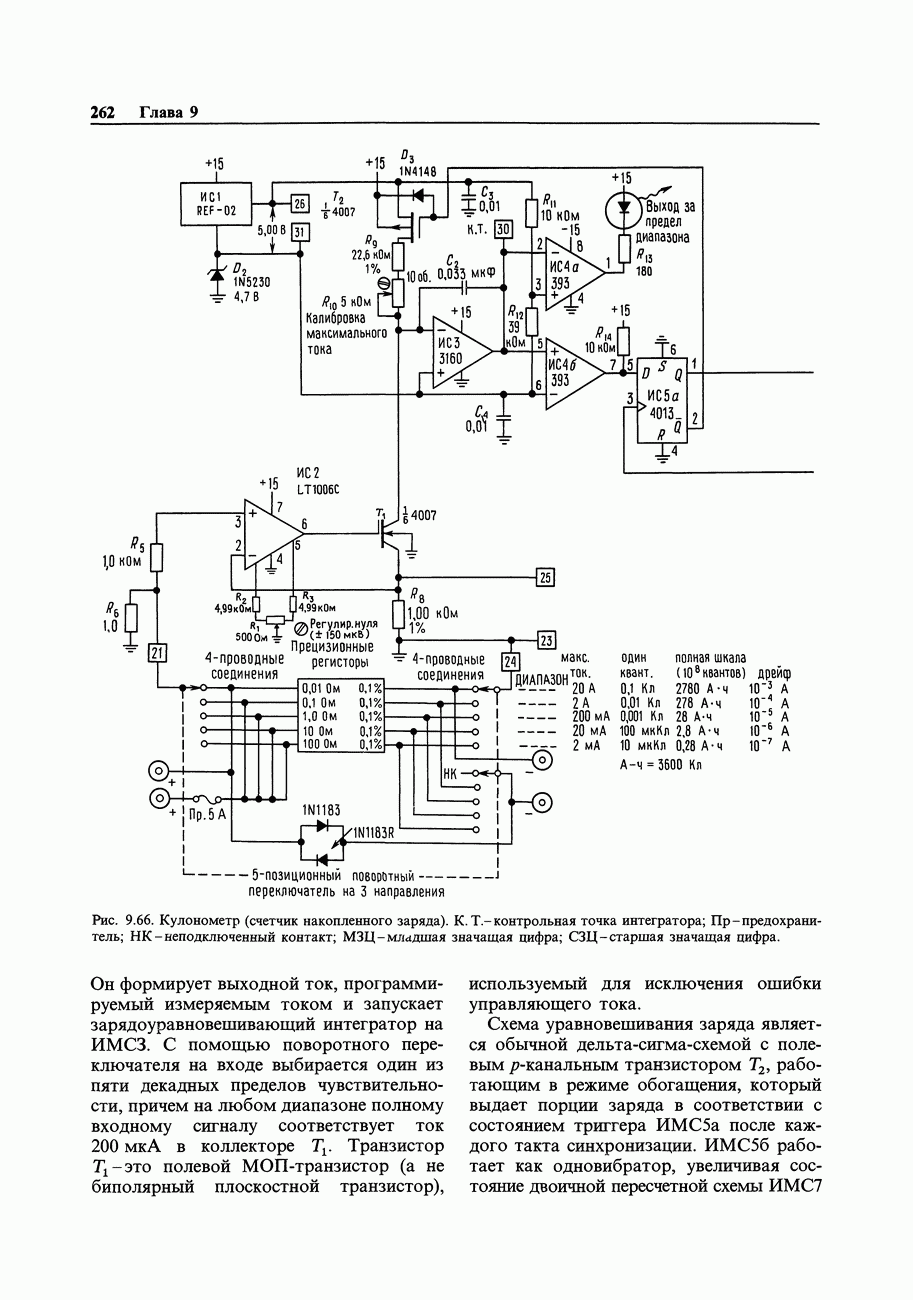
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
- 10.08. Программируемый ввод-вывод: регистры состояний
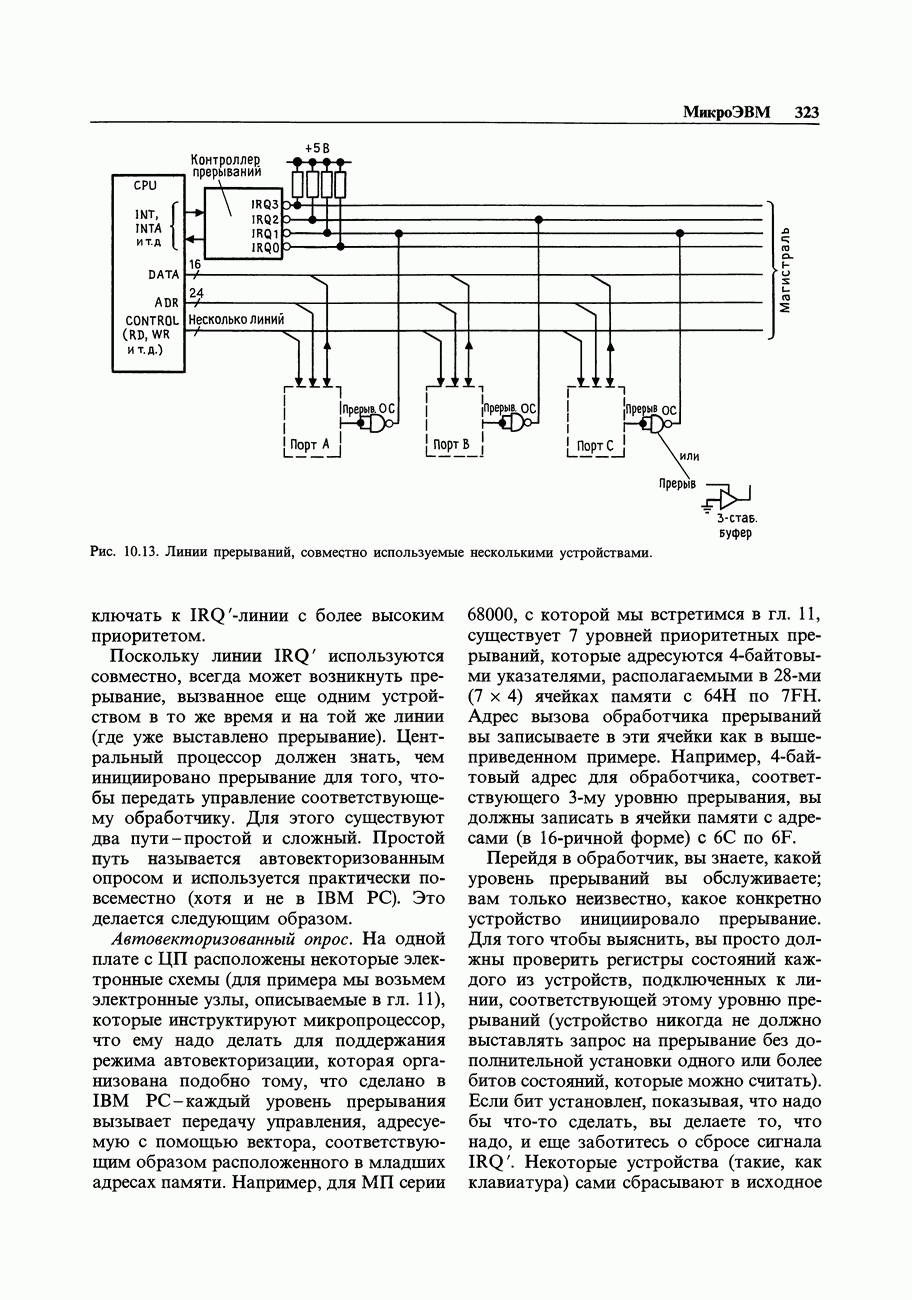
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
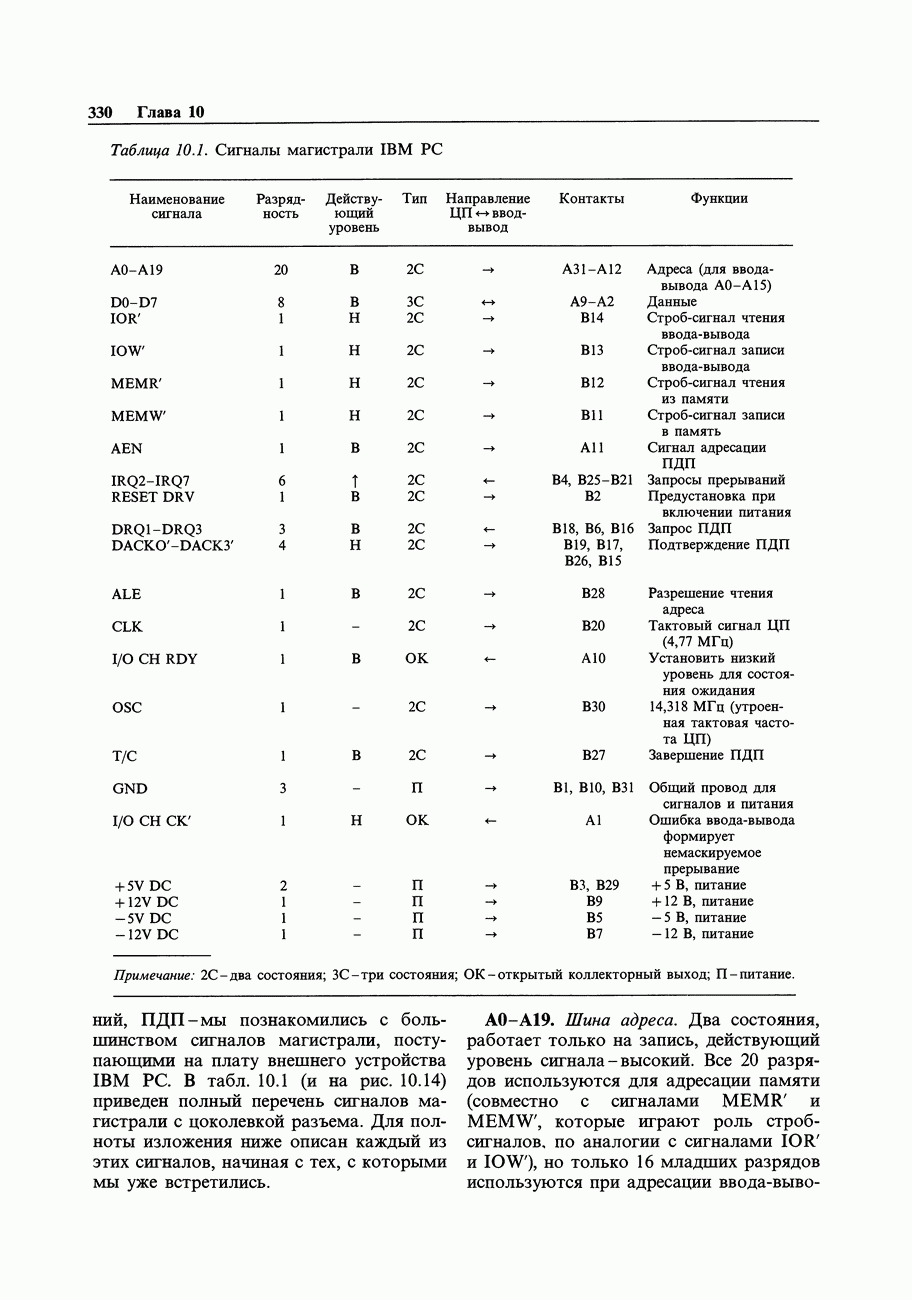
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
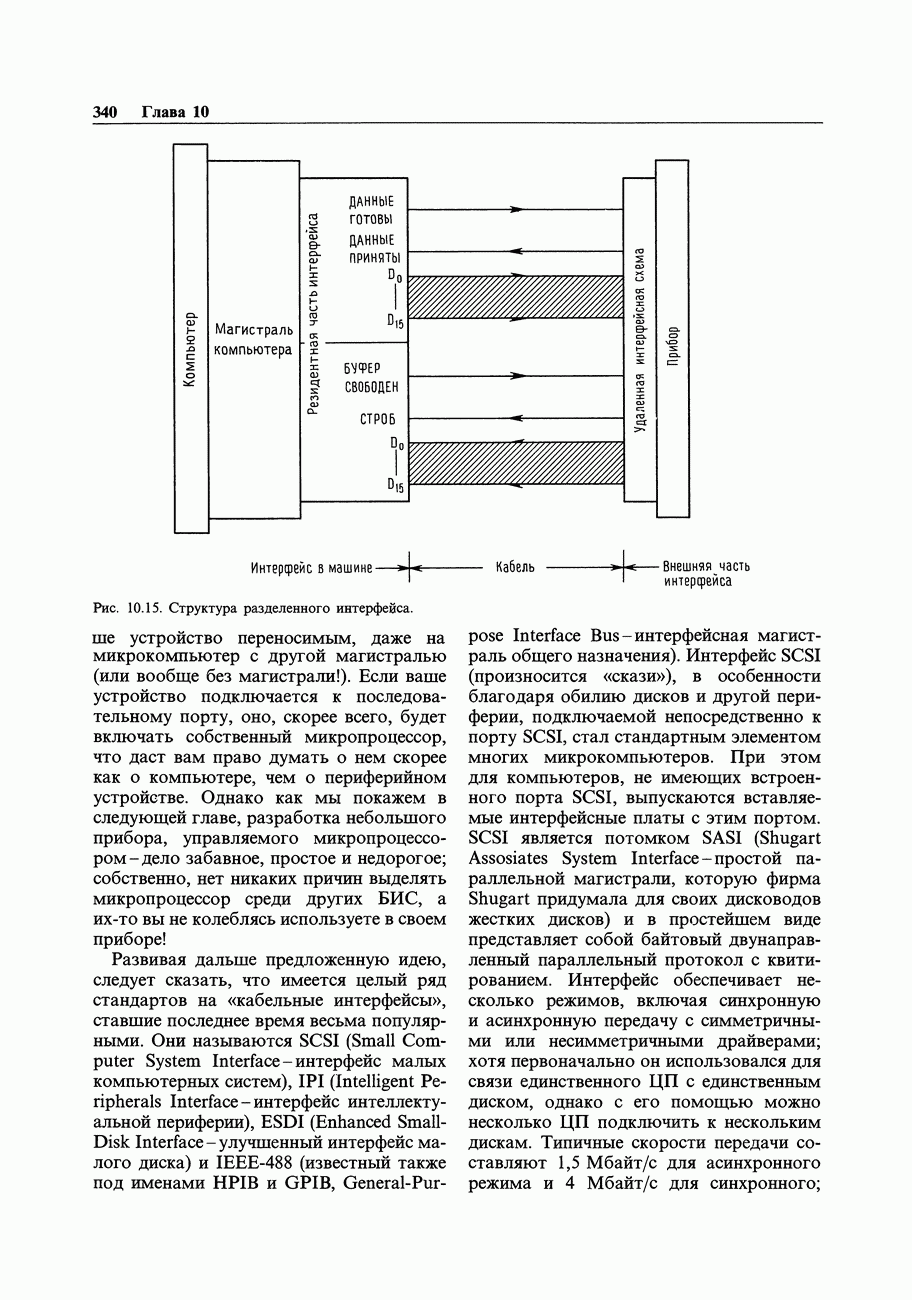
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
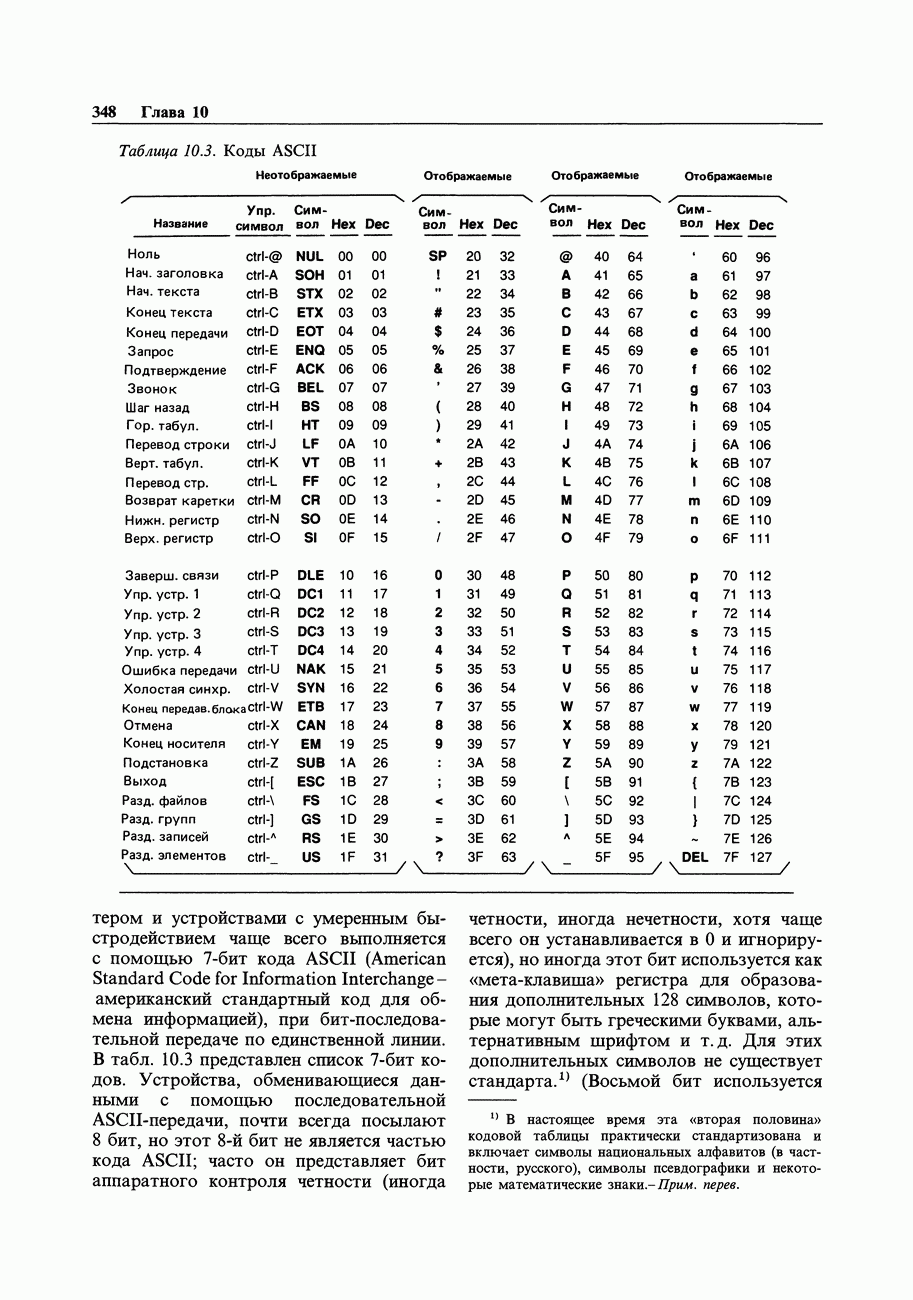
- 10.19. Последовательная связь и коды ASCII
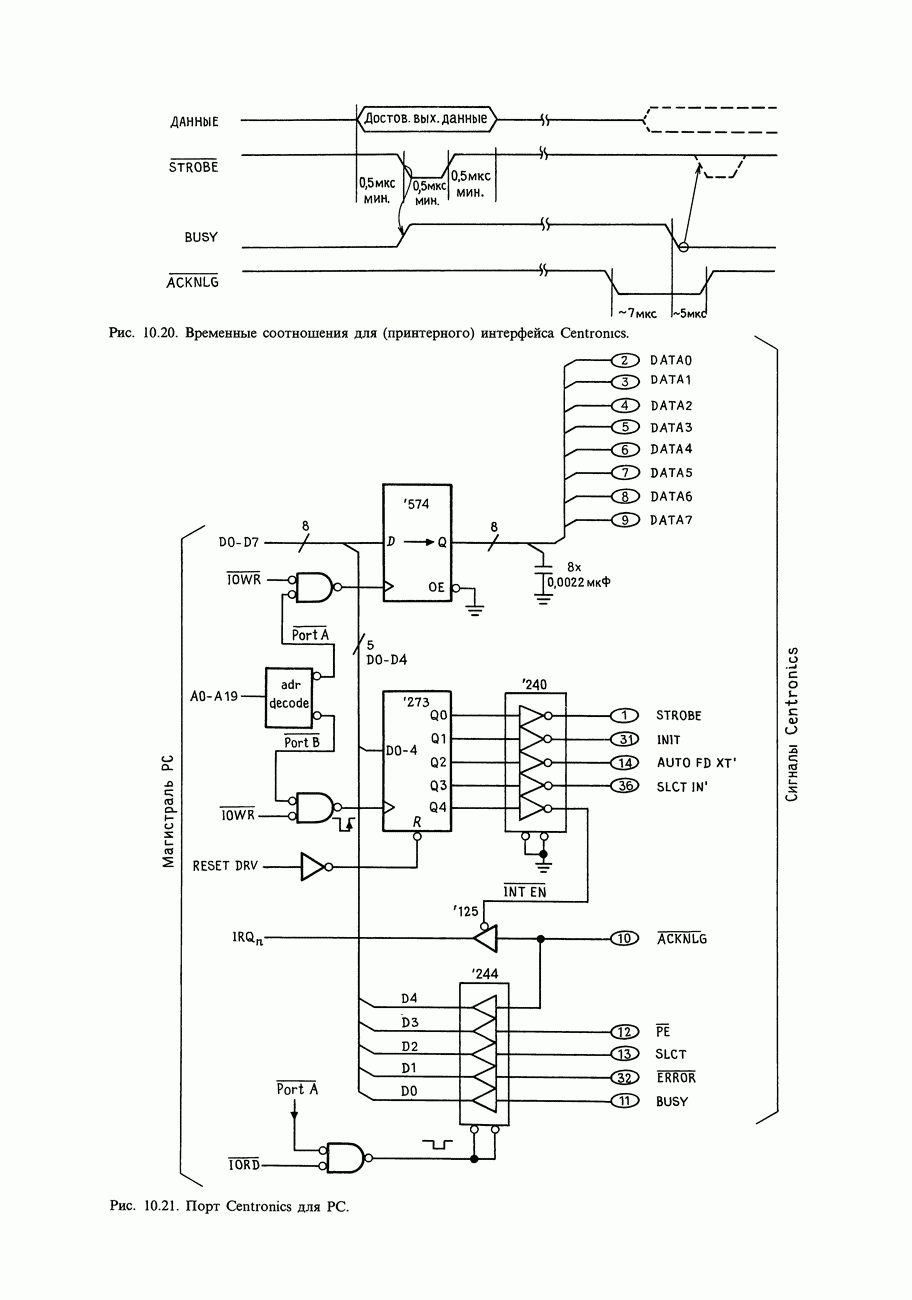
- 10.20. Параллельная связь
- 10.21. Локальные вычислительные цепи
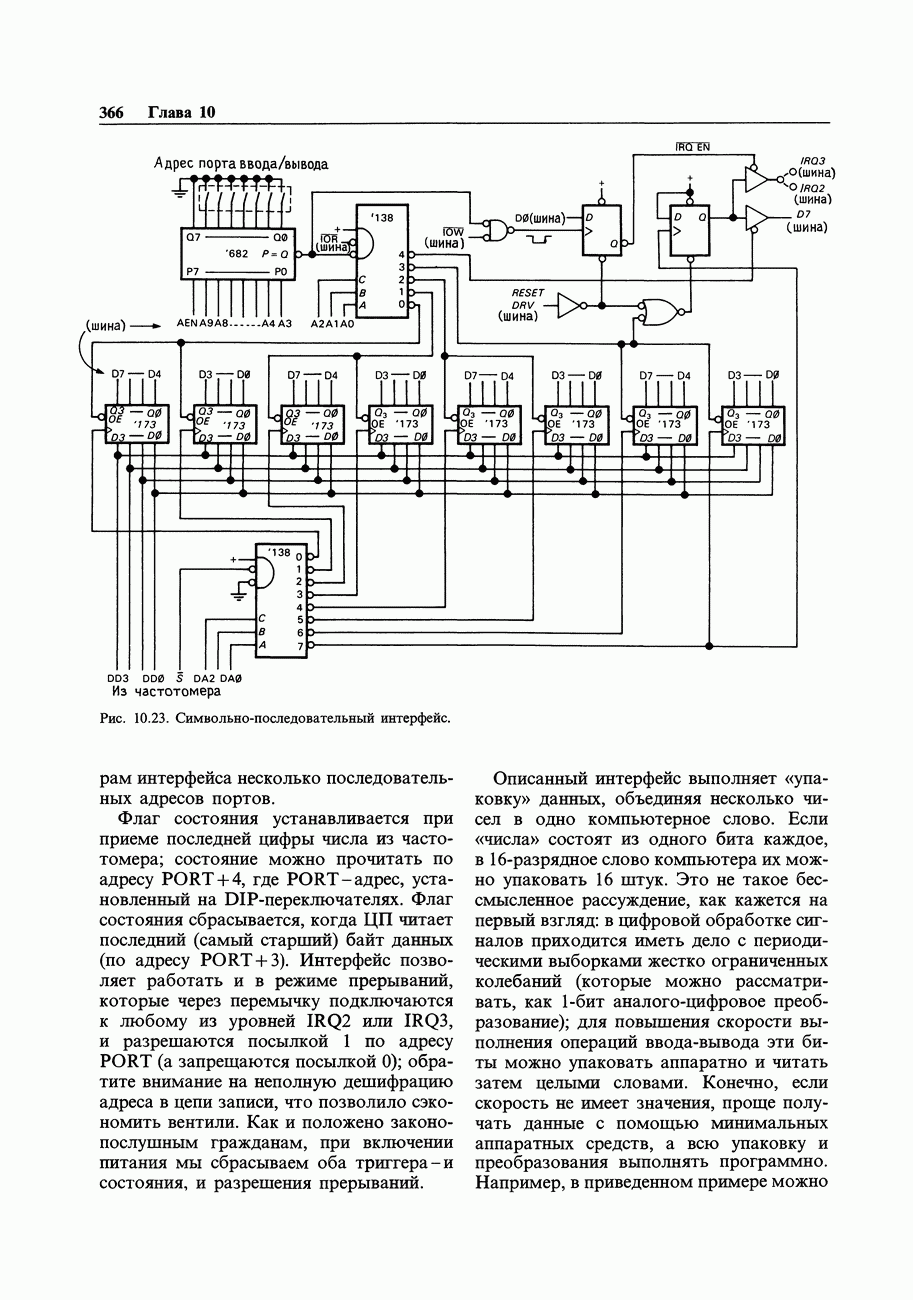
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел