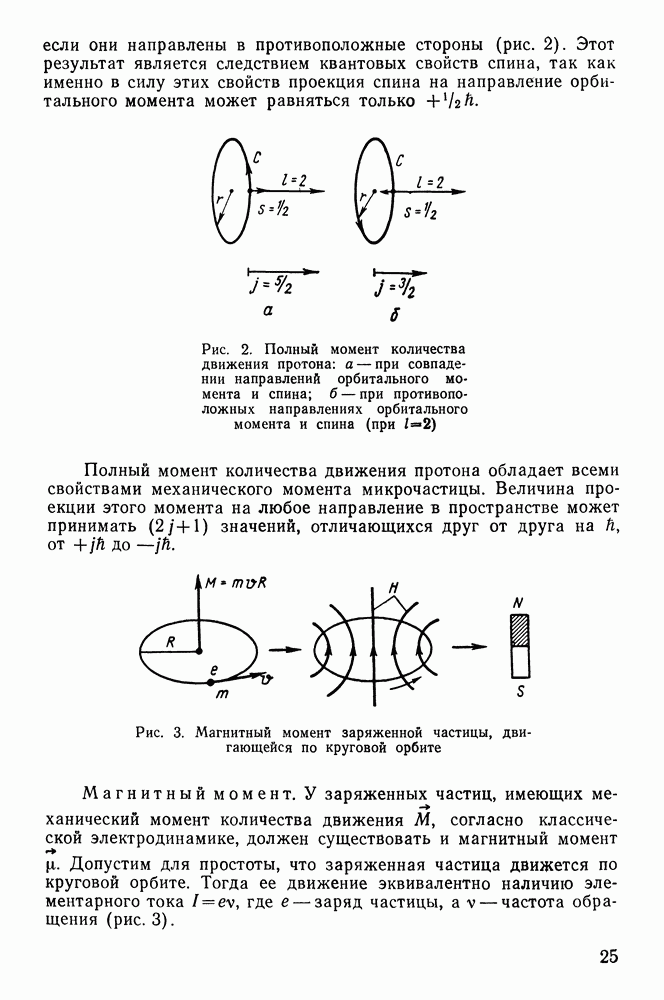
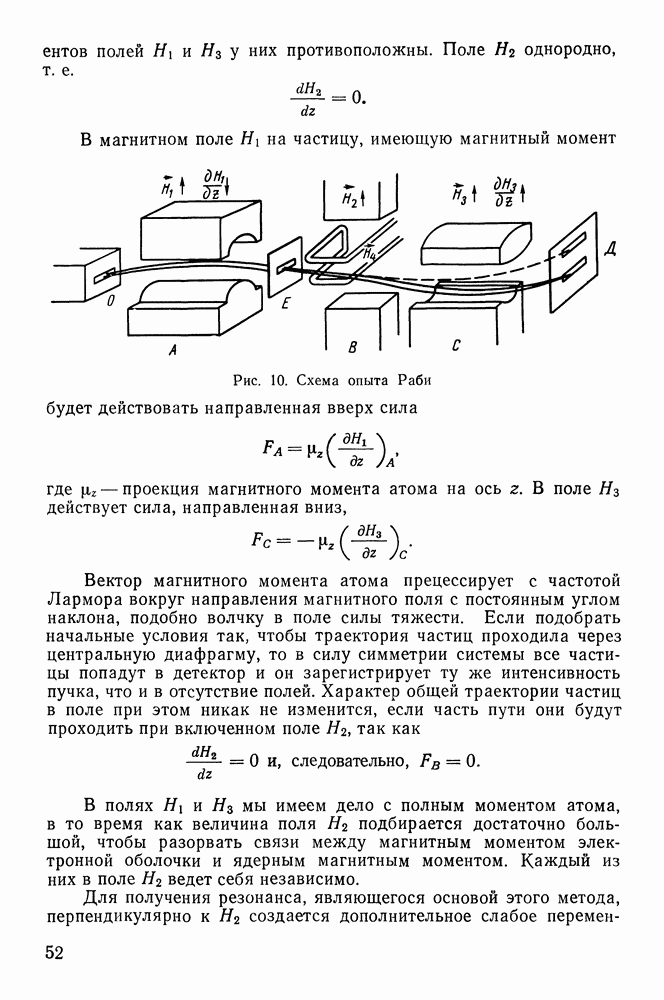
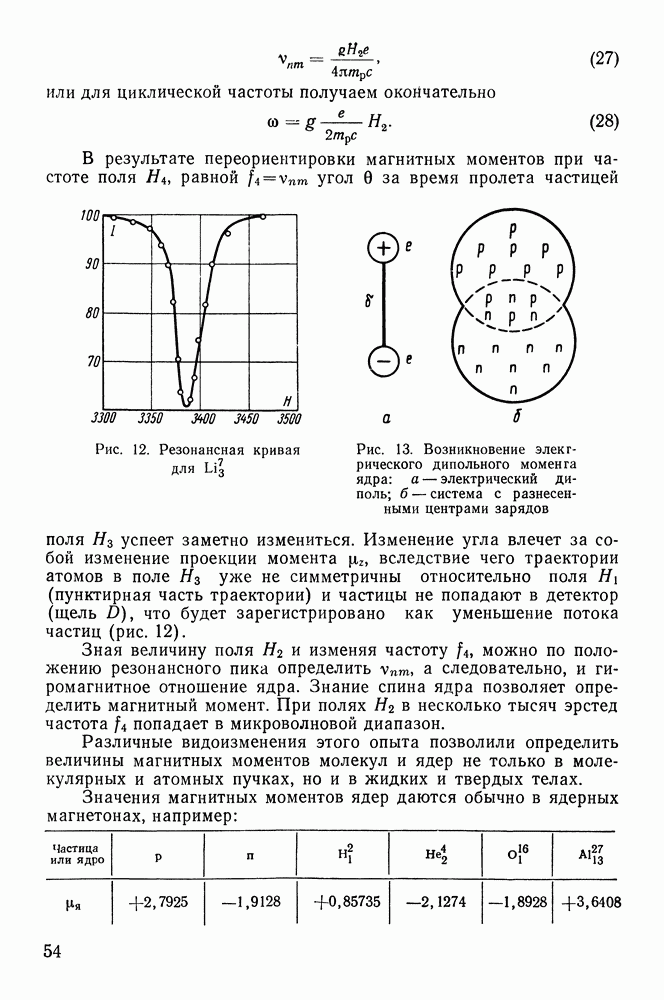
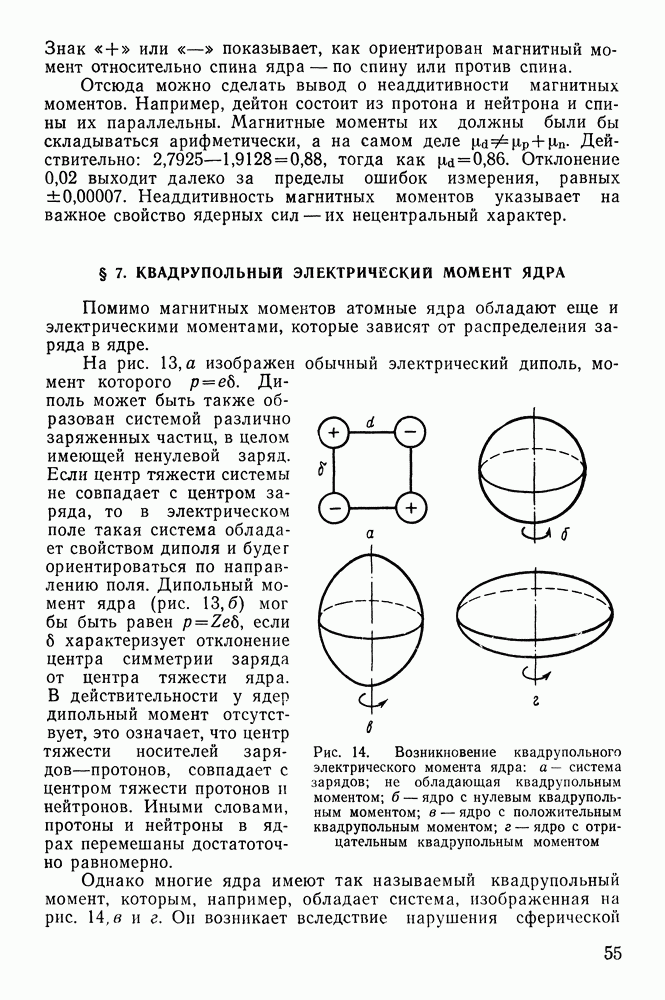
§ 18. АЛЬФА-РАСПАД

Основные характеристики а-распада. Явление -распада состоит в том, что ядро самопроизвольно испускает -частицу и превращается в другое ядро с массовым числом, на 4 единицы меньшим, и с атомным номером, меньшим на 2 единицы:

Ранее (§ 4) было показано, что ядро может самопроизвольно разделиться на две части, если энергия его связи относительно этих составных частей отрицательна. Или, другими словами, (масса исходного ядра больше суммы масс образующихся ядер. Таким образом, энергетическое условие возможности самопроизвольного -распада записывается в виде

Разность энершй покоя исходного ядра и продуктов распада, равная по абсолютной величине энергии связи, выделяется в виде кинетической энергии -частицы и ядра отдачи:

Покажем, что первая значительно больше второй. Законы сохранения энергии и импульса для -распада дают

Считая, что распадающееся ядро находится в состоянии покоя, получим

откуда

Таким образом,

для кинетической энергии -частиц получим выражение

Так как то подавляющую часть кинетической энергии, выделяющейся при -распаде, уносит -частица и лишь незначительную долю энергии приобретает ядро — првцукт распада.

Например, при распаде ядра энергия связи

Перечислим основные особенности -распада, установленные опытным путем.

В большинстве случаев -частицы, вылетающие при распаде данного элемента, имеют одинаковые энергии, т. е. являются моноэнергетическими. Например, распадаясь, испускает -частицы с кинетической энергией

Однако некоторые ядра испускают несколько типов моноэнергетических -частиц, что получило название тонкой структурой -спектров. Например, испускает -частицы двух энергий:

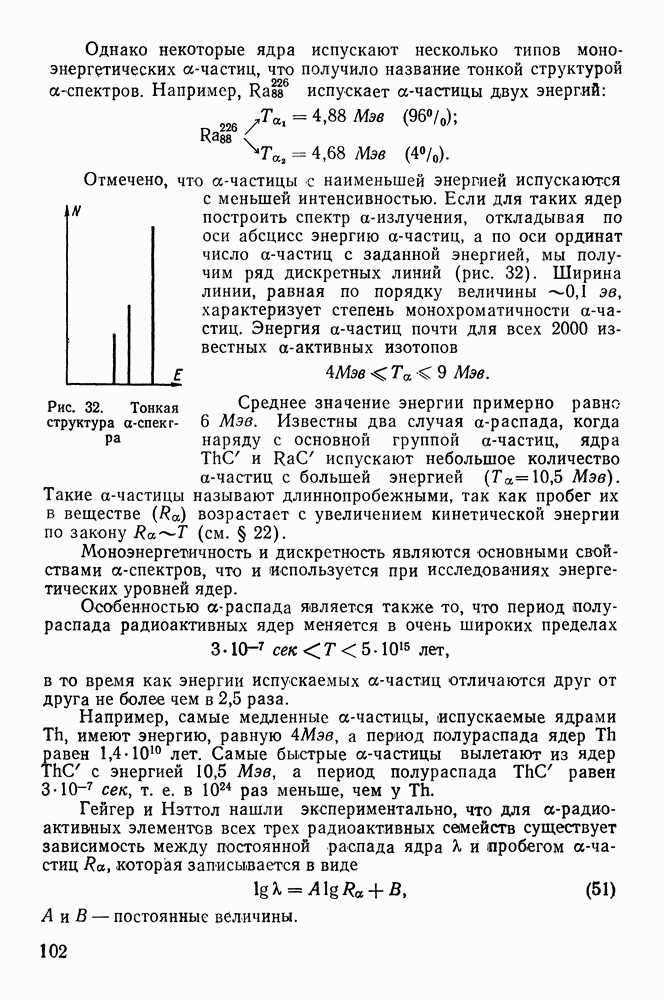
Отмечено, что -частицы с наименьшей энергией испускаются с меньшей интенсивностью. Если для таких ядер построить спектр -излучения, откладывая по оси абсцисс энергию -частиц, а по оси ординат число -частиц с заданной энергией, мы получим ряд дискретных линий (рис. 32). Ширина линии, равная по порядку величины характеризует степень монохроматичности -частиц. Энергия -частиц почти для всех 2000 известных -активных изотопов

Рис. 32. Тонкая структура -спектра

Среднее значение энергии примерно равно Известны два случая -распада, когда наряду с основной группой -частиц, ядра испускают небольшое количество -частиц с большей энергией Такие -частицы называют длиннопробежными, так как пробег их в веществе возрастает с увеличением кинетической энергии по закону (см. § 22).

Моноэнергетичность и дискретность являются основными свойствами -спектров, что и используется при исследованиях энергетических уровней ядер.

Особенностью -распада является также то, что период полураспада радиоактивных ядер меняется в очень широких пределах

в то время как энергии испускаемых -частиц отличаются друг от друга не более чем в 2,5 раза.

Например, самые медленные -частицы, испускаемые ядрами имеют энергию, равную а период полураспада ядер равен лет. Самые быстрые -частицы вылетают из ядер с энергией а период полураспада равен сек, т. е. в раз меньше, чем у

Гейгер и Нэттол нашли экспериментально, что для -радио-активных элементов всех трех радиоактивных семейств существует зависимость между постоянной распада ядра К и пробегом -частиц которая записывается в виде

— постоянные величины.

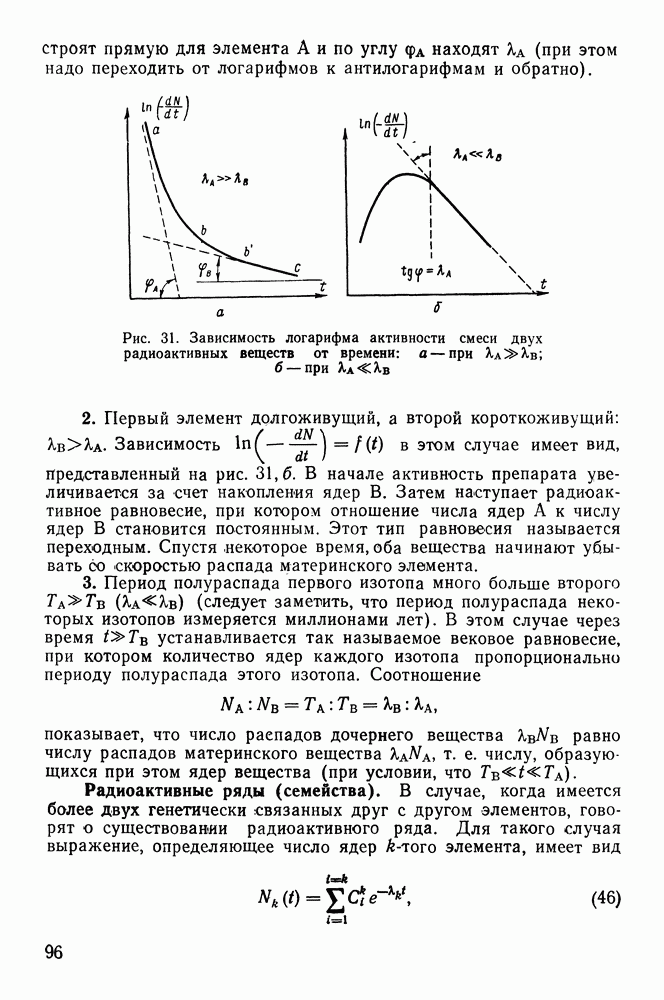
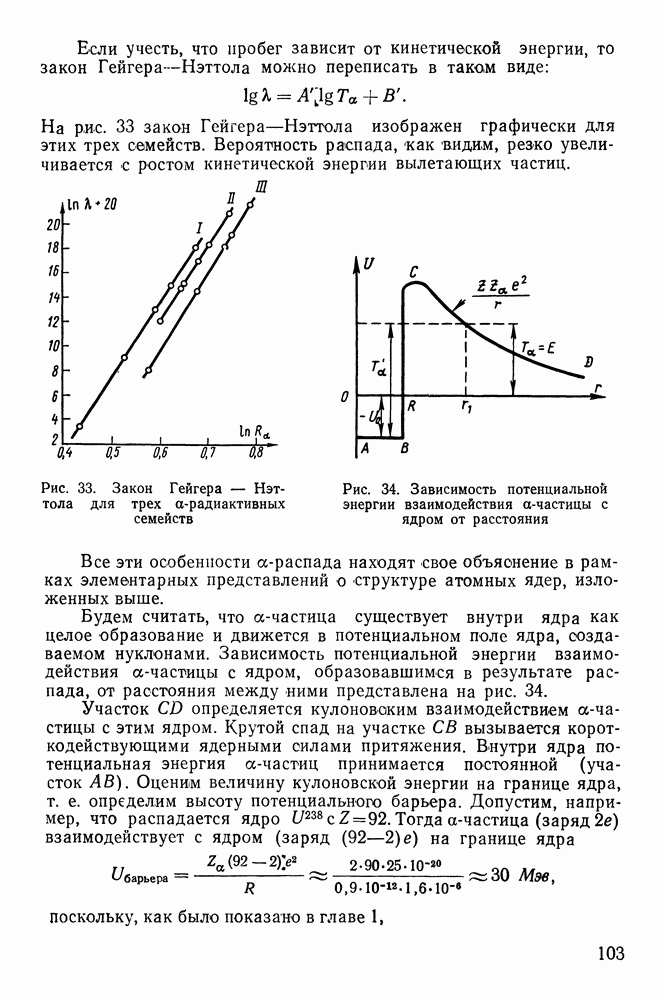
Если учесть, что пробег зависит от кинетической энергии, то закон Гейгера-Нэттола можно переписать в таком виде:

На рис. 33 закон Гейгера-Нэттола изображен графически для этих трех семейств. Вероятность распада, как видим, резко увеличивается с ростом кинетической энергии вылетающих частиц.

Рис. 33. Закон Гейгера — Нэттола для трех -радиактивных семейств

Рис. 34. Зависимость потенциальной энергии взаимодействия -частицы с ядром от расстояния

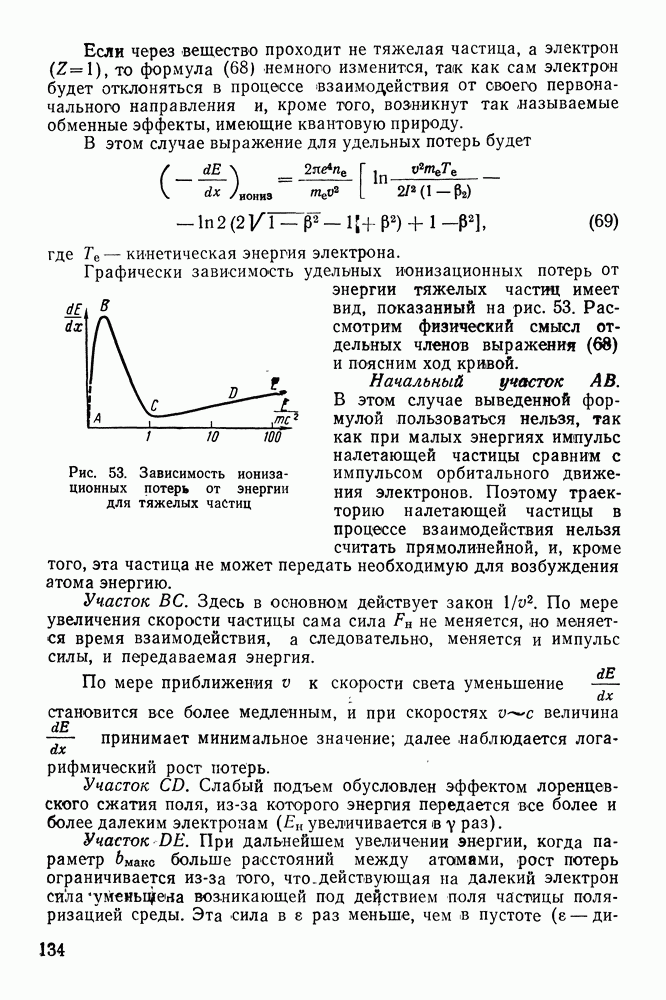
Все эти особенности -распада находят свое объяснение в рамках элементарных представлений о структуре атомных ядер, изложенных выше.

Будем считать, что -частица существует внутри ядра как целое образование и движется в потенциальном поле ядра, создаваемом нуклонами. Зависимость потенциальной энергии взаимодействия -частицы с ядром, образовавшимся в результате распада, от расстояния между «ими представлена на рис. 34.

Участок определяется кулоновсжим взаимодействием -частицы с этим ядром. Крутой спад на участке вызывается короткодействующими ядерными силами притяжения. Внутри ядра потенциальная энергия -частиц принимается постоянной (участок Оценим величину кулоновской энергии на границе ядра, т. е. определим высоту потенциального барьера. Допустим, например, что распадается ядро -частица (заряд взаимодействует с ядром (заряд (92—2) на границе ядра

поскольку, как было показано в главе 1,

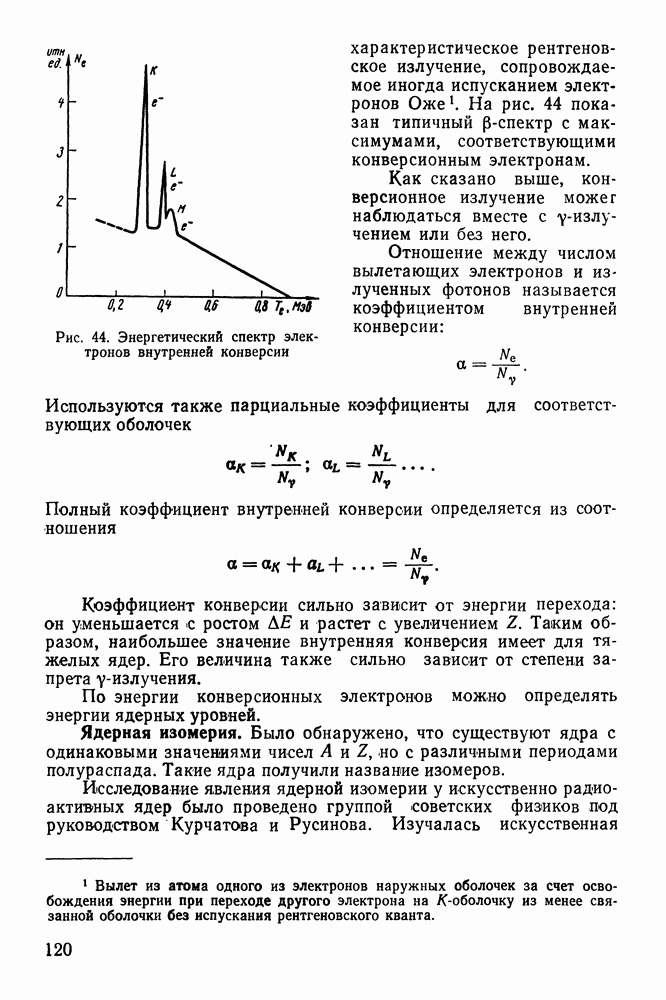
Вылетающие из ядер -частицы имеют в среднем кинетические энергии порядка т. е. намного меньше высоты кулоновского барьера. Этот факт никак не может быть понят в рамках классической механики.

Если энергия вылетавшей -частицы равна а потенциальная энергия барьера то это означает, что кинетическая энергия -частицы, пока она проходит барьер, отрицательна, поскольку

Согласно классической механике, если шарик с массой и скоростью имеет кинетическую энергию, меньшую потенциальной энергии, которую он имел бы на вершине барьера то, приблизившись к барьеру, он отразится от него и повернет назад (рис. 35).

Рис. 35. Потенциальный барьер в классической механике

Иное положение имеет место для частиц, обладающих волновыми свойствами. Квантовая механика показывает, что при любой конечной высоте потенциального барьера падающая на него заряженная частица, полная энергия которой положительна, имеет хотя и малую, но конечную вероятность «просочиться» сквозь барьер. Наличие такого чисто квантового эффекта, называемого «туннельным переходом», и лежит в основе -распада.

Здесь имеется аналогия с волновыми процессами, происходящими при прохождении света через границу раздела двух сред с разными коэффициентами преломления Из курса общей физики известно, что условия прохождения фотонов будут зависеть от угла их падения. При и угол падения (рис. 36), таком, что

где угол называется углом полного внутреннего отражения, фотоны целиком отражаются . Условие внутреннего отражения соответствует «в механике случаю, когда кинетическая энергия частицы оказывается меньше ее потенциальной энергии (равной высоте потенциального барьера).

Согласно представлениям геометрической оптики отражение происходит на поверхности раздела двух сред, и луч не проникает в отражающую среду (рис. 36,а). Однако в действительности

благодаря волновым свойствам света отражение идет не только на границе раздела, а по всей глубине отражающей среды, так как волны, затухая, все же проникают в нее.

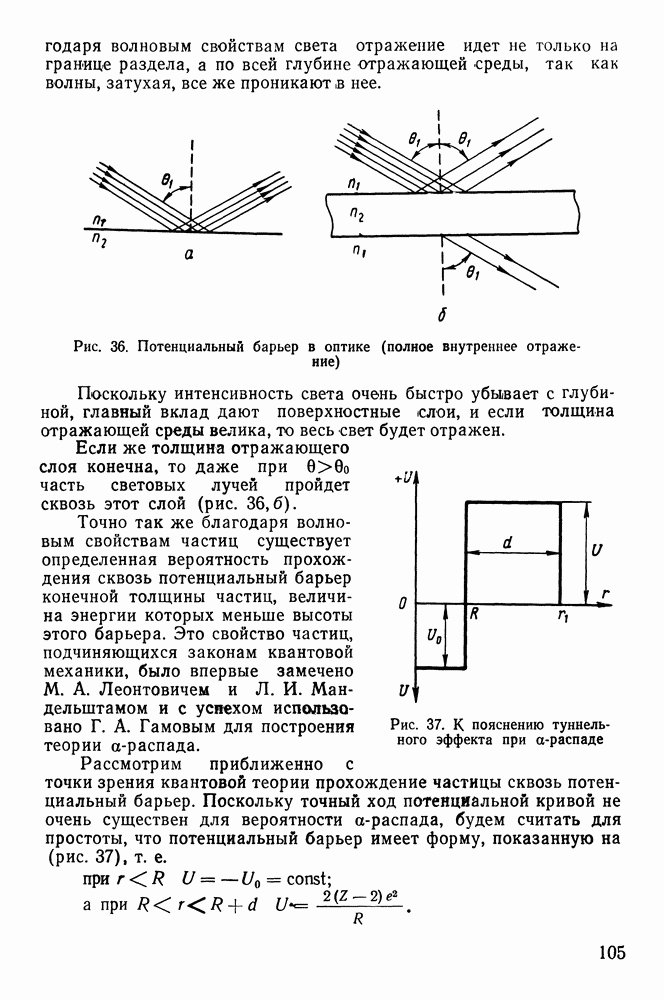
Рис. 36. Потенциальный барьер в оптике (полное внутреннее отражение)

Поскольку интенсивность света очень быстро убывает с глубиной, главный вклад дают поверхностные слои, и если толщина отражающей среды велика, то весь свет будет отражен.

Если же толщина отражающего слоя конечна, то даже при часть световых лучей пройдет сквозь этот слой (рис. 36,б).

Рис. 37. К пояснению туннельного эффекта при -распаде

Точно так же благодаря волновым свойствам частиц существует определенная вероятность прохождения сквозь потенциальный барьер конечной толщины частиц, величина энергии которых меньше высоты этого барьера. Это свойство частиц, подчиняющихся законам квантовой механики, было впервые замечено М. А. Леонтовичем и Л. И. Мандельштамом и с успехом использовано Г. А. Гамовым для построения теории -распада.

Рассмотрим приближенно с точки зрения квантовой теории прохождение частицы сквозь потенциальный барьер. Поскольку точный ход потенциальной кривой не очень существен для вероятности -распада, будем считать для простоты, что потенциальный барьер имеет форму, показанную на (рис. 37), т. е.

Состояние микрочастицы в квантовой механике описывается волновой функцией квадрат модуля которой характеризует плотность вероятности нахождения частицы в данном месте.

В ядре (при ), поскольку потенциальная энергия не зависит от координат, частица движется свободно, и ее волновая функция представляет собой волну де Бройля

где — кинетическая энергия частицы в ядре,

Попадая внутрь барьера, волна быстро затухает. Это можно понять, если учесть, что здесь формально кинетическая энергия отрицательна и импульс а становится мнимым

Так как мы приняли, что барьер прямоугольный, т. е. постоянно, то значение функции в интервале может быть записано в виде

Вне барьера при волновая функция будет иметь тот же вид что и в ядре, но с

Вероятность просачивания частицы сквозь барьер определяется, как отношение вероятности нахождения частицы за барьером на расстоянии к вероятности нахождения частицы внутри барьера, т. е. на расстоянии от центра ядра:

Это отношение называют коэффициентом проницаемости барьера, или просто прозрачностью. Прозрачность характеризует вероятность прохождения частицы сквозь потенциальный барьер.

Полученный результат легко обобщается на барьер произвольной формы, который разбивается на ряд прямоугольных барьеров толщиной и высотой Тогда вероятность прохождения частицы через весь барьер равна произведению коэффициентов прозрачности каждого из слоев.

В пределе при

где радиус ядра, а (рис. 34). Пределами интегрирования служат границы барьера или границы той области, где кинетическая энергия отрицательна.

Имея скорость -частица в ядре радиуса в среднем раз в секунду подходит к границе ядра. При каждом подходе вероятность пройти скзозь потенциальный барьер и выйти из ядра равна Поэтому постоянная распада (вероятность распада в единицу времени)

Выполняя интегрирование по для кулоновского барьера, можно получить зависимость постоянной распада от энергии -частицы, которая экспериментально была найдена Гейгером и Нэттолом.

Пользуясь выражением (54), можно достаточно точно определясь размеры ядер.

При выводе формулы для прозрачности потенциального барьера нужно, строго говоря, сделать два уточнения.

А. Ранее предполагалось, что -частица существует в ядре в виде самостоятельной частицы. Однако более вероятно, что -частица образуется в момент вылета из ядра и поэтому необходимо дополнительно учитывать вероятность образования -частицы в ядре. (Фактически в ядре существует некоторое динамическое равновесие, при котором -частицы непрерывно создаются и распадаются.)

Б. Следует также учитывать возможность вылета -частицы с угловым моментом, отличным от нуля и равным Такой случай возникает, если при -распаде ядро переходит в состояние с измененным угловым моментом. Тогда разность угловых моментов уносится -частицей. Теоретическое рассмотрение приводит к выводу, что в этом случае вероятность вылета уменьшается в раз.

Происходит это благодаря эффективному увеличению потенциального барьера из-за появления кроме кулоновского, также и центробежного барьера. Дело в том, что когда частица имеет определенный орбитальный момент количества движения, то возникает центробежная сила, которую можно описать центробежным потенциалом. Центробежная сила 1 в классической механике равна

где модуль вектора момента количества движения. Согласно квантовой механике

поэтому при потенциал взаимодействия -частицы с ядром возрастает

что приводит к возрастанию интеграла в формуле (53) и уменьшению коэффициента прозрачности

Однако эффект центробежного барьера, величину которого можно оценить из выражения (55), не может быть большим, поскольку быстро убывает с расстоянием.

Неучет этих двух факторов, а также некоторых других более тонких эффектов приводит к тому, что для некоторых ядер значения постоянной распада , полученные на основе элементарной теории -распада оказываются на несколько порядков больше величин, найденных из экспериментов, -переходы, для которых Ятеор много больше Яэксп называются запрещенными, а отношение коэффициентом запрета ( период полураспада).

Наличие запрещенных переходов приводит к нарушению закона монотонного роста постоянной распада с энергией частиц, который следует из формулы (54).

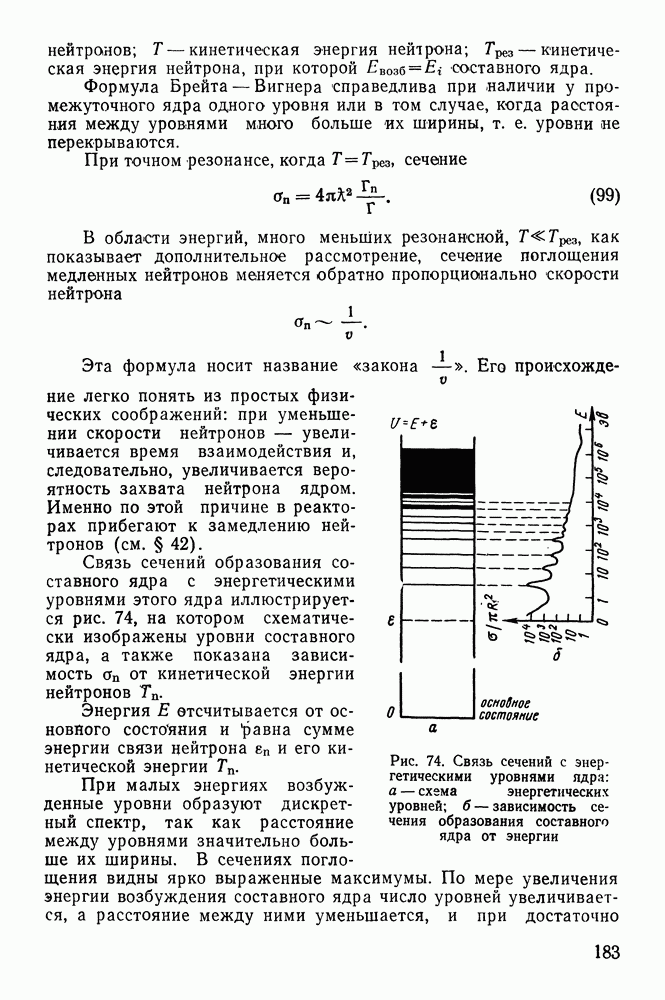
Тонкая структура а-спектров. До сих пор мы предполагали, что ядро распадается из основного состояния и новое ядро тоже образуется в основном состоянии. Напомним, что основным называется состояние, которому соответствует наименьшая возможная для данного ядра энергия, определяемая минимальной массой покоя ядра. Все остальные энергетические состояния ядра называются возбужденными. Многие возбужденные состояния отличаются от основного не только энергией, но и другими параметрами — спином, четностью и пр.

Для характеристики уровней вводятся обозначения: где указывает величину полного момента количества движения, знак четность; показывает номер энергетического уровня.

Испускание основной группы -частиц соответствует энергетическим переходам между основными состояниями исходного и конечного ядер. Возникновение других моноэнергетических групп -частиц объясняется тем, что образующиеся в результате -распада ядра получаются в различных возбужденных состояниях.

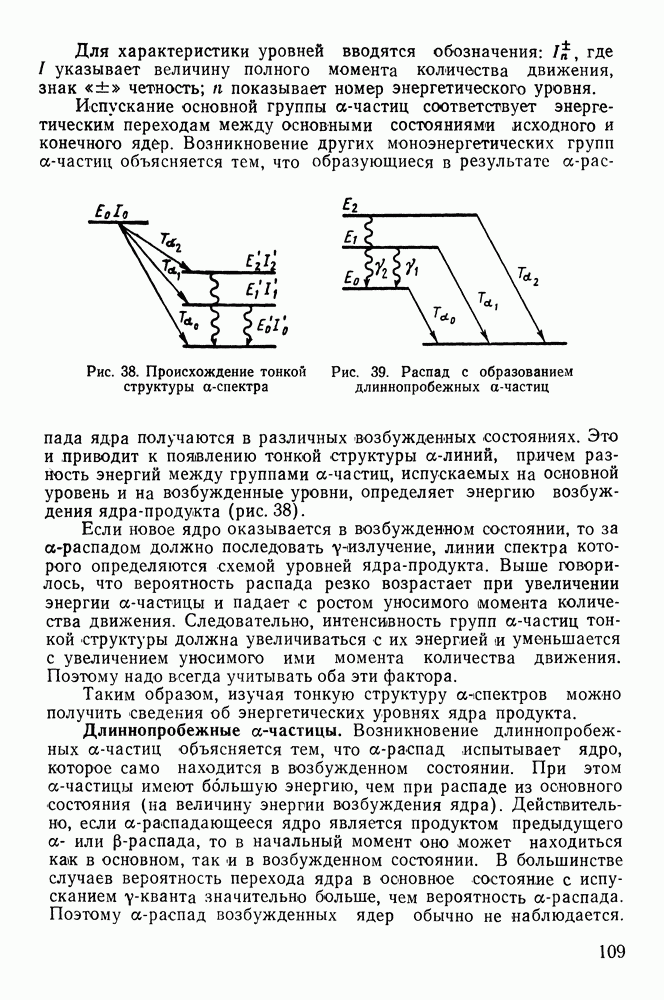
Рис. 38. Происхождение тонкой структуры -спектра

Рис. 39. Распад с образованием длиннопробежных -частиц

Это и приводит к появлению тонкой структуры -линий, причем разность энергий между группами -частиц, испускаемых на основной уровень и на возбужденные уровни, определяет энергию возбуждения ядра-продукта (рис. 38).

Если новое ядро оказывается в возбужденном состоянии, то за -распадом должно последовать излучение, линии спектра которого определяются схемой уровней ядра-продукта. Выше говорилось, что вероятность распада резко возрастает при увеличении энергии -частицы и падает с ростом уносимого момента количества движения. Следовательно, интенсивность групп -частиц тонкой структуры должна увеличиваться с их энергией и уменьшается с увеличением уносимого ими момента количества движения. Поэтому надо всегда учитывать оба эти фактора.

Таким образом, изучая тонкую структуру -спектров можно получить сведения об энергетических уровнях ядра продукта.

Длиннопробежные а-частицы. Возникновение длиннопробежных -частиц объясняется тем, что -распад испытывает ядро, которое само находится в возбужденном состоянии. При этом -частицы имеют большую энергию, чем при распаде из основного состояния (на величину энергии возбуждения ядра). Действительно, если -распадающееся ядро является продуктом предыдущего или -распада, то в начальный момент оно может находиться как в основном, так и в возбужденном состоянии. В большинстве случаев вероятность перехода ядра в основное состояние с испусканием -кванта значительно больше, чем вероятность -распада. Поэтому -распад возбужденных ядер обычно не наблюдается.

Имеются, однако, два случая, когда вероятности обоих процессов сравнимы, и -распад наблюдается как из основного, так и из возбужденного состояния ядра. Это происходит при больших энергиях распада, т. е. у наиболее короткоживущих элементов: и

Из сказанного следует, что разности энергий длиннопробежных групп непосредственно определяют схему расположения уровней уже не ядра-продукта, а исходного ядра (рис. 39).

Радиоактивные изотопы, дающие длиннопробежные -частицы, также создают -излучение, которое в отличие от случая, приводящею к образованию тонкой структуры, принадлежит не конечному ядру, а исходному. При этом

— энергия -частицы, вылетающей с -того уровня, — частота -кванта.

Итак, при распаде возбужденных ядер, вообще говоря, конкурируют два процесса: -распад и испускание -лучей. Но только одно ядро из 10000 переходит в основное состояние ядра-продукта с испусканием -частины, прежде чем успеет отдать избыточную энергию в виде -квантов. Изучая спектры длиннопробежных -частиц, можно получить сведения об энергетических уровнях исходного ядра.