3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ

В 30-х годах Андерсон обратил внимание на то, что формула (3.1) сильно занижает энергетические потери электронов, когда они становятся релятивистскими. Скоро осознали, что здесь имеет место какой-то дополнительный механизм потерь, включающий взаимодействие между электроном и ядром. Он получил название тормозного излучения. Физический смысл такого процесса прост. Когда заряд ускоряется или замедляется, он излучает электромагнитные волны, а тормозное излучение испускается при любых электромагнитных взаимодействиях между зарядом и ядрами вещества, через которое он проходит.

Мы проведем достаточно подробный теоретический анализ, во-первых, потому что сам по себе этот процесс имеет огромное значение для астрофизики и, во-вторых, потому что можно развить достаточно строгий математический аппарат для описания почти любого процесса излучения с участием свободных электронов.

3.3.1. излучение ускоряющегося электрона. Об ускоряющихся заряженных частицах необходимо знать следующее:

1. Полная скорость излучения в мгновенной инерциальной системе отсчета ускоренного электрона равна

Здесь собственное ускорение электрона. Мощность излучения зависит только от ускорения электрона. Эта формула справедлива только для электронов, движущихся со скоростями Покажите, что если частица движется с релятивистской скоростью, то мощность излучения в системе отсчета наблюдателя равна

где измеряются в системе отсчета наблюдателя (это полезное упражнение по теории относительности). Преобразуйте ускорение V из мгновенной инерциальной системы отсчета в систему отсчета наблюдателя помня, что инвариантно относительно преобразований Лоренца (см. п. 3.3.5). Как будет показано ниже, нам потребуются результаты только для системы покоя электрона. Единственное ограничение применимости Уравнения (3.2) состоит в предположении, что за период ускорения электрон теряет только малую долю своей энергии. В противном случае мы Должны учитывать торможение излучением, но применительно к нашим задачам последнее значения не имеет.

2. График излучения в полярных координатах имеет тот же вид, что и в случае дипольного излучения в мгновенной системе покоя электрона, т.е. напряженность электрического поля больших расстояниях от электрона пропорциональна где — угол между направлением на наблюдателя и Вектором собственного ускорения электрона. Для мощности, излучаемой в пределах телесного угла на можно написать

Рис. 3.1. График в полярных координатах излучения движущейся ускоренно заряженной частицы. Показана также поляризация излучения. Отметим, что оба эти параметра зависят от ускорения

3. Излучение поляризовано, причем вектор электрического поля параллелен вектору ускорения электрона в картинной плоскости (рис. 3.1).

Хотя частица может быть релятивистской, силы, вызывающие ускорение, могут дать в результате нерелятивистское ускорение в системе отсчета, в которой частица покоится. Это тот важный момент, который позволяет упростить многие астрофизические задачи. Поэтому мы полностью опишем излучение в системе покоя электрона, а затем преобразуем результат к лабораторной системе отсчета.

Нас будут интересовать темп полных энергетических потерь на излучение и спектральное распределение излучения. Чтобы найти спектр, применим теорему Парсеваля.

3.3.2. Теорема парсеваля и спектральное разложение излучения ускоряющегося электрона. Введем преобразование Фурье для ускорения частицы, т.е. пару преобразований

Применим теперь теорему Парсеваля, утверждающую, что ускорение и его разложение Фурье связаны следующим образом:

Доказательство можно найти в любом учебнике фурье-анализа. Отсюда полная энергия, излучаемая при электростатических столкновениях между электроном и ядром, выражается, как

Но нам нужно проинтегрировать в пределе от до Поскольку ускорение — действительная величина, согласно другой теореме анализа Фурье,

Отсюда

Поэтому

есть полная энергия в единичном интервале длин волн, выделяемая при столкновении. Это очень полезная формула.

3.3.3. Дальнейшая программа. Выше было выведено выражение для ускорения электрона в электрическом поле. Осуществим преобразование Фурье ускорения в мгновенной системе покоя электрона. Уравнение (3.7) дает распределение по частотам для излучения при единичном столкновении с прицельным параметром Наконец, проинтегрируем результат по прицельному параметру, предварительно позаботившись о пределах интегрирования Ьтах и В релятивистском случае нужно перейти в лабораторную систему координат. Чтобы получить темп полных потерь, следует проинтегрировать спектр по всем частотам.

Как релятивистский, так и нерелятивистский случай сначала совпадают, поэтому начнем с рассмотрения общей задачи. Электрон космических лучей движется мимо покоящихся ядер, тем не менее в соответствии с нашим подходом выясним, какие силы действуют на электрон в его системе покоя. В этой системе мимо него проносятся ядра со скоростью и с прицельным параметром Мы уже определили электрическое поле, создаваемое движущейся заряженной частицей и воздействующее на неподвижный электрон. Точное релятивистское выражение имеет вид

где заряд ядра. Обе эти величины являются нерелятивистскими возмущениями. Нет нужды включать сюда магнитное поле В, поскольку электрон первоначально покоится в выбранной системе отсчета и во время столкновения до релятивистских скоростей не ускоряется.

При больших значениях у составляющая электрического сильно превосходит так что в релятивистском случае нужно рассмотреть толькс

излучение, вызываемое составляющей Движение под действием составляющей порождает излучение, потому что частица ускоряется, а в случае ионизационных потерь энергия вдоль оси х в конечном счете не передается.

Теперь преобразование Фурье даст спектр излучения в системе отсчета, в которой электрон покоится. Точно проинтегрируем а затем проанализируем, как можно получить такой же результат с помощью более приближенных методов:

Замена переменных дает

По таблицам преобразований Фурье найдем, что интеграл равен

где модифицированная функция Бесселя первого рода. Асимптотические разложения следующие:

Таким образом, для низких частот находим

Фактор Лоренца отсутствует в окончательном выражении! Но это и неудивительно, поскольку, как мы помним, импульсы в нерелятивистском и релятивистском случаях совпадают [см. уравнение (2.13)]. На высокочастотном конце наблюдается экспоненциальный завал Итак, спектр получен и имеет форму, показанную на рис. 3.2. Обратите внимание на происхождение экспоненциального завала. Длительность релятивистского столкновения приближенно равна Поэтому преобладающий фурье-компонент в спектре излучения должен соответствовать частотам откуда т.е. по порядку величины Величина определяется на единичный интервал частот.

Рис. 3.2.

Поскольку спектр в области низких частот плоский (не зависит от , большая часть энергии выделяется вблизи самой высокой частоты

Можно было бы раньше догадаться, что низкочастотный спектр должен быть плоским, так как на этих частотах импульс представляется дельта-функцией, фурье-образ которой совершенно плоский. Поэтому на низких частотах энергетический спектр имеет вид

Этот спектр плоский вплоть до частоты

Наконец, нужно произвести интегрирование по всем значениям прицельного параметра, которые могут вносить вклад в излучение на частоте До сих пор мы проводили анализ совершенно общего характера в системе покоя электрона. Если же электрон движется с релятивистской скоростью, то концентрация ядер увеличивается в у раз из-за релятивистского сокращения длин. Отсюда где — концентрация ядер в лабораторной системе отсчета. Число столкновений в секунду равно поскольку все параметры измеряются в системе покоя электрона, будем снабжать их штрихами:

3.3.4. Нерелятивистское и тепловое тормозное излучение. Представляют интерес два случая: скорость полных энергетических потерь вследствие тормозного излучения нерелятивистских электронов высоких энергий, движущихся в среде; непрерывное тормозное излучение полностью ионизованного газа, в котором электроны имеют максвелловское распределение по скорости при температуре В обоих случаях релятивистские поправки обращаются в нуль, и мы получаем

Здесь снова необходимо правильно выбрать предельные значения прицельных параметров. Что касается Ьтах, то можно интегрировать только до таких значений при которых Бблыыие значения соответствуют экспоненциальному хвосту распределения, поэтому вклад в излучение, наблюдаемый на данной частоте пренебрежимо мал (рис. 3.2). Значение определяется так же, как в разд. 2.2, т.е. при низких скоростях, Примем классическое значение Это соответствует тормозному излучению в областях с температурой На больших скоростях следует учитывать квантовые эффекты и эти значения соответствуют рентгеновскому излучению горячего межгалактического газа в скоплениях галактик. Таким образом, нам предстоит выбрать из

где для низких скоростей,

Мы упростили выкладки, ограничившись анализом плоской низкочастотной области спектра излучения. Есть, конечно, экспоненциальный завал на высоких частотах, соответствующий

Нерелятивистские тормозные потери. Чтобы найти темп полных энергетических потерь для электрона, обладающего высокой энергией, проинтегрируем уравнение (3.13) по всем частотам. На практике это означает интегрирование от до где итах соответствует экспоненциальному завалу Это значение приблизительно равно

или с точностью до порядка величины или кинетической энергии электрона, т.е. максимально возможной энергии, теряемой при отдельном столкновении. Таким образом,

Эта формула для нас не так уж важна, но, как мы видим, темп полных потерь энергии электроном пропорционален т.е. корню квадратному из кинетической энергии с обратным случаем релятивистских тормозных потерь, п. 3.3.б, уравнение (3.25)].

Тепловое тормозное излучение. Чтобы описать тормозное (или свободно-свободное) излучение газа с температурой следует проинтегрировать уравнение (3.13) по максвелловскому распределению электронов по скоростям:

Математические выкладки в этом случае несколько громоздки. Чтобы получить правильный по порядку величины ответ, подставим в формулу (3.13). Тогда излучательная способность плазмы с электронной концентрацией имеет на низкочастотном пределе вид

где поправочный коэффициент, называемый фактором Гаунта, он равен из формулы (3.13), проинтегрированному по скоростям. При высоких энергиях имеется экспоненциальный завал который следует включить в соотношение (3.14). Темп полных энергетических потерь плазмы можно найти, проинтегрировав излучательную способность по всем частотам. На практике из-за экспоненциального завала к правильной форме функции приводит интегрирование соотношения (3.14) от до как было описано выше, т.е.

Результаты точных расчетов дают следующее: спектральная излучательная способность плазмы равна

На частотах фактор Гаунта зависит от частоты только логарифмически. Для радио- и рентгеновского диапазонов имеются следующие удобные формулы соответственно:

для где постоянная Эйлера. Оба логарифмических члена легко выводятся из уравнений (3.13). Для эта формула следует из приближенных выражений для функций Бесселя, использовавшихся при выводе уравнения (3.9). Высокочастотное приближение отличается от низкочастотного на коэффициент а в формуле (3.16) для излучательной способности тормозного излучения учитывается только множитель в пределе Таким образом, в факторе Гаунта преобладает член

Полная скорость энергетических потерь плазмой равна

при

Вопрос о форме фактора Гаунта, удобной для использования в формулах для теплового тормозного излучения, большой и очень сложный. Значительное число полезных результатов собрано в [6].

Поглощение теплового тормозного излучения. Выведем коэффициент поглощения для теплового тормозного излучения. Это важно, поскольку По результирующему спектру в радиодиапазоне можно судить о свойствах

компактных областей ионизованного водорода. Вывод иллюстрирует также общий подход к установлению связи между коэффициентами излучения и поглощения.

Прежде всего запишем уравнение переноса излучения. Будем рассматривать интенсивность излучения т.е. энергию излучения, падающего на единичную площадку в единичном телесном угле за 1 с в единичном диапазоне длин волн. На пути уменьшение интенсивности составит где коэффициент поглощения, приращение за счет излучения где излучательная способность плазмы (мощность на единицу объема в единичном интервале длин волн), т.е.

В термодинамическом равновесии при температуре и каждому акту излучения соответствует поглощение посредством того же физического процесса, т.е. выполняется принцип детального равновесия. Спектр излучения должен быть равновесным, поэтому

где спектр интенсивности излучения абсолютно черного тела при температуре В радиодиапазоне и поэтому можно использовать приближение Рэлея — Джинса к закону Планка: Отсюда

Таким образом, коэффициент поглощения для теплового тормозного излучения имеет вид

По определению оптическая толщина среды

Чтобы найти точный спектр излучения в данной области, проинтегрируем уравнение переноса по области с постоянной концентрацией электронов, т.е.

Предполагается, что фоновое излучение отсутствует и при Интегрирование осуществляется просто:

Получен вполне разумный результат. Если , то

Рис. 3.3. Спектр теплового тормозного излучения в области малых частот, при которых становится заметным самопоглощение.

При

Полный спектр имеет вид, показанный на рис. 3.3. Оказалось, что такую форму имеют спектры компактных областей расположенных вблизи областей звездообразования. Температуру такой области можно оценить по части спектра, в которой справедливо приближение Рэлея — Джинса, и усредненному, взвешенному по температуре значению измеренному в точке, в которой область становится оптически толстой,

3.3.5. Полезный релятивистский инвариант. Прежде чем перейти к случаю релятивистского тормозного излучения, выведем очень полезный инвариант. Нам часто придется совершать релятивистские преобразования величины т.е. темпа радиационных потерь частицы. Эта величина — инвариант, что в огромной степени упрощает многие задачи. Для специалиста по теории относительности инвариантность вытекает из того факта, что и суть четвертые компоненты -векторов, по отношению к которым выполняются одни и те же преобразования Лоренца при переходе из одной системы отсчета в другую.

Можно получить этот результат из иных рассуждений. В движущейся системе отсчета излучение возникает вследствие ускорения, и в полярных координатах оно пропорционально Поэтому в системе покоя электрона излучение импульса не имеет, а -вектор импульса есть Отрезок собственного времени, в течение которого происходит излучение, входит в -вектор интервала Применяя обратные преобразования Лоренца, получим, что в лабораторной системе координат

и, следовательно,

3.3.6. Релятивистское тормозное излучение. Анализ этой проблемы чрезвычайно важен для электронов космических лучей. Начнем с уравнения (3.11) для излучения на единицу длины в системе отсчета движущегося электрона. Здесь также необходимо выбрать подходящие пределы для прицельного параметра Ьтгх и Эта величина перпендикулярна направлению движения электрона, поэтому ее значения и в 5 совпадают.

Нижний предел На первый взгляд может показаться, что значение должно быть таким же, как и прежде Однако сейчас мы рассматриваем излучение электрона и требуем, чтобы оно было когерентным. Размер электрона Если длительность импульса меньше, чем время, необходимое для преодоления расстояния то различные участки распределения вероятности будут давать импульсы в различные моменты времени и мы не получим когерентного излучения. Поэтому длительность импульса должна быть по крайней мере равной времени пролета расстояния равного размеру электрона.

Следовательно,

т.е. в знаменатель минимального значения прицельного параметра не входит множитель у. Смысл этого результата в следующем. В системе покоя электрона этот прицельный параметр соответствует угловой частоте значит, энергии фотона Переходя к другой системе отсчета, получим т.е. энергия, которую электрон теряет в процессе соударения в виде излучения, не может превышать его собственную кинетическую энергию. Именно этот простой физический аргумент применялся при выводе нерелятивистского значения

Верхний предел Ьтгх. Выше значение предела было Данный случай слегка отличается тем, что электрон взаимодействует с ядром, которое постоянно экранируется облаком электронов, если только прицельный параметр не мал. Альтернативные оценки можно получить, рассмотрев атомную модель Ферми — Томаса [7].

Электростатическое поле ядра можно приближенно представить в виде

где

Таким образом, для нейтральных атомов удобно принять следующее значение:

Теперь рассмотрим отношение этих двух прицельных параметров

В каждом частном случае в качестве следует принимать меньшее из этих значений. В ультрарелятивистском пределе следовательно

нужно использовать предел, учитывающий экранирование Ферми — Томаса.

Ультрарелятивистский предел дает

Теперь нужно записать это выражение в лабораторной системе. Выше (п. 3.3.5) было показано, что релятивистский инвариант. В данном случае имеет следующую размерность: энергия в единицу времени на единицу длины волны. Поэтому возникает лишь один вопрос: как изменяется при преобразовании координат. Легко заметить, что преобразуется в точности так же, как поэтому, как было показано в п. 3.3.5,

т.е. в системе ширина полосы увеличивается в у раз. Следовательно, в интенсивность в единичном диапазоне меньше в у раз, т.е.

Спектр интенсивности не зависит от частоты вплоть до энергии которая соответствует случаю, когда электрон отдает всю свою кинетическую энергию за одно столкновение. Теперь, интегрируя по частоте, можно найти скорость полных энергетических потерь на излучение

Поскольку

Сравним полученное выражение с точной формулой, выведенной Бете и Гайтлером, с учетом всех аспектов релятивистской квантовой механики

Несмотря на объем приближенных вычислений, мы получили результат, очень близкий к правильному. Член учитывает взаимодействия космического электрона со связанными электронами атомов окружающего вещества.

3.3.7. Релятивистское тормозное излучение в практических исследованиях электронов космических лучей. Релятивистские потери на тормозное излучение имеют экспоненциальную форму

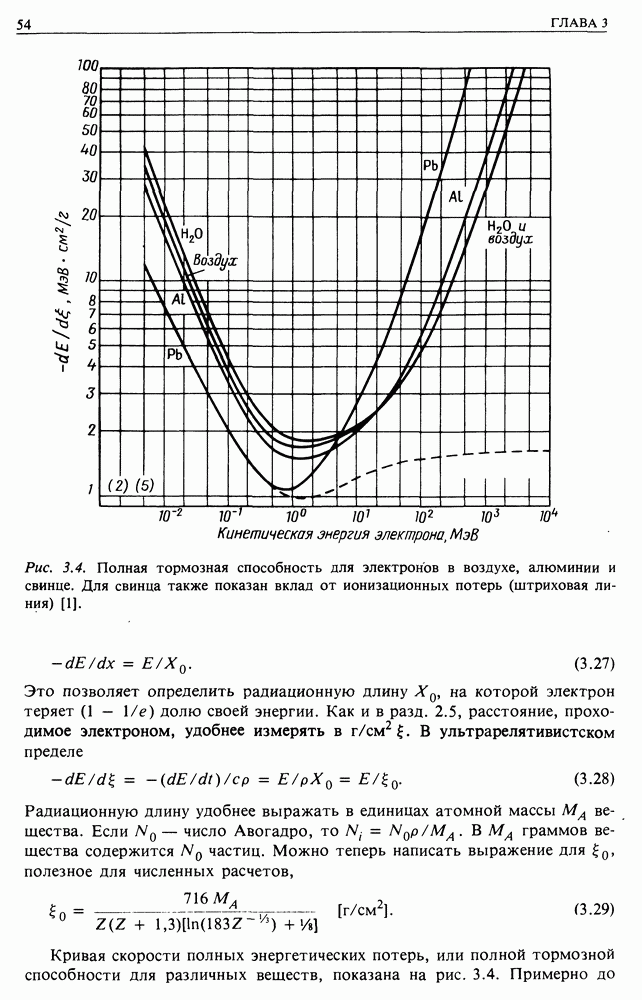
Рис. 3.4. Полная тормозная способность для электронов в воздухе, алюминии и свинце. Для свинца также показан вклад от ионизационных потерь (штриховая линия) [1].

Это позволяет определить радиационную длину на которой электрон теряет долю своей энергии. Как и в разд. 2.5, расстояние, проходимое электроном, удобнее измерять в В ультрарелятивистском пределе

Радиационную длину удобнее выражать в единицах атомной массы вещества. Если число Авогадро, то граммов вещества содержится частиц. Можно теперь написать выражение для полезное для численных расчетов,

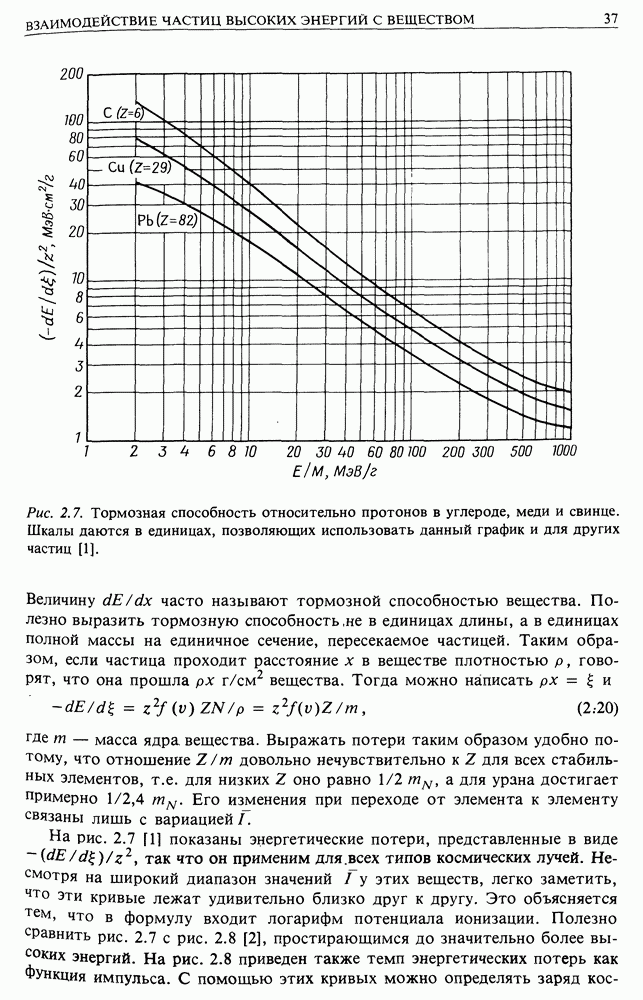
Кривая скорости полных энергетических потерь, или полной тормозной способности для различных веществ, показана на рис. 3.4. Примерно до

Рис. 3.5. Плотность вероятности испускания фотона в процессе торможения как функция частоты излучаемого фотона.

где электроны только становятся релятивистскими, ионизационные потери преобладают, но выше этого значения релятивистские потери быстро начинают преобладать. Можно определить критическую энергию при которой тормозные потери становятся равными ионизационным. Для воздуха, свинца и водорода равно соответственно Это очень важный результат для анализа атмосферных ливней.

Приводим радиационные длины для некоторых типичных веществ: воздух — свинец — водород —

Радиационная длина для воздуха играет особую роль, поскольку полная глубина атмосферы равна и поэтому электроны космических лучей могут претерпеть катастрофические тормозные потери, войдя в атмосферу.

Другим решающим фактором является спектр излучения, на получение которого мы потратили столько усилий. Перепишем его в виде вероятности испускания фотона, тогда

Это означает, что вероятность расходится в области нулевой частоты (рис. 3.5). Однако это не играет роли, так как энергия здесь нулевая. Хотя вероятность испускания фотона мала, но зато он уносит значительную часть энергии электрона. Поскольку энергетический спектр плоский, можно ожидать, что на каждой радиационной длине будет испущен один или два энергичных фотона. Это очень важно, потому что это означает, что электрон очень высокой энергии оставляет, скажем, около половины своей энергии в виде одного или двух энергичных фотонов еще в самом начале своего пути в атмосфере. Это естественно приводит нас к рассмотрению взаимодействия фотонов высоких энергий.