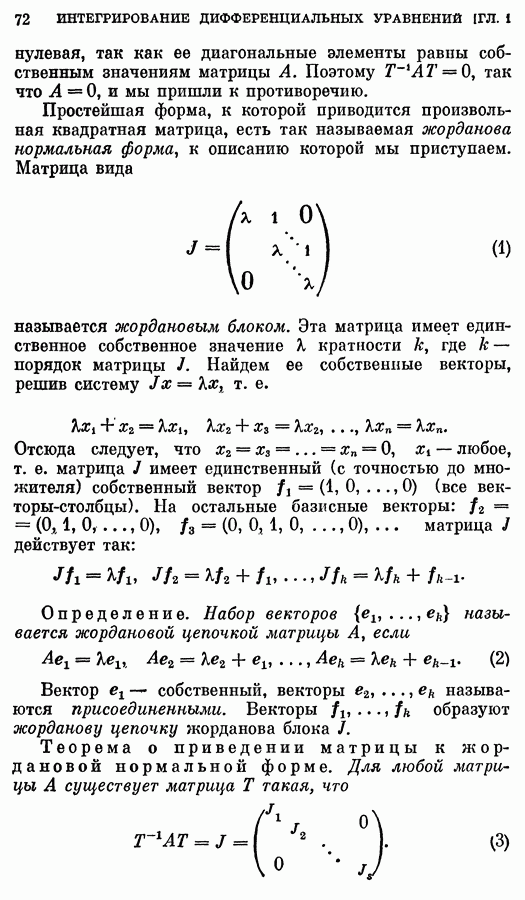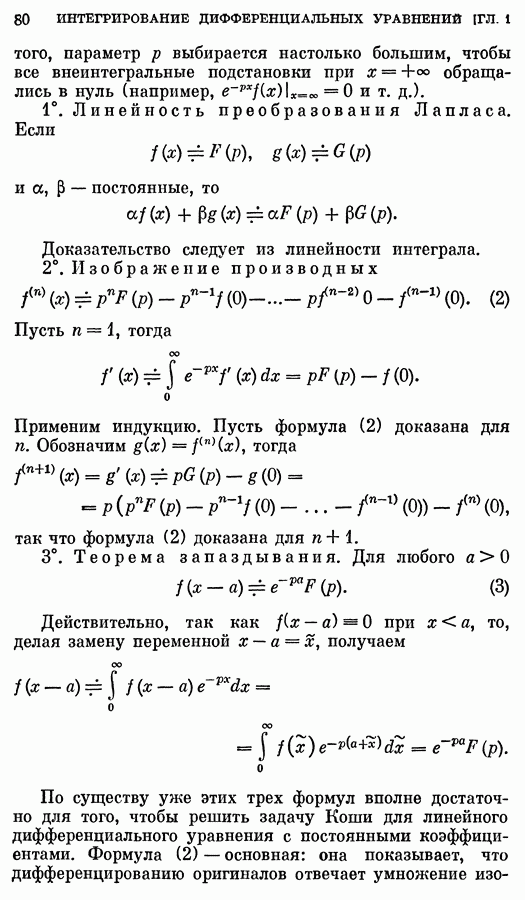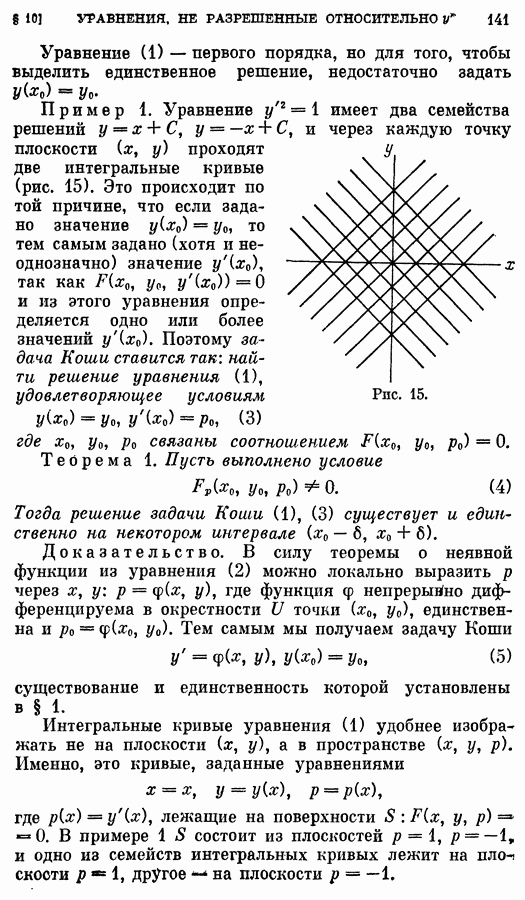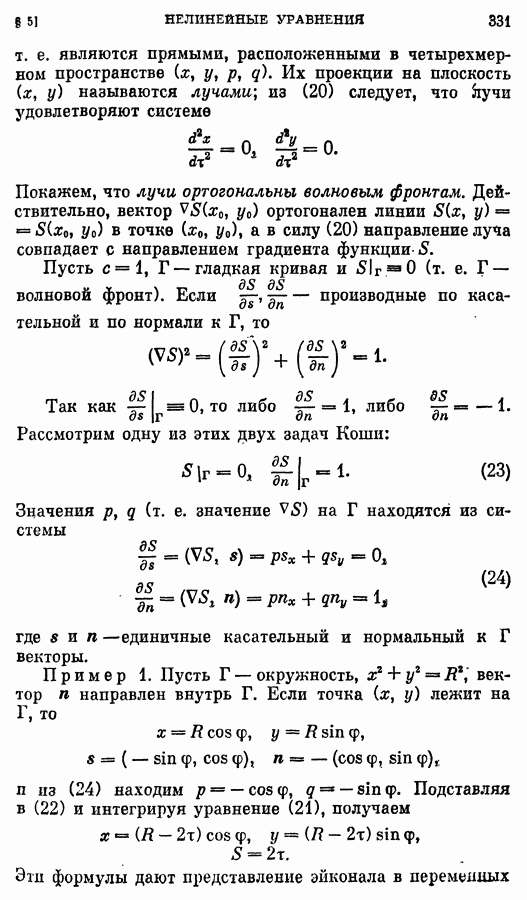| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
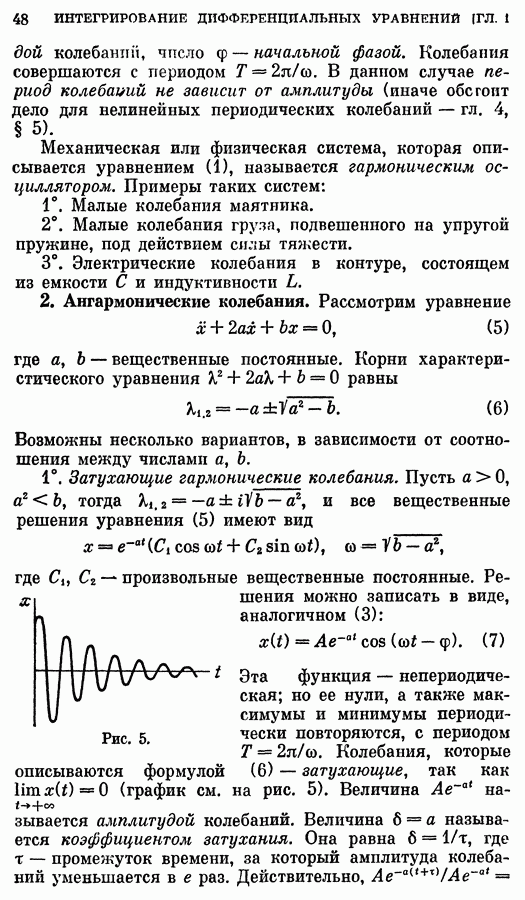
ZADANIA.TO
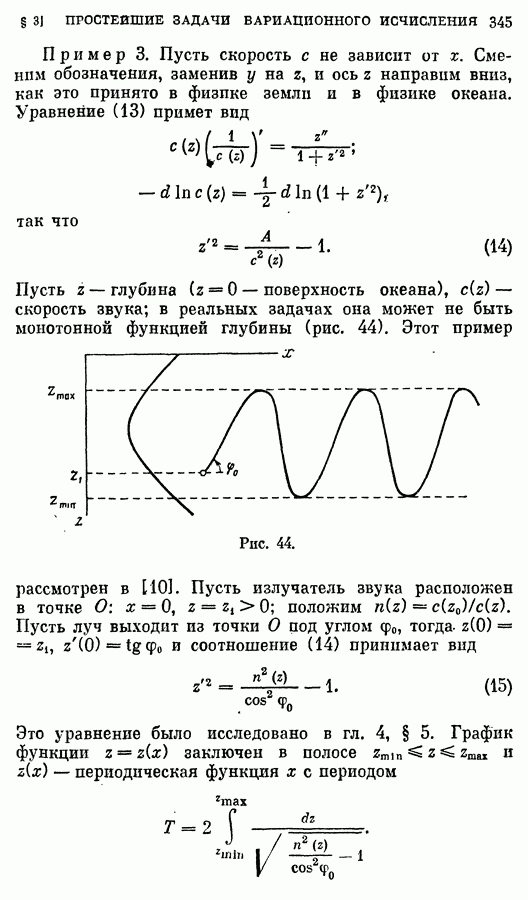
§ 12. Дельта-функция и ее применения
1. Дельта-функция Дирака.
Эта функция — она обозначается  — была введена английским физиком П. Дираком. Ее определение таково:
— была введена английским физиком П. Дираком. Ее определение таково:

Дельта-функцию можно рассматривать, например, как плотность единичной массы, сосредоточенной в точке  (это только одна из известных физических интерпретаций дельта-функции). Действительно, обозначим эту плотность
(это только одна из известных физических интерпретаций дельта-функции). Действительно, обозначим эту плотность  тогда
тогда  при
при  (вся масса сосредоточена в точке
(вся масса сосредоточена в точке  , ибо масса равна единице, так что
, ибо масса равна единице, так что  .
.
Разумеется, дельта-функция не есть функция в обычном смысле слова. Это обобщенная функция. Теория обобщенных функций была построена советским математиком С. Л. Соболевым и французским математиком П. Шварцем.
Основы теории обобщенных функций читатель может тйти в [15, 18]. Мы ограничимся тем, что приведем сновные формулы, относящиеся к дельта-функции, и не будем излагать строгую теорию обобщенных функций. Читатель, незнакомый с обобщенными функциями, будет находиться примерно в том же положении, в каком находились в начале нашего века инженеры, которые использовали метод Хевисайда (см. гл. 1, § 11). Впрочем, это не совсех М так: математического обоснования метода Хевисайда тогда не было, а математическое обоснование приведенных ниже результатов — теория обобщенных функций — существует.
Введем понятие обобщенной функции. Пусть К — множество всех функций  которые бесконечно дифференцируемы на всей оси
которые бесконечно дифференцируемы на всей оси  и финитны. Последнее означает, что каждая функция
и финитны. Последнее означает, что каждая функция  тождественно равна нулю вне некоторого отрезка:
тождественно равна нулю вне некоторого отрезка:  если
если  числа
числа  — свои для каждой функции
— свои для каждой функции  Множество К есть линейное пространство; его элементы
Множество К есть линейное пространство; его элементы  называются основными (или пробными) функциями.
называются основными (или пробными) функциями.
Обобщенной функцией  (над пространством К) называется линейный функционал, определенный на пространстве К. Именно, каждой функции
(над пространством К) называется линейный функционал, определенный на пространстве К. Именно, каждой функции  ставится в соответствие число
ставится в соответствие число  причем
причем

для любых основных функций  и для любых чисел «
и для любых чисел « От функционала
От функционала  требуется также непрерывность; мы не будем вводить соответствующее определение, поскольку во всех рассматриваемых примерах это свойство выполняется.
требуется также непрерывность; мы не будем вводить соответствующее определение, поскольку во всех рассматриваемых примерах это свойство выполняется.
Будем употреблять обозначения, принятые в физической литературе. Именно, значение  будем записывать в виде интеграла
будем записывать в виде интеграла

Класс обобщенных функций содержит все «обычные» функции. Действительно, если  — непрерывная на оси
— непрерывная на оси  функция, то интеграл из (3) существует и обладает свойством линейности. Если
функция, то интеграл из (3) существует и обладает свойством линейности. Если  — непрерывные на всей оси функции и
— непрерывные на всей оси функции и

 любой
любой  функции
функции  (гл. 6, § 3, основная лемма вариационного исчисления). По аналогии с этим фактом будем считать, что две обобщенные функции
(гл. 6, § 3, основная лемма вариационного исчисления). По аналогии с этим фактом будем считать, что две обобщенные функции  равны:
равны:  если соотношение (4) выполняется для любой основной функции
если соотношение (4) выполняется для любой основной функции 
Введем производные от обобщенных функций. Пусть  — непрерывно дифференцируемая на всей оси функция,
— непрерывно дифференцируемая на всей оси функция,  — основная функция. Интегрируя по частям,
— основная функция. Интегрируя по частям,
получаем

поскольку внеинтегральная подстановка  равна нулю — функция
равна нулю — функция  финитна. Формулу (5) примем в качестве определения обобщенной функции
финитна. Формулу (5) примем в качестве определения обобщенной функции  Заметим, что правая часть формулы (5) определена, так как
Заметим, что правая часть формулы (5) определена, так как  — основная функция, и потому интеграл
— основная функция, и потому интеграл  определен. Аналогично определяются высшие
определен. Аналогично определяются высшие  из водные:
из водные:

Приведем основные формулы для дельта-функции и поясним их.

Здесь  — непрерывная на всей оси функция. Эта формула есть определение дельта-функции.
— непрерывная на всей оси функция. Эта формула есть определение дельта-функции.
Дельта-функцию можно представить как «предел» обычных функций.
Пусть  — ступенчатая функция (рис. 18):
— ступенчатая функция (рис. 18):

так что


Рис. 18.
Функцию  можно интерпретировать как плотность единичной массы, «размазанной» да интервал
можно интерпретировать как плотность единичной массы, «размазанной» да интервал  . Покажем, что
. Покажем, что

где предел понимается так:

для любой непрерывной на всей оси функции  Действительно, по теореме о среднем
Действительно, по теореме о среднем

откуда следует (8).
Обозначим символом  ступенчатую функцию Хевисайда:
ступенчатую функцию Хевисайда:

Действительно, пусть  — основная функция. Согласно определению (5),
— основная функция. Согласно определению (5),

(так как  — финитная функция)
— финитная функция)

Поскольку первый и последний интегралы равны для любой основной функции  то
то  согласно определению равенства обобщенных функций (см. (4)).
согласно определению равенства обобщенных функций (см. (4)).
3°. Пусть функция  непрерывно дифференцируема на полуосях
непрерывно дифференцируема на полуосях  в точке а может иметь разрыв. Тогда
в точке а может иметь разрыв. Тогда

Здесь  (т. е. величина скачка функции
(т. е. величина скачка функции  — обычная производная.
— обычная производная.
Действительно, по определению (5) имеем

(интегрируем по частям)

Последнее слагаемое равно  , и формула 3° доказана.
, и формула 3° доказана.

Здесь  — любая основная функция; если
— любая основная функция; если  фиксировано, то достаточно, чтобы функция
фиксировано, то достаточно, чтобы функция  была
была  раз непрерывно дифференцируема на оси х.
раз непрерывно дифференцируема на оси х.

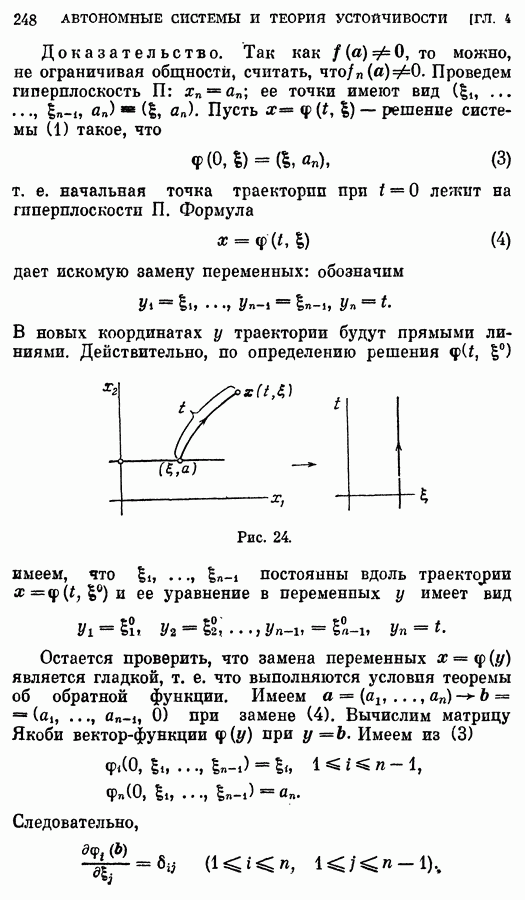
Пусть  (для определенности),
(для определенности),  — непрерывная на оси х функция. Тогда
— непрерывная на оси х функция. Тогда

(мы сделали замену 

Так как первый последний интегралы равны при любой непрерывной функции  то 5° доказано.
то 5° доказано.

Здесь мы ограничимся совсем уже формальным выводом. Воспользуемся формулой обращения для преобразования Фурье:

где  преобразование Фурье функции
преобразование Фурье функции 

Пусть  тогда
тогда  подставляя это выражание в формулу обращения, получаем 6°.
подставляя это выражание в формулу обращения, получаем 6°.
7°. Пусть  — гладкая функция, имеющая конечно число нулей
— гладкая функция, имеющая конечно число нулей  и все нули — простые
и все нули — простые  Тогда
Тогда

Рассмотрим вначале случай, когда функция  имеет ровно один нуль
имеет ровно один нуль  Так как
Так как  при
при  то
то

где  может быть выбрано сколь угодно малым. Сделаем в интеграле замену переменной
может быть выбрано сколь угодно малым. Сделаем в интеграле замену переменной  тогда существует обратная функция
тогда существует обратная функция  и
и

Действительно, числа  положительны,
положительны,  Если
Если  то получим
то получим

так что в обоих случаях

Тем самым формула доказана при  Так как
Так как  при
при  то
то

со доказанному выше.
Формула из п. 7° верна и в том случае, когда функция  имеет бесконечно много нулей, и все они изолированы. Например,
имеет бесконечно много нулей, и все они изолированы. Например,

Приведем еще одну формулу, связанную с дельтафункцией. Пусть  — целое число, тогда
— целое число, тогда

Действительно,

Формул 1° — 7° вполне достаточно для решения большинства прикладных вадач, связанных с обыкновенными дифференциальными уравнениями.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
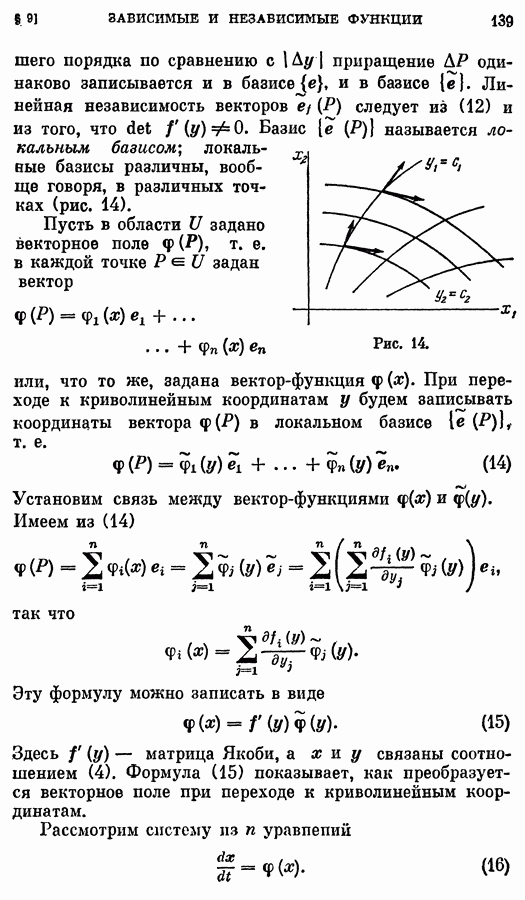
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
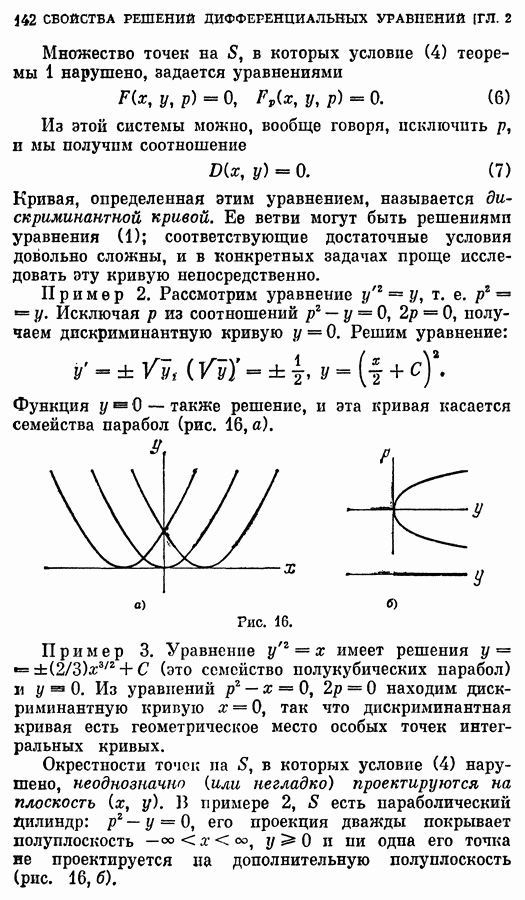
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
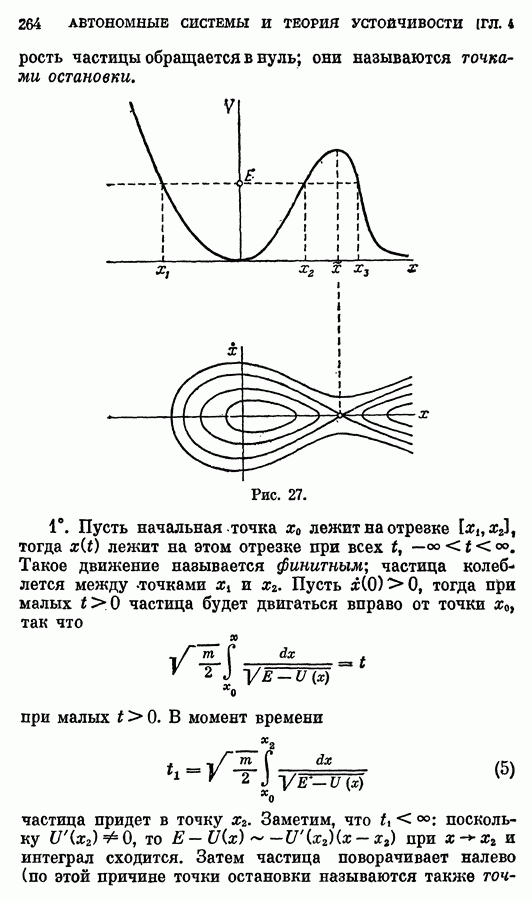
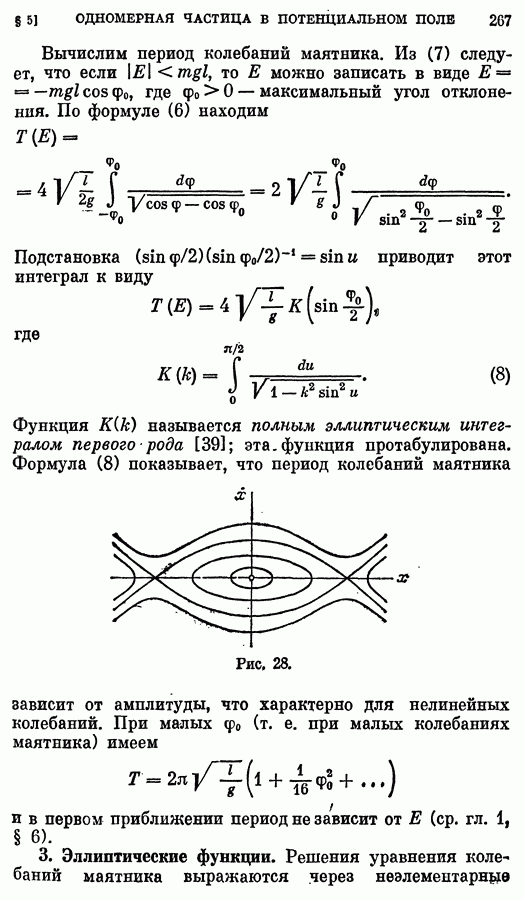
- § 5. Одномерное движение частицы в потенциальном поле
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
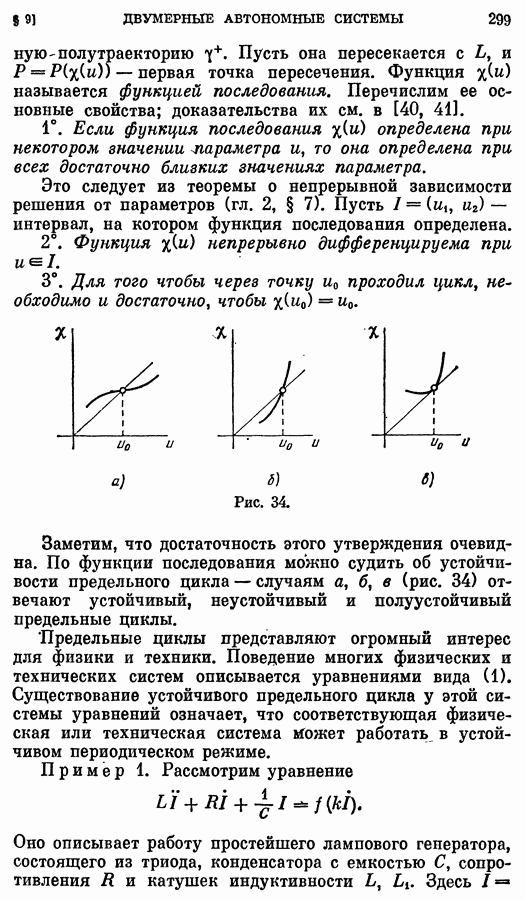
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
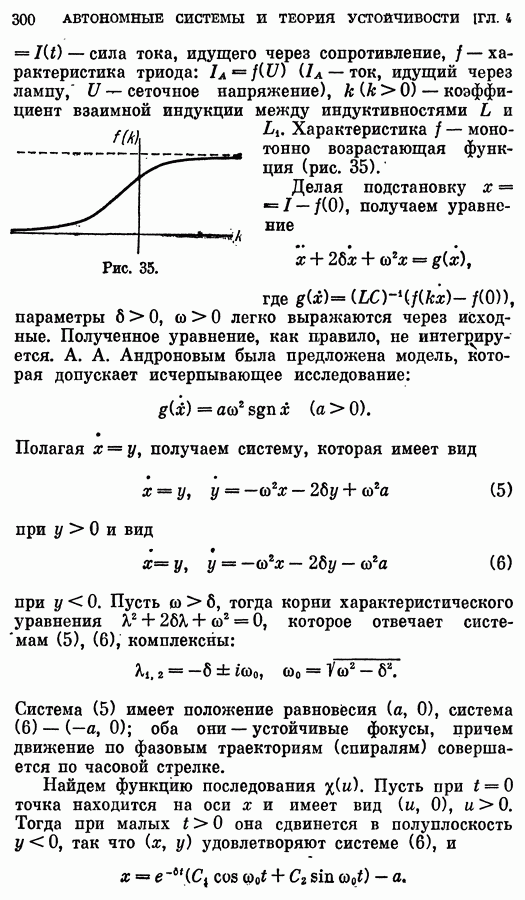
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ