| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
При равновероятных передаваемых сигналах средняя вероятность ошибки воспроизведения сигнала на выходе приемника  где
где  вероятность ошибки при передаче сигнала
вероятность ошибки при передаче сигнала 
Согласно теории потенциальной помехоустойчивости минимум  достигается при оптимальном приеме, основанном на вычислении апостериорных вероятностей
достигается при оптимальном приеме, основанном на вычислении апостериорных вероятностей  принимаемый сигнал с помехой. Алгоритм работы оптимального приемника М позиционных сигналов имеет вид
принимаемый сигнал с помехой. Алгоритм работы оптимального приемника М позиционных сигналов имеет вид

При выполнении неравенства приемник выносит решение о передаче сигнала  Он содержит М каналов обработки, в каждом из которых вычисляется квадрат расстояния
Он содержит М каналов обработки, в каждом из которых вычисляется квадрат расстояния  и решающее устройство, в котором производится вынесение решения о посылаемом сигнале по наименьшему из расстояний.
и решающее устройство, в котором производится вынесение решения о посылаемом сигнале по наименьшему из расстояний.
Для сигналов с одинаковыми энергиями алгоритм приема преобразуется к виду

В каналах обработки такого приемника содержатся корреляторы, поэтому прием называется корреляционным.
Работу приемника можно представить геометрически. Сигналы  отображаются сигнальными точками. Пространство сигналов разбивается на М областей. Границами сигнальных областей служат плоскости, равноотстоящие от сигнальных точек, соответствующих парам сигналов
отображаются сигнальными точками. Пространство сигналов разбивается на М областей. Границами сигнальных областей служат плоскости, равноотстоящие от сигнальных точек, соответствующих парам сигналов  Оптимальному приему соответствует такое разбиение пространства на области сигналов, при котором достигается минимум средней вероятности ошибки
Оптимальному приему соответствует такое разбиение пространства на области сигналов, при котором достигается минимум средней вероятности ошибки  На
На  показаны примеры расположения границ областей сигналов. Ошибка при передаче сигнала происходит, когда вектор принимаемого сигнала с помехой выходит за пределы области сигнала. Оптимальным выбором расположения сигнальных точек достигается минимум средней вероятности ошибки
показаны примеры расположения границ областей сигналов. Ошибка при передаче сигнала происходит, когда вектор принимаемого сигнала с помехой выходит за пределы области сигнала. Оптимальным выбором расположения сигнальных точек достигается минимум средней вероятности ошибки 
Разделение сигналов ФМ-4 в соответствии с алгоритмом (2.12) можно упростить. Как видно из  для решения о том, в какой из четырех областей находится вектор, достаточно определить проекции на его орты и
для решения о том, в какой из четырех областей находится вектор, достаточно определить проекции на его орты и  Решения выносят по знакам проекций, совокупность которых совпадает со знаками перед ортами в формулах (2.11). Если например,
Решения выносят по знакам проекций, совокупность которых совпадает со знаками перед ортами в формулах (2.11). Если например,  то выносят решение о посылке сигнала
то выносят решение о посылке сигнала  Схема демодулятора при этом содержит два канала
Схема демодулятора при этом содержит два канала  с опорными колебаниями
с опорными колебаниями  интеграторами И и решающими
интеграторами И и решающими

Рис. 2.6. Манипуляционные коды
устройствами РУ, в которых определяют полярности символов в каналах. Для работы этих устройств необходимы сигналы тактовой синхронизации ТС. Сигналы опорной несущей и ТС вырабатываются вспомогательными устройствами демодулятора. В коммутаторе К происходит преобразование решений в квадратурных каналах в последовательности символов на выходе демодулятора.
Аналогично выполняют демодуляцию сигналов АФМ-16 (рис.2.6,б), однако в этом случае решающие устройства РУ многоуровневые. Демодуляция сигналов многопозиционной ФМ требует большого числа двоичных решений. В частности, при ФМ-16, как это видно из конфигураций областей сигналов на рис.2.6,б, необходимо  канала с двоичными решающими устройствами.
канала с двоичными решающими устройствами.
Сигналы ММС принимают с учетом формы элементарных модулирующих сигналов (2.8), которые играют роль весовых функций опорных колебаний  Схема демодулятора показана на рис.2.7,б. При интегрировании результатов обработки в каналах должно быть учтено смещение сигналов в квадратурных каналах на интервал Т. Такое же смещение необходимо учитывать в схеме на рис.2.7,а при приеме сигналов смещенной ФМ.
Схема демодулятора показана на рис.2.7,б. При интегрировании результатов обработки в каналах должно быть учтено смещение сигналов в квадратурных каналах на интервал Т. Такое же смещение необходимо учитывать в схеме на рис.2.7,а при приеме сигналов смещенной ФМ.
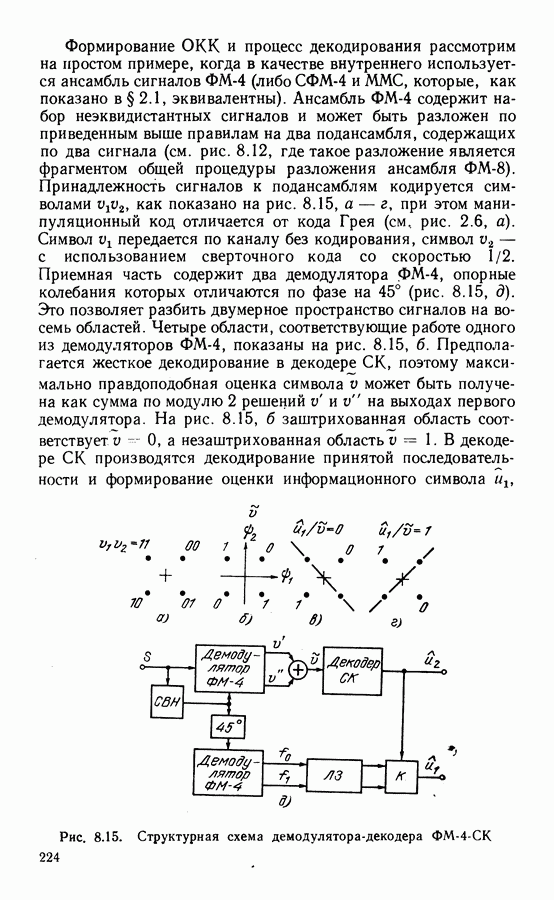
В многопозиционных ансамблях каждый сигнал содержит информацию о нескольких двоичных информационных символах. Для минимизации вероятности ошибки на двоичный символ  необходимо оптимизировать манипуляционный код, сопоставляющий каждому передаваемому сигналу набор двоичных информационных символов. Ошибки чаще происходят за счет переходов в области соседних сигналов. Поэтому информационные комбинации, соответствующие соседним сигналам, должны отличаться наименьшим числом двоичных символов. Этому условию удовлетворяет код Грея, пример которого для сигналов ФМ-4 показан на
необходимо оптимизировать манипуляционный код, сопоставляющий каждому передаваемому сигналу набор двоичных информационных символов. Ошибки чаще происходят за счет переходов в области соседних сигналов. Поэтому информационные комбинации, соответствующие соседним сигналам, должны отличаться наименьшим числом двоичных символов. Этому условию удовлетворяет код Грея, пример которого для сигналов ФМ-4 показан на

Рис. 2.7. Структурные схемы демодуляторов: а — ФМ-4; б - ММС

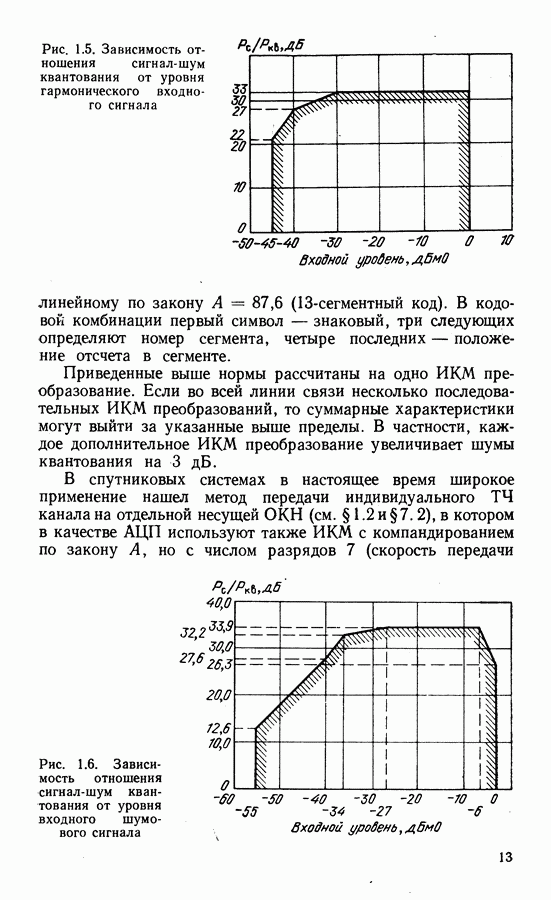
Рис. 2.8. К оценке энергетических потерь

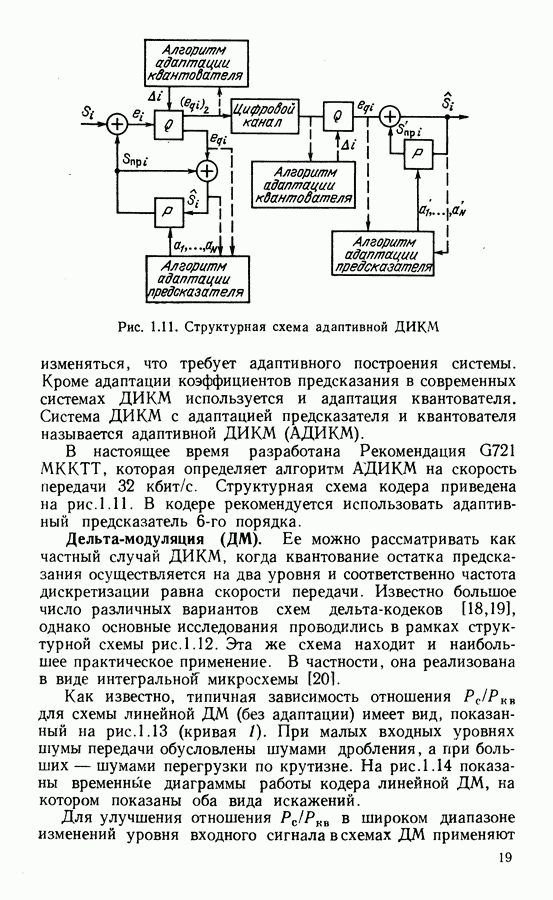
Рис. 2.9. Кривые помехоустойчивости приема дискретных сигналов
рис. 2.6,а. Здесь переход из любой сигнальной точки в соседнюю область приводит к ошибке в одном двоичном символе. В табл. 2.1 приведен код Грея для сигналов ФМ-8. Пример кода для сигналов АФМ-16 показан на рис.2.6.в. Оптимальный манипуляционный код получим, если координаты сигнальных точек по горизонтали и по вертикали кодировать одномерным кодом Грея, а затем объединить двоичные символы в четырехзначные кодовые комбинации.
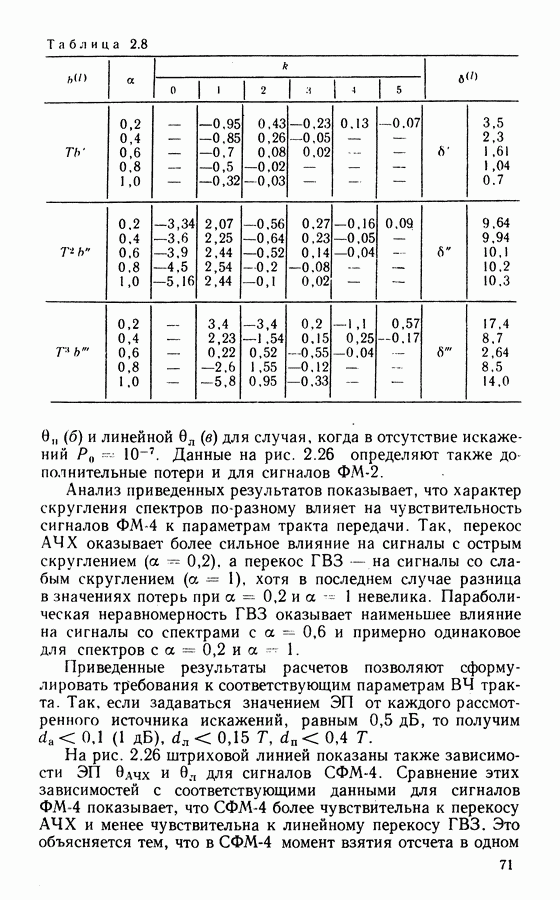
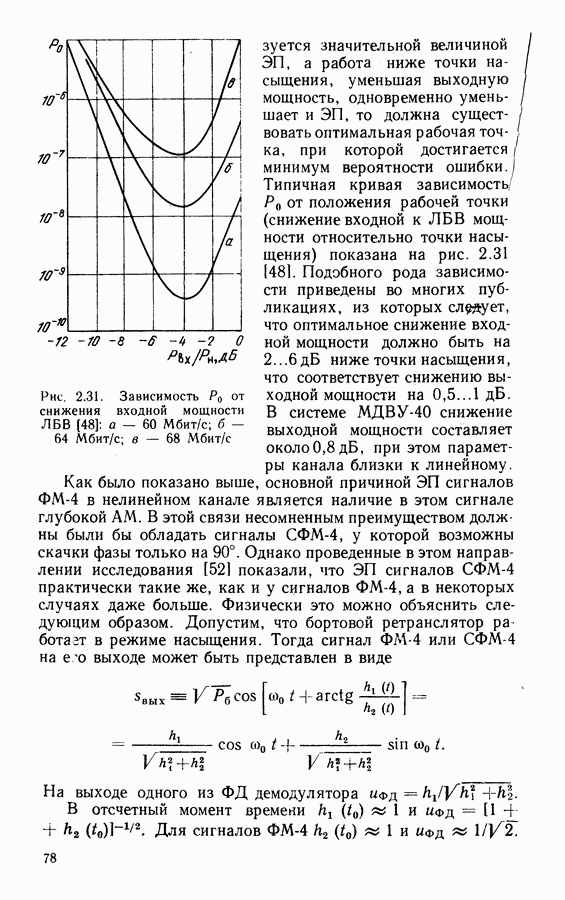
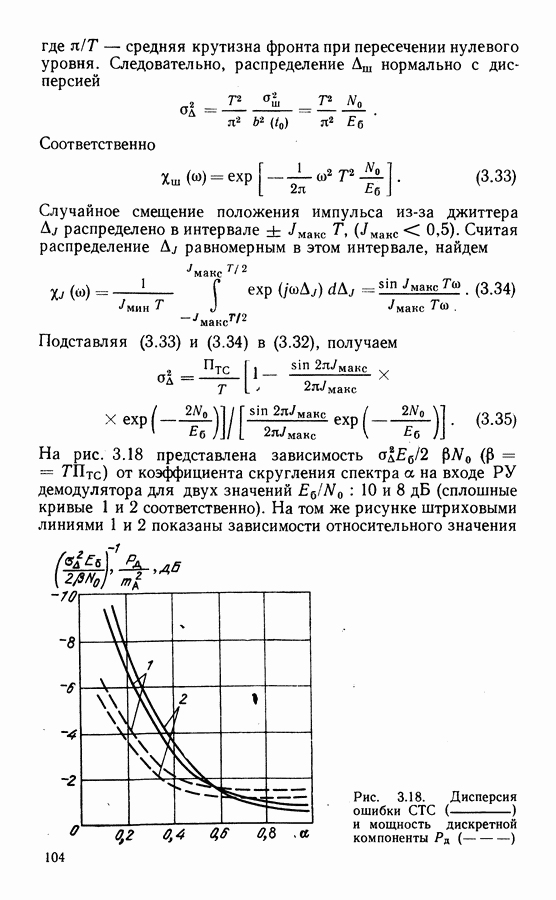
При идеальной демодуляции полагают, что параметры принимаемого сигнала (временные границы посылок, значения частот и начальных фаз и др.) известны точно. В реальных условиях сведения о параметрах сигнала формируются при действии помех. Кроме того, в реальных трактах действуют дестабилизирующие факторы (нестабильности частот гетеродинов, скачки фазы, колебания уровней сигналов и др.), что увеличивает погрешность оценки параметров. Рекомендуемые теорией оптимального приема алгоритмы могут быть реализованы лишь приближенно. Иногда в целях снижения сложности аппаратуры оптимальные алгоритмы упрощают. Влияние перечисленных выше факторов учитывается величиной энергетических потерь. Пусть зависимость  при идеальной демодуляции, определяемая потенциальной помехоустойчивостью, изображается на рис. 2.8 сплошной кривой. Помехоустойчивость в реальных условиях будет хуже и кривая на рис. 2.8 будет смещена вправо (штриховая линия). Энергертические потери (ЭП) показывают, насколько необходимо увеличить отношение сигнал-шум на входе реального демодулятора по сравнению с идеальным, чтобы вероятность ошибки
при идеальной демодуляции, определяемая потенциальной помехоустойчивостью, изображается на рис. 2.8 сплошной кривой. Помехоустойчивость в реальных условиях будет хуже и кривая на рис. 2.8 будет смещена вправо (штриховая линия). Энергертические потери (ЭП) показывают, насколько необходимо увеличить отношение сигнал-шум на входе реального демодулятора по сравнению с идеальным, чтобы вероятность ошибки  осталась на прежнем уровне. Величина
осталась на прежнем уровне. Величина
потерь 0 совместно с кривой потенциальной помехоустойчивости позволяет оценить отношение сигнал-шум на входе демодулятора, необходимое для получения заданной вероятности ошибки в реальных условиях.
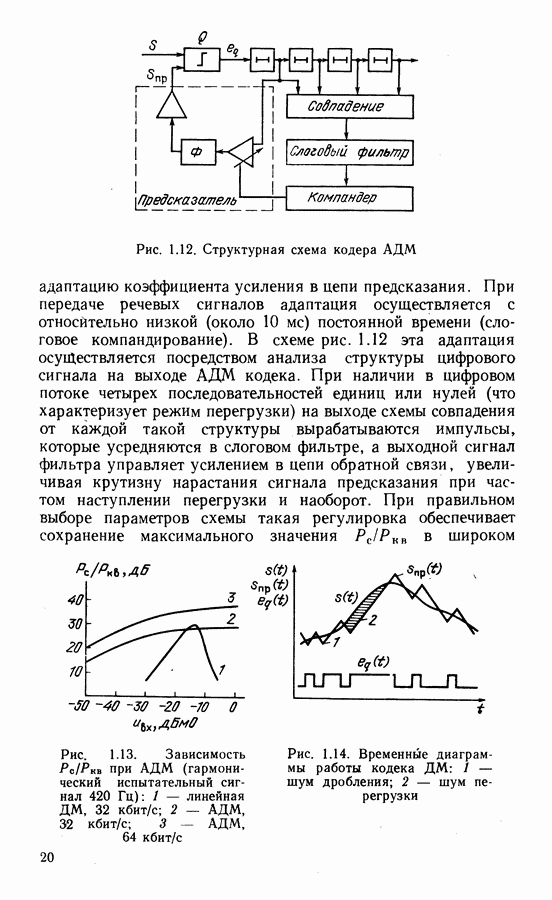
Вероятность ошибки при оптимальном когерентном приеме двоичных сигналов и действии аддитивной гауссовской помехи с равномерным энергетическим спектром зависит от расстояния между сигналами  и односторонней спектральной плотности помехи
и односторонней спектральной плотности помехи  и имеет вид
и имеет вид  где
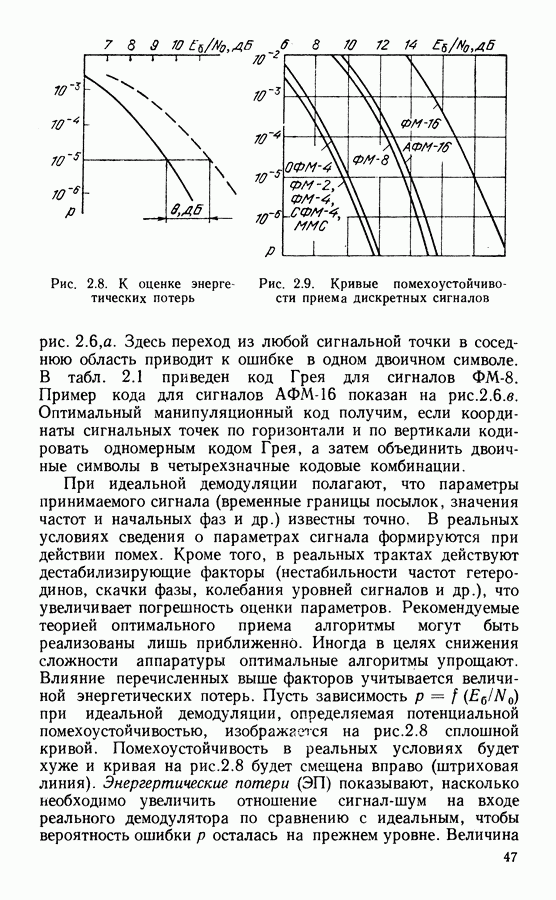
где  дополнение интеграла вероятности до единицы. При ФМ-2 расстояние между сигналами
дополнение интеграла вероятности до единицы. При ФМ-2 расстояние между сигналами  а вероятность ошибки в приеме сигнала
а вероятность ошибки в приеме сигнала  и вероятность ошибки на бит
и вероятность ошибки на бит  совпадают. Поэтому помехоустойчивость определяется выражением
совпадают. Поэтому помехоустойчивость определяется выражением

Зависимость  для ФМ-2 приведена на рис. 2.9. Вероятность ошибки в двоичном символе
для ФМ-2 приведена на рис. 2.9. Вероятность ошибки в двоичном символе  при оптимальном приеме сигналов ФМ-4 можно также определить по формуле (2.13), поскольку канал с ФМ-4, как было показано выше, содержит два независимых канала с ФМ-2. При числе позиций фазы
при оптимальном приеме сигналов ФМ-4 можно также определить по формуле (2.13), поскольку канал с ФМ-4, как было показано выше, содержит два независимых канала с ФМ-2. При числе позиций фазы  выражение для расчета вероятности ошибки усложняется, однако при большом отношении сигнал-шум и оптимальном манипуляционном коде используют приближенную формулу:
выражение для расчета вероятности ошибки усложняется, однако при большом отношении сигнал-шум и оптимальном манипуляционном коде используют приближенную формулу:  Точные выражения для расчетов вероятности ошибки можно найти в [33, 34]. На рис. 2.9 показаны кривые помехоустойчивости при оптимальном приеме сигналов ФМ-8 и ФМ-16. С ростом числа фаз помехоустойчивость снижается. Переход к смещенной фазовой модуляции взаимных расстояний между сигналами не изменяет, в этом случае вероятность ошибки при СФМ-4 определяется выражением (2.13).
Точные выражения для расчетов вероятности ошибки можно найти в [33, 34]. На рис. 2.9 показаны кривые помехоустойчивости при оптимальном приеме сигналов ФМ-8 и ФМ-16. С ростом числа фаз помехоустойчивость снижается. Переход к смещенной фазовой модуляции взаимных расстояний между сигналами не изменяет, в этом случае вероятность ошибки при СФМ-4 определяется выражением (2.13).
Помехоустойчивость приема сигналов с частотной модуляцией и непрерывной фазой зависит от индекса модуляции  а также от того, насколько учитывается фазовая связь между символами при вынесении решения в демодуляторе. Если интервал интегрирования в когерентном оптимальном приемнике сигналов
а также от того, насколько учитывается фазовая связь между символами при вынесении решения в демодуляторе. Если интервал интегрирования в когерентном оптимальном приемнике сигналов  составляет длительность двух двоичных символов
составляет длительность двух двоичных символов  то сигналы образуют биортогональный ансамбль (2.10), для которого вероятность ошибки определяется выражением (2.13). При интегрировании на большем интервале и индексе
то сигналы образуют биортогональный ансамбль (2.10), для которого вероятность ошибки определяется выражением (2.13). При интегрировании на большем интервале и индексе  возможно некоторое улучшение помехоустойчивости (около 1 дБ).
возможно некоторое улучшение помехоустойчивости (около 1 дБ).
Помехоустойчивость приема сигналов с АФМ при большом отношении сигнал-шум можно оценивать выражением  Здесь
Здесь  расстояние между сигналами с номерами
расстояние между сигналами с номерами  Точные выражения и оценки погрешности при использовании приближенных формул приведены в [33, 34]. На рис. 2.9 даны результаты расчетов для сигналов АФМ-16. Сравнение с ФМ-16 показывает, что при одинаковой вероятности ошибки
Точные выражения и оценки погрешности при использовании приближенных формул приведены в [33, 34]. На рис. 2.9 даны результаты расчетов для сигналов АФМ-16. Сравнение с ФМ-16 показывает, что при одинаковой вероятности ошибки  при АФМ-16 необходимо меньшее отношение
при АФМ-16 необходимо меньшее отношение  При многопозиционной ФМ сигнальные точки расположены на окружности и пространство сигналов используется плохо. АФМ сигналы характеризуются более плотным и равномерным расположением сигнальных точек по всему сигнальному пространству, что при равной средней энергии обеспечивает большие значения минимального расстояния
При многопозиционной ФМ сигнальные точки расположены на окружности и пространство сигналов используется плохо. АФМ сигналы характеризуются более плотным и равномерным расположением сигнальных точек по всему сигнальному пространству, что при равной средней энергии обеспечивает большие значения минимального расстояния  и более высокую помехоустойчивость.
и более высокую помехоустойчивость.
Применение ОФМ приводит к некоторому возрастанию вероятности ошибки, поскольку демодуляция основана на сравнении параметров соседних символов. В частности, при ОФМ-2 и ОФМ-4 число ошибок на выходе демодулятора возрастает примерно вдвое, так что  Зависимость
Зависимость  для когерентного приема сигналов ОФМ-4 показана на рис. 2.9. Результаты исследования статистики ошибок при ОФМ произвольной кратности можно найти в [34, 37]. Удвоение ошибок приводит к незначительным энергетическим потерям по сравнению с абсолютной ФМ (около
для когерентного приема сигналов ОФМ-4 показана на рис. 2.9. Результаты исследования статистики ошибок при ОФМ произвольной кратности можно найти в [34, 37]. Удвоение ошибок приводит к незначительным энергетическим потерям по сравнению с абсолютной ФМ (около  )
)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
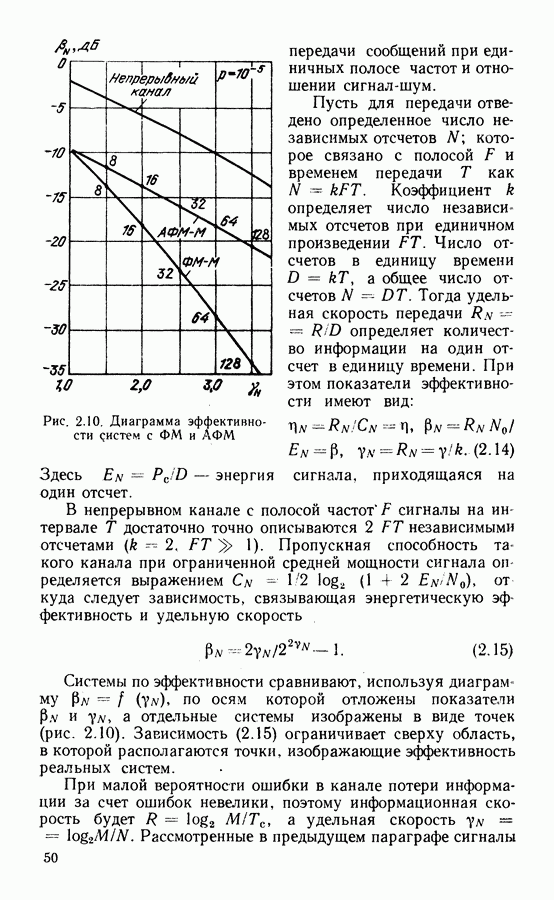
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
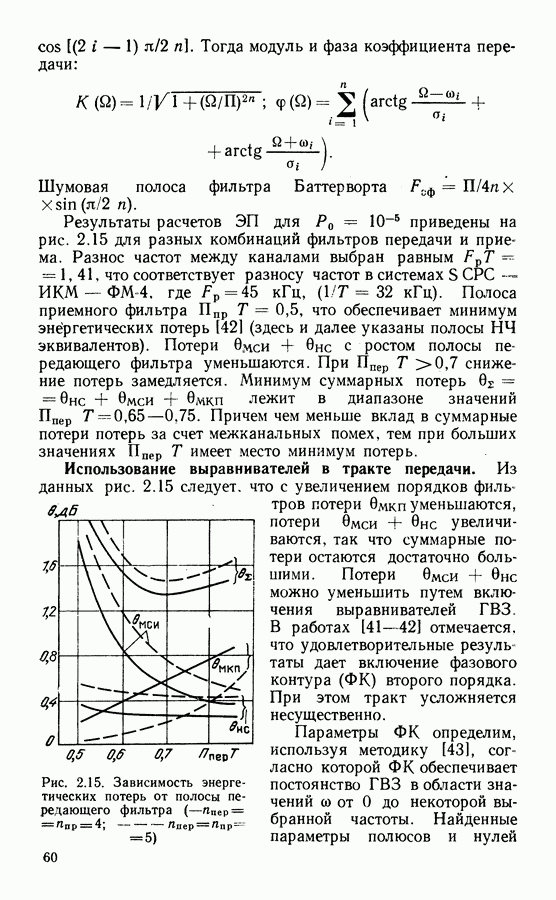
- Использование выравнивателей в тракте передачи.
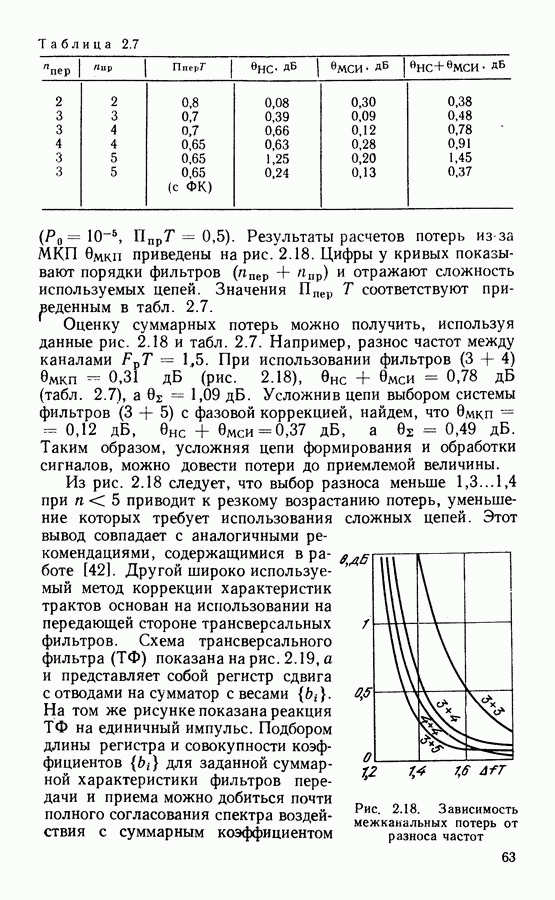
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
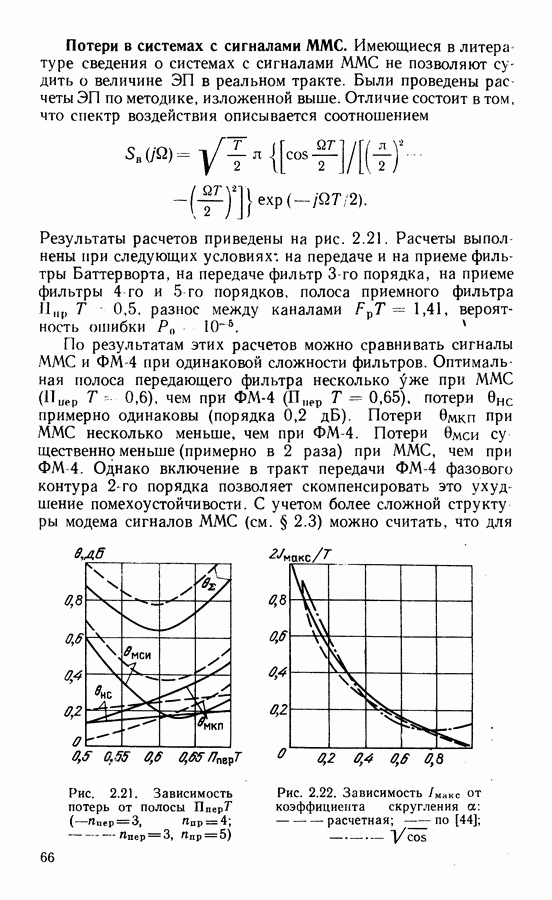
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
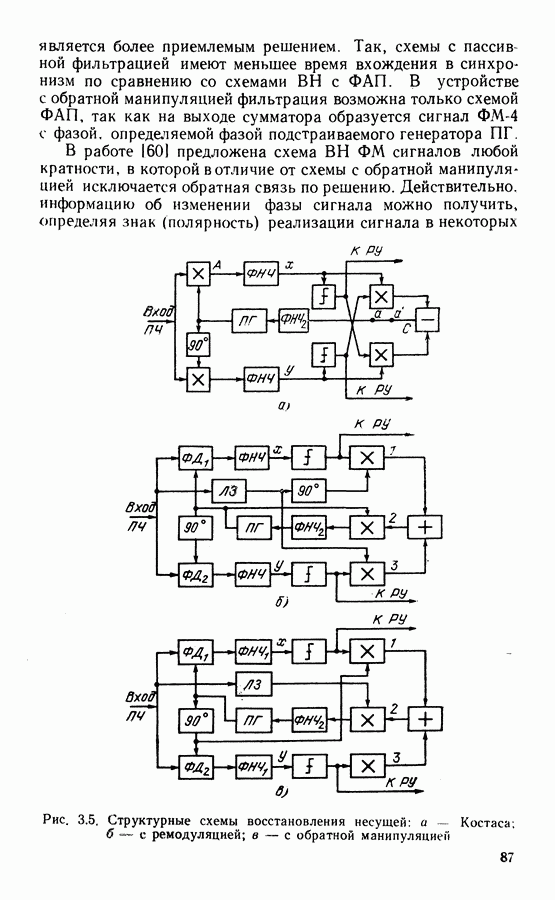
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
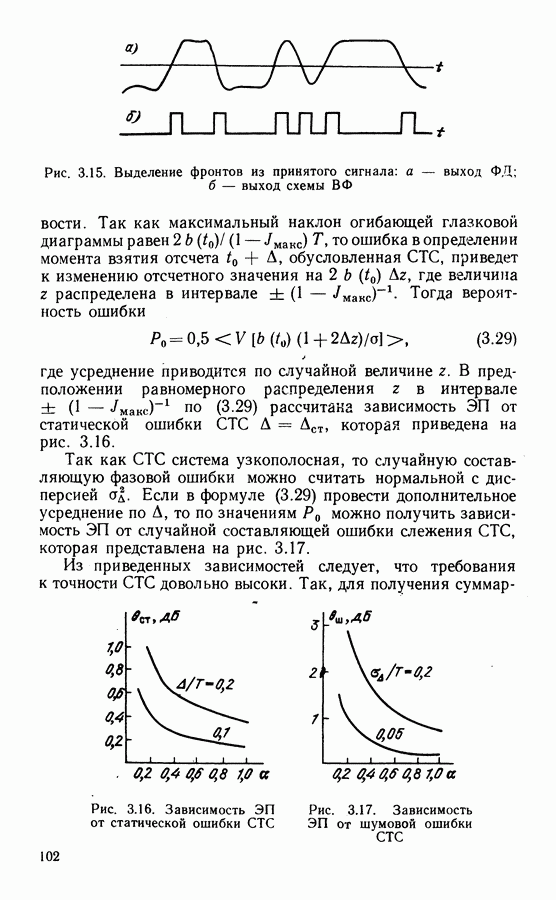
- Требования к точности работы системы ВН.
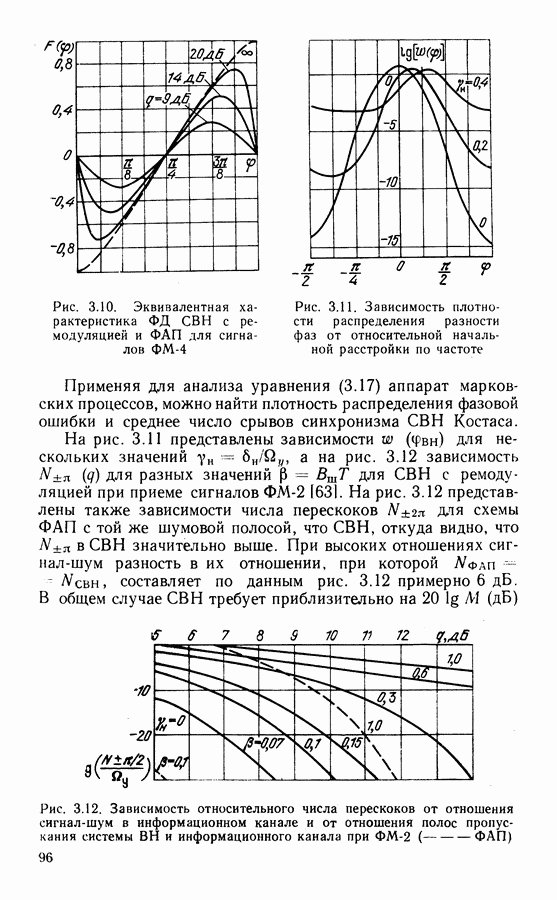
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
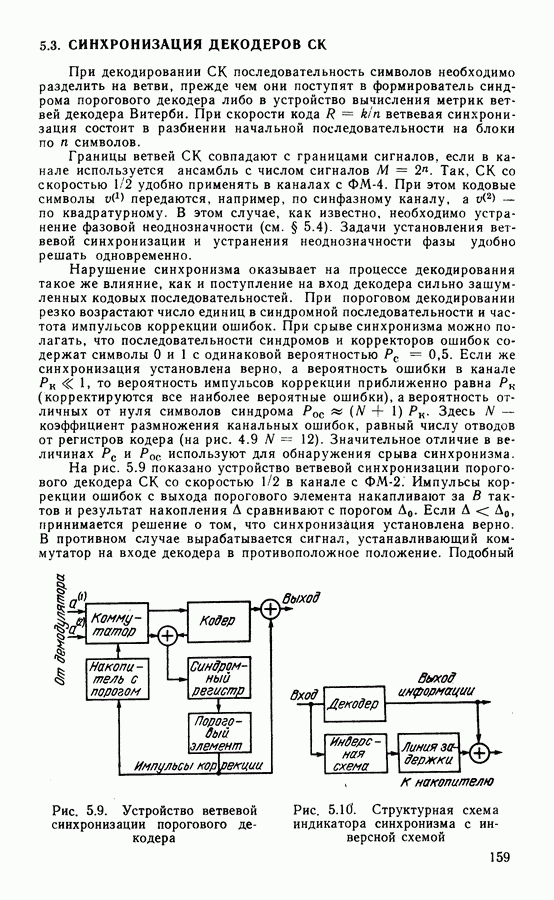
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
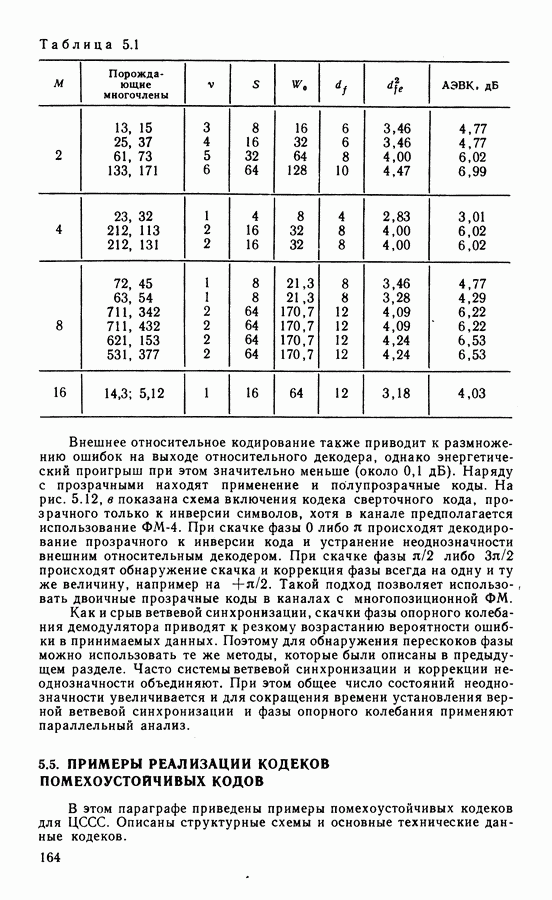
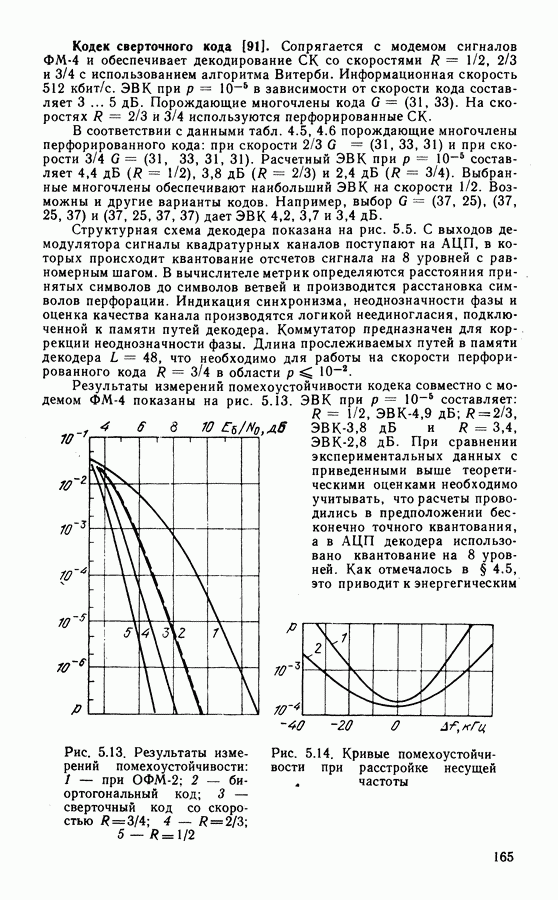
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
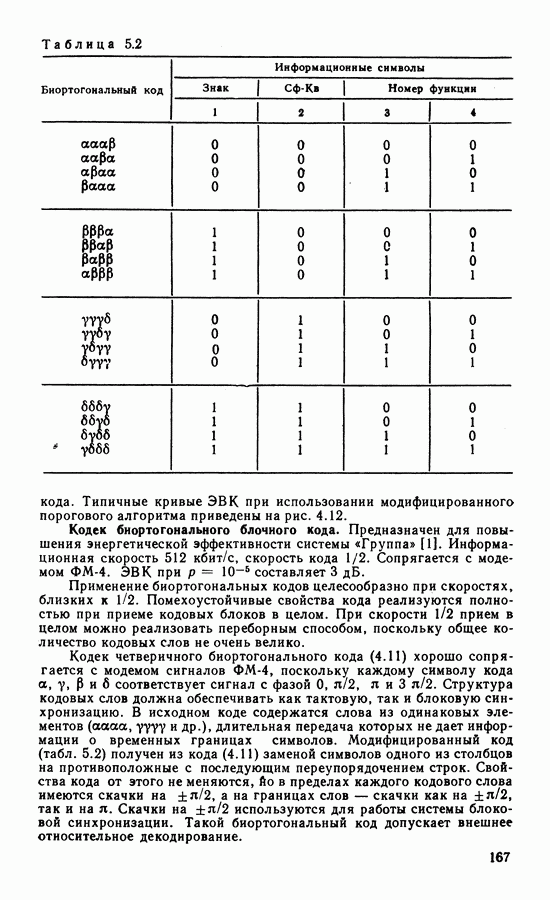
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
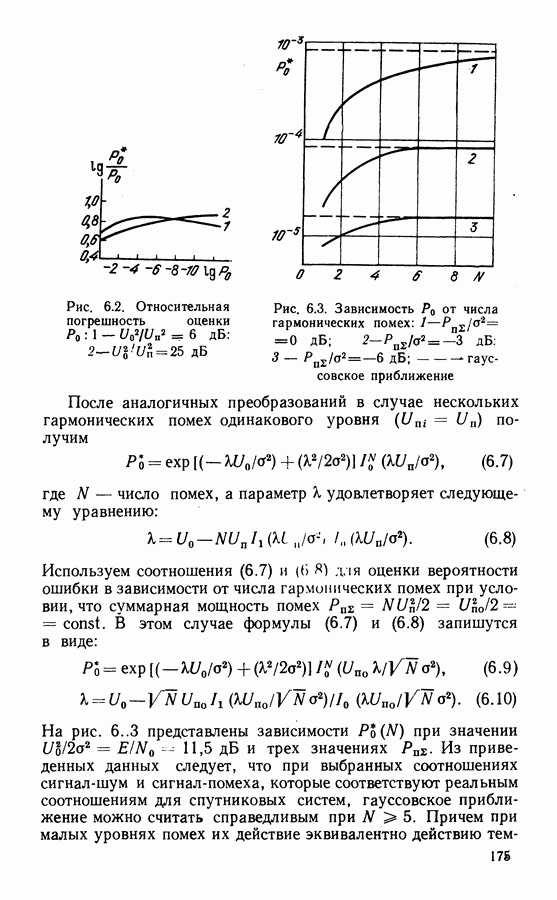
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
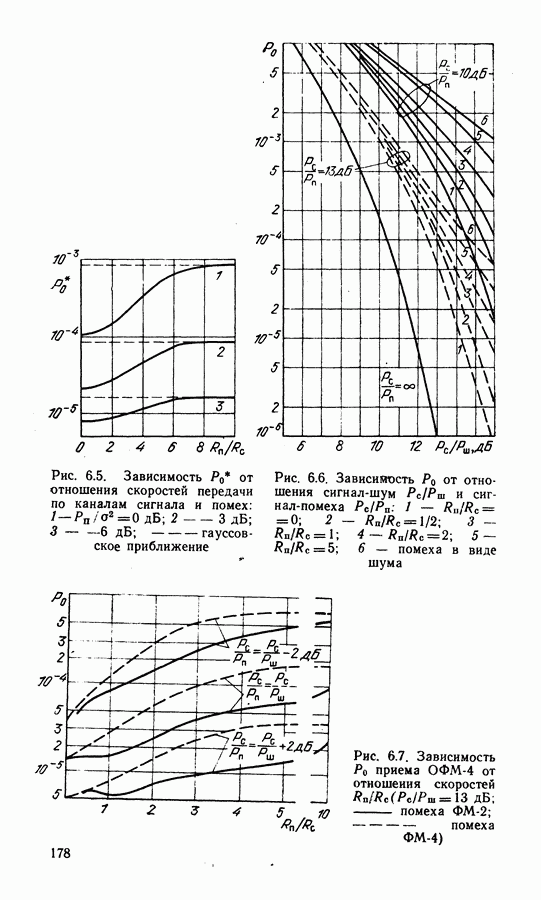
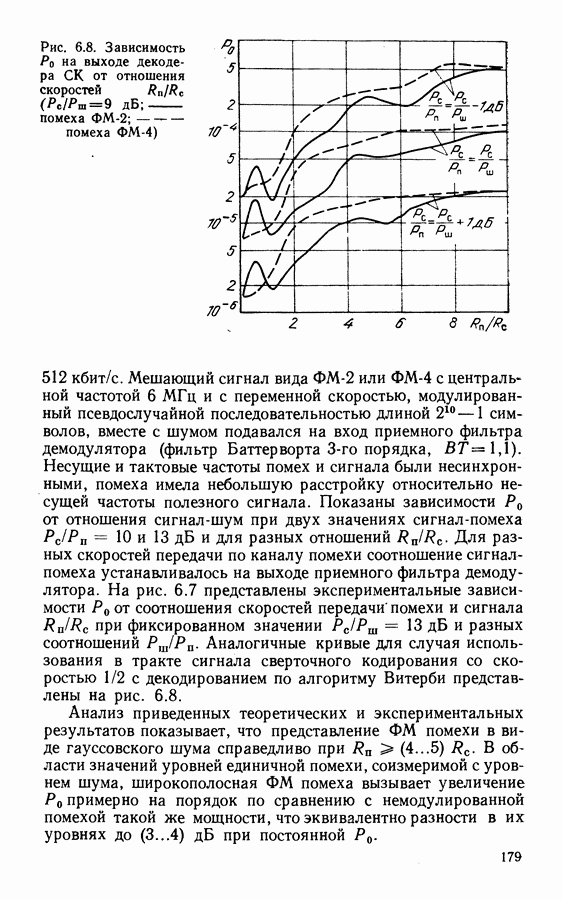
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
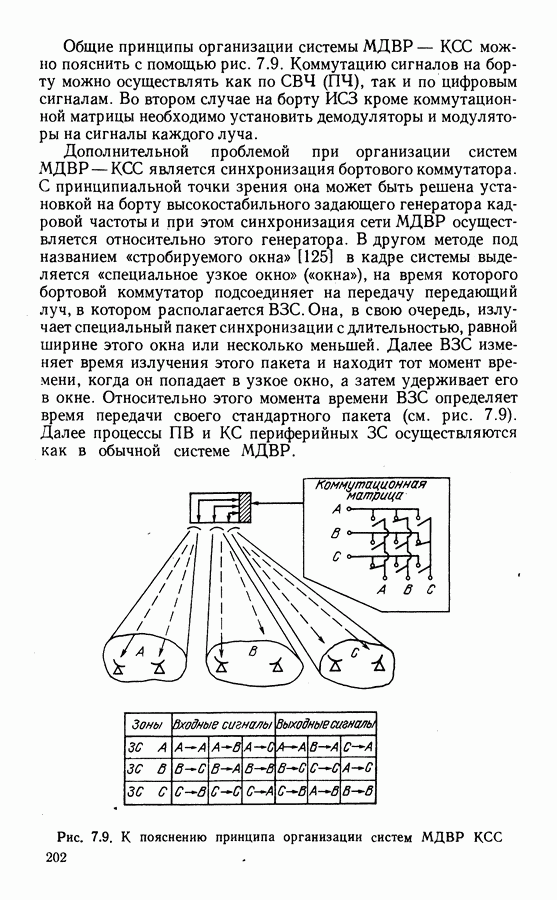
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
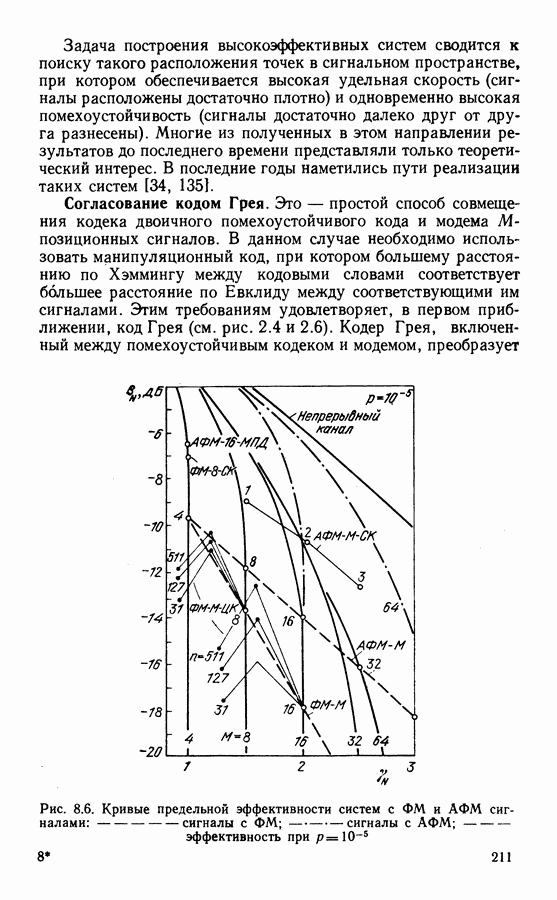
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ