| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
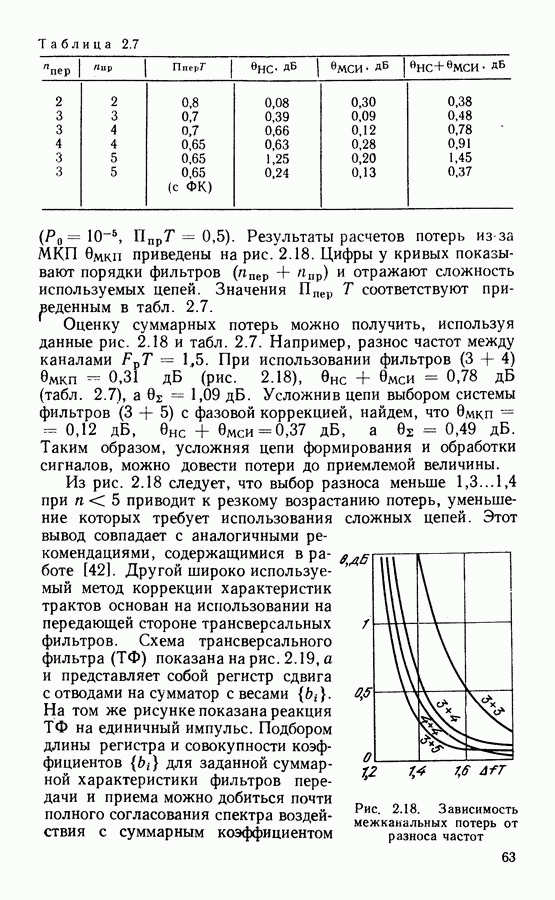
4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
Рассмотренная в § 4.1 общая классификация методов декодирования применима и к сверточным кодам. Из вероятностных алгоритмов наиболее разработаны алгоритм последовательного декодирования и алгоритм Витерби.
Алгоритм последовательного декодирования [87] реализует поиск пути, соответствующего переданной информационной последовательности. Существенным является то, что информация, полученная в процессе декодирования, используется для оптимизации дальнейшего поиска наиболее правдоподобных продолжений пути. Для сглаживания неравномерности вычислений декодер содержит буферную память, переполнение которой при интенсивном потоке ошибок ведет к отказу от декодирования. Кроме того, последовательный алгоритм чувст.
вителен к искажениям сигнала в канале (изменения уровня сигнала, флуктуации фазы и т. д.). Поэтому в ЦССС последовательный алгоритм широкого распространения не получил, несмотря на то, что сложность реализации такого алгоритма пропорциональна малой степени длины кодового ограничения 
Другим алгоритмом декодирования, основанным на использовании вероятностных характеристик принимаемых сигналов, является алгоритм максимального правдоподобия, предложенный А. Витерби [78]. Алгоритм имеет ряд преимуществ перед другими и его широко используют для декодирования коротких  Рассмотрим алгоритм на примере кода со скоростью
Рассмотрим алгоритм на примере кода со скоростью 
Пусть, начиная с момента времени  на вход кодера подается информационная последовательность длиной в
на вход кодера подается информационная последовательность длиной в  символов
символов  На выходе кодера последовательность символов
На выходе кодера последовательность символов  . Состояние кодера в момент
. Состояние кодера в момент  определяют как набор из
определяют как набор из  информационных символов
информационных символов  Решетчатая диаграмма кода однозначно связывает информационную последовательность
Решетчатая диаграмма кода однозначно связывает информационную последовательность  последовательность состояний кодера
последовательность состояний кодера  и последовательность символов на его выходе
и последовательность символов на его выходе 
Каждой ветви кода  в канале соответствует сигнал, который может быть представлен набором координат в
в канале соответствует сигнал, который может быть представлен набором координат в  -мерном пространстве
-мерном пространстве  . В канале действует аддитивная помеха и поступающая на вход декодера последовательность
. В канале действует аддитивная помеха и поступающая на вход декодера последовательность  где
где  -мерный вектор помехи. Декодирование состоит в прослеживании по кодовой решетке пути с максимальной апостериорной вероятностью. Декодированный путь можно указать одним из способов: набором оценок кодовых ветвей
-мерный вектор помехи. Декодирование состоит в прослеживании по кодовой решетке пути с максимальной апостериорной вероятностью. Декодированный путь можно указать одним из способов: набором оценок кодовых ветвей  составляющих путь; последовательностью оценок состояний кодера
составляющих путь; последовательностью оценок состояний кодера  либо последовательностью оценок информационных символов на входе кодера
либо последовательностью оценок информационных символов на входе кодера  которые совпадают с первыми символами оценок состояний
которые совпадают с первыми символами оценок состояний  Последовательность
Последовательность  будет декодирована с минимальной вероятностью ошибки, если из всех возможных путей выбрать оценку
будет декодирована с минимальной вероятностью ошибки, если из всех возможных путей выбрать оценку  для которой максимальна апостериорная вероятность
для которой максимальна апостериорная вероятность 
Передачу всех вариантов наборов  считают равновероятной. В этом случае декодирование по критерию максимума апостериорной вероятности равносильно декодированию по
считают равновероятной. В этом случае декодирование по критерию максимума апостериорной вероятности равносильно декодированию по
критерию максимального правдоподобия, когда выбирается оценка  обеспечивающая выполнение условия
обеспечивающая выполнение условия

В канале без памяти апостериорной вероятности  пропорционально произведение условных плотностей вероятностей суммы сигнала и помехи
пропорционально произведение условных плотностей вероятностей суммы сигнала и помехи  . В гауссовском канале при действии белого шума с односторонней спектральной плотностью мощности
. В гауссовском канале при действии белого шума с односторонней спектральной плотностью мощности  каждый сомножитель этого произведения имеет вид
каждый сомножитель этого произведения имеет вид  Для отыскания максимума выражения (4.14) удобно прологарифмировать
Для отыскания максимума выражения (4.14) удобно прологарифмировать 
При декодировании по критерию (4.14) выбирают такую последовательность сигналов  и однозначно связанную с ней последовательность ветвей
и однозначно связанную с ней последовательность ветвей  которая обеспечивает минимум суммы
которая обеспечивает минимум суммы

называемой метрикой декодированного пути. Метрика пути содержит в качестве слагаемых метрики ветвей:  где метрики ветвей
где метрики ветвей  . В гауссовском канале метрика ветви пропорциональна квадрату Евклидова расстояния между вектором принимаемой суммы сигнала и помехи
. В гауссовском канале метрика ветви пропорциональна квадрату Евклидова расстояния между вектором принимаемой суммы сигнала и помехи  и вектором сигнала
и вектором сигнала  соответствующего ветви кода
соответствующего ветви кода  . В дискретном канале для оценки расстояний используют метрику Хэмминга.
. В дискретном канале для оценки расстояний используют метрику Хэмминга.
Периодическая структура решетчатой диаграммы существенно упрощает сравнение и выбор путей в соответствии с правилами (4.15). Число состояний на решетке ограничено, и два наугад выбранных достаточно длинных пути имеют, как правило, общие состояния. Отрезки путей, входящих в эти состояния, необходимо сравнить и выбрать путь с наименьшей метрикой. Такой путь называют выжившим. В соответствии с алгоритмом Витерби сравнение и отбрасывание отрезков путей производится периодически на каждом шаге декодирования.
Рассмотрим декодирование кода (7.5), символы которого передаются по дискретному каналу. В этом случае метрика ветви  равна расстоянию Хэмминга между набором символов
равна расстоянию Хэмминга между набором символов  на входе декодера и набором символов
на входе декодера и набором символов  соответствующих данной ветви на решетчатой диаграмме. Если
соответствующих данной ветви на решетчатой диаграмме. Если  то возможные значения
то возможные значения  для кода (7,5) с решеткой, изображенной на рис. 4.5, будут:
для кода (7,5) с решеткой, изображенной на рис. 4.5, будут:  Метрика пути есть сумма метрик ветвей, образующих некоторый путь на решетчатой диаграмме. Путь конечной длины оканчивается в определенном состоянии. Метрика состояния
Метрика пути есть сумма метрик ветвей, образующих некоторый путь на решетчатой диаграмме. Путь конечной длины оканчивается в определенном состоянии. Метрика состояния  равна
равна  который заканчивается в данном состоянии. Шаг декодирования состоит в обработке декодером принимаемых из канала данных в интервале между двумя соседними уровнями узлов.
который заканчивается в данном состоянии. Шаг декодирования состоит в обработке декодером принимаемых из канала данных в интервале между двумя соседними уровнями узлов.
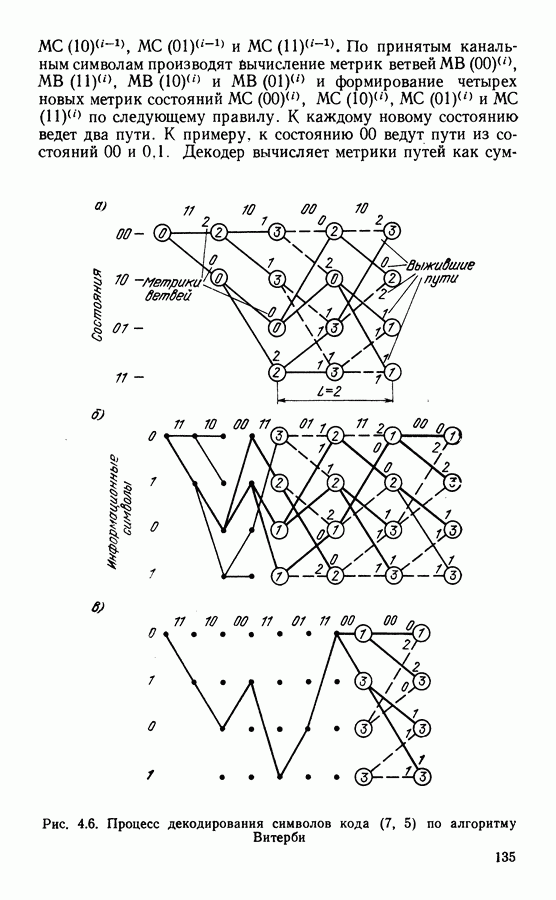
На рис. 4.6 показано развитие процесса декодирования символов кода (7.5). На вход декодера поступают пары символов из канала  Цифрами около ветвей обозначены метрики ветвей, цифры в кружках обозначают метрики состояний. В начальный момент времени полагаем, что декодер находится в состоянии 00 и исходная метрика
Цифрами около ветвей обозначены метрики ветвей, цифры в кружках обозначают метрики состояний. В начальный момент времени полагаем, что декодер находится в состоянии 00 и исходная метрика  (рис. 4.6, а). Если из канала поступили символы 11, то метрики двух ветвей, выходящих из этого состояния,
(рис. 4.6, а). Если из канала поступили символы 11, то метрики двух ветвей, выходящих из этого состояния,  Это отмечено на первом шаге декодирования. Так как других ветвей из состояния 00 в состояния 00 и И нет, то метрики этих состояний принимают равными метрикам входящих ветвей:
Это отмечено на первом шаге декодирования. Так как других ветвей из состояния 00 в состояния 00 и И нет, то метрики этих состояний принимают равными метрикам входящих ветвей:  и
и  Аналогично и на следующем шаге, когда из канала поступают символы 10. Здесь
Аналогично и на следующем шаге, когда из канала поступают символы 10. Здесь  Метрики состояний на этом шаге определяются теперь как суммы метрик входящих ветвей с метриками предыдущих состояний:
Метрики состояний на этом шаге определяются теперь как суммы метрик входящих ветвей с метриками предыдущих состояний:  На этом развитие решетчатой диаграммы заканчивается.
На этом развитие решетчатой диаграммы заканчивается.
Далее алгоритм периодически повторяет один основной шаг.. На каждой из диаграмм он изображен в правой части рисунка. В момент времени  в памяти декодера хранятся метрики состояний, вычисленных на предыдущем шаге:
в памяти декодера хранятся метрики состояний, вычисленных на предыдущем шаге: 
 и
и  По принятым канальным символам производят бычисление метрик ветвей
По принятым канальным символам производят бычисление метрик ветвей  и формирование четырех новых метрик состояний
и формирование четырех новых метрик состояний  и
и  по следующему правилу. К каждому новому состоянию ведет два пути. К примеру, к состоянию 00 ведут пути из состояний 00 и 0,1. Декодер вычисляет метрики путей как
по следующему правилу. К каждому новому состоянию ведет два пути. К примеру, к состоянию 00 ведут пути из состояний 00 и 0,1. Декодер вычисляет метрики путей как

Рис. 4.6. Процесс декодирования символов кода (7, 5) по алгоритму Витерби
суммы метрик предыдущих состояний и метрик входящих ветвей:

Далее производят попарное сравнение метрик путей, входящих в каждое состояние (пары показаны фигурными скобками). В результате сравнения выбирают меньшую метрику и ее считают метрикой данного состояния для последующего шага декодирования. Путь, входящий в данное состояние с меньшей метрикой, считают выжившим. На рис. 4.6, б отрезки выживших путей показаны сплошными линиями. Пути, входящие в состояния с большими метриками, считают оборванными. Они показаны на решетчатой диаграмме штриховыми линиями.
Таким образом, на каждом шаге декодирования в соответствии с алгоритмом Витерби в каждом из состояний решетчатой диаграммы производят однотипные операции: 1) сложение метрик предыдущих состояний с метриками соответствующих ветвей; 2) сравнение метрик входящих путей и 3) выбор путей с наименьшими метриками, величины которых используют как метрики состояний на последующем шаге декодирования (сокращенно ССВ). Если метрики сравниваемых путей одинаковы, выбор одного из двух путей производят случайным образом. На каждом шаге в результате сравнения половина возможных путей отбрасывается и в дальнейшем не используется. Другая половина образует продолжения путей для следующего шага декодирования. Из каждого состояния на следующем шаге вновь появляются два варианта продолжения путей. Это обеспечивает постоянство вычислений, производимых на каждом шаге. Декодер прослеживает по кодовой решетке путь, имеющий минимальное расстояние от пути, который генерирует кодер.
Типовая схема декодера содержит вычислитель метрик, подключенный к выходу демодулятора, где производится формирование метрик ветвей по изложенным выше правилам.

Рис. 4.7. Модификация решетчатой диаграммы: а — диаграмма кода со скоростью  выделение
выделение  ветвей; в — образование промежуточного узла;
ветвей; в — образование промежуточного узла;  диаграмма перфорированного кода
диаграмма перфорированного кода
В процессоре осуществляется вычисление метрик путей, входящих в каждое состояние, их сравнение и выбор по правилам, представленным формулами (4.16). Данные о выживших в результате такого сравнения путях хранятся в оперативной памяти, а решение о передаваемых информационных символах выносят на основе сравнения метрик выживших путей.
При прослеживании на достаточно большую глубину выжившие пути, как правило, сливаются. Это видно из рис. 4.6, в, где показаны варианты выживших путей, которые сливаются в один. Поэтому часто для упрощения процедуры вынесения решения производят прослеживание на несколько большей глубине, но выносят решение по пути, который заканчивается в произвольном состоянии. Память реального декодера конечна и хранит пути длиной  (в зависимости от параметров кода). Старший символ на выбранном пути считают выходным символом декодера. Часто используют мажоритарный метод, когда решение выносят по большинству символов, определяемых совокупностью выживших путей.
(в зависимости от параметров кода). Старший символ на выбранном пути считают выходным символом декодера. Часто используют мажоритарный метод, когда решение выносят по большинству символов, определяемых совокупностью выживших путей.
Использование мягкого решения дает определенный выигрыш по сравнению с квантованием на два уровня выхода демодулятора. Применение восьмиуровневого квантования дает выигрыш по сравнению с двухуровневым порядка  Квантование на восемь уровней всего на
Квантование на восемь уровней всего на  хуже по сравнению со случаем использования неквантованных входных символов в соответствии с формулой (4.15). Подробнее выбор параметров и определение характеристик декодирования рассмотрены в § 4.6.
хуже по сравнению со случаем использования неквантованных входных символов в соответствии с формулой (4.15). Подробнее выбор параметров и определение характеристик декодирования рассмотрены в § 4.6.
Сложность реализации алгоритма определяется в основном структурой решетчатой диаграммы. Фрагменты диаграмм СК с параметрами  приведены на рис. 4.5 и 4.7, а. Если скорость двоичного кода
приведены на рис. 4.5 и 4.7, а. Если скорость двоичного кода  то число состояний кодера (узлов диаграммы)
то число состояний кодера (узлов диаграммы)  а число
а число
ветвей, выходящих (входящих) из каждого состояния,  Число сложений при декодировании равно общему числу ветвей на шаге
Число сложений при декодировании равно общему числу ветвей на шаге  Число сравнений (вычитаний), выполняемых на каждом шаге,
Число сравнений (вычитаний), выполняемых на каждом шаге,  Общее число арифметических операций
Общее число арифметических операций  , а число операций на один декодируемый символ
, а число операций на один декодируемый символ  Видно, что удельное число операций возрастает не только с увеличением длины кода
Видно, что удельное число операций возрастает не только с увеличением длины кода  но и с ростом числителя скорости
но и с ростом числителя скорости  Наиболее простыми по структуре реализации кодеков являются коды со скоростью
Наиболее простыми по структуре реализации кодеков являются коды со скоростью  1/2. Однако во многих случаях применение кодов со скоростями более 1/2 предпочтительнее.
1/2. Однако во многих случаях применение кодов со скоростями более 1/2 предпочтительнее.
Решетчатая диаграмма кода со скоростью 2/3 (рис. 4.7, а) может быть модифицирована. Выделим четыре ветви, показанные на рис.  Набор таких ветвей допускает образование промежуточного узла, как показано на рис. 4.7, в. Объединение отрезков ветвей возможно, поскольку пары ветвей, выходящих из узлов, имеют совпадающие первые два символа
Набор таких ветвей допускает образование промежуточного узла, как показано на рис. 4.7, в. Объединение отрезков ветвей возможно, поскольку пары ветвей, выходящих из узлов, имеют совпадающие первые два символа  и соответственно пары ветвей, входящие в узлы, содержат совпадающий третий символ
и соответственно пары ветвей, входящие в узлы, содержат совпадающий третий символ  Аналогично возможно образование промежуточных узлов и на других наборах ветвей, как показано на рис.
Аналогично возможно образование промежуточных узлов и на других наборах ветвей, как показано на рис.  Модифицированная диаграмма по структуре совпадает с диаграммой кода в
Модифицированная диаграмма по структуре совпадает с диаграммой кода в  Кодовые последовательности исходного кода с
Кодовые последовательности исходного кода с  могут быть получены из последовательностей кода с
могут быть получены из последовательностей кода с  1/2 путем периодического вычеркивания (перфорации) символов. Такие коды называются перфорированными [88].
1/2 путем периодического вычеркивания (перфорации) символов. Такие коды называются перфорированными [88].
На рис. 4.8 показан процесс перфорации. При поступлении на вход кодера информационного символа и на его выходе образуется пара символов  . В перфораторе, состоящем из четырех тактируемых регистров, производится такое преобразование последовательностей
. В перфораторе, состоящем из четырех тактируемых регистров, производится такое преобразование последовательностей  в кодовые
в кодовые

Рис. 4.8. Образование символов перфорированного кода

Рис. 4.9. Кодек с пороговым декодированием
последовательности  пр
пр  котором символы
котором символы  на выходе отсутствуют. Четырем информационным символам на входе кодера соответствуют восемь символов на его выходах
на выходе отсутствуют. Четырем информационным символам на входе кодера соответствуют восемь символов на его выходах  шесть символов на выходах перфоратора
шесть символов на выходах перфоратора  При этом скорость перфорированного кода 2/3. На приемной стороне необходимо обратное преобразование и вместо вычеркнутых символов в ячейки регистра вписываются, например, нули. Многочлены перфорированного кода обозначают как
При этом скорость перфорированного кода 2/3. На приемной стороне необходимо обратное преобразование и вместо вычеркнутых символов в ячейки регистра вписываются, например, нули. Многочлены перфорированного кода обозначают как  где знак
где знак  указывает положение вычеркнутого символа. Решетчатая диаграмма перфорированного кода состоит из двух повторяющихся шагов (рис. 4.7, г). Первый шаг образуют ветви, состоящие из символов, порождаемых многочленами
указывает положение вычеркнутого символа. Решетчатая диаграмма перфорированного кода состоит из двух повторяющихся шагов (рис. 4.7, г). Первый шаг образуют ветви, состоящие из символов, порождаемых многочленами  На втором шаге вычеркнутый символ заменен произвольным символом X (0 либо 1). Декодирование кодов, полученных перфорацией исходного кода со скоростью 1/2, можно производить декодером, рассчитанным на эту скорость Необходимо лишь предусмотреть правильную расстановку символов перфорации.
На втором шаге вычеркнутый символ заменен произвольным символом X (0 либо 1). Декодирование кодов, полученных перфорацией исходного кода со скоростью 1/2, можно производить декодером, рассчитанным на эту скорость Необходимо лишь предусмотреть правильную расстановку символов перфорации.
Вероятностные методы декодирования достаточно сложны в реализации, хотя и обеспечивают высокую помехоустойчивость. Наряду с ними в ЦСС широко применяют более простые алгоритмы. Для этой цели используют класс СК, допускающих пороговое декодирование [75].
Пороговый алгоритм имеет много общего с мажоритарным декодированием блоковых кодов. Рассмотрим систематический код со скоростью 1/2 и многочленами  Схема кодека кода с многочленами,
Схема кодека кода с многочленами,  показана на рис. 4.9. Моделью двоичного канала являются сумматоры по
показана на рис. 4.9. Моделью двоичного канала являются сумматоры по
модулю 2, на входы которых кроме кодовых последовательностей  поступают ошибки
поступают ошибки  Декодер содержит аналог кодера, в котором по принимаемым символам
Декодер содержит аналог кодера, в котором по принимаемым символам  формируется копия проверочной последовательности
формируется копия проверочной последовательности  . В формирователе синдрома (сумматоре по модулю 2) образуется последовательность синдромов
. В формирователе синдрома (сумматоре по модулю 2) образуется последовательность синдромов  которая поступает на вход синдромного регистра. Наборам ошибок соответствуют определенные конфигурации синдромов последовательности
которая поступает на вход синдромного регистра. Наборам ошибок соответствуют определенные конфигурации синдромов последовательности  Если число ненулевых синдромов превышает определенный порог, на выходе порогового элемента появляется символ коррекции, который в корректоре используется для исправления ошибки в информационном символе.
Если число ненулевых синдромов превышает определенный порог, на выходе порогового элемента появляется символ коррекции, который в корректоре используется для исправления ошибки в информационном символе.
В отсутствие ошибок в канале последовательности на входе формирователя синдромов  всегда совпадают и синдром
всегда совпадают и синдром  Прослеживая прохождение символов ошибок
Прослеживая прохождение символов ошибок  через регистр кодера и формирователь синдрома, представим значения синдромов в последовательные моменты времени
через регистр кодера и формирователь синдрома, представим значения синдромов в последовательные моменты времени  следующим образом:
следующим образом:

Набор равенств (4.17) выражает ошибочный символ в информационном подканале  через символы синдромов несколькими различными способами, образуя набор проверок:
через символы синдромов несколькими различными способами, образуя набор проверок:

Подобно уравнениям (4.19), ошибочный символ  входит в каждую из них, а другие символы входят в проверки только по одному разу. Такие проверки, как и в случае блоковых кодов, называются ортогональными относительно
входит в каждую из них, а другие символы входят в проверки только по одному разу. Такие проверки, как и в случае блоковых кодов, называются ортогональными относительно  Кроме того, проверки А непосредственно равны синдромам 5. Коды, у которых некоторая совокупность синдромов ортогональна
Кроме того, проверки А непосредственно равны синдромам 5. Коды, у которых некоторая совокупность синдромов ортогональна
относительно  называют самоортогональными. Проверки для самоортогонального кода вида (4.18) называют простыми.
называют самоортогональными. Проверки для самоортогонального кода вида (4.18) называют простыми.
Иногда получить набор ортогональных проверок без преобразования синдромов не удается. Однако линейная комбинация синдромов может дать набор ортогональных проверок. Такие коды относятся к классу полностью ортогонализируемых кодов, и проверки в этом случае являются составными. Как и при декодировании блоковых кодов, ортогонализация возможна и за несколько шагов (ступеней линейного преобразования) [75].
На выходе порогового элемента формируется оценка ошибочного символа на основе сравнения количества ненулевых символов проверок  определенным порогом Т.Как и в примере (4.9), выберем
определенным порогом Т.Как и в примере (4.9), выберем  чтобы при
чтобы при  решение на выходе порогового элемента
решение на выходе порогового элемента  а при
а при  решение
решение  . В общем случае, если число ортогональных проверок
. В общем случае, если число ортогональных проверок  задано, на выходе порогового элемента
задано, на выходе порогового элемента  если
если  четное) либо
четное) либо  нечетное). Реализуемое расстояние при пороговом декодировании
нечетное). Реализуемое расстояние при пороговом декодировании  а число исправляемых ошибок на длине ограничения
а число исправляемых ошибок на длине ограничения  равно
равно  Код с проверками (4.18) имеет параметры
Код с проверками (4.18) имеет параметры  и позволяет исправить однократные и двукратные ошибки любой конфигурации на длине
и позволяет исправить однократные и двукратные ошибки любой конфигурации на длине  символов. Кроме того, при пороговом декодировании исправляются некоторые конфигурации ошибок и более высокой кратности.
символов. Кроме того, при пороговом декодировании исправляются некоторые конфигурации ошибок и более высокой кратности.
Проверки (4.18) контролируют И различных символов ошибок  Общее количество символов, контролируемых набором ортогональных проверок, называется эффективной длиной ограничения кода
Общее количество символов, контролируемых набором ортогональных проверок, называется эффективной длиной ограничения кода  . В рассматриваемом примере
. В рассматриваемом примере 
Решение об ошибочном символе  используют для коррекции символа
используют для коррекции символа  На выход декодера поступает сумма
На выход декодера поступает сумма  Кроме того, оценка
Кроме того, оценка  может быть использована для коррекции синдромов
может быть использована для коррекции синдромов  в состав которых входит ошибочный символ
в состав которых входит ошибочный символ  На следующем такте модифицированное множество синдромов дополняется вновь вычисленным синдромом
На следующем такте модифицированное множество синдромов дополняется вновь вычисленным синдромом  и декодирование осуществляется по такому же алгоритму. Так реализуют декодирование с обратной связью. При этом возможно распространение ошибок, если при декодировании вынесено неверное решение
и декодирование осуществляется по такому же алгоритму. Так реализуют декодирование с обратной связью. При этом возможно распространение ошибок, если при декодировании вынесено неверное решение  которое поступило по цепи обратной связи в синдромный регистр. Распространение ошибок возможно и в декодерах
которое поступило по цепи обратной связи в синдромный регистр. Распространение ошибок возможно и в декодерах
блоковых кодов (рис. 4.2), но там оно сказывается лишь в пределах декодируемого блока. При декодировании СК тактируемый регистр с нелинейными обратными связями через пороговые элементы может переходить в режим возбуждения даже после исключения ошибок в канале. Это приведет к бесконечной глубине распространения ошибок. Можно показать, что в декодерах самоортогональных кодов глубина распространения ошибок всегда конечна. В остальных случаях устойчивость синдромного регистра требует дополнительного анализа [75].
Известно несколько способов ограничения распространения ошибок. Возможен анализ числа ненулевых синдромов на длине кодового ограничения: когда число ошибок превышает корректирующую способность кода, анализатор отключает цепи коррекции синдрома. Другой способ основан на использовании самоортогональных кодов, в которых распространение ошибок минимально. Иногда применяют дефинитное декодирование, при котором обратная связь на синдромный регистр вообще не используется. Поскольку в этом случае влияние обнаруженной ошибки на значения последующих синдромов не исключается, здесь возможно ограниченное распространение ошибок. При скорости кода, отличной от 1/2 структура порогового декодера не отличается от описанной выше.
При пороговом декодировании используют систематические коды. Для реализации чаще всего выбирают самоортогональные коды, порождающие многочлены которых определяются на основе теории совершенных разностных множеств [75]. Применение этой теории позволяет строить системы ортогональных проверок. Подробные таблицы самоортогональных кодов приведены в [75, 92].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
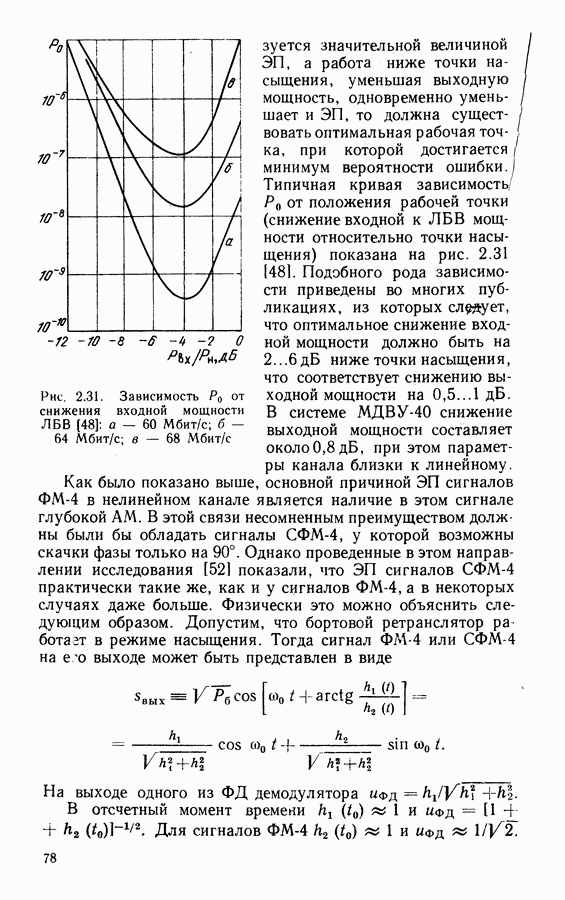
- Энергетические потери в системе с ФМ-4.
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
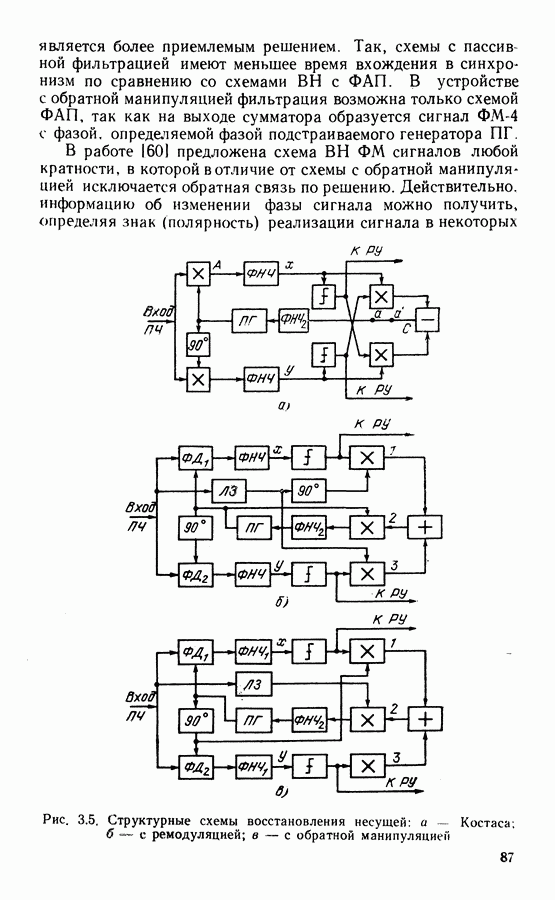
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
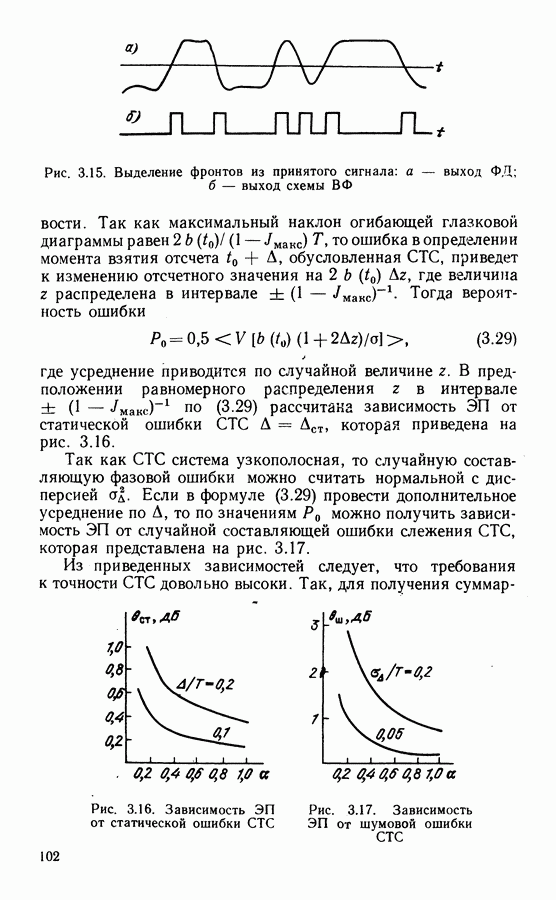
- Требования к точности работы системы ВН.
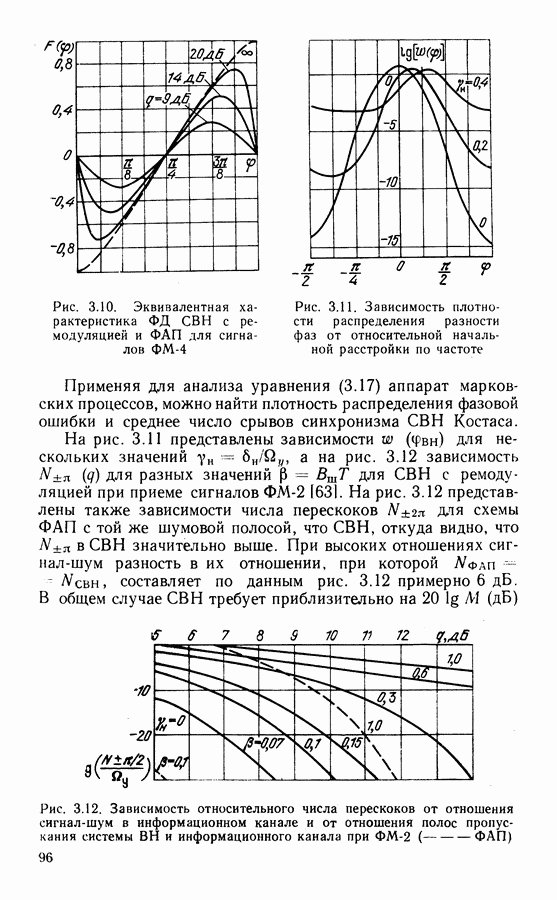
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
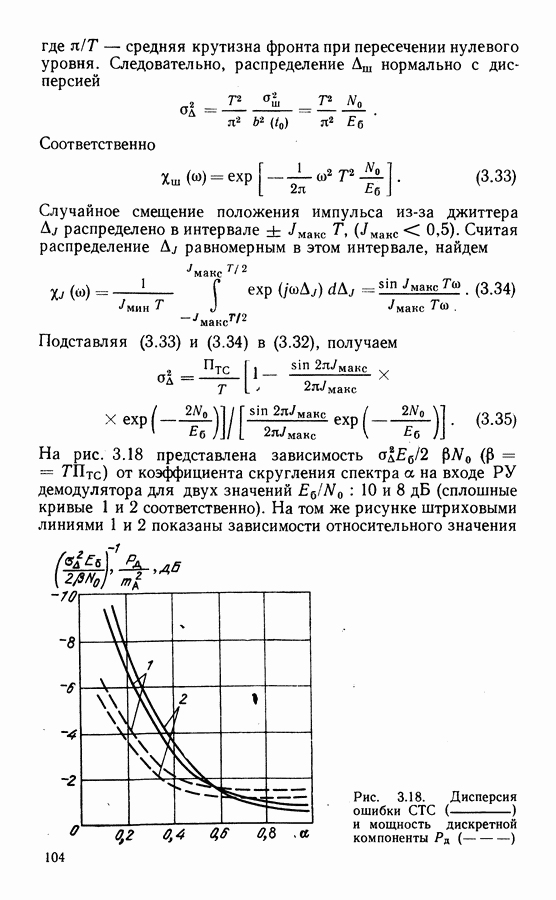
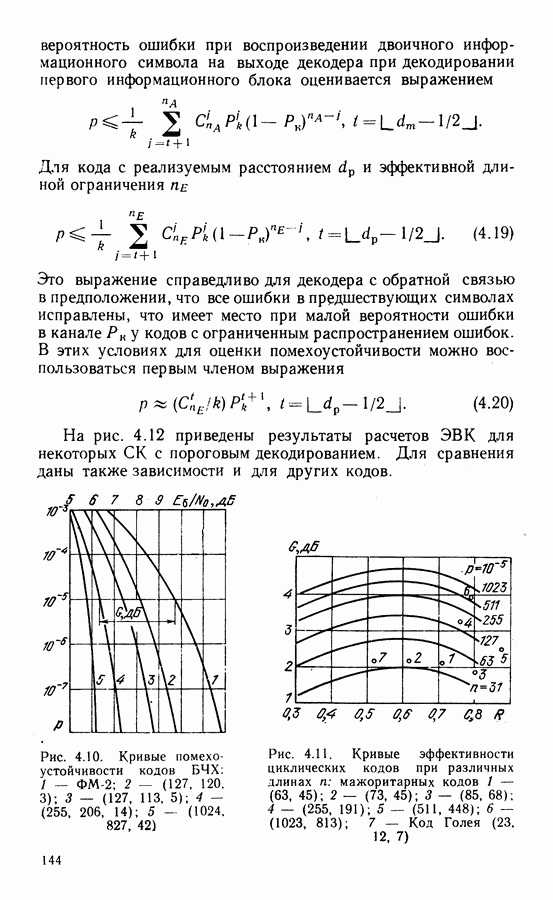
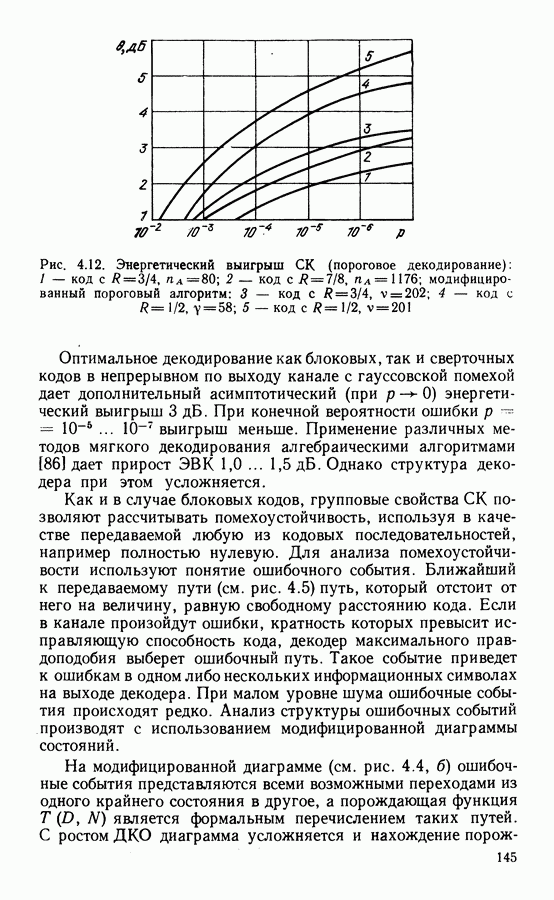
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
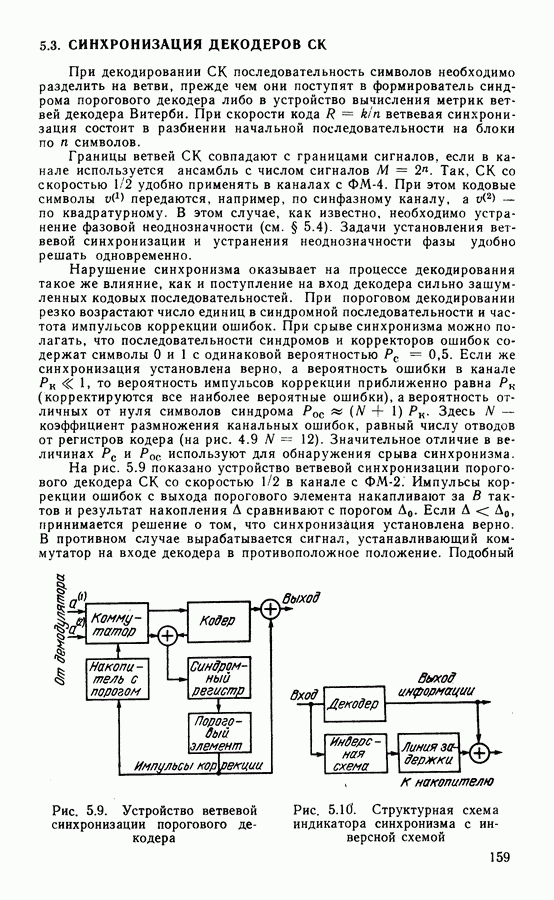
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
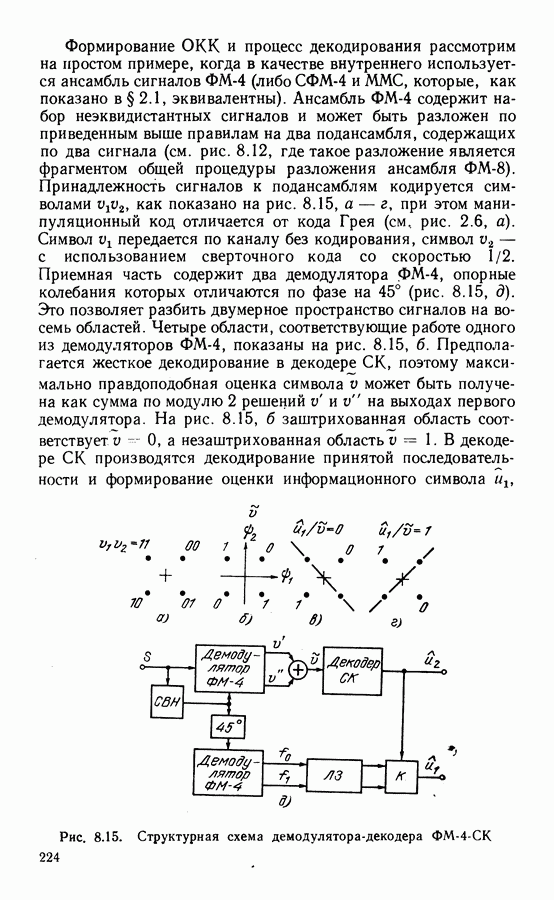
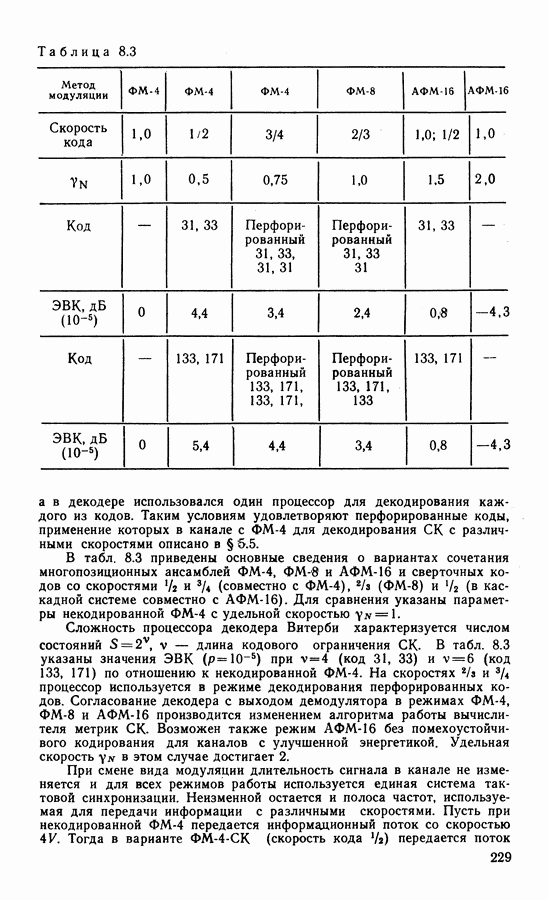
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ