| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
Коды Хэмминга — циклические коды с параметрами  Это совершенные коды, исправляющие однократные ошибки. Если в соответствии с выражением
Это совершенные коды, исправляющие однократные ошибки. Если в соответствии с выражением  остаток от деления
остаток от деления  на многочлен
на многочлен  то в результате деления
то в результате деления  на
на  получаем
получаем  Таким образом, если по синдрому
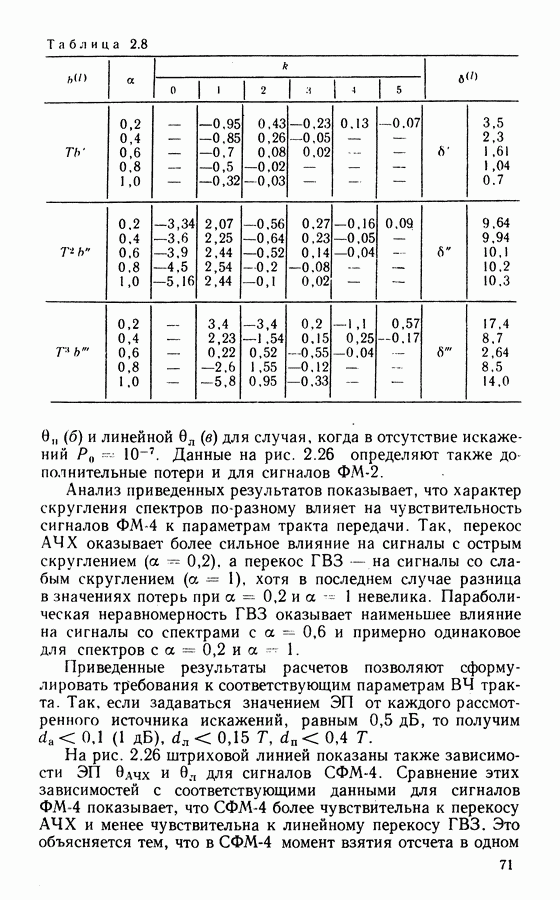
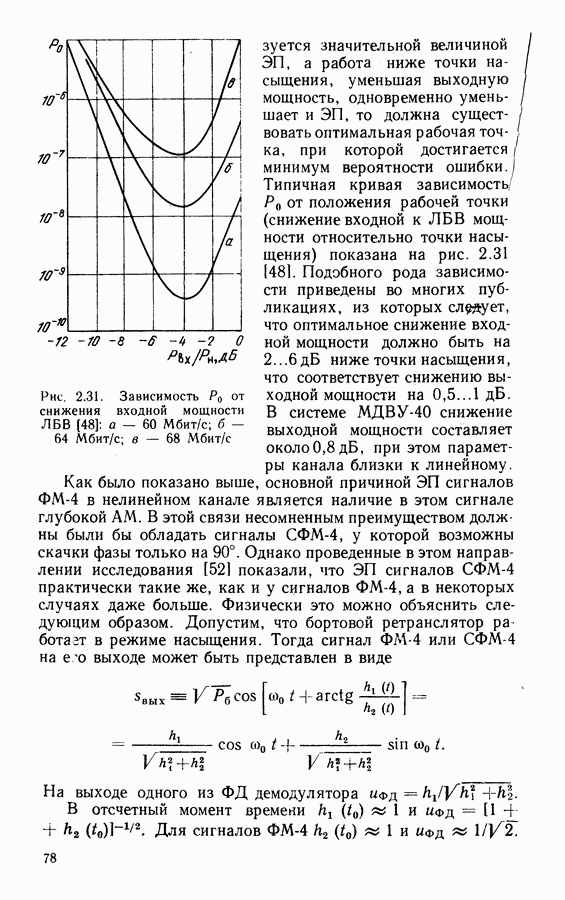
Таким образом, если по синдрому  удается установить наличие ошибки в каком-либо символе блока циклического кода, то, используя простые схемы формирователей синдрома на регистрах сдвигов с обратными связями, это можно сделать и для любого символа блока. По этому принципу работает декодер Мэггита, схема которого для кода Хэмминга (7, 4, 3) показана на рис. 4.1. При поступлении на вход декодера принимаемого кодового слова (ключ К замкнут) символы запоминаются в ячейках буферного регистра. Одновременно происходит формирование синдрома.
удается установить наличие ошибки в каком-либо символе блока циклического кода, то, используя простые схемы формирователей синдрома на регистрах сдвигов с обратными связями, это можно сделать и для любого символа блока. По этому принципу работает декодер Мэггита, схема которого для кода Хэмминга (7, 4, 3) показана на рис. 4.1. При поступлении на вход декодера принимаемого кодового слова (ключ К замкнут) символы запоминаются в ячейках буферного регистра. Одновременно происходит формирование синдрома.
Анализатор синдрома — комбинационная схема, предназначенная для обнаружения ошибок определенной конфигурации. Пусть в принятом слове ошибка в символе  т. е. многочлен ошибок
т. е. многочлен ошибок  Определим остаток от деления
Определим остаток от деления  на
на  на основе равенства:
на основе равенства:  откуда синдром
откуда синдром 

Рис. 4.1. Структурная схема декодера кода (7, 4, 3)
 Вектор синдрома
Вектор синдрома  . В анализаторе синдрома реализуется логическая функция умножения
. В анализаторе синдрома реализуется логическая функция умножения  (черта означает инверсию). Таким образом, если символы синдрома
(черта означает инверсию). Таким образом, если символы синдрома  то оценка ошибки
то оценка ошибки  и символ на выходе декодера корректируется:
и символ на выходе декодера корректируется:  Одновременно коррекции подвергается и вектор синдрома. Далее происходит сдвиг на один такт и процедуру повторяют. Декодер такого типа, рассчитанный на исправление простых конфигураций ошибок, несложен и поэтому широко используется для коррекции однократных ошибок либо пакетов ошибок. Возможны различные модификации этого алгоритма [74, 81]. Однако с увеличением кратности исправляемых ошибок сложность анализатора и декодера в целом резко возрастает.
Одновременно коррекции подвергается и вектор синдрома. Далее происходит сдвиг на один такт и процедуру повторяют. Декодер такого типа, рассчитанный на исправление простых конфигураций ошибок, несложен и поэтому широко используется для коррекции однократных ошибок либо пакетов ошибок. Возможны различные модификации этого алгоритма [74, 81]. Однако с увеличением кратности исправляемых ошибок сложность анализатора и декодера в целом резко возрастает.
Код Голея (23, 12, 7) — совершенный циклический код с порождающим многочленом  Расширенный код Голея (24, 12, 8) получают при добавлении общей проверки на четность. Алгоритм декодирования и простая схема декодера описаны в книгах [74, 81].
Расширенный код Голея (24, 12, 8) получают при добавлении общей проверки на четность. Алгоритм декодирования и простая схема декодера описаны в книгах [74, 81].
Коды Боуза — Чоудхури — Хоквингема (БЧХ) образуют обширный класс  Двоичные коды имеют параметры:
Двоичные коды имеют параметры:  Порождающий многочлен кода определяется как наименьшее общее кратное минимальных многочленов
Порождающий многочлен кода определяется как наименьшее общее кратное минимальных многочленов  Число
Число  называется конструктивным расстоянием,
называется конструктивным расстоянием,  кратность исправляемых ошибок. Подробные таблицы минимальных многочленов приведены в [741. В табл. 4.1 даны параметры и порождающие многочлены некоторых кодов БЧХ. Многочлены приведены в восьмеричной форме записи, старшая степень расположена слева. Например, коду (15,7) соответствуют: восьмеричное представление
кратность исправляемых ошибок. Подробные таблицы минимальных многочленов приведены в [741. В табл. 4.1 даны параметры и порождающие многочлены некоторых кодов БЧХ. Многочлены приведены в восьмеричной форме записи, старшая степень расположена слева. Например, коду (15,7) соответствуют: восьмеричное представление  двоичное представление
двоичное представление  и многочлен
и многочлен  Подробные таблицы кодов БЧХ можно найти в [74—76].
Подробные таблицы кодов БЧХ можно найти в [74—76].
Декодирование кодов БЧХ производят на основе решения алгебраических уравнений. Каждой позиции кодового слова ставится в соответствие локатор ошибки. Декодирование состоит в отыскании локаторов, а в случае недвоичных кодов и значений ошибок в символах, отмеченных локаторами. Сначала вычисляют символы синдрома, которые содержат информацию об ошибках, затем находят многочлен локаторов. Этот этап представляет наибольшую трудность в реализации. При использовании алгоритма Питерсона либо Бэрлекампа — Мэсси и большом числе исправляемых ошибок декодирующая
Таблица 4.1

схема достаточно сложная. Поэтому часто используют запоминающие устройства  куда заносят все варианты входных данных и решений основного уравнения декодирования. На высокой тактовой частоте применяют алгоритм Ченя, который удобен при небольшом числе исправляемых кодом ошибок. Коэффициенты многочлена локаторов ошибок определяют подстановкой значений символов синдрома в многочлен локаторов ошибок. Декодирование кодов БЧХ возможно и декодером Меггита, в котором анализатор синдрома часто выполняют в виде ЗУ. Подробные сведения по алгоритмам декодирования кодов БЧХ можно найти в [74—76 , 81, 82, 140], по спектральным методам декодирования — в книге [140].
куда заносят все варианты входных данных и решений основного уравнения декодирования. На высокой тактовой частоте применяют алгоритм Ченя, который удобен при небольшом числе исправляемых кодом ошибок. Коэффициенты многочлена локаторов ошибок определяют подстановкой значений символов синдрома в многочлен локаторов ошибок. Декодирование кодов БЧХ возможно и декодером Меггита, в котором анализатор синдрома часто выполняют в виде ЗУ. Подробные сведения по алгоритмам декодирования кодов БЧХ можно найти в [74—76 , 81, 82, 140], по спектральным методам декодирования — в книге [140].
Коды Рида — Соломона  подкласс недвоичных кодов БЧХ с параметрами: символы кода из поля
подкласс недвоичных кодов БЧХ с параметрами: символы кода из поля  целое, длина блока (число
целое, длина блока (число  -ичных символов)
-ичных символов)  количество информационных символов
количество информационных символов  минимальное расстояние
минимальное расстояние  При фиксированной скорости кода и длине блока коды
При фиксированной скорости кода и длине блока коды  обеспечивают наибольшее минимальное расстояние между словами. Их удобно использовать для исправления пакетов ошибок, а также в каскадных системах кодирования в качестве внешних кодов. В кодеках кодов
обеспечивают наибольшее минимальное расстояние между словами. Их удобно использовать для исправления пакетов ошибок, а также в каскадных системах кодирования в качестве внешних кодов. В кодеках кодов  используют описанные выше алгоритмы декодирования кодов
используют описанные выше алгоритмы декодирования кодов  дополнительное усложнение обусловлено необходимостью вычислений в недвоичных полях [82].
дополнительное усложнение обусловлено необходимостью вычислений в недвоичных полях [82].
Мажоритарно декодируемые коды образуют класс кодов, позволяющих реализовать наиболее простой и быстродействующий алгоритм декодирования. Рассмотрим циклический  код с проверочной матрицей Н. Строки этой матрицы
код с проверочной матрицей Н. Строки этой матрицы
линейно независимы и их линейные комбинации образуют векторы  каждый из которых согласно (4.4) ортогонален каждому вектору кода. Если в канале действуют ошибки, то принимаемый вектор
каждый из которых согласно (4.4) ортогонален каждому вектору кода. Если в канале действуют ошибки, то принимаемый вектор  Образуем проверочные суммы
Образуем проверочные суммы  которые зависят только от ошибочных символов:
которые зависят только от ошибочных символов: 
Из множества векторов  выберем
выберем  таких
таких

которые удовлетворяют следующим условиям:
 символ каждого вектора равен 1, т. е.
символ каждого вектора равен 1, т. е.

2) для любого  существует не более одного вектора
существует не более одного вектора  с символом 1 на позиции с номером
с символом 1 на позиции с номером  Таким образом, если
Таким образом, если  то
то 
Множество векторов  удовлетворяющих этому условию, называется ортогональным относительно символа на
удовлетворяющих этому условию, называется ортогональным относительно символа на  позиции. С его помощью образуется набор из
позиции. С его помощью образуется набор из  ортогональных проверок
ортогональных проверок  кода:
кода:

Значение символа  можно определить по большинству проверочных сумм, ортогональных к символу на позиции
можно определить по большинству проверочных сумм, ортогональных к символу на позиции  Предположим, что произошло
Предположим, что произошло  или меньше ошибок в кодовом слове
или меньше ошибок в кодовом слове  означает наибольшее целое, не превышающее
означает наибольшее целое, не превышающее  . В этом случае
. В этом случае  или менее символов вектора
или менее символов вектора  равны 1. Если
равны 1. Если  то другие ненулевые символы
то другие ненулевые символы  распределены в
распределены в  суммах А. Следовательно, оставшиеся
суммах А. Следовательно, оставшиеся  или более половины всего числа проверочных сумм содержат только
или более половины всего числа проверочных сумм содержат только  и соответственно равны 1. Если же
и соответственно равны 1. Если же  то отличные от нуля символы
то отличные от нуля символы  распределены в
распределены в  проверочных суммах. Следовательно, более
проверочных суммах. Следовательно, более  т. е. более половины сумм, содержат
т. е. более половины сумм, содержат  и сами равны 0. Вынесение решения по большинству лежит в основе мажоритарного алгоритма декодирования.
и сами равны 0. Вынесение решения по большинству лежит в основе мажоритарного алгоритма декодирования.
Рассмотрим этот алгоритм на примере циклического кода (15, 7) с проверочным многочленом  . В соответствии с (4.6) представим проверочную матрицу этого кода в несистематической форме:
. В соответствии с (4.6) представим проверочную матрицу этого кода в несистематической форме:

Для образования проверок используем следующие линейные комбинации строк:

Проверки с использованием векторов  имеют вид
имеют вид

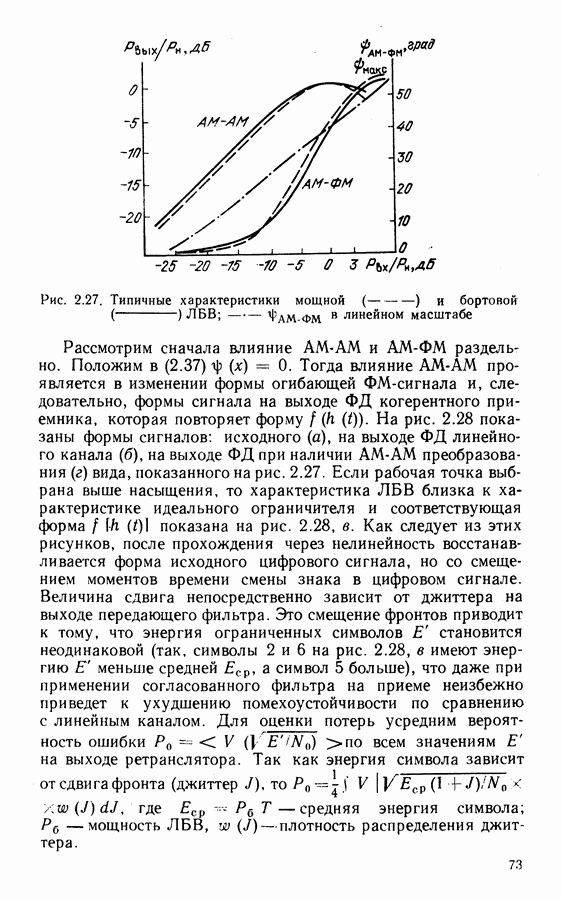
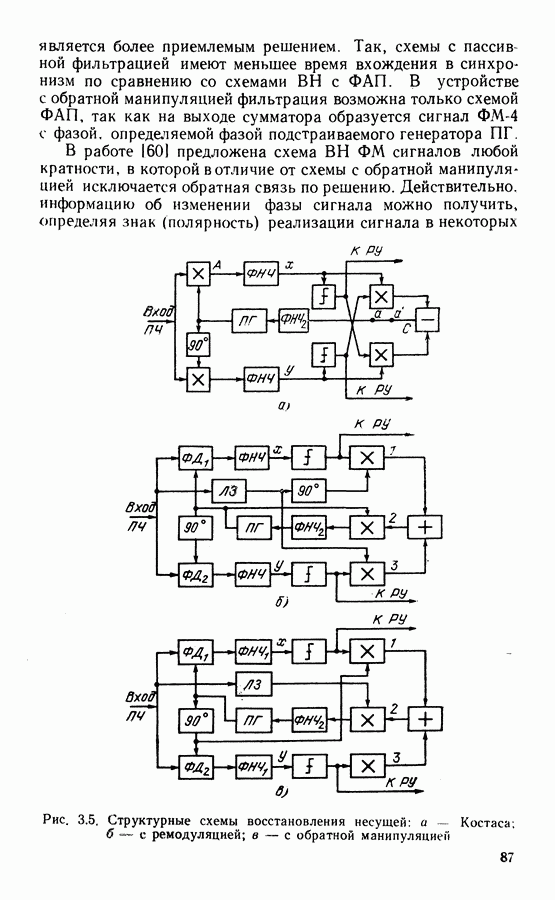
Схема мажоритарного декодера показана на рис. 4.2. Вначале в регистр через ключи в положении 3 (запись) вписываются принимаемые символы  Четыре сумматора по модулю 2 формируют проверки
Четыре сумматора по модулю 2 формируют проверки  в соответствии с уравнениями (4.9), которые поступают на мажоритарный элемент
в соответствии с уравнениями (4.9), которые поступают на мажоритарный элемент  Здесь выносится решение о символе ошибки
Здесь выносится решение о символе ошибки  по большинству и далее оценка
по большинству и далее оценка  поступает на корректор символа
поступает на корректор символа  На выходе декодера будет символ
На выходе декодера будет символ  Затем ключи устанавливают в положения
Затем ключи устанавливают в положения  (декодирование) и происходит
(декодирование) и происходит

Рис. 4.2. Структурная схема мажоритарного декодера кода (15, 7)
циклический сдвиг символов вправо, так что на следующем такте вырабатывается оценка  и корректируется символ
и корректируется символ  а в начало регистра вписывается откорректированный символ
а в начало регистра вписывается откорректированный символ  Эта процедура повторяется до тех пор, пока на выходе не окажется последний символ блока
Эта процедура повторяется до тех пор, пока на выходе не окажется последний символ блока  Далее ключи вновь устанавливаются в положения 3 и происходит запись следующего блока. Для двоичных кодов вынесение решения по большинству проверок (4.9) можно заменить сравнением суммы
Далее ключи вновь устанавливаются в положения 3 и происходит запись следующего блока. Для двоичных кодов вынесение решения по большинству проверок (4.9) можно заменить сравнением суммы  с порогом Т. При
с порогом Т. При  мажоритарная функция реализуется следующим образом:
мажоритарная функция реализуется следующим образом:  при
при  при
при 
Код (15, 7) имеет минимальное расстояние  и при полном декодировании позволяет исправить все ошибки кратности
и при полном декодировании позволяет исправить все ошибки кратности  и меньше. При мажоритарном декодировании корректирующая способность кода определяется реализуемым расстоянием
и меньше. При мажоритарном декодировании корректирующая способность кода определяется реализуемым расстоянием  которое зависит от числа ортогональных проверок
которое зависит от числа ортогональных проверок  Если строки порождающей матрицы Н позволяют образовать
Если строки порождающей матрицы Н позволяют образовать  ортогональных проверок, то гарантированно исправляется
ортогональных проверок, то гарантированно исправляется  ошибок и
ошибок и  Мажоритарно декодируемый код считается хорошим, если реализуемое расстояние
Мажоритарно декодируемый код считается хорошим, если реализуемое расстояние  достигает минимального расстояния кода
достигает минимального расстояния кода 
Проверочные суммы могут быть сформированы при декодировании и на основе синдромов. Как следует из формулы (4.5), каждый синдром есть скалярное произведение вектора принимаемого слова на вектор-строку проверочной матрицы: 
Проверки формируются на основе линейных комбинаций строк  Определим проверочную сумму
Определим проверочную сумму 
 Из этого выражения следует, что наборы проверок
Из этого выражения следует, что наборы проверок  могут быть сформированы с использованием синдромов
могут быть сформированы с использованием синдромов  как линейные комбинации, причем весовые коэффициенты
как линейные комбинации, причем весовые коэффициенты  входящие в эти суммы, равны коэффициентам, входящим в уравнения для образования проверок.
входящие в эти суммы, равны коэффициентам, входящим в уравнения для образования проверок.
Описанный способ мажоритарного декодирования основан на использовании набора проверок вида (4.8), когда каждый из  проверочных векторов ортогонален относительно декодируемого символа. При этом для вынесения решения необходим один уровень мажоритарной логики и коды называются ортогонализуемыми в один шаг. Вместе с тем известны коды, когда для вынесения решения о каждом символе необходимо производить мажоритарную обработку в несколько последовательных этапов. Такие коды называются ортогонализуемыми в
проверочных векторов ортогонален относительно декодируемого символа. При этом для вынесения решения необходим один уровень мажоритарной логики и коды называются ортогонализуемыми в один шаг. Вместе с тем известны коды, когда для вынесения решения о каждом символе необходимо производить мажоритарную обработку в несколько последовательных этапов. Такие коды называются ортогонализуемыми в  шагов.
шагов.
Известно несколько классов мажоритарно декодируемых кодов. Дважды транзитивно-инвариантные коды ортогонализуемы в один шаг [83]. Используются также коды максимальной длины с параметрами  [74]. Комбинации кода МД порождаются
[74]. Комбинации кода МД порождаются  -разрядным регистром сдвигов с обратной связью как последовательности максимальной длины. Коды Хэмминга, рассмотренные ранее, также относятся к классу мажоритарно декодируемых. Код (7,4) ортогонализуем в один шаг, а код (7,3) ортогонализуем в два шага. Ряд кодов строится на основе разностных множеств. Параметры этих кодов:
-разрядным регистром сдвигов с обратной связью как последовательности максимальной длины. Коды Хэмминга, рассмотренные ранее, также относятся к классу мажоритарно декодируемых. Код (7,4) ортогонализуем в один шаг, а код (7,3) ортогонализуем в два шага. Ряд кодов строится на основе разностных множеств. Параметры этих кодов:  [83]. Обширный класс образуют коды, построенные на основе конечных проектной и евклидовой геометрий [83]. Конечно-геометрические коды имеют следующие параметры:
[83]. Обширный класс образуют коды, построенные на основе конечных проектной и евклидовой геометрий [83]. Конечно-геометрические коды имеют следующие параметры: 
Евклидово-геометрические коды имеют параметры:  Подкласс таких кодов составляют коды Рида Маллера, для которых:
Подкласс таких кодов составляют коды Рида Маллера, для которых:  Классификация, способы построения систем проверок и параметры кодов приведены в монографии [81], а также в статье [84]. В табл. 4.2 приведены основные данные по мажоритарным кодам, декодируемым за один или два шага.
Классификация, способы построения систем проверок и параметры кодов приведены в монографии [81], а также в статье [84]. В табл. 4.2 приведены основные данные по мажоритарным кодам, декодируемым за один или два шага.
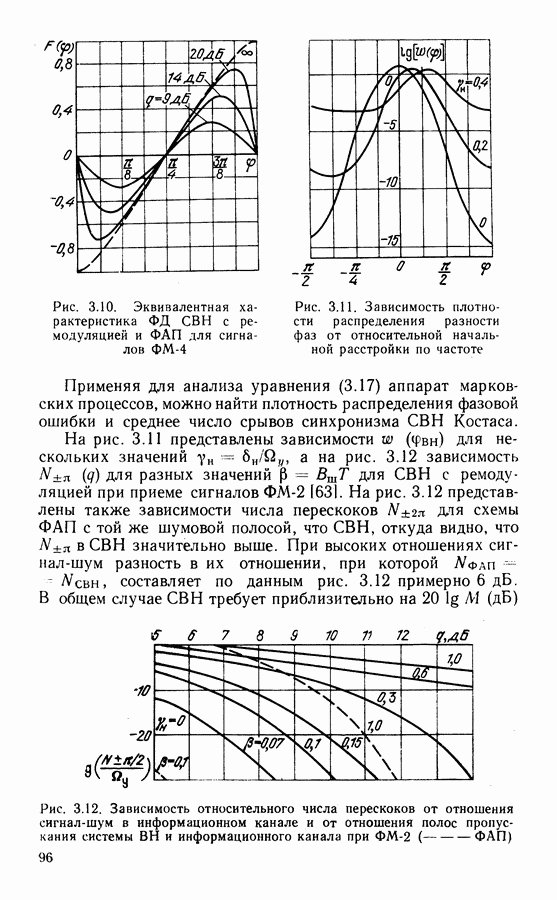
Рассмотрим пример построения нелинейных кодов. К ним относятся, в частности, ортогональные и биортогональные
Таблица 4.2 (см. скан)
коды, получаемые на основе матриц Адамара. Матрица Адамара размеров  имеет вид
имеет вид  Повторение
Повторение  трижды в позитивной и один раз в негативной форме дает
трижды в позитивной и один раз в негативной форме дает

Продолжая подобное построение, можно получить матрицы Адамара  где
где  порядок матрицы,
порядок матрицы,  целое число. Строки матриц Адамара ортогональны. Перейдем к четверичному представлению строк, полагая, что двоичные на» боры соответствуют четверичным символам по следующему правилу:
целое число. Строки матриц Адамара ортогональны. Перейдем к четверичному представлению строк, полагая, что двоичные на» боры соответствуют четверичным символам по следующему правилу:  Векторы
Векторы  образуют биортогональную систему, поскольку каждому из них ортогональны два других и противоположен третий вектор [33]. Из матрицы (4.10) получаем
образуют биортогональную систему, поскольку каждому из них ортогональны два других и противоположен третий вектор [33]. Из матрицы (4.10) получаем

Повторением  образуем матрицу
образуем матрицу  и матрицу
и матрицу  составленную из инверсий символов
составленную из инверсий символов

Строки матриц  образуют биортогональный четверичный код. Такие коды имеют следующие параметры: основание кода
образуют биортогональный четверичный код. Такие коды имеют следующие параметры: основание кода  длина блока
длина блока  число разрешенных кодовых слов
число разрешенных кодовых слов  скорость кода
скорость кода  . Каждая из матриц (4.11) представляет набор ортогональных кодовых слов. Декодирование ортогональных и биортогональных кодов производят, как правило, с использованием евклидовой метрики [34]. Если символы кода являются координатами векторов в 2
. Каждая из матриц (4.11) представляет набор ортогональных кодовых слов. Декодирование ортогональных и биортогональных кодов производят, как правило, с использованием евклидовой метрики [34]. Если символы кода являются координатами векторов в 2  -мерном пространстве с евклидовой метрикой, то алгоритм приема в целом, минимизирующий вероятность ошибки декодирования блока при действии аддитивных помех, имеет вид
-мерном пространстве с евклидовой метрикой, то алгоритм приема в целом, минимизирующий вероятность ошибки декодирования блока при действии аддитивных помех, имеет вид

где  значения символов с помехой на аналоговом выходе канала;
значения символов с помехой на аналоговом выходе канала;  символы передаваемых кодовых блоков с номерами
символы передаваемых кодовых блоков с номерами  Таким образом, алгоритм сводится к весовому накоплению результатов обработки отдельных символов
Таким образом, алгоритм сводится к весовому накоплению результатов обработки отдельных символов  в согласованных фильтрах, причем весовыми коэффициентами являются символы кодовых блоков. В решающем устройстве производится сравнение выходов согласованных фильтров и в соответствии с алгоритмом (4.12) вынесение решения о кодовом блоке с наибольшим скалярным произведением
в согласованных фильтрах, причем весовыми коэффициентами являются символы кодовых блоков. В решающем устройстве производится сравнение выходов согласованных фильтров и в соответствии с алгоритмом (4.12) вынесение решения о кодовом блоке с наибольшим скалярным произведением  Сравнение производится методом перебора, поэтому сложность реализации такого алгоритма возрастает экспоненциально с увеличением длины кода. Возможно некоторое уменьшение объема перебора примерно вдвое, вытекающее из биортогональных свойств кода [85]. Из-за сложности алгоритма декодирования на практике применяют короткие
Сравнение производится методом перебора, поэтому сложность реализации такого алгоритма возрастает экспоненциально с увеличением длины кода. Возможно некоторое уменьшение объема перебора примерно вдвое, вытекающее из биортогональных свойств кода [85]. Из-за сложности алгоритма декодирования на практике применяют короткие
ортогональные и биортогональные коды. Кроме того, с увеличением длины блока скорость кода резко падает.
Рассмотренные в этом параграфе алгебраические методы декодирования достаточно просты и объем оборудования декодера растет как небольшая степень длины блока. Поэтому применение этих алгоритмов возможно для декодирования достаточно длинных кодов. Алгебраические алгоритмы хорошо согласованы с дискретным выходом канала. Возможно также декодирование с мягким решением, когда помимо информации о двоичных символах при декодировании используют сведения о надежности символа. Различные варианты применения мягкого решения при алгебраическом декодировании блоковых кодов рассмотрены в ряде работ [86].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
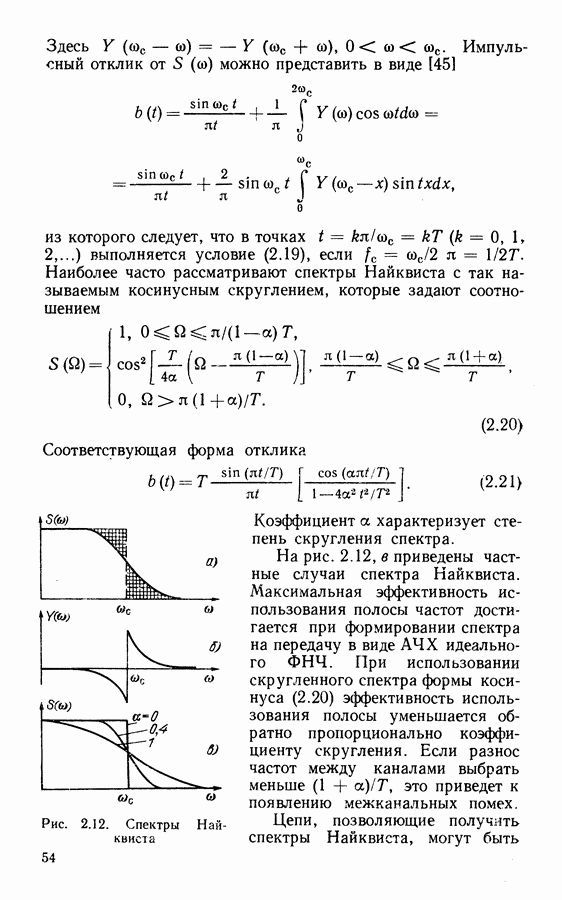
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
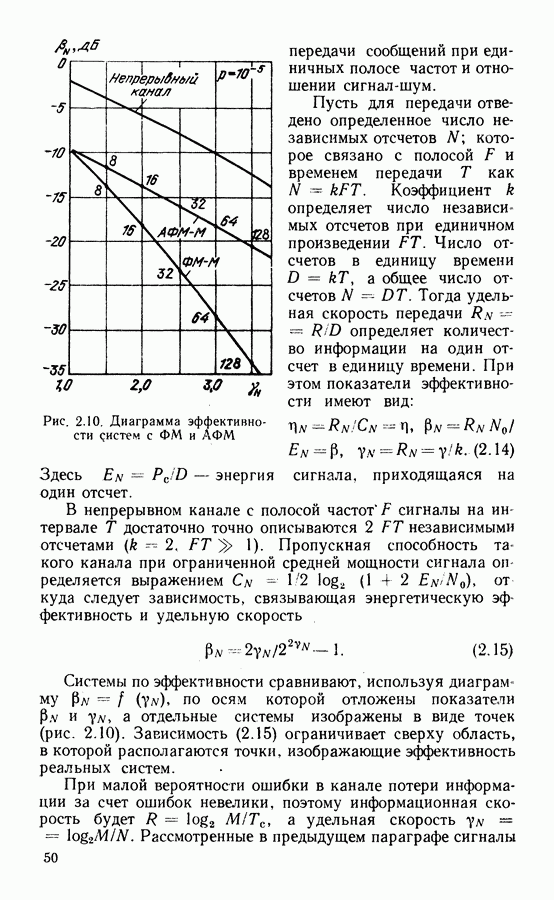
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
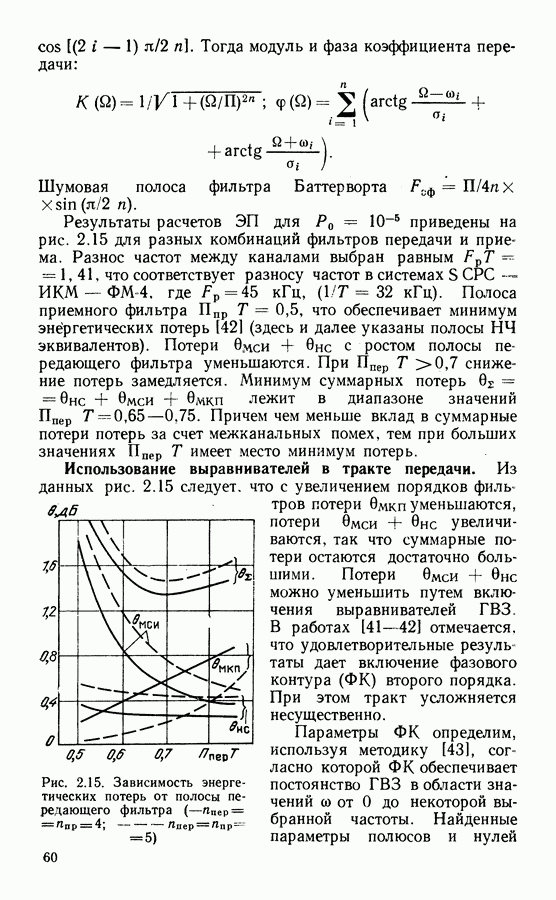
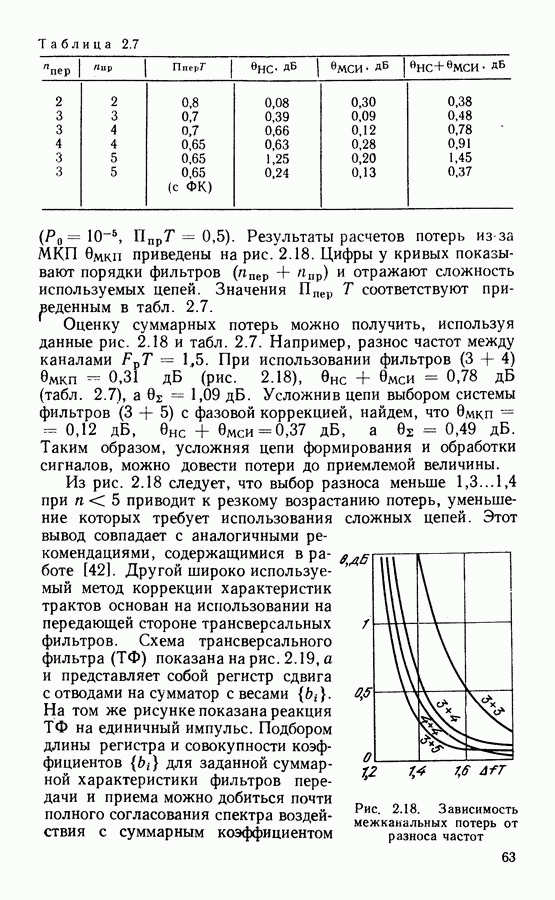
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
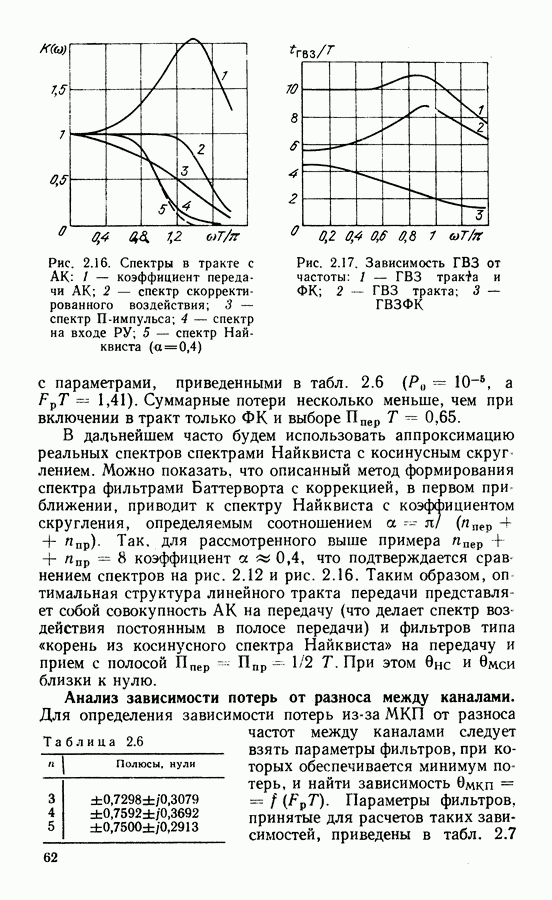
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
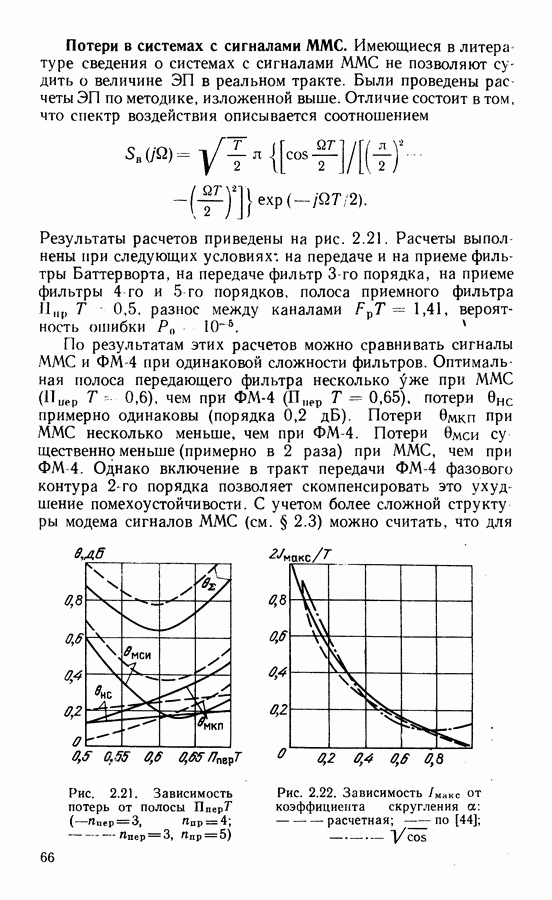
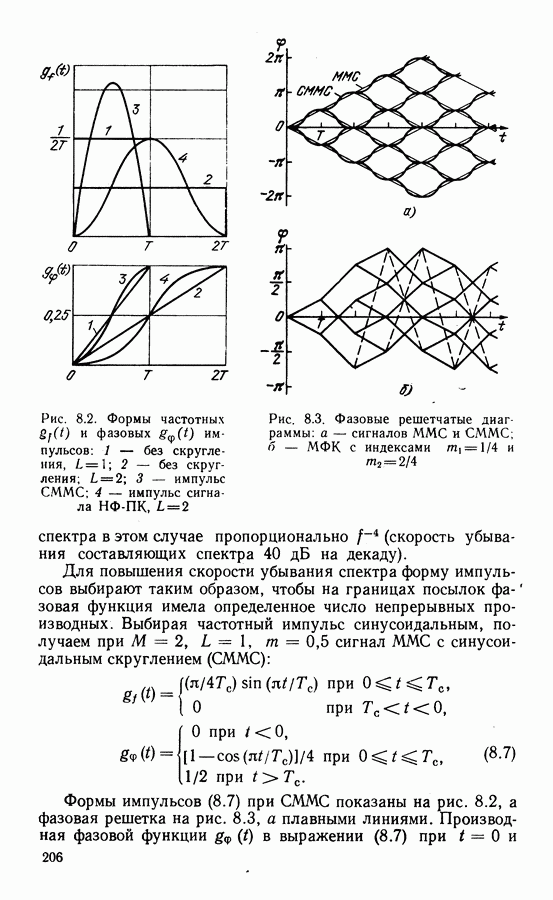
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
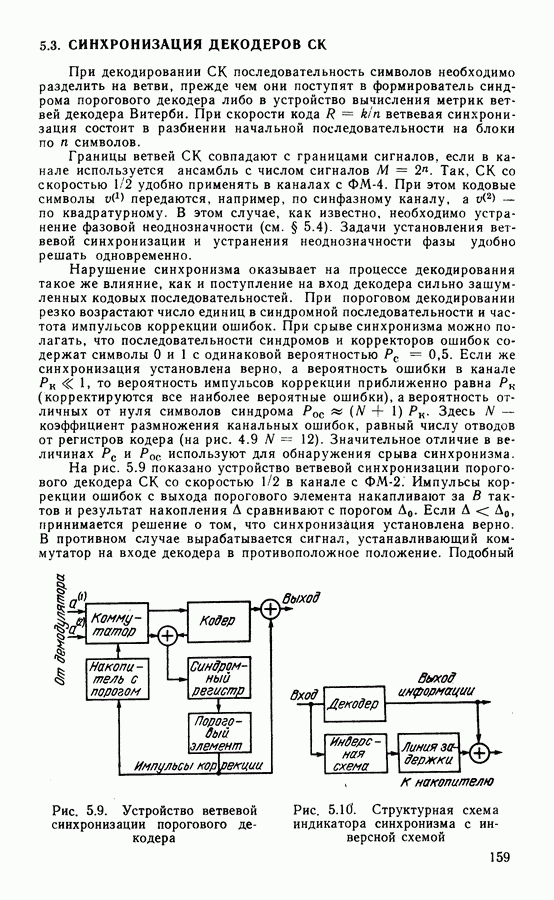
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
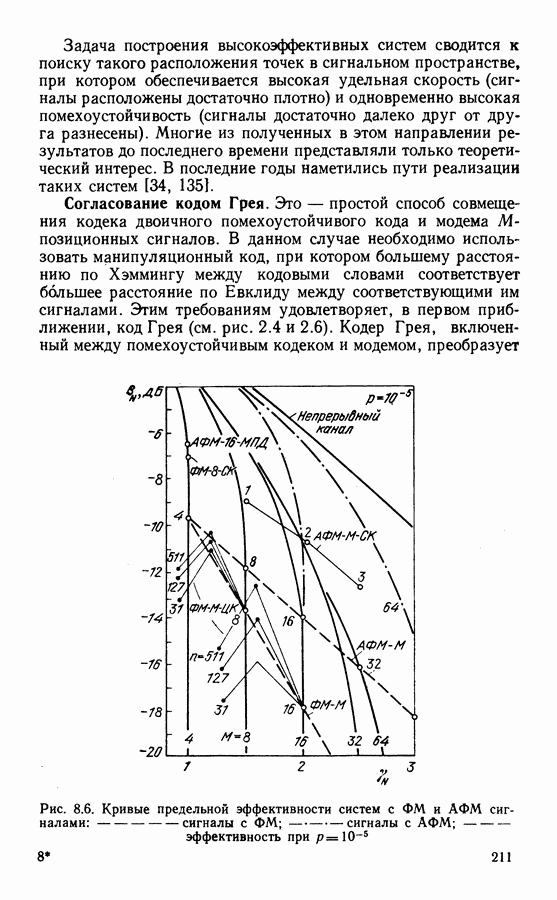
- Согласование кодом Грея.
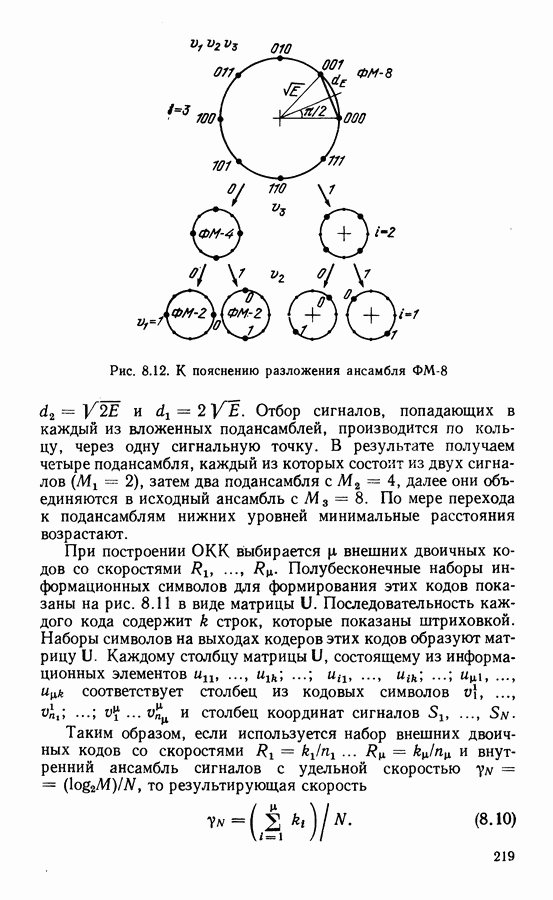
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ