| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. Многомерные оптимальные системы
Вначале подытожим основные результаты, полученные при решении задачи синтеза одномерной оптимальной реализуемой системы управления.
Пусть входное воздействие g(t)
представляется реализацией случайного процесса с энергетическим спектром ![]() и в сумме
z(t)=g(t)+n(t) с белым шумом (помехой) n(t) поступает на систему управления. В
соответствии с методом Винера оптимальная реализуемая система имеет передаточную
функцию
и в сумме
z(t)=g(t)+n(t) с белым шумом (помехой) n(t) поступает на систему управления. В
соответствии с методом Винера оптимальная реализуемая система имеет передаточную
функцию
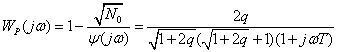 ,
,
где ![]() , x(jw)=WP(jw)Z(jw).
, x(jw)=WP(jw)Z(jw).
Р.Калман
предложил другое представление того же решения в виде дифференциального
уравнения ![]() .
.
При этом входное воздействие g(t)
удобно представить в виде выходного сигнала фильтра (рис.38), описываемого
дифференциальным уравнением ![]() .
.
Фильтр, с помощью которого моделируется входное воздействие g(t), обычно называют формирующим фильтром. Само же входное воздействие g(t) при этом является состоянием формирующей системы.
Было установлено, что при описании
входных сигналов в виде состояния некоторой системы всегда получается решение в
виде точно такой же по виду системы с обратной связью. При этом структура САУ
сохраняется для любого интервала времени, в том числе и во время переходного
процесса, при изменении коэффициентов ![]() во времени, а также в случае, когда x(t)
является вектором, т.е. при одновременном управлении по нескольким параметрам.
И во всех этих случаях структура системы управления оказывается оптимальной в
смысле минимума дисперсии ошибки
во времени, а также в случае, когда x(t)
является вектором, т.е. при одновременном управлении по нескольким параметрам.
И во всех этих случаях структура системы управления оказывается оптимальной в
смысле минимума дисперсии ошибки ![]() .
.
В этом разделе вначале рассматриваются математические модели входных многомерных нестационарных воздействий. После этого обсуждается структура оптимальной многомерной системы, которая называется фильтром Калмана.
Описание входных воздействий
Пусть нам необходимо осуществлять
управление одновременно n выходными сигналами системы ![]() При этом мы хотим получить
наименьшие отличия этих сигналов от заданных функций – входных воздействий
При этом мы хотим получить
наименьшие отличия этих сигналов от заданных функций – входных воздействий 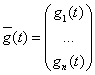 . Будем описывать
входные воздействия с помощью системы линейных дифференциальных уравнений
состояния:
. Будем описывать
входные воздействия с помощью системы линейных дифференциальных уравнений
состояния:
![]() ,
,
где A(t) – (n ![]() n) – матрица:
n) – матрица: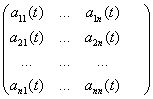 ;
; 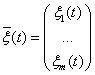 – векторный белый шум с
энергетическим спектром каждой компоненты
– векторный белый шум с
энергетическим спектром каждой компоненты ![]() соответственно.
соответственно.
V(t) - (n ![]() m)-матрица V(t)=
m)-матрица V(t)=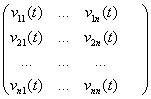 .
.
Рассмотрим примеры.
Пример 1. Уравнение состояния для трех независимых параметров.
Предположим, что необходимо обеспечить измерение траектории по 3 координатам, не связанным друг с другом. Эти координаты описываются случайными процессами, соответствующими дифференциальным уравнениям:
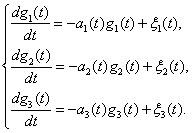
Введем вектор 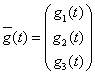 , матрицу
, матрицу 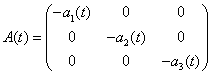 и белый шум
и белый шум 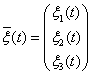 . Тогда одновекторное
уравнение состояния
. Тогда одновекторное
уравнение состояния ![]() в точности описывает все заданные
входные воздействия Для проверки достаточно раскрыть в этом уравнении матричные
и векторные обозначения.
в точности описывает все заданные
входные воздействия Для проверки достаточно раскрыть в этом уравнении матричные
и векторные обозначения.
Пример 2. Входное воздействие с дробно-рациональным энергетическим спектром.
Пусть g(t) описывается дифференциальным уравнением вида:
![]() .
.
Найдем энергетический спектр такого
воздействия. Для этого вначале выполним преобразование Лапласа ![]() и запишем
передаточную функцию формирующего фильтра
и запишем
передаточную функцию формирующего фильтра
![]() .
.
Энергетический спектр входного воздействия находится
по формуле ![]() .
При выборе различных коэффициентов
.
При выборе различных коэффициентов ![]() могут быть получены энергетические
спектры разнообразной формы. Но рассматриваемое уравнение имеет третий порядок.
Преобразуем его в одно векторное уравнение. Введем вспомогательные переменные:
могут быть получены энергетические
спектры разнообразной формы. Но рассматриваемое уравнение имеет третий порядок.
Преобразуем его в одно векторное уравнение. Введем вспомогательные переменные:![]() . Тогда исходное
уравнение перепишется в форме:
. Тогда исходное
уравнение перепишется в форме:
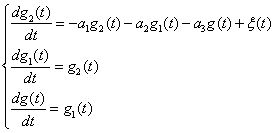 .
.
Введем теперь вектор 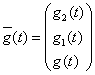 и тогда
и тогда 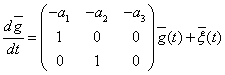 , где
, где 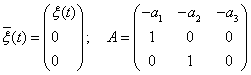 . Таким образом
дифференциальное уравнение третьего порядка удается преобразовать к стандартной
векторной форме. Очевидно, что точно так же к векторному уравнению первого
порядка можно преобразовать дифференциальное уравнение произвольного порядка.
. Таким образом
дифференциальное уравнение третьего порядка удается преобразовать к стандартной
векторной форме. Очевидно, что точно так же к векторному уравнению первого
порядка можно преобразовать дифференциальное уравнение произвольного порядка.
Пример 3. Полиномиальное воздействие.
Пусть ![]() . Такой входной сигнал получается как
решение следующего дифференциального уравнения
. Такой входной сигнал получается как
решение следующего дифференциального уравнения ![]() . Заметим, что этот результат можно
рассматривать как частный случай предыдущего примера, полагая
. Заметим, что этот результат можно
рассматривать как частный случай предыдущего примера, полагая ![]() . Тогда
. Тогда ![]() ,
, ![]() – начальные условия.
– начальные условия.
Введем вспомогательные переменные ![]() . Тогда уравнения состояния
запишутся в виде:
. Тогда уравнения состояния
запишутся в виде:
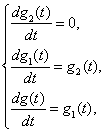
или в стандартной форме:
![]() ,
,
где 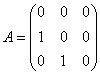 ,
, 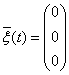 .
.
Таким образом, исходное дифференциальное
уравнение состояния ![]() описывает широкий класс реальных случайных
процессов.
описывает широкий класс реальных случайных
процессов.
Пусть теперь ![]() передается по каналу связи и
вместе с помехой поступает на вход системы управления:
передается по каналу связи и
вместе с помехой поступает на вход системы управления:
![]() , где
, где 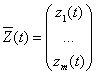 , C(t)=
, C(t)=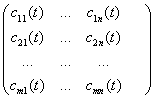 ;
;
![]() =
=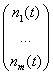 – помеха в виде векторного белого шума со
спектральными плотностями каждой компоненты
– помеха в виде векторного белого шума со
спектральными плотностями каждой компоненты ![]() соответственно.
соответственно.
Рассмотренная векторная модель позволяет дать математическое описание различных ситуаций, возникающих при формировании входных сигналов проектируемых САУ.
Пример 4.
Предположим, что один и тот же входной сигнал g(t)
передается по двум независимым каналам связи. При этом на выходе первого канала
наблюдается смесь ![]() сигнала
сигнала
![]() с помехой
с помехой ![]() , а на выходе второго
канала наблюдается процесс
, а на выходе второго
канала наблюдается процесс ![]() . Для того, чтобы представить такие
наблюдения в стандартной векторной форме, введем векторы
. Для того, чтобы представить такие
наблюдения в стандартной векторной форме, введем векторы ![]() и матрицу
и матрицу 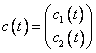 . В этом случае одно векторное
уравнение
. В этом случае одно векторное
уравнение ![]() или
или
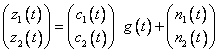 описывает
двухканальную систему наблюдений скалярного процесса
описывает
двухканальную систему наблюдений скалярного процесса ![]() .
.
Пример 5.
Пусть входной сигнал ![]() имеет сложный энергетический спектр и
описывается дифференциальным уравнением третьего порядка (см. пример 2). В этом
случае уравнение состояния включает трехмерный вектор
имеет сложный энергетический спектр и
описывается дифференциальным уравнением третьего порядка (см. пример 2). В этом
случае уравнение состояния включает трехмерный вектор 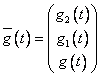 . Производятся наблюдения
сигнала
. Производятся наблюдения
сигнала ![]() на
фоне помехи
на
фоне помехи ![]()
![]() . Для того, чтобы
получить стандартное представление наблюдений
. Для того, чтобы
получить стандартное представление наблюдений ![]() необходимо ввести матрицу
необходимо ввести матрицу ![]() .
.
Многомерный фильтр Калмана
Наблюдаемый многомерный сигнал ![]() поступает на систему
управления. В наилучшей системе обеспечивается минимум суммарной ошибки:
поступает на систему
управления. В наилучшей системе обеспечивается минимум суммарной ошибки:
![]() .
.
Структура оптимальной системы описывается следующим уравнением:
![]() ,
,
где 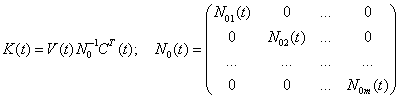 ,
,
а ![]() . Последнее уравнение является
дифференциальным уравнением Риккати и обычно требует ЭВМ для решения. Но это
решение находится, как правило, один раз до проведения эксперимента. После
этого значения V(t) могут храниться в памяти. Уравнение для матрицы V(t)
называется дисперсионным, поскольку V(t) – точная матрица
дисперсий и взаимных ковариаций ошибок управления.
. Последнее уравнение является
дифференциальным уравнением Риккати и обычно требует ЭВМ для решения. Но это
решение находится, как правило, один раз до проведения эксперимента. После
этого значения V(t) могут храниться в памяти. Уравнение для матрицы V(t)
называется дисперсионным, поскольку V(t) – точная матрица
дисперсий и взаимных ковариаций ошибок управления.
Итак, и в многомерном нестационарном
случае система управления сохраняет свою структуру (рис. 39). По-прежнему это
система, в которой формируется сигнал ошибки ![]() . Он поступает на фильтр, включающий
переменный коэффициент усиления K(t) и интеграторы, охваченные обратной связью.
. Он поступает на фильтр, включающий
переменный коэффициент усиления K(t) и интеграторы, охваченные обратной связью.
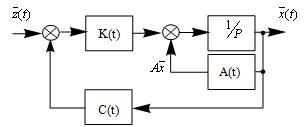
Рис. 39
При этом часть системы в точности соответствует формирующему фильтру.
Пример 6. Еще раз рассмотрим систему управления при входном сигнале, заданном уравнением:
![]() ,
, ![]() ,
,
где ![]() .
.
В этом случае уравнение Калмана для наблюдений z(t)=g(t)+n(t) запишется в виде:
![]() ,
,
где K(t)=V(t)![]() ;
;
![]() .
.
Существенной особенностью записанного уравнения фильтрации является зависимость коэффициента усиления K(t) от времени. Это связано с тем, что фильтр Калмана учитывает переходный процесс в системе и оптимален для каждого момента времени t. Характерную зависимость V(t) можно проиллюстрировать графиком на рис. 40.
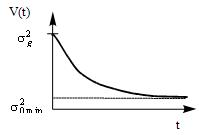
Рис. 40
В начальный момент времени (t=0) рассогласование
между выходным сигналом x(t=0)=0 системы управления и заданной траекторией
движения g(t=0)=g(0) может быть большим. Поэтому и коэффициент усиления
К(t=0)=![]() в
этот момент наибольший. По мере уменьшения динамической ошибки в процессе
работы системы коэффициент усиления уменьшается и стремится к оптимальному для
установившегося режима значению
в
этот момент наибольший. По мере уменьшения динамической ошибки в процессе
работы системы коэффициент усиления уменьшается и стремится к оптимальному для
установившегося режима значению ![]() . Это значение можно найти, полагая
. Это значение можно найти, полагая ![]() =0 в установившемся
режиме. Тогда из уравнения Риккати получаем:
=0 в установившемся
режиме. Тогда из уравнения Риккати получаем: ![]() , где
, где ![]() или
или ![]() . Решение этого уравнения
. Решение этого уравнения 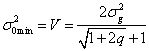 совпадает с
известной величиной дисперсии ошибки стационарного реализуемого фильтра Винера.
совпадает с
известной величиной дисперсии ошибки стационарного реализуемого фильтра Винера.
Итак, для одномерного случая отличием приведенного решения является учет переходного процесса и выбор оптимальных параметров системы управления в каждый момент времени.
Оптимальное управление предполагает точное знание моделей входных воздействий и характеристик помех. Однако на практике численные значения параметров моделей известны не точно. Кроме того, вычислительные трудности ограничивают применение сложных моделей высокой размерности, предопределяя применение более грубых и более простых приближений к реальным процессам.
Указанные причины приводят к отклонению действительных характеристик эффективности от расчетных. Величина отклонений действительных характеристик систем управления от потенциальных за счет изменения параметров внешних воздействий называется чувствительностью системы управления.
Предположим, что Q – некоторый
показатель качества, например, средний квадрат ошибки системы, зависящий от
некоторого параметра ![]() входного сигнала. При отклонении
входного сигнала. При отклонении ![]() от заданного значения
от заданного значения
![]() 0 показатель
качества Q также отклоняется от оптимального значения Q0. В этом
случае чувствительность можно характеризовать отношением:
0 показатель
качества Q также отклоняется от оптимального значения Q0. В этом
случае чувствительность можно характеризовать отношением:![]() а при малых отклонениях –
величиной
а при малых отклонениях –
величиной ![]() Чем
выше чувствительность, тем больше опасений, что в реальных условиях система
управления будет иметь худшие характеристики качества по сравнению с
расчетными. Если, наоборот, величина
Чем
выше чувствительность, тем больше опасений, что в реальных условиях система
управления будет иметь худшие характеристики качества по сравнению с
расчетными. Если, наоборот, величина ![]() мала, то допустимы значительные
отклонения параметров внешних воздействий. В предельном случае, когда
мала, то допустимы значительные
отклонения параметров внешних воздействий. В предельном случае, когда ![]() =0, показатель
качества системы вообще не зависит от параметра
=0, показатель
качества системы вообще не зависит от параметра ![]() . В таком случае говорят, что система
управления инвариантна относительно параметра
. В таком случае говорят, что система
управления инвариантна относительно параметра ![]() .
.
В этом разделе рассмотрены два подхода к построению оптимальных систем управления. Первый подход связан с именем Н. Винера и основан на нахождении структуры оптимальной системы с помощью решения интегрального уравнения. Главные недостатки этого метода – сложность решения задач синтеза САУ и требования к стационарности входных воздействий. Поэтому при проектировании современных нестационарных систем управления применяется метод пространства состояний, предложенный Р. Калманом. Этот метод позволяет на инженерном уровне решать сложные задачи построения оптимальных многомерных систем с учетом переходных процессов в условиях нестационарных помех и нестационарных воздействий.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- 1. Основные понятия теории управления
- 1.1. Управляемые системы
- 1.2. Линейные системы управления
- 2. Автоматическое управление системами
- 2.1. Устойчивость систем управления
- 2.2. Динамические ошибки систем управления
- 2.3. Эффективность систем управления при воздействии помех
- 3. Оптимальные системы управления
- 3.1. Оптимальные стационарные системы. Фильтр Винера
- 3.2. Оптимальные реализуемые системы управления. Фильтр Калмана
- 3.3. Многомерные оптимальные системы
- 4. Дискретные и цифровые системы управления
- 4.1. Цифровые системы управления
- 4.2. Цифровые фильтры
- 4.3. Действие помех на цифровые системы управления
- Список литературы
