4.3. Действие помех на цифровые системы управления

Рассмотрим особенности анализа цифровых систем  управления, находящихся под воздействием помех. Вначале приведем основные формулы, позволяющие определить дисперсию ошибки сопровождения, обусловленную действием помех. Затем кратко проанализируем методы построения оптимальных линейных дискретных систем,  которые в настоящее время широко используются при проектировании и анализе цифровых систем управления.

Дисперсия ошибки в цифровых системах управления

            Цифровую систему управления с учетом действия помех можно представить в виде рис. 50.

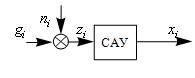
Рис. 50

            На вход системы действует сумма  управляющего воздействия    и помех Ni = N(ti).   В результате действия помехи в выходном сигнале xi  содержится случайная составляющая, которую  можно охарактеризовать    величиной дисперсии  . При этом цифровая система управления описывается разностным уравнением:

  .  

            Поскольку система управления линейна, то можно отдельно рассматривать прохождение сигналов и помех через эту систему. Таким образом, достаточно найти дисперсию процесса, описываемого следующим уравнением общего вида:

.

            Помехой в системе управления обычно служат независимые отсчеты  Ni  гауссовских случайных величин с нулевым средним и дисперсией  .   В общем случае дисперсия результирующего процесса xi  находится с помощью известных методов теории вероятностей. Действительно, разностное уравнение представляет собой закон преобразования случайных величин    в случайные величины . Поэтому любые вероятностные характеристики    выражаются через известные характеристики помех.

            Пример.   Система первого порядка.

            Пусть система управления описывается простейшим разностным уравнением вида   .

            Найдем дисперсию ошибки на выходе такой системы. Для этого возведем левую и правую части в квадрат и найдем математическое ожидание. После возведения в квадрат получаем  .  

            Теперь находим математическое ожидание левой и правой частей:.

            Таким образом, дисперсия ошибки за счет действия помех   .  Заметим, что , т.к. в противном случае система управления будет неустойчивой.

Оптимальные цифровые системы. Описания динамики движения объектов в цифровых системах

            В непрерывных системах для описания динамики движения объекта или входного сигнала системы управления используется следующее стохастическое дифференциальное уравнение: , где    – белый шум.  В этом случае траектория движения объекта представляет собой одну из множества реализаций случайного процесса g(t) .

            В цифровых системах дифференциальному уравнению первого порядка будет соответствовать разностное уравнение  , где   – постоянный коэффициент;   – гауссовские независимые случайные величины с дисперсией . Определим вероятностные характеристики возможных траекторий объекта  в дискретном времени. Так же, как и в рассмотренном примере, возведем левую и правую части уравнения движения объекта в квадрат и найдем математическое ожидание. Получим    или   .  Эта величина дисперсии  определяет динамический диапазон возможных отклонений  траектории от среднего значения.

            Другим параметром, описывающим движение объекта, является характеристика скорости изменения  траектории.  В рассматриваемом случае мерой этой скорости может быть коэффициент корреляции двух соседних значений  g(ti–1) =gi–1 и g(ti) = gi траектории. Для его нахождения умножим левую и правую части уравнения на  gi–1  и найдем их средние значения: .   Поскольку  , то коэффициент корреляции 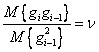  .  Таким образом, параметр   оказывается  равным значению коэффициента корреляции двух соседних значений траектории.

             Нормированная корреляционная функция последовательности   описывается при этом   простым выражением   .         

            Допустим, что с помощью приведенного уравнения  мы хотим описать траекторию движения объекта, значительно изменяющегося за 100 тактовых интервалов. Это  означает, что . В этом случае можно выбрать  .

Оптимальная цифровая линейная система управления

            Пусть на вход линейной системы управления действует сумма   zi =gi + ni                 управляющего сигнала gi , который описывается уравнением    и помехи  ni    в виде независимых отсчетов  мешающего процесса с дисперсией  .

            Состояние цифровой линейной системы управления  xi связано с входным сигналом следующим разностным уравнением   .

            Основной задачей системы является минимизация дисперсии ошибки    управления. Рассмотрим возможности построения оптимальной системы, для которой дисперсия ошибки минимальна. Для минимизации дисперсии имеется возможность выбора коэффициентов     и   системы управления.

            Итак, необходимо найти   Подставим в формулу для ошибки известные соотношения:

            Величины   gi–1  имеют большие значения. Если необходимо минимизировать ошибки, то нужно положить . Тогда  или  .

            В этой формуле отражены три составляющие ошибки системы управления. Первое слагаемое учитывает ошибку    на предыдущем шаге работы системы.  Второе слагаемое – динамическая ошибка за счет изменения траектории движения. Третье слагаемое     – ошибка, вызванная действием помех на систему управления. Поскольку все слагаемые являются независимыми, то дисперсия будет равна сумме дисперсий ошибок всех трех слагаемых: 

    ,

где   ,    , .

            Продифференцируем  Di  по bi  и приравняем производную к нулю. Легко подсчитать, что минимальное значение   Pi = Di min     дисперсии ошибки достигается  при ,  где . После подстановки оптимального значения  bi   в уравнение системы получаем следующий алгоритм функционирования оптимальной цифровой системы управления:

,      ,       ,

где  .

            В этом уравнении величина  является экстраполированной на один шаг траекторией объекта или прогнозом значения траектории.  Действительно, на предыдущем шаге состояние системы было   .   Динамика изменения траектории описывается уравнением  . Лучшее, что мы можем сделать с точки зрения прогноза траектории движения gi – предсказать, что сигнал gi будет иметь величину хэi =.  

            Таким образом, в найденной системе управления вначале формируется прогноз   траектории движения. Затем определяется рассогласование   между сделанным прогнозом и очередным сигналом управления ,  искаженном помехами. После этого очередное состояние системы    формируется как сумма прогноза  и взвешенного рассогласования.

            Весовым коэффициентом   служит отношение дисперсии ошибки системы управления   рi   и   дисперсии помех, действующих на систему управления.

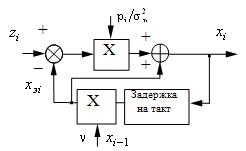
Рис. 51

            Структурная схема рассмотренной оптимальной цифровой системы управления может быть представлена в виде рис.51.

* * *

            Рассмотренные вопросы действия помех на цифровые системы управления позволяют решить две важные задачи. Во–первых, для любой заданной линейной системы управления можно дать оценку ее эффективности, т.е. оценить дисперсию ошибки за счет действия помех. Вторая важная задача – построение оптимальной цифровой системы управления, учитывающей как динамику движения объекта, так и величину помехи, действующей на систему управления.