| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14. Преобразование Карунена-Лоэва
В задачах сжатия
изображений лучшим преобразованием является то, в котором на первый базисный
вектор, в среднем, приходилась бы наибольшая информация об изображении, на
второй максимум из оставшейся и т.д. Рассмотрим построение такого пространства
со следующих позиций. Без потери общности предположим, что у нас имеется набор
из ![]() одномерных
векторов
одномерных
векторов ![]() ,
, ![]() . Для них требуется
найти такой вектор
. Для них требуется
найти такой вектор ![]() ,
чтобы минимизировалась квадратическая разность
,
чтобы минимизировалась квадратическая разность
![]() , (1)
, (1)
где ![]() - некоторые пока неизвестные весовые
коэффициенты. Очевидно, что
- некоторые пока неизвестные весовые
коэффициенты. Очевидно, что ![]() можно найти путем дифференцирования
данного выражения по
можно найти путем дифференцирования
данного выражения по ![]() и приравнивания результата нулю:
и приравнивания результата нулю:
 . (2)
. (2)
Но в этом выражении остаются
неизвестными коэффициенты ![]() . Однако они также должны быть выбраны из
соображений минимума квадратической ошибки, следовательно,
. Однако они также должны быть выбраны из
соображений минимума квадратической ошибки, следовательно, ![]() находится как
находится как
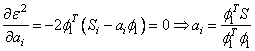
и полагая ![]() , получим
, получим ![]() , т.е.
, т.е. ![]() есть не что иное как проекция сигнала
есть не что иное как проекция сигнала ![]() на вектор
на вектор ![]() . Подставляя данное
выражение в (2), можно записать следующее рекуррентное выражения для нахождения
. Подставляя данное
выражение в (2), можно записать следующее рекуррентное выражения для нахождения
![]() :
:
 . (3)
. (3)
В последнем выражении опущен множитель ![]() , т.к. это число
определяет лишь масштаб вектора
, т.к. это число
определяет лишь масштаб вектора ![]() , который нами был уже задан в виде
соотношения
, который нами был уже задан в виде
соотношения ![]() ,
а значит
,
а значит ![]() =1.
=1.
Выражение (3)
описывает рекуррентное выражение для вычисления вектора ![]() , минимизирующего (1), которое
сходится до установившегося значения уже на 20-30 итерации. В качестве
начальных условий можно выбрать любой не нулевой вектор, например
, минимизирующего (1), которое
сходится до установившегося значения уже на 20-30 итерации. В качестве
начальных условий можно выбрать любой не нулевой вектор, например ![]() . Таким образом,
нашли первый базисный вектор, на который будет приходиться максимум информации
о сигналах
. Таким образом,
нашли первый базисный вектор, на который будет приходиться максимум информации
о сигналах ![]() в
виде проекций
в
виде проекций ![]() .
По условию второй базисный вектор должен содержать максимум оставшейся
информации, т.е. той, которая не вошла в
.
По условию второй базисный вектор должен содержать максимум оставшейся
информации, т.е. той, которая не вошла в ![]() . Для нахождения
. Для нахождения ![]() достаточно из векторов
достаточно из векторов ![]() вычесть информацию,
находящуюся в
вычесть информацию,
находящуюся в ![]() ,
получим:
,
получим:
![]() ,
, ![]() ,
, ![]() .
.
Используя теперь уже векторы ![]() , базисный вектор
, базисный вектор ![]() будет вычисляться по
аналогии с
будет вычисляться по
аналогии с ![]() по
формуле
по
формуле
 .
.
Следуя этому правилу, можем вычислить
полный набор базисных векторов ![]() , которые наилучшим образом будут
локализовывать информацию о сигналах
, которые наилучшим образом будут
локализовывать информацию о сигналах ![]() в проекциях. Благодаря этому будет
достигнут минимум ошибки восстановления (1) по неполному набору коэффициентов
разложения.
в проекциях. Благодаря этому будет
достигнут минимум ошибки восстановления (1) по неполному набору коэффициентов
разложения.
Полученный
алгоритм вычисления векторов ![]() соответствует алгоритму вычисления
собственных векторов матрицы
соответствует алгоритму вычисления
собственных векторов матрицы 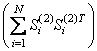 . Следовательно, можно заключить, что
наилучшая локализация сигналов достигается в пространстве собственных векторов,
вычисленных на основе суммарной матрицы автокорреляции набора векторов
. Следовательно, можно заключить, что
наилучшая локализация сигналов достигается в пространстве собственных векторов,
вычисленных на основе суммарной матрицы автокорреляции набора векторов ![]() .
.
Следует также
отметить, что при ![]() матрица
матрица
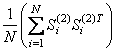 переходит
в автоковариационную матрицу векторов
переходит
в автоковариационную матрицу векторов ![]() . Это значит, что если известна
автокорреляционная матрица изображений, то оптимальное преобразование будет
определяться собственными векторами этой матрицы.
. Это значит, что если известна
автокорреляционная матрица изображений, то оптимальное преобразование будет
определяться собственными векторами этой матрицы.
Учитывая, что базисные векторы преобразования КЛ вычисляются исходя из статистических свойств кодируемых изображений, то в конкретном методе сжатия эти векторы следует записывать в сжатый файл для использования декодером. Кроме того, не существует быстрого алгоритма вычисления этих векторов. Все эти факты делают метод КЛ сугубо теоретическим без реальных приложений. В связи с этим возникает проблема поиска преобразования, которое обладало бы малой вычислительной сложностью и давало бы результаты преобразования близкие к преобразованию Карунена-Лоэва. Этим условиям удовлетворяет преобразование Фурье.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- 1. Коды Хаффмана
- 2. Адаптивные коды Хаффмана
- 3. Арифметическое кодирование
- 4. Алгоритм RLE
- 5. Алгоритм LZW
- 6. LZW в GIF
- 7. Цветовые пространства
- 8. Сжатие изображений. Основные понятия
- 9. Критерий визуального восприятия
- 10. Среднеквадратичный критерий
- 11. PSNR
- 12. ДИКМ и JPEG-LS
- 13. Иерархическая сеточная интерполяция
- 14. Преобразование Карунена-Лоэва
- 15. Стандарт сжатия JPEG
- 16. Квантование
- 17. Стандарт JPEG2000
- 18. Особенности сжатия в алгоритме SPIHT
- 19. Сжатие изображений с использованием СИФ
- 20. Основы видеокодирования
- 21. Нахождение векторов движения
- 22. Кодирование векторов движения
- 23. Методы подоптимального поиска векторов движения
