| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Адаптивные коды Хаффмана
Работа рассмотренного выше алгоритма предполагает, что нам известны частоты появления символов. Для этого обычно просматривают кодируемую последовательность и подсчитывают число появлений того или иного символа, затем строят коды Хаффмана, а потом кодируют заданную последовательность. Такой подход имеет два недостатка: во-первых, приходится дважды просматривать кодируемую последовательность, что приводит к снижению скорости работы алгоритма, и, во-вторых, найденные частоты необходимо передавать декодеру для корректного декодирования данных. Поэтому на практике применяют другой метод формирования кодов переменной длины, который позволяет «на лету», по мере кодирования данных уточнять коды Хаффмана. В этом случае нет необходимости дважды просматривать последовательность и передавать коды приемной стороне, но за это приходится платить несколько худшим качеством сжатия. Такой алгоритм, например, лежит в основе программы compact операционной системы UNIX.
Основная идея адаптивного кодирования заключается в том, что компрессор и декомпрессор начинают работать с «пустого» дерева Хаффмана, а потом модифицируют его по мере чтения и обработки символов. Соответственно, и кодер и декодер должны модифицировать дерево одинаково, чтобы все время использовать один и тот же код, который может меняться по ходу процесса. Итак, в начале кодер строит пустое дерево Хаффмана, т.е. никакому символу коды еще не присвоены. Поэтому первый символ просто записывается в выходной поток в незакодированной форме, что обычно соответствует 8 битному коду ASCII. Затем, этот символ помещается в дерево и ему присваивается код, например, 0. После этого кодируется следующий символ во входном потоке, и если этот символ встретился впервые, то он также записывается в выходной поток в виде 8 битного ASCII символа, и помещается в дерево Хаффмана, где ему присваивается определенный код в соответствии с его текущей частотой появления, равной 1. По мере того как поступают символы на вход кодера, происходит подсчет числа их появления и их количества и в соответствии с этой информацией выполняется перестройка дерева Хаффмана. Но здесь есть один нюанс: как отличить 8 битный ASCII символ от кода переменной длины в момент декодирования последовательности? Чтобы разрешить эту коллизию используют специальный esc (escape) символ, который показывает, что за ним следует незакодированный символ. Соответственно код самого esc символа должен находиться в дереве Хаффмана и будет меняться каждый раз по мере кодирования информации (перестройки дерева).
Рассмотрим пример реализации адаптивных кодов Хаффмана на последовательности символов AFFAADB. Так как вначале кодирования дерево Хаффмана пустое, то в выходной поток записывается 8-битовый код символа A (01000001), который затем добавляется в дерево Хаффмана (рис. 1, а). Следующий символ входного потока F также отсутствует в дереве Хаффмана, поэтому он записывается в выходной поток как код ASCII-символа, но перед ним ставится еще и esc-символ (рис. 1, б). Следующий, третий символ, снова F и для него имеется код в дереве Хаффмана, поэтому этот код записывается в выходной поток, счетчик для символа F увеличивается на единицу и становится равный двум и дерево Хаффмана принимает вид (рис. 1, в). Четвертый символ входного потока А также имеется в дереве Хаффмана, поэтому его код заносится в выходной поток, а счетчик принимает значение 2 (рис. 1, г). Аналогичные действия выполняются и при считывании следующего символа А (рис. 1, д).
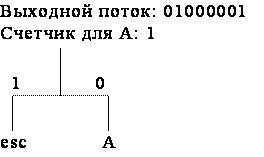
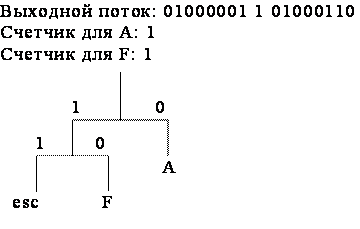
а) б)
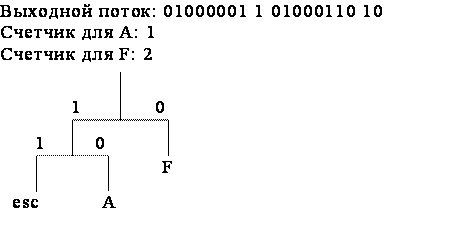
в)
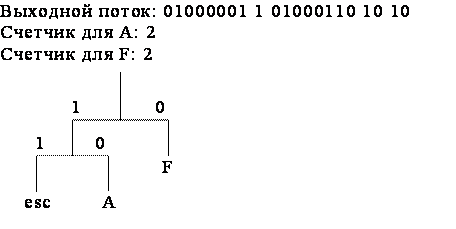
г)
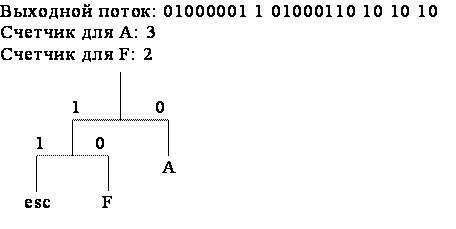
д)
Следующий символ D является новым, поэтому он должен быть записан в выходной поток как ASCII-символ, перед которым следует поставить esc-символ (рис. 1, е). Здесь в дереве Хаффмана появляется третий уровень, т.к. сумма счетчиков для esc-символа и D равна 1 (счетчик esc всегда 0) и это меньше суммы значений счетчиков F и А. Наконец, последний символ B записывается в незакодированном виде в выходной поток и добавляется в дерево Хаффмана (рис. 1, ж).

е)
 ж)
ж)
В результате проведенного кодирования выходной поток составил 44 бит вместо 56, что соответствует сжатию в 1,27 раза. При кодировании более длинных последовательностей это значение будет увеличиваться, т.к. дерево Хаффмана будет содержать все больше и больше символов, которые будут представлены в выходном потоке как коды переменной длины, а не парами esc и ASCII символов.
Декодер при восстановлении исходной последовательности работает подобно кодеру, т.е. он также последовательно строит дерево Хаффмана по мере декодирования последовательности, что позволяет корректно определять исходные символы.
Адаптивное кодирование Хаффмана имеет ряд особенностей при своей работе. Первая связана с хранением значений счетчиков символов, при кодировании длинных последовательностей. Дело в том, что языки высокого уровня, обычно, оперируют с числами максимум в 32 бит, в которых можно записывать числа от 0 до 4294967296, т.е. можно работать с файлами размером 4Гб. Но иногда этих значений недостаточно и приходится вырабатывать дополнительные меры по предотвращению переполнения счетчиков символов. Вторая особенность связана с постоянным перестроением дерева Хаффмана, что влияет на скорость работы алгоритма. Вместе с тем можно заметить, что при считывании очередного символа из входного потока, дерево Хаффмана может остаться прежним и его перестраивать не имеет смысла. Это бывает, когда новое значение счетчика символа не влияет на его местоположении в дереве Хаффмана. Следовательно, при кодировании и декодировании необходимо определять: нужно или нет пересчитывать дерево Хаффмана и в зависимости от результата выполнять нужные действия. Вот две основные особенности работы адаптивного алгоритма кодирования Хаффмана, но, несмотря на указанные сложности, он часто применяется на практике, например, в известном протоколе V.32 передачи данных по модему со скоростью 14400 бод.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- 1. Коды Хаффмана
- 2. Адаптивные коды Хаффмана
- 3. Арифметическое кодирование
- 4. Алгоритм RLE
- 5. Алгоритм LZW
- 6. LZW в GIF
- 7. Цветовые пространства
- 8. Сжатие изображений. Основные понятия
- 9. Критерий визуального восприятия
- 10. Среднеквадратичный критерий
- 11. PSNR
- 12. ДИКМ и JPEG-LS
- 13. Иерархическая сеточная интерполяция
- 14. Преобразование Карунена-Лоэва
- 15. Стандарт сжатия JPEG
- 16. Квантование
- 17. Стандарт JPEG2000
- 18. Особенности сжатия в алгоритме SPIHT
- 19. Сжатие изображений с использованием СИФ
- 20. Основы видеокодирования
- 21. Нахождение векторов движения
- 22. Кодирование векторов движения
- 23. Методы подоптимального поиска векторов движения
