| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
Устанавливаемая в этом параграфе формула замены переменной является одним из важнейших средств вычисления  -кратного интеграла.
-кратного интеграла.
Предположим, что функция  интегрируема в некоторой замкнутой, ограниченной кубируемой области D в пространстве
интегрируема в некоторой замкнутой, ограниченной кубируемой области D в пространстве  Предположим, далее, что от переменных
Предположим, далее, что от переменных  мы переходим к переменным
мы переходим к переменным  т. е. совершаем преобразование
т. е. совершаем преобразование

которое кратко можно записать в виде

понимая под у точку  -мерного пространства
-мерного пространства  под х точку
под х точку  -мерного пространства
-мерного пространства  а под
а под  совокупность
совокупность  функций
функций 
Обозначим через D ту область в  которая при преобразовании (3.21) или (3.21) переводится в D, т. е. положим
которая при преобразовании (3.21) или (3.21) переводится в D, т. е. положим  При этом мы всегда будем требовать, чтобы преобразование (3.21) или
При этом мы всегда будем требовать, чтобы преобразование (3.21) или  допускало обратное, так что
допускало обратное, так что 
Докажем, что если функции (3.21) имеют в области D непрерывные частные производные первого порядка и если в этой области D отличен от нуля якобиан (см. § 2 гл. 14 ч. 1).

то для  -кратного интеграла от функции
-кратного интеграла от функции  по области D справедлива следующая формула замены переменных.
по области D справедлива следующая формула замены переменных.

которая в подробной записи принимает следующий вид:

Точнее, мы докажем следующую основную теорему.
Теорема 3.8. Если преобразование (3.21) переводит область D в D и является взаимно однозначным и если функции (3.21) имеют в области D непрерывные частные производные первого порядка по всем переменным и отличный от нуля якобиан (3.22), то для каждой интегрируемой в D функции  справедлива формула замены переменных (3.23).
справедлива формула замены переменных (3.23).
Отметим, что при условиях теоремы 3.8 существует преобразование  обратное преобразованию
обратное преобразованию
Доказательству теоремы 3.8 предпошлем семь лемм. Сначала дадим обоснование формулы (3.23) для случая, когда преобразование (3.21) является линейным (леммы 1—4), а затем сведем к этому случаю общее преобразование (3.21) (леммы 5-7).
Лемма 1. Если преобразование  является суперпозицией (или произведением) двух преобразований
является суперпозицией (или произведением) двух преобразований  причем все участвующие в этих преобразованиях функции имеют непрерывные частные производные первого порядка, то якобиан
причем все участвующие в этих преобразованиях функции имеют непрерывные частные производные первого порядка, то якобиан  взятый в точке
взятый в точке  равен произведению якобиана
равен произведению якобиана  взятого в точке х, на якобиан
взятого в точке х, на якобиан  , взятый в точке
, взятый в точке  где
где  т. е.
т. е.

или в подробной записи:

Доказательство леммы 1. Заметим, что для любых  элемент
элемент  стоящий на пересечении
стоящий на пересечении  строки и
строки и  столбца якобиана
столбца якобиана  и взятый в точке
и взятый в точке  по правилу дифференцирования сложной функции равен
по правилу дифференцирования сложной функции равен

где 
Но по правилу перемножения определителей равенство (3.25) и означает, что якобиан  , взятый в точке х, равен произведению якобиана взятого в точке х, на якобиан
, взятый в точке х, равен произведению якобиана взятого в точке х, на якобиан  взятый в точке
взятый в точке  . Лемма 1 доказана.
. Лемма 1 доказана.
Напомним, что линейным преобразованием координат называется преобразование вида

где  — произвольные постоянные числа.
— произвольные постоянные числа.
Для линейного преобразования (3.26) якобиан  падает с определителем матрицы этого преобразования
падает с определителем матрицы этого преобразования  т. е.
т. е.

Если этот определитель отличен от нуля, то линейное преобразование (3.26) называется невырожденным. В этом случае существует обратное преобразование, также линейное и невырожденное, и уравнения (3.26) можно разрешить относительно  Кратко будем обозначать линейное преобразование (3.26) символом
Кратко будем обозначать линейное преобразование (3.26) символом  а обратное ему преобразование символом
а обратное ему преобразование символом 
Основной целью следующих трех лемм является доказательство того факта, что для невырожденного линейного преобразования (3.26) и для каждой непрерывной функции  справедлива формула замены переменных (3.23), которую с учетом соотношения (3.27) можно представить в следующем виде:
справедлива формула замены переменных (3.23), которую с учетом соотношения (3.27) можно представить в следующем виде:

где 
Сначала рассмотрим два линейных преобразования частного вида:
1) линейное преобразование  заключающееся в том, что к
заключающееся в том, что к  координате добавляется
координате добавляется  координата, а все остальные координаты при этом сохраняются:
координата, а все остальные координаты при этом сохраняются:

или  (краткая запись);
(краткая запись);
2) линейное преобразование  заключающееся в том, что
заключающееся в том, что  координата умножается на число
координата умножается на число  а все остальные координаты при этом не меняются:
а все остальные координаты при этом не меняются:

или  (краткая запись).
(краткая запись).
Легко видеть, что

поэтому преобразования  и
и  невырожденные.
невырожденные.
Лемма 2. Для преобразований  и
и  при любой непрерывной в области D функции
при любой непрерывной в области D функции  справедлива формула замены переменных (3.28).
справедлива формула замены переменных (3.28).
Доказательство леммы 2. Пусть  —
—  -мерный прямоугольный параллелепипед, содержащий D, функция
-мерный прямоугольный параллелепипед, содержащий D, функция  имеет вид
имеет вид

Достаточно доказать, что

где символом Т обозначено одно из преобразований  или
или  Заметим, что если
Заметим, что если  — прямоугольный параллелепипед
— прямоугольный параллелепипед  то
то  — снова прямоугольный параллелепипед
— снова прямоугольный параллелепипед

а  — кубируемая область
— кубируемая область

На основании формулы повторного интегрирования (3.18)

Применяя к однократному интегралу по переменной  формулу замены переменной
формулу замены переменной  для случая преобразования
для случая преобразования  для случая преобразования
для случая преобразования  (см § 5 гл. 9 ч. 1), получим
(см § 5 гл. 9 ч. 1), получим
а) для случая преобразования 

б) для случая преобразования 

Подставим (3.30) или (3.30) в (3.29); затем, воспользовавшись формулой повторного интегрирования (3.18) и тем, что

а также полагая  при
при  придем к равенству (3.28). Лемма 2 доказана.
придем к равенству (3.28). Лемма 2 доказана.
Лемма 3. Всякое невырожденное линейное преобразование (3.26) представимо в виде суперпозиции конечного числа Преобразований вида  и
и  при
при 
Доказательство леммы 3. Разобьем доказательство на три этапа.
1. Покажем, что линейное преобразование Г, заключающееся в перестановке местами  координат (при сохранении всех остальных координат), представимо в виде суперпозиции шести преобразований типа
координат (при сохранении всех остальных координат), представимо в виде суперпозиции шести преобразований типа 
В самом деле, сохраняя при записи  только
только  координаты (остальные не меняются), можем записать:
координаты (остальные не меняются), можем записать:

2) Отметим, что путем конечного числа перестановок местами двух строк или двух столбцов (т. е. путем конечного числа преобразований типа Т) мы можем привести любое линейное невырожденное преобразование к линейному преобразованию с матрицей  которой отличны от нуля все главные миноры, т. е. определители
которой отличны от нуля все главные миноры, т. е. определители

3) Остается доказать, что линейное преобразование с отличными от нуля главными мннорами можно представить в виде конечного числа преобразований типа  Докажем это по индукции.
Докажем это по индукции.
Для  рассмотрим преобразование Т с матрицей
рассмотрим преобразование Т с матрицей

Преобразование переводит  утверждение справедливо. Рассмотрим теперь преобразование Т с матрицей
утверждение справедливо. Рассмотрим теперь преобразование Т с матрицей

Предположим, что это преобразование Т можно представить в виде конечного числа преобразований типа  т. е. что существует конечное число преобразований вида
т. е. что существует конечное число преобразований вида  переводящие
переводящие  в
в

Для завершения индукции достаточно доказать, что путем суперпозиции конечного числа преобразований типа 
можно привести последовательность координат (3.31) к виду 

т. e. представить преобразование T с матрицей

в виде суперпозиции конечного числа преобразований вида; 
Для доказательства этого, сначала для каждого номера.  для которого элемент
для которого элемент  произведем преобразование, представимое суперпозицией трех преобразований:
произведем преобразование, представимое суперпозицией трех преобразований:  (для тех
(для тех  , для которых
, для которых  этого преобразования не производим). Суперпозиция всех указанных троек преобразований для всех
этого преобразования не производим). Суперпозиция всех указанных троек преобразований для всех  переведет элемент (3.31) в
переведет элемент (3.31) в

Далее заметим, что поскольку минор А. матрицы (3.33) отличен от нуля, то отличен от нуля и равный ему определитель, матрицы

По теореме о базисном миноре существуют числа  линейная комбинация с которыми строк матрицы (3.35) равная
линейная комбинация с которыми строк матрицы (3.35) равная

т. е. равна первым  элементам
элементам  строки матрицы (3.33). Это означает, что если мы для каждого
строки матрицы (3.33). Это означает, что если мы для каждого  для которого
для которого  произведем преобразование, представимое суперпозицией. трех преобразований:
произведем преобразование, представимое суперпозицией. трех преобразований:  (для тех
(для тех  для которых
для которых  соответствующую тройку преобразований:
соответствующую тройку преобразований:
не производим), то суперпозиция  и всех произведенных троек преобразований переведет элемент (3.34) в (3.32). Индукция завершена. Лемма 3 доказана.
и всех произведенных троек преобразований переведет элемент (3.34) в (3.32). Индукция завершена. Лемма 3 доказана.
Лемма 4. Для любого невырожденного линейного преобразования (3.26) и любой непрерывной в области D функции  справедлива формула замены переменных (3.28).
справедлива формула замены переменных (3.28).
В самом деле, формула (3.28) справедлива для каждого из преобразований вида  (лемма 2), но любое линейное невырожденное преобразование представимо в виде суперпозиции конечного числа таких преобразований (лемма 3), причем якобиан этой суперпозиции преобразований равен произведению якобианов (лемма 1).
(лемма 2), но любое линейное невырожденное преобразование представимо в виде суперпозиции конечного числа таких преобразований (лемма 3), причем якобиан этой суперпозиции преобразований равен произведению якобианов (лемма 1).
Следствие из леммы 4. Если  — произвольная кубируемая область в
— произвольная кубируемая область в  — произвольное невырожденное линейное преобразование, то
— произвольное невырожденное линейное преобразование, то  -мерный объем
-мерный объем  области
области  и
и  -мерный объем
-мерный объем  ее образа
ее образа  связаны равенством
связаны равенством

Для доказательства этого утверждения достаточно в формуле (3.28) взять  в области
в области 
Пусть теперь дано любое преобразование  и выполнены условия теоремы 3.8. При этом оба интеграла в (3.23) существуют, если только
и выполнены условия теоремы 3.8. При этом оба интеграла в (3.23) существуют, если только  — кубируемая область, так что нам нужно доказать кубируемость D и равенство интегралов в (3.23).
— кубируемая область, так что нам нужно доказать кубируемость D и равенство интегралов в (3.23).
Пусть  — элементы
— элементы

матрицы Якоби, взятые в точке  саму матрицу Якоби
саму матрицу Якоби  обозначим символом
обозначим символом  Назовем нормой точки
Назовем нормой точки  величину
величину  Назовем нормой матрицы
Назовем нормой матрицы  величину
величину

Кроме того, для единичной матрицы 
Лемма 5. Если выполнены условия теоремы 3.8 и С —  -мерный координатный куб, принадлежащий области D, то
-мерный координатный куб, принадлежащий области D, то  -мерные объемы куба С и его образа
-мерные объемы куба С и его образа  связаны неравенством
связаны неравенством

Доказательство леммы 5. Пусть С —  -мерный куб с центром в точке
-мерный куб с центром в точке  и с ребром
и с ребром  Тогда куб С. можно определить неравенством
Тогда куб С. можно определить неравенством

В силу формулы Тейлора для функции  переменных
переменных  (см. п. 3 § 5 гл. 12 ч. 1) найдется число 0; из интервала
(см. п. 3 § 5 гл. 12 ч. 1) найдется число 0; из интервала  такое, что
такое, что

Отсюда и из соотношения (3.37) заключаем, что

Полагая  получим из (3.40) и (3.39):
получим из (3.40) и (3.39):

Таким образом, если точка находится в кубе С с ребром  и с центром в точке
и с центром в точке  то образ
то образ  точки находится в кубе с центром в точке у и с ребром
точки находится в кубе с центром в точке у и с ребром  Поэтому множество
Поэтому множество  кубируемо и
кубируемо и

Лемма 5 доказана.
Следствие 1 из леммы 5. Если выполнены условия теоремы 3.8 и область  кубируема, то и ее образ
кубируема, то и ее образ  кубируем. В частности, если D кубируема, то и
кубируем. В частности, если D кубируема, то и  кубируема.
кубируема.
Действительно, граница любого кубируемого множества  является множеством
является множеством  -мерного объема нуль, а такое множество согласно доказанному утверждению преобразуется в множество,
-мерного объема нуль, а такое множество согласно доказанному утверждению преобразуется в множество,  -мерный объем которого также равен нулю.
-мерный объем которого также равен нулю.
Кубируемость области  следует из того, что в условиях теоремы 3.8 для преобразования
следует из того, что в условиях теоремы 3.8 для преобразования  выполнены те же условия, что и для
выполнены те же условия, что и для 
Следствие 2 из леммы 5. Если функция  интегрируема в области
интегрируема в области  и выполнены условия теоремы 3.8, то
и выполнены условия теоремы 3.8, то  а потому и
а потому и  интегрируемы. в D.
интегрируемы. в D.
Лемма 6. Пусть выполнены все условия теоремы 3.8 и пусть  — произвольное кубируемое подмножество D, а
— произвольное кубируемое подмножество D, а  — его образ при преобразовании (3.21). Тогда для
— его образ при преобразовании (3.21). Тогда для  -мерного объема области
-мерного объема области  справедливо неравенство
справедливо неравенство

Доказательство леммы 6. Разобьем доказательство на два этапа.
1) Докажем, что для любого невырожденного линейного преобразования Т и для любого  -мерного куба
-мерного куба  справедливо неравенство
справедливо неравенство

В силу следствия из леммы 4 для любого кубируемого множества  и для линейного преобразования Т справедливо равенство (3.36). Положим
и для линейного преобразования Т справедливо равенство (3.36). Положим  тогда
тогда  и
и

Оценив правую часть (3.43) с помощью неравенства (3.38), в котором вместо преобразования возьмем суперпозицию преобразований  получим
получим

По лемме  ибо матрица Якоби линейного преобразования совпадает с матрицей этого преобразования. Но это и означает, что неравенство (3.44) может быть переписано в виде (3.42). Неравенство (3.42) доказано.
ибо матрица Якоби линейного преобразования совпадает с матрицей этого преобразования. Но это и означает, что неравенство (3.44) может быть переписано в виде (3.42). Неравенство (3.42) доказано.
2) Докажем теперь непосредственно неравенство (3.41). Покроем пространство  сеткой
сеткой  -мерных кубов с ребром
-мерных кубов с ребром  Пусть
Пусть  те кубы, которые целиком содержатся в
те кубы, которые целиком содержатся в  и пусть
и пусть 
В каждом кубе  фиксируем произвольную точку
фиксируем произвольную точку  и запишем для этого куба
и запишем для этого куба  неравенство (3.42), полагая при этом
неравенство (3.42), полагая при этом  Получим
Получим

Поскольку элементы матрицы Якоби  являются непрерывными функциями переменной х во всей области D, а следовательно, и равномерно непрерывными в D, то
являются непрерывными функциями переменной х во всей области D, а следовательно, и равномерно непрерывными в D, то  — равномерно непрерывная функция в
— равномерно непрерывная функция в  Отсюда заключаем,
Отсюда заключаем,
что функция  также равномерно непрерывна в
также равномерно непрерывна в  Учитывая, что
Учитывая, что  получаем, что для любого
получаем, что для любого  найдется
найдется  Такое, что для всех
Такое, что для всех  для которых
для которых  выполняется неравенство
выполняется неравенство  е. Таким образом, если выбрать
е. Таким образом, если выбрать  то
то  (для всех
(для всех  и оценку (3.45) можно записать в виде
и оценку (3.45) можно записать в виде

Суммируя последнее неравенство по всем  , получим
, получим

Из утверждения, сформулированного в конце § 4 этой главы, следует, что предел при  всей правой части (3.46) существует и равен
всей правой части (3.46) существует и равен  — произвольное число). Кроме того,
— произвольное число). Кроме того,  так что в пределе при 0 из неравенства (3.46) получается неравенство (3.41). Лемма 6 доказана.
так что в пределе при 0 из неравенства (3.46) получается неравенство (3.41). Лемма 6 доказана.
Лемма 7. Если выполнены все условия теоремы 3.8 и дополнительно предполагается, что функция  неотрицательна в D, то справедлива формула замены переменных (3.23).
неотрицательна в D, то справедлива формула замены переменных (3.23).
Доказательство леммы 7. Покроем пространство  сеткой
сеткой  -мерных кубов с ребром
-мерных кубов с ребром  и обозначим через
и обозначим через  те из этих кубов, которые целиком содержатся в
те из этих кубов, которые целиком содержатся в  . Пусть
. Пусть  . Для каждой области
. Для каждой области  запишем неравенство (3.41):
запишем неравенство (3.41):

Умножим обе части (3.47) на  где
где

и просуммируем полученные неравенства по всем  от 1 до
от 1 до 

По теореме о среднем значении

где  . Поэтому
. Поэтому

и неравенство (3.48) можно усилить:

В силу утверждения, сформулированного в конце § 4, левак часть (3.49) при  имеет предел, равный
имеет предел, равный  и поскольку
и поскольку  где
где  то в пределе при
то в пределе при  получается
получается

Меняя в этих рассуждениях ролями  рассматривая в D функцию
рассматривая в D функцию  и используя лемму 1 и теорему об определителе произведения двух матриц, получи» противоположное неравенство
и используя лемму 1 и теорему об определителе произведения двух матриц, получи» противоположное неравенство

Из (3.50) и (3.51) вытекает доказываемая формула замены переменных. Лемма 7 доказана.
Доказательство теоремы 3.8. Пусть  — произвольная интегрируемая по области D функция и выполнены все условия теоремы 3.8.
— произвольная интегрируемая по области D функция и выполнены все условия теоремы 3.8.
Из интегрируемости функции  в области D получаем, что существует постоянная
в области D получаем, что существует постоянная  такая, что
такая, что 
Для каждой из неотрицательных функций  теорема 3.8 справедлива (в силу леммы 7). На тогда из линейного свойства интеграла вытекает справедливость формулы (3.23) и для разности
теорема 3.8 справедлива (в силу леммы 7). На тогда из линейного свойства интеграла вытекает справедливость формулы (3.23) и для разности  Теорема 3.8 доказана.
Теорема 3.8 доказана.
Замечание 1. В условиях теоремы 3.8 можно допустить обращение в нуль якобиана (3.22) на некотором принадлежащем D множестве точек  имеющем
имеющем  -мерный объем нуль. В самом деле, множество
-мерный объем нуль. В самом деле, множество  лежит внутри элементарной фигуры С как угодно малого объема, причем согласно доказанному выше справедлива формула
лежит внутри элементарной фигуры С как угодно малого объема, причем согласно доказанному выше справедлива формула

Осуществляя в формуле (3.52) предельный переход по последовательности элементарных фигур  n-мерный объем
n-мерный объем  которых стремится к нулю, убедимся в справедливости формулы (3.23) и для рассматриваемого случая.
которых стремится к нулю, убедимся в справедливости формулы (3.23) и для рассматриваемого случая.
Замечание 2. Имеет место следующее утверждение, являющееся частным случаем так называемой теоремы Сарда.
Утверждение. Пусть  — замкнутая ограниченная аудируемая область в
— замкнутая ограниченная аудируемая область в  а функции (3.21) имеют в
а функции (3.21) имеют в  непрерывные частные производные первого порядка по всем переменным. Пусть
непрерывные частные производные первого порядка по всем переменным. Пусть  Тогда
Тогда  -мерный объем множества А равен нулю.
-мерный объем множества А равен нулю.
Это утверждение и замечание 1 позволяют освободиться в теореме 3.8 от требования необращения якобиана (3.22) в нуль в области D.
Замечание 3. Как показывает рассматриваемый ниже пример, требование взаимной однозначности преобразования  существенно даже в случае связной области и условия
существенно даже в случае связной области и условия  для всех
для всех 
Пример. Пусть  определено равенствами
определено равенствами

Тогда  . Легко подсчитать, что якобиан преобразования
. Легко подсчитать, что якобиан преобразования  не равен нулю для всех
не равен нулю для всех  . Сравним между собой интегралы в формуле (3.23) для
. Сравним между собой интегралы в формуле (3.23) для 

Таким образом, формула замены переменных не имеет места.
Замечание 4. В условиях теоремы 3.8 можно допустить неоднозначность преобразования  yа некотором принадлежащем D множестве
yа некотором принадлежащем D множестве  имеющем
имеющем  -мерный объем нуль.
-мерный объем нуль.
Доказательство этого факта полностью аналогично доказательству утверждения в замечании 1.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
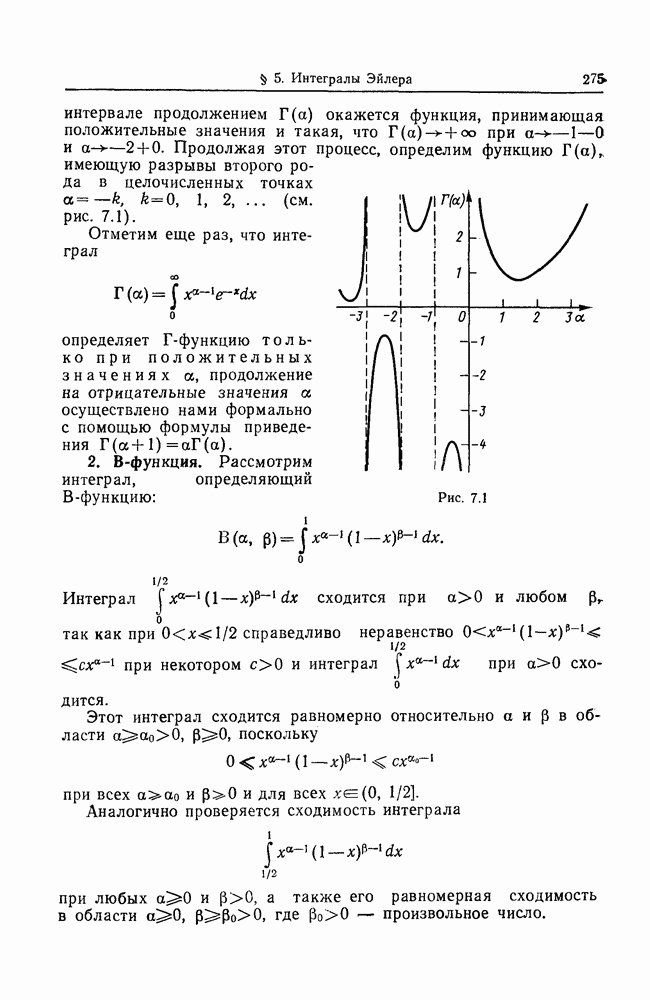
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
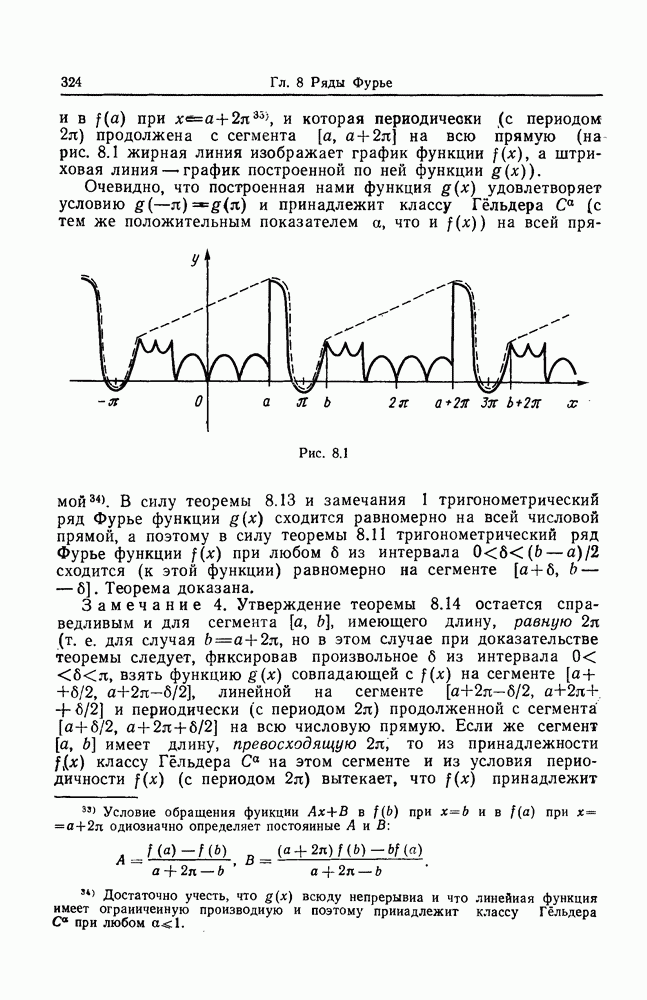
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ