| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.4. Лучшие границы для дерева поиска
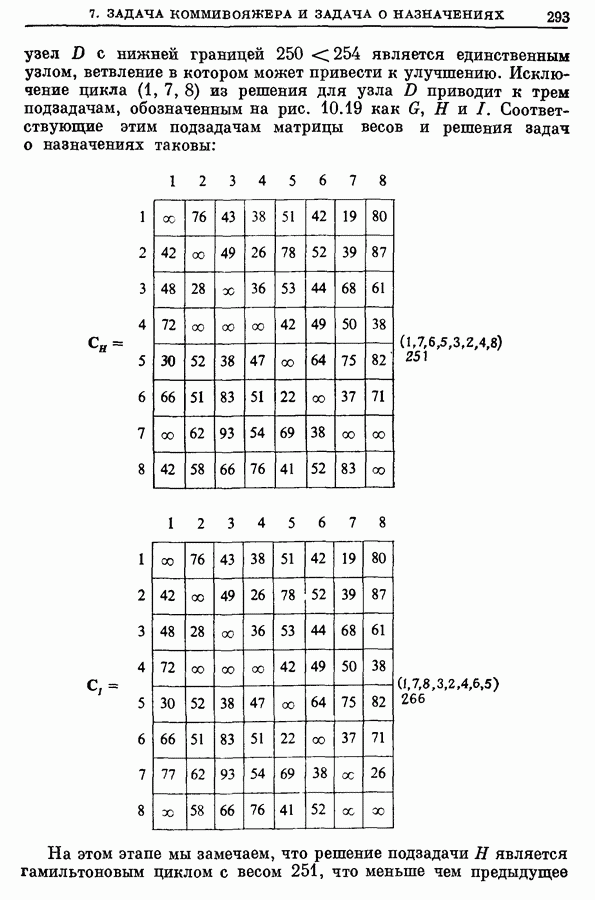
Мы описали в разд. 7.1 алгоритм поиска, в котором в качестве нижней границы в узле берется значение из решения соответствующей задачи о назначениях. На самом то деле совершенно очевидно, что метод исключения циклов остается неизменным независимо от того, какая нижняя граница используется для ограничения поиска. Но так как процесс ветвления в узле прекращается только тогда, когда или решение подзадачи, отвечающей этому узлу, является гамильтоновым циклом, или когда нижняя граница в узле превосходит значение полученного до этого наилучшего решения, то очевидно, что качество оценки границы оказывает заметное влияние на число ветвлений в дереве решений и, следовательно, на вычислительную эффективность метода. Целью настоящего раздела является описание метода получения нижней границы, вычисляемой по решению задачи о назначениях с небольшими дополнительными усилиями и являющейся более точной, чем ранее используемые границы. Пусть решение задачи о назначениях содержит некоторое число циклов, как это показано в качестве примера на рис. 10.20 (а). Пусть  цикл обозначается
цикл обозначается  и пусть число циклов равно
и пусть число циклов равно  (Мы будем использовать один и тот же символ
(Мы будем использовать один и тот же символ  как для обозначения цикла, так и для обозначения множества его вершин.)
как для обозначения цикла, так и для обозначения множества его вершин.)
Определим стягивание как замену цикла единственной вершиной. Полученный граф содержит  вершин
вершин  . В качестве матрицы весов нового графа берется
. В качестве матрицы весов нового графа берется  -матрица
-матрица  с элементами вида
с элементами вида

где  окончательная матрица относительных весов, полученная в конце решения задачи венгерским (например) методом (см. гл. 12).
окончательная матрица относительных весов, полученная в конце решения задачи венгерским (например) методом (см. гл. 12).

(кликните для просмотра скана)
На рис. 10.20 (а), например,

Теперь второе решение задачи о назначениях в случае задачи с матрицей  все еще может содержать циклы, в качестве вершин которых выступают предыдущие циклы. Рис. 10.20 (б) показывает один из возможных способов образования новых циклов
все еще может содержать циклы, в качестве вершин которых выступают предыдущие циклы. Рис. 10.20 (б) показывает один из возможных способов образования новых циклов  где
где  их общее число (на рис.
их общее число (на рис.  Эти циклы опять могут быть стянуты в вершины и дать новую задачу с новой матрицей весов
Эти циклы опять могут быть стянуты в вершины и дать новую задачу с новой матрицей весов  вычисленной так же, как и в (10.19), т. е.
вычисленной так же, как и в (10.19), т. е.

где множества  являются объединениями всех множеств
являются объединениями всех множеств  образующих «частные» циклы, и где
образующих «частные» циклы, и где  матрица относительных весов, полученная в конце решения второй задачи о назначениях.
матрица относительных весов, полученная в конце решения второй задачи о назначениях.
Решение задачи о назначениях для нового, дважды стянутого, графа все еще может содержать циклы, и итерационный процесс решения — стягивания можно продолжать до тех пор, пока задача не сведется к единственной вершине.
Определим компрессию как преобразование матрицы, не удовлетворяющей аксиоме треугольника в метрическом пространстве, в матрицу, удовлетворяющую этой аксиоме. Таким образом, для компрессии матрицы нужно заменить каждый элемент  для которого
для которого

элементом  и продолжать эту замену до тех пор, пока для всякого к не будут справедливы неравенства
и продолжать эту замену до тех пор, пока для всякого к не будут справедливы неравенства 
Теорема 5. Сумма значений решений задач о назначениях, полученных во время процесса «решение — стягивание — компрессия» осуществляемого вплоть до момента, когда «стянутая» задача будет содержать единственную точку), является точной нижней границей для задачи коммивояжера.
Доказательство. В гл. 12 показано, что элемент  в матрице относительных весов, полученной в конце решения задачи о назначениях, дает нижнюю границу для дополнительного веса, который получается из-за включения дуги
в матрице относительных весов, полученной в конце решения задачи о назначениях, дает нижнюю границу для дополнительного веса, который получается из-за включения дуги  в решение.
в решение.
Рассмотрим цикл  полученный] в конце решения первой задачи о назначениях. Любой гамильтонов цикл, проходящий
полученный] в конце решения первой задачи о назначениях. Любой гамильтонов цикл, проходящий
через все  вершин, будет иметь по крайней мере две дуги (одну направленную внутрь цикла
вершин, будет иметь по крайней мере две дуги (одну направленную внутрь цикла  другую — наружу), инцидентные вершинам, не лежащим в
другую — наружу), инцидентные вершинам, не лежащим в  и «приходящие» в одну или более вершин из
и «приходящие» в одну или более вершин из  Число таких дуг будет, очевидно, четным.
Число таких дуг будет, очевидно, четным.

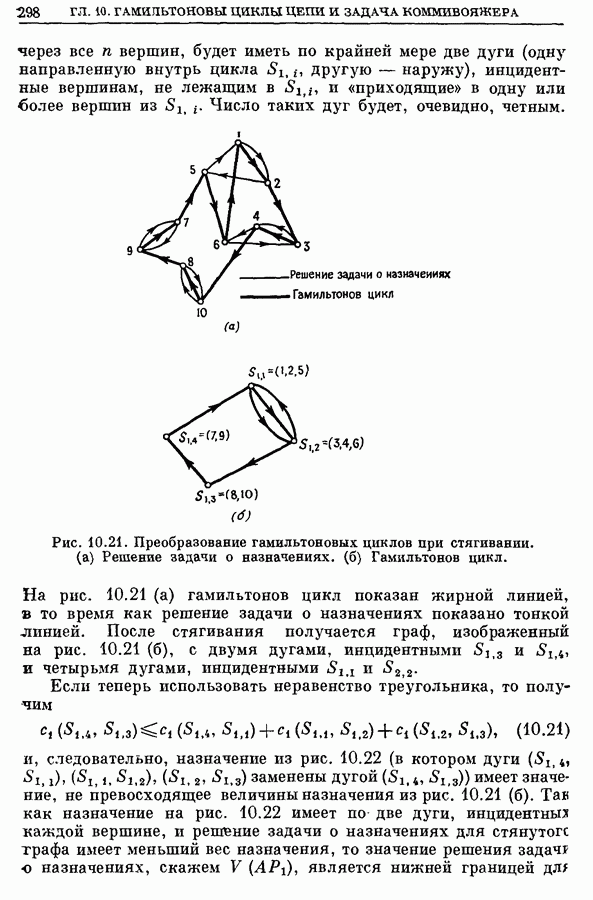
Рис. 10.21. Преобразование гамильтоновых циклов при стягивании. (а) Решение задачи о назначениях, (б) Гамильтонов цикл.
На рис. 10.21 (а) гамильтонов цикл показан жирной линией, в то время как решение задачи о назначениях показано тонкой линией. После стягивания получается граф, изображенный на рис. 10.21 (б), с двумя дугами, инцидентными  и
и  и четырьмя дугами, инцидентными
и четырьмя дугами, инцидентными 
Если теперь использовать неравенство треугольника, то получим

и, следовательно, назначение из рис. 10.22 (в котором дуги  заменены дугой
заменены дугой  имеет значение, не превосходящее величины назначения из рис.
имеет значение, не превосходящее величины назначения из рис.  Так как назначение на рис. 10.22 имеет по две дуги, инцидентны? каждой вершине, и решение задачи о назначениях для стянутогс графа имеет меньший вес назначения, то значение решения задачи о назначениях, скажем
Так как назначение на рис. 10.22 имеет по две дуги, инцидентны? каждой вершине, и решение задачи о назначениях для стянутогс графа имеет меньший вес назначения, то значение решения задачи о назначениях, скажем  является нижней границей для
является нижней границей для
величины назначения на рис.  для значения приращения веса, которое было бы необходимо для объединения вместе различных циклов.
для значения приращения веса, которое было бы необходимо для объединения вместе различных циклов.

Рис. 10.22. Назначение, соответствующее рис. 10.21 (б), с двумя дугами в каждой вершине.
Очевидно, что поскольку граф назначения, полученный с помощью любого гамильтонова цикла, содержит после первого стягивания (т. е. в случае назначения, соответствующего рис. 10.21 (б)) эйлеров цикл, то его всегда можно преобразовать в граф с меньшим (или равным) весом, в котором каждой вершине индицентны только две дуги. Это делается с помощью замены цепи, образованной дугами, ведущими из одной вершины в другую, единственной дугой между этими вершинами (как было продемонстрировано выше).
Если, с другой стороны, матрица относительных весов  не удовлетворяет условию треугольника, то соотношение (10.21) может быть не выполнено. В этом случае матрица
не удовлетворяет условию треугольника, то соотношение (10.21) может быть не выполнено. В этом случае матрица  должна быть сначала подвергнута компрессии. Значение решения задачи о назначениях с компрессированной матрицей следует взять тогда в качестве нижней границы величины приращения веса, что необходимо при объединении циклов. Это так, ибо компрессия матрицы может лишь уменьшить или оставить без изменения вес любого назначения для первоначальной матрицы.
должна быть сначала подвергнута компрессии. Значение решения задачи о назначениях с компрессированной матрицей следует взять тогда в качестве нижней границы величины приращения веса, что необходимо при объединении циклов. Это так, ибо компрессия матрицы может лишь уменьшить или оставить без изменения вес любого назначения для первоначальной матрицы.
Аналогично  вес решения задачи о назначениях после второго стягивания является нижней границей веса связываемых циклов, получаемых при этом стягивании, и так далее для третьего, четвертого и остальных стягиваний. Поэтому величина
вес решения задачи о назначениях после второго стягивания является нижней границей веса связываемых циклов, получаемых при этом стягивании, и так далее для третьего, четвертого и остальных стягиваний. Поэтому величина

где  - значение начального решения задачи о назначениях с начальной матрицей С, а к — число стягиваний, необходимых для преобразования графа задачи в единственную вершину, равное весу решения задачи коммивояжера. Теорема доказана.
- значение начального решения задачи о назначениях с начальной матрицей С, а к — число стягиваний, необходимых для преобразования графа задачи в единственную вершину, равное весу решения задачи коммивояжера. Теорема доказана.
Вообще здесь следует отметить, что даже если начальная матрица весов удовлетворяет условию треугольника, то последующие матрицы относительных весов могут не удовлетворять этому условию и на каком-то этапе может потребоваться компрессия.
Пример вычисления границы
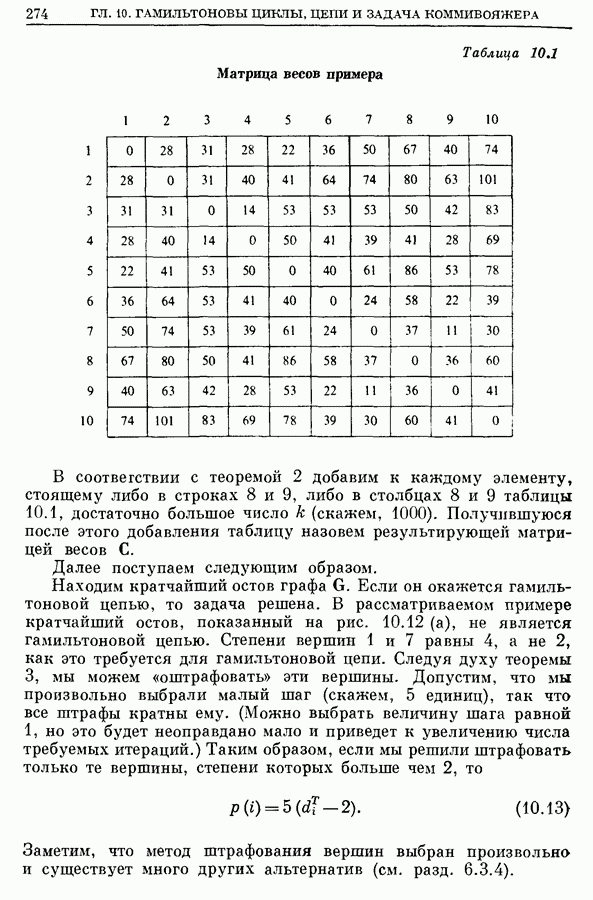
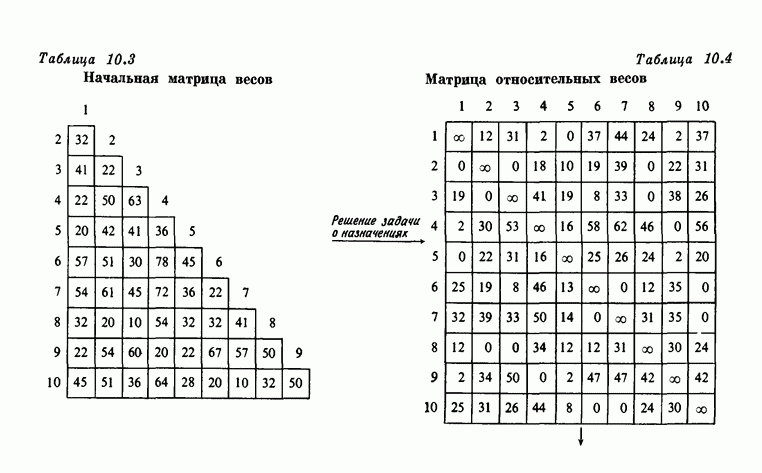
Рассмотрим задачу коммивояжера с 10 вершинами, матрица весов которой симметрична и приведена в табл. 10.3.
Решение начальной задачи о назначениях дает величину  Результирующая матрица относительных весов дана в табл. 10.4, а решение дается графом на рис. 10.23.
Результирующая матрица относительных весов дана в табл. 10.4, а решение дается графом на рис. 10.23.

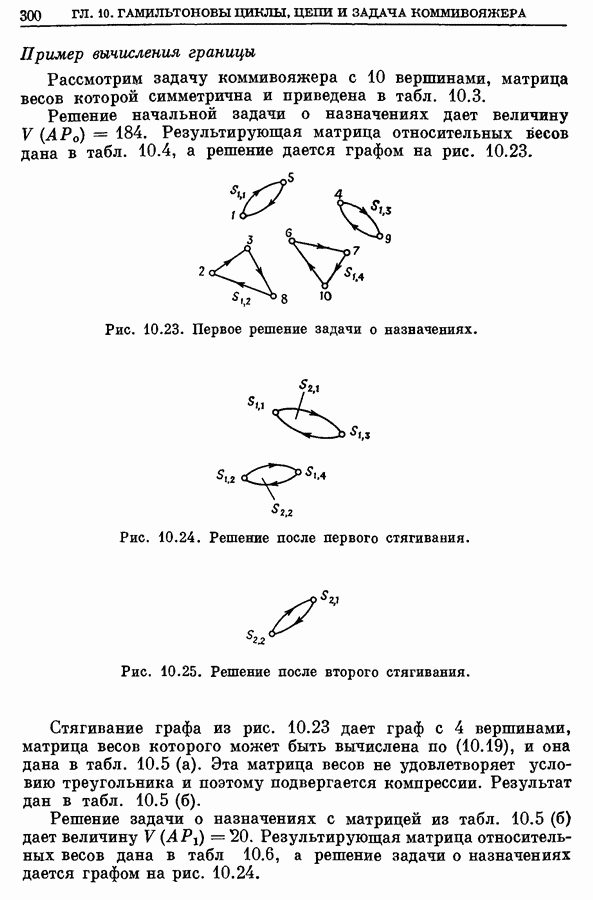
Рис. 10.23. Первое решение задачи о назначениях.

Рис. 10.24. Решение после первого стягивания.

Рис. 10.25. Решение после второго стягивания.
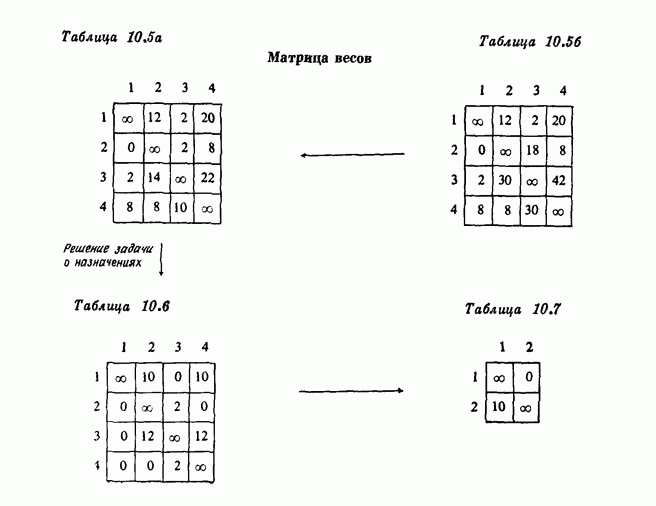
Стягивание графа из рис. 10.23 дает граф с 4 вершинами, матрица весов которого может быть вычислена по (10.19), и она дана в табл. 10.5 (а). Эта матрица весов не удовлетворяет условию треугольника и поэтому подвергается компрессии. Результат дан в табл. 10.5 (б).
Решение задачи о назначениях с матрицей из табл. 10.5 (б) дает величину  Результирующая матрица относительных весов дана в табл 10.6, а решение задачи о назначениях дается графом на рис. 10.24.
Результирующая матрица относительных весов дана в табл 10.6, а решение задачи о назначениях дается графом на рис. 10.24.
(см. скан)
(см. скан)
Стягивание графа из рис. 10.24 дает граф с 2 вершинами, матрица весов которого (вычисленная по (10.20)) дана в табл. 10.7 (Эта тривиальная (2 X 2)-матрица не должна подвергаться Компрессии, так как она удовлетворяет условию треугольника.)
Решение задачи о назначениях с матрицей из табл. 10.7 имеет значение  а само решение дается графом на рис. 10.25, который переходит в единственную вершину после следующего сжатия. Таким образом, нижняя граница значения для задачи коммивояжера с матрицей из табл. 10.3 равна
а само решение дается графом на рис. 10.25, который переходит в единственную вершину после следующего сжатия. Таким образом, нижняя граница значения для задачи коммивояжера с матрицей из табл. 10.3 равна

Сравнив ее со значением оптимального решения задачи коммивояжера, равного 216, получим ошибку в  в то время как использование в качестве нижней границы величины
в то время как использование в качестве нижней границы величины  дает ошибку в
дает ошибку в  Хотя настоящая нижняя граница и не является в общем случае такой близкой, как в приведенном примере, но результаты [8] показывают, что эта граница в среднем значительно лучше, чем
Хотя настоящая нижняя граница и не является в общем случае такой близкой, как в приведенном примере, но результаты [8] показывают, что эта граница в среднем значительно лучше, чем 
Время вычисления границы в задаче коммивояжера в среднем только на 9% больше времени, требуемого для решения задачи о назначениях с той же самой матрицей весов. Время вычисления при решении задачи о назначениях с использованием венгерского метода оценивается как  (см. гл. 12), где k — некоторая постоянная,
(см. гл. 12), где k — некоторая постоянная,  порядок матрицы. Самый плохой случай при вычислении границы (что касается времени вычисления) возникает тогда, когда все циклы при каждом стягивании содержат только по две вершины. В этом случае общее время вычисления при решении задачи о назначениях таково:
порядок матрицы. Самый плохой случай при вычислении границы (что касается времени вычисления) возникает тогда, когда все циклы при каждом стягивании содержат только по две вершины. В этом случае общее время вычисления при решении задачи о назначениях таково:

Из (10.23) видно, что в худшем случае требуемое время для вычисления предложенной границы в задаче коммивояжера только на  больше, чем время, требуемое для решения задачи о назначениях того же самого размера. (Здесь следует заметить, что время, необходимое для выполнения той части процесса, которая связана с «стягиванием» и «компрессией», оценивается как
больше, чем время, требуемое для решения задачи о назначениях того же самого размера. (Здесь следует заметить, что время, необходимое для выполнения той части процесса, которая связана с «стягиванием» и «компрессией», оценивается как 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
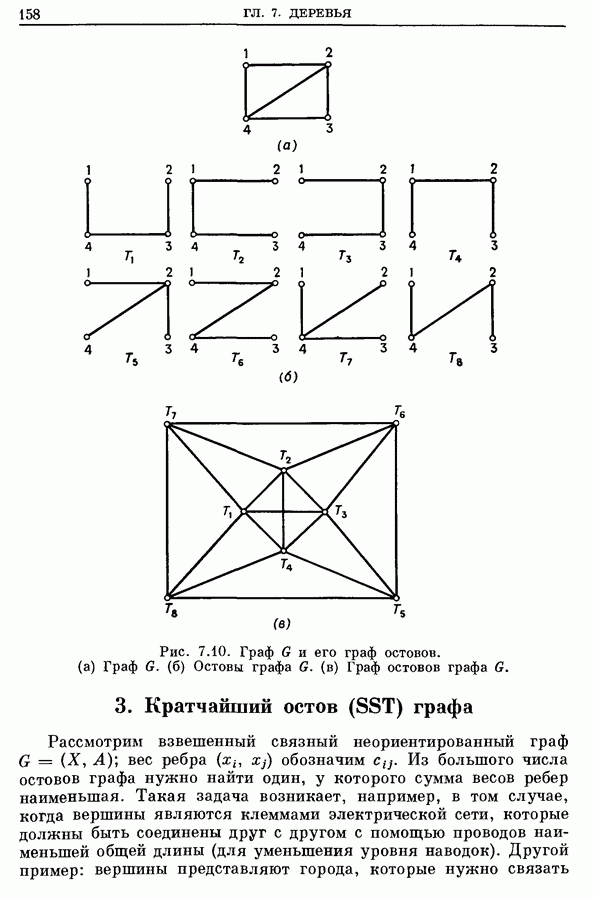
- 2.4. Граф остовов
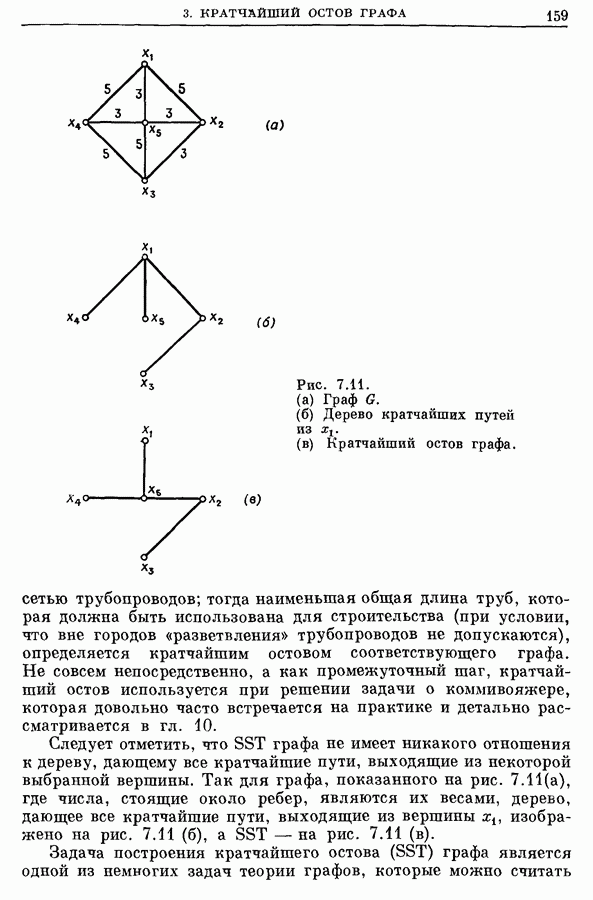
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
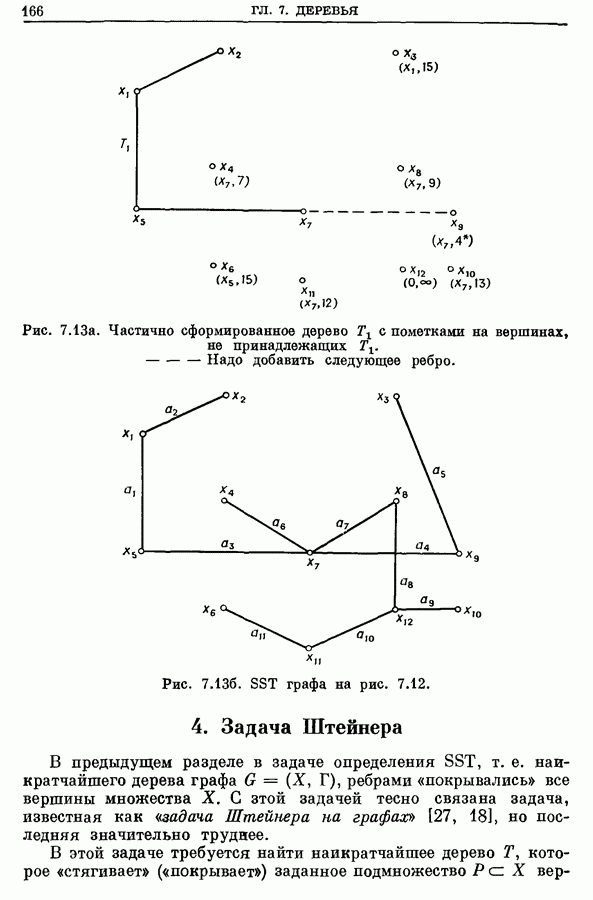
- 3.3. Родственные задачи
- 3.4. Пример [48]
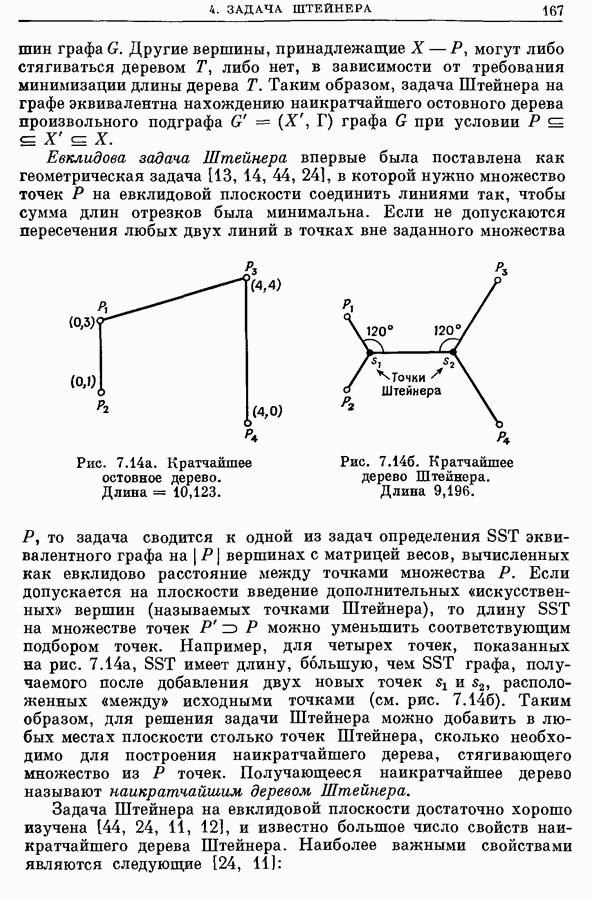
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
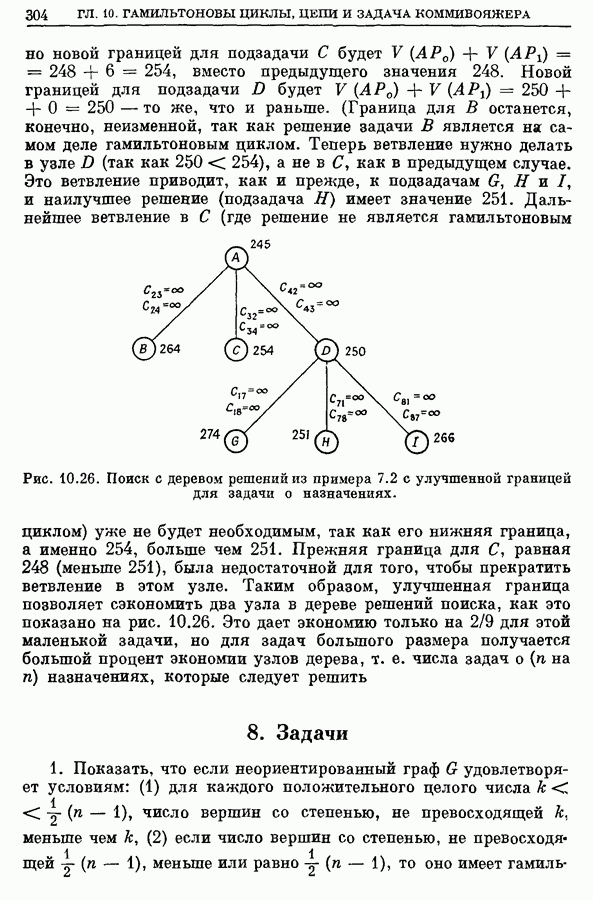
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
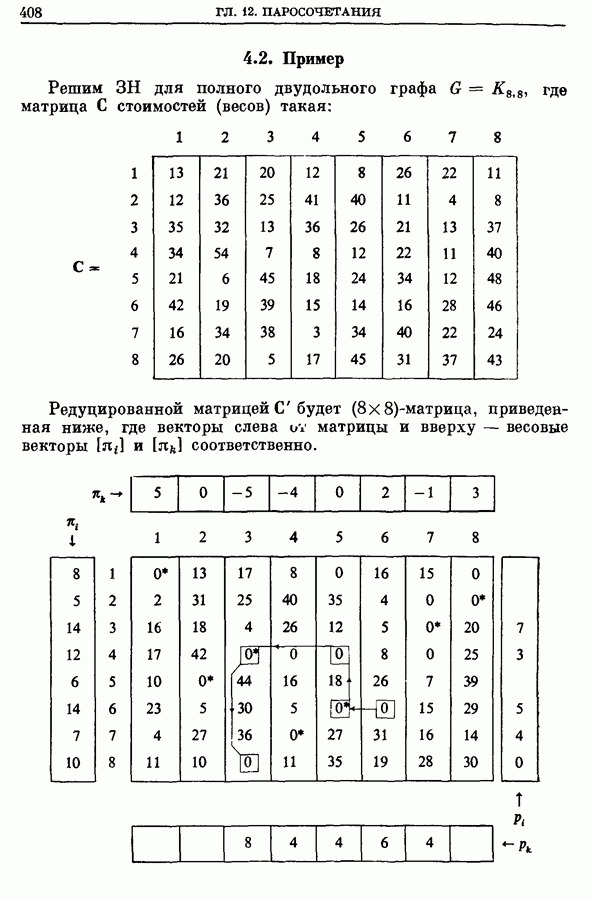
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
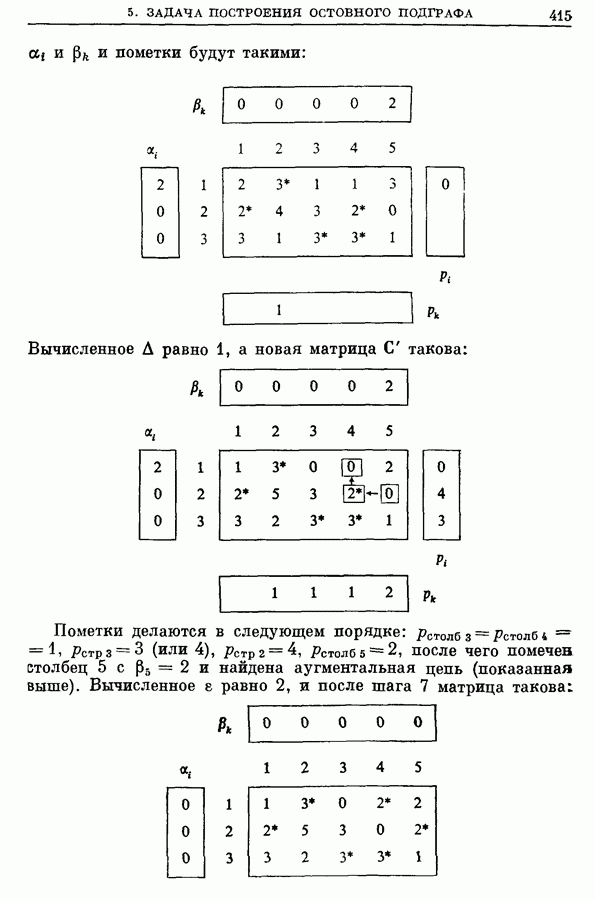
- 5.2. Пример
- 6. Задача о покрытии
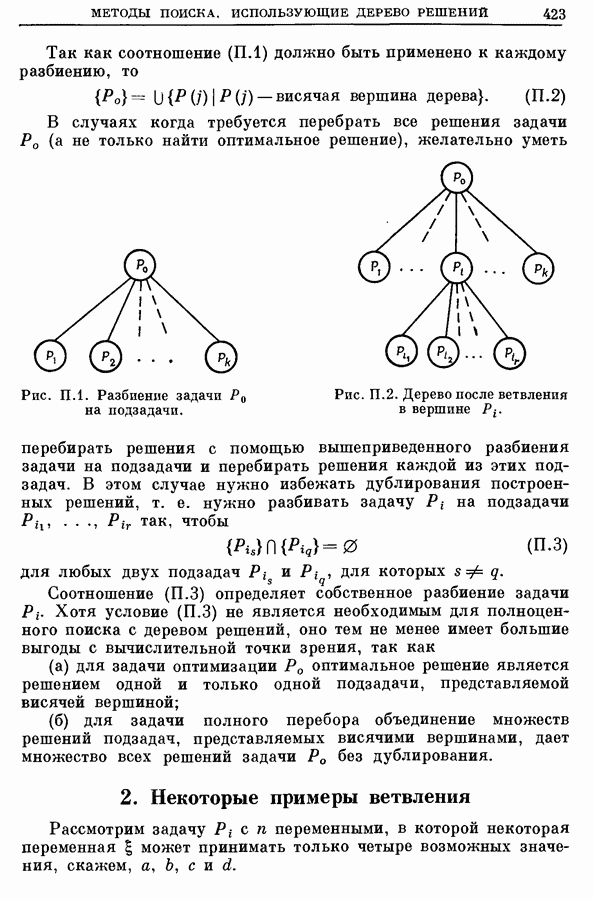
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
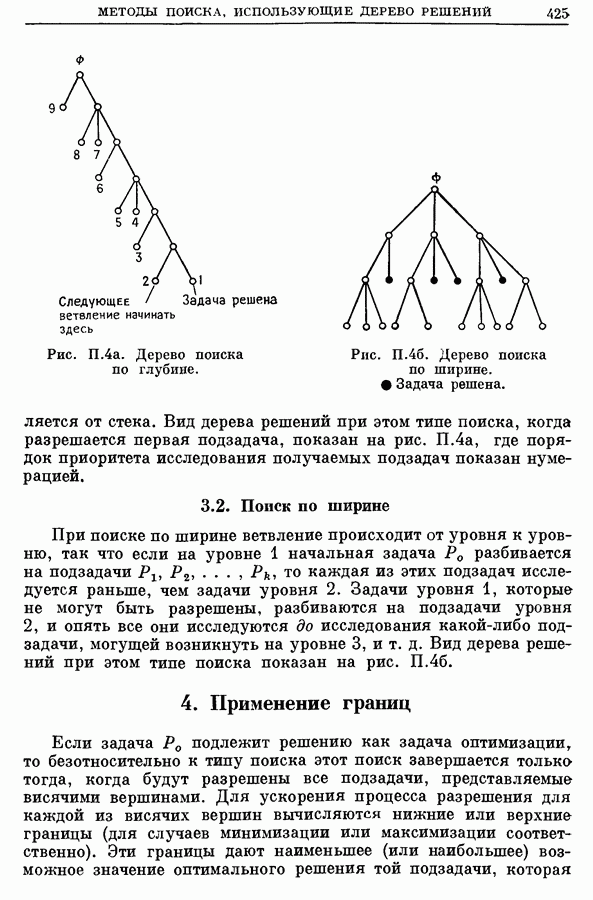
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления